Аналитическая геометрия. Линии на плоскости и их уравнения

1.

МАТЕМАТИКА
СТРОИТЕЛЬСТВО
БАКАЛАВРИАТ
1 семестр
2020

2.

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
3.1 Линии на плоскости и их уравнения
3.2 Прямая линия на плоскости
3.3 Кривые второго порядка
3.4 Уравнение поверхности и уравнения линии в
пространстве
3.5 Плоскость
3.6 Прямая линия в пространстве
3.7 Взаимное расположение прямой и плоскости

3.

3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
3.3 Кривые второго порядка
3.3.1 Эллипс
3.3.2 Гипербола
3.3.3 Парабола
3.3.4 Общее уравнение кривой второго порядка и
приведение его к каноническому виду

4.

3.3.1 ЭЛЛИПС
Эллипсом называется множество всех точек плоскости, сумма
расстояний от каждой из которых до двух фиксированных точек
(фокусов) есть величина постоянная, большая, чем расстояние между
фокусами.
F1 и F2
- фокусы эллипса
2a (a 0) - сумма расстояний от любой точки эллипса до фокусов
2c (c 0, a c) - расстояние между фокусами
y
M x; y - текущая точка эллипса
M
Тогда F1M F2 M 2a
Введём декартову систему координат так,
чтобы фокусы лежали на оси Ох на
одинаковом расстоянии от начала координат:
x
F1
O
F1 c;0 , F2 c;0
2
x c y2
2
x c y2
F1M x c; y
F1M F1M
F2 M x c; y
F2 M F2 M
F2

5.

3.3.1 ЭЛЛИПС
x c
2
2
y
x c
2
y 2 2a
– уравнение эллипса
При помощи алгебраических преобразований и использования
замены
a 2 c 2 b 2 (a b)
x2 y 2
2 1
2
a
b
это уравнение можно упростить
каноническое уравнение эллипса
Подробный вывод канонического уравнения эллипса приведён на с. 129
учебника.
Примеры
x2 y2
1
16 4
a 4, b 2
x2 y2
1
41 8
a 41, b 2 2

6.

3.3.1 ЭЛЛИПС
x2 y 2
2 1
2
a
b
y
B2
a b
a – большая полуось эллипса
b – малая полуось эллипса
x
A1 F1
Свойства эллипса
O
F2 A2
B1
1. Эллипс симметричен относительно координатных
осей и относительно начала координат.
2. Эллипс расположен внутри прямоугольника
a x a, b y b.
3. Эллипс пересекает координатные оси в точках
A1 a;0 , A2 a;0 , B1 0; b , B2 0; b .
4. Чем больше
x,
тем меньше
y.
Это вершины эллипса.

7.

3.3.1 ЭЛЛИПС
Эксцентриситет эллипса
Отношение
c
a
называется эксцентриситетом эллипса, оно
характеризует степень сжатия эллипса.
0 c a 0 1
Чем больше эксцентриситет, тем ближе фокусы к вершинам, лежащим на
оси Ох, тем более сплющен эллипс.
Чем меньше эксцентриситет, тем ближе фокусы друг к другу и к началу
координат, тем более эллипс приближается к окружности.

8.

3.3.1 ЭЛЛИПС
Замечание
Если ввести декартову систему координат так, чтобы фокусы лежали на
оси Оу на одинаковом расстоянии от начала координат, то
2b (b 0)
- сумма расстояний от любой точки эллипса до фокусов
F1 0; c , F2 0; c
- фокусы эллипса
2c 2b b 2 c 2 a 2 (b a)
b – большая полуось эллипса
a – малая полуось эллипса
c
b
- эксцентриситет эллипса
x2 y2
2 1 b a
2
a
b

9.

3.3.1 ЭЛЛИПС
Пример
Построить эллипс в декартовой системе
координат и указать координаты его фокусов
a 5, b 7, b a
b 2 c 2 a 2 c 2 b 2 a 2 c b2 a 2
c 7 2 52 24 2 6 4,9
F1 0; 2 6 , F2 0;2 6
- фокусы эллипса
x2 y2
1
25 49

10.

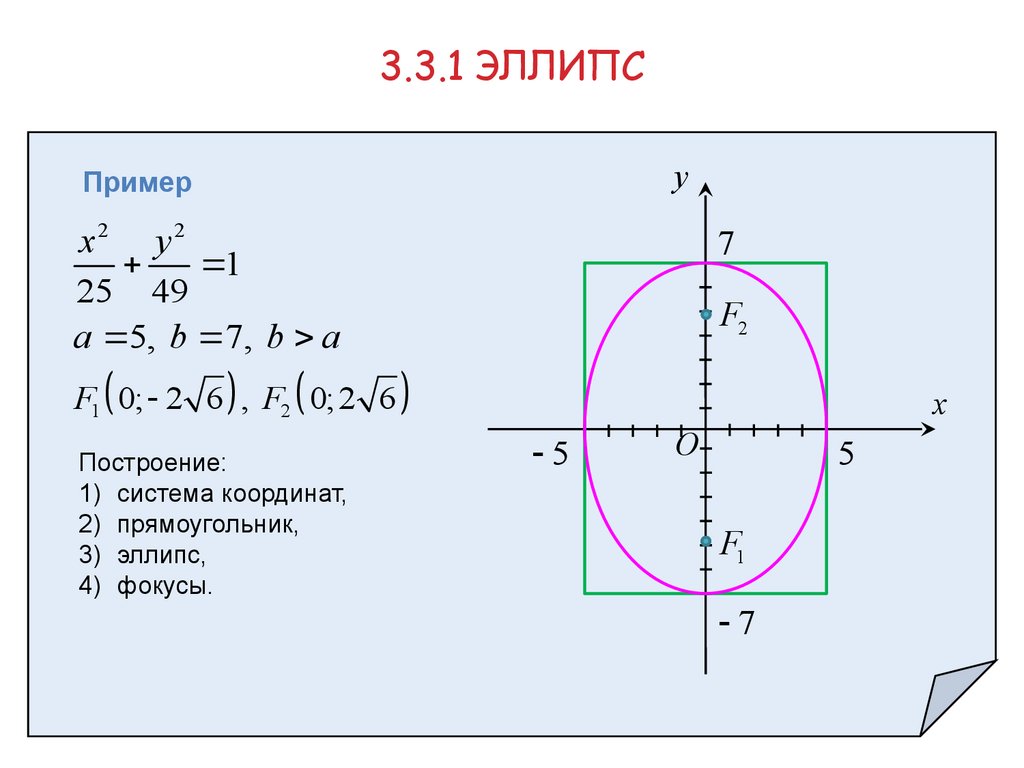
3.3.1 ЭЛЛИПС
y
Пример
x2 y2
1
25 49
a 5, b 7, b a
F1 0; 2 6 , F2 0;2 6
Построение:
1) система координат,
2) прямоугольник,
3) эллипс,
4) фокусы.
7
F2
x
5
O
5
F1
7

11.

3.3.2 ГИПЕРБОЛА
Гиперболой называется множество всех точек плоскости, разность
расстояний от каждой из которых до двух фиксированных точек
(фокусов) есть величина постоянная, меньшая, чем расстояние между
фокусами.
F1 и F2
- фокусы гиперболы
2a (a 0) - разность расстояний от любой точки гиперболы до фокусов
2c (c 0, a c) - расстояние между фокусами
y
M x; y - текущая точка гиперболы
M
Тогда F1M F2 M 2a
Введём декартову систему координат так,
x
чтобы фокусы лежали на оси Ох на
F2
F1 O
одинаковом расстоянии от начала координат:
F1 c;0 , F2 c;0
2
x c y2
2
x c y2
F1M x c; y
F1M F1M
F2 M x c; y
F2 M F2 M

12.

3.3.2 ГИПЕРБОЛА
x c
2
2
y
x c
2
y 2 2a
– уравнение гиперболы
При помощи алгебраических преобразований и использования
замены
c 2 a 2 b 2
x2 y 2
2 1
2
a
b
это уравнение можно упростить
каноническое уравнение гиперболы
Подробный вывод канонического уравнения гиперболы предлагается
провести самостоятельно.
Примеры
x2 y2
1
16 49
a 4, b 7
x2 y2
1
12 31
a 2 3, b 31

13.

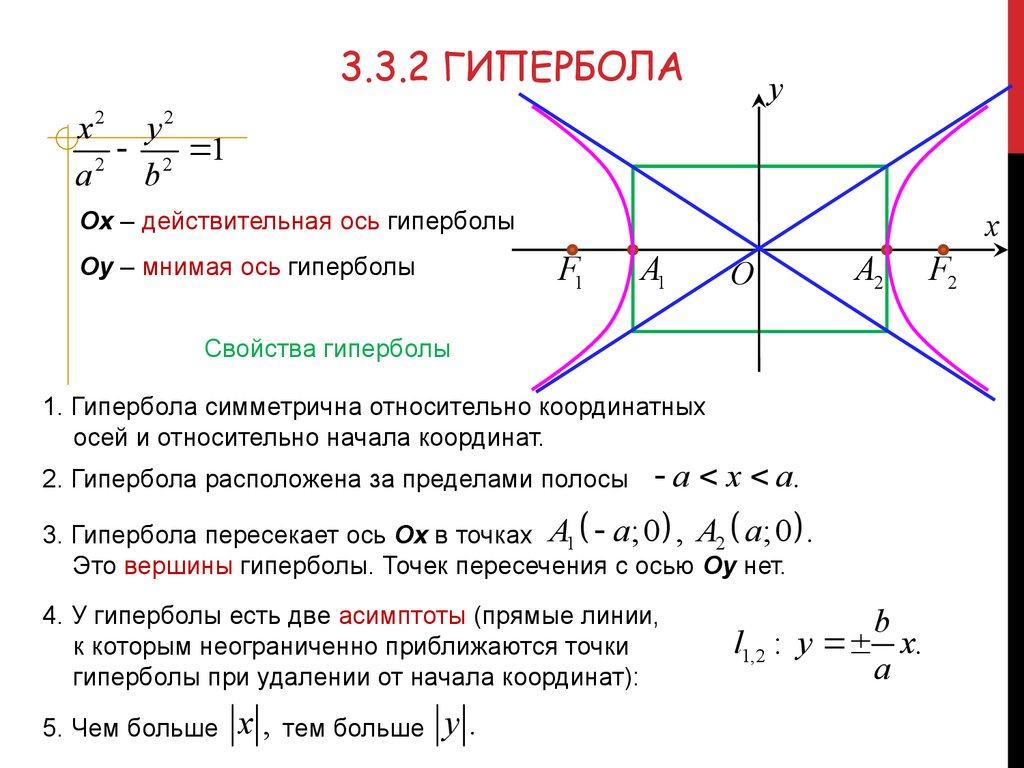
3.3.2 ГИПЕРБОЛА
y
x2 y 2
2 1
2
a
b
Ох – действительная ось гиперболы
x
F1
Оу – мнимая ось гиперболы
A1
A2
O
Свойства гиперболы
1. Гипербола симметрична относительно координатных
осей и относительно начала координат.
2. Гипербола расположена за пределами полосы
a x a.
3. Гипербола пересекает ось Ох в точках A1 a;0 , A2 a;0
Это вершины гиперболы. Точек пересечения с осью Оу нет.
4. У гиперболы есть две асимптоты (прямые линии,
к которым неограниченно приближаются точки
гиперболы при удалении от начала координат):
5. Чем больше
x,
тем больше
y.
.
b
l1,2 : y x.
a
F2

14.

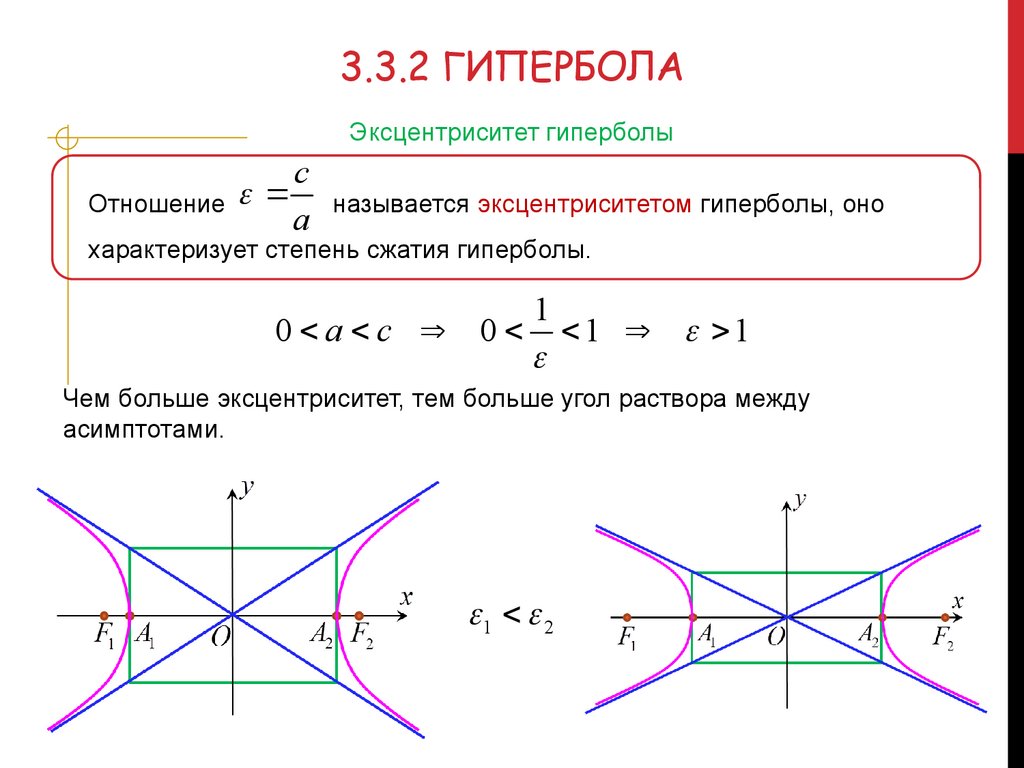
3.3.2 ГИПЕРБОЛА
Эксцентриситет гиперболы
Отношение
c
a
называется эксцентриситетом гиперболы, оно
характеризует степень сжатия гиперболы.
1
0 a c 0 1 1
Чем больше эксцентриситет, тем больше угол раствора между
асимптотами.
1 2

15.

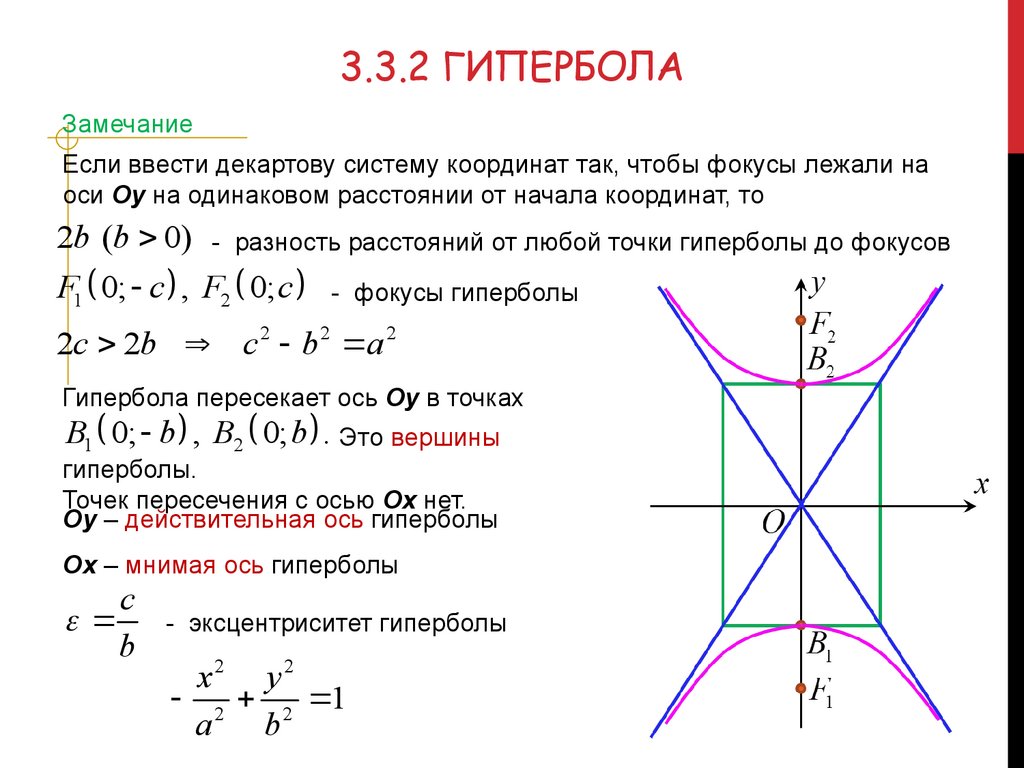
3.3.2 ГИПЕРБОЛА
Замечание
Если ввести декартову систему координат так, чтобы фокусы лежали на
оси Оу на одинаковом расстоянии от начала координат, то
2b (b 0)
- разность расстояний от любой точки гиперболы до фокусов
F1 0; c , F2 0; c
- фокусы гиперболы
2c 2b c 2 b 2 a 2
Гипербола пересекает ось Оу в точках
B1 0; b , B2 0; b . Это вершины
гиперболы.
Точек пересечения с осью Ох нет.
Оу – действительная ось гиперболы
Ох – мнимая ось гиперболы
c
b
- эксцентриситет гиперболы
x2 y 2
2 2 1
a
b

16.

3.3.2 ГИПЕРБОЛА
Пример
Построить гиперболу в декартовой системе
координат и указать координаты её фокусов
a 5, b 7
c 2 a 2 b 2 c 2 b 2 a 2 c b2 a 2
c 7 2 52 74 8,6
F1 74;0 , F2
74;0
- фокусы гиперболы
Ох – действительная ось гиперболы
Оу – мнимая ось гиперболы
x2 y2
1
25 49

17.

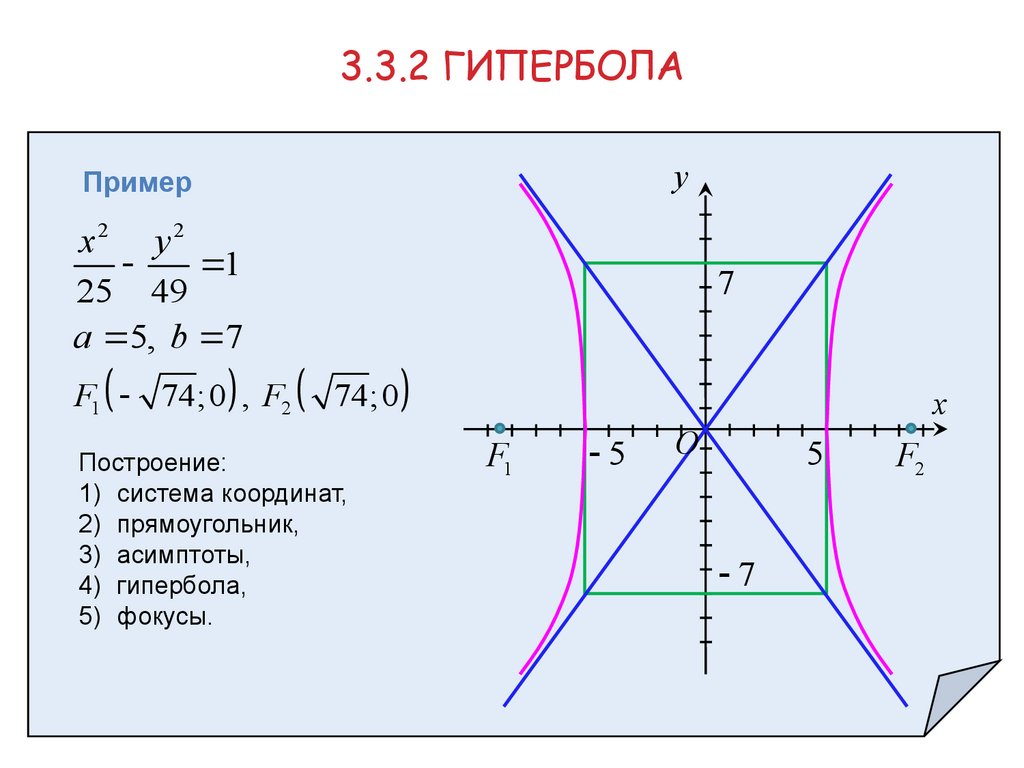
3.3.2 ГИПЕРБОЛА
y
Пример
x2 y2
1
25 49
a 5, b 7
F1 74;0 , F2
7
74;0
Построение:
1) система координат,
2) прямоугольник,
3) асимптоты,
4) гипербола,
5) фокусы.
x
F1
5
O
5
7
F2

18.

3.3.3 ПАРАБОЛА
Параболой называется множество всех точек плоскости, равноудалённых
от фиксированной точки (фокуса) и прямой (директрисы).
F - фокус параболы
p ( p 0)
M x; y
- расстояние между фокусом и директрисой d
- текущая точка параболы
Введём декартову систему координат так,
чтобы фокус лежал на положительном
направлении оси Ох, директриса
перпендикулярна оси Ох, расстояния от
директрисы до начала координат и от фокуса
до начала координат равны:
y
M
N
x
O
F
p
d
p
F ;0 , d : x
2
2
2
p
p
p
2
NM x ; FM
x
;
y
FM
FM
x
y
2
2
2

19.

3.3.3 ПАРАБОЛА
2
p
p
2
x y x
2
2
– уравнение параболы
Возведём обе части в квадрат и приведём подобные
2
2
p
p
2
x
y
x
2
2
2
2
p
p
x 2 px
y 2 x 2 px
4
4
y 2 2 px
каноническое уравнение параболы
Примеры
2
y 18 x, p 9
1
1
y 2 x, p
3
6

20.

3.3.3 ПАРАБОЛА
y 2 2 px
Свойства параболы
1. Парабола симметрична относительно оси Ох.
2. Парабола проходит через начало координат
Это вершина параболы.
O 0;0 .
y
3. Парабола расположена в I и IV четвертях.
4. Ветви параболы направлены вправо.
x
O
d
F

21.

3.3.3 ПАРАБОЛА
Замечание
Если расположить систему координат по-другому, то получим ещё три
канонических уравнения параболы.
p
p
1) F ;0 , d : x
y 2 2 px
2
2
p
p
2) F 0; , d : y
x 2 2 py
2
2
p
p
3) F 0; , d : y
x 2 2 py
2
2

22.

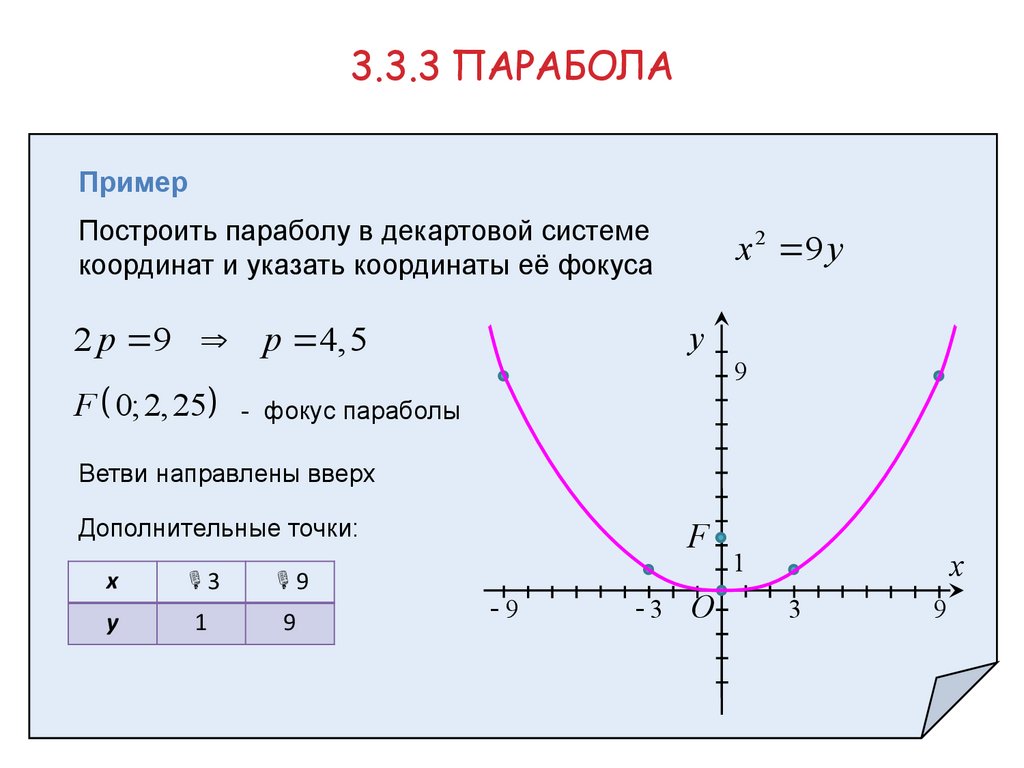
3.3.3 ПАРАБОЛА
Пример
Построить параболу в декартовой системе
координат и указать координаты её фокуса
2 p 9 p 4,5
F 0; 2, 25
x 2 9 y
y
9
- фокус параболы
Ветви направлены вверх
Дополнительные точки:
х
3
9
у
1
9
F
9
3
O
x
1
3
9

23.

3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО
ПОРЯДКА
И ПРИВЕДЕНИЕ ЕГО К КАНОНИЧЕСКОМУ ВИДУ
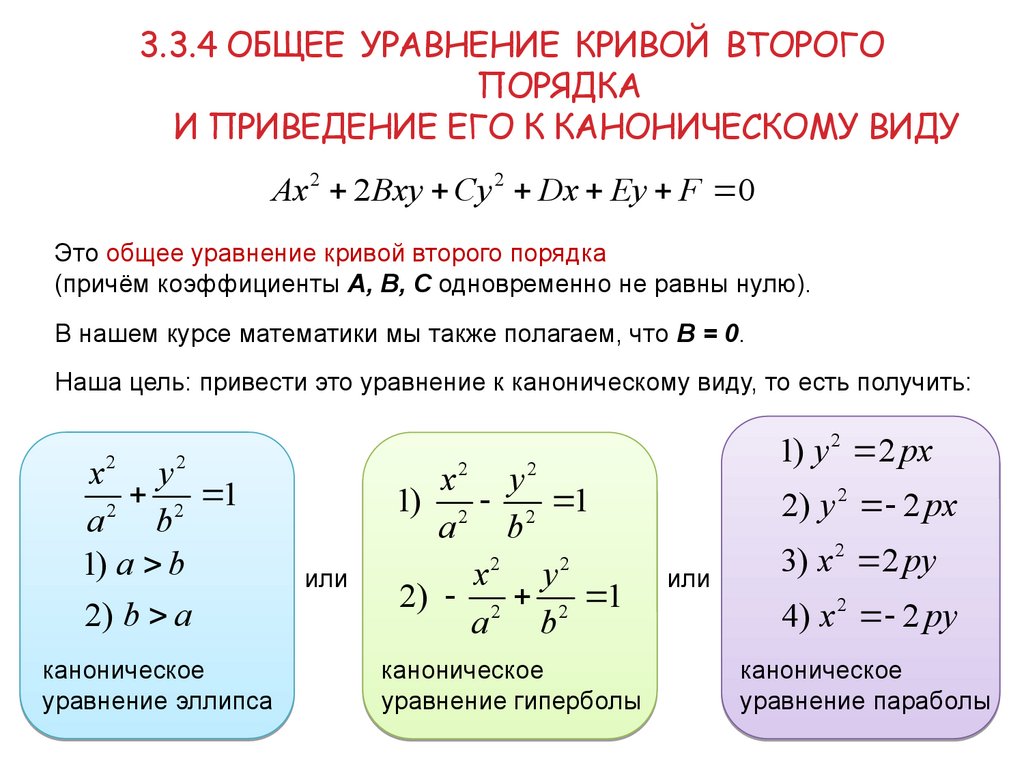
Ax 2 2 Bxy Cy 2 Dx Ey F 0
Это общее уравнение кривой второго порядка
(причём коэффициенты А, В, С одновременно не равны нулю).
В нашем курсе математики мы также полагаем, что В = 0.
Наша цель: привести это уравнение к каноническому виду, то есть получить:
x2 y2
2 1
2
a
b
1) a b
2) b a
каноническое
уравнение эллипса
или
x2 y 2
1) 2 2 1
a b
x2 y 2
2) 2 2 1
a
b
каноническое
уравнение гиперболы
1) y 2 2 px
2) y 2 2 px
или
3) x 2 2 py
4) x 2 2 py
каноническое
уравнение параболы

24.

3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО
ПОРЯДКА
И ПРИВЕДЕНИЕ ЕГО К КАНОНИЧЕСКОМУ ВИДУ
Пример
Привести к каноническому виду уравнение
4 x 2 9 y 2 8 x 18 y 23 0.
Указать тип кривой и сделать чертёж в системе координат.
Решение:
1) Сгруппируем переменные
4x
2
8 x 9 y 2 18 y 23 0.
2) Вынесем за скобки коэффициенты при квадратах
4 x 2 2 x 9 y 2 2 y 23 0.
3) Дополним выражения в скобках до полных квадратов
4 x 2 2 x 1 1 9 y 2 2 y 1 1 23 0.

25.

3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО
ПОРЯДКА
И ПРИВЕДЕНИЕ ЕГО К КАНОНИЧЕСКОМУ ВИДУ
Пример
Решение (продолжение):
4) Свернём полные квадраты, используя формулы сокращённого умножения
2
2
4 x 1 1 9 y 1 1 23 0
5) Раскроем внешние скобки
2
2
4 x 1 4 9 y 1 9 23 0
6) Приведём подобные и перенесём свободный член в правую часть
2
2
4 x 1 9 y 1 36
7) Разделим обе части уравнения на 36 и упростим
2
2
4 x 1
9 y 1
36
36
36
36
2
2
x 1 y 1 1
9
4

26.

3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО
ПОРЯДКА
И ПРИВЕДЕНИЕ ЕГО К КАНОНИЧЕСКОМУ ВИДУ
Пример
Решение (продолжение):
8) Сделаем замену
x 1 x1
y 1 y1
9) Подставим в уравнение и получим
x12 y12
1
9
4
- каноническое уравнение эллипса
10) Выразим в замене х и у, найдём координаты начала новой системы
координат
x x1 1
y y1 1
O1 1;1

27.

3.3.4 ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ ВТОРОГО
ПОРЯДКА
И ПРИВЕДЕНИЕ ЕГО К КАНОНИЧЕСКОМУ ВИДУ
Пример
Решение (продолжение):
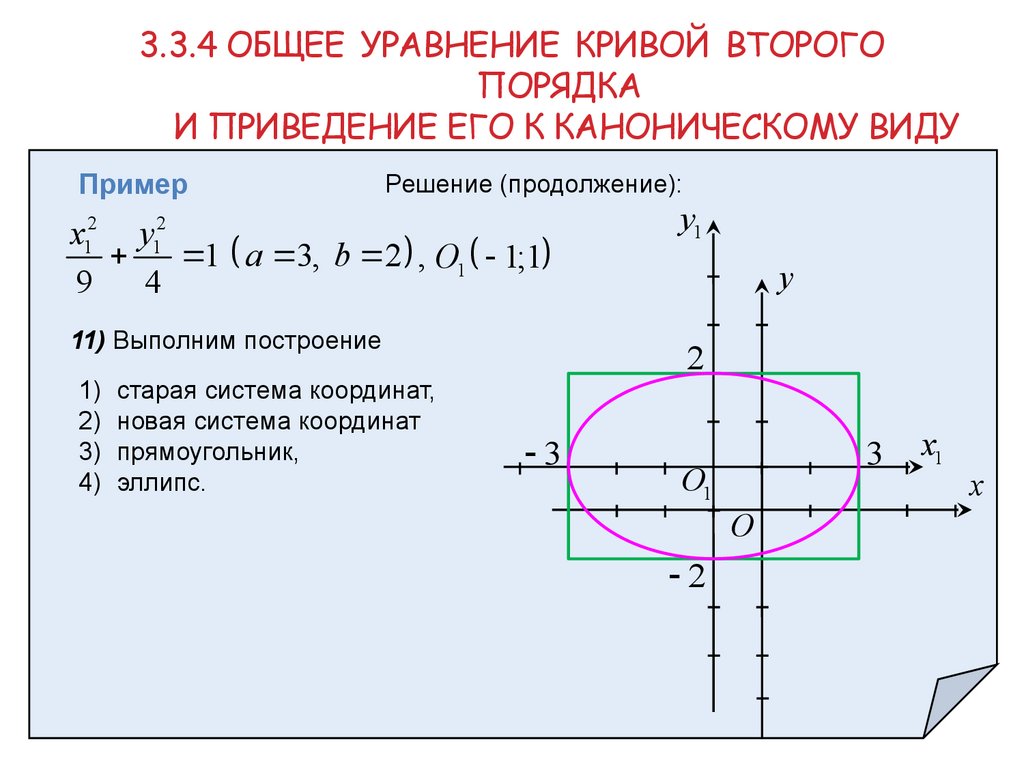
x12 y12
1 a 3, b 2 , O1 1;1
9
4
y1
11) Выполним построение
2
1)
2)
3)
4)
старая система координат,
новая система координат
прямоугольник,
эллипс.
3
y
3
O1
O
2
x1
x

28.

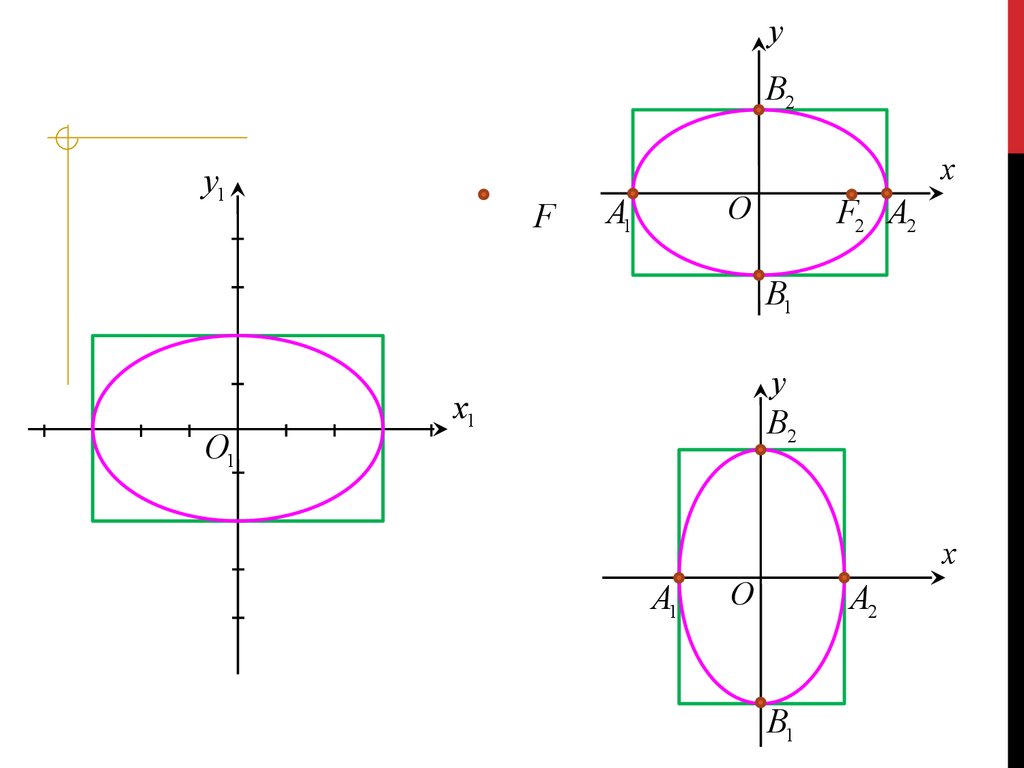
y
B2
x
y1
F
O
A1
F2 A2
B1
O1
y
B2
x1
x
A1
O
A2
B1

29.

Лекция выложена впервые.
Если Вы заметили ошибку, то сообщите мне на эл. почту.