Расчет простых цепей методом свертывания

1. Расчет цепей постоянного тока со смешанным соединением резисторов

Данный тип задач входит в экзаменационные задания
Выполнение задания является подготовкой к сдаче
экзамена по электротехнике и электронике
Студенту необходимо:
- внимательно изучить методику решения,
представленную в следующем примере, подробно
записать пример решения в учебную тетрадь
- решить задачу по данным своего варианта и выслать на
проверку

2. Соединение потребителей электрической энергии

Существуют два вида соединений:
• Последовательное
• Параллельное

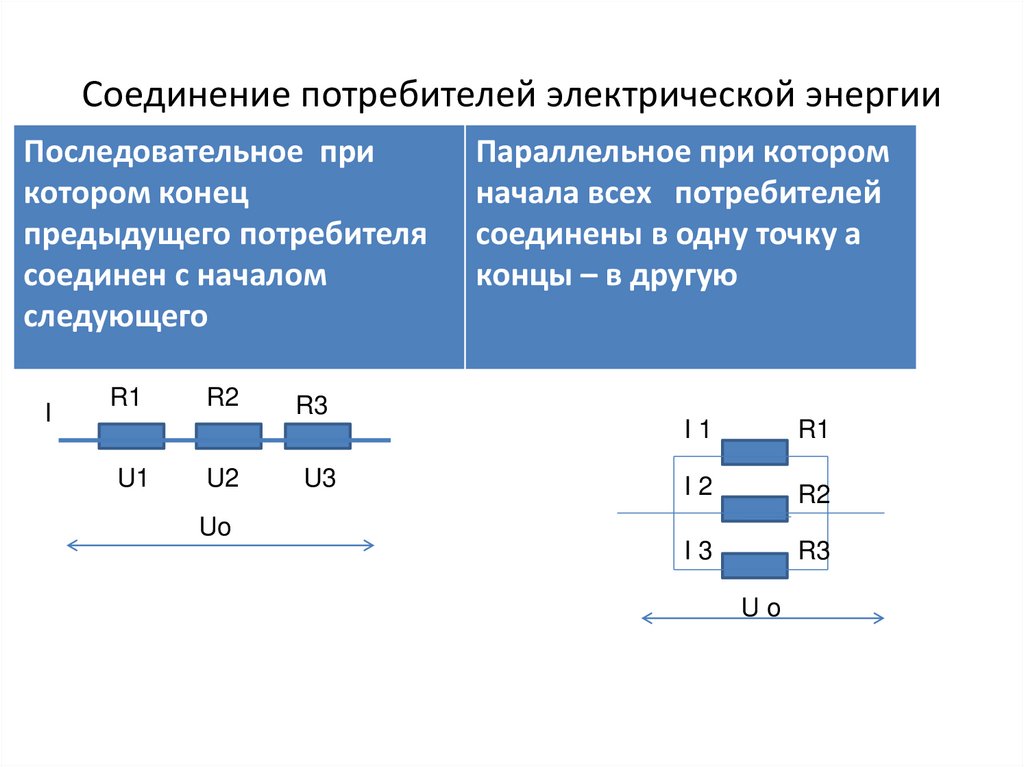
3. Соединение потребителей электрической энергии

Последовательное при
котором конец
предыдущего потребителя
соединен с началом
следующего
I
R1
U1
R2
U2
Параллельное при котором
начала всех потребителей
соединены в одну точку а
концы – в другую
R3
U3
I1
R1
I2
R2
I3
R3
Uo
Uo

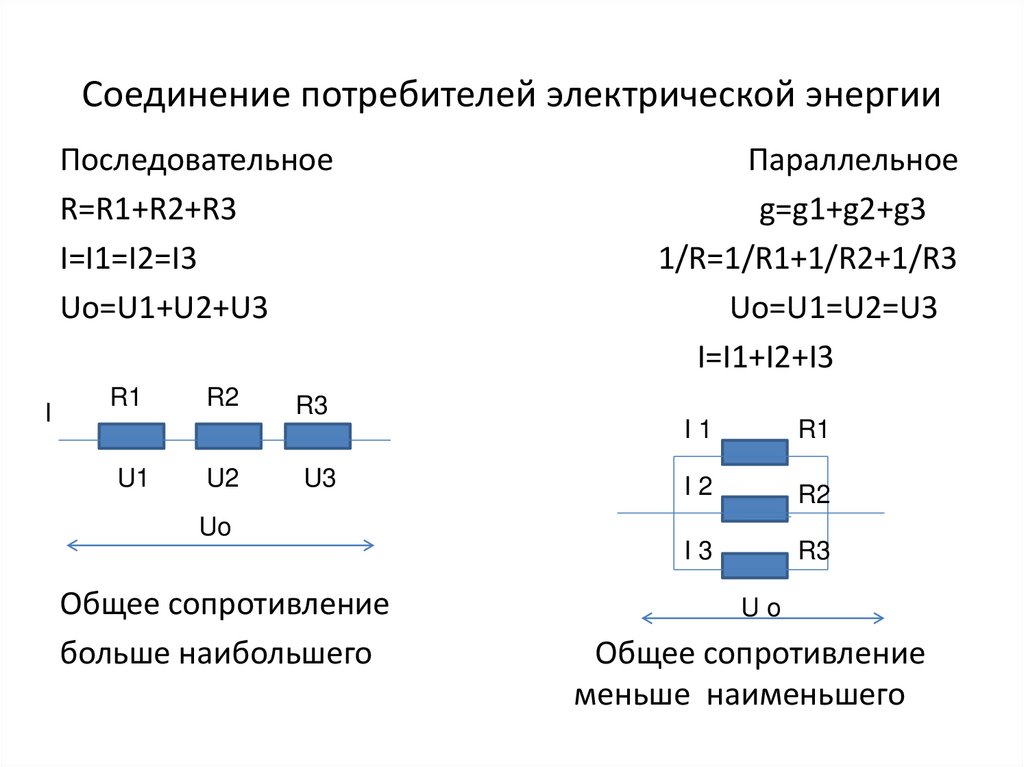
4. Соединение потребителей электрической энергии

Последовательное
R=R1+R2+R3
I=I1=I2=I3
Uo=U1+U2+U3
I
R1
U1
R2
U2
Параллельное
g=g1+g2+g3
1/R=1/R1+1/R2+1/R3
Uo=U1=U2=U3
I=I1+I2+I3
R3
U3
I1
R1
I2
R2
I3
R3
Uo
Общее сопротивление
больше наибольшего
Uo
Общее сопротивление
меньше наименьшего

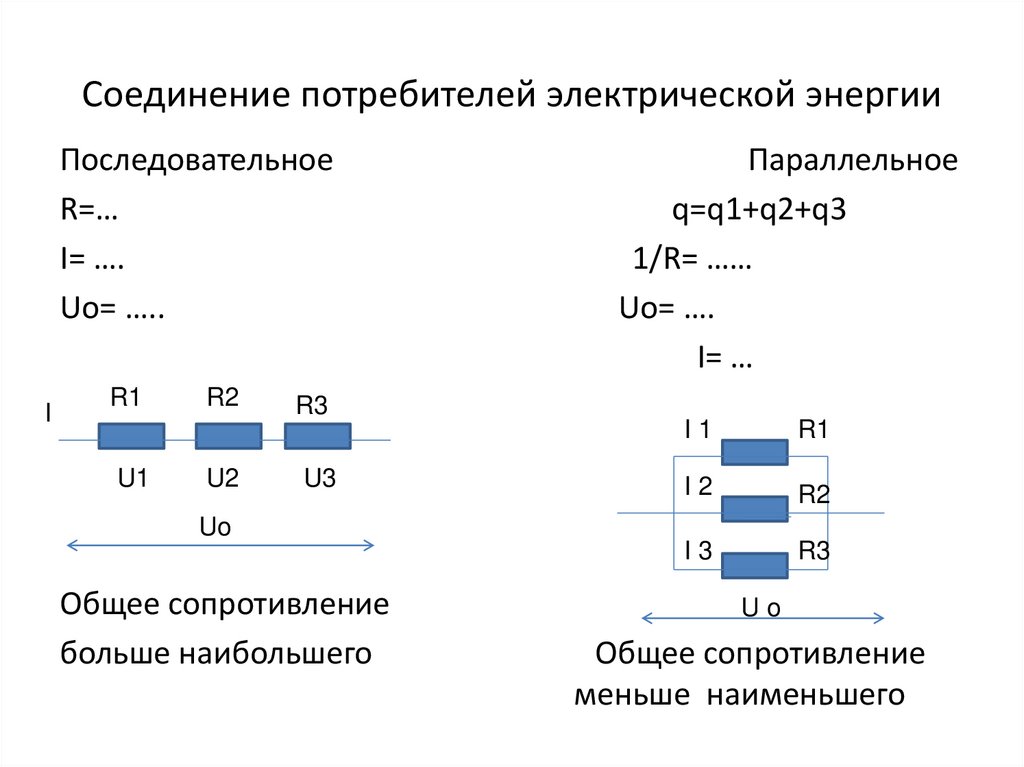
5. Соединение потребителей электрической энергии

Последовательное
R=…
I= ….
Uo= …..
I
R1
U1
R2
U2
Параллельное
q=q1+q2+q3
1/R= ……
Uo= ….
I= …
R3
U3
I1
R1
I2
R2
I3
R3
Uo
Общее сопротивление
больше наибольшего
Uo
Общее сопротивление
меньше наименьшего

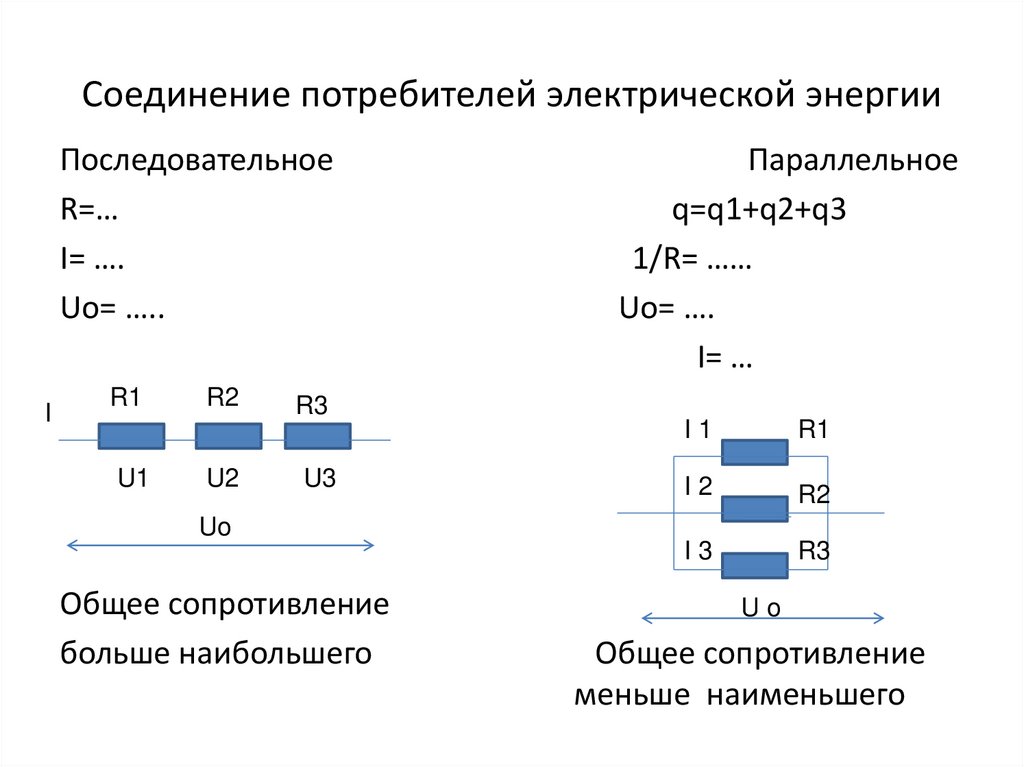
6. Соединение потребителей электрической энергии

Последовательное
R=…
I= ….
Uo= …..
I
R1
U1
R2
U2
Параллельное
q=q1+q2+q3
1/R= ……
Uo= ….
I= …
R3
U3
I1
R1
I2
R2
I3
R3
Uo
Общее сопротивление
больше наибольшего
Uo
Общее сопротивление
меньше наименьшего

7. Расчёт простых цепей методом «свёртывания»

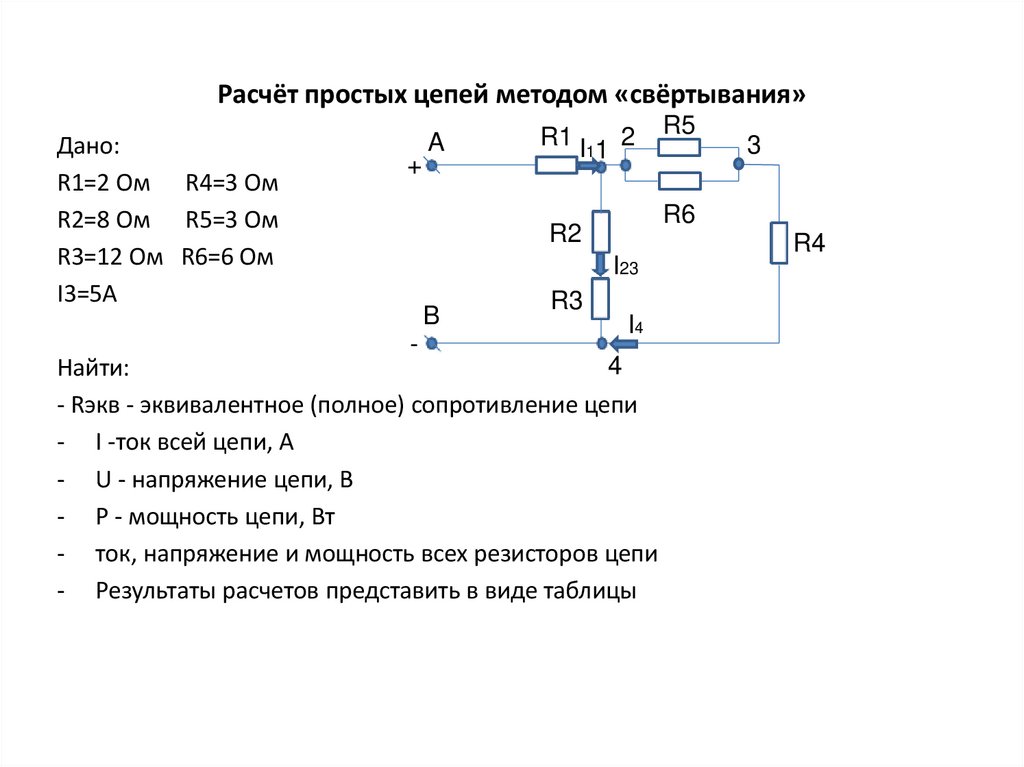
Дано:
R1=2 Ом R4=3 Ом
R2=8 Ом R5=3 Ом
R3=12 Ом R6=6 Ом
I3=5A
+
A
R1 I1
1
2
I23
-
3
R6
R2
B
R5
R3
I4
4
Найти:
- Rэкв - эквивалентное (полное) сопротивление цепи
- I -ток всей цепи, А
- U - напряжение цепи, В
- P - мощность цепи, Вт
- ток, напряжение и мощность всех резисторов цепи
- Результаты расчетов представить в виде таблицы
R4

8. Расчёт простых цепей методом «свёртывания»

Преобразуем первоначальную схему таким образом, чтобы характер соединения элементов стал
очевиден. Для этого схему удобнее представить так, чтобы ее условное начало (клемма А) была слева, а
условный конец (клемма В) – справа.
При этом преобразовании возможны разные последовательности действий, но результаты будут
схожими.
В данном случае, для получения преобразованного варианта сделано
следующее:
A
R1 1 R2
R5
2
R6
R3
4
B
3 R4
1. Изображена ветвь цепи содержащая: клемма А-R1-R2-R3-клемма В ( в
одну линию)
2. В соответствии с исходной схемой, между R1 и R2 (точка1) и между R3
и В (точка 4) подсоединяем участок, содержащий R4, R5 и R6, без
изменений.

9. Расчёт простых цепей методом «свёртывания»

Проанализируем полученную схему и рассчитаем сопротивления отдельных
ветвей и схемы в целом:
R2 и R3 соединены последовательно: R23=R2+R3=8+12=20 Ом
R5 и R6 соединены параллельно: 1/R56=1/R5+1/R6=1/3+1/6=1/2 R56=2 Ом
R56 и R4 соединены последовательно: R564=R56+R4=2+3=5 Ом
R23 и R564 соединены параллельно: 1/R23+1/R564=1/20+1/5=1/4 R23564=4 Ом
R1 и R23564 соединены последовательно, тогда Rэкв= R1+ R23564=2+4=6 Ом
A
R1 1 R2
R5
2
R6
R3
3 R4
Полное сопротивление найдено.
4
B

10. Расчёт простых цепей методом «свёртывания»

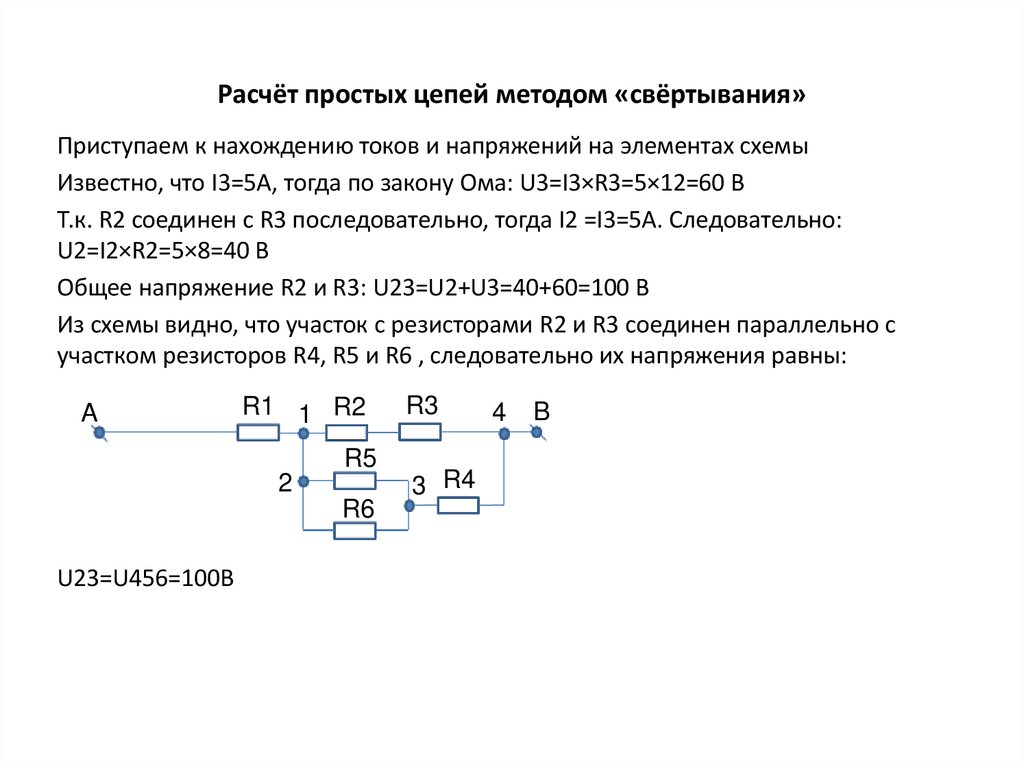
Приступаем к нахождению токов и напряжений на элементах схемы
Известно, что I3=5A, тогда по закону Ома: U3=I3×R3=5×12=60 В
Т.к. R2 соединен с R3 последовательно, тогда I2 =I3=5А. Следовательно:
U2=I2×R2=5×8=40 В
Общее напряжение R2 и R3: U23=U2+U3=40+60=100 В
Из схемы видно, что участок с резисторами R2 и R3 соединен параллельно с
участком резисторов R4, R5 и R6 , следовательно их напряжения равны:
A
R1 1 R2
R5
2
R6
U23=U456=100В
R3
3 R4
4
B

11. Расчёт простых цепей методом «свёртывания»

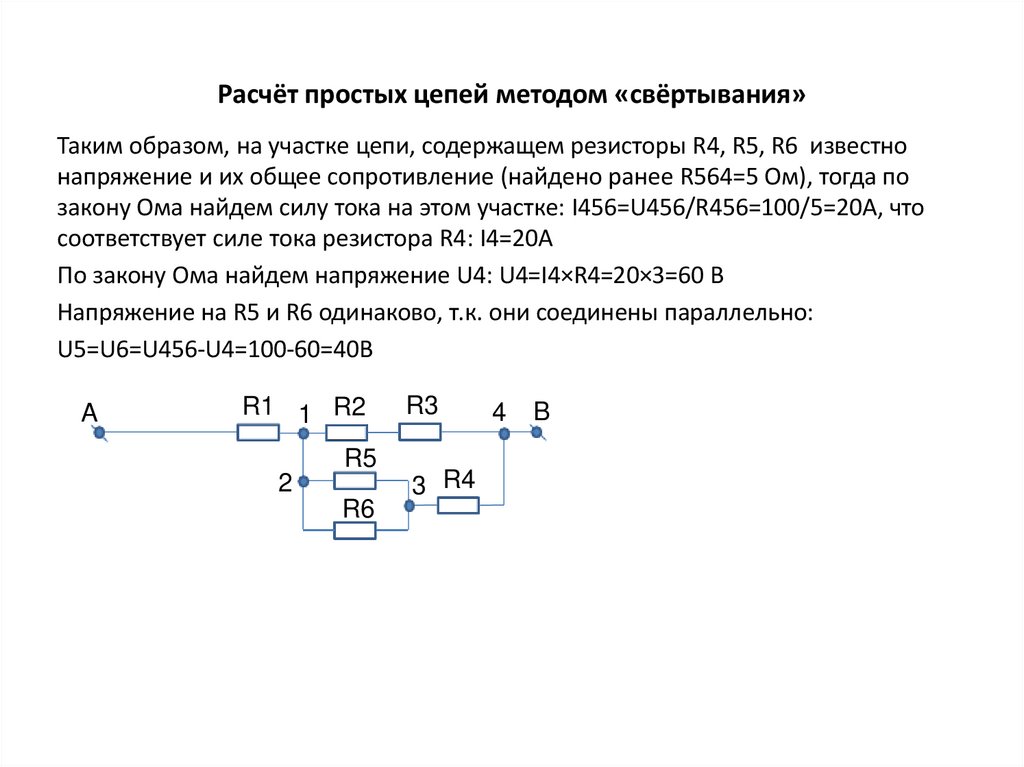
Таким образом, на участке цепи, содержащем резисторы R4, R5, R6 известно
напряжение и их общее сопротивление (найдено ранее R564=5 Ом), тогда по
закону Ома найдем силу тока на этом участке: I456=U456/R456=100/5=20A, что
соответствует силе тока резистора R4: I4=20А
По закону Ома найдем напряжение U4: U4=I4×R4=20×3=60 В
Напряжение на R5 и R6 одинаково, т.к. они соединены параллельно:
U5=U6=U456-U4=100-60=40В
A
R1 1 R2
R5
2
R6
R3
3 R4
4
B

12. Расчёт простых цепей методом «свёртывания»

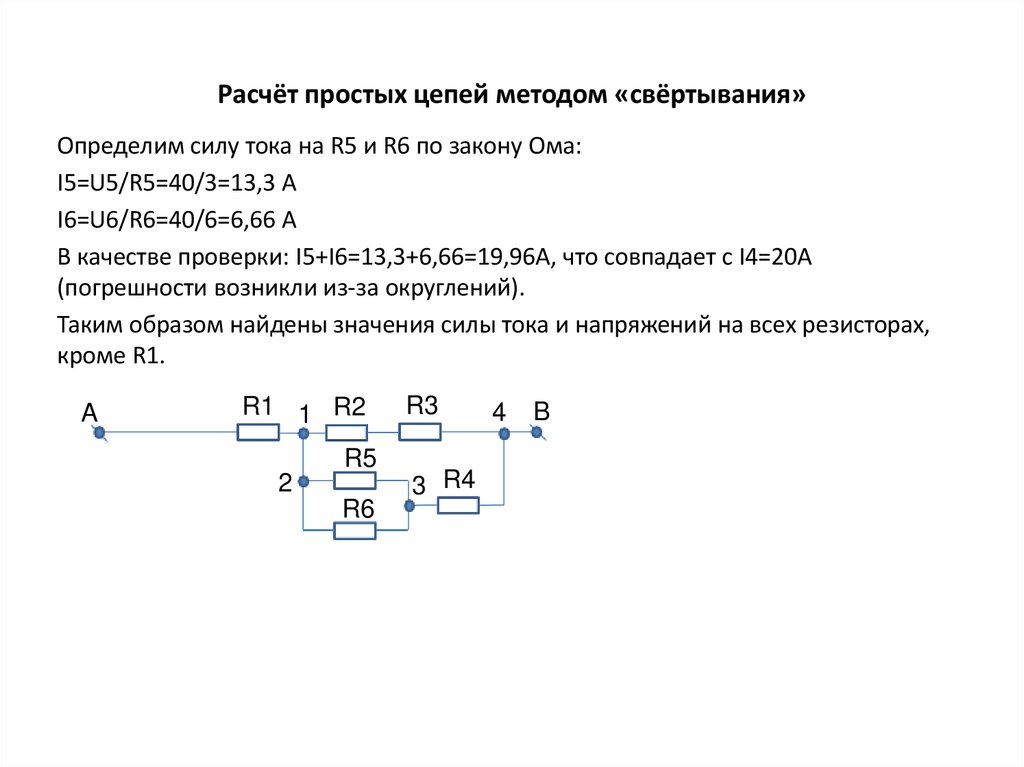
Определим силу тока на R5 и R6 по закону Ома:
I5=U5/R5=40/3=13,3 А
I6=U6/R6=40/6=6,66 А
В качестве проверки: I5+I6=13,3+6,66=19,96А, что совпадает с I4=20А
(погрешности возникли из-за округлений).
Таким образом найдены значения силы тока и напряжений на всех резисторах,
кроме R1.
A
R1 1 R2
R5
2
R6
R3
3 R4
4
B

13. Расчёт простых цепей методом «свёртывания»

Из схемы видно, что I1 соответствует полному току данной цепи, а с другой
стороны – сумме токов, протекающих через R2 (или R3) и R4:
I=I1=I2+I4=5+20=25А
Напряжение на R1 найдем по закону Ома: U1=I1×R1=25×2=50В
Полное напряжение цепи: U=I×Rэкв=25×6=150В
В качестве проверки: U=U1+U2+U3=50+40+60=150В. Все верно!
A
R1 1 R2
R5
2
R6
R3
3 R4
4
B

14. Расчёт простых цепей методом «свёртывания»

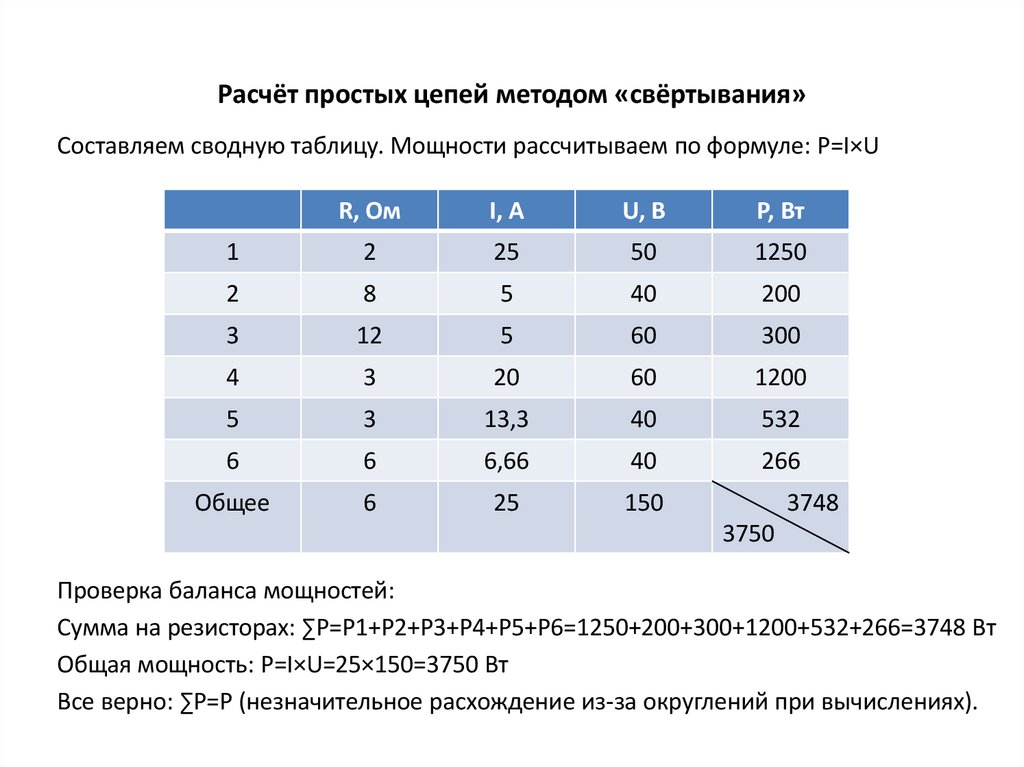
Составляем сводную таблицу. Мощности рассчитываем по формуле: P=I×U
R, Ом
I, А
U, В
P, Вт
1
2
25
50
1250
2
8
5
40
200
3
12
5
60
300
4
3
20
60
1200
5
3
13,3
40
532
6
6
6,66
40
266
Общее
6
25
150
3748
3750
Проверка баланса мощностей:
Сумма на резисторах: ∑Р=Р1+Р2+Р3+Р4+Р5+Р6=1250+200+300+1200+532+266=3748 Вт
Общая мощность: P=I×U=25×150=3750 Вт
Все верно: ∑P=P (незначительное расхождение из-за округлений при вычислениях).

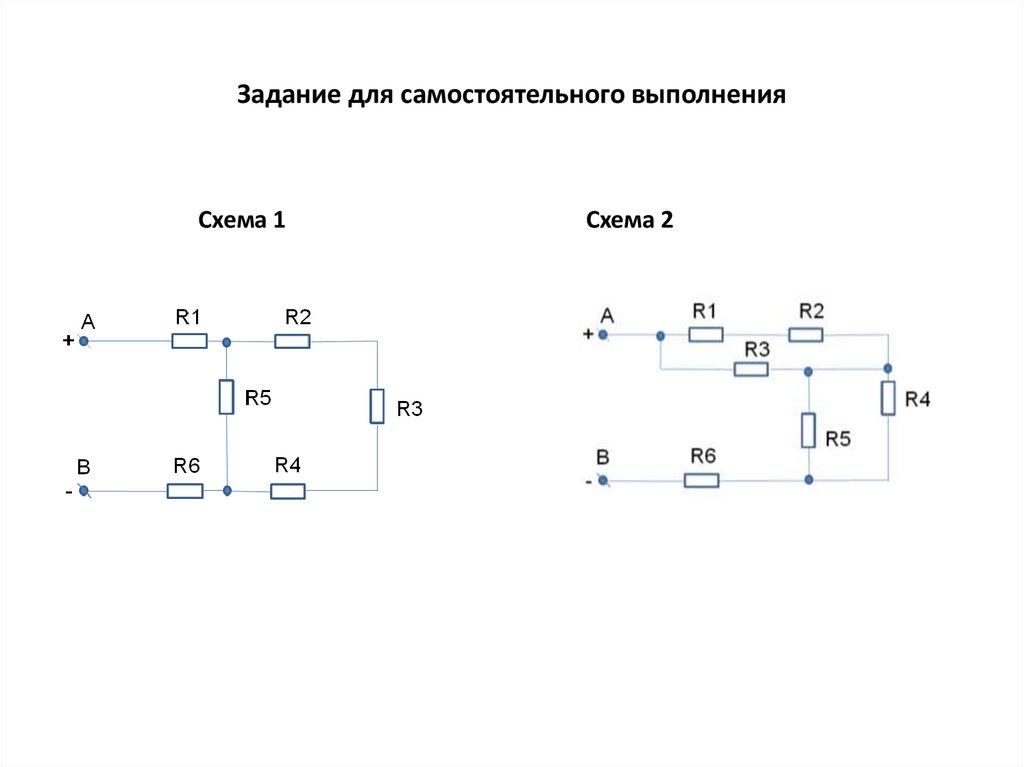
15. Задание для самостоятельного выполнения

Решить задачу, используя данные своего варианта.
Номер варианта соответствует номеру фамилии студента в списке группы.
На проверку прислать полное решение, включая исходную схему, номер и данные
своего варианта, сводную таблицу и проверку баланса мощностей.
В решении должны быть все расчетные формулы в общем виде, с подставленными
значениями параметров, результатом, единицами измерения.
Словесные комментарии, наименования параметров в решении писать не надо.
Выслать выполненное задание на проверку (адрес: davidov.sv@att.edu.ru),
убедившись в хорошем качестве фотографии.
Работы, выполненные с нарушением данных требований, будут возвращены для
исправлений.
Срок выполнения задания – до 19 декабря т.г.

16. Задание для самостоятельного выполнения

Схема 1
Схема 2

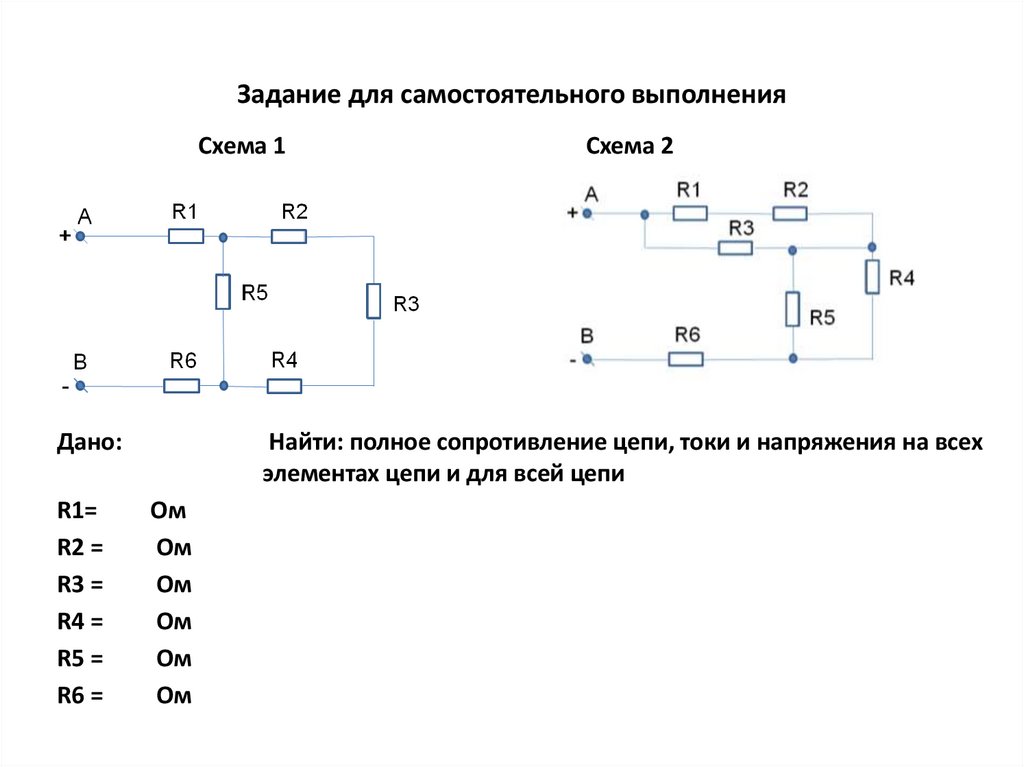
17. Задание для самостоятельного выполнения

Схема 1
Дано:
R1=
R2 =
R3 =
R4 =
R5 =
R6 =
Схема 2
Найти: полное сопротивление цепи, токи и напряжения на всех
элементах цепи и для всей цепи
Ом
Ом
Ом
Ом
Ом
Ом

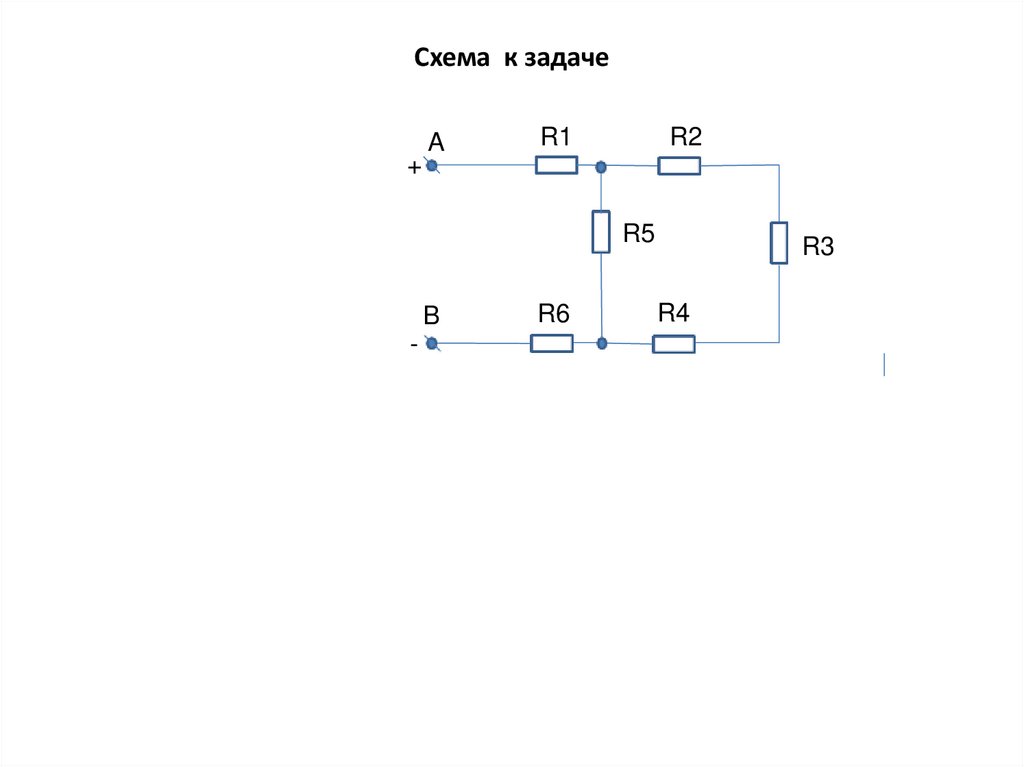
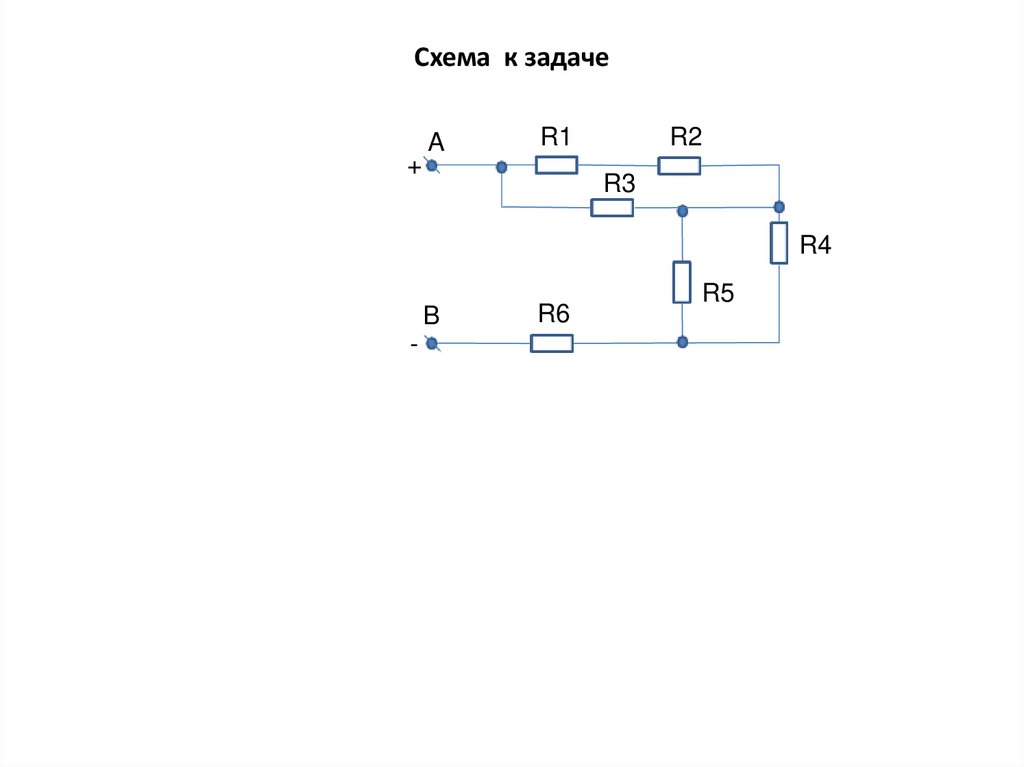
18. Схема к задаче

+
A
R1
R2
R5
B
-
R6
R3
R4

19. Схема к задаче

+
A
R1
R2
R3
R4
B
-
R6
R5

20.

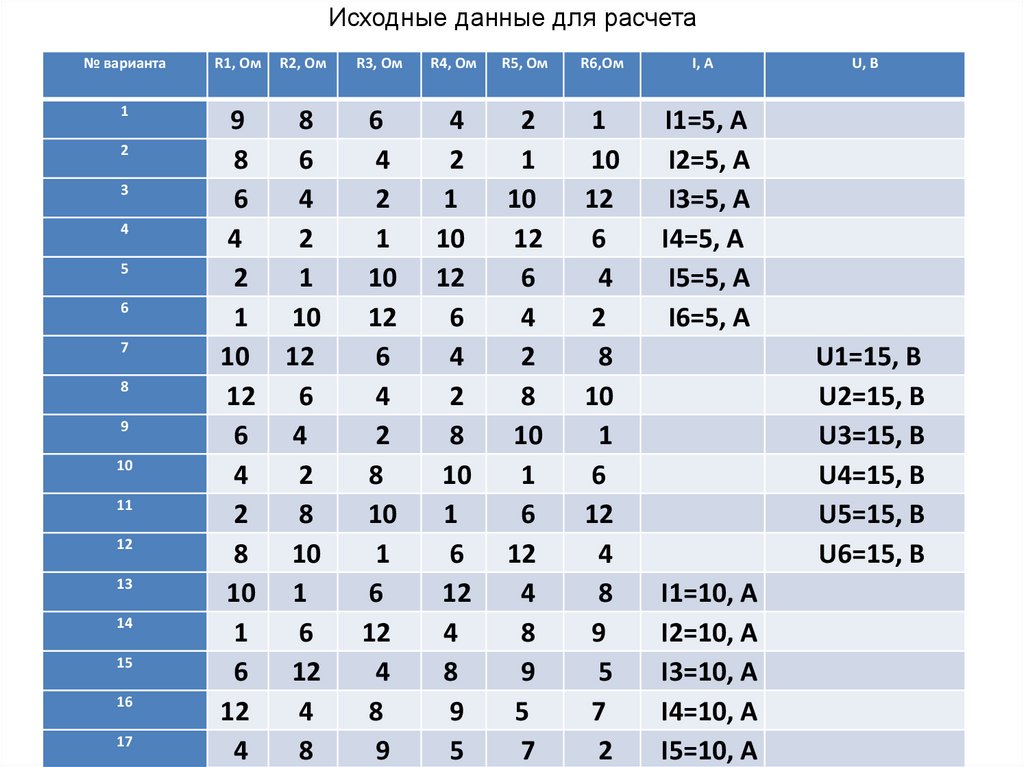
Исходные данные для расчета
№ варианта
R1, Ом
R2, Ом
R3, Ом
R4, Ом
R5, Ом
R6,Ом
I, А
1
9
8
6
4
2
1
10
12
6
4
2
8
10
1
6
12
4
8
6
4
2
1
10
12
6
4
2
8
10
1
6
12
4
8
6
4
2
1
10
12
6
4
2
8
10
1
6
12
4
8
9
4
2
1
10
12
6
4
2
8
10
1
6
12
4
8
9
5
2
1
10
12
6
4
2
8
10
1
6
12
4
8
9
5
7
1
10
12
6
4
2
8
10
1
6
12
4
8
9
5
7
2
I1=5, А
I2=5, А
I3=5, А
I4=5, А
I5=5, А
I6=5, А
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
U, В
U1=15, В
U2=15, В
U3=15, В
U4=15, В
U5=15, В
U6=15, В
I1=10, А
I2=10, А
I3=10, А
I4=10, А
I5=10, А

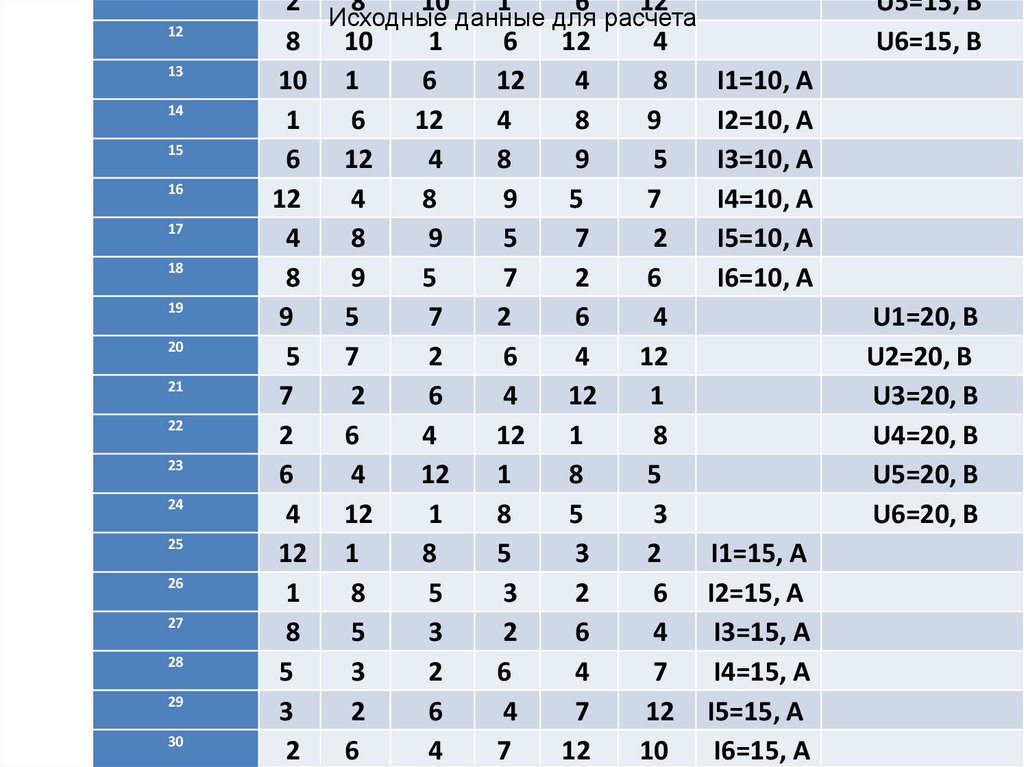
21.

12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2
8
10
1
6
12
Исходные данные для расчета
8
10
1
6
12
4
10 1
6
12
4
8
I1=10, А
1
6
12
4
8
9
I2=10, А
6
12
4
8
9
5
I3=10, А
12
4
8
9
5
7
I4=10, А
4
8
9
5
7
2
I5=10, А
8
9
5
7
2
6
I6=10, А
9
5
7
2
6
4
5
7
2
6
4
12
7
2
6
4
12
1
2
6
4
12
1
8
6
4
12
1
8
5
4
12
1
8
5
3
12 1
8
5
3
2
I1=15, А
1
8
5
3
2
6 I2=15, А
8
5
3
2
6
4
I3=15, А
5
3
2
6
4
7
I4=15, А
3
2
6
4
7
12 I5=15, А
2
6
4
7
12
10
I6=15, А
U5=15, В
U6=15, В
U1=20, В
U2=20, В
U3=20, В
U4=20, В
U5=20, В
U6=20, В

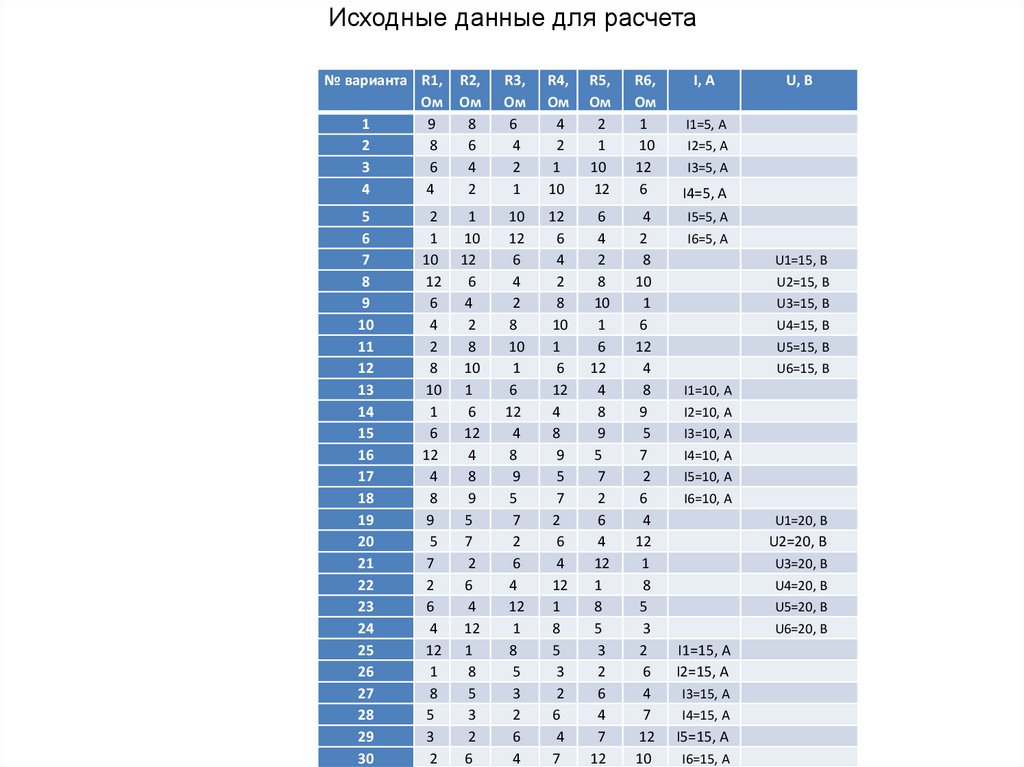
22.

Исходные данные для расчета
№ варианта R1,
Ом
1
9
2
8
3
6
4
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2
1
10
12
6
4
2
8
10
1
6
12
4
8
9
5
7
2
6
4
12
1
8
5
3
2
R2,
Ом
8
6
4
2
R3,
Ом
6
4
2
1
R4,
Ом
4
2
1
10
R5,
Ом
2
1
10
12
R6,
Ом
1
10
12
6
1
10
12
6
4
2
8
10
1
6
12
4
8
9
5
7
2
6
4
12
1
8
5
3
2
6
10
12
6
4
2
8
10
1
6
12
4
8
9
5
7
2
6
4
12
1
8
5
3
2
6
4
12
6
4
2
8
10
1
6
12
4
8
9
5
7
2
6
4
12
1
8
5
3
2
6
4
7
6
4
2
8
10
1
6
12
4
8
9
5
7
2
6
4
12
1
8
5
3
2
6
4
7
12
4
2
8
10
1
6
12
4
8
9
5
7
2
6
4
12
1
8
5
3
2
6
4
7
12
10
I, А
U, В
I1=5, А
I2=5, А
I3=5, А
I4=5, А
I5=5, А
I6=5, А
U1=15, В
U2=15, В
U3=15, В
U4=15, В
U5=15, В
U6=15, В
I1=10, А
I2=10, А
I3=10, А
I4=10, А
I5=10, А
I6=10, А
U1=20, В
U2=20, В
U3=20, В
U4=20, В
U5=20, В
U6=20, В
I1=15, А
I2=15, А
I3=15, А
I4=15, А
I5=15, А
I6=15, А