Расчет цепи постоянного тока

1.

Параметры схемы:
E1 = 10 В, E2 = 36 В, E3 = 12 В;
R01 = 1 Ом, R02 = 1 Ом, R03 = 1 Ом;
R1 = 3 Ом, R2= 5 Ом, R3 = 3 Ом,
R4 = 5 Ом, R5 = 6 Ом, R6 = 5 Ом
Порядок расчета:
1. Обозначим узлы схемы a, b, c, d. Произвольно укажем направления токов во всех
ветвях. Обозначим направление обхода контура для составления уравнений по второму
закону Кирхгофа.
2. С целью упрощения последовательные и параллельные соединения сопротивлений,
содержащиеся в цепи, заменяются эквивалентными:
RЭ1 = (R1+R01) = 4 Ом
RЭ2 = (R2+R02) = 6 Ом
RЭ3= (R3+R03) = 4 Ом

2.

3. Составляются уравнения по первому закону Кирхгофа, количество которых равно
(n–1), где n – количество узлов в схеме, знак тока зависит от ориентации тока,
относительно узла:
2-й закон Кирхгофа:
1-й закон Кирхгофа:
a : I1 I 2 I 3 0;
b : I1 I 4 I 5 0;
c : I 2 I 5 I 6 0.
Iк : I 2 RЭ 2 I 6 R6 I 3 RЭ 3 E2 E3 ;
IIк : I 3 RЭ 3 I 4 R4 I1RЭ1 E3 E1;
IIIк : I 4 R4 I 5 R5 I 6 R6 0.
4. Остальные три уравнения для независимых контуров составляются по второму
закону Кирхгофа. Знак слагаемых в уравнении зависит от совпадения или не
совпадения с принятым направлением обхода контура.
5. Решая полученные системы уравнений совместно, определим значения токов в
ветвях (задача решается в MS Excel методом обратной матрицы). Запишем матрицу
коэффициентов при неизвестных токах и матрицу-столбец правой части уравнений.
Матрица коэффициентов левой части
системы:
•I1
•I2
•I3
•I4
•I5
•I6
-1
-1
-1
0
0
0
1
0
0
1
-1
0
0
1
0
0
1
-1
0
6
-4
0
0
5
-4
0
4
5
0
0
0
0
0
5
6
5
Матрица-столбец
правой части системы:
и
0
0
0
24
2
0
Значения
токов:
I1 = -1,31 А
I2 = 2,33 А
I3 = -1,02 А
I4 = 0,17 А
I5 = -1,14 А
I6 = 1,19 А

3.

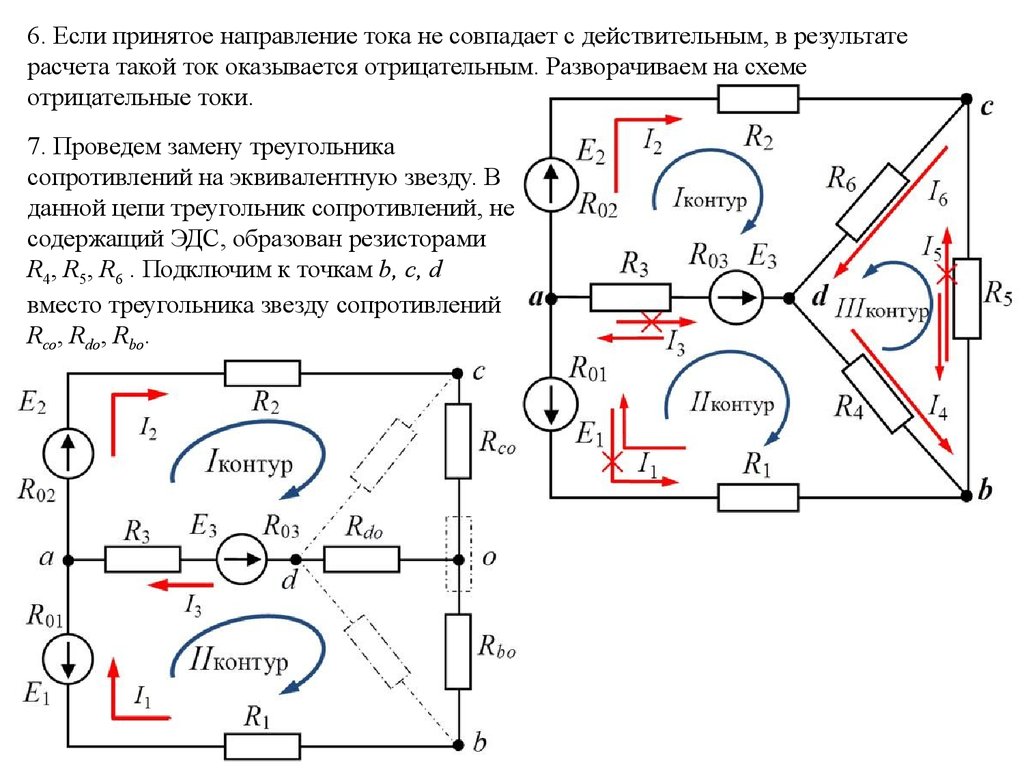
6. Если принятое направление тока не совпадает с действительным, в результате
расчета такой ток оказывается отрицательным. Разворачиваем на схеме
отрицательные токи.
7. Проведем замену треугольника
сопротивлений на эквивалентную звезду. В
данной цепи треугольник сопротивлений, не
содержащий ЭДС, образован резисторами
R4, R5, R6 . Подключим к точкам b, c, d
вместо треугольника звезду сопротивлений
Rсо, Rdo, Rbo.

4.

8. Для преобразованной схемы рассчитаем значения эквивалентных сопротивлений.
R5 R6
R4 R6
Rсo
1,875 Ом Rdo
1,56 Ом
R4 R5 R6
R4 R5 R6
R4 R5
Rbo
1,875 Ом
R4 R5 R6
9. Составляем по законам Кирхгофа уравнения для расчета токов.
o : I1 I 2 I 3 0;
Iк. : I 2 ( RЭ 2 Rco ) I 3 ( RЭ 3 Rdo ) E2 E3 ;
IIк. : I1 ( RЭ1 Rbo ) I 3 ( RЭ 3 Rdo ) E3 E1.
10. Определим значения токов в ветвях (в MS Excel).
Матрица коэффициентов левой
Матрица-столбец
части системы:
правой части системы:
•I1
•I2
•I3
-1
1
-1
0
0
7,875
5,56
и
24
5,875
0
-5,56
2
Значения
токов:
I1 = 1,31 А
I2 = 2,33 А
I3 = 1,02 А
Значения полученных токов совпадают с ранее найденными, значит расчет
произведен верно.

5.

11. Произвольно задаемся направлением контурных токов Ik1, Ik2, Ik3 в контурах.
Составляем для каждого контура уравнение по второму закону Кирхгофа, учитывая
действие как внутреннего контурного тока, действующего на все резистивные элементы
контура, так и внешние контурные токи, действующие на резистивные элементы,
расположенные на смежных сторонах контура.
I к1 ( R1 R01 R3 R03 R4 ) I к 2 ( R3 R03 ) I к 3 R4 E3 E1
I к 2 ( R2 R02 R3 R03 R6 ) I к1 ( R3 R03 ) I к 3 R6 E2 E3
I к 3 ( R4 R5 R6 ) I к1 ( R4 ) I к 2 R6 0
Определим значения контурных токов (в MS Excel).
Если контурный ток оказался отрицательным, он
разворачивается на схеме.
Токи во внешних ветвях схемы I1, I2, I5 равны
соответствующим контурным токам Ik1, Ik2, Ik3.
Токи во внутренних ветвях схемы I1, I2, I3
определяются как сумма или разность
соответствующих контурных токов. Если
контурные токи во внутренней ветви совпадают по
направлению, берется их сумма; если не
Значения токов:
совпадают, берется их разность:
Iк1 = I1 = 1,31 А
Iк2 = I2 = 2,33 А
Iк3 = I5 = 1,14 А
I 3 I к 2 I к1 1,02 A
I 4 I к1 I к 3 0,17 A
I 6 I к 2 I к 3 1,19 A

6.

12. Составляем баланс мощностей цепи. Для исходной схемы баланс мощностей имеет
вид:
P P
И
П
E1 I1 E2 I 2 E3 I 3
I12 ( R1 R01 ) I 22 ( R2 R02 ) I 32 ( R3 R03 ) I 42 R4 I 52 R5 I 62 R6 .
50,16 50,09
13. Рассчитаем потенциалы точек внешнего контура цепи. Разделим дополнительными
точками элементы в ветвях (k, m). Примем потенциал точки a равным 0. Расчет
потенциалов ведется по закону Ома.
E U
E
I
ba
r0
I
b
a
r0
U ba b a
R
R
a 0 В
k a ( E2 I 2 R02 ) 36 2,33 1 33,67 В
с k I 2 R2 33,67 2,33 5 22,02 В
b c I 5 R5 22,02 1,14 6 15,18 В
m b I1 R1 15,18 1,31 3 11,25 В
a m ( E1 I1 R01 ) 11,25 (10 1,31 1) 0,06 0 В

7.

В результате расчета потенциалов точек строится в масштабе потенциальная диаграмма.