Лекция 10

1.

Центр дистанционного обучения
1 Часть курса физики
Профессор кафедры физики,
доктор физико-математических наук
Сайт кафедры физики
online.mirea.ru

2.

Центр дистанционного обучения
ЛЕКЦИЯ 10.
РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО ПАРАМЕТРАМ.
ВНУТРЕННЯЯ ЭНЕРГИЯ И РАБОТА ИДЕАЛЬНОГО ГАЗА
10.1. Барометрическая формула. Классическое распределение
Больцмана
Рассмотрим газ в сосуде (см. рис.10.1). Как молекулы распределены по высоте
Слой dH создаёт дополнительное давление dP gdH , но плотность
m P P m0 N A P m0
,
V T R T k NA
kТ
где m0 - масса молекулы. Тогда dP
P m0g
dH
kT
или
m g
dP
0 dH .
P
kT
Рисунок 10.1 Слой dH оказывает дополнительное давление dP online.mirea.ru

3.

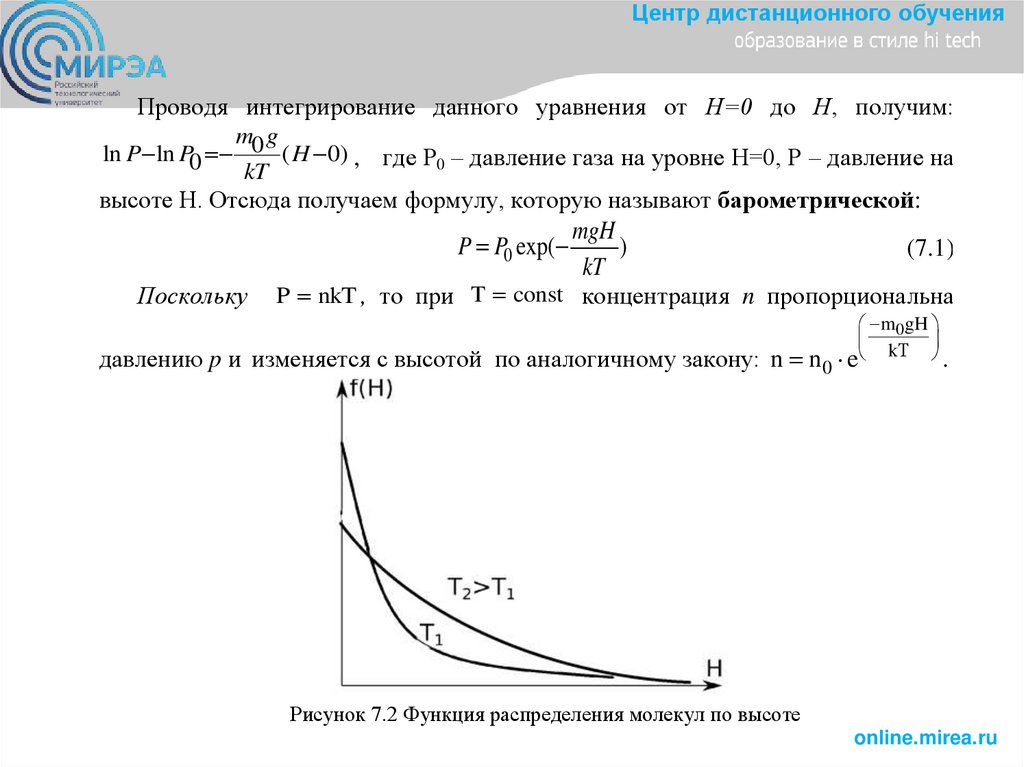
Центр дистанционного обучения
Проводя интегрирование данного уравнения от Н=0 до Н, получим:
m g
ln P ln P0 0 ( H 0) , где Р0 – давление газа на уровне Н=0, Р – давление на
kT
высоте Н. Отсюда получаем формулу, которую называют барометрической:
mgH
P P0 exp(
)
(7.1)
kT
Поскольку P nkT , то при T const концентрация n пропорциональна
давлению p и изменяется с высотой по аналогичному закону: n n 0
m0gH
e kТ .
Рисунок 7.2 Функция распределения молекул по высоте
online.mirea.ru

4.

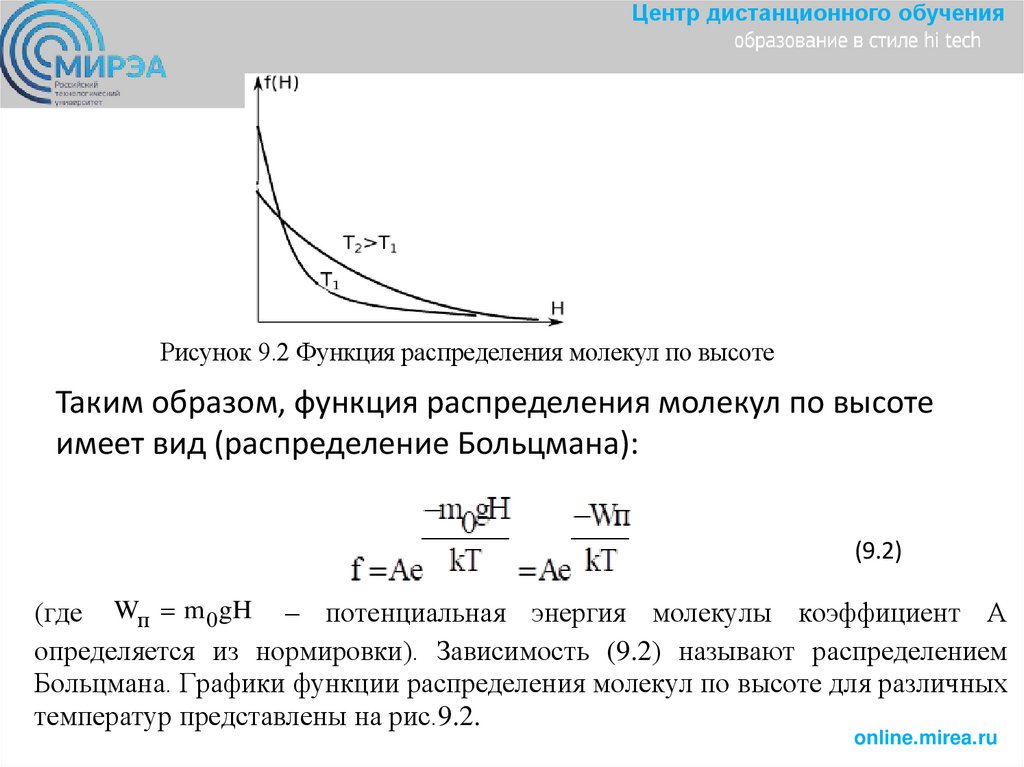
Центр дистанционного обучения
Рисунок 9.2 Функция распределения молекул по высоте
Таким образом, функция распределения молекул по высоте
имеет вид (распределение Больцмана):
(9.2)
(где Wп m 0gH – потенциальная энергия молекулы коэффициент А
определяется из нормировки). Зависимость (9.2) называют распределением
Больцмана. Графики функции распределения молекул по высоте для различных
температур представлены на рис.9.2.
online.mirea.ru

5.

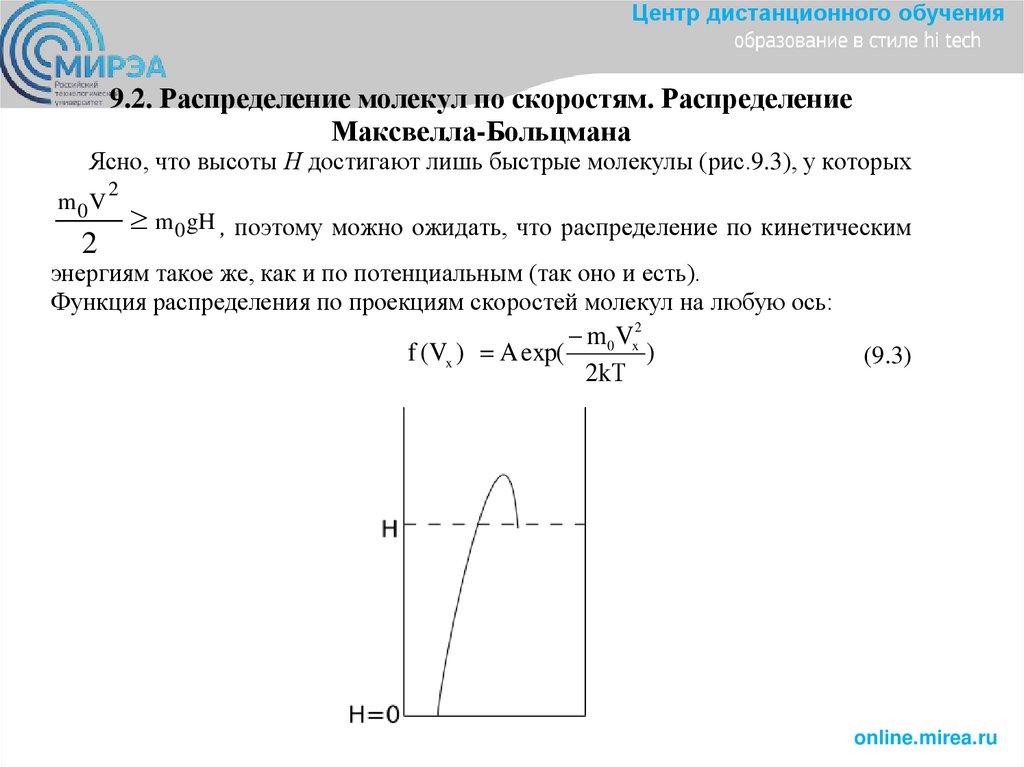
Центр дистанционного обучения
9.2. Распределение молекул по скоростям. Распределение
Максвелла-Больцмана
Ясно, что высоты Н достигают лишь быстрые молекулы (рис.9.3), у которых
m0V
2
2
m 0gH , поэтому можно ожидать, что распределение по кинетическим
энергиям такое же, как и по потенциальным (так оно и есть).
Функция распределения по проекциям скоростей молекул на любую ось:
m0 Vx2
f (Vx ) A exp(
)
2kТ
(9.3)
online.mirea.ru

6.

Центр дистанционного обучения
Можно показать, что распределение молекул по абсолютным скоростям имеет
следующий вид:
Это называется распределением Максвелла по абсолютным скоростям
(рис.9.4).
Рисунок 9.4 Распределение Максвелла по скоростям
Распределения Максвелла и Больцмана можно объединить:
W Wп
(9.5)
f A exp( k
),
kТ
где Wп,Wk – потенциальная и кинетическая энергии молекулы. Это
распределение носит имя Максвелла - Больцмана.
При температуре абсолютного нуля Т=0 молекулы падают на дно сосуда и
online.mirea.ru
перестают двигаться.

7.

Центр дистанционного обучения
9.3. Степени свободы молекулы. Внутренняя энергия и
теплоёмкость идеального газа
Напомним: степени свободы - это минимальное число независимых переменных,
которые однозначно описывают положение системы в пространстве.
Примеры: 1 точка - 3 степени свободы (Х, У, Z)
2 свободные точки - 6 степеней свободы
2 жёстко связанные точки - 5 степень свободы (каждая связь уменьшает число
степеней свободы на 1)
3 свободные точки - 9 степеней свободы
3 жёстко связанные точки 9 - 3 = 6 степеней свободы. (3 связи)
Положение твёрдого тела в пространстве можно полностью задать 3-мя точками,
связанными с телом, следовательно, у твердого тела 6 степеней свободы.
Поскольку молекулы идеального газа не взаимодействуют на расстоянии, то
потенциальной энергии взаимодействия у идеального газа нет. Можно принять, что
внутренняя энергия идеального газа складывается из кинетической энергии атомов.
online.mirea.ru

8.

Центр дистанционного обучения
Выполняется принцип равного распределения тепловой энергии по
степеням свободы. На каждую степень свободы у одной молекулы приходится
1
в среднем энергия равная: 2 kT .
Если у молекулы i степеней свободы, то энергия молекулы составит:
Wмолек. (i 2) kT
(9.6)
Внутренняя энергия для 1 моля складывается из кинетической энергии NA
молекул. (Напомним, что в 1 моле любого вещества содержится NA=6.1023
молекул)
i
i
U N A Wмолек N A kT RT
(9.7)
2
2
Внутренняя энергия для произвольной массы m идеального газа равна:
m
mi
U U
RT
(9.8)
2
В общем случае, для неидеальных газов и тел внутренняя энергия включает
энергию всевозможных видов движения и взаимодействия всех частиц
термодинамической системы (кинетическая энергия атомов и молекул,
потенциальная энергия всех частиц, включая ядра и т. д.). Внутренняя энергия
не включает кинетическую энергию и потенциальную энергию
термодинамической системы как целого.
online.mirea.ru

9.

Центр дистанционного обучения
9.4. Работа идеального газа
Рассмотрим газ в цилиндре с поршнем, площадь которого равна S. (рис.7.5).
Пусть газ сдвигает поршень на расстояние dX.
Рисунок 7.5. Работа идеального газа при расширении.
При квазистатическом (квазиравновесном) расширении газа он совершит
работу: А Fdx P Sdx PdV
Итак, мы получили выражение для элементарной работы газа:
A PdV
(9.9)
При медленном квазистатическом расширении внешние силы равны силе
давления газа, но противоположно направлены. Поэтому работа внешних сил:
Aвнеш A
(9.10)
Работа при конечном приращении объёма складывается (интегрируется) из
элементарных работ:
V2
А12 PdV
V1
(А12 > 0, А21 < 0)
(9.11)
online.mirea.ru

10.

Центр дистанционного обучения
Рисунок 9.6 Элементарная работа на графике соответствует площади заштрихованного
столбца. Вся работа газа А12 равна площади под кривой 1-2.
Если при переходе газа из точки 1 в точку 2 газ расширяется dV>0, работа
газа получится положительной А12 >0. При обратном процессе, переходе из
точки 2 в точку 1, газ сжимается dV<0, и работа газа отрицательна А21 <0.
Работа равна площади под кривой перехода в координатах Р,V (см. рис.9.6).
Работа зависит от пути перехода, значит, не является функцией
состояния (см. рис.7.7).
Рисунок 9.7 а) работа газа А12>0; б) работа газа А21<0; в) работа в замкнутом
цикле А121>0 и равна площади внутри замкнутой кривой; г) в обратном цикле
А121<0
online.mirea.ru

11.

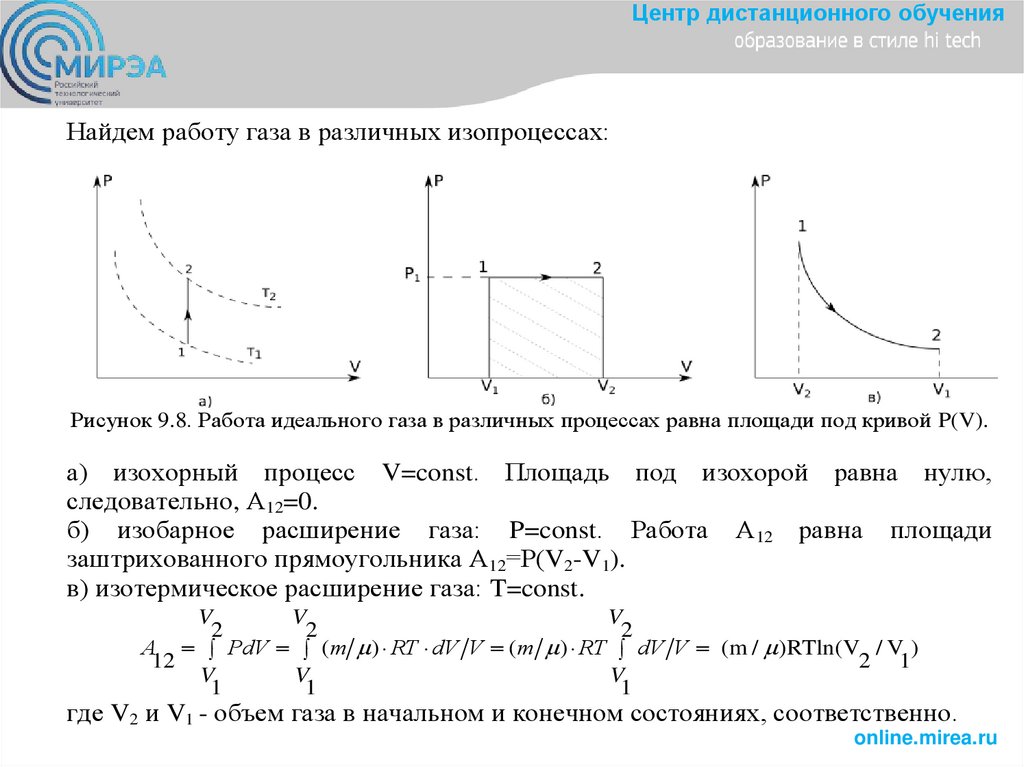
Центр дистанционного обучения
Найдем работу газа в различных изопроцессах:
Рисунок 9.8. Работа идеального газа в различных процессах равна площади под кривой P(V).
а) изохорный процесс V=const. Площадь под изохорой равна нулю,
следовательно, А12=0.
б) изобарное расширение газа: P=const. Работа А12 равна площади
заштрихованного прямоугольника А12=Р(V2-V1).
в) изотермическое расширение газа: T=const.
V
V
V
2
2
2
А PdV (m ) RT dV V (m ) RT dV V (m / )RTln(V / V )
12
2 1
V
V
V
1
1
1
где V2 и V1 - объем газа в начальном и конечном состояниях, соответственно.
online.mirea.ru

12.

Центр дистанционного обучения
online.mirea.ru

13.

Центр дистанционного обучения
Не забудьте себя похвалить!!
Спасибо за внимание.
online.mirea.ru