2 геометрия 8 27.11.2025

1.

21 ноября
Классная работа
“Учиться можно только весело…
Чтобы переваривать знания, надо
поглощать их с аппетитом”.
Анатоль Франс

2.

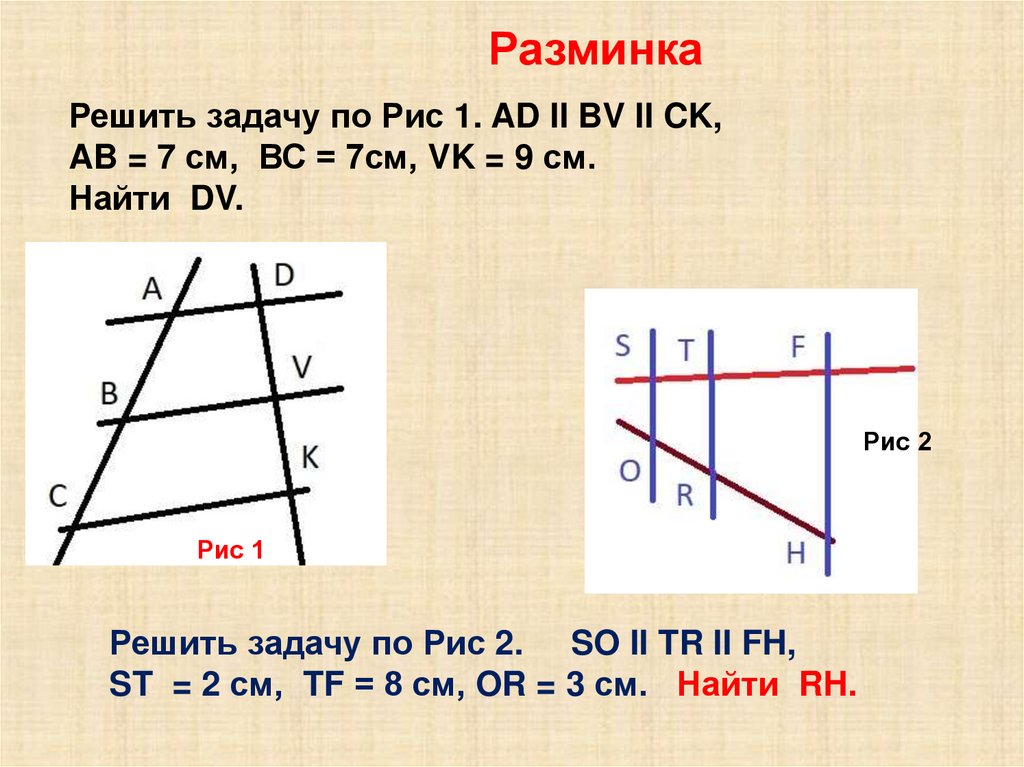
Разминка
Решить задачу по Рис 1. AD II BV II CK,
AB = 7 см, ВС = 7см, VK = 9 см.
Найти DV.
Рис 2
Рис 1
Решить задачу по Рис 2. SO II TR II FH,
ST = 2 см, TF = 8 см, OR = 3 см. Найти RH.

3.

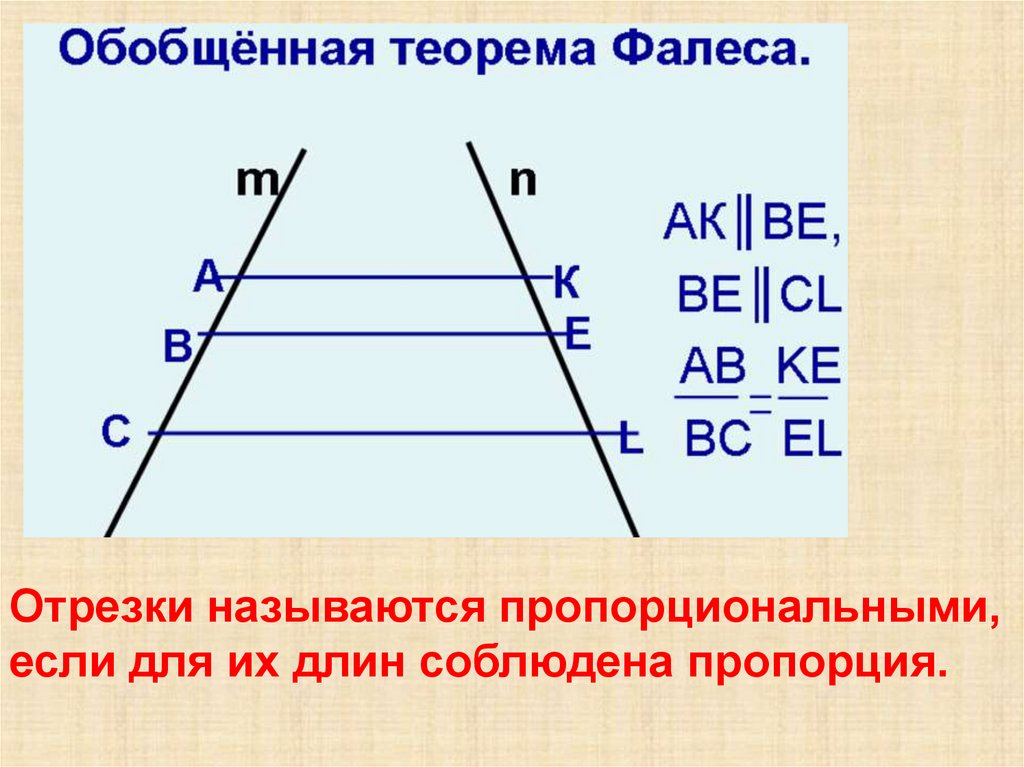
Отрезки называются пропорциональными,
если для их длин соблюдена пропорция.

4.

Похожесть?
Что
объединяет
эти
фотографии?

5.

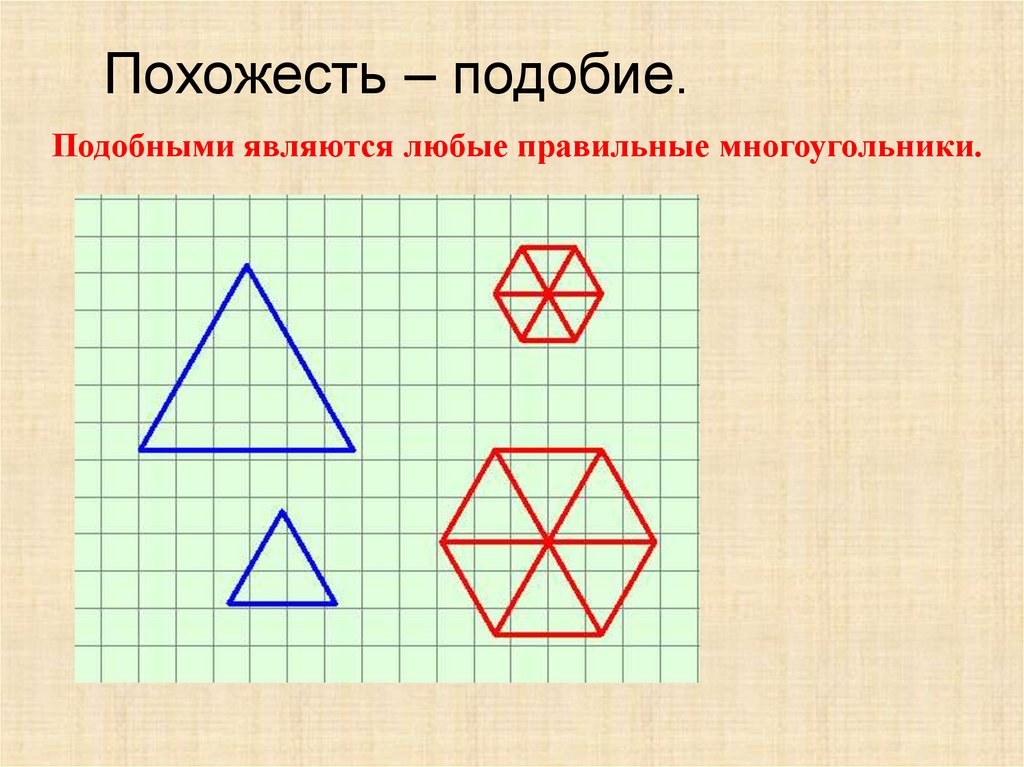
Похожесть – подобие.
Подобными являются любые правильные многоугольники.

6.

Тема урока.
Подобные треугольники.
Признаки подобия.

7.

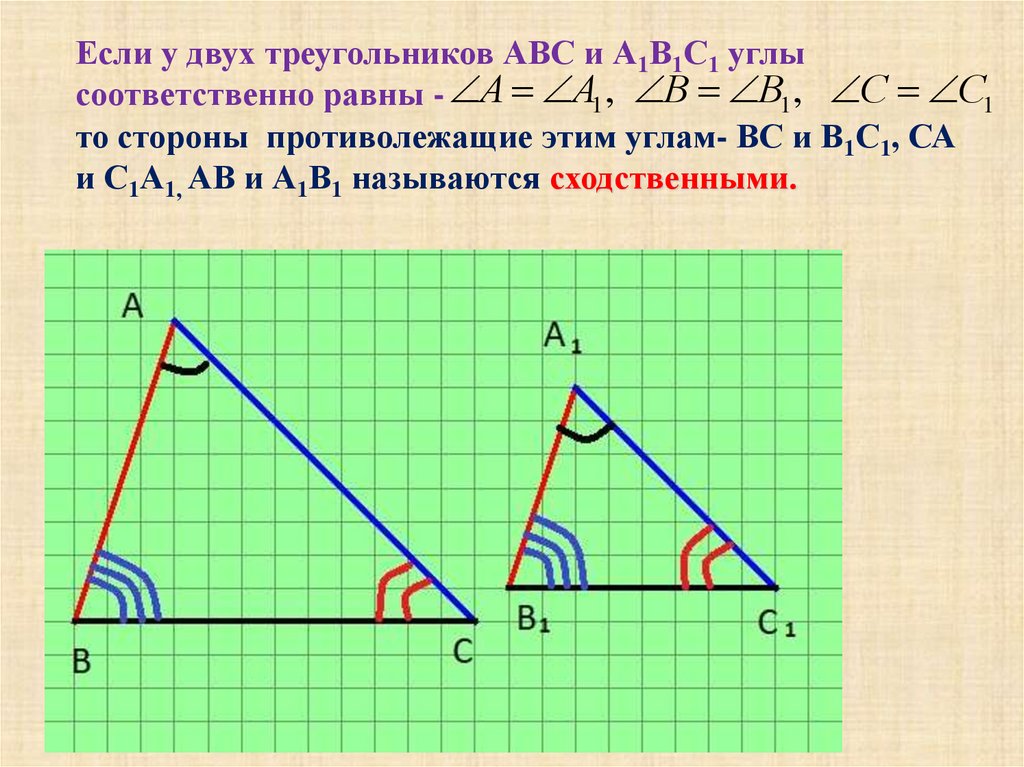
Если у двух треугольников АВС и А1В1С1 углы
соответственно равны - А А1 , В В1 , С С1
то стороны противолежащие этим углам- ВС и В1С1, СА
и С1А1, АВ и А1В1 называются сходственными.

8.

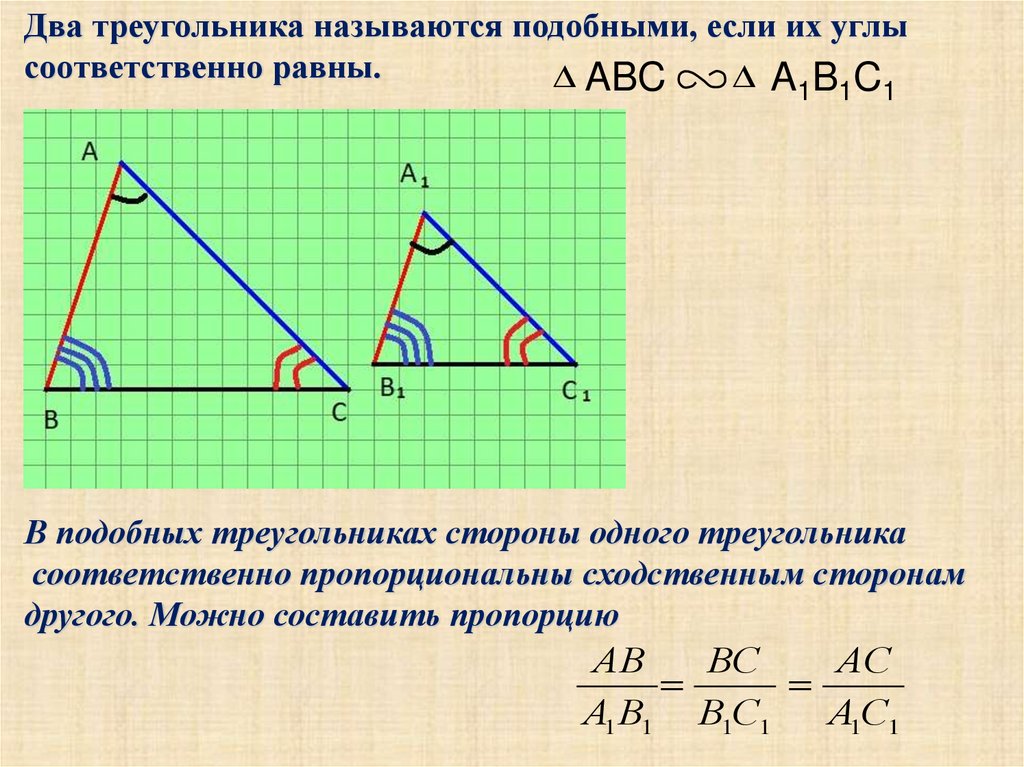
Два треугольника называются подобными, если их углы
соответственно равны.
ABC
A B C
1 1
1
В подобных треугольниках стороны одного треугольника
соответственно пропорциональны сходственным сторонам
другого. Можно составить пропорцию
АВ
ВС
АС
А1 В1 В1С1
А1С1

9.

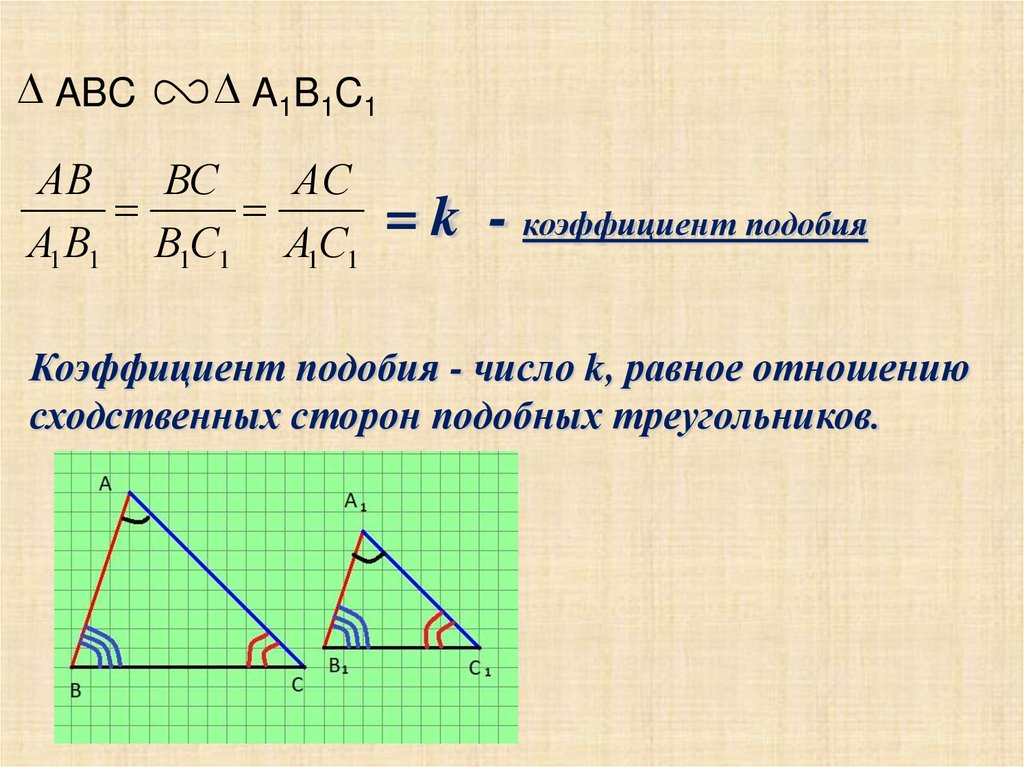
ABC
A1B1C1
АВ
ВС
АС
=
k
коэффициент подобия
А1 В1 В1С1 А1С1
Коэффициент подобия - число k, равное отношению
сходственных сторон подобных треугольников.

10.

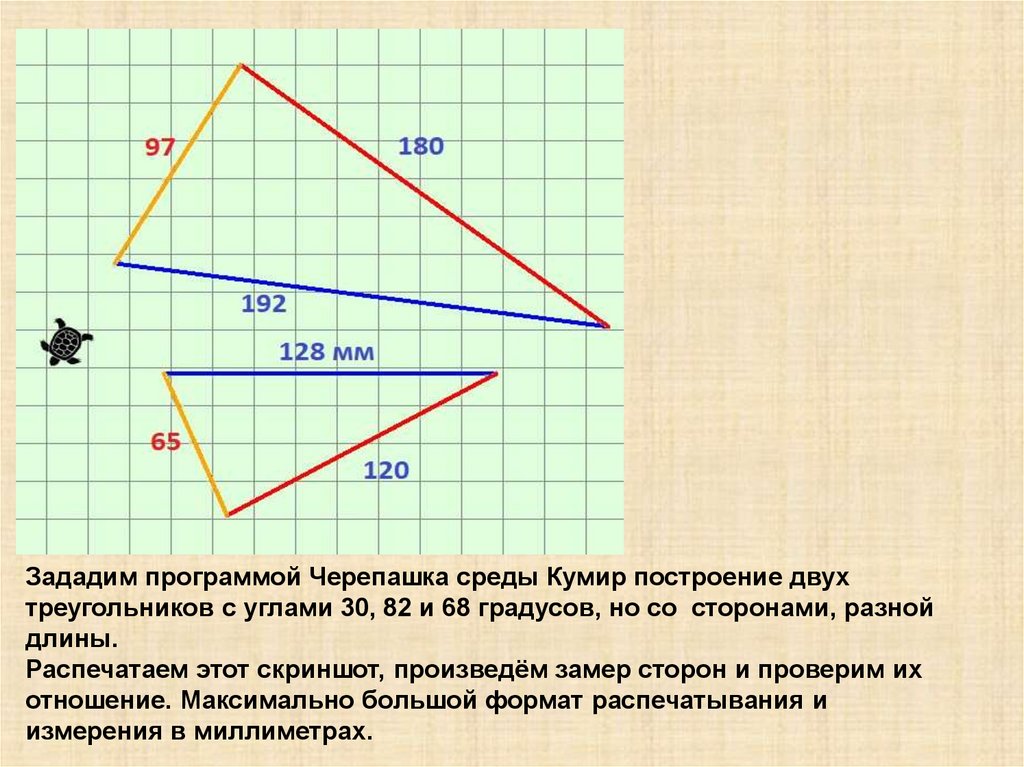
Зададим программой Черепашка среды Кумир построение двух
треугольников с углами 30, 82 и 68 градусов, но со сторонами, разной
длины.
Распечатаем этот скриншот, произведём замер сторон и проверим их
отношение. Максимально большой формат распечатывания и
измерения в миллиметрах.

11.

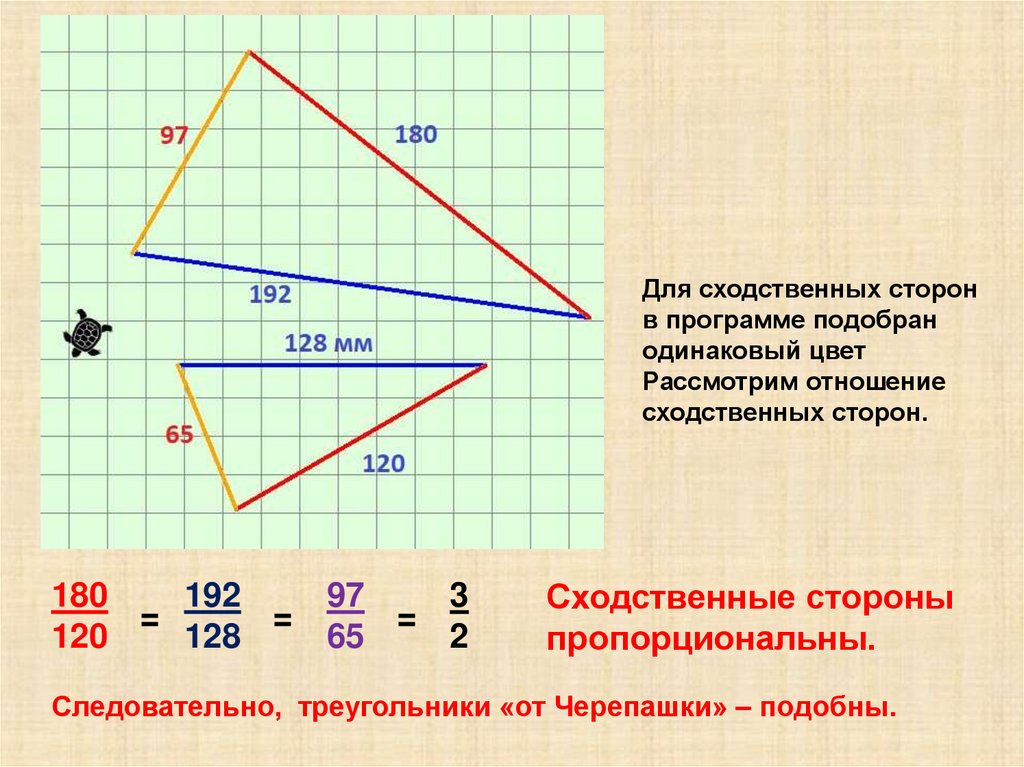
Для сходственных сторон
в программе подобран
одинаковый цвет
Рассмотрим отношение
сходственных сторон.
180
192
97
3
=
=
=
120
128
65
2
Сходственные стороны
пропорциональны.
Следовательно, треугольники «от Черепашки» – подобны.

12.

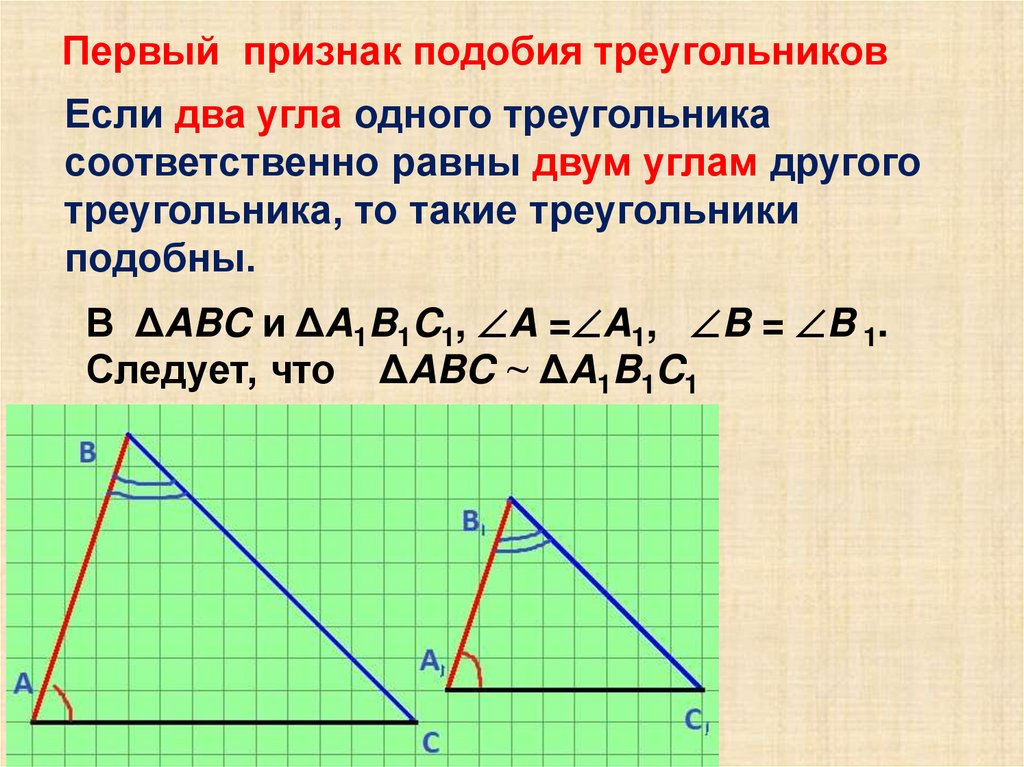
Первый признак подобия треугольников
Если два угла одного треугольника
соответственно равны двум углам другого
треугольника, то такие треугольники
подобны.
В ΔABC и ΔA1B1C1, A = A1, B = B 1.
Следует, что ΔABC ~ ΔA1B1C1

13.

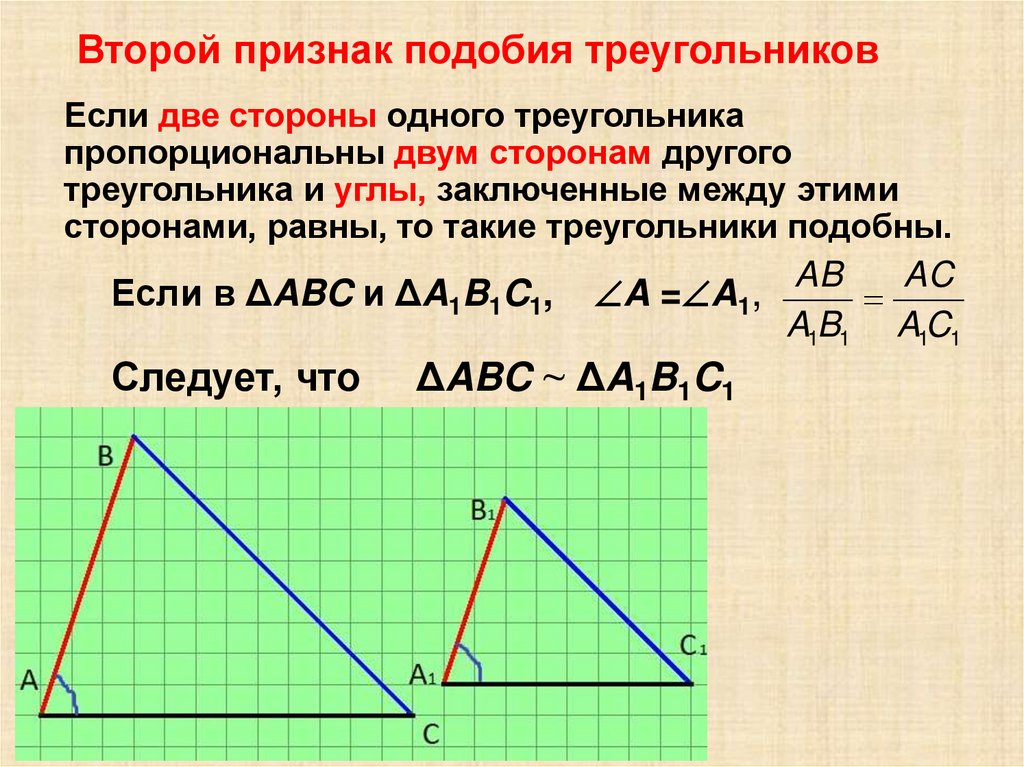
Второй признак подобия треугольников
Если две стороны одного треугольника
пропорциональны двум сторонам другого
треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники подобны.
AB
AC
Если в ΔABC и ΔA1B1C1, A = A1,
A1B1 A1C1
Следует, что
ΔABC ~ ΔA1B1C1

14.

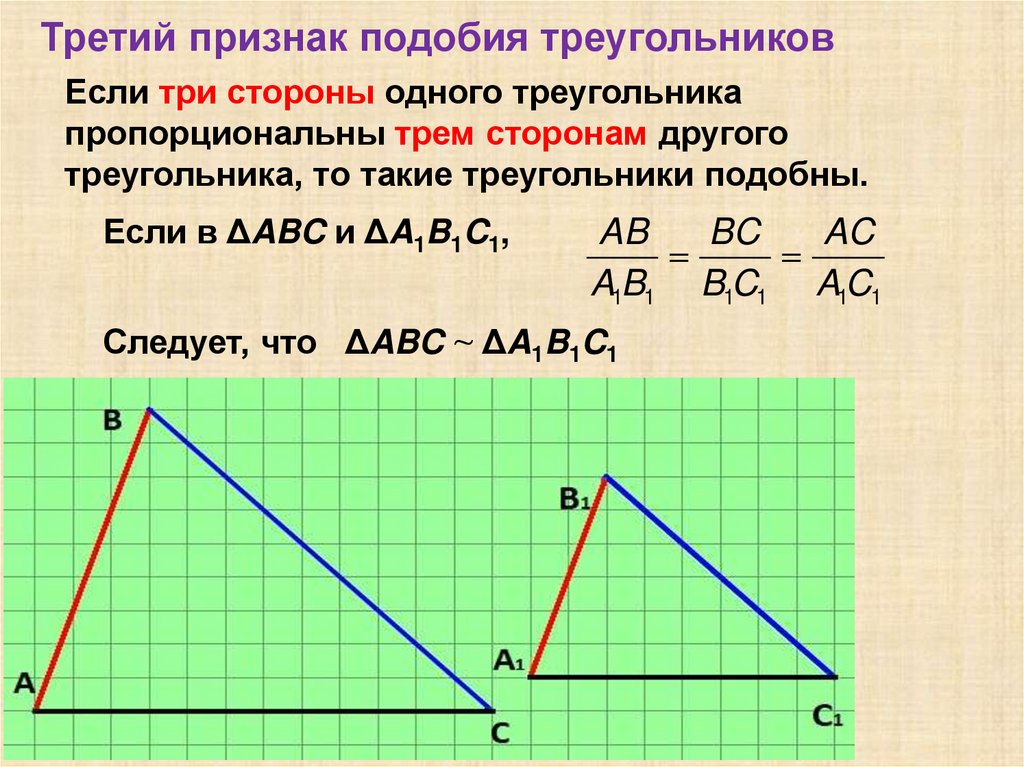
Третий признак подобия треугольников
Если три стороны одного треугольника
пропорциональны трем сторонам другого
треугольника, то такие треугольники подобны.
Если в ΔABC и ΔA1B1C1,
AB
BC
AC
A1B1 B1C1 A1C1
Следует, что ΔABC ~ ΔA1B1C1

15.

Хороший рисунок помогает быстро найти решение задачи.
Как правильно построить подобные треугольники?
1) Если вы при построении соблюдаете параллельность
сходственных сторон, у вас получатся подобные фигуры.
2) Другой интересный способ, векторный. Вспоминаем навыки,
полученные при использовании программы КУМИР. Два
вектора , например m(1; 3) и b ( -3; 3) прикладывают к базовым
сторонам различной длины. Затем вектора продолжают до
пересечения, намеченных векторами, сторон.

16.

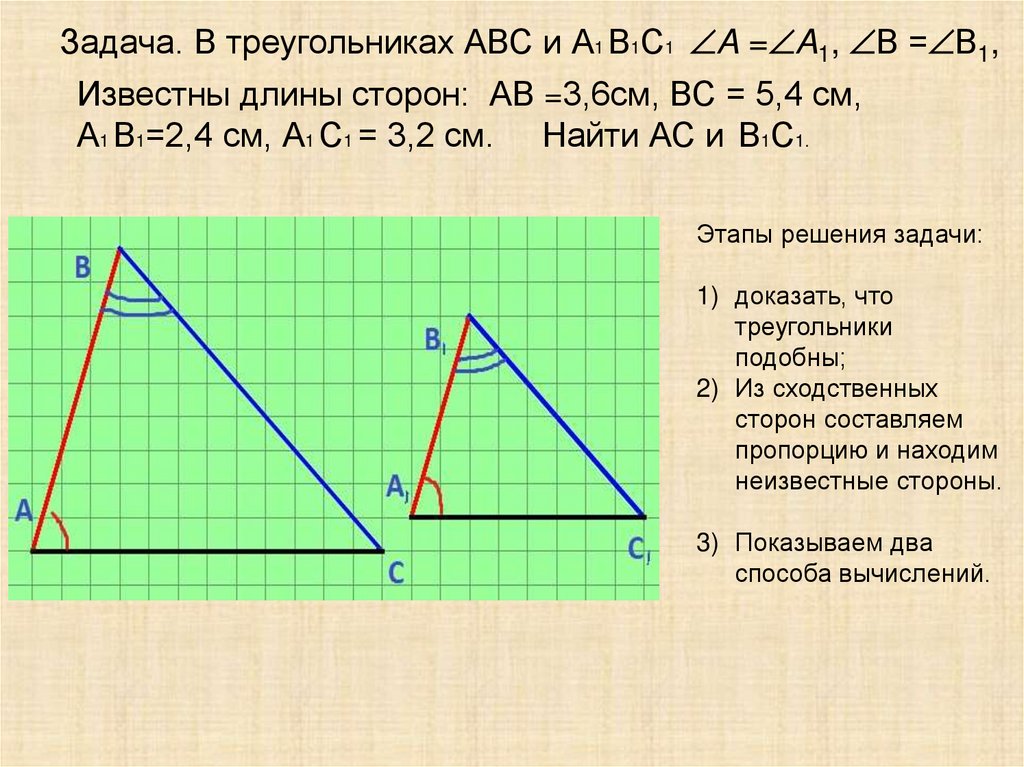
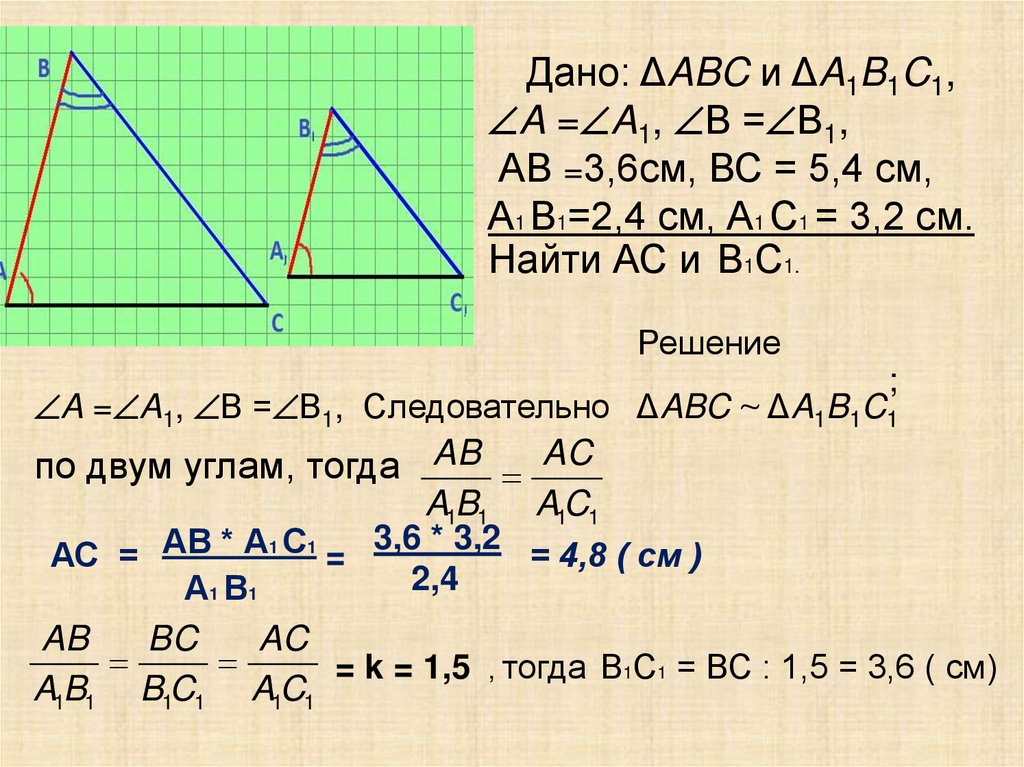
Задача. В треугольниках АВС и А1 В1С1 A = A1, В = В1,
Известны длины сторон: АВ =3,6см, ВС = 5,4 см,
А1 В1=2,4 см, А1 С1 = 3,2 см. Найти АС и В1С1.
Этапы решения задачи:
1) доказать, что
треугольники
подобны;
2) Из сходственных
сторон составляем
пропорцию и находим
неизвестные стороны.
3) Показываем два
способа вычислений.

17.

Дано: ΔABC и ΔA1B1C1,
A = A1, В = В1,
АВ =3,6см, ВС = 5,4 см,
А1 В1=2,4 см, А1 С1 = 3,2 см.
Найти АС и В1С1.
Решение
;
A = A1, В = В1, Следовательно ΔABC ~ ΔA1B1C1
по двум углам, тогда AB AC
A1B1 A1C1
3,6 * 3,2
АС = АВ * А1 С1 =
= 4,8 ( см )
2,4
А1 В1
AB
BC
AC
= k = 1,5 , тогда В1С1 = ВС : 1,5 = 3,6 ( см)
A1B1 B1C1 A1C1

18.

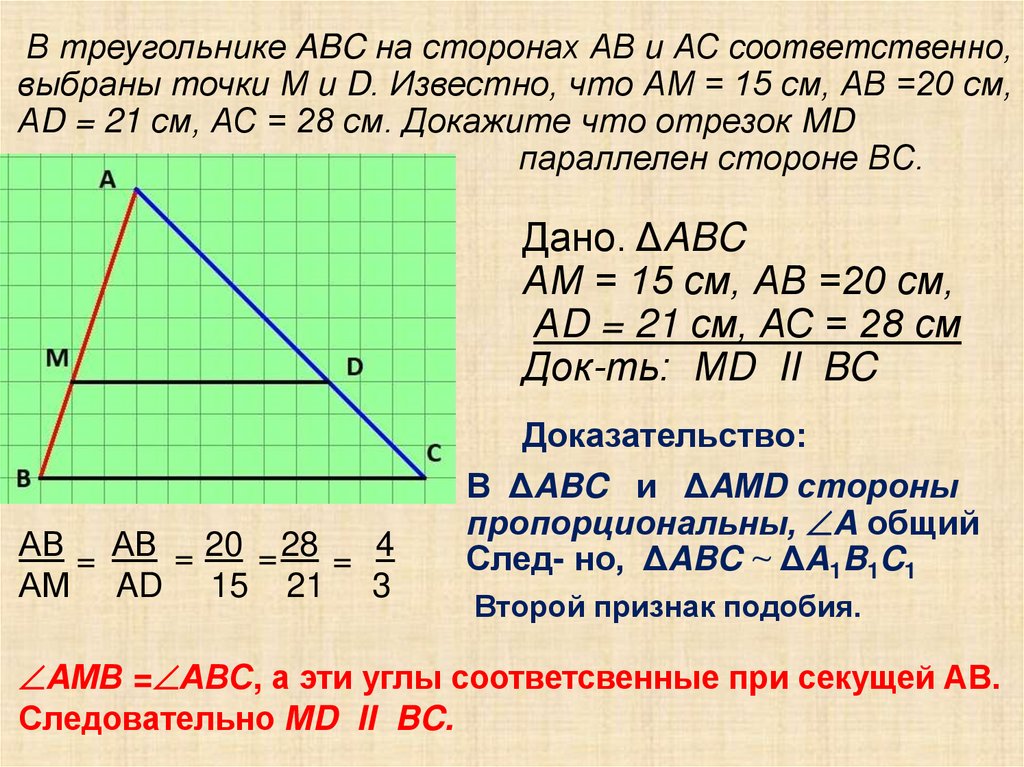
В треугольнике ABC на сторонах АВ и АС соответственно,
выбраны точки М и D. Известно, что АМ = 15 см, АВ =20 см,
АD = 21 см, АС = 28 см. Докажите что отрезок MD
параллелен стороне ВС.
Дано. ΔABC
АМ = 15 см, АВ =20 см,
АD = 21 см, АС = 28 см
Док-ть: МD II BC
АВ = АВ = 20 = 28 = 4
АМ AD 15 21 3
Доказательство:
В ΔABC и ΔAМD стороны
пропорциональны, A общий
След- но, ΔABC ~ ΔA1B1C1
Второй признак подобия.
AМВ = АВС, а эти углы соответсвенные при секущей АВ.
Следовательно МD II BC.

19. Домашнее задание:

Изучить пункты 61-63; решить
№ 550, 560