Лекция 5 Поверхность как объект пространства

1. Поверхность как объект пространства Понятие «поверхность» в начертательной геометрии связано с представлением о кинематическом

способе ее
образования:
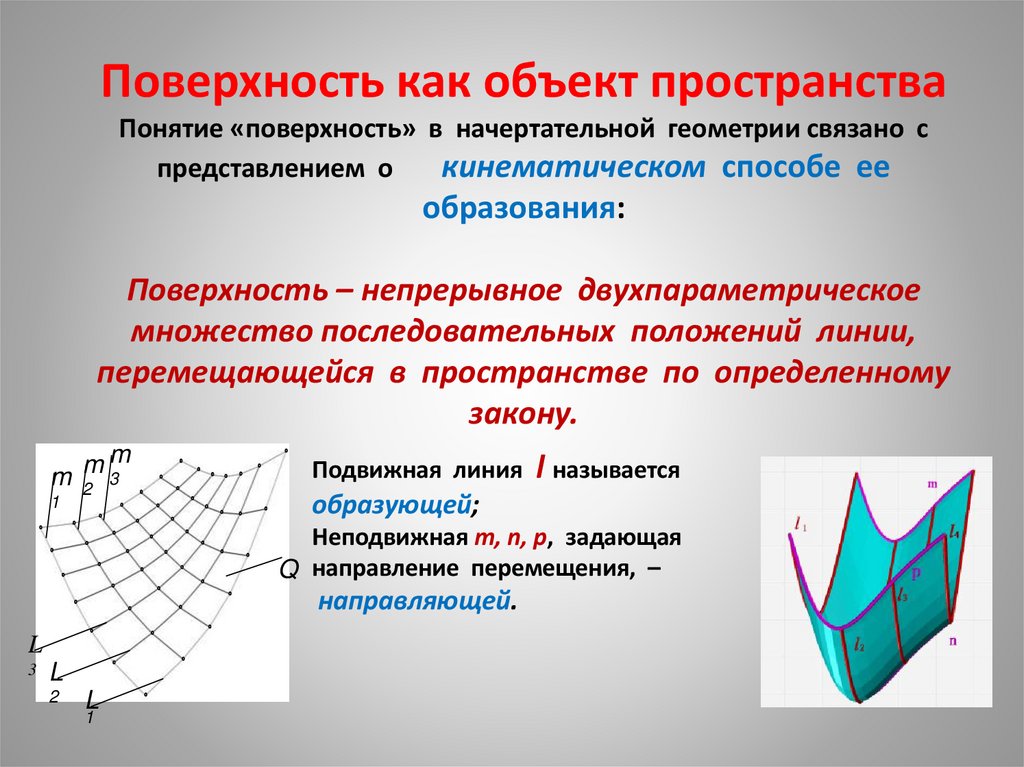
Поверхность – непрерывное двухпараметрическое
множество последовательных положений линии,
перемещающейся в пространстве по определенному
закону.
m
m
m 3
Подвижная линия l называется
1
образующей;
2
Неподвижная m, n, p, задающая
Q направление перемещения, –
направляющей.
L
3 L
2
L
1

2. Для задания поверхности на чертеже выбирают такую совокупность независимых геометрических условий, которая однозначно

определяет данную поверхность в
пространстве.
Эта совокупность называется определителем
поверхности.
Обозначим определитель буквой G. Формула определителя выглядит так:
G = { Г х А }, где Г – геометрическая часть
А – алгоритмическая часть
Геометрическая часть - совокупность геометрических фигур, с помощью
которых можно образовать поверхность.
Алгоритмическая часть - алгоритм формирования поверхности при помощи
фигур, входящих в геометрическую часть определителя.
Определитель часто задают словесно.

3. Одна и та же поверхность может быть образована различными способами, следовательно иметь несколько определителей.

а) цилиндр образован
вращением прямой образующей
L вокруг неподвижной оси i;
направляющая m – окружность,
центр которой лежит на оси
цилиндра.
G1 = { (L,i,m ) ( A1 ) }
б) образующая - окружность с
центром на оси цилиндра.
G2 = { ( m, i ) ( A2 ) }
i
i
m
m
O
L

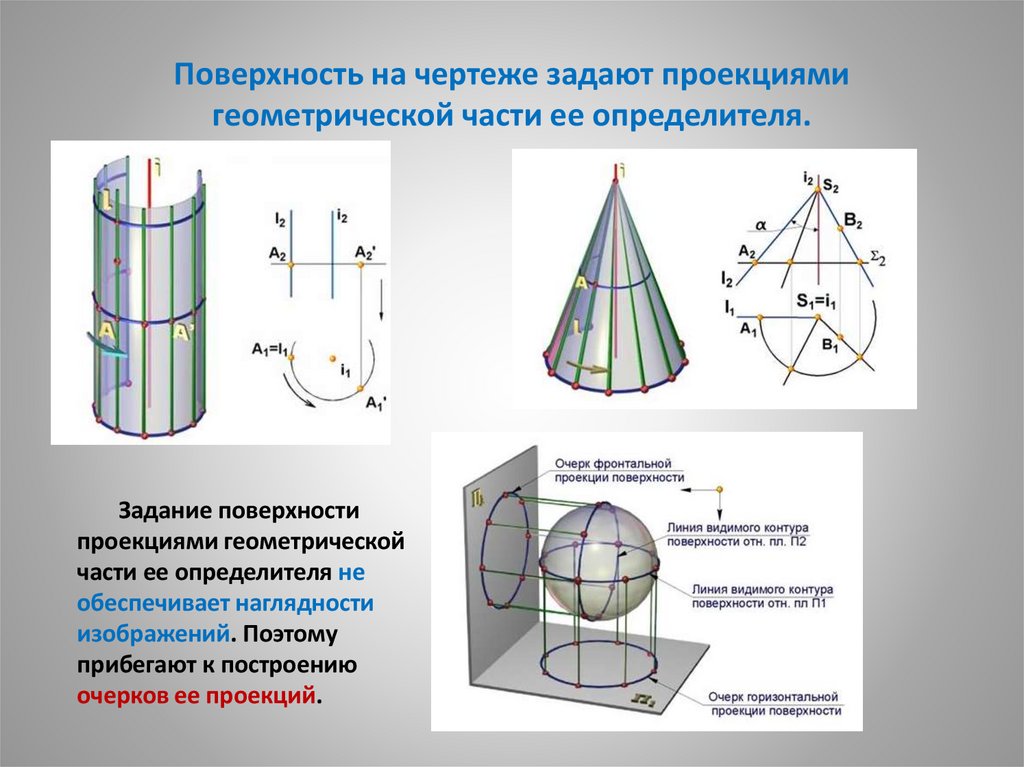
4. Поверхность на чертеже задают проекциями геометрической части ее определителя.

Задание поверхности
проекциями геометрической
части ее определителя не
обеспечивает наглядности
изображений. Поэтому
прибегают к построению
очерков ее проекций.

5. Классификация поверхностей При классификации поверхностей основополагающим является способ образования и свойства поверхности.

По виду образующей:
• Линейчатые (образующая – прямая линия)
• Нелинейчатые (образующая – кривая линия)

6. Линейчатые поверхности:

• Развертывающиеся
• Неразвертывающиеся
Нелинейчатые поверхности:
• С образующей постоянной формы (поверхности
вращения и трубчатые поверхности)
• С образующей переменной формы
(циклические поверхности)
Циклическая поверхность

7. По закону движения образующей линии: ● поверхности вращения; ● винтовые поверхности; ● поверхности с плоскостью параллелизма; ●

поверхности параллельного переноса.
Поверхности вращения
созданы при вращении образующей m вокруг оси i
G = { (i,m ) ( A1 ) }

8.

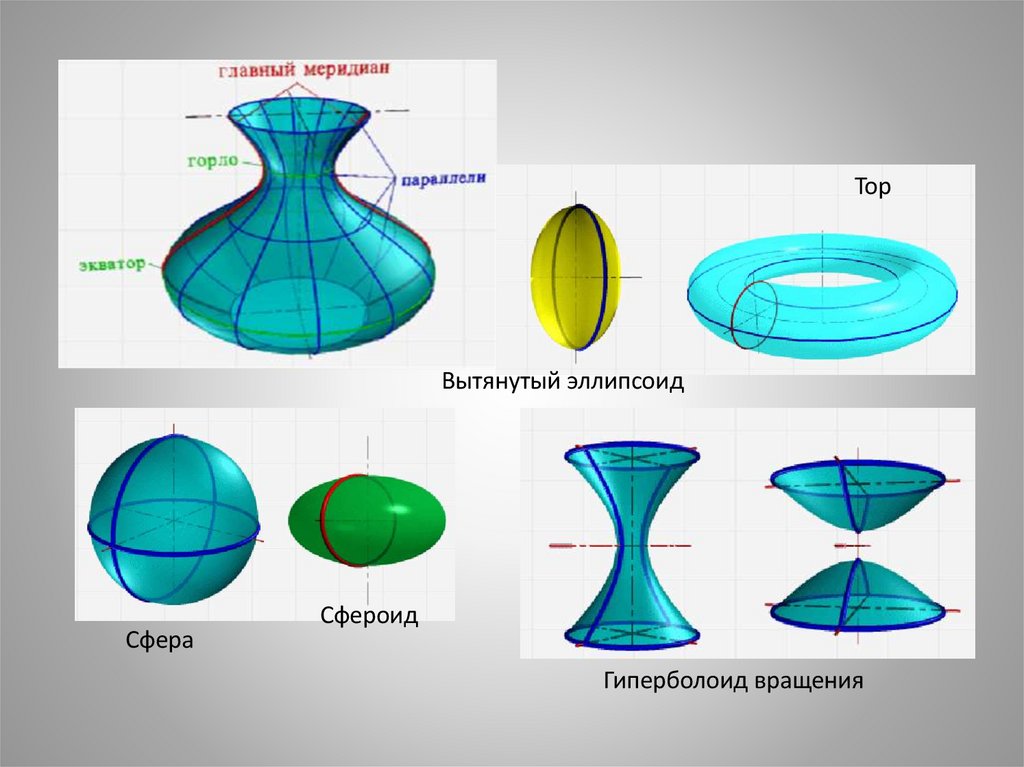
Тор
Вытянутый эллипсоид
Сфера
Сфероид
Гиперболоид вращения

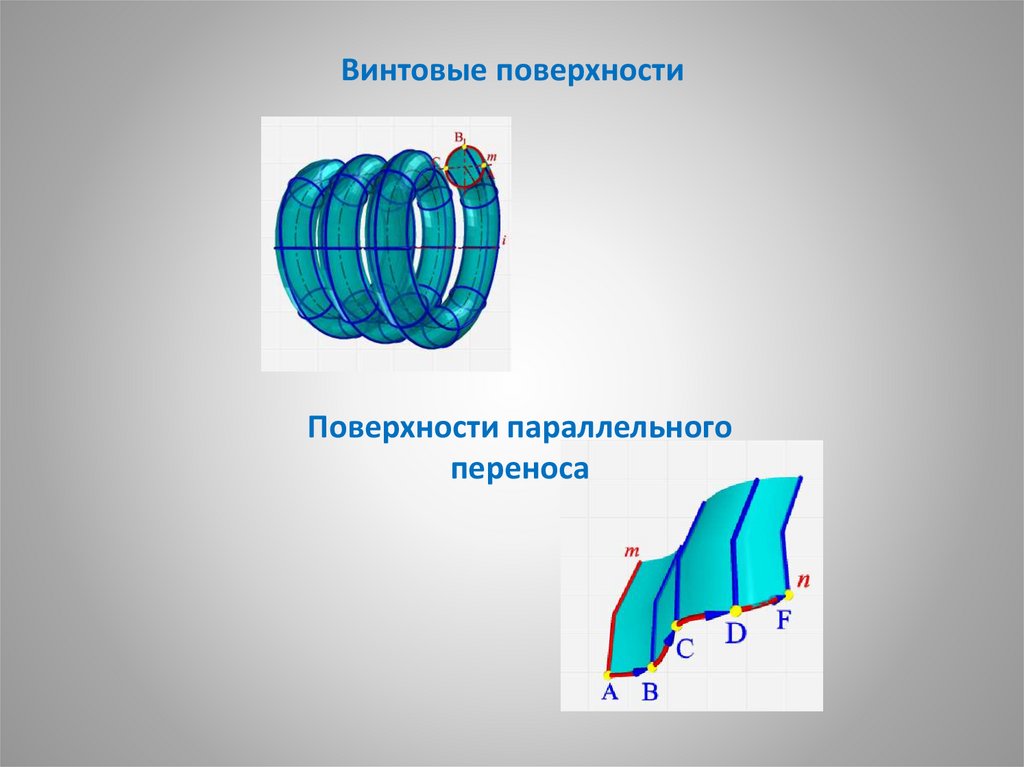
9. Винтовые поверхности

Поверхности параллельного
переноса

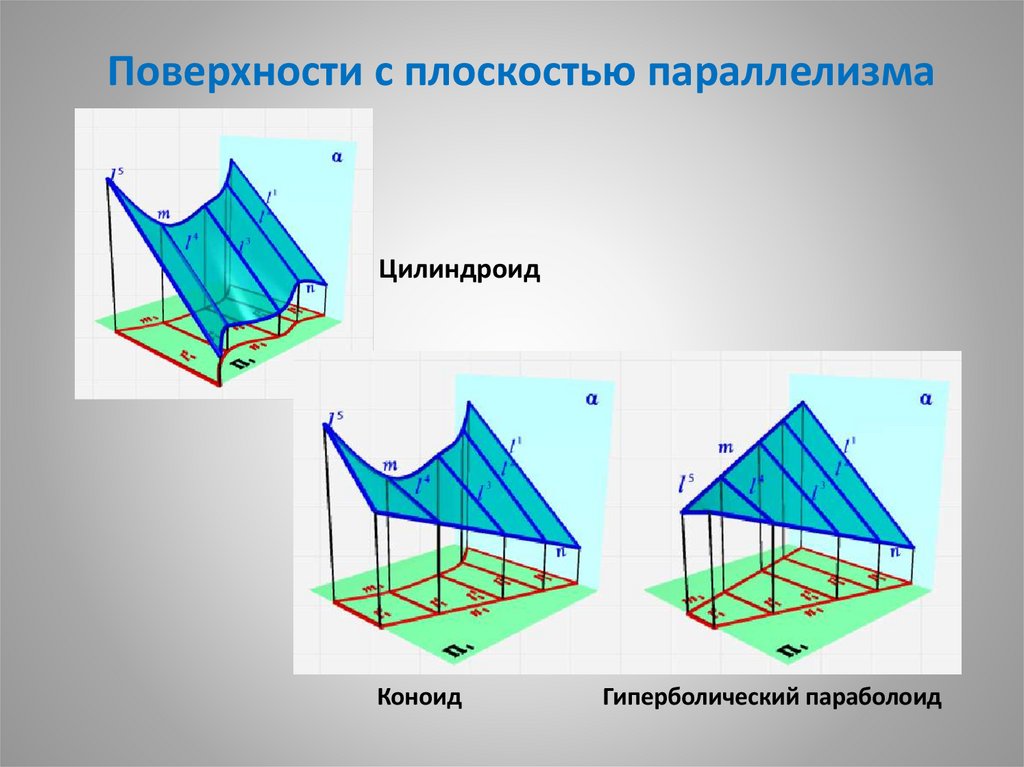
10. Поверхности с плоскостью параллелизма  

Поверхности с плоскостью параллелизма
Цилиндроид
Коноид
Гиперболический параболоид

11. Задачи позиционные

• Задачи на взаимную принадлежность
геометрических образов
• Задачи на взаимное пересечение
геометрических образов

12.

Точка и линия на поверхности
Точка принадлежит плоскости, если она принадлежит
прямой, лежащей в данной плоскости.
Точка принадлежит поверхности, если она принадлежит
линии, лежащей в данной поверхности.
Прямая принадлежит плоскости, если она имеет с ней две
общие точки
Линия принадлежит поверхности, если имеет с ней n-ное
количество общих точек.

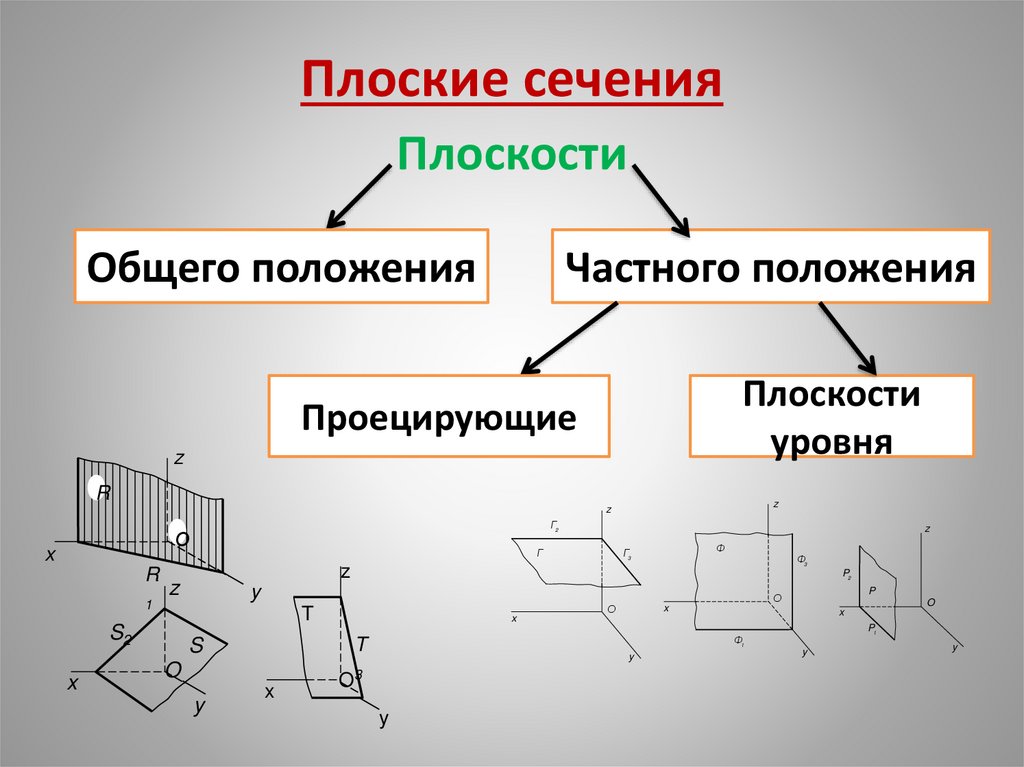
13. Плоские сечения

Плоскости
Общего положения
Частного положения
Плоскости
уровня
Проецирующие
z
R
z
z
Г2
О
x
R
Г
Ф3
P2
y
1
x
Г3
z
z
T
S2
z
Ф
O
x
x
y
O3
y
O
x
Ф1
T
S
y
x
P
О
О
P1
y
y

14.

Пересечение проецирующей поверхности
с проецирующей плоскостью

15.

Методические указания
• Плоскость, пересекающая поверхность, может занимать
общее и частное положение относительно плоскостей
проекций
• В общем случае вид сечения – кривая линия
• Сечение поверхности вращения плоскостью является
фигурой симметричной. Ось симметрии фигуры сечения
лежит в плоскости общей симметрии заданной
поверхности и плоскости, при условии:
- проходит через ось вращения поверхности;
- перпендикулярности секущей плоскости
• Сечением многогранной поверхности является ломаная
линия, вершины которой лежат на ребрах поверхности

16. Пересечение поверхности плоскостью

• При пересечении поверхности или какойлибо геометрической фигуры плоскостью
получается фигура, которая называется
сечением.
• Сечение поверхности плоскостью в общем
случае представляет собой кривую (или
прямую, если пересекаются плоскости),
принадлежащую секущей плоскости.

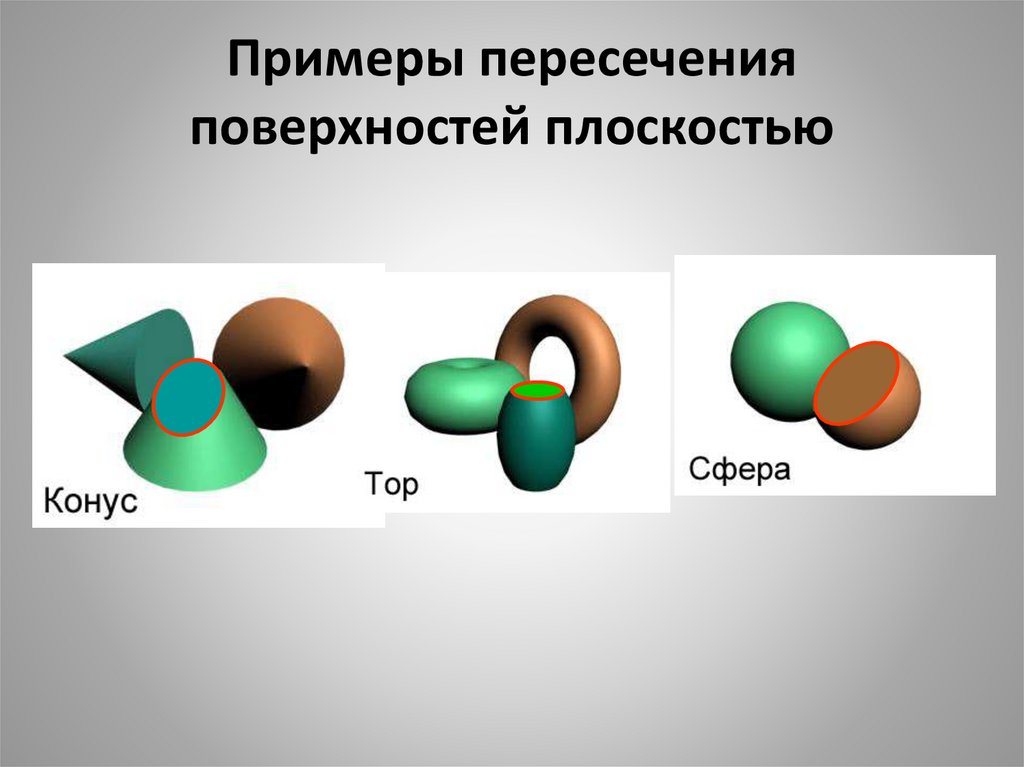
17. Примеры пересечения поверхностей плоскостью

18. Алгоритм определения линии сечения поверхности плоскостью

• Определение проекций линий сечения
следует выполнять по следующему
алгоритму:
• Определить опорные точки – точки
расположенные на очерковых
образующих поверхности (эти точки
определяют границы видимости проекции
кривой);

19.

• Экстремальные точки, удаленные на
минимальные и максимальные
расстояния от плоскостей проекций;
• Произвольные (промежуточные) точки
линии сечения
• В зависимости от положения плоскости по
отношению к плоскостям проекций,
сложность решения позиционной задачи,
по определению линии пересечения ее с
поверхностью существенно меняется.
Наиболее простым представляется
случай, когда плоскость проецирующая.

20. Пересечение многогранников плоскостью.

• При пересечении поверхности плоскостью получается
плоская фигура, которую называют сечением. Сечение
поверхности плоскостью - плоская кривая,
принадлежащая секущей плоскости.
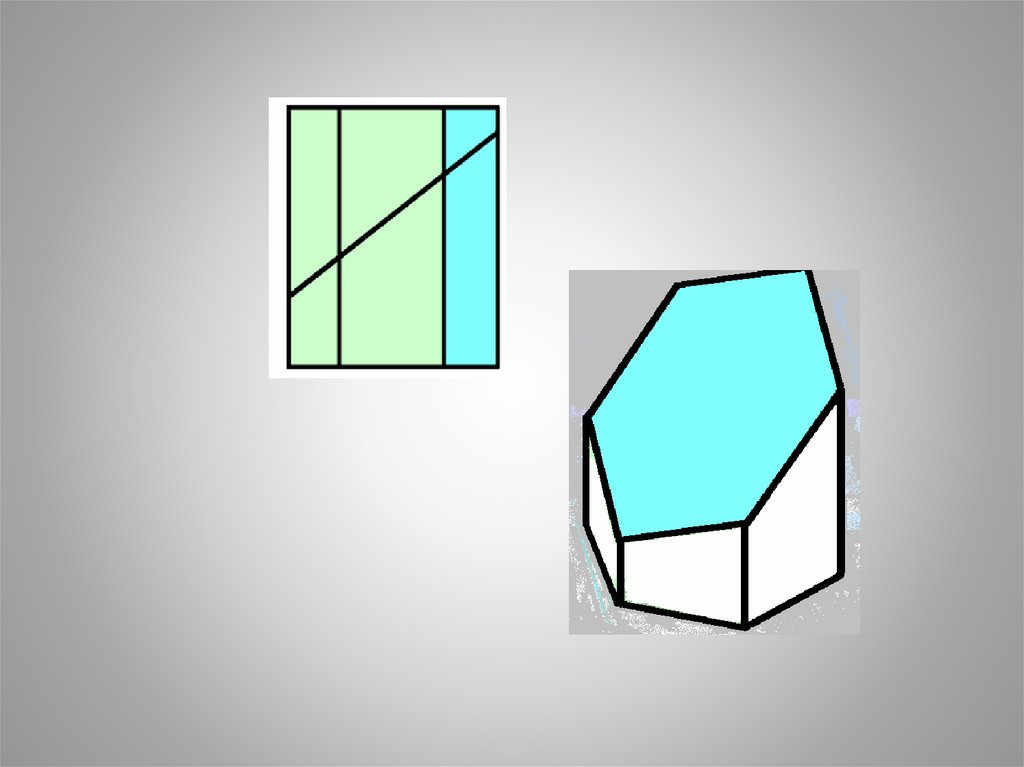
• При сечении многогранника плоскостью образуется
ломаная линия, при сечении кривой поверхности - кривая
линия.
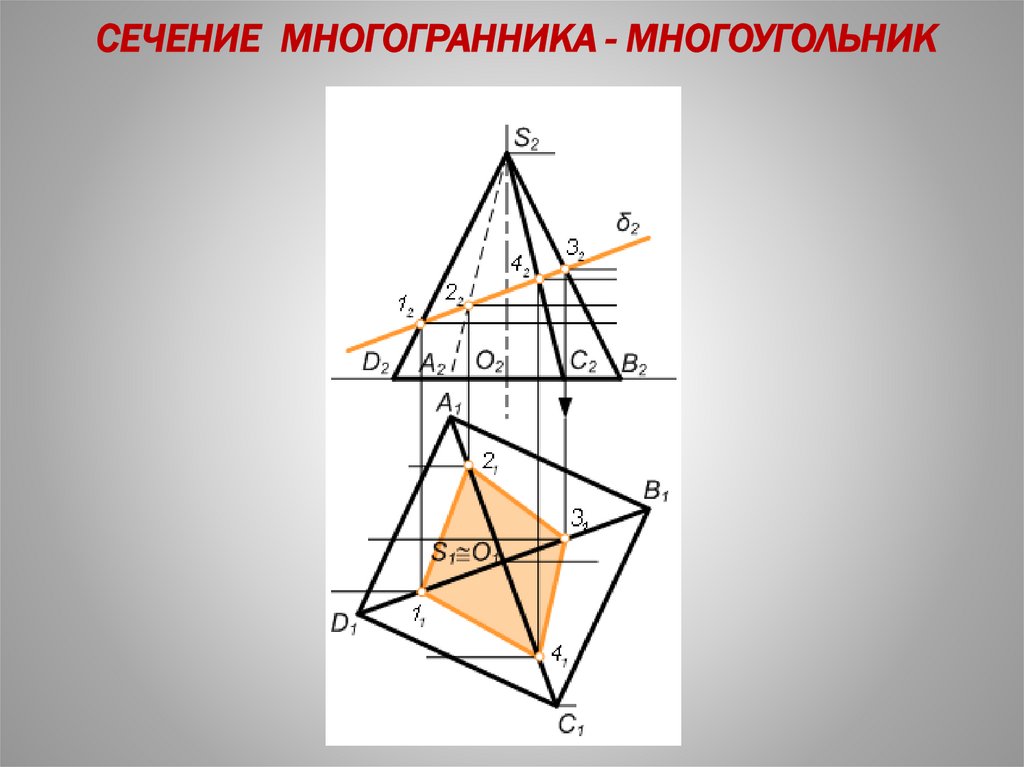
• Проекциями сечения многогранников, в общем случае
являются многоугольники, вершины которых принадлежат
ребрам, а стороны – граням многогранника.

21.

• Задача по определению сечения
многогранника сводится к многократному
решению задач:
• а) по определению точки встречи прямой
(ребер многогранника) с плоскостью; или
• б)по нахождению линии пересечения двух
плоскостей (грани многогранника и
секущей плоскости).

22.

• При решении задачи на пересечение
поверхности плоскостью необходимо
выполнить следующий анализ:
1.Определить какого положения плоскость и
поверхность относительно плоскостей
проекций.
• Если плоскость проецирующая, то на одной
из плоскостей проекций линия пересечения
уже имеется. Её нужно обозначить, а на
второй положение определить по
принадлежности.

23.

Прямой круговой цилиндр занимает
горизонтально проецирующее положение

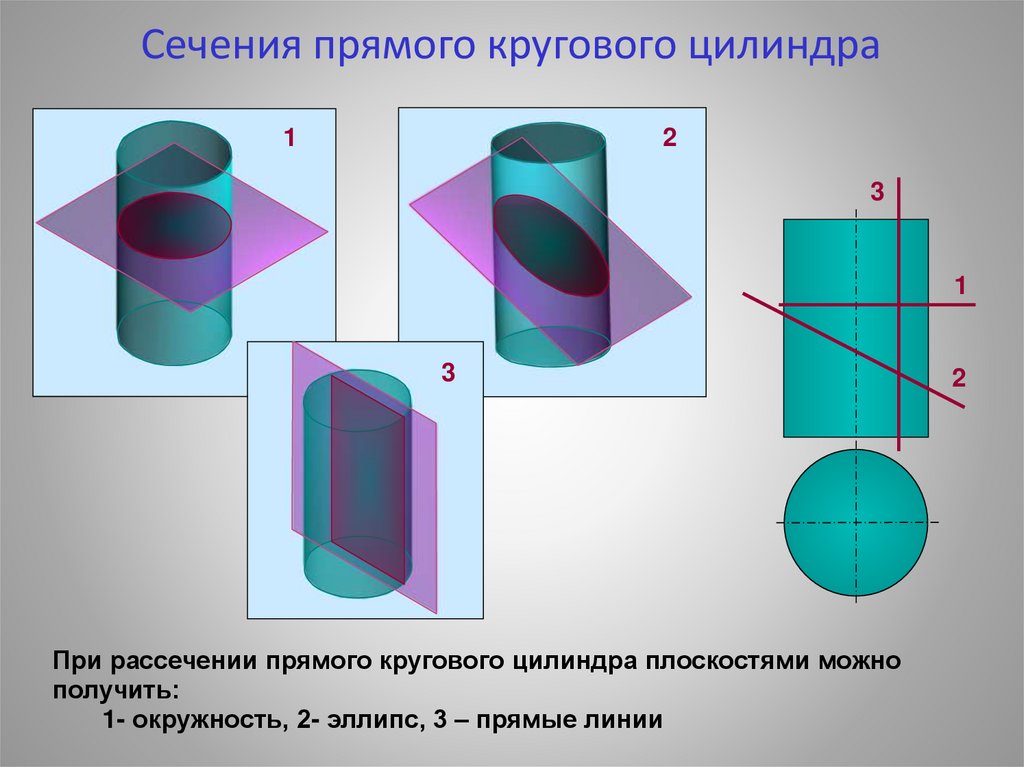
24.

Сечения прямого кругового цилиндра
1
2
3
1
3
При рассечении прямого кругового цилиндра плоскостями можно
получить:
1- окружность, 2- эллипс, 3 – прямые линии
2

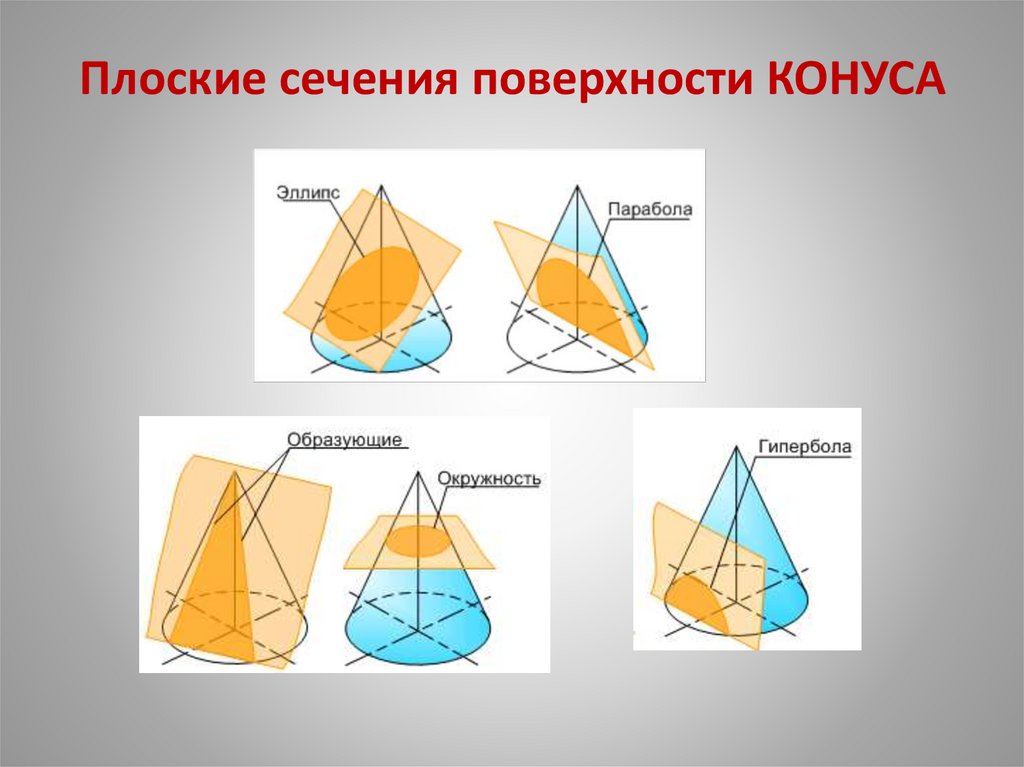
25. Плоские сечения поверхности КОНУСА

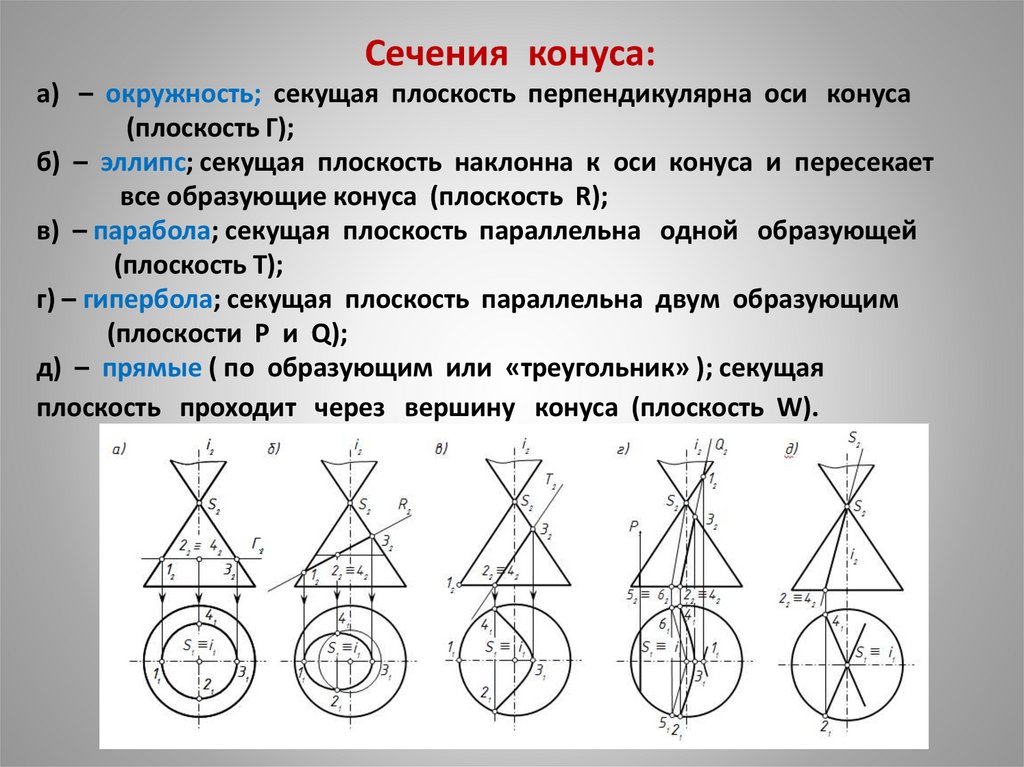
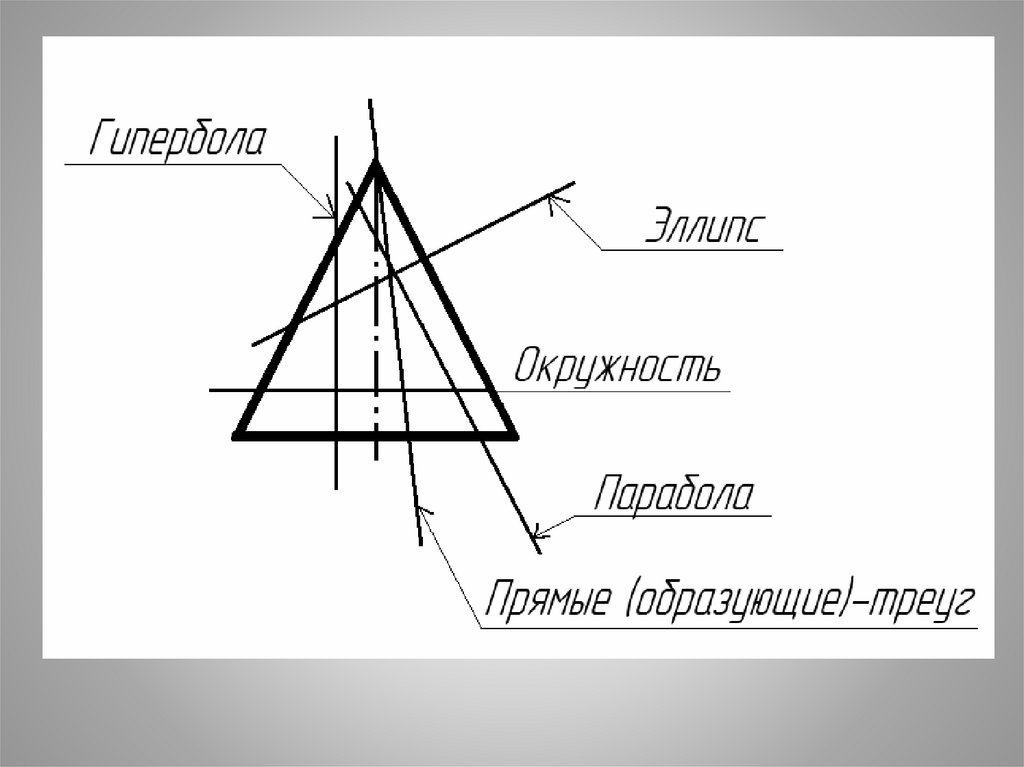
26. Сечения конуса: а) – окружность; секущая плоскость перпендикулярна оси конуса (плоскость Г); б) – эллипс; секущая плоскость

наклонна к оси конуса и пересекает
все образующие конуса (плоскость R);
в) – парабола; секущая плоскость параллельна одной образующей
(плоскость Т);
г) – гипербола; секущая плоскость параллельна двум образующим
(плоскости Р и Q);
д) – прямые ( по образующим или «треугольник» ); секущая
плоскость проходит через вершину конуса (плоскость W).

27.

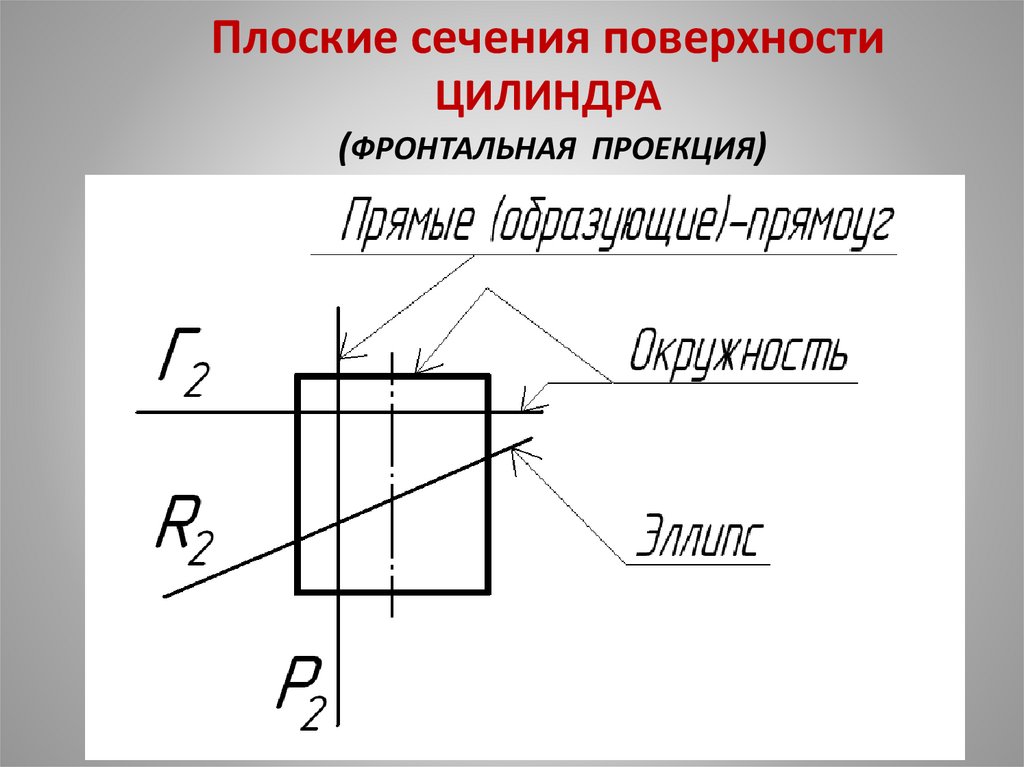
28. Плоские сечения поверхности ЦИЛИНДРА (ФРОНТАЛЬНАЯ ПРОЕКЦИЯ)

29.

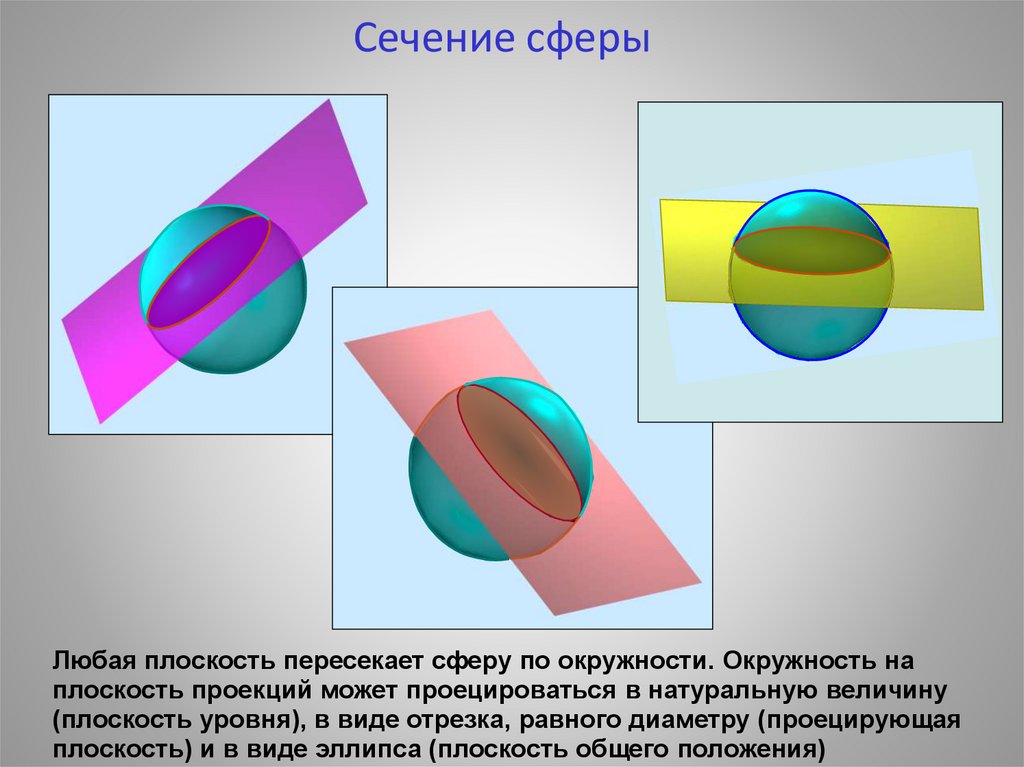
Сечение сферы
Любая плоскость пересекает сферу по окружности. Окружность на
плоскость проекций может проецироваться в натуральную величину
(плоскость уровня), в виде отрезка, равного диаметру (проецирующая
плоскость) и в виде эллипса (плоскость общего положения)

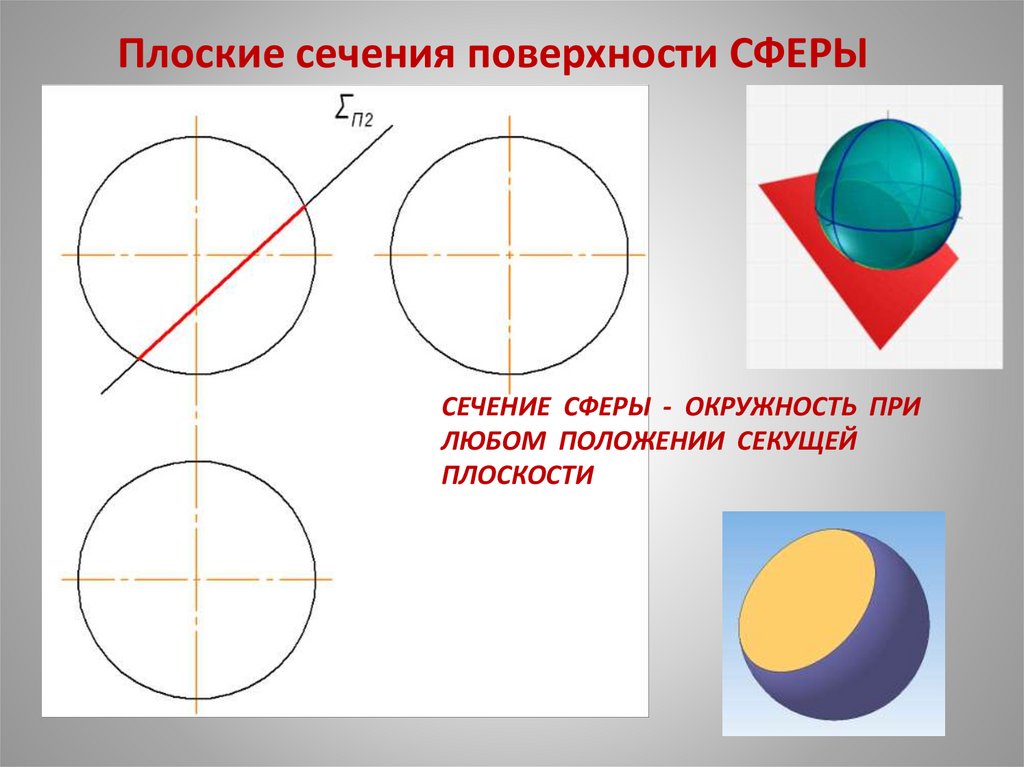
30. СЕЧЕНИЕ СФЕРЫ - ОКРУЖНОСТЬ ПРИ ЛЮБОМ ПОЛОЖЕНИИ СЕКУЩЕЙ ПЛОСКОСТИ

Плоские сечения поверхности СФЕРЫ
СЕЧЕНИЕ СФЕРЫ - ОКРУЖНОСТЬ ПРИ
ЛЮБОМ ПОЛОЖЕНИИ СЕКУЩЕЙ
ПЛОСКОСТИ

31. СЕЧЕНИЕ МНОГОГРАННИКА - МНОГОУГОЛЬНИК