ya_rgrrrr_ti_mne

1.

Применение интегрального исчисления векторных
полей в фотонике и оптоинформатике
Расчётно-графическая работа №2
Работу выполнил Срывкин Никита Александрович | ИСУ 467577 | Группа V3203

2.

Введение: Мост между математикой и оптикой
Настоящая работа посвящена применению методов интегрального исчисления векторных полей для решения актуальных задач фотоники и оптоинформатики. Мы будем исследовать
распространение света, потоки излучения и электростатические поля, используя математический анализ для получения физически значимых результатов.
Основной целью является демонстрация того, как теоремы Стокса и Остроградского–Гаусса, а также криволинейные и поверхностные интегралы, позволяют рассчитывать ключевые физические
величины.
Мы сфокусируемся на таких понятиях, как фазовый набег, мощность излучения, циркуляция поля и разность потенциалов. Все расчеты будут выполняться для конкретного варианта, параметры
которого задаются индивидуально.
Определение параметров варианта
Для каждого студента параметры задачи определяются уникальным номером ИСУ. На основе этих цифр вычисляются вспомогательные величины, которые задают конкретную конфигурацию
оптической системы.
1
2
Геометрические размеры
Коэффициенты полей
Радиусы траектории, линзы, контура и размер детектора.
Константы, входящие в выражения для векторных полей и вектора Пойнтинга.
Определение параметров варианта
Эти параметры определяют все — от численных значений интегралов до физической интерпретации результатов в контексте конкретной оптической конфигурации, будь то спиральная траектория
луча, сферическая линза или кулоновское поле.

3.

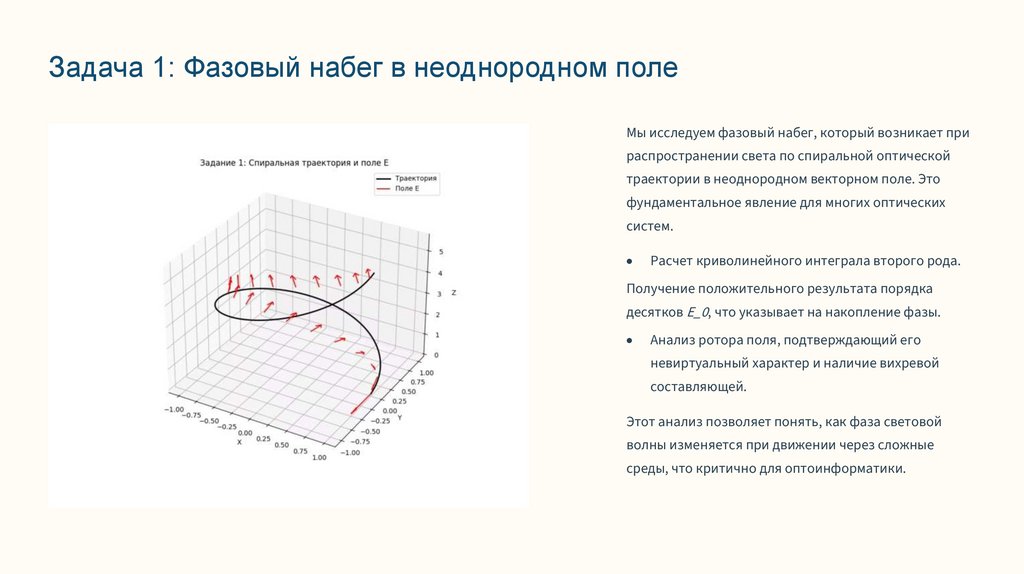
Задача 1: Фазовый набег в неоднородном поле
Мы исследуем фазовый набег, который возникает при
распространении света по спиральной оптической
траектории в неоднородном векторном поле. Это
фундаментальное явление для многих оптических
систем.
Расчет криволинейного интеграла второго рода.
Получение положительного результата порядка
десятков E_0, что указывает на накопление фазы.
Анализ ротора поля, подтверждающий его
невиртуальный характер и наличие вихревой
составляющей.
Этот анализ позволяет понять, как фаза световой
волны изменяется при движении через сложные
среды, что критично для оптоинформатики.

4.

Задача 2: Поток излучения через линзу
В этой задаче мы рассчитываем поток излучения через полусферическую линзу при условии однородного вектора Пойнтинга.
1
Теорема Остроградского–
Гаусса
2
Нормальная компонента
3
Независимость от наклона
Поток определяется исключительно
Наклон поля не влияет на интегральную
Применяется для демонстрации
нормальной компонентой вектора
мощность излучения.
равенства полного потока через линзу и
Пойнтинга.
потока через её основание.
Это демонстрирует, как теорема Гаусса упрощает расчет мощности излучения в оптических системах.
Задача 3: Вихревое электрическое поле
Используя теорему Стокса, находим ненулевую циркуляцию по круговому контуру. Это интерпретируется как наличие орбитального углового
момента у светового пучка — ключевого свойства для оптических манипуляций.
Задача 4: Разность потенциалов точечного заряда
По формуле потенциала вычисляется разность потенциалов между двумя точками. Подчеркивается путевая независимость результата в
потенциальном поле, что является фундаментальным принципом электростатики.

5.

Задача 5: Моделирование кулоновского поля
Рассчитывается мощность на плоском
квадратном детекторе. Показано, что на
величину сигнала влияет только
нормальная к детектору компонента
потока, а при нулевой дивергенции
поток через различные сечения остается
постоянным.

6.

Заключение
Таким образом, методы векторного анализа предоставляют последовательный и мощный инструмент для описания сложных явлений в фотонике и
оптоинформатике.
Описание фазовых эффектов
Точное моделирование изменения фазы световых волн.
Анализ распределения мощности
Количественная оценка энергии, переносимой излучением.
Свойства вихревых и потенциальных полей
Понимание фундаментальной природы оптических и электростатических полей.
Мы продемонстрировали тесную связь между абстрактными математическими теоремами (Стокса, Остроградского–Гаусса) и физическими законами
сохранения. Выбор геометрии и параметров поля напрямую влияет на измеряемые величины, что делает эти методы незаменимыми для инженеров и
ученых в области фотоники и оптоинформатики.