11 геометрия 8

1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ

11 класс

2. Взаимное расположение прямых и плоскостей в пространстве

Две прямые
Две плоскости
Прямая и плоскость

3.

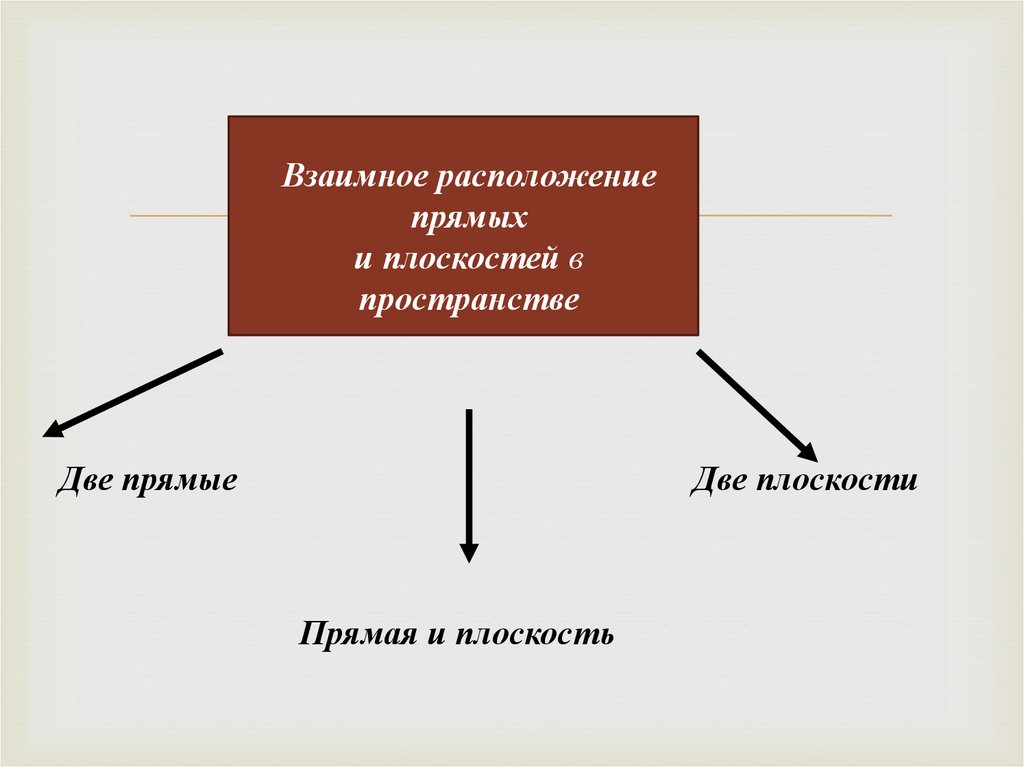
Взаимное расположение прямых в
пространстве
Имеют общую точку
лежат в одной плоскости
пересекаются
а
А
в
Не имеют общую точку
лежат в одной плоскости
параллельны
не имеют общую точку
а вв одной плоскости
не лежат
скрещиваются
в
а
в
а в А
а || b
m –― n
а

4. 1. Параллельные прямые

2. Пересекающиеся прямые
3. Скрещивающиеся прямые

5.

K
B1
C1
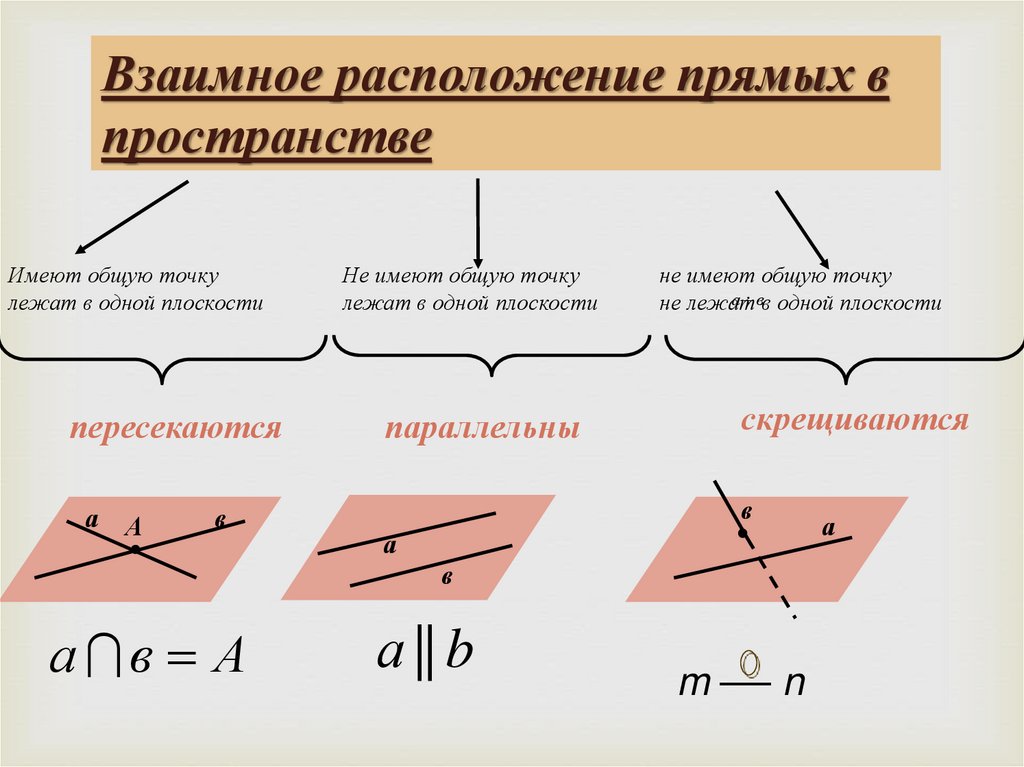
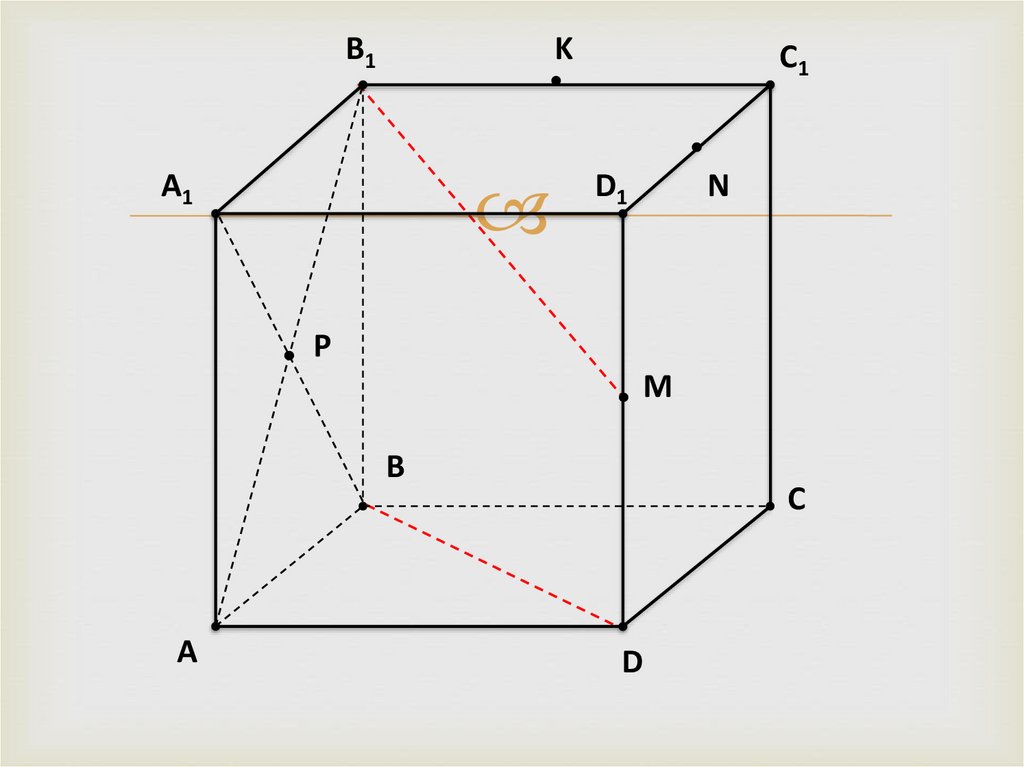
Дано:
A1
ABCDA1B1C1D1 – КУБ.
D1
N
K, M, N – СЕРЕДИНЫ РЕБЕР
P
M
B1C1, D1D, D1C1 СООТВЕТСТВЕННО,
B
C
P – ТОЧКА ПЕРЕСЕЧЕНИЯ ДИАГОНАЛЕЙ
ГРАНИ AA1B1B.
A взаимное расположение прямых.
Определите
D

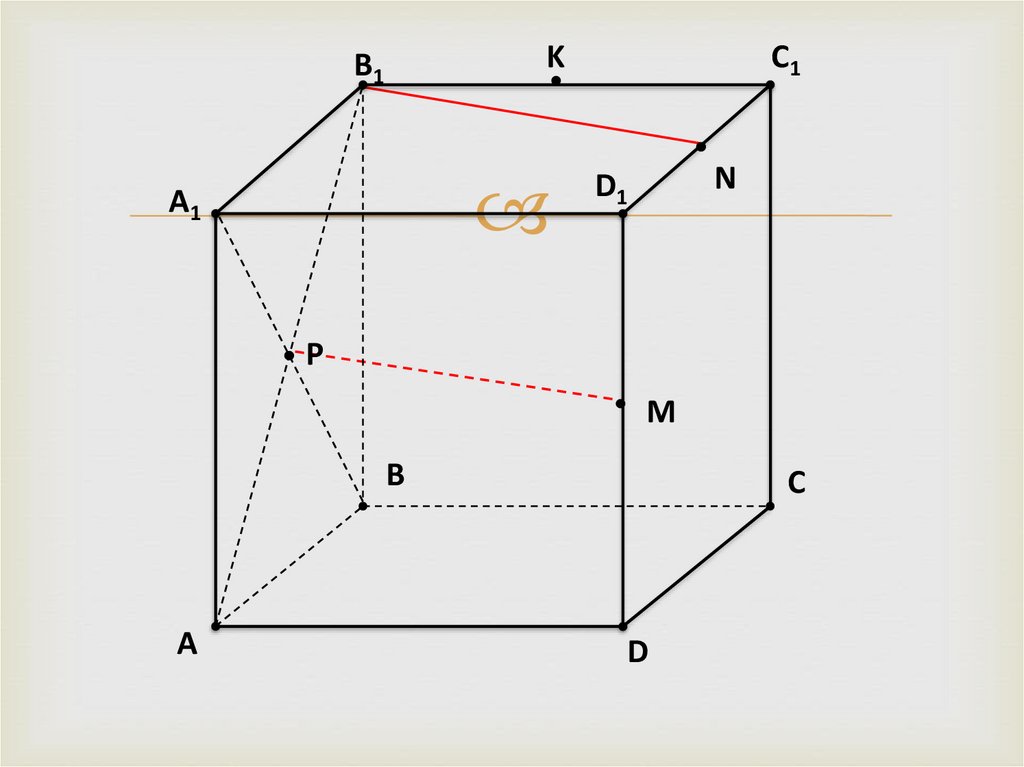
6.

B1
K
A1
C1
D1
N
P
M
B
A
C
D

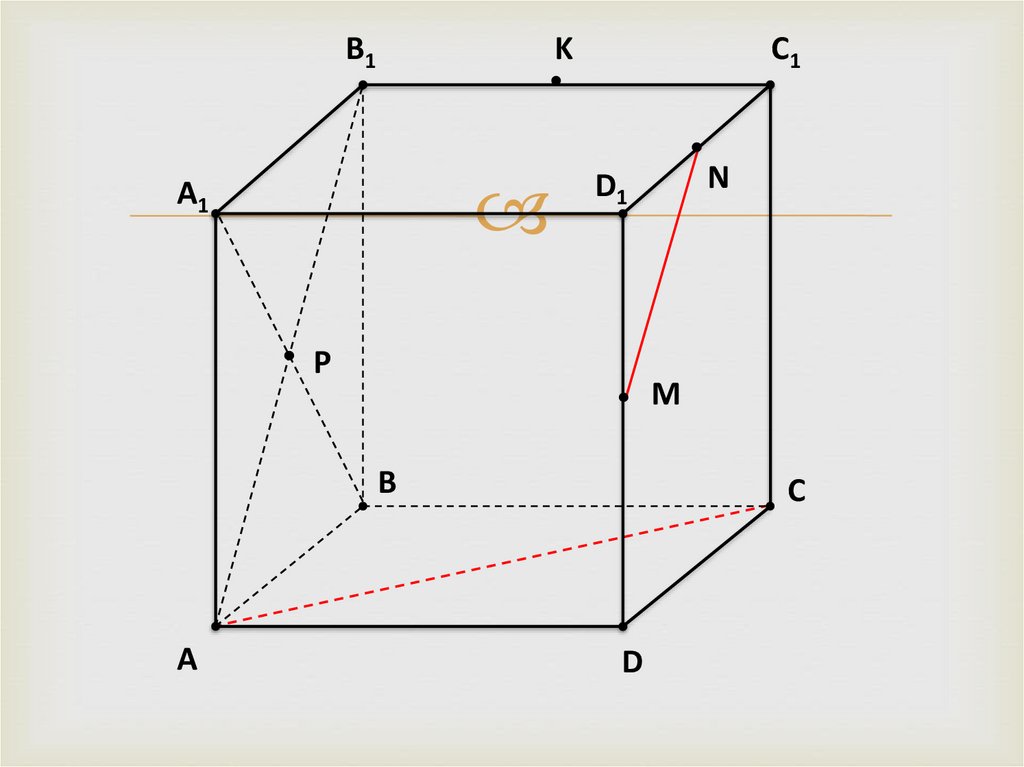
7.

K
B1
A1
C1
N
D1
P
M
B
A
C
D

8.

B1
K
A1
C1
P
M
B
A
N
D1
C
D

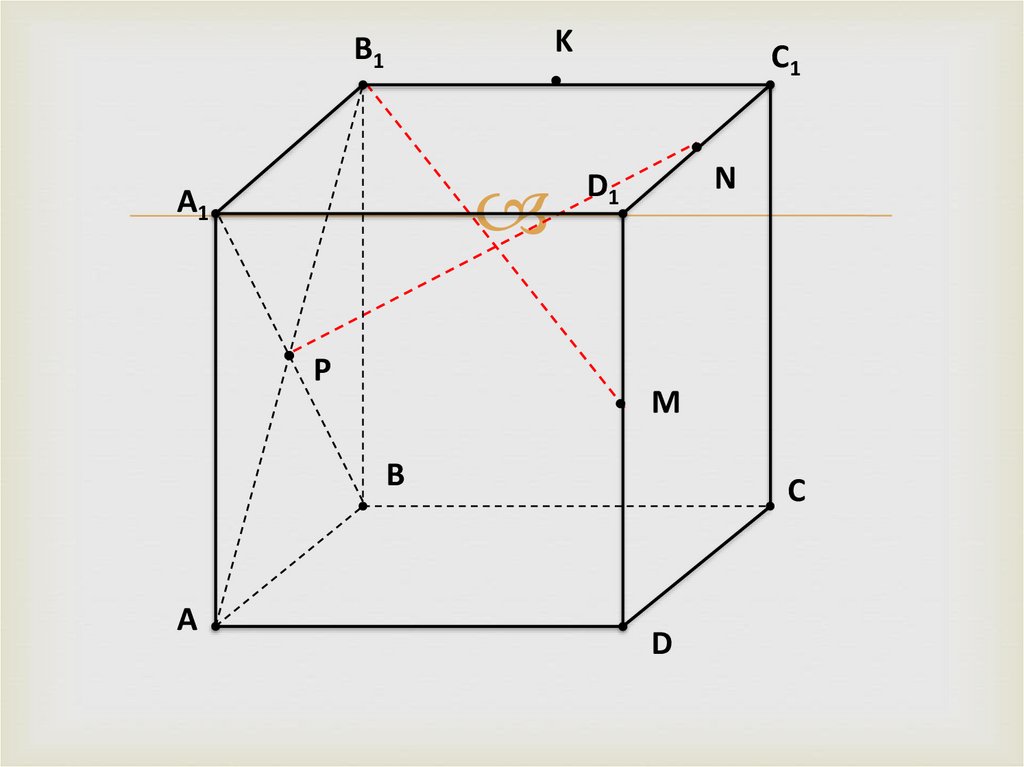
9.

K
B1
A1
P
C1
N
D1
M
B
A
C
D

10. Проверь себя

1. Пересекаются
2. Параллельны
3. Скрещиваются
4. Пересекаются

11.

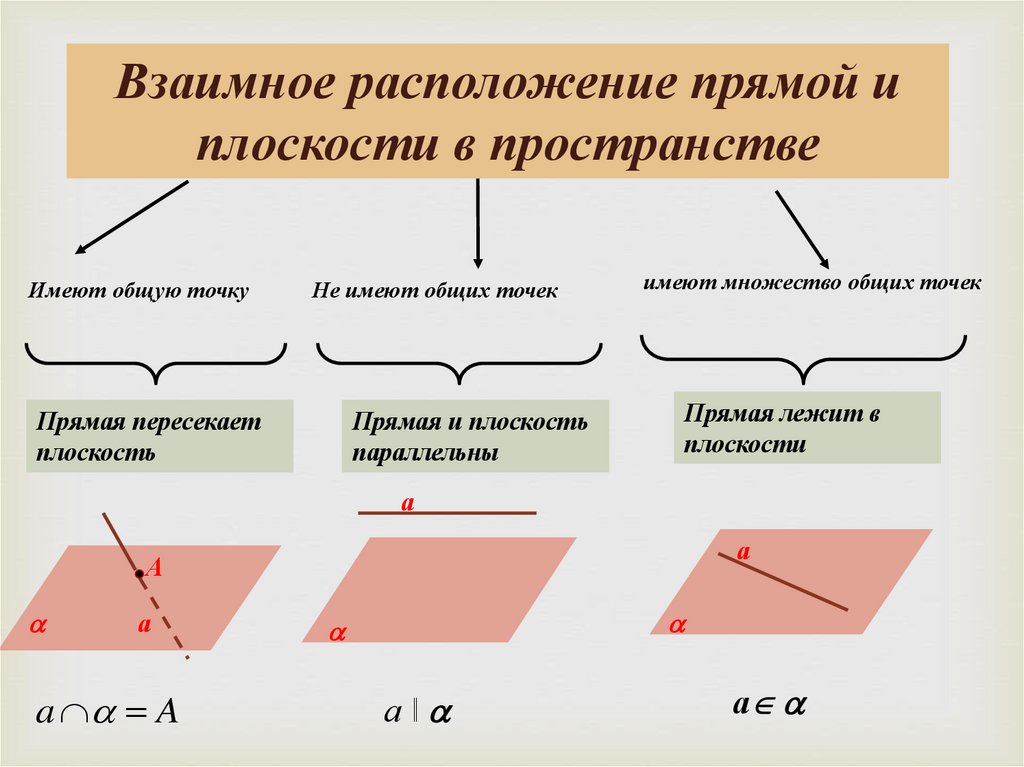
Взаимное расположение прямой и
плоскости в пространстве
Имеют общую точку
Не имеют общих точек
Прямая пересекает
плоскость
имеют множество общих точек
Прямая лежит в
плоскости
Прямая и плоскость
параллельны
а
а
А
а
a A
а‖
а

12. 1. Параллельность плоскости и прямой

2. Пересечение плоскости и прямой
3. Перпендикулярность плоскости и прямой

13.

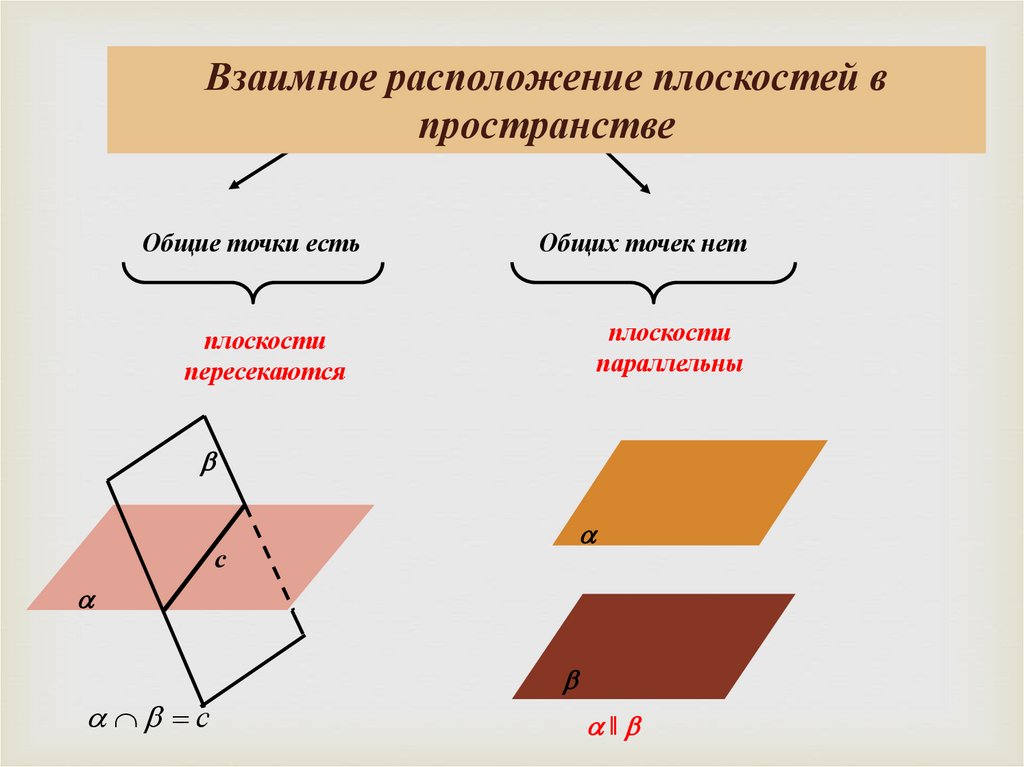
Взаимное расположение плоскостей в
пространстве
Общие точки есть
Общих точек нет
плоскости
пересекаются
плоскости
параллельны
с
с
‖

14.

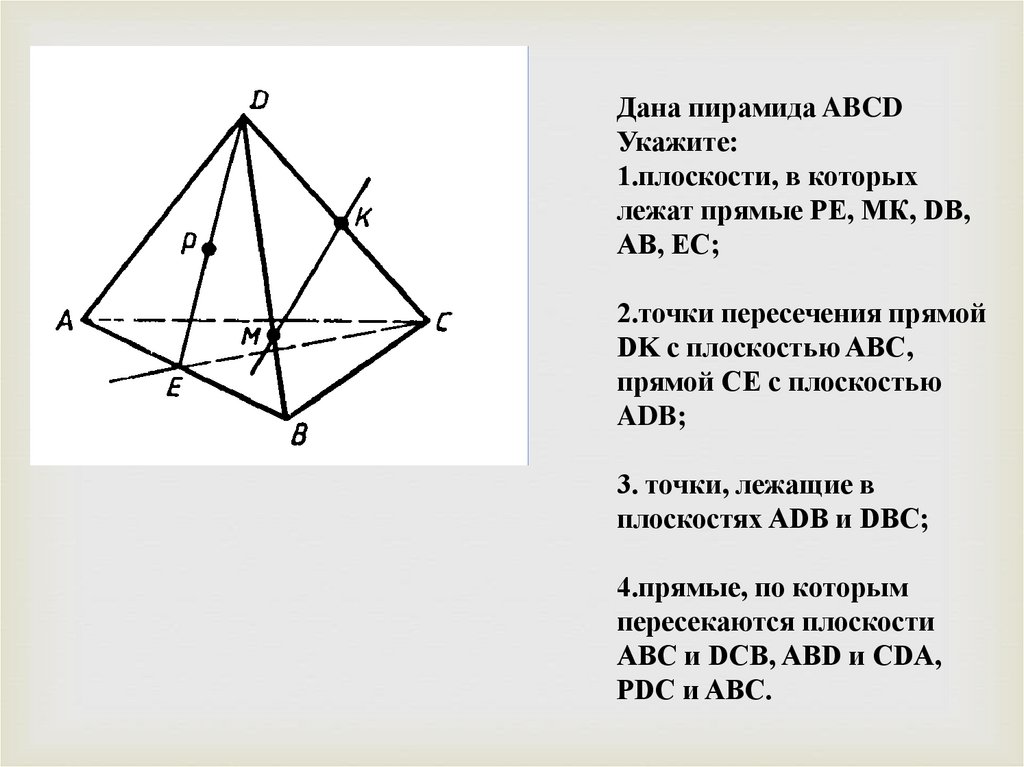
Дана пирамида ABCD
Укажите:
1.плоскости, в которых
лежат прямые РЕ, МК, DB,
АВ, ЕС;
2.точки пересечения прямой
DK с плоскостью ABC,
прямой СЕ с плоскостью
ADB;
3. точки, лежащие в
плоскостях ADB и DBC;
4.прямые, по которым
пересекаются плоскости
ABC и DCB, ABD и CDA,
PDC и ABC.

15.

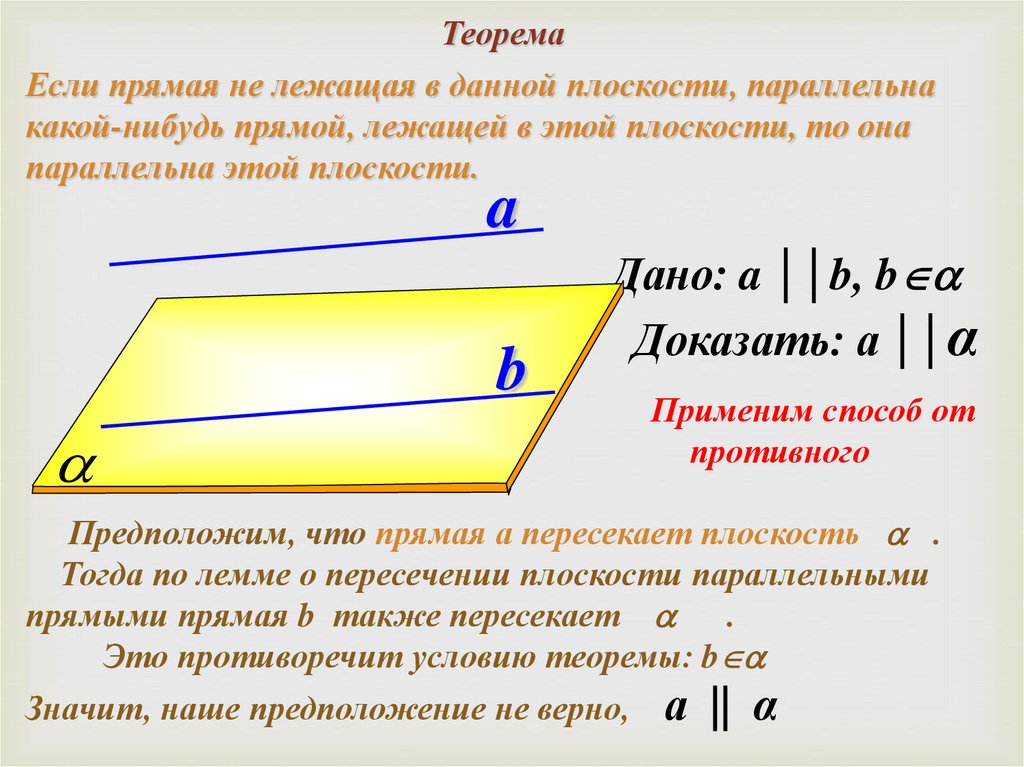
Теорема
Если прямая не лежащая в данной плоскости, параллельна
какой-нибудь прямой, лежащей в этой плоскости, то она
параллельна этой плоскости.
a
b
Дано: a ││b, b
Доказать: a ││α
Применим способ от
противного
Предположим, что прямая а пересекает плоскость .
Тогда по лемме о пересечении плоскости параллельными
прямыми прямая b также пересекает .
Это противоречит условию теоремы: b
Значит, наше предположение не верно,
а || α

16.

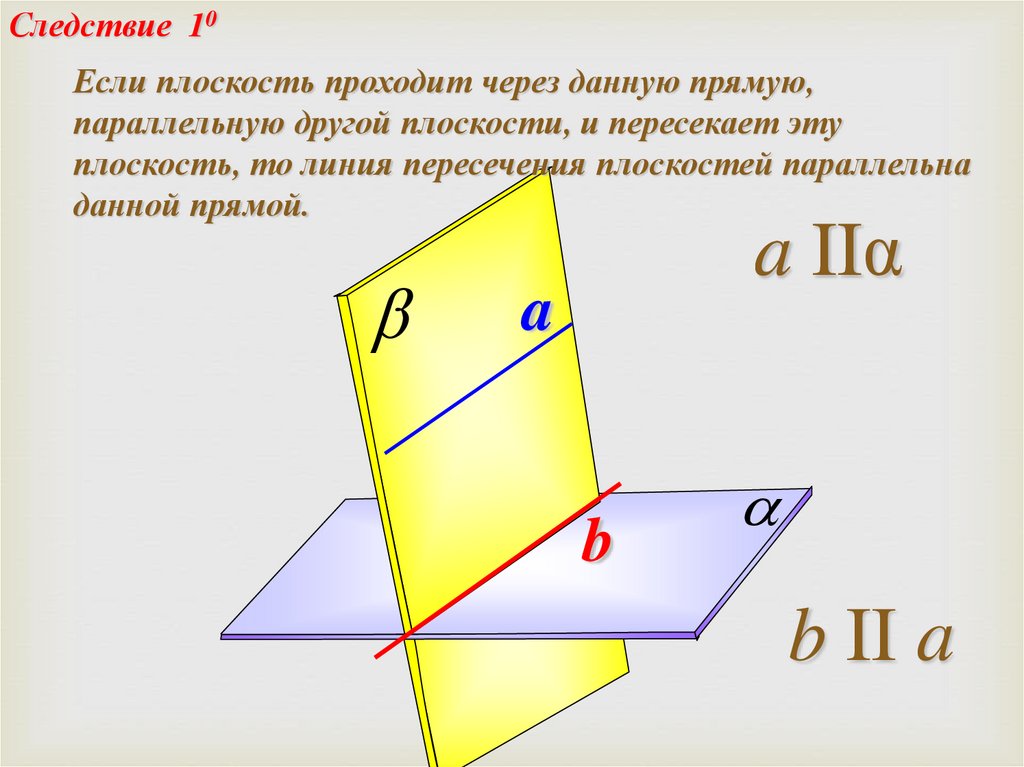
Следствие 10
Если плоскость проходит через данную прямую,
параллельную другой плоскости, и пересекает эту
плоскость, то линия пересечения плоскостей параллельна
данной прямой.
a IIα
II
a
b
b II a

17.

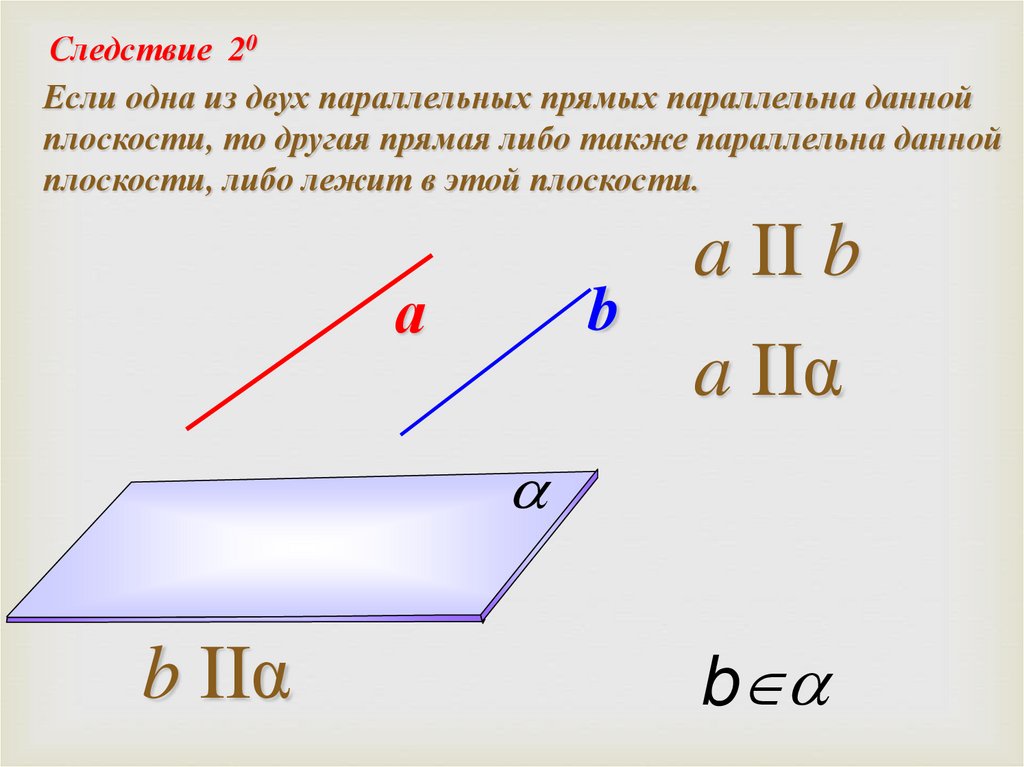
Следствие 20
Если одна из двух параллельных прямых параллельна данной
плоскости, то другая прямая либо также параллельна данной
плоскости, либо лежит в этой плоскости.
а
b
a II b
a IIα
b IIα
b

18.

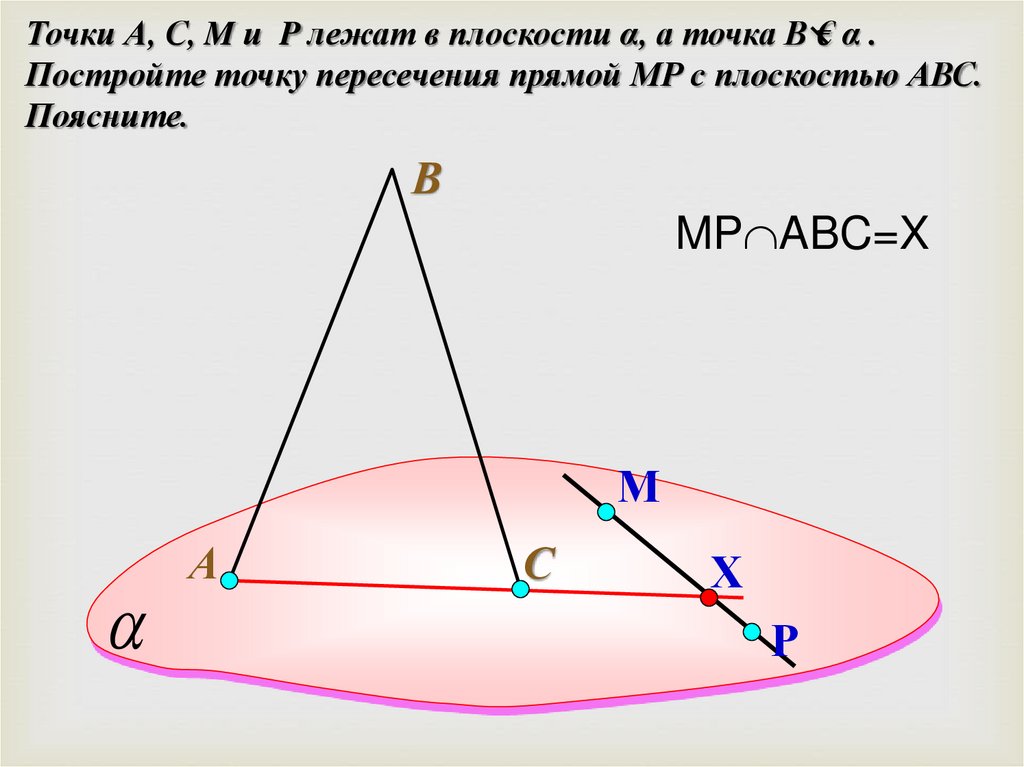
Точки А, С, M и P лежат в плоскости α, а точка В € α .
Постройте точку пересечения прямой МР с плоскостью АВС.
Поясните.
В
MP ABC=X
М
А
С
Х
Р

19. Практикум

Через концы отрезка AB, принадлежащего
плоскости α, и точку C – середину этого отрезка –
проведены параллельные прямые, пересекающие
плоскость β в
точках A1, B1 и C1 соответственно. AA1 = 8см, CC1 =
10см. Найди длину отрезка BB1.

20. Практикум

21. Практикум

В кубе ABCDA1B1C1D1 найди угол между
прямыми A1B и B1C.

22. Практикум

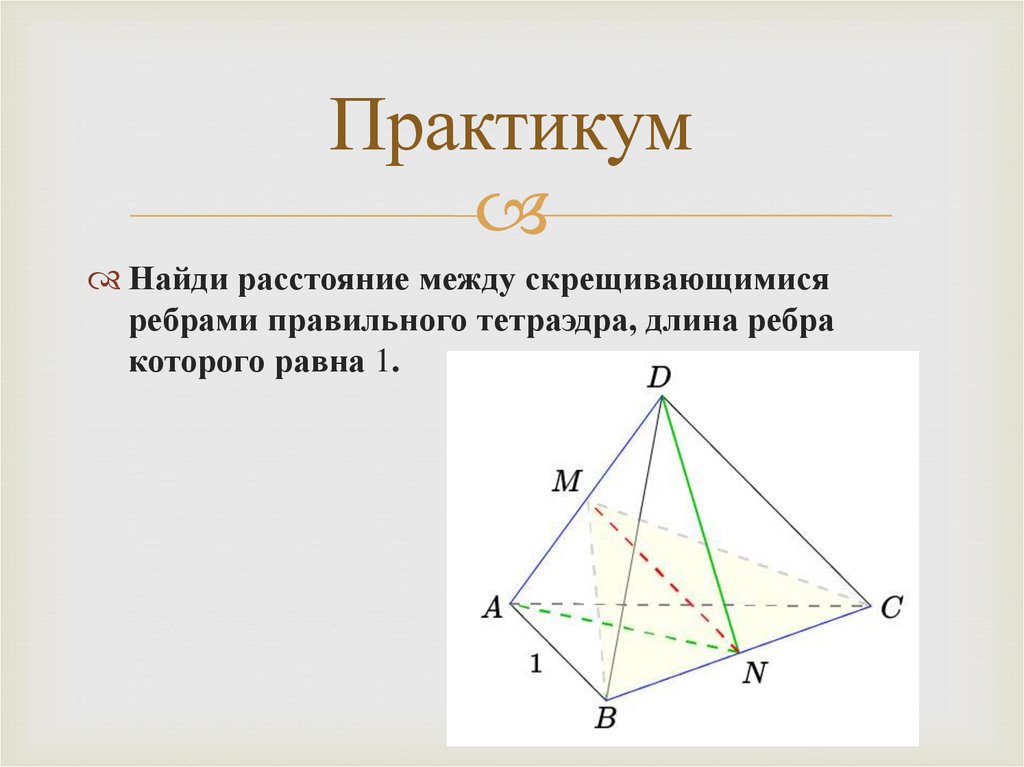
Найди расстояние между скрещивающимися
ребрами правильного тетраэдра, длина ребра
которого равна 1.

23. Практикум