8.07M

Category:

programming

АиСД_Лекция 3

1.

Алгоритмы и структуры данных
Преподаватель:
Ряскова Елена Борисовна
Кафедра АПУ СПбГЭТУ «ЛЭТИ»
1

Дерево
Дерево – конечное множество Т, состоящее из одного или более узлов,
таких, что:
имеется один специально обозначенный узел, называемый корнем данного
дерева;
остальные узлы (исключая корень) содержатся в m 0 попарно не
пересекающихся множествах Т1, Т2, ..., Тm, каждое из которых, в свою
очередь, является деревом. Деревья Т1, Т2, ..., Тm называются
поддеревьями данного дерева.
a
b
i
c
j
h
d
e
f
g
k
АиСД
3

4.

Виды вершин дерева
Корень
А
B
D
Узлы
E
C
F
H
G
Листья
АиСД
4

5.

Упорядоченное дерево. Лес
Если в определении дерева существен порядок перечисления поддеревьев
Т1, Т2, ..., Тm, то дерево называют упорядоченным и говорят о
«первом» (Т1), «втором» (Т2) и т. д. поддеревьях данного корня (старший брат и
т.п.).
В терминологии теории графов это «конечное ориентированное (корневое)
упорядоченное дерево».
Лес – это множество (обычно упорядоченное), состоящее из некоторого (быть
может, равного нулю) числа непересекающихся деревьев.
Тогда, следуя пункту 2 определения дерева: узлы дерева, за исключением
корня, образуют лес.
Дерево T = (корень, лес поддеревьев)
АиСД
5

6.

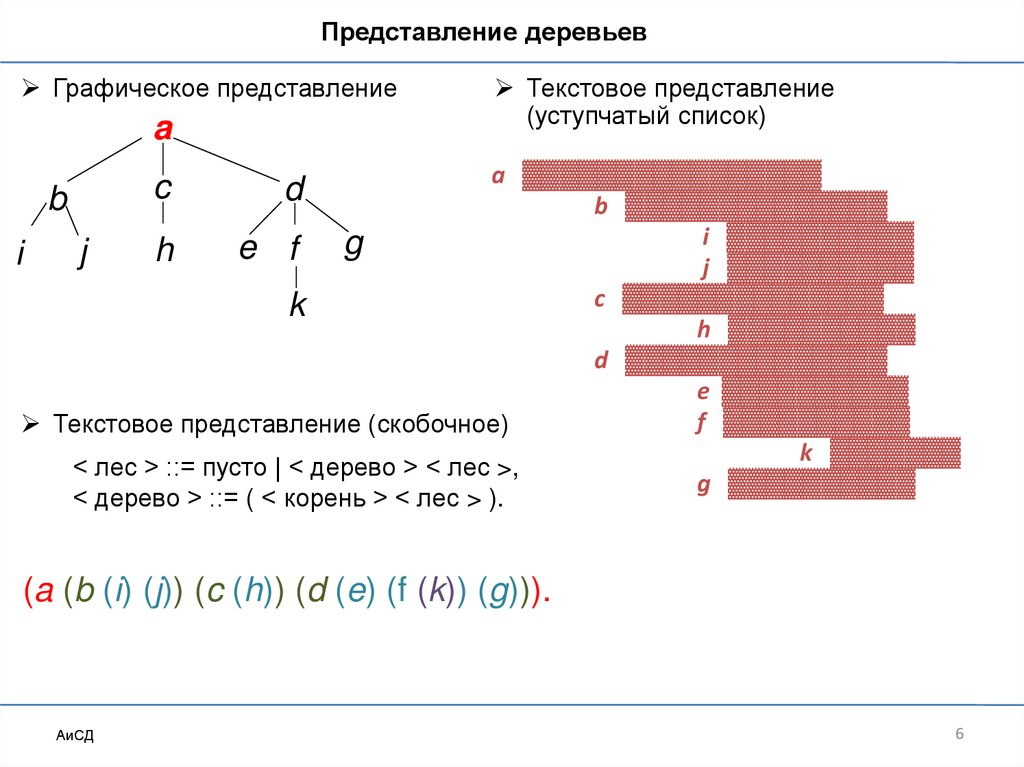
Представление деревьев
Графическое представление
a
Текстовое представление
(уступчатый список)
a ▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
b
b ▓▓▓▓▓▓▓▓▓▓▓▓▓▓
i ▓▓▓▓▓▓▓▓▓▓
e f g
h
j
i
j ▓▓▓▓▓▓▓▓▓▓
c ▓▓▓▓▓▓▓▓▓▓▓▓▓▓
k
h ▓▓▓▓▓▓▓▓▓▓
d ▓▓▓▓▓▓▓▓▓▓▓▓▓▓
e ▓▓▓▓▓▓▓▓▓▓
f ▓▓▓▓▓▓▓▓▓▓
Текстовое представление (скобочное)
k ▓▓▓▓▓▓▓
< лес > ::= пусто | < дерево > < лес >,
g ▓▓▓▓▓▓▓▓▓▓
< дерево > ::= ( < корень > < лес > ).
c
d
(a (b (i) (j)) (c (h)) (d (e) (f (k)) (g))).
АиСД
6

7.

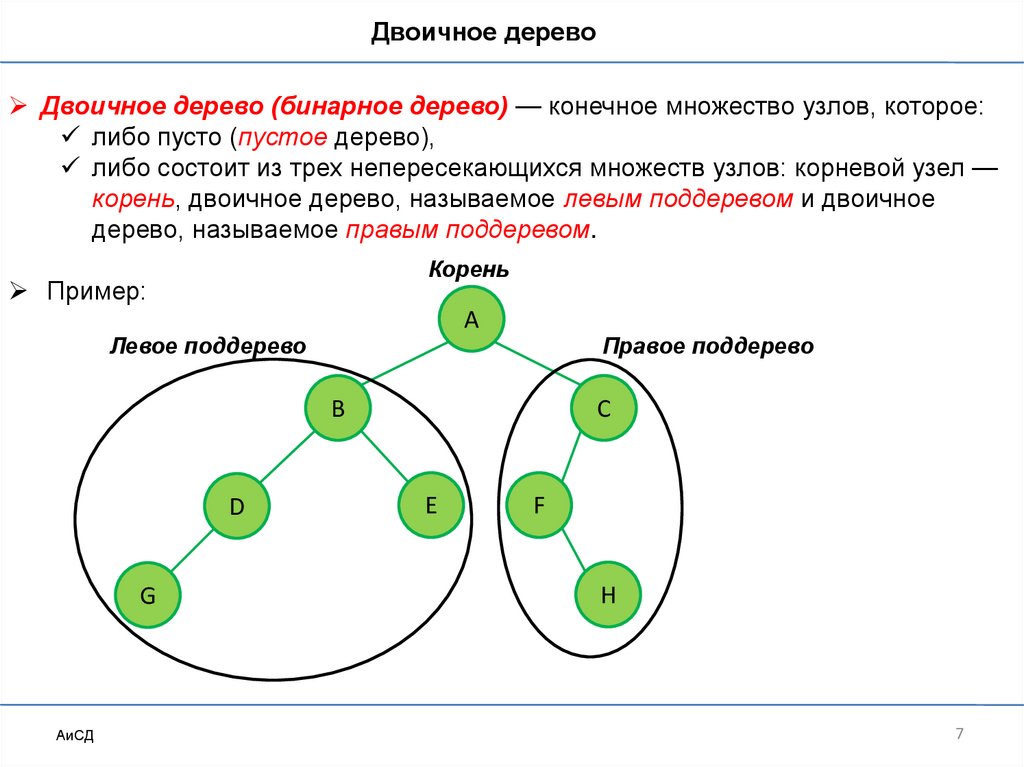
Двоичное дерево
Двоичное дерево (бинарное дерево) — конечное множество узлов, которое:
либо пусто (пустое дерево),
либо состоит из трех непересекающихся множеств узлов: корневой узел —
корень, двоичное дерево, называемое левым поддеревом и двоичное
дерево, называемое правым поддеревом.
Корень
Пример:
А
Левое поддерево
Правое поддерево
B
D
G
АиСД
C
E
F
H
7

8.

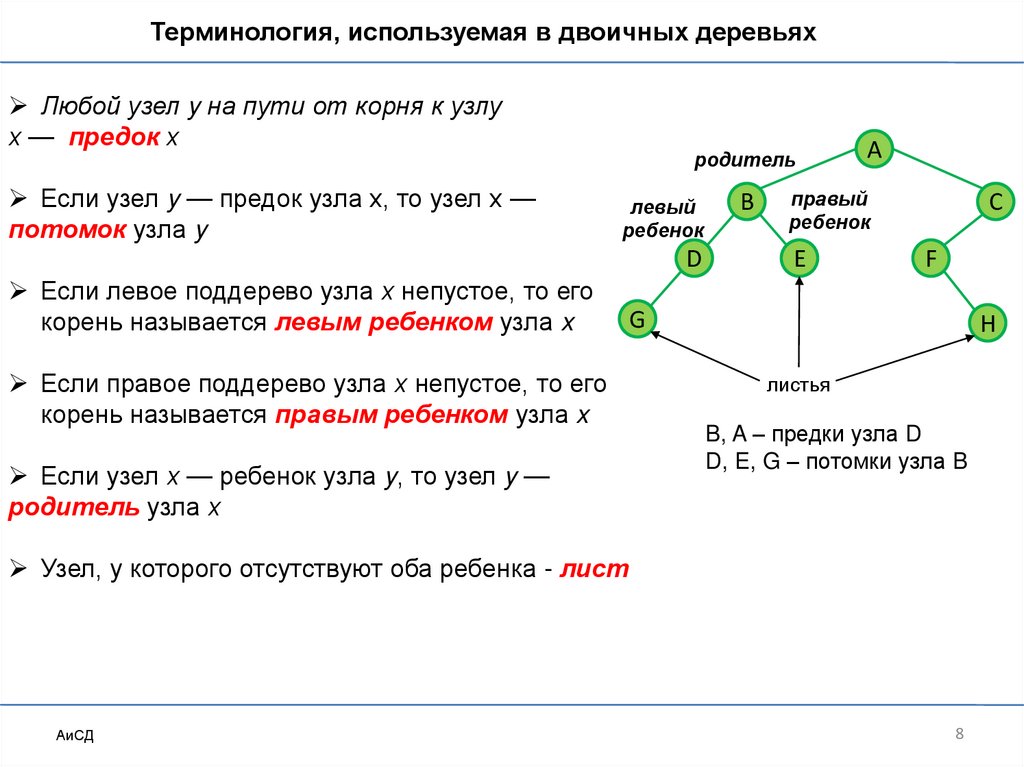
Терминология, используемая в двоичных деревьях
Любой узел y на пути от корня к узлу
х — предок х
Если узел y — предок узла х, то узел х —
потомок узла y
родитель
левый
ребенок
D
Если левое поддерево узла х непустое, то его
корень называется левым ребенком узла x
Если правое поддерево узла х непустое, то его
корень называется правым ребенком узла x
Если узел х — ребенок узла y, то узел y —
родитель узла х
B
А
правый
ребенок
E
C
F
G
H
листья
B, A – предки узла D
D, E, G – потомки узла B
Узел, у которого отсутствуют оба ребенка - лист
АиСД
8

9.

Терминология, используемая в двоичных деревьях
глубина = 0
А
B
C
глубина = 1
высота= 3
D
E
G
глубина = 2
F
H
глубина = 3
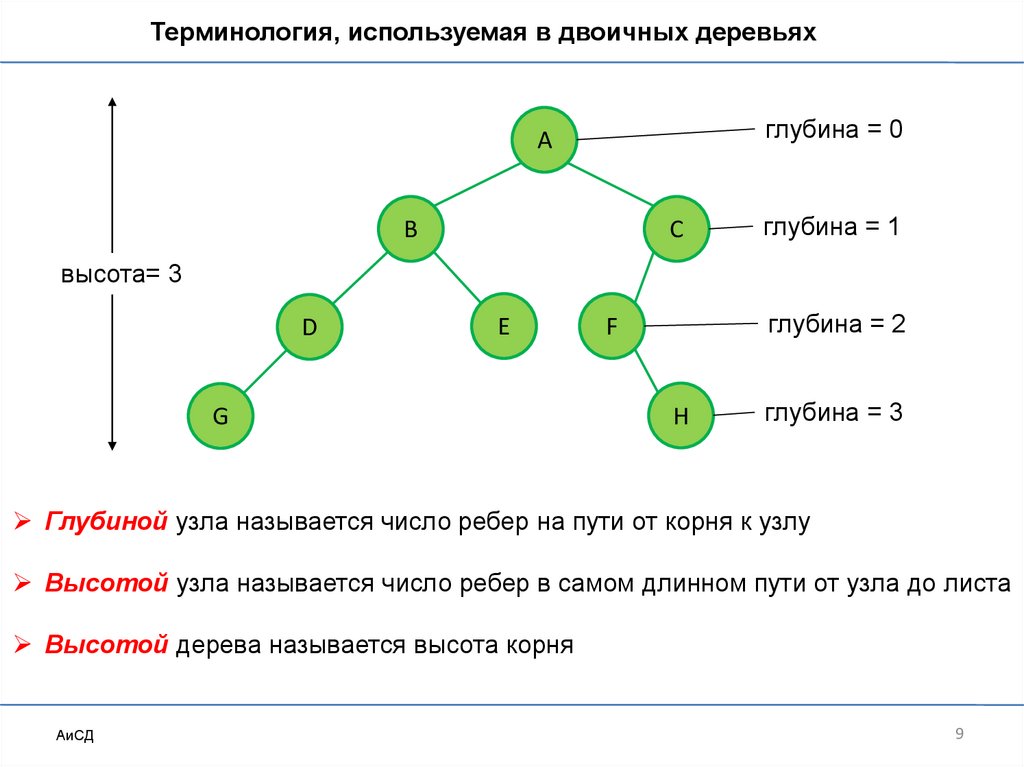
Глубиной узла называется число ребер на пути от корня к узлу
Высотой узла называется число ребер в самом длинном пути от узла до листа
Высотой дерева называется высота корня
АиСД
9

10.

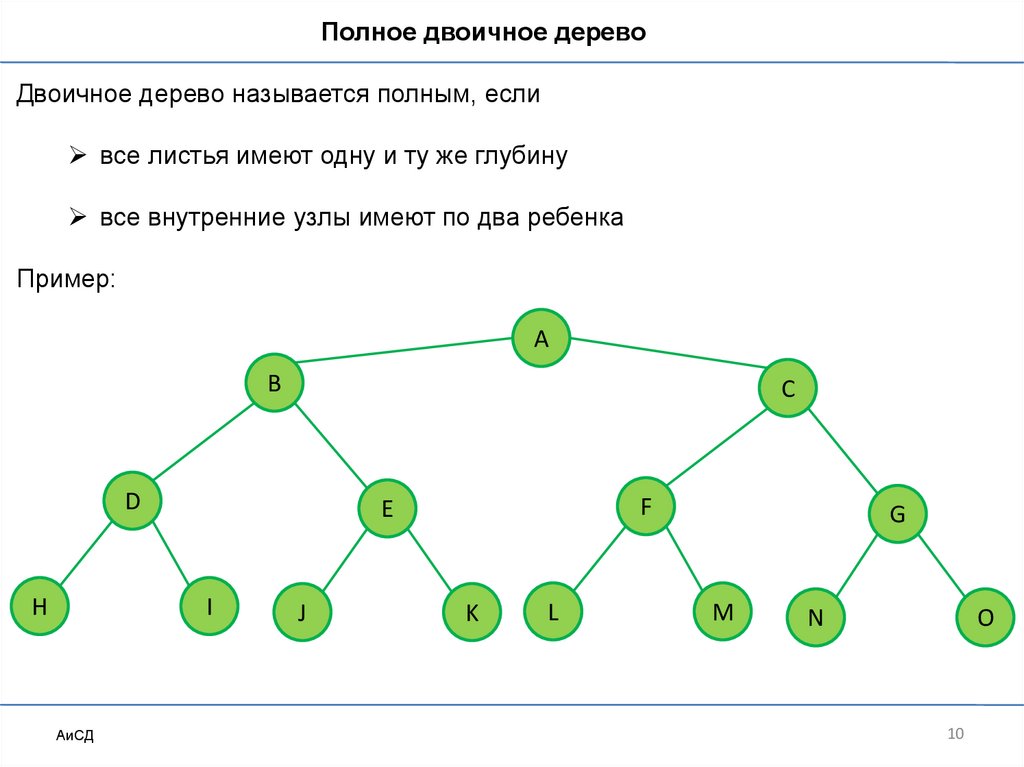
Полное двоичное дерево
Двоичное дерево называется полным, если
все листья имеют одну и ту же глубину
все внутренние узлы имеют по два ребенка
Пример:
А
B
C
D
H
I
АиСД
F
E
J
K
L
G
M
N
O
10

11.

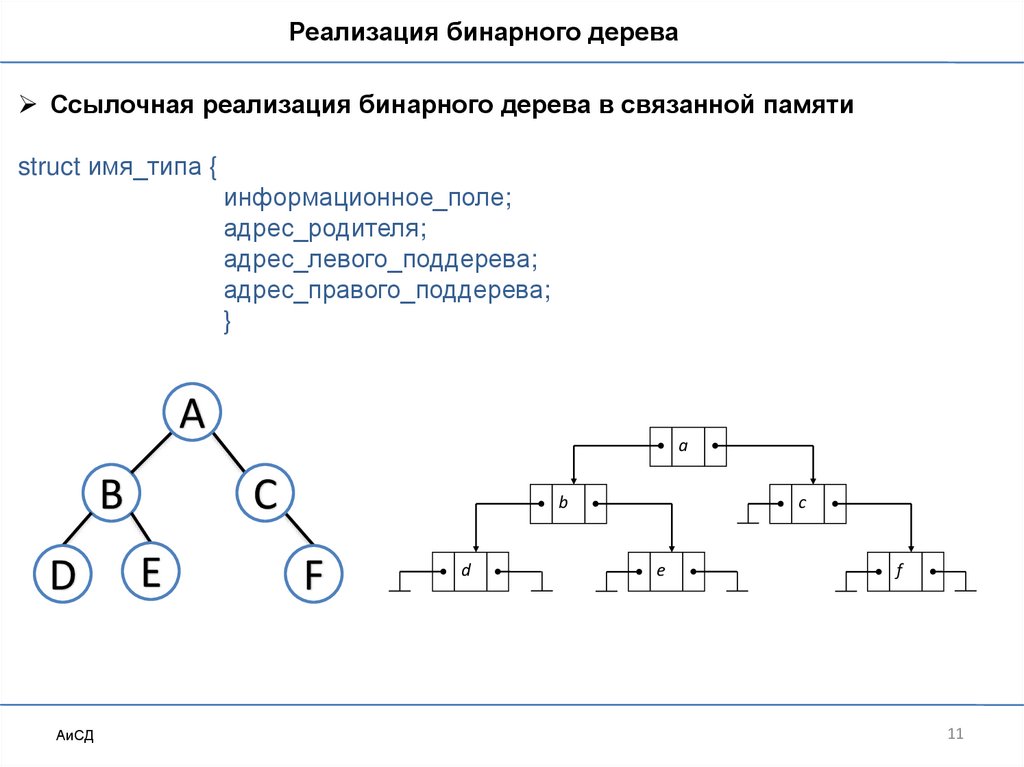
Реализация бинарного дерева
Ссылочная реализация бинарного дерева в связанной памяти
struct имя_типа {
информационное_поле;
адрес_родителя;
адрес_левого_поддерева;
адрес_правого_поддерева;
}
A
B
D
АиСД
a
C
E
b
F
d
c
e
f
11

12.

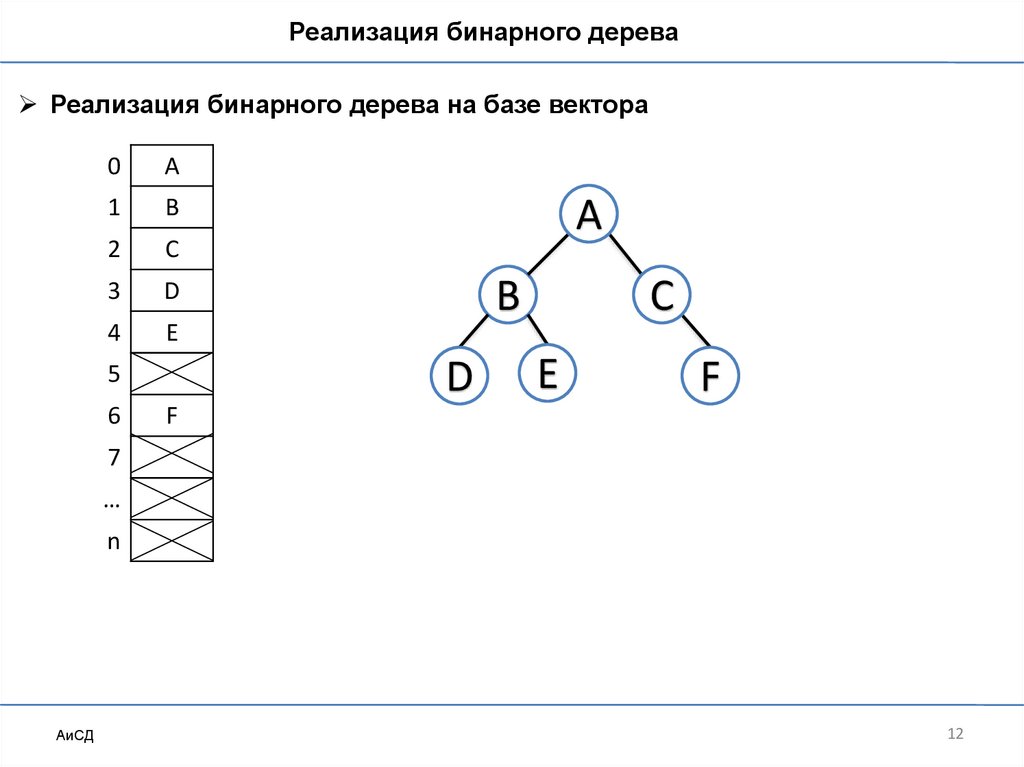
Реализация бинарного дерева
Реализация бинарного дерева на базе вектора
0
A
1
B
2
C
3
D
4
E
B
D
5
6
A
C
E
F
F
7
…
n
АиСД
12

13.

Обходы бинарных деревьев
Обход дерева – это упорядоченная последовательность вершин дерева, в
которой каждая вершина встречается только один раз.
Терминология в различных источниках:
прямой, обратный, концевой;
КЛП, ЛКП, ЛПК;
прямой, симметричный, обратный;
сверху вниз, слева направо, снизу вверх;
префиксный (PreOrder), инфиксный (InOrder), постфиксный (PostOrder).
АиСД
13

14.

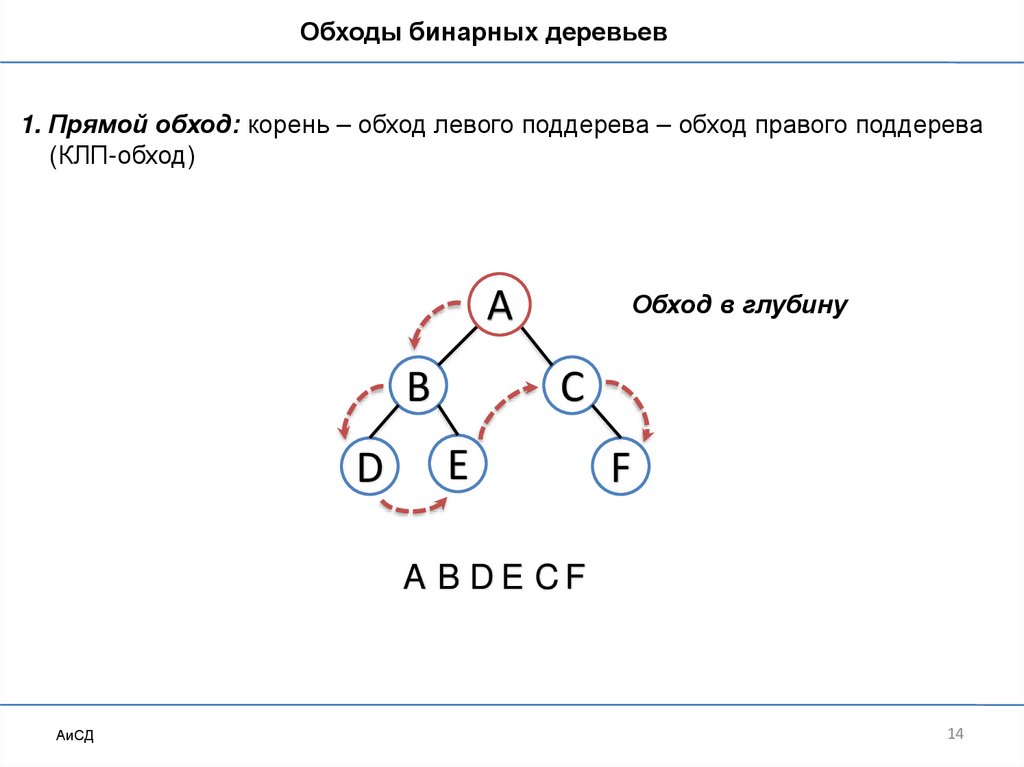
Обходы бинарных деревьев
1. Прямой обход: корень – обход левого поддерева – обход правого поддерева
(КЛП-обход)
A
B
D
Обход в глубину
C
E
F
A B DE CF
АиСД
14

15.

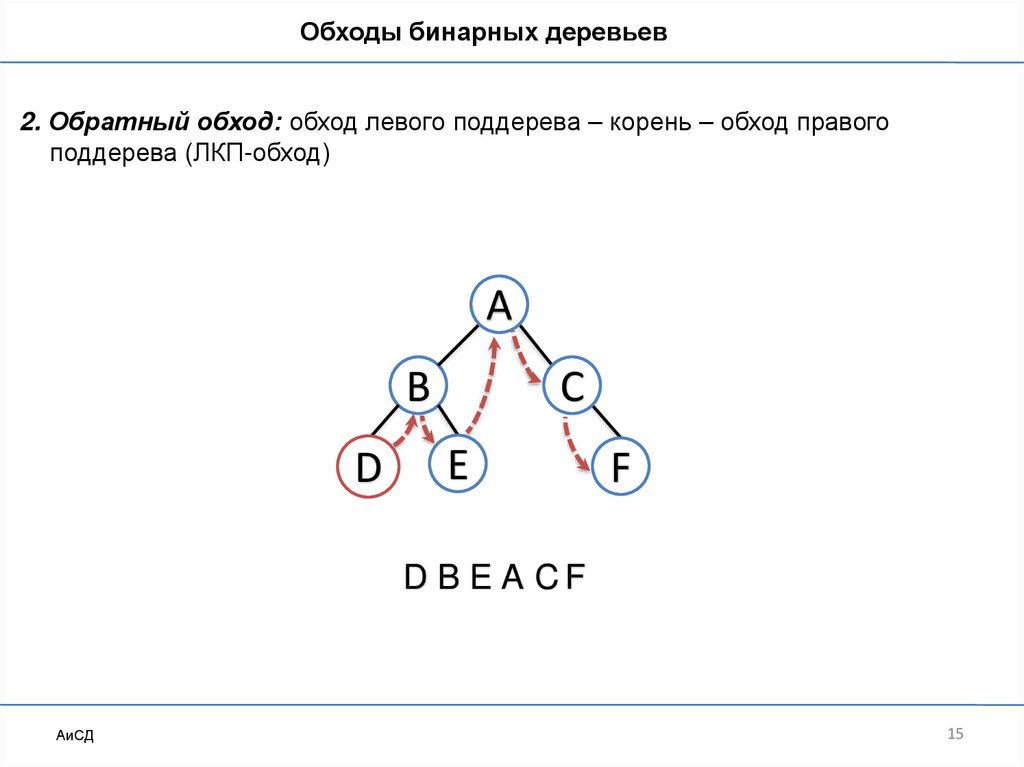
Обходы бинарных деревьев
2. Обратный обход: обход левого поддерева – корень – обход правого
поддерева (ЛКП-обход)
A
B
D
C
E
F
D B E A CF
АиСД
15

16.

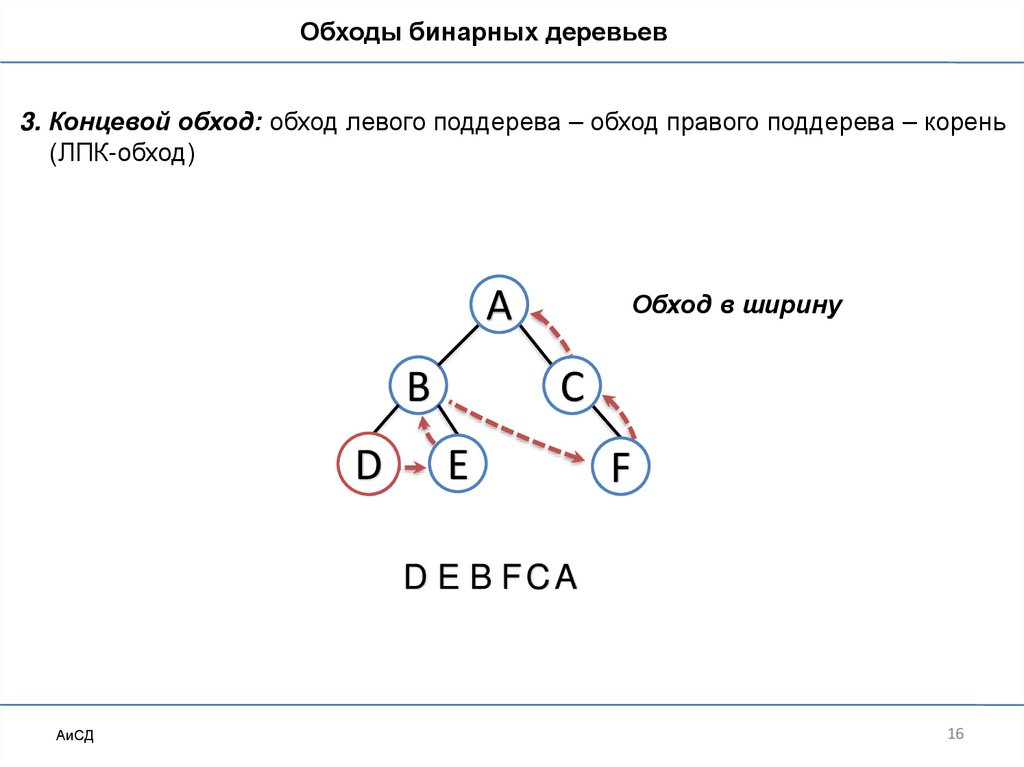
Обходы бинарных деревьев
3. Концевой обход: обход левого поддерева – обход правого поддерева – корень
(ЛПК-обход)
A
B
D
Обход в ширину
C
E
F
D E B FCA
АиСД
16

17.

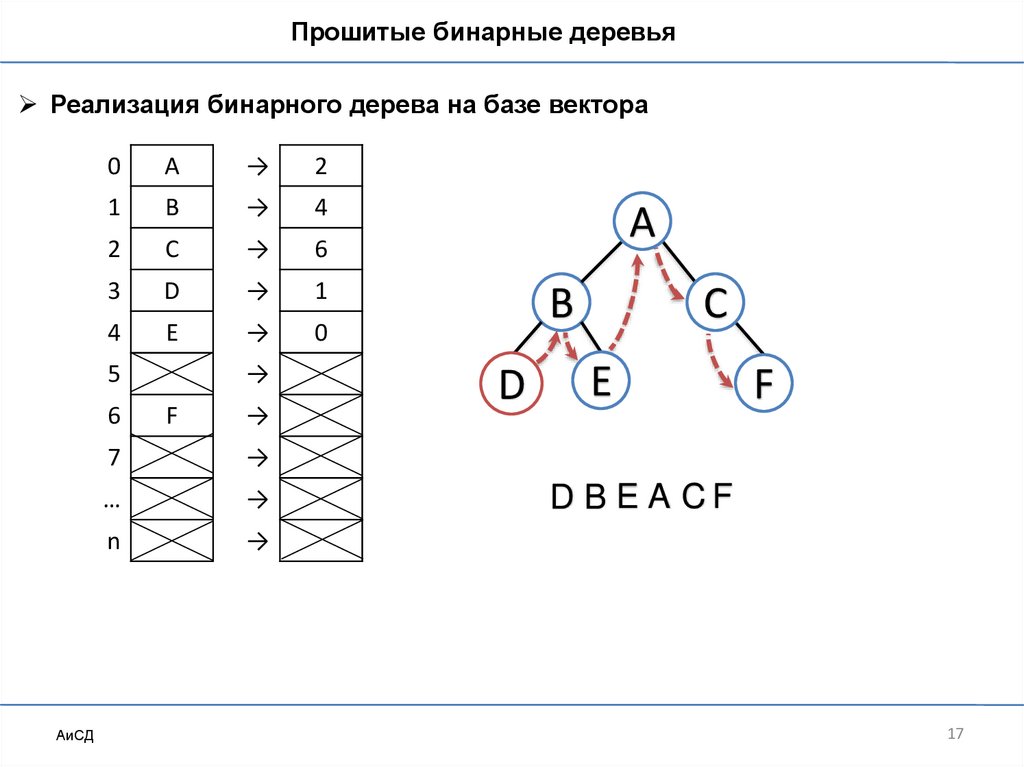
Прошитые бинарные деревья
Реализация бинарного дерева на базе вектора
0
A
→
2
1
B
→
4
2
C
→
6
3
D
→
1
4
E
→
0
5
6
АиСД
→
F
→
7
→
…
→
n
→
A
B
D
C
E
F
D B E A CF
17

18.

Тема 4. Алгоритмы сортировки, их
классификация. Простые варианты
сортировки.
18

19.

Алгоритм сортировки по возрастанию
Задача сортировки чисел в порядке возрастания:
Вход: последовательность из n чисел <a1, a2,…, an>
Выход: перестановка входной последовательности <a1‘, a2‘,…,
an‘>, такая что a1‘≤ a2‘≤…≤ an‘
Пример экземпляра задачи сортировки:
Вход: <10, 8, 2, 12, 5, 100>
Выход: <2, 5, 8, 10, 12, 100>
АиСД
19

20.

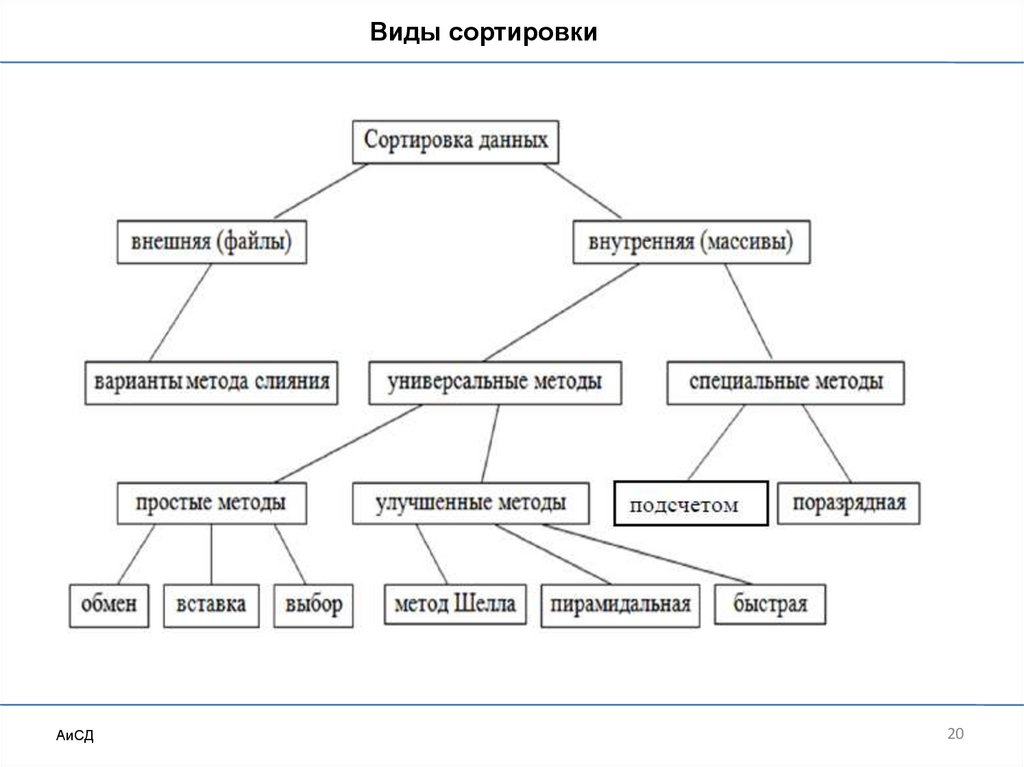
Виды сортировки
АиСД
20

21.

Виды сортировки
Основные алгоритмы внутренних сортировок
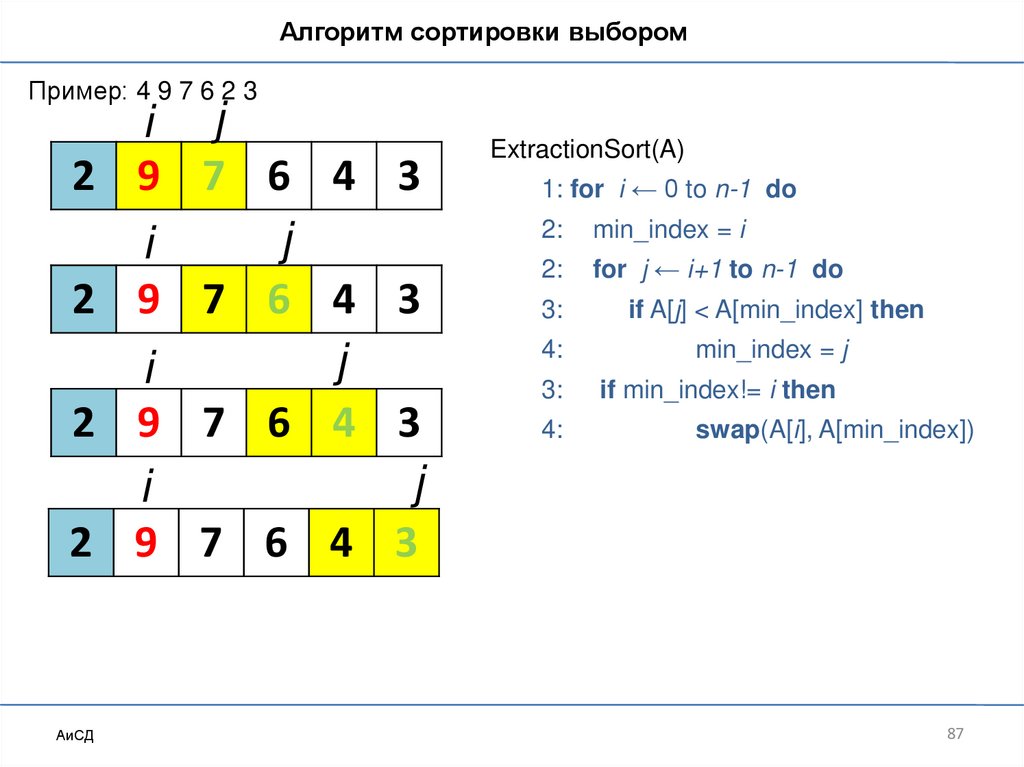
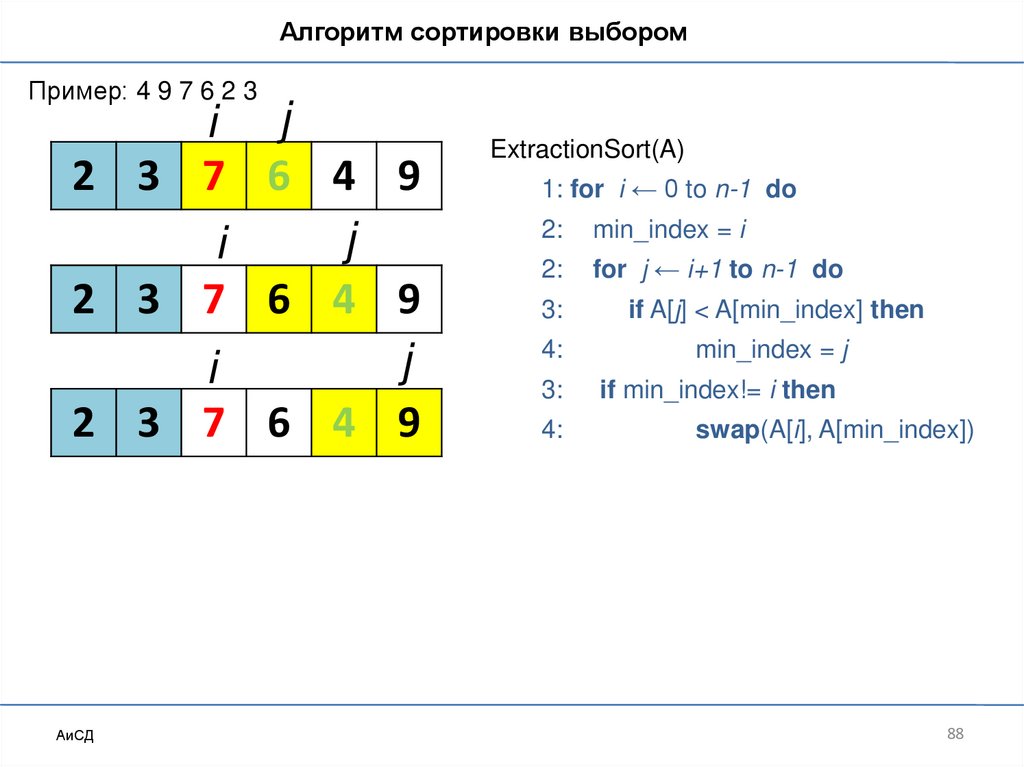
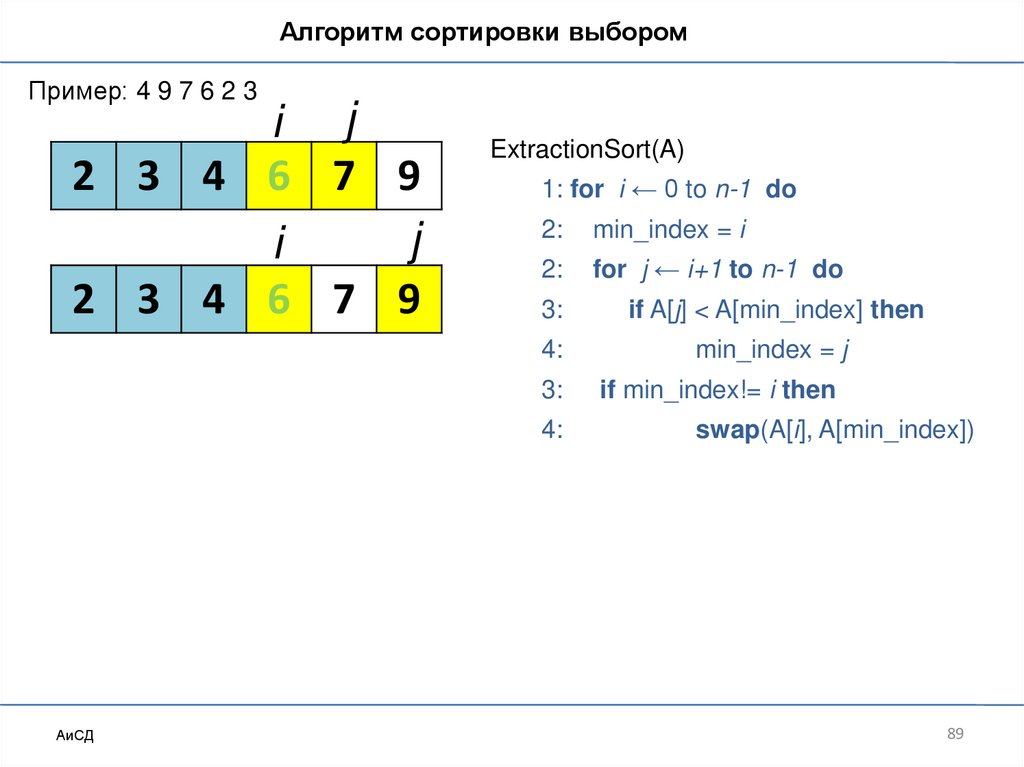
Сортировка выбором
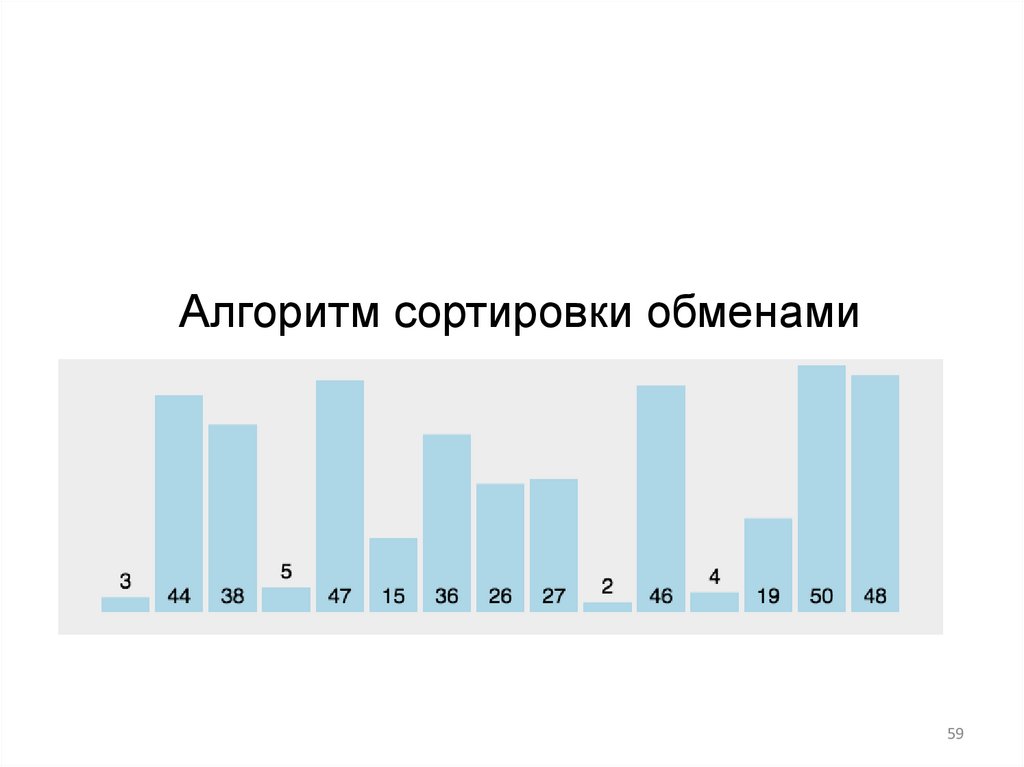
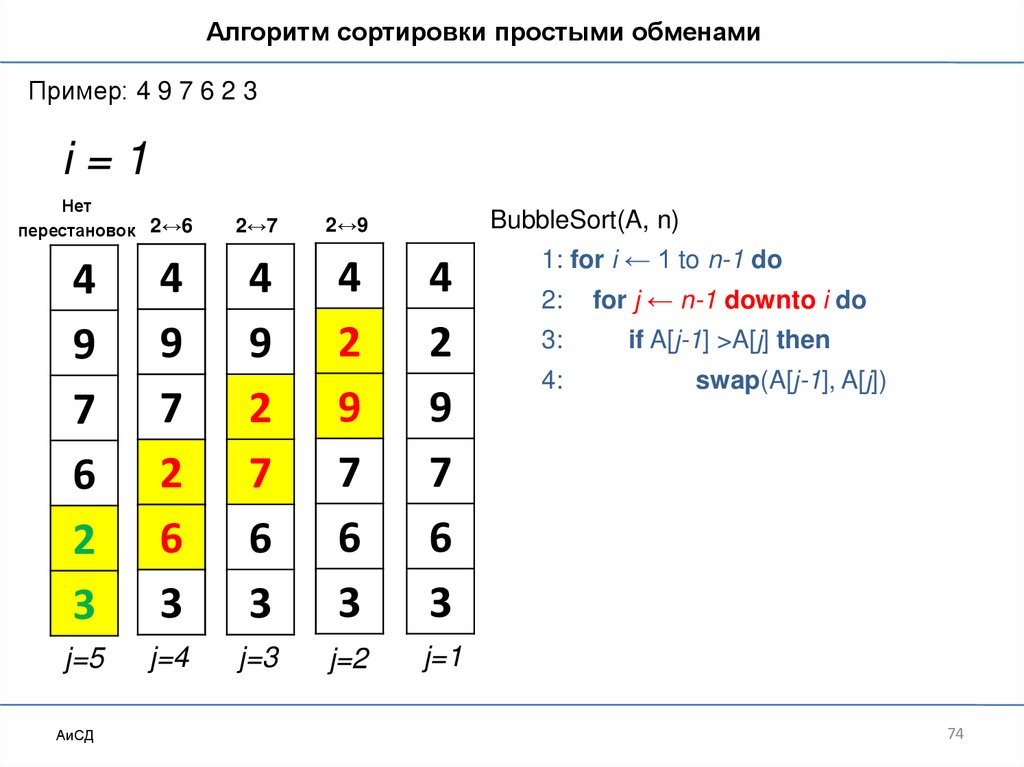
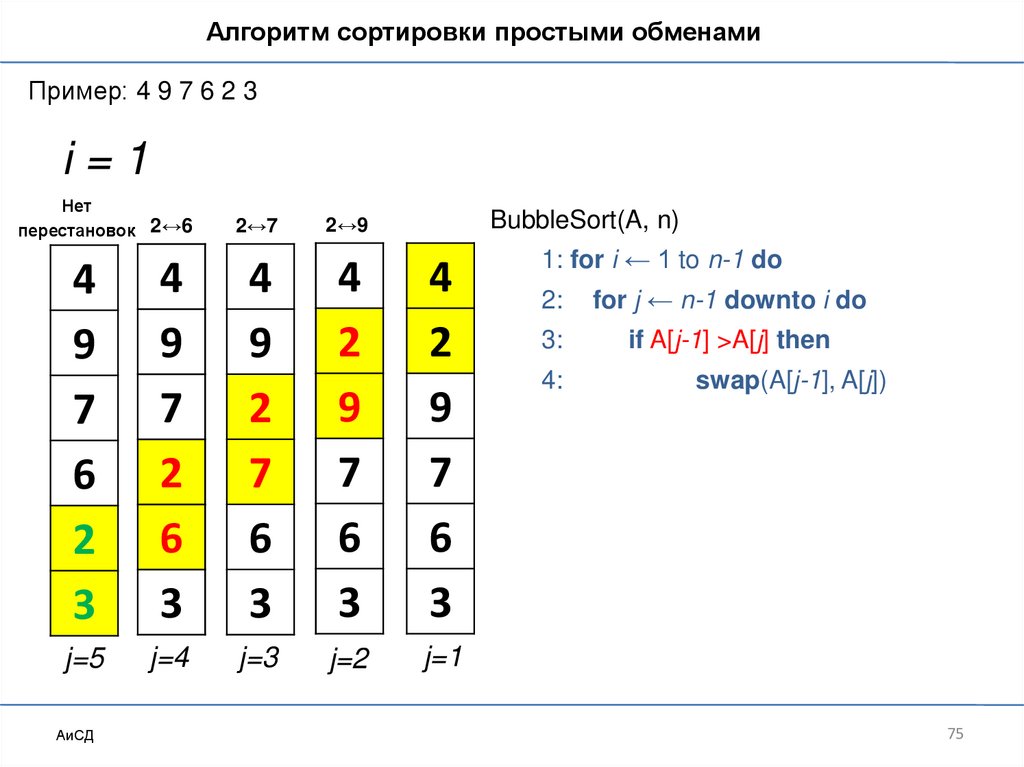
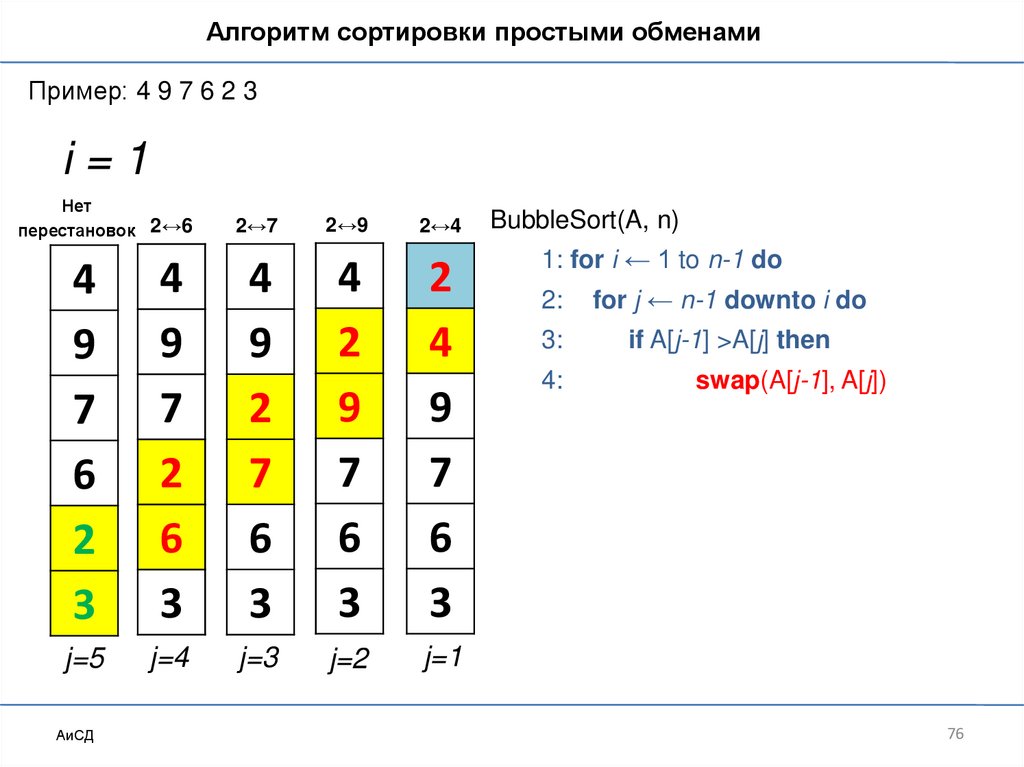
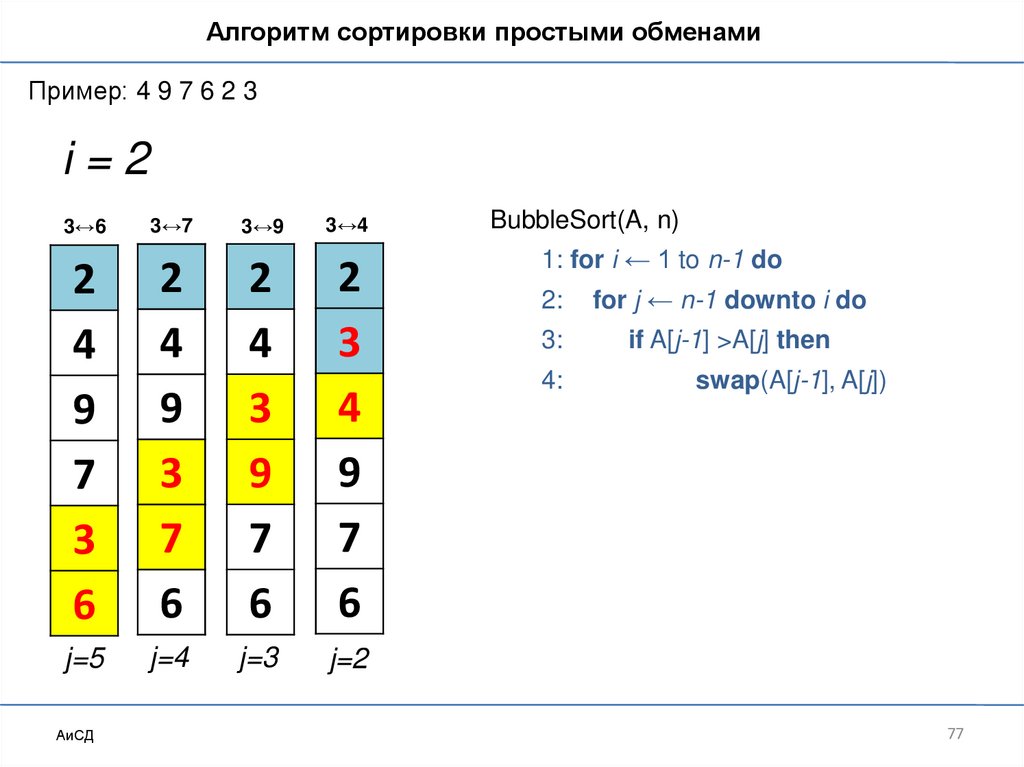
Сортировка обменами («пузырьковая»)
Сортировка вставкой
Поразрядная сортировка
Бинарная пирамидальная сортировка
Сортировка методом Шелла
Быстрая сортировка Хоара
Сортировка слиянием
Внешние сортировки
Сортировка простым слиянием
Сортировка естественным слиянием
АиСД
21

22.

Алгоритм сортировки вставками
22

23.

Алгоритм сортировки вставками
Пример:
524613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
23

24.

Алгоритм сортировки вставками
Пример:
524613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
24

25.

Алгоритм сортировки вставками
Пример:
254613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
temp ← A[i]
6:
A[i] ← A[i+1]
7:
A[i+1] ← temp
8:
АиСД
i←i−1
25

26.

Алгоритм сортировки вставками
Пример:
254613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
26

27.

Алгоритм сортировки вставками
Пример:
254613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
27

28.

Алгоритм сортировки вставками
Пример:
245613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
28

29.

Алгоритм сортировки вставками
Пример:
245613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
29

30.

Алгоритм сортировки вставками
Пример:
245613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
30

31.

Алгоритм сортировки вставками
Пример:
245613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
31

32.

Алгоритм сортировки вставками
Пример:
245613
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
32

33.

Алгоритм сортировки вставками
Пример:
124563
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
33

34.

Алгоритм сортировки вставками
Пример:
123456
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
34

35.

Оценка времени работы сортировки вставками
Оценим время однократного выполнения каждой строки псевдокода
алгоритма сортировки вставками
Время
InsertionSort(A)
1: for j ← 2 to n do
2:
i←j −1
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
с1
35

36.

Оценка времени работы сортировки вставками
Оценим время однократного выполнения каждой строки псевдокода
алгоритма сортировки вставками
Время
InsertionSort(A)
1: for j ← 2 to n do
с1
2:
i←j −1
с2
3:
while i>0 and A[i] >A[i+1] do
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
36

37.

Оценка времени работы сортировки вставками
Оценим время однократного выполнения каждой строки псевдокода
алгоритма сортировки вставками
Время
InsertionSort(A)
1: for j ← 2 to n do
с1
2:
i←j −1
с2
3:
while i>0 and A[i] >A[i+1] do
с3
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
37

38.

Оценка времени работы сортировки вставками
Оценим время однократного выполнения каждой строки псевдокода
алгоритма сортировки вставками
Время
InsertionSort(A)
1: for j ← 2 to n do
с1
2:
i←j −1
с2
3:
while i>0 and A[i] >A[i+1] do
с3
4:
swap(A[i], A[i+1])
5:
i←i−1
АиСД
с4
38

39.

Оценка времени работы сортировки вставками
Оценим время однократного выполнения каждой строки псевдокода
алгоритма сортировки вставками
Время
InsertionSort(A)
1: for j ← 2 to n do
с1
2:
i←j −1
с2
3:
while i>0 and A[i] >A[i+1] do
с3
4:
swap(A[i], A[i+1])
с4
5:
i←i−1
с5
АиСД
39