Similar presentations:
Структуры и алгоритмы компьютерной обработки данных
1. Структуры и алгоритмы компьютерной обработки данных
Специальность«Математическое обеспечение и администрирование
информационных систем»
2 курс
52 часа лекций
54 часов лабораторных работ,
курсовая работа, экзамен
14.06.2025
1
2. Литература:
Д. Кнут. Искусство программирования для ЭВМ. Т. 1-3, М.: Мир, 1978, 1995, 2006 и др..Н. Вирт. Алгоритмы и структуры данных. М.: Мир, 1989.
Л.Н. Королев, А.И. Миков. Информатика. Введение в компьютерные науки. М.: Высшая
школа, 2003.
Дж. Бакнелл. Фундаментальные алгоритмы и структуры данных в Delphi. СПб.: Питер,
2006.
Дж. Макконел. Основы современых алгоритмов. Москва, Техносфера, 2004.
А. Ахо, Д.Хопкрофт, Д. Ульман. Структуры данных и алгоритмы. Москва, Вильямс,
2003.
Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн. Алгоритмы. Построение и анализ. 3-е
издание. М: Изд. Дом «Вильямс», 2013.
Р. Стивенс. Алгоритмы. Теория и практическое применение. М.: Эксмо, 2020.
14.06.2025
2
3. Концепция типа данных
Данные, которые должны обрабатываться на компьютере являютсяабстракцией, отображением некоторого фрагмента реального мира. А
именно того фрагмента, который является предметной областью решаемой
задачи. Для ее решения вначале строится информационная, а в общем случае математическая модель изучаемой предметной области и выбирается
существующий или строится новый алгоритм решения задачи.
Информация всегда материализуется, представляется в форме сообщения. Сообщение в общем случае представляет собой некоторый зарегистрированный физический сигнал. Сигнал — это изменение во времени или
пространстве некоторого объекта, в частности, параметра некоторой
физической величины, например индукции магнитного поля (при хранении
информации, точнее сообщения на магнитных носителях) или уровня напряжения в электрической цепи (в микросхемах процессора или оперативной
памяти).
Дискретное сообщение — это последовательность знаков (значений сигнала) из некоторого конечного алфавита (конечного набора значений параметра сигнала), в частности, для компьютера это последовательность
знаков двоичного алфавита, то есть последовательность битов.
14.06.2025
3
4.
Компьютерные данные это дискретные сообщения, которые представлены вформе, используемой в компьютере, понятной компьютеру. Для процессора
компьютера любые данные представляют собой неструктурированную
последовательность битов (иногда используют термин поток битов).
Конкретная интерпретация этой последовательности зависит от программы, от
формы представления и структуры данных, которые выбраны программистом. Это выбор, в конечном счёте, зависит от решаемой задачи и удобства выполнения действий над данными.
К данным в программах относятся:
Непосредственные значения это неизменные объекты программы, которые
представляют сами себя: числа (25, 1.34E-20), символы (‘A’, ‘!’) , строки (‘Введите
элементы матрицы’);
Константы – это имена, закрепляемые за некоторыми значениями (const
pi=3.1415926).
Переменные это объекты, которые могут принимать значение, сохранять его
без изменения, и изменять его при выполнении определенных действий (var
k:integer, x:real, a:array[1..3,1..5]).
Значения выражений и функций. Выражения и функции– это записанные
определённым способом правила вычисления значений: k*x+ sqrt(x). Функции
имеют имена, выражения имен не имеют.
14.06.2025
4
5.
Для отображения особенностей представления в компьютере данных различнойприроды в информатике, в компьютерных дисциплинах используется важнейшая
концепция типа данных.
Тип данных представляет собой важнейшую характеристику,
которая определяет:
множество допустимых значений;
множество операций, которые могут выполняться над значением;
структуру значения (скаляр, вектор и т.д.);
способ машинного представления значения.
Основные принципы концепции типа данных
в языках программирования:
Тип константы, переменной, функции или выражения может быть определен
по внешнему виду (по изображению) или по описанию без выполнения какихлибо вычислений.
Любая операция или функция требует аргументов и возвращает результат
вполне определенного типа. Типы аргументов и результатов операций
определяется по вполне определенным правилам языка.
14.06.2025
5
6.
Обобщением рассмотренных понятий в современных языках программированияявляется понятие объекта, который представляется как объединение в целое
данных и действий над ними.
Самостоятельными объектами объявляются непосредственные значения,
различные структуры из таких значений (списки, множества и т.д), функции,
библиотеки функций,
программные модули и любые другие программные
конструкции. Абсолютно всё в языке программирования объявляется объектами.
В ряде языков принципиально меняется понятие переменной, точнее это понятие
вообще отменяется. Понятие имени остаётся, но имя просто закрепляется за
объектом, причём некоторые объекты могут менять значение, а другие не могут.
14.06.2025
6
7.
Разновидности типов и структур данныхВ информатике используется большое количество различных типов, различных
структур
данных, которые применяются для моделирования объектов,
встречающихся в рассматриваемых задачах.
Данные
По значению
Скалярные
Структурированные
По времени жизни
Статические
Динамические
Значение скалярного (простого, атомарного) типа представлено ровно
одним компонентом ( пример: время, температура).
Значение структурированного (составного) типа представлено более чем
одним компонентом (пример: вектор, матрица, таблица и т.д.).
Если структура данного по ходу выполнения алгоритма не изменяется, то такая
структура считается статической, Статические структуры данных существуют
в неизменном виде в течение всего времени исполнения алгоритма.
Динамические структуры создаются, изменяются и уничтожаются по мере
необходимости в любой момент исполнения алгоритма.
14.06.2025
7
8.
Различают предопределенные (предварительно определенные) – стандартные,фундаментальные и определяемые в программе типы. Для стандартных
типов в описании языка программирования заданы все его характеристики –
множество значений, множество операций, структура и машинное представление
значения. Для вновь определяемых типов в языке предусмотрен механизм
указания в программе множества значений, множества операций и структуры
значения. Обычно новый тип строится на базе имеющихся стандартных. Поэтому
машинное представление значений таких типов фиксировано в описании языка.
Основные базовые статические типы (структуры данных)
скалярные (простые, атомарные) типы:
целый;
вещественный;
логический (булевский);
символьный;
структурированные (составные) типы:
массив;
запись;
файл (последовательность);
множество;
объектовый (класс) тип;
всевозможные комбинации скалярных и структурированных типов;
ссылочный тип (указатель).
14.06.2025
8
9.
Наиболее часто используемые предопределенные скалярные типы: целый(integer), вещественный (real), символьный (char), логический (boolean).
Тип integer (int)
Целочисленные точные значения. Примеры: 73, -98, 5, 19674.
Машинное представление: формат с фиксированной точкой. Диапазон значений
определяется длиной поля. Операции: +, -, *, div, mod,=, <, и т.д.
Тип real (float)
Нецелые приближенные значения. Примеры: 0.195, -91.84, 5.0
Машинное представление: формат с плавающей точкой. Диапазон и точность
значений определяется длиной поля. Операции: +, -, *, /, =, <, и т.д.
Тип char
Одиночные символы текстов. Примеры: ‘a’, ‘!’, ‘5’.
Машинное представление: формат ASCII. Множество значений определяется
кодовой таблицей и возможностями клавиатуры. Операции: +, =, <, и т.д.
Тип boolean (bool)
Два логических значения false и true. Причем, false<true.
Машинное представление ─ нулевое и единичное значение бита: false
кодируется 0, true ─ 1. Операции: , , , =, < и т.д.
14.06.2025
9
10.
Различают дискретные и непрерывные скалярные типы. Множествозначений дискретного типа конечное или счетное. Множество значений
непрерывного типа более чем счетное. К дискретным стандартным типам
относятся целый, символьный и логический. К непрерывным стандартным типам относится вещественный.
Основные механизмы построения новых скалярных дискретных типов:
перечисление, ограничение. В определении перечисляемых типов
фиксируется список всех возможных значений, множество операций
определяется в языке заранее. В определении ограниченных типов в
качестве множества допустимых значений фиксируется подмножество
множества значений некоторого дискретного типа, который в этом случае
называется базовым типом по отношению к определяемому.
14.06.2025
10
11.
Структурированные (составные) типы характеризуются: количеством ивозможным типом компонентов значения, а также способом доступа к
отдельному компоненту значения.
Массив (регулярный тип, вектор)
Структуры аналогичные векторам и матрицам в информатике принято называть
массивами. Все элементы массива должны быть одного и того же типа.
a11a12a13
x {x1 , x2 , x3}; w ( w1 , w2 , w3 , w4 , w5 , w6 , w7 , w8 , w9 ); A a21a22a23
a31a32a33
Для доступа (обращения) к отдельному элементу массива используется
индекс или несколько индексов (w[5]; w[i+2]; A[1][2]). Индексы могут быть
выражениями, значения которых могут произвольным образом изменяться
в заранее заданных границах. Поэтому говорят, что к элементам массивов
имеется прямой доступ.
w[1]
w[2]
w[3]
w[4]
w[5]
w[6]
w[7]
w[8]
w[9]
6
18
42
43
55
63
82
94
42
14.06.2025
11
12.
Записи ( комбинированный тип, структура, объединение)День Победы:
Полёт Гагарина:
День
Месяц
Год
9
май
1945
12
апрель
1961
Структуры, аналогичные строкам таблицы, называют записями. Компоненты
записей принято называть полями. Различные поля (столбцы таблицы) могут
быть разных типов. Для доступа к отдельным полям записи используются их
фиксированные и неизменные имена. Например: День Победы. Месяц := май.
Поля могут выбираться для обработки в произвольном порядке, поэтому говорят,
что доступ к компонентам записи прямой.
Файл (последовательность)
Основной структурой данных, которая используется для хранения информации
на внешних устройствах (магнитных дисках, лентах и т.д.) являются файлы или
последовательности. Считается, что файл всегда находится на внешнем
устройстве. При этом количество компонентов файла неизвестно, все
компоненты должны быть одного и того же типа. Доступ к компонентам ─
последовательный.
14.06.2025
12
13.
МножествоВо многих математических и информационных задачах возникает необходимость
в прямом или косвенном использовании основного математического объекта
множества. Соответствующая множеству тип данных по определению относится к структурированным, так как в общем случае множество может состоять
более чем из одного элемента, и при этом со всеми элементами множества
приходится выполнять операции как с единым целым. Количество элементов в
множестве заранее не определяется, и с течением времени оно может
изменятся. Все элементы множества должны быть одного и того же типа.
Доступа к отдельным элементам множества нет. Можно только узнать принадлежит элемент множеству или нет, включить элемент в множество или исключить его из множества. Предусмотрены также стандартные операции над множествами: объединение, пересечение, вычитание и т.д.
X
X3
?
X17
X3
?
X17
14.06.2025
X1
X5
X4
X2
13
14.
В современных языках программирования используются более мощные повозможностям составные типы. Так, в язык Python включены списки, кортежи и
словари.
Списки в языке Python – это изменяемая последовательность объектов
произвольных типов. Например, L= [123, ‘орех’, 1.17] # список из трех объектов
Кортежи в языке Python – это неизменяемая последовательность объектов
произвольных типов. Например, L= (123, ‘орех’, 1.17) # кортеж из трех объектов
Словарь языка Python представляет собой неупорядоченный набор объектов,
доступ
к
которым
осуществляется
по
их
именам
(ключам).
Например: D={‘food’: ‘cutlet’, ‘quantity’: 4, ‘color’: ‘brown’} # словарь из трёх объектов
14.06.2025
14
15.
Динамические структуры данныхУ данных с динамической структурой с течением времени изменяется сама
структура, а не только количество элементов, как у файлов или последовательностей. Базовыми динамическими структурами данных являются:
объект;
линейный список;
дерево;
граф.
Линейный список
У линейного списка каждый элемент связан с предшествующим ему. У
линейного списка известно, какой элемент находится в начале списка, какой
в конце, а также, какой элемент стоит перед текущим. В линейном списке
переходить от текущего элемента к следующему можно только с помощью
указанных связей между соседними элементами.
В целом получается цепочка элементов, в которой можно осуществлять
поиск, в которую можно вставлять элементы или исключать их.
14.06.2025
15
16.
На базе линейного списка организуются много других типов динамическихструктур. Это в частности: кольца, очереди, деки и стеки.
Структура кольца
Отличие кольца от линейного списка в том, что у кольца имеется связь между
последним элементов списка и его первым элементом.
У линейного списка и у кольца возможен доступ к любому элементу структуры. Для этого нужно последовательно перемещаться от одного элемента к
другому. Во многих реальных ситуациях такой доступ отсутствует. Можно
взаимодействовать только с первым и последним элементами или же только
с одним из них. Для моделирования таких объектов используются очереди,
деки и стеки.
14.06.2025
16
17.
Структура очередиУ очереди доступен для включения конец, а для исключения (выборки) ─ начало.
Элемент, поступивший в очередь раньше и обслуживается раньше. Говорят, что
очередь это структура с дисциплиной обслуживания FIFO (First In, First Out) ─
«первый пришёл, первый ушел».
Структура дека
У дека оба конца доступны, как для включения, так и для выборки. Таким образом, можно сказать, что дек ─ это двусторонняя очередь.
14.06.2025
17
18.
Структура стекаУ стека для взаимодействия доступна только один конец структуры ─ вершина
стека. И включение нового элемента в стек и выборка последнего ранее
включенного идет через вершину стека. Таким образом на обслуживание
попадает первым элемент, поступивший последним. Говорят, что стек ─ это
структура с дисциплиной обслуживания LIFO (Last In, First Out) ─ «последним
пришёл, первым ушёл».
Структура дерева
Деревом называется структура данных, элементы которой связаны отношениями подчиненности, когда одному элементу может быть подчинено несколько,
но при этом он может сам быть подчинен только одному. В структуре имеется
только один элемент, не подчиняющийся никаким другим. Это элемент называется корнем дерева.
14.06.2025
18
19.
Корнем дерева является элемент a, он находится на самом высоком уровне. Вдереве нет элементов, которым подчиняется корень. Узлы b, c и d подчиняются
(порождаются, являются дочерними узлами) узлу а. Узел а является для них
родительским, порождающим. В свою очередь узлы b и d имеют по несколько дочерних узлов, а узел с таковых не имеет.
Структура графа
Структурой данных наиболее общего вида является граф. Любые элементы
графа могут быть связаны с любыми другими элементами.
14.06.2025
19
20.
Основные операции над статическими структурами данных :присваивание
сравнение
Основные операции над динамическими структурами данных :
создание структуры
включение нового элемента
уничтожение структуры
исключение элемента
полный перебор структуры
поиск элемента
упорядочение (сортировка) структуры.
Существенным моментом эффективного решения задачи с
помощью компьютера является адекватный выбор структуры
данных, разработка нового или выбор существующего алгоритма
ее решения, реализация этого алгоритма в виде правильной
программы.
14.06.2025
20
21.
Эффективность алгоритмовВ курсе информатики рассматривались несколько различных алгоритмов
решения одной и той же задачи поиска. При этом, вообще говоря,
бездоказательно, только на основе внешнего вида алгоритмов
утверждалось, что, например, быстрый алгоритм и алгоритм с барьером
лучше, эффективнее, чем классический алгоритм.
В связи с этим возникает ряд вопросов. Что понимать под
эффективностью алгоритма? Как можно выяснить, какой алгоритм лучше,
эффективнее, а какой хуже? Вообще, как можно сравнивать алгоритмы
между собой?
В настоящее время алгоритмы принято сравнивать друг с другом по двум
критериям — затраченному на выполнение алгоритма времени и
потребовавшийся для этого выполнения объём памяти. Первый критерий
связан с временной эффективностью алгоритма, а второй — с
объёмной эффективностью или эффективностью по памяти.
14.06.2025
21
22.
При сравнении нескольких алгоритмов решения одной и той же задачи покритерию временной эффективности лучшим считается тот алгоритм, на
выполнение которого одним и тем же исполнителем на одном и том же
наборе исходных данных требуется меньшее время.
Аналогичным образом по критерию объёмной эффективности лучшим
является тот алгоритм, на выполнение которого одним и тем же
исполнителем на одном и том же наборе исходных данных потребовался
меньший объём памяти.
Временная и объёмная эффективности довольно сложным образом
связаны и с самим алгоритмом и друг с другом.
14.06.2025
22
23.
Важнейшим фактором, влияющим на время выполнения алгоритма, атакже на требуемую память является набор исходных данных, для
которого осуществляется исполнение алгоритма. Такой набор состоит из
значений переменных, имена которых указаны в процедурах ввода
алгоритма.
main ( )
{
const int Nmax=1000;
int n, a, x[Nmax+1];
scan (n, x, a);
bool Flag=false; //Элемент ещё не найден
int IndexFoundElem=0, i=1;
while ( (i<=n) && ! Flag )
{
if (x[i]==a)
{//Элемент найден, завершение поиска
Flag=true; IndexFoundElem=i;}
else i++; //Продолжение поиска
}
print (Flag, IndexFoundElem);
14.06.2025
}
23
24.
Набор входных данных (n, x, a) алгоритма линейного поиска включает всебя: значение переменной n, которое определяет фактическую размерность массива x, значения всех его элементов и искомое значение a.
Выберем в качестве тестового набор (n 8, x (43, 55, 82, 43, 94, 18, 6,
63), а=25). В результате получим, что элемент, совпадающий с a=25, в
рассматриваемом массиве отсутствует и для получения результата
потребовалось просмотреть все элементы массива и выполнить 8
итераций цикла.
Выберем в качестве тестового набор (n 8, x (43, 55, 82, 43, 94, 18, 6,
63), а=18). В результате получим, что элемент, совпадающий с a=18
имеется, значение IndexFoundElement=6, и получения результата потребовалось 6 итераций цикла, а следовательно, он получен за меньшее
время.
Для набора (n 2, x (14, 69), a=12) требуется меньше места в памяти,
чем для только что рассмотренных.
Таким образом, понятия временной и объемной эффективности алгоритма
необходимо точно определять.
14.06.2025
24
25.
Пусть DA — множество допустимых для данного алгоритма A наборовисходных данных. Конкретный набор исходных данных d DA, для которого осуществляется фактическое исполнение алгоритма, принято для
краткости называть входом алгоритма, экземпляром задачи или конкретной проблемой.
Для алгоритмов поиска множество входов
представляет собой
совокупность допустимых наборов исходных данных (n, x, a).
Допустимость набора определяется смыслом, входящих в набор величин,
и их использованием в алгоритме решения задачи.
Так для переменной n, определяющей размерность вектора x, допустимы
только целые положительные значения. Элементы массива x и искомое
значение a не могут быть вещественными, поскольку для вещественного
типа некорректно сравнение на равенство. Но в отличие от n они могут
быть равными нулю и отрицательными.
14.06.2025
25
26.
Примеры входов алгоритмов поиска:d1=(n 8, x (55, 43, 82, 43, 94, 18, 6, 63), a 25)
d2=(n 8, x (55, 43, 82, 43, 94, 18, 6, 63), a 18)
d3= (n 2, x (14, 69), a 12)
Определение временной эффективности
Фактически затраченное на выполнение алгоритма время, которое
определяет его временную эффективность, существенно зависит от
конкретного исполнителя, например, от модели компьютера, от его
возможностей, скоростей выполнения различных действий и т.д.
Чтобы при анализе алгоритма отделить его собственные свойства от
неодинаковых свойств различных исполнителей для сравнения между
собой алгоритмов используется не время как таковое в секундах, минутах
или часах, а общее количество действий, которые должны быть
осуществлены при исполнении алгоритма. Однако остается зависимость
от набора действий, доступных исполнителю, которую необходимо
учитывать специальным образом.
14.06.2025
26
27.
Пусть имеется несколько алгоритмов решения одной и той же задачи идля их выполнения используется один и тот же вход . Тогда более
эффективным по времени считается тот алгоритм, при исполнении
которого для получения результата требуется выполнить меньше
действий.
К отдельным действиям алгоритма при таком подсчёте относятся:
арифметические операции (+, –, , /), операции сравнения (=, , >, < , , ),
логические операции ( , , ), а также присваивание и некоторые другие
действия. А вот действия, связанные с организацией обмена (ввода или
вывода данных), как правило, не учитываются.
Таким образом, для улучшения алгоритма, для повышения его
временной эффективности следует каким-либо образом уменьшить
общее количество действий, связанных с его исполнением, но при этом
правильность результата не должна пострадать.
Описанный подход позволяет в основном исключить влияние
индивидуальных особенностей исполнителя на сравнение алгоритмов и
принимать во внимание только важнейшие особенности самих алгоритмов.
14.06.2025
27
28.
В связи с тем, что временная эффективность алгоритма и количестводействий в нём связаны друг с другом противоположной зависимостью,
пользоваться характеристикой эффективность не совсем удобно.
Поэтому на практике для анализа алгоритмов применяют другую
характеристику, которая называется трудоёмкостью алгоритма.
Трудоёмкостью алгоритма A называется характеристика, численно
равная
количеству действий, которые потребуется выполнить для
получения результа во время исполнения алгоритма A на некотором его
входе .d DA
Трудоёмкость обратна эффективности: чем больше операций приходится
выполнять для получения результата, тем выше трудоёмкость алгоритма,
и тем менее он эффективен по времени
Поскольку на различных входах
трудоёмкость одного и того же
алгоритма различна, естественно ввести в рассмотрение функцию
трудоёмкости, отражающую эту зависимость
14.06.2025
28
29.
Функция трудоёмкости T (d ) представляет собой отображение множесAтва допустимых наборов данных
DA на множество целых положительных
чисел N, которое для каждого конкретного входа d D определяет
A
трудоёмкость алгоритма A.
Таким образом, можно утверждать, что вход алгоритма d является
аргументом, а сам алгоритм A определяет вид функциональной зависимости для функции трудоёмкости T
. A (d )
В качестве характерного примера определения вида функции
трудоёмкости, рассмотрим алгоритм накопления суммы. В соответствии с
приведёнными выше указаниями для определения трудоёмкости
требуется подсчитать только количество действий из фрагмента
алгоритма, в который не входят описания и операции обмена:
S=0.0; i=1; while (i<=n) {a=1.0/(i*i+1.0); S=+a; i++; }
14.06.2025
29
30.
Этот фрагмент содержит:1. два действия присваивания на этапе инициализации (S=0.0 и i=1);
2. одну операцию сравнения, входящую в условие повторения i<=n;
3. три арифметические
a=1.0/(i*i+1.0);
операции
и
присваивание
в
операторе
4. одну арифметическую операцию и присваивание в операторе S=+a;
5. одну арифметическую операцию и присваивание в операторе i++;
Суммарное количество перечисленных в пунктах 1–5 действий равно
одиннадцати.
Но девять действий пунктов 2–5 (определение значения условия
повторения и действия, входящие в тело цикла) выполняются на каждой
итерации цикла, а количество итераций равно n.
Получаем, что функция трудоёмкости алгоритма равна T ( d ) 9n 2
14.06.2025
30
31.
В рассматриваемом случае любой вход алгоритма состоит из однойпеременной n: d=(n), значение которой определяет количество слагаемых
в сумме. Естественно, что она же и оказалась аргументом функции
трудоёмкости T ( d ) T ( n )
14.06.2025
31
32.
Для решения одной и той же задачи можно построить алгоритмы разнойтрудоёмкости.
Пример: оценка сложности алгоритма вычисления значения полинома в точке.
Алгоритм, использующий прямое вычисление p(x)=anxn+an-1xn-1+…+a1x1+a0.
Для вычисления anxn требуется n умножений.
Для вычисления всех слагаемых нужно 1+2+3+…+n =n(n+1)/2 умножений.
Для вычисления окончательного значения еще n сложений.
Обще количество операции n(n+1)/2+n =O(n2).
Алгоритм, использующий схему Горнера, например, для полинома 4 степени:
p(x)=(((a4x+a3)x+a2)x+a1)+a0 требует 4 сложения и 4 умножения.
В общем случае по методу индукции получим n умножений и n сложений, или
всего 2n операций.
Таким образом сложность алгоритма порядка O(n). Класс сложности также
полиномиальный.
14.06.2025
32
33.
Не для всех алгоритмов функция трудоёмкости является непрерывнойфункцией своих аргументов. Так в ветвлении
if (a[1]>a[2]) {c=a[1]; a[1]=a[2]; a[2]=c;}
функция трудоёмкости T(d)=4 в случае выполнения условия a[1]>a[2], а
при его невыполнении T(d)=1.
Конечно, можно записать такую функцию в традиционном для кусочнонепрерывных функций виде:
4, a1 a2
T (d )
1, a1 a2
Но это более или менее приемлемый способ для двух-трёх ветвей, а при
наличии большого их количества работать с функцией в таком виде
становится очень неудобно.
14.06.2025
33
34.
Причём, в подавляющем большинстве случаев точное распределениезначений функции по ветвям не представляет интереса. Как правило,
важно знать наименьшее и наибольшее количество операций, которые
придётся выполнить для получения результата.
При этом наименьшее значение считается лучшим случаем
и
обозначается TA (d ),
а наибольшее считается худшим случаем и
обозначается TA (d )
С использованием введённых обозначений для предыдущего алгоритма
получим: TA (d ) =1 и TA (d ) =4.
Вместе с тем существуют
алгоритмы, для которых рассчитать функцию
трудоёмкости описанным способом вообще невозможно. Поэтому место точного
расчёта количества операций используется приближённая оценка, приближённый
вид функции при дополнительном условии, выражающемся в том, что аргумент
функции стремится к бесконечности. В этом случае говорят о сложности
алгоритма, а не о функции трудоёмкости.
14.06.2025
34
35.
Используем теперь введенные понятия для анализа алгоритмаопределения максимального элемента, основная часть которого имеет
вид:
MaxElem=a[1]; i=2; while (i<=n) { if (a[i]>MaxElem) MaxElem=a[i]; i++;}
При подсчёте количества действий, выполняемых на одной итерации
цикла, возникает осложнение, связанное с тем, что внутри цикла имеется
ветвление Неравенство a[i]>MaxElem удовлетворяется для одних
элементов массива и не удовлетворяется для других.
Следовательно, сколько именно раз окажется выполненным оператор
MaxElem=a[i] существенно зависит от исходного массива a.
Получается, что в этом алгоритме невозможно в принципе определить вид
обычной функции трудоёмкости.
Но зато очень просто определить лучший и худший случаи. А именно: в
лучшем случае оператор MaxElem=a[i] не выполнится ни разу, а в худшем
случае этот оператор будет выполняться каждый раз, для каждого
очередного элемента массива.
14.06.2025
35
36.
В лучшем случае на каждой итерации выполняется всего четыре действия(i<=n, a[i]>MaxElem, i++), следовательно, функция трудоёмкости лучшего
случая имеет вид TA (d )=4n+2
Худший случай возникает, когда каждый следующий элемент массива
оказывается больше предыдущего, то есть исходный массив упорядочен
по возрастанию значений его элементов. Именно в этой ситуации
неравенство a[i]>MaxElem
удовлетворяется каждым следующим
элементом массива и, следовательно, на каждой итерации
цикла
добавляется ещё одно действие MaxElem=a[1]. Отсюда функция
трудоёмкости худшего случая имеет вид TA (d ) =5n+2
Аналогичные ситуации возникают и для функции объёма памяти и из тех
же самых соображений приходится рассматривать наименьший и
наибольший объём памяти, который потребуется алгоритму, и обсуждать
функцию объёма памяти лучшего и худшего случаев.
При анализе алгоритмов обычно интересуются самым плохим вариантом
— худшим случаем, в котором для получения результата требуется
выполнить максимально возможное количество действий, или выделить
максимально возможный объём памяти.
14.06.2025
36
37.
КлассическийБыстрый
Алгоритм с
барьером
Лучший случай
11
9
4
Худший случай
8n 3
5n 1
3n 4
Функция
объёма памяти
4n+20
4n+12
4n+16
Во всех рассмотренных вариантах построения алгоритма поиска
максимальное количество операций, которое необходимо выполнить для
получения результата, линейно зависит от количества элементов в
рассматриваемом массиве. Поэтому все эти алгоритмы называются
алгоритмами линейного поиска. Говорят также, что эти алгоритмы
имеют линейную вычислительную сложность.
14.06.2025
37
38.
Найдём, например, трудоёмкость худшего случая для классическогоалгоритма, если на его вход подается массив с размерностью, скажем,
n=10. По второй строке таблицы находим, что трудоёмкость классического
алгоритма в этом случае равна 83.
Теперь найдем трудоёмкость худшего случая алгоритма с барьером для
массива из 20 элементов (то есть для n=20). По этой же таблице получаем,
что трудоёмкость в этом случае равна 84.
Другими словами, получается, что не для любых входов алгоритм с
барьером лучше, чем классический.
Для того чтобы результат сравнения оказался корректным у всех
неодинаковых входов, которые используются для выбора лучшего и
худшего случаев функции трудоёмкости алгоритма, должно быть нечто
общее, чтобы разница, например, в количестве элементов в массиве не
повлияла на значение функции.
Корректно выбирать лучший и худший случай только на всех входах с
одинаковым характерным размером. Для примеров с массивами это
означает, что при выборе лучшего и худшего случаев в качестве исходных
могут выбираться любые массивы, но с одной и той же размерностью n.
14.06.2025
38
39.
Функция трудоёмкости лучшего случая TA ( d ), d DnA представляетсобой минимальное значение функции трудоёмкости по всем возможным
входам с одной и той же длиной n : TA (d ) min TA (d )
d DnA
Функция трудоёмкости худшего случая TA ( D ), d DnA представляет
собой максимальное значение функции трудоёмкости по всем возможным
входам с одной и той же длиной n: TA (d ) max TA (d )
d DnA
Точно также с помощью выбора соответственно минимального и
максимального значений функции объёма памяти по всем возможным
входам с одной и той же длиной n вводятся функция объёма памяти
лучшего случая VA (d ) min VA (d ) и функция объёма памяти худшего
случая VA (d ) max VA (d ) d DnA
d DnA
Заметим, что практический интерес, в основном, представляют функции
худшего случая, поскольку именно они даёт верхнюю границу количества
операций и объёмов памяти, которые потребуются для алгоритма: меньше
может быть, но больше — никогда.
14.06.2025
39
40.
Вычислительная сложность алгоритмов и задачОдним из существенных моментов решения задачи на компьютере
является определение необходимых для выполнения программы, которая
реализует её решение, аппаратных и программных ресурсов. Нехватка
любого из необходимых ресурсов может сделать невозможным
выполнение такой программы
Вычислительными ресурсами называются любые компоненты
компьютера: процессоры, оперативная память, дисковые накопители,
дисплеи, принтеры, линии связи и т.д., а также программы и данные,
которые выделяются, расходуются или занимаются программой в
процессе её выполнения.
Требования алгоритмов и программ к таким компонентам, как принтер,
сканер, микрофон, звуковые колонки и т.д., а также программные ресурсы
операционной системы и стандартных библиотек обычно не обсуждаются,
и под вычислительными ресурсами понимают только запросы к времени
выполнения и памяти.
Потребности задач в ресурсах компьютера определяются
потребности в них алгоритмов и программ решения этих задач.
14.06.2025
через
40
41.
Самый существенный вычислительный ресурс — процессорное время невсегда может быть выделен выполняющейся программе в необходимом
количестве, прежде всего потому, что неудачно разработанная программа
может занять процессор не только на несколько часов, но и на несколько
тысяч лет и даже более, что физически невозможно осуществить
Необходимо учитывать, что в целом ряде проблемных областей время
выполнения программы является критически значимым фактором. Это, в
основном, системы реального времени (бортовые авиационные и
космические, оборонные системы, системы управления технологическими
процессами — выплавкой стали, химическим производством и т.д.), в
которых несвоевременное получение результатов выполнения программы,
осуществляющей управление системой, может привести к самым тяжёлым
последствиям, вплоть до физической потери объекта управления. Для
таких программ доступ к процессору должен быть предоставлен
мгновенно, как только он потребуется, и на всё необходимое для
выполнения программы время.
14.06.2025
41
42.
Вместе с тем совершенно некорректно говорить об общей эффективностипрограммы, учитывая только временные требования, поскольку они
сложным образом связаны с требованиями к памяти. Причём требования к
памяти, также как и потребности в процессорном времени могут оказаться
неудовлетворёнными как из-за их физической нехватки в компьютере, так
и из-за плохой организации программы.
Определение требований алгоритма или его программной реализации к
вычислительным ресурсам, особенно к процессорному времени и объёму
памяти является необходимым этапом в разработке и реализации
алгоритмов.
Умение
определять требования алгоритма к ресурсам позволяет
разобраться с ещё одной проблемой. Если для решения одной и той же
задачи построено несколько различных алгоритмов, то закономерно
возникает вопрос: какой из них лучше?
Более эффективным логично считать алгоритм,
наименьшую память и выполняющийся быстрее всех.
14.06.2025
занимающий
42
43.
В определении трудоёмкости фигурирует ещё одно понятие «количестводействий», которое, вообще говоря, необходимо обсуждать отдельно,
уточняя, о каких именно действиях идёт речь.
Дело в том, что различные исполнители алгоритмов обладают разными
наборами доступных им действий — разными системами команд. Кроме
того, различные исполнители одно и то же действие выполняют за разное
физическое время.
14.06.2025
43
44.
В общем случае потребности во времени и в памяти существеннымобразом зависят от возможностей исполнителя алгоритма, от того какие
действия ему доступны, как много времени он затрачивает на их
выполнение, и какой объём памяти ему для этого требуется.
Поэтому вначале необходимо определить вычислительные возможности
исполнителя, и только после этого искать обсуждаемые функции.
Моделью вычислений называется множество операций, входящих в
систему команд исполнителя алгоритмов, для каждой из которых известны
временные и объёмные расходы на выполнение.
Выше была использована модель вычислений, ориентированная на язык
программирования высокого уровня. В этой модели к отдельным
действиям во время подсчёта их количества относятся различные
операции, которые допускаются к использованию в программах
конкретным языком программирования, причём фрагменты текста
программ, связанные с организацией обмена данными, не учитываются.
Для краткости такую модель будем называть языковой моделью
вычислений.
14.06.2025
44
45.
Языковая модель вычислений предполагает, что программа выполняетсяна однопроцессорном, одноядерном компьютере фон Неймановской
архитектуры. Это означает, что все действия выполняются строго
последовательно.
В теоретических построениях, если это не оговорено явно, в качестве
модели вычислений используется детерминированная машина Тьюринга,
которая
выполняет
все
действия
программы
также
строго
последовательно.
Вычислительной сложностью называется характеристика алгоритма,
которая задаётся парой функций,
определяющих зависимости
трудоёмкости и объёма памяти от характерного размера входа алгоритма.
Изучение зависимости вычислительной сложности от характерного
размера входа алгоритма является предметом теории вычислительной
сложности. В этой теории ищется ответ на один из важнейших вопросов
разработки алгоритмов: «Как изменяется время исполнения алгоритма и
объём требуемой памяти в зависимости от размера входа?».
14.06.2025
45
46.
В настоящее время основными задачами, решаемыми в теории сложностивычислений, являются:
практическое получение явного вида функций трудоёмкости и объёма
памяти конкретных алгоритмов и программ;
асимптотический анализ вычислительной сложности алгоритмов при
неограниченном возрастании размеров их входов;
классификация алгоритмов и задач по классам сложности;
получение нижних оценок, которые задают минимально возможное
время получения решения анализируемых задач на компьютере.
14.06.2025
46
47.
Асимптотическая сложность алгоритмовНа практике выявлена общая закономерность анализа вычислительной
сложности алгоритмов: несмотря на то, что функции трудоёмкости и
объёма памяти в ряде случаев могут быть определены точно, усилия на их
нахождение не всегда оправдываются.
Кропотливая работа по анализу текста алгоритма может оказаться
проведённой впустую, так как при больших размерах входа вклад
постоянных множителей и слагаемых низших порядков становится весьма
малым, и, следовательно, можно ограничиться только рассмотрением
старшего члена полиномиального выражения функции трудоёмкости или
объёма памяти.
Точный вид функций вычислительной сложности приходится отыскивать
только в тех случаях, когда необходимо надёжно прогнозировать время
выполнения реальных программ на реальных входах, а также сравнивать
эффективности алгоритмов при относительно малых размерах входа. В
подавляющем большинстве остальных случаев можно ограничиться
только приближенной оценкой этих функций.
14.06.2025
47
48.
Способы получения приближенных оценок, которые обеспечиваютвозможность проведения упрощённого обсуждения вычислительной
сложности алгоритмов, рассматриваются в теории асимптотического
анализа алгоритмов.
Асимптота — (от др. греч. ἀσύμπτωτος) прямая, неограниченно
приближающаяся, но не касающаяся кривой, которая имеет уходящую на
бесконечность ветвь.
В асимптотическом анализе сложности алгоритмов ищется оценка порядка
роста функций вычислительной сложности при неограниченном
увеличении характерного размера входа n.
Здесь термин «оценка» подразумевает приближённость получаемых
результатов, а «порядок роста» — скорость увеличения значений функции
при увеличении размера входа.
Причём эта скорость не определяется, как в стандартном математическом
анализе с помощью нахождений производной.
В асимптотическом анализе сравнивают исследуемую функцию с
некоторой
стандартной
элементарной
функцией,
которая
рассматривается как образец скорости роста. Это гораздо проще и
нагляднее, чем вычисление производной и её дальнейший анализ.
14.06.2025
48
49.
Например, говорят:«растёт не быстрее, чем n2», «имеет порядок роста 2n»Приближённые оценки порядков роста функций трудоёмкости и объёма
памяти при неограниченном увеличении характерного размера входа
называются асимптотической сложностью, или более кратко
сложностью алгоритма.
Таким образом, когда говорят «сложность алгоритма» обычно
подразумевается не «вычислительная сложность», представленная
функциями трудоёмкости и объёма памяти, а «асимптотическая
сложность», то есть приближённая оценка порядка роста этих функций.
Асимптотическая сложность является:
приближенной оценкой увеличения значений функций трудоёмкости и
объёма памяти при увеличении размера входа алгоритма;
эти оценки справедливы только в области больших значений аргумента.
Практический смысл использования асимптотической сложности состоит в
том, что находить такие оценки значительно проще, чем определять
точный вид функции трудоёмкости и объёма памяти.
14.06.2025
49
50.
Кроме того, алгоритм с меньшей асимптотической сложностью обычноявляется более эффективным для всех входных данных, за исключением,
возможно, данных с малым характерным размером входа. Это позволяет
не только характеризовать алгоритмы с позиции достаточности ресурсов,
но и сравнивать их между собой с точки зрения эффективности.
Асимптотические обозначения
В асимптотическом анализе сложности алгоритмов используются
стандартные обозначения, принятые в математическом асимптотическом
анализе. Исходными в этом анализе являются довольно простые
математические понятия мажоранты и миноранты.
Мажоранта F1 и миноранта F2 для множества функций
14.06.2025
{ 1 ( x ), 2 ( x ), 3 ( x )}
50
51.
Мажоранта некоторого набора функций это функция, ограничивающая нарассматриваемом промежутке весь набор функций сверху, а
миноранта — функция, ограничивающая этот же набор снизу.
Пусть функции f(n) и g(n) определены и имеют область значений на
множестве натуральных чисел N. Говорят, что функция g(n) мажорирует
функцию f(n) (или является мажорантой функции f(n)), если существуют
действительное число c>0 и натуральное N такие, что для 0 f(n) cg(n)
для n N.
Аналогичным образом, функция g(n) минорирует функцию f(n) (или
является минорантой функции f(n)), если существуют действительное
число c>0 и натуральное N такие, что для f(n) cg(n) 0 для n N.
14.06.2025
51
52.
С понятием мажоранты тесно связано одно из основных асимптотическихпонятий O(g(n)), которое читается так: «O большое от g(n) ».
Запись f(n)=O(g(n)) означает, что функция cg(n) является мажорантой для
функции f(n). Обычно для краткости говорят, что мажорантой является
функция g(n), а не cg(n).
В асимптотическом анализе алгоритмов обозначение « O большое»
используется для сравнения поведения функций трудоёмкости и объёма
памяти с некоторыми стандартными функциями при больших значениях
аргумента, точнее при n ∞.
Отметим, что:
умноженная на константу с мажорирующая функция g(n) не обязана
быть больше функции f(n) для всех натуральных n. Достаточно, чтобы
нашлось некоторое целое число N, после которого выполняется f(n)<cg(n).
значение константы с может выбираться достаточно произвольным
образом, главное, что бы нашлось хотя бы одно такое значение, для
которого неравенство 0 f(n) cg(n) удовлетворяется для всех достаточно
больших n.
14.06.2025
52
53.
если существует хотя бы одна константа с, для которой выполненоосновное требование определения, то таких констант найдется
бесконечно много, причём от выбора константы зависит граничное
значение N.
С математической точки зрения определение означает, что f ( n ) O ( g ( n ))
является несимметричным отношением функций f(n) и g(n), которое
можно считать аналогом отношения a<b действительных чисел a и b.
С точки зрения асимптотического анализа сложности алгоритмов можно
считать, что обозначение f ( n ) O ( g ( n )) является краткой формальной
записью следующих эквивалентных утверждений:
для всех достаточно больших значений аргумента функция f(n) меньше,
чем функция g(n), умноженная на некоторое число c;
f(n) растёт со скоростью, имеющей порядок g(n) ;
f(n) растёт со скоростью не превышающей g(n).
14.06.2025
53
54.
Для полного понимания рассматриваемого обозначения необходимоуточнить один важный момент: в асимптотических обозначениях отдельно
взятая запись вида O(g(n)) обозначает множество функций, для которых
g(n) является мажорантой, то есть множество функций, которые растут
медленнее, чем g(n) с точностью до постоянного множителя.
Такая запись может означать ещё и какую-либо неопределённую функцию,
про которую известно только то, что она принадлежит множеству O(g(n))
Запись вида
f(n)=O(g(n)) указывает, что конкретная функция f(n)
принадлежит
указанному
множеству
G(g(n)).
В
стандартных
математических обозначениях этот факт записывается так: f ( n ) O ( g ( n ))
При рассмотрении асимптотики функций трудоёмкости используется
следующая терминология:
запись вида T(n)=O(g(n)) означает, что мажоранта g(n) представляет
собой верхнюю асимптотическую оценку;
про отдельно взятую запись вида O(g(n)) говорят: «O большое от g(n)
является временно́й асимптотической сложностью», при этом
прилагательное «асимптотический» чаще всего опускают и говорят
«временна́я сложность» алгоритма.
14.06.2025
54
55.
С практической точки зрения, найденная для некоторого алгоритмаасимптотическая оценка O(g(n)) сложности обеспечивает уверенность в
том, что ни при каких обстоятельствах даже в наихудшем случае время
выполнения или объём памяти этого алгоритма не окажется больше, чем
c(g(n)).
Из сказанного следует, что O(g(n)) является приближённой оценкой
функции трудоёмкости или объёма памяти худшего случая.
В точки зрения техники проведения анализа асимптотическая оценка
исключает из рассмотрения в функции трудоёмкости или объёма памяти
различные коэффициенты и все члены младших порядков, оставляя
только старший член.
14.06.2025
55
56.
На практике довольно часто возникает необходимость в нахождении нетолько верхних, но и нижних оценок сложности, которые должны
определять минимально необходимую потребность в процессорном
времени и объёме памяти.
Для этого в асимптотическом анализе используется связанное с
минорантой понятие «Омега большое».
Отношение f ( n ) ( g ( n )) указывает, что g(n) это нижняя асимптотическая граница роста функции f(n), и при этом определяет множество
функций, которые растут быстрее, чем g(n) c точностью до постоянного
множителя.
С математической точки зрения f ( n ) ( g ( n )) является несимметричным отношением функций f(n) и g(n), которое является аналогом
отношения a>b для вещественных чисел a и b.
С практической точки зрения, найденная для некоторого алгоритма
асимптотическая оценка Ω(g(n)) обеспечивает уверенность в том, что ни
при каких обстоятельствах, даже в лучшем случае время выполнения или
объём памяти этого алгоритма не окажется меньше, чем cg(n).
Таким образом, эта оценка является приближением для функции
трудоёмкости или объёма памяти лучшего случая .
14.06.2025
56
57.
Особенности использования асимптотических обозначенийВсе асимптотические обозначения имеют некоторые особенности в их
толковании и использовании. Эти особенности одинаковы для всех
обозначений, поэтому обсудим их только на примере обозначения O(g(n))
Итак, O(g(n)) является:
указанием, на то, что g(n) это мажоранта для некоторого множества
функций;
определяет верхнюю асимптотическую оценку границы роста сложности;
обозначает множество функций ограниченных сверху функцией g(n) ;
обозначает некоторую неопределённую функцию из этого множества.
Запись T(n)=O(g(n)) показывает, что:
функция g(n) является мажорантой для конкретной функции T(n);
функция T(n) имеет скорость роста не больше, чем функция g(n);
функция T(n) принадлежит множеству O(g(n)).
14.06.2025
57
58.
Для всех асимптотических обозначений записи вида T(n)=O(g(n)) иT(n) O(g(n)) являются эквивалентными.
Толкование O(g(n)) как некоторой неопределённой функции позволяет
включать это обозначение в выражения.
Например, в математических справочниках можно встретить выражения
для приближённого вычисления n!, которые называют формулами
Стирлинга: ln n! n ln n n O (ln n )
В этой формуле, как и во всех аналогичных ситуациях, применение
асимптотического обозначения имеет следующий смысл.
Любое асимптотическое обозначение, включённое в некоторое
выражение, следует рассматривать, как некоторую функцию, которая
принадлежит соответствующему множеству, причём имя и точный вид её
не имеет никакого значения.
Поэтому, например, в приведённом варианте формулы Стирлинга O(lg n)
следует понимать, как прибавляемую к n ln(n)-n некоторую функцию f(n),
относительно которой известно только то, что она не превышает ln(n) при
n ∞.
ln n! n ln n n f ( n ) f (n ) O (ln n )
14.06.2025
58
59.
Получение верхних асимптотических оценокПрактическое определение верхних асимптотических оценок опирается на
ряд математических свойств отношения O(g(n)):
Отношение «O большое»:
транзитивно, то есть, из
f(n)=O(h(n));
f(n)=O(g(n)) и g(n)=O(h(n)) следует, что
рефлексивно, то есть f(n)=O(f(n));
несимметрично, так как если f(n)=O(g(n)), то g(n)=Ω(f(n)).
замкнуто относительно операций сложения и умножения на скаляр.
Если f1(n)=O(g(n)) и f2(n)=O(g(n)), то f1(n)+f2(n)=O(g(n)) и сf1(n)=O(g(n)), для
любого с>0.
Последнее свойство означает, что любые линейные комбинации функций,
которые имеют порядок роста не больший, чем g(n), имеют тот же самый
порядок роста.
14.06.2025
59
60.
Для основных элементарных функций, которые используются васимптотическом анализе сложности в качестве образцов скорости роста,
доказаны следующие утверждения:
Если числа a>1 и b>1, то log a n O(log b n ) и log b n O(log a n )
Это позволяет в асимптотической оценке сложностей вообще не
указывать основание у логарифмов: можно выбрать любое большее
единицы основание, оценка от этого не измениться.
Для любого основания a>1, log a n O ( n )
Если n>1, и для целых показателей степеней r и s выполнено
неравенство r s, то nr=O(ns). Например, n2=O(n3). Это свойство, вместе со
свойством замкнутости позволяет утверждать, что любой полином
мажорируется его старшим членом. Точнее: пусть имеется полином
k
k
k 1
p
(
n
)
O
(
n
)
,
тогда
pk (n ) ak n ak 1n ... a1n a0
k
Для a>1 n O (a )
n
Для a>0 a
n
O(n!)
Для n>0 n! O(n )
n
14.06.2025
60
61.
Перечисленные свойства дают возможность сформулировать простыеправила, с помощью которых находятся верхние асимптотические оценки
алгоритмов.
Правило 1. Не содержащие вызовов подпрограмм линейные участки
алгоритмов и участки с ветвлениями всегда определяют некоторое
конечное количество действий, поэтому их асимптотическая сложность
O(1).
Запись O(1) означает, что мажорантой является функция g(n)=1.
Константа c, на которую в соответствии с определением требуется
умножить эту функцию, может быть выбрана как угодно большой, такой
большой, чтобы её значение превысило любое количество действий
любого линейного участка или участка с ветвлением, поэтому для всех
таких алгоритмов O(1) является верхней оценкой сложности.
Правило 2. Асимптотическая сложность правильно построенных простых
циклов с параметром и их аналогов в других формах записи операторов
циклов есть O(n).
Оборот «правильно построенный цикл» подразумевает, что при записи
оператора цикла не нарушены синтаксические правила языка, а также
обеспечена завершаемость цикла.
14.06.2025
61
62.
Правило 3. Асимптотическая сложность правильно построенных кратныхциклов с параметром и их аналогов в других формах записи оператора
цикла есть O(nk) , где k — кратность цикла.
Например, опираясь только на тот факт, что в алгоритме нахождения
суммы матриц потребовалось построить двойной цикл, можно сразу
записать, что асимптотическая сложность этого алгоритма O(n2), а для
алгоритма умножения матриц эта сложность равна O(n3).
Сказанное относится только к циклам, для которых известно точное, либо
максимально возможное количество итераций. Для более сложных
вариантов построения цикла, как, например, в алгоритме решения задачи
о
накоплении
сумм с
бесконечным
количеством
слагаемых,
асимптотический анализ сложности проводится с привлечением
соответствующих задаче математических методов.
14.06.2025
62
63.
Правило 4. Получение асимптотических оценокподпрограмм, полученных разбиением на подзадачи.
для
рекурсивных
Довольно часто при решении задачи осуществляется её разделение на
несколько подзадач, с соответствующим уменьшением характерного
размера входа для каждой из подзадач. С применением этого способа в
его простейшем варианте построен, например, алгоритм бинарного
поиска, в котором область поиска на каждом шаге сужается в два раза.
Для определённости будем считать, что исходная задача разбивается на
a 1 подзадач, и при этом характерный размер входа каждой из подзадач
уменьшается в c>1 раз.
В этом случае может быть сформулировано рекуррентное уравнение вида
T (n) aT (n / c) bn k
В уравнении учтено, что при рекурсивном разбиении на a подзадач в
подпрограмме возникает столько же рекурсивных вызовов, причём у
каждого из них размер входа уменьшается в c раз.
Кроме того, само разбиение потребовало
некоторого количество
дополнительных действий, которые учтены с помощью слагаемого bnk.
14.06.2025
63
64.
Пусть r=ac-k, доказано, чтоуравнения имеет вид:
решение обсуждаемого рекуррентного
T(n)=O(nk), если r<1;
T(n)=O(nk logcn) , если r=1;
T (n ) O(n
logc a
) , если r>1
Например, для алгоритма бинарного поиска имеем: деление на
подзадачи не выполнялось, следовательно, a=1; характерный размер
входа уменьшен в два раза — c=2; дополнительные действия равны
некоторой константе b и от n не зависят, поэтому k=0. Для найденных
значений коэффициентов параметр r=ac-k=1, поэтому сразу же получаем
T(n)=O(log n).
14.06.2025
64
65.
Пример оценки сложности алгоритмов. Задача сложения матрицi=1;
while (i<=n)
{j=1;
while (j <=m) {c[i][j]=a[i][j]+b[i][j]; j++;}
i++;}
Подсчёт с помощью нахождения функции трудоёмкости
До внешнего цикла одно присваивание. Во внешнем цикле: одно сравнение, одно
сложение и два присваивания ─ 4 n. Во внутреннем цикле: одно сравнение, два
сложения и два присваивания ─ 5 n m. Таким образом общее количество
операций P равно P=5 n m+4 n+1. Пусть N=max(n,m) – интегральный аргумент
функции сложности. Тогда количество операций имеет порядок О(N2). Таким
образом алгоритм имеет полиномиальную сложность, относится к классу
сложности P.
Асимптотическая оценка по правилу 3: правильный цикл кратности 2 ─ оценка
сложности O(N2).
14.06.2025
65
66.
Классификация функций вычислительной сложностиОписанные способы определения функций трудоёмкости и объёма памяти
дают возможность определить вычислительную сложность большинства
алгоритмов, программ и подпрограмм.
В рассмотренных примерах были получены различные виды функций
трудоёмкости:
логарифмическая в алгоритме бинарного поиска;
линейная в алгоритме классического линейного поиска;
квадратичная в алгоритме сложения матриц;
кубическая в алгоритме умножения матриц;
алгоритмы с показательной функцией.
Чтобы определить, какой вид функции может привести к принципиальной
нехватке ресурсов, целесообразно хотя бы приблизительно оценить
требуемое процессорное время в зависимости от характерных размеров
входов.
14.06.2025
66
67.
Шкала оценок асимптотических сложностейПеречисленные правила и примеры их применения показывают, что в
процессе анализа алгоритмов получается довольно много схожих и даже
одинаковых оценок, которые тесно связаны со структурой изучаемого
алгоритма.
Это наблюдение позволяет выбрать типичные результаты анализа в
качестве своеобразных образцов скоростей роста для исследуемых
алгоритмов.
1. log a N, a>1
2. N
3. N log a N, a>1
4. Nk, k≥1
5. aN, a>1
6. N!
7. NN
Если уровни этой шкалы соотнести с введенными выше полиномиальным
и экспоненциальным классами сложностей алгоритмов, легко обнаружить,
что алгоритмы с оценками уровней 2–4 относятся к полиномиальному
классу P, а алгоритмы 5-го уровня — к экспоненциальному классу EXP
14.06.2025
67
68.
Сложность алгоритмов с логарифмическими оценками O(log n) возрастаетзначительно медленнее, чем у любого алгоритма класса P, следовательно,
такие алгоритмы обладают очень низкими требованиями к ресурсам и
имеют очень хорошие вычислительные свойства.
Сложность алгоритмов с оценками O(n!) и O(nn) увеличивается
значительно быстрее, чем даже у алгоритмов класса EXP. Поэтому,
алгоритмы с такими оценками на практике почти не применимы, они имеют
в основном теоретический интерес.
Замечания к использованию асимптотических оценок
Пользуясь легко определяемыми асимптотическими оценками для
сравнения алгоритмов с точки зрения их эффективности, необходимо
проявлять осторожность и всегда помнить о том, что эти оценки
справедливы только для больших значений характерных размеров входов.
Если алгоритмы планируется сравнивать и для малых размеров входов,
то для определения более эффективного алгоритма необходимо
учитывать ещё и существование мультипликативной константы c, на
которую при формировании неравенства T(n)<cg(n) умножается
мажорирующая функция g(n)
14.06.2025
68
69.
Если например, сравнивать два алгоритма решения одной и той жезадачи, A1 с оценкой O(n2) и A2 с оценкой O(n3), то с точки зрения
асимптотической теории алгоритм A1 эффективнее алгоритма A2, так как
для любых констант c1 и c2 подбором N можно добиться выполнения
неравенства c1n2<c2n3 , например, достаточно взять очевидное решение
этого неравенства N>c1/c2.
С другой стороны, если, предположим c1=1000000, а с2=100, то с2n3<c1n2
вплоть до достаточно большого размера входа n=10000.
Пусть теперь алгоритм A2 имеет
оценку O(2n) с той
же самой
мультипликативной константой c2. Тогда с22n<c1n2 вплоть до n=22. То есть
алгоритм с экспоненциальной сложностью окажется для этих входов
эффективнее, чем алгоритм с квадратичной сложность!
Следовательно, общий вывод о большей эффективности алгоритма без
учёта требования больших значений размера входа оказался ошибочным.
Значение мультипликативной константы может оказаться настолько
большим, что при малых размерах входов её роль перевесит роль
мажорирующей функции.
14.06.2025
69
70.
Кроме игнорирования роли мультипликативной константы при оценкесложности достаточно часто ограничиваются только получением
временны́х оценок, забывая о том, что существуют ещё и объёмные
оценки. Известны примеры, когда эффективные с временно́й точки зрения
алгоритмы требуют таких больших объёмов оперативной памяти, что этот
фактор полностью уничтожает преимущество от выигрыша во времени,
поскольку для хранения данных приходится использовать очень
медленную внешнюю память.
Таким образом, важно помнить, о том, что вычислительная сложность
требует нахождения оценки не только для функции трудоёмкости, но и
функции объёма памяти
Если создаваемая программа будет использоваться для единичных
расчетов, то стоимость и время написания и отладки программы окажется
преобладающим фактором. В этом случае более медленный, но более
простой в реализации алгоритм может оказаться в целом эффективнее,
чем более быстрый, но требующий огромных вложений в его создание.
И, наконец, имеется особый класс численных алгоритмов, связанный с
научно-техническими
расчётами,
в
которых
кроме
временно́й
эффективности необходимо учитывать достигаемую точность расчётов и
устойчивость алгоритмов к различного рода погрешностям данных
14.06.2025
70
71.
Верификация программ. Инвариант цикла.Инвариантом цикла называется выражение, значение которого остается
постоянным во время всех выполнений тела цикла.
Пример инварианта для цикла накопления суммы.
S:=0; {Начальное значение накапливаемой суммы}
i:=1; {накопление суммы с первого слагаемого }
1) while i N do {пока есть еще не рассмотренные слагаемые}
begin
S:=S + x[i];
{добавление очередного слагаемого}
i:=i+1 {переход к следующему слагаемому}
2) end;
3)
Для данного цикла инвариантом является выражение I:
N
I S x[k ]
k i
До цикла в точке 1) программы S=0, i=1, инвариант I равен искомой сумме.
Внутри цикла в точке 2) программы. После первого прохода S=x[1], i=2,
суммирование идет от второго слагаемого. Величина I не изменилась.
После цикла в точке 3) программы величина I не изменилась, i>N, второе
слагаемое равно нулю и следовательно, S есть искомый результат.
14.06.2025
71
72.
Для одного и того же цикла можно построить несколько инвариантов.Желательно подобрать такой инвариант, который связан с конечной целью
выполнения цикла.
Если такой инвариант существует и, кроме того, показано, что цикл
выполняется конечное число раз, то можно утверждать, что алгоритм
правильный и результаты его выполнения являются верными искомыми
результатами. Такие рассуждения называются верификацией алгоритма
В стандартных операторах цикла while B do S требование конечности
означает, что после конечного количества проходов по циклу условие B
должно стать ложным. Для доказательства оканчиваемости с циклом обычно
связывается некоторая ограниченная целочисленная убывающая функции
или последовательность, элементы которой зависят от переменных
программы, и показывается, 1) что ее начальное значение или начальный
элемент положительны и при этом B=true; 2) при каждом выполнении цикла
значение функции уменьшается (происходит переход к следующему элементу
последовательности); 3) при достижении конечного значения (элемента
последовательности) (обычно 0 или -1) условие В=false
В нашем случае, в качестве такой последовательности можно взять bi=N-i+1
Имеем: 1) b1=N>0; i N = true; 2) при увеличении i bi уменьшается; 3) при
i=N+1, bi=0 и i N = false.
14.06.2025
72
73.
Тема 3. РЕКУРСИЯВ математике для решения подавляющего большинства задач используются
методы, которые в конечном счете могут быть сведены к одному из двух
базовых способов: итерации или рекурсии.
Итерация означает неоднократное повторение одних и тех же действий,
которое после некоторого количества шагов приводит к желаемому результату.
Характерным примером итерационного способа решения задачи являются
методы последовательных приближений решения нелинейных уравнений, в том
числе метод касательных, метод хорд и т.д.
f ( x ) 0;
x (x );
x0 a;
xn ( xn 1 ), n 1,2,... | xk xk 1 |
С точки зрения структуры алгоритма итерация
представляет собой циклический алгоритм
Рекурсия представляет собой ссылку при описании объекта, действия на
описываемый объект, действие. Рекурсия означает решение задачи с помощью
сведения решения к самому себе. При этом вычисления зависят от других, в некотором смысле более простых (обычно меньших) значений аргумента или аргументов задачи. Полностью аналогичные механизмы используются в базовой
теории рекурсивных функций, в методе математической индукции, а также в рекуррентных последовательностях, например, ak=2ak-1+k, k>0, a0=1
14.06.2025
73
74.
Пример 1. Вычисление факториала P=n!, n – целое число.Обычно для вычисления факториала целого числа используется итерационный
способ, основанный на многократном домножении величины, в которой
накапливается результат, на очередной сомножитель: Pi := Pi-1 i, i=1,2,…,k.
int factorial ( int k)
//итерационная подпрограмма вычисления k!
{
int P=1; //Начальное значение накапливаемого результата
for ( int i=1; k<=n; i++ ) {P*=i; } //цикл по накоплению произведения
return P; // Возвращаемое значение
}
L=factorial(5);
k
5
14.06.2025
P
i
24
120
16
2
2
1
4
5
3
6
i<=k
i=6≤k=5
i=1≤k=5
true
i=2≤k=5
i=4≤k=5
i=5≤k=5
i=3≤k=5→→false
factorial
120
74
75.
def ft(n):p=1
for i in range(2, n+1):
p*=i
return p
14.06.2025
75
76.
Эту задачу можно решить и с помощью рекурсии, базируясь на следующихсоображениях:
k! 1 2 3 ... k 1 2 3 ... (k 1) k (k 1)! k
Следовательно, P(k)=k! можно определить таким образом:
1, k 1
P(k )
P(k 1) k , k 1
int factorial1 (int k)
// рекурсивная подпрограмма вычисления k!
{
return1;
1;// терминальная ветвь
if (k==1) return
else return
return factorial1(k-1)*k;
factorial1(k-1)*k; // рекурсивная ветвь
}
Рекурсивные алгоритмы обычно получаются на основе математической постановки задачи. Самое важное при построении рекурсивного алгоритма: увидеть
одинаковые действия на текущем и предыдущем шаге вычислений (действий).
14.06.2025
76
77.
def ftr(k):if k==1:
return 1
else:
return ftr(k-1)*k
14.06.2025
77
78.
L=factorial(5);Первый экземпляр описания
k1=5
if (k1==1) then return 1; else return factorial1(k1-1)*k1;
result= 120
Второй экземпляр описания k2=4
if (k2==1) then return 1; else return factorial1(k2-1)*k2;
result= 24
Третий экземпляр описания
k3=3
if (k3==1) then return 1; else return factorial1(k3-1)*k3;
result= 6
Четвёртый экземпляр описания
k4=2
if (k4==1) then return 1; else return factorial1(k4-1)*k4;
result= 2
Пятый экземпляр описания
k5=1
if (k5==1) then return 1; else return factorial1(k5-1)*k5;
1
14.06.2025
78
79.
Исполнитель рекурсивного алгоритма сводит неизвестное к другому неизвестному,накапливая информацию (прямой ход) и откладывая фактические вычисления до
момента, когда выполнится условие, позволяющие напрямую вычислить искомое
значение. Затем выполняется обратный ход рекурсии.
Основные достоинства рекурсии:
простота математической формулировки;
простота алгоритма и его реализации
Основные недостатки рекурсии:
дополнительные расходы оперативной памяти;
дополнительные временные расходы;
возможен переход сложности в класс EXP.
14.06.2025
79
80.
Пример 2. Задача вычисления суммыN
S xi x1 x2 x3 ... x N
i 1
Итерационный подход
Переменная S рассматривается как текущее значение накапливаемой суммы.
Организуется перебор слагаемых. Каждое очередное слагаемое вычисляется
и добавляется к величине S. После добавления последнего слагаемого
значение S будет представлять собой искомый результат.
Тело цикла образуют следующие действия: вычисление очередного слагаемого,
добавление его к текущему значению S и переход к следующему слагаемому.
Условие, при котором выполняются эти действия ─ наличие еще не вычисленных и
не добавленных слагаемых.
До начала вычислений уже накопленное значение суммы равно нулю, а
накапливать сумму можно начать с первого слагаемого.
14.06.2025
80
81.
const N=100;type massiv = array [1..N] of real;
function SumI( A: massiv): real;
{Функция итерационного вычисления суммы элементов массива A}
var i:integer; S:real;
begin
{Инициализация цикла}
S:=0; {Начальное значение накапливаемой суммы}
i:=1; {накопление суммы с первого слагаемого }
while i N do {пока есть еще не рассмотренные слагаемые}
begin
S:=S + x[i];
{добавление очередного слагаемого}
i:=i+1 {переход к следующему слагаемому}
end;
result:=S {Возврат результата}
end.
14.06.2025
81
82.
Рекурсивный подходСхема рассуждений:
S= a1+a2+…+aN-1+aN = (a1+a2+…+aN-1)+aN =SN-1+aN
Отсюда непосредственно следует рекурсия:
0, k 0
S (k )
S (k 1) ak , k 1,2,..., N
Реализация алгоритма:
const N=100;
type massiv = array [1..N] of real;
function SumR( A: massiv;k:integer): real;
{Функция рекурсивного вычисления суммы элементов массива A,
k-количество элементов, K≤N}
begin
if k≤N then
{Проверка на превышение размерности массива}
if k=0 then {терминальная ветвь} result:=0
else {рекурсивная ветвь} result:=SumR(A,k-1)+A[K]
end.
14.06.2025
82
83.
const int n=100;float SumR(int k, float *A)
/* Функция рекурсивного вычисления суммы элементов массива A,
k-количество элементов, k≤n */
{
if (k<n) //проверка на превышение размерности
{
if (k < 0) return 0; //терминальная ветвь
else return SumR (k-1, A)+A[k]; // рекурсивная ветвь
}
}
main()
{ float A[n],S;
…
S=SumR(n-1,A);
…
}
14.06.2025
83
84.
def sum(x):’’’ Итерационное суммирование элементов списка x’’’
s=0.0
for c in x:
s+=c
return s
def sumr(x):
’’’Рекурсивное суммирование элементов списка x.’’’
if len(x)==0:
return 0
else:
return x.pop( )+sumr(x)
def sumr(x):
’’’Рекурсивное суммирование элементов списка x.’’’
b=x[:]
if len(b)==0:
return 0
else:
return b.pop( )+sumr(b)
14.06.2025
84
85.
Пример 3. Нахождение экстремального элемента массиваЗадан массив x ={x1,x2,…,xn}. Необходимо найти его наибольший элемент.
Итерационный подход
Пусть max ─ переменная, которая играет роль «кандидата на должность»
наибольшего элемента, i ─ номер очередного элемента массива.
const N=100;
type massiv = array [1..N] of real;
function MaxI( A: massiv): real;
{Функция итерационного вычисления наибольшего элемента массива A}
var i: integer; max:real;
begin
max:=A[1]; {назначение кандидатом первого элемента массива}
for i:=2 to N do {пока есть ещё не рассмотренные элементы}
if A[i]>max then max:=A[i]; {сравнение очередного с кандидатом и
при необходимости замена кандидата}
result := max
end.
14.06.2025
85
86.
Проведем проверку (тестирование) алгоритма на примере x={5, 3, 8, -1, 9, 7}x: array of integer; N, i, max: integer;
x[1]
x[2]
x[3]
x[4]
x[5]
x[6]
5
3
8
-1
9
7
N
i
max
6
2
3
4
5
6
7
5
8
9
i N
(i=7)
(i=2)
(i=3)
(i=4) (N=6)
(i=5)
(i=6)
(N=6)
false
true
x[i]>max
(x[4]=-1)
(x[2]=3)
(x[3]=8) >> (max=9)
(x[5]=9)
(max=5)
(max=8)
(max=5)
false
false
true
(x[6]=7)
read (N, x); {ввод размерности и значений элементов массива}
max:=x[1]; {назначение кандидатом первого элемента массива}
i:=2: {перебор остальных элементов массива, начиная со второго}
while i N do {пока есть ещё не рассмотренные элементы}
begin
if x[i]>max then max:=x[i]; {сравнение очередного с кандидатом}
i:=i+1 {переход к следующему элементу массива}
end;
write (max)
14.06.2025
86
87.
Рекурсивный подходСхема рассуждений:
max (a1,a2,…aN)=
max (a1,a2,…,aN-1,aN)= max(max(a1, a2,…,aN-1), aN)
Отсюда непосредственно следует рекурсия:
Пусть Mk=max(a1,…,ak),
a1, k 1
M (k )
max( M (k 1), ak ), k 2,3,..., N
Реализация алгоритма:
const N=100;
type massiv = array [1..N] of real;
function MaxR( A: massiv; k:integer): real;
{Функция рекурсивного вычисления максимального элемента массива A,
k-количество элементов, K≤N}
var m1:real;
begin
if k≤N then {проверка на превышение размерности массива}
end;
14.06.2025
if k=1 then {терминальная ветвь } result := A[1]
else begin {рекурсивная ветвь}
m1:=MaxR(A,k-1);
if m1>A[k] then result := m1 else result:=A[k];
end
87
88.
const int n=100;float MaxR(int k, float * a)
/* Функция рекурсивного вычисления максимального элемента массива a,
k-количество элементов, k<=n */
{
if (k<=n) // проверка на превышение размерности массива
{
if (k==1) return a[0]; // терминальная ветвь
else { // рекурсивная ветвь
float m1=MaxR(k-1 a);
if (m1>a[k]) return m1; else return a[k];
}
}
}
14.06.2025
88
89.
Пример 4.Рекурсивная печать элементов файла в обратном (или прямом) направлении
Схема рассуждений. Если файл не пуст, то выделяем головной элемент файла и
его хвостовую часть. Печатаем головной (текущий) элемент файла и совершаем
переход к его хвостовой части. Хвостовую часть можно рассматривать как самостоятельный файл. По-этому над хвостовой частью выполняем те же самые действия, что и над целым файлом.
Реализация алгоритма:
type fint=file of integer; var f:fint;
procedure printback (var f:fint); {рекурсивная печать элементов файла}
begin
if not eof(f) then
begin {рекурсивная ветвь}
read(f,a);
printback(f);
write(a)
{в Delphi}
write
(f^);
get(f);
printback(f)
read(f,a);
write(a);
printback(f)
Delphi}
get(f);
printback(f);
write(f^)
{в {в
обратном
порядке}
end
end;
begin reset(f); printback(f)
end.
14.06.2025
89
90.
Общие соображения по построению рекурсивных подпрограмм.Рекурсия может быть прямой:
procedure P(n); begin … P(n-1) … end;
или косвенной:
procedure P(n); begin … Q(n) … end;
procedure Q(n); begin … P(n-1) … end;
Должно существовать, по крайней мере, две ветви. Одна, содержащая
рекурсивное прямое или косвенное обращение к самой себе. Вторая
(терминальная) — не рекурсивное прямое задание. Если не будет первой ветви,
то очевидно что подпрограмма не рекурсивна. Если нет второй ветви, то
выполнение программы никогда не завершится.
Рекурсивной и терминальной ветвей может быть более одной. Если функция
возвращает логическое значение, то приходится формировать по крайней мере
две терминальные ветви по одной для возвращения значений true и false.
Даже при наличии только одной рекурсивной ветви может быть более одного вызова рекурсивной подпрограммы.
14.06.2025
90
91.
Пример 5. Числа Фиббоначи. Эти числа образуют элементы рекуррентнойпоследовательности, заданной по правилу: F1=1; F2=1; Fk=Fk-1+Fk-2, K≥3.
function Fib(k:integer):integer;
{Функция рекурсивного вычисления n-го числа Фиббоначи}
begin
if (k=1) or (k=2) then {терминальная ветвь} result:=1
else {рекурсивная ветвь} result:=Fib(k-1)+Fib(k-2)
end;
Рекурсивные вызовы функции Fib,
относящиеся к одному уровню рекурсии
inf Fib (int k)
// Функция рекурсивного вычисления n-го числа Фиббоначи
{
if ((k==1) || (k==2) ) return 1; //терминальная ветвь
else return Fib(k-1)+Fib(k-2); //рекурсивная ветвь
}
14.06.2025
91
92.
def fibr(n):’’’Рекурсивное нахождение n-го числа Фибоначчи’’’
if n==1 or n==2:
return 1
else:
return fibr(n-1)+fibr(n-2)
14.06.2025
92
93.
Рекурсивные вызовы, находящиеся в теле одной и той же подпрограммы, относятся к одному и тому же уровню рекурсии.На одном уровне рекурсии может находиться более одного рекурсивного вызова.
Глубиной рекурсии считается количество рекурсивных вызовов прямого хода,
находящихся на различных уровнях рекурсии.
14.06.2025
93
94.
Если каждый рекурсивный вызов изображать узлом дерева, то можно построитьдерево рекурсивных вызовов, высота которого равна глубине рекурсии.
L = Fib(5)
k=5
k=4
k=3
H=3
k=3
k=2
k=2
k=2
k=1
k=1
Высота дерева вызовов = глубина рекурсии = 3
14.06.2025
94
95.
Анализ дерева показывает возможные недостатки рекурсивного подхода:Неэффективность реализации рекурсивного алгоритма вычисления
чисел Фиббоначи из-за многочисленных дублирований вызовов с
одним и тем же значение аргумента.
Экспоненциальное нарастание количества вызовов, если на одном
уровне рекурсии находится более одного вызова
Экспоненциальное количество вызовов означает принадлежность алгоритма к
классу сложности EXP.
В данном случае целесообразно использовать итерационный подход. Введём в
рассмотрение текущий элемент последовательности T, предыдущий элемент P,
и элемент, находящийся перед предыдущим PP.
PP:=1; P:=1;
Получен алгоритм полиномиальной сложности
for i:=3 to n do
begin
T:=P+PP; {текущий элемент равен сумме двух предыдущих}
PP:=P; {после этого стоящий перед предшествующим заменяется}
P:=T {после этого заменяется предшествующий}
end;
14.06.2025
95
96.
def fib(n):‘’’Итерационное нахождение n-го числа Фибоначчи’’’
a,b=1,1
for i in range(3, n+1):
a,b=b,a+b
return b
14.06.2025
96
97.
Пример 6. Задача о ханойских башнях.Имеются N колец, расположенных в порядке убывания диаметра на одном стержне (А). Требуется переместить эти кольца на другой стержень (В), используя для
перемещения только один вспомогательный стрежень (C). При этом за один ход
можно перемещать только одно кольцо, а кольцо большего диаметра не может
размещаться на кольце меньшего диаметра.
C
A
B
N=3
Способ рассуждений полностью аналогичен способу, используемому в методе
математической индукции. При N=1 способ решения задачи очевиден: единственное кольцо сразу же перемещается с исходного стержня A на конечный B
без вспомогательного. Допустим, что известен способ перемещения для N-1.
Тогда, верхние N-1 колец перемещаются со стержня А на вспомогательный
стержень С, затем самое большое нижнее кольцо перемещается на целевой
диск В и, наконец, группа из N-1 колец со вспомогательного диска С перемещается на свое место.
14.06.2025
97
98.
Схема рекурсивных рассужденийA
B
C
N-1
N
14.06.2025
98
99.
Для упрощения разработки и формализации (обеспечения возможности записи)алгоритма обозначим стержни не буквами {A,B,C}, а номерами {1,2,3} соответственно. Перемещение кольца можно отображать текстом, содержащим номера
стержней, участвующих в перемещении. Например: «Перемещение кольца со
стержня 2 на стрежень 3».
Заметим, что в перемещениях исходный и конечный стержни могут иметь любые
номера. При разных перемещениях стержни играют разные роли. Исходный
может стать вспомогательным, а конечный – исходным.
Обозначим Cbeg – исходный стержень, Сend – конечный, и Cmid –
промежуточный.
Тогда Cbeg, Сend и Cmid могут принимать только значения 1, 2 или 3. Отметим,
при этом, что если, например, Cbeg=2, а Сend=3, то Cmid=1. Можно показать, что
в общем случае Cbeg +Cmid+ Сend=6.
Напишем в соответствии с приведёнными выше рассуждениями рекурсивную
процедуру перемещения N колец со стержня Cbeg на стержень Сend.
14.06.2025
99
100.
type pivot=1..3; {Тип номеров стержней}procedure H(Сbeg,Cend:pivot; N:integer);
{Рекурсивная процедура перемещения N колец со стрежня Cbeg на
стрежень Cend}
var Cmid:pivot;{промежуточный стержень}
begin
if N=1 then {терминальная ветвь}
writeln(‘Перемещение кольца со стрежня ’, Сbeg:1,’ на стержень ‘,Cend:1)
else {рекурсивная ветвь}
begin
Сmid:=6-Cbeg-Cend; {Определение номера промежуточного стержня}
H(Cbeg,Cmid,N-1); {Перемещение N-1 кольца на промежуточный}
writeln(‘Перемещение кольца со стрежня ’, Сbeg:1,’
на стержень ‘,Cend:1); {Перемещение самого большого кольца}
H(Cmid,Cend,N-1); {Перемещение N-1 кольца на конечный}
end
end;
14.06.2025
100
101.
void H( int Сbeg, int Cend, int N)/* Рекурсивная процедура перемещения N колец со стрежня Cbeg на
стрежень Cend/*
{
if (N==1) // терминальная ветвь
cout << “Перемещение со стрежня” << Сbeg << “на стержень” << Cend;
else // рекурсивная ветвь
{
int Сmid=6-Cbeg-Cend; // Определение номера промежуточного стержня
H(Cbeg,Cmid,N-1); // Перемещение N-1 кольца на промежуточный
\\ Перемещение самого большого кольца
cout << “Перемещение со стрежня” << Сbeg << “на стержень” <<Cend;
H(Cmid,Cend,N-1); \\ Перемещение N-1 кольца на конечный
}
return; }
14.06.2025
101
102.
14.06.2025102
103.
Определим количество перемещений M для разных N.Для N=1 требуется только одно перемещение M(1)=1.
Пусть известно количество перемещений для N-1: M(N-1).
Тогда количество перемещений для N колец: M(N)=M(N-1)+1+M(N-1).
Прямое вычисление дает M(2)=3; M(3)=7; M(4)=15; M(5)=31
Можно предположить, что M(N)=2N -1. Доказать это методом индукции.
Произведенный подсчёт показывает, что
экспоненциальному классу сложности EXP.
алгоритм
относится
к
Для N=64 и при перекладывании одного кольца в секунду на полное
перемещение потребуется 584 942 417 355 лет.
Задание. 1. Проверить выполнение программы на небольшом N.
2. Написать анимационную программу, которая не только печатает
протокол перемещений, но и графически отображает перемещения.
14.06.2025
103
104.
Пример 7. Простой синтаксический анализатор.Дана цепочка определений некоторой грамматики:
<Формула> ::= <Цифра>|(<Формула><Знак операции><Формула>)
<Цифра> ::= 0|1|2|3|4|5|6|7|8|9
<Знак операции> ;;= -|+|
Написать программу, которая определяет является ли последовательность
символов до первой точки в заданном файле символов правильной формулой.
Примеры цепочек символов, являющимися в соответствии с этой грамматикой правильными формулами (удовлетворяющих этой грамматике).
5
(3-7)
((3-7) (4+5))
(((3-7) (4+5))-(9-6))
Анализ определения и примеров показывает, что формула правильная: если прочитана цифра и за ней точка или если прочитана скобка, правильная формула,
знак операции, опять правильная формула, вновь скобка и за ней точка. Во всех
остальных случаях формула неправильная.
Это определение по своей сути рекурсивно. Поэтому алгоритм анализа не
может быть построен итерационным способом.
14.06.2025
104
105.
Нужно построить рекурсивную функцию, определяющую является ли уже прочитанная из файла последовательность символов правильной формулой или нет.Проверка нахождения в файле точки за такой последовательностью не может быть
включена в эту функцию, так как в определении формулы такая проверка
отсутствует. Следовательно, эту проверку нужно организовать в основной программе.
Очевидно, что обсуждаемая функция должна иметь логический тип. Из структуры
определения вытекает, что следует построить две вспомогательные подпрограммы, которые должны определять, является ли очередной прочитанный из файла
символ цифрой, а также является ли он знаком операции.
В соответствии с определениями эти подпрограммы могут быть логическими
функциями, содержащими сложное ветвление. Однако есть более простой вариант:
function IsDigit (x:char): boolean;
begin result:= x in [‘0’.. ‘9’] end;
function IsOperation (x:char): boolean;{Является ли символ x знаком операции?}
begin result:= x in [‘+’,’-’,‘ ’] end;
14.06.2025
105
106.
bool IsDigit( char x)\\ Является ли символ x цифрой?
{
return (x>=‘0’ ) && (x<=‘9’ );
}
bool IsOperation( char x)
\\ Является ли символ x знаком операции?
{
return (x== ‘+’ ) || (x== ‘-’ ) || (x == ‘ ’ );
}
def IsOperation(s):
return s=='+' or s=='-' or s=='*'
def IsOperation(s):
return s in set([‘+’,’-’,’*’])
14.06.2025
106
107.
Основная рекурсивная функция должна иметь хотя бы одну рекурсивную ветвьи не менее двух терминальных (логический тип). Она должна определять
является ли прочитанная последовательность символов (возможно состоящая
из одного символа) правильной формулой.
Более точно: эта функция должна сама последовательно читать символы из
файла и смотреть, является ли то что она уже прочитала формулой? Эта функция
должна считывать символы из файла до тех пор, пока после считывания очередного символа не получится либо правильная, либо неправильная формула. Пока
прочитанное можно рассматривать как начальную часть правильной формулы,
функция должна продолжать считывание.
Какие формальные параметры могут быть у обсуждаемой функции? Вообще говоря, только анализируемый файл. Однако, его можно также сделать глобальным
объектом подпрограммы. В этом случае у функции формальных параметров не
будет. Для рекурсивных подпрограмм, работающих с файлом, такой вариант
предпочтительнее.
Действия формируем прямо по определению. Читаем символ из файла. Если этот
символ цифра, то ответ готов ― истина. Если этот символ открывающая круглая
скобка, то это может быть началом рекурсивной части определения и нужно
смотреть дальше. Во всех остальных случаях ответ также готов ― возвращается
ложь, так как прочитанное не является правильной формулой.
14.06.2025
107
108.
function IsFormula: boolean;{является ли последовательность символов формулой}
var c: char: {очередной считанный символ} f1,f2,f3:boolen; {вспомог. перем}
begin
read(f,c); {чтение очередного символа}
if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then
begin {начинается рекурсивная часть определения}
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
end; {Конец функции IsFormula}
14.06.2025
108
109.
В основной программе открываем файл, вызываем функцию, если она возвращает значение true, считываем еще один символ и если это точка, то делаем вывод о правильности результата.f: file of char; {анализируемый файл}
x:char;{очередной символ файл}
begin
reset(f);{открываем файл для чтения}
if IsFormula then {функция вернула ответ – в файле правильная формула}
begin
read(f,x); {следующий символ x должен быть точкой}
if x=‘.’ then
writeln(‘Файл содержит правильную формулу’)
else
writeln(‘Файл не содержит точки за правильной формулой’)
end
else
writeln(‘Файл не содержит правильную формулу’)
end.
14.06.2025
109
110.
bool IsFormula ()// является ли последовательность символов формулой
{
char c;
cin>>c; // чтение очередного символа
if (IsDigit(c)) then return true// терминальная ветвь определения
else { if (c==‘(‘ )
/* начинается рекурсивная часть определения
после скобки должна идти правильная формула */
bool f1=IsFormula( );
// затем знак операции
cin>>c; bool f2=IsOperation(c);
// затем ещё правильная формула
bool f3=IsFormula();
// затем закрывающая скобка.
// результат есть конъюнкция всех определений
cin>>c; return f1 && f2 && f3 && (c==‘)’)
}
else return false; // вторая терминальная ветвь
} // Конец функции IsFormula
14.06.2025
110
111.
После написания и отладки программы следует проанализировать её текст сцелью улучшить программу, упростить её или повысить её эффективность.
В данном случае немного усложнив ветвление в подпрограмме можно повысить
эффективность за счёт выхода из ветвления сразу после обнаружения ошибки.
Рассмотренный вариант предполагает вычисление f1, f2 и f3 и только после этого
фиксируется результат. С другой стороны ясно, что если f1 = false, то выполнять
дальнейшие вычисления бессмысленно.
if IsFormula then {Первая формула в скобке правильная}
begin {Надо смотреть дальше}
read(f,c); if IsOperation(c) then {Далее правильный знак операции}
if IsFormula then {2 формула -правильная}
begin read(f,c); result c=‘)’ end
else {не формула}result := false
else {не знак операции }result := false
end else {уже первая часть в скобках не формула} result := false
Можно ещё упростить основную программу, чтобы только один раз выводить результат, соответствующий неправильной формуле.
Это можно сделать следующим образом: вызвать функцию IsFormula и запомнить
возвращаемое значение в некоторой переменной. Затем образовать конъюнкцию
из этого значения и отношения x=‘.’. Далее идёт обычное ветвление на две ветви.
14.06.2025
111
112.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
(
Проверка
result
false
true
14.06.2025
112
113.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
с
f3
(
(
Проверка
Второй уровень
f1
f2
result
Проверка
result
false
true
14.06.2025
113
114.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
(
Проверка
14.06.2025
Второй уровень
f1
f2
с
(
result
с
3
tr
Проверка
f3
Третий уровень
f1
f2
result
Проверка
result
true
true
114
f3
115.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
14.06.2025
с
-(
(
Проверка
Второй уровень
f1
f2
result
tr
Проверка
f3
tr
result
115
116.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
(
Проверка
14.06.2025
Второй уровень
f1
f2
с
(
result
tr
Проверка
tr
f3
с
tr
7
result
Третий уровень
f1
f2
Проверка
result
true
true
116
f3
117.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1=:IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
(
с
()
tr
Проверка
Второй уровень
f1
f2
result
tr
Проверка
tr
f3
tr
result
true
14.06.2025
117
118.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
(
tr
Проверка
14.06.2025
tr
result
118
119.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
tr
Проверка
tr
result
с
Второй уровень
f1
f2
(
Проверка
f3
result
false
true
14.06.2025
119
120.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
tr
Проверка
14.06.2025
Второй уровень
f1
f2
с
tr
tr
(
result
Проверка
f3
Третий уровень
f1
f2
с
4
result
Проверка
result
true
true
120
f3
121.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
true
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
tr
Проверка
14.06.2025
tr
result
Второй уровень
f1
f2
с
+(
tr
Проверка
f3
tr
result
121
122.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
tr
Проверка
14.06.2025
tr
result
с
Второй уровень
f1
f2
+
tr
Проверка
tr
f3
tr
result
Третий уровень
f1
f2
с
5
Проверка
result
true
true
122
f3
123.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula
;
{затем
закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
tr
Проверка
tr
result
tr
Второй уровень
f1
f2
с
)+
tr
Проверка
tr
f3
tr
result
true
14.06.2025
123
124.
read(f,c); {чтение очередного символа}if IsDigit(c) then {терминальная ветвь определения} result:=true
else if c=‘(‘ then { рекурсивная ветвь определения}
begin
{после скобки должна идти правильная формула}
f1:=IsFormula;
{затем знак операции}
read(f,c);f2:=IsOperation(c);
{затем ещё правильная формула}
Файл f: ( ( 3 – 7 ) ( 4 + 5 ) ) .
f3:=IsFormula;
{затем закрывающая скобка}.
{результат есть конъюнкция всех определений}
read(f,c);result:=f1 and f2 and f3 and c=‘)’
end
else {вторая терминальная ветвь } result:=false;
Первый уровень
f1
f2
f3
с
)
tr
Проверка
tr
tr
result
true
14.06.2025
124
125.
Рекурсия «вперёд»Основное требование к построению рекурсивных подпрограмм состоит в том, чтобы в подпрограмме имелось ограничивающее глубину рекурсии условие (одно или
несколько), которое в некоторый момент времени становится истинным и
обрывает цепочку рекурсивных вызовов.
Следовательно, в общем случае, можно строить рекурсию не только «назад», к
меньшим значениям параметров, к «предшествующим» ситуациям, но и «вперёд»,
к большим значениям параметров, к условно «будущим» ситуациям.
Пример 8.Постороение всех размещений с повторениями из n чисел по m.
Некоторые определения.
Пусть имеется N предметов различных видов, «сортов»: {a1,a2,…,aN}. Структура,
представляющая из себя несколько предметов, распложенных последовательно
друг за другом, называется расстановкой. Например, пусть имеется три предмета {a, b, c}. Тогда ccabc – расстановка. Пуcть {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, тогда
801281 – расстановка. (Характерные особенности – допускаются повторения,
порядок важен, количество – любое).
14.06.2025
125
126.
Расстановка, состоящая из m возможно повторяющихся предметов иотличающиеся друг от друга видом или порядком предметов, называются
размещениями с повторениями. По сравнению с общим случаем расстановки
– введено ограничение на количество предметов. Количество различных
размещений с повторениями Ānm = nm, n≤m или n≥m.
Расстановка, состоящая из m неповторяющихся предметов и отличающиеся
друг от друга видом или порядком предметов, называются размещениями без
повторений. По сравнению с общим случаем расстановки – введено
ограничение на количество предметов и на повторение. Количество различных
размещений с повторениями Anm = n(n-1)(n-2)…(n-m+1), m≤n.
Размещение без повторений, состоящее из n предметов называется
перестановкой. Перестановки отличаются друг от друга только порядком.
Количество различных перестановок Pn=Ann = n(n-1)(n-2)…1 =n!.
Размещение без повторений, состоящее из m предметов для которых порядок не
существенен называется сочетанием. Количество различных сочетаний
Cnm = n! /(n-m)!/m!
14.06.2025
126
127.
Пусть количество различных предметов n=5 и предметы это цифры {1, 2, 3, 4, 5}.Построим все размещения с повторениями из m=3 предметов.
Из определения этого вида расстановок следует, что нужно построить все
трёхзначные числа, состоящие из указанных цифр. Всего получим 53=125
различных вариантов
111 121 131 141 151
211 221 231 241 251
511 521 531 541 551
112 122 132 142 152
212 222 232 242 252
512 522 532 542 552
113 123 133 143 153
513 523 533 543 553
114 124 134 144 154
213 223 233 243 253 …
214 224 234 244 254
115 125 135 145 155
215 225 235 245 255
515 525 535 545 555
Первая цифра 1
Первая цифра 2
Первая цифра 5
514 524 534 544 554
Итак, как получены эти размещения? Итерационный способ рассуждений:
Организуем цикл по перебору всех возможных цифр, размещаемых на первом
месте. Затем организуем внутренний цикл по перебору всех возможных цифр на
втором месте. И, наконец, организуется внутренний цикл второго уровня
вложенности по перебору всех возможных цифр на третей позиции. В каждом
варианте образуем конкатенацию соответствующих цифр.
14.06.2025
127
128.
for i1:=‘1’ to ‘5’ do {перебор первых цифр}for i2:= ‘1’ to ‘5’ do {перебор вторых цифр}
for i3:= ‘1’ to ‘5’ do {перебор третьих цифр}
writelln(i1+i2+i3:3); {Печать очередного размещения}
В чём недостаток предложенного варианта построения алгоритма?
Он подходит только для конкретного значения m=3, так как реализован именно
тройной цикл. Во всех остальных случаях результат не будет получен.
Рекурсивный способ рассуждений. Организуем цикл по перебору всех
возможных цифр, размещаемых на первом месте (то есть начало выглядит
точно также, как и для итерационного способа). Далее рассуждаем по способу:
найти действия над некоторой частью, такие же как и над целым. Здесь можно
найти аналогию с файлом. Выделили голову файла – первую цифру и хвост
файла – все остальные цифры. В каждом случае после выбора первой цифры
для получения остальной части размещения действуем точно таким же
способом, как и для построения всего размещения, а это значит, что нужно
рекурсивно вызывать создаваемую подпрограмму.
14.06.2025
128
129.
Для формирования результата предлагается использовать массив A из m элементов, при этом k-й элемент массива соответствует k-й цифре размещения.Пусть к – номер текущего элемента массива, то есть номер позиции, на
которую осуществляется выбор очередной цифры, Gen(k) – подпрограмма
формирующая часть размещения, начинающуюся с цифры k. Тогда набросок
оговоренной части алгоритма можно изобразить так:
for i :=1 to n do {перебор вариантов постановки цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
end;
Это рекурсивная ветвь подпрограммы. Терминальная ветвь содержит вывод
полученного размещения на печать.
Необходимо еще сформировать условие перехода к терминальной ветви, то
есть условие, ограничивающее глубину рекурсии.
Если k – номер цифры, с которой подпрограмма формирует оставшуюся часть
размещения, а всего используется m цифр, то ясно, что это условие k>m
14.06.2025
129
130.
Подпрограмму следует реализовать как процедуру. Формируемый массив Aцелесообразно объявить глобальной величиной.
const n=5; m=3;
var A: array [1..m] of 1..n;
procedure Gen(k:integer);{Подпрограмма рекурсивного формирования
части размещения, начинающейся с k-й позиции}
var i:integer;
begin
if k>m then {терминальная ветвь}
begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {пер-р. вар-в. пост. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
end;
begin {основная программа} Gen(1) end.
14.06.2025
130
131.
const int n=5, m=3;int A [m+1];
void Gen( int k)
{
/* рекурсивное формирования части размещения, начинающейся с k-й позиции */
if (k>m) // терминальная ветвь
{ for ( int i=1; i<=m; i++) cout<<A[i]; cout <<“\n”;
else
{ // рекурсивная ветвь
for ( int i=1; i<=n; i++) // перебор цифр на k-м месте
{
A[k]=i; // На k-е место ставится очередная цифра i
/* Рекурсивный вызов для формирования оставшейся
части размещения, начинающейся с k+1-й цифры */
Gen(k+1);
}
} //конец рекурсивной ветви
}
14.06.2025
main () {Gen(1); return;}
131
132.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
begin {основная программа} Gen(1) end.
n
5
m
3
1
A
1
1
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
Проверка
Третий уровень
i
k
3
1
Проверка
false
false
false
14.06.2025
Четвёртый ур.
i
k
4
Проверка
true
132
133.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
begin {основная программа} Gen(1) end.
n
5
m
3
1
A
1
1
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
Проверка
Третий уровень
i
k
3
1
Проверка
false
false
false
14.06.2025
Четвёртый уров.
i
k
4
Проверка
true
133
134.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
begin {основная программа} Gen(1) end.
n
5
m
3
1
A
1
1
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
Проверка
Третий уровень
i
k
3
1
Проверка
false
false
false
14.06.2025
Четвёртый уров.
i
k
4
Проверка
true
134
135.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
begin {основная программа} Gen(1) end.
n
5
m
3
1
A
1
1
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
Проверка
Третий уровень
i
k
3
1
Проверка
false
false
false
14.06.2025
Четвёртый уров.
i
k
4
Проверка
true
135
136.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
begin {основная программа} Gen(1) end.
n
5
m
3
1
A
1
1
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
Проверка
Третий уровень
i
k
3
1
Проверка
false
false
false
14.06.2025
Четвёртый уров.
i
k
4
Проверка
true
136
137.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
112
begin {основная программа} Gen(1) end.
n
5
m
3
1
A
1
2
1
Четвёртый уров.
i
k
4
Проверка
Третий уровень
i
k
3
2
1
Проверка
false
false
true
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
false
14.06.2025
Проверка
137
138.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
112
113
begin {основная программа} Gen(1) end.
n
5
m
3
1
A
1
32
Четвёртый уров.
i
k
4
Проверка
Третий уровень
i
k
3
32
Проверка
false
false
true
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
false
14.06.2025
Проверка
138
139.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
112
113
begin {основная программа} Gen(1) end.
114
m
n
A
5
3
1 1 34
Четвёртый уров.
i
k
4
Проверка
Третий уровень
i
k
3
43
Проверка
false
false
true
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
false
14.06.2025
Проверка
139
140.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111
end;
112
113
begin {основная программа} Gen(1) end.
114
m
n
A
115
5
3
1 1 54
Четвёртый уров.
i
k
4
Проверка
Третий уровень
i
k
3
45
Проверка
false
false
true
Первый уровень
i
k
1
1
Второй уровень
i
k
2
1
Проверка
false
14.06.2025
Проверка
140
141.
if k>m then {терминальная ветвь}begin for i:=1 to m do write(A[i]:1); writeln end;
else
for i :=1 to n do {перебор вар-ов постан. цифры на k-е место место}
begin
A[k]:=i; {На k-е место ставится очередная цифра i}
{Рекурсивный вызов для формирования оставшейся части
размещения, начинающейся с k+1-й цифры }
Gen(k+1)
111 121
end;
112
113
begin {основная программа} Gen(1) end.
114
m
n
A
115
1
5
3
1 1
2 5
Первый уровень
i
k
1
1
Второй уровень
i
k
2
2
1
Проверка
Проверка
14.06.2025
Третий уровень
i
k
5
3
1
Проверка
Четвёртый уров.
i
k
4
false
true
Проверка
141
142.
Какова сложность построенного алгоритма? Какой алгоритм сложнее, задачи оХанойских башнях или задачи о размещениях?
Сколько различных размещений можно получить? Ānm = nm – это нижняя грани-ца
сложности. Для n=2 и m=64 получим Ānm =264., то есть класс сложности EXP.
Какие структуры данных можно использовать в данном случае для фиксации
результата?
14.06.2025
142
143.
АЛГОРИТМЫ С ВОЗВРАТОМВо многих случаях решение задачи получается в результате полного перебора всех возможных вариантов решения задачи.
Например, задача линейного поиска ― в случае когда искомого объекта в
совокупности нет, то результат получается только после полного перебора всех
её элементов. Класс сложности полиномиальный.
Существует класс задач, в которых получить решение за приемлемое время
не удается. Так, решения задач о Ханойских башнях и о размещениях тоже
получаются только как результат полного перебора всех возможных вариантов,
но у них класс сложности экспоненциальный.
В первом примере полный перебор не доставляет проблем. Но в последних
двух примерах этот полный перебор уже катастрофически увеличивает время
получения решения. К сожалению, ни в задаче о получении всех размещений,
ни в более простой задаче о Ханойских башнях уйти от полного перебора,
приводящего к экспоненциальной сложности, не удается.
Вместе с тем существует множество задач, в которых пользуясь специальными приёмами можно избежать полного перебора и уйти от экспоненциальной сложности.
14.06.2025
143
144.
Одним из таких специальных приёмов является применение алгоритмов свозвратом, которые фактически представляют собой реализацию одного из
вариантов метода проб и ошибок.
Общая схема организации алгоритмов с возвратом
1. Решение задачи получается в результате выполнения нескольких шагов.
2. На каждом шаге осуществляется полный, линейный перебор всех
допустимых, возможных вариантов действий.
3. После выбора очередного допустимого варианта действий фиксируются
все последствия, вытекающие из такого выбора.
4. Осуществляется рекурсивный вызов вперёд подпрограммы для выполнения по точно такой же схеме всех последующих шагов.
5. В реализации алгоритма с возвратом важную роль играет специальная
величина ― формальный параметр, который играет роль индикатора
успешного выбора варианта действий на текущем шаге.
14.06.2025
144
145.
6. Если в результате сделанного на текущем шаге выбора на одном изпоследующих шагов (на одном из следующих уровней рекурсивного
вызова) не окажется ни одного допустимого варианта действий, то такой
параметр должен возвратить на текущий шаг сообщение об ошибке. В
этом случае на текущем шаге нужно отменить все зафиксированные
последствия выбора и перейти к выбору следующего допустимого
варианта.
7. Если же на каждом последующем шаге, вплоть по последнего существуют
допустимые варианты действий, такой параметр должен возвратить на
текущий шаг сообщение об успешном решении задачи.
Задача решена успешно, поскольку на каждом шаге от первого до последнего
выбраны допустимые варианты действий.
В качестве параметра ― индикатора можно взять переменную логического типа и договориться, что значение false у этой переменной означает , что произошла ошибка и допустимых вариантов нет.
Естественно в этом алгоритме, как и в любом рекурсивном алгоритме
необходимо контролировать достижение предельного уровня глубины
рекурсии (достижение последнего шага) и осуществлять выход на терминальную ветвь.
14.06.2025
145
146.
Пример: задача о восьми ферзяхТребуется расставить на шахматной доске восемь ферзей так, чтобы
они не находились под боем друг у друга.
8
7
6
5
4
3
2
1
a
14.06.2025
b
c
d
e
f
g
h
146
147.
Полный перебор всех вариантов дает число 64 63 62 61 60 59 58 57, чтопримерно равно 1015 расположений ферзей на доске.
Если на анализ одой позиции тратить 1 секунду, то для решения задачи полным
перебором потребуется 5 609 024 года.
Вместе с тем очевидно, что в этот полный перебор попадают и заведомо неудовлетворительные позиции, когда, например, все восемь ферзей расположены на
одной горизонтали.
8
7
6
5
4
3
2
1
14.06.2025
a
b
c
d
e
f
g
h
147
148.
Ясно, что огромное количество таких вариантов нужно отбрасывать на как можно более ранних этапах выбора позиций, а точнее, как только обнаружится первый случай попадания под удар.Систематический подход к выбору позиций для ферзей дает общая схема построения алгоритмов с возвратами.
Поскольку ясно, что на одной вертикали не может находится более одного ферзя, в качестве шагов построения решения возьмем выбор позиции очередного
ферзя на очередной вертикали: первый шаг – выбор позиции первого ферзя на
первой вертикали, второй шаг – выбор позиции второго ферзя на второй вертикали, и т.д., на последнем восьмом шаге выбирается позиция последнего восьмого ферзя на восьмой вертикали.
Заметим, что выбор позиции на некоторой вертикали фактически означает выбор горизонтали для размещения ферзя.
14.06.2025
148
149.
87
6
5
4
3
2
1
a
14.06.2025
b
c
d
e
f
g
h
149
150.
87
6
5
4
3
2
1
a
14.06.2025
b
c
d
e
f
g
h
150
151.
Допустим выбраны позиции для k-1-го ферзя и на k-м шаге осуществляетсяпоиск позиции для k-го ферзя.
Тогда по общей схеме рассуждений выбор осуществляется последовательным просмотром горизонталей (начиная с первой) с целью выявления
позиции не находящейся под боем.
Если такой горизонтали нет, то организуется возврат на предыдущий шаг
(уровень рекурсии) с сообщением о неудаче.
Если допустимые позиции есть, то считаем первую допустимую позицию
выбранной и фиксируем попавшие под удар поля на остальной части доски.
После чего рекурсивно вызывается процедура, которая проводит те же самые
действия на следующей k+1-й вертикали для следующего ферзя.
Рекурсивно вызванная процедура может возвратить со следующих шагов
сообщение о том, что на хотя бы одном из них не нашлось ни одного
допустимого поля.
Тогда нужно отменить попадание под удар с текущей позиции и выбрать для
ферзя следующую допустимую позицию
Если рекурсивная процедура возвращает сообщение об успешности попытки,
это означает, что решение уже получено, так как на каждой вертикали
нашлись допустимые поля.
14.06.2025
151
152.
Общий набросок подпрограммы, реализующей рекурсию с возвратомРеализуем подпрограмму в виде процедуры, хотя в некоторых частных случаях
подпрограмма может быть реализована и как функция.
Формальный параметр подпрограммы, возвращающий два значения (есть ошибка,
нет ошибки), должен быть логического типа, это выходной параметр, следовательно, он должен быть параметром-переменной.
Будем считать, что этот параметр получает значение true, если ошибки нет, и
значение false, если ошибка обнаружена.
Заметим, что отсутствие ошибки (true) означает, что на каждом из шагов алгоритма найден допустимый вариант, а это в свою очередь означает, что решение
задачи уже получено. Наличие ошибки (false) означает, что на каком то из
последующих шагов допустимого варианта не нашлось, то есть решение ещё не
получено и нужно продолжать его поиск.
Зададимся вопросом, когда такой параметр должен получить значение true?
Ответ: если на последнем шаге (при достижении последнего уровня рекурсии)
найдется хотя бы один допустимый вариант. Во всех остальных случаях он
должен иметь значение false. Это значение параметр может получить либо в
начале подпрограммы, либо из основной программы при вызове подпрограммы.
14.06.2025
152
153.
В соответствии с общей схемой метода, подпрограмма описывает действия,выполняемые на текущем шаге.
Нужно организовать цикл перебора всех (вообще всех, а не только допустимых)
вариантов текущего шага.
По общей схеме организации цикла, нужно: выбрать его конкретную форму,
произвести инициализацию цикла, определить действия составляющие тело цикла
и условие выполнения этих действий.
В данном случае цикл в форме с параметром (for) не подходит, так как перебор
вариантов может быть прекращен сразу после получения из рекурсивного вызова
ответа, соответствующего получению решения.
Следовательно, нужно использовать либо цикл с предусловием (while), либо с постусловием (repeat). Для
определенности используем вариант c постусловием.
Выполнение тела цикла следует продолжать до тех пор пока не будет получено
сообщение о получении результата, либо пока не будут исчерпаны все варианты
действий.
В теле цикла нужно: а)выбирать следующий вариант, б)если он допустим,
фиксировать последствия выбора, в)рекурсивно вызывать процедуру для
выполнения аналогичных действий на следующем шаге, г)проводить анализ
результатов вызова, если возвращенное процедурой значение параметра-индикатора сигнализирует об ошибке, то отменять последствия выбора.
14.06.2025
153
154.
procedure BackTrace (var q: boolean); {Рекурсивный алгоритм с возвратом,q – индикатор результата }
begin
q := false;{решение ещё не получено}
{Инициализация перебора всех вариантов текущего шага}
repeat {цикл по всем вариантам}
{выбор следующего варианта}
if <условие допустимости варианта> then
begin {вариант допустим}
{фиксация последствий выбора}
BackTrace(q); {Рекурсивный вызов}
if not q then {рекурсивная подпрограмма вернула сообщение об ошибке}
{отмена последствий выбора}
end
until {условие завершения цикла} q or <вариантов больше нет>
end;
Проанализируйте, что будет, если очередной вариант недопустим?
Проанализируйте, что будет, если рекурсия вернула значение q=true?
В чём принципиальная ошибка этого наброска алгоритма?
Этот набросок, не контролирует достижение последнего шага. Необходимо
включить такой контроль.
14.06.2025
154
155.
Для организации контроля введем k – формальный параметр, определяющийномер текущего шага, и N – глобальную величину, определяющую общее
количество шагов (предельную глубину рекурсии).
Контроль достижения предельной глубины рекурсии следует проводить перед
рекурсивным вызовом подпрограммы. Если предельный уровень (последний
шаг) ещё не достигнут, то рекурсивный вызов производится. Если последний
шаг достигнут, то с помощью параметра-индикатора q фиксируется получение
решения задачи, так как на последнем шаге найден допустимый вариант.
14.06.2025
155
156.
procedure BackTrace (k:integer; var q: boolean);{Рекурсивный алгоритм с возвратом, k – номер текущего шага, q – индикатор
результата}
begin
q := false;{решение ещё не получено}
Можно ли убрать этот оператор?
{Инициализация перебора всех вариантов текущего шага}
repeat {цикл по всем вариантам}
{выбор следующего варианта}
if <условие допустимости варианта> then
begin {вариант допустим}
{фиксация последствий выбора}
if k<N then {не последний шаг}
begin
BackTrace(k+1, q); {Рекурсивный вызов}
if not q then {рек. подпр-ма вернула сообщение об ошибке }
{отмена последствий выбора}
end
else {решение найдено} q := true
end
until {условие завершения цикла} q or <вариантов больше нет>
end;
14.06.2025
156
157.
void BackTrace ( int k, int* q)/* Рекурсивный алгоритм с возвратом, k – номер текущего шага, q – индикатор
результата */
{
*q = 0; \\ решение ещё не получено
Можно ли убрать этот оператор?
\\ Инициализация перебора всех вариантов текущего шага
do \\ цикл по всем вариантам
{\\ выбор следующего варианта
if (<условие допустимости варианта>)
{ \\ вариант допустим
\\ фиксация последствий выбора
if (k<N) \\ не последний шаг
{
BackTrace (k+1, q); \\ Рекурсивный вызов
if (! *q) then \\ рек. подпр-ма вернула сообщение об ошибке
{\\ отмена последствий выбора}
}
else *q =1; \\ решение найдено
}
}
} while ( (!*q) && <есть непросмотренные варианты>) \\ решение найдено
14.06.2025
157
158.
Пример 9. Решение задачи о восьми ферзях.Для упрощения формализации решения рассматриваемой задачи обозначим
вертикали доски также как и горизонтали – цифрами.
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
Пусть ферзь находится в поле (k, j), где k – номер вертикали, j – горизонтали.
Например, в поле (4, 3)
Какие поля доски при этом находятся под ударом ферзя?
14.06.2025
158
159.
Ответ:• все поля вертикали с номером k=4;
• все поля горизонтали с номером j=3;
• все поля «убывающей» диагонали: (1, 6); (2, 5); (3, 4); (5, 2); (6, 1);
• все поля «возрастающей диагонали» (2, 1); (3, 2); (5, 4); (6, 5); (7, 6); (8, 7).
Общее свойство полей «убывающей» диагонали: k+j= 7 (в данном примере). В
общем случае k+j= const. Причём, 2 ≤ const ≤ 16.
Общее свойство полей «возрастающей» диагонали: k-j= 1 (в данном примере).
В общем случае k-j= const. Причём, -7 ≤ const ≤ 7.
Поле может находится под ударом или нет. Следовательно, свойство полей
горизонталей, вертикалей и диагоналей «находится под ударом» можно описать с
помощью массивов с элементами логического типа.
Поля горизонталей можно описать с помощью массива H: array [1..8] of boolean.
Тогда, например, H[1] = false означает, что поля первой горизонтали находится
под ударом, а H[1] = true, означает, что эти поля не находятся под ударом.
14.06.2025
159
160.
Поля «убывающей» диагонали можно описать с помощью массиваDdn: array [2..16] of boolean, а поля «возрастающей» диагонали ― массивом
Dup: array [-7..7] of boolean.
Например, Ddn[3] = false означает, что под ударом находятся все поля «убывающей» диагонали, для которой k+j=3, то есть поля (1, 2) и (2, 1), а Dup[3]=false
означает, что под ударом находятся все поля «возрастающей» диагонали, для
которой k-j=3, то есть поля (4,1); (5, 2); (6, 3); (7,4); (8, 5).
Поля вертикалей текущего шага всегда находятся под ударом ферзя, который
выставляется на эту вертикаль. В соответствии с предыдущими рассуждениями на k-ом шаге ферзя ставиться на k-ю вертикаль. При этом
позицию ферзя можно однозначно задать номером Q горизонтали. Таким
образом получаем, что расстановка ферзей на шахматной доске может быть
описана массивом Q: array [1..8] of 1..8.
Например, Q[3]=5 означает, что ферзь находится на поле (3, 5). Следовательно, под ударом этого ферзя находятся все поля третьей вертикали. При этом
H[5]=false, Ddn[8]= false, Dup[-2]= false.
В общем случае, если Q[k]=j, то ферзь находится на поле (k, j) и при этом
H[j]= false, Ddn[k+j]]= false, Dup[k-j]= false.
14.06.2025
160
161.
program EightQueen; {Расстановка восьми ферзей}var i:integer; {для инициализации массивов}
q: boolean;{фактический параметр вызова подпрограммы }
Queens : array [1..8] of 1..8; {Массив, описывающий расстановку ферзей}
H : array [1..8] of boolean; {Состояние горизонталей}
Ddn :array [2..16] of boolean; {Состояние «убывающих» диагоналей}
Dup :array [-7..7] of boolean; {Состояние «возрастающих» диагоналей}
procedure BackTraceQueen (k:integer; var q: boolean);
{Рекурсивный алгоритм с возвратом расстановки восьми ферзей, k – номер
текущего шага, q – индикатор результата}
var j: 1..8; {для перебора полей текущей вертикали}
begin
q := false;{решение ещё не получено}
j := 0; {Инициализация перебора всех горизонталей текущего шага}
repeat {цикл по перебору всех вариантов текущего шага}
14.06.2025
161
162.
repeat {цикл по перебору всех вариантов текущего шага}j:=j+1; {выбор следующего варианта ― следующего поля вертикали }
if H[j] and Ddn[k+j] and Dup[k-j] then {выбранное поле не под ударом}
begin {фиксация последствий выбора}
Queens [k]:=j; H[j]:=false; Ddn[k+j]:=false; Dup[k-j]:=false;
if k<8 then {последняя вертикаль еще не достигнута}
begin {рекурсивная ветвь}
BackTraceQueen (k+1, q); {вызов для к+1-й вертикали}
if not q then {обнаружена ошибка}
begin {отмена последствий выбора}
H[j]:=true; Ddn[k+j]:= true; Dup[k-j]:= true
end
end
else {терминальная ветвь }
q:=true {решение получено}
end
until q or j=8 {пока решение не найдено или вариантов больше нет}
end {конец рекурсивной подпрограммы BackTraceQueen};
14.06.2025
162
163.
begin {основная программа}{все поля доски не под ударом}
for i := 1 to 8 do H[i]:=true;
for i := 2 to 16 do Ddn[i]:=true;
for i := -7 to 7 do Dup[i]:=true;
BackTraceQueen(1,q); {Вызов подпрограммы расстановки ферзей}
if q then {решение найдено}
for i := 1 to 8 do writeln(i:4, Queens[i]:1); {вывод расстановки ферзей}
end.
Задание начального значения параметра-индикатора q можно перенести из
подпрограммы в основную программу.
••
for i := -7 to 7 do Dup[i]:=true;
q:= false; {Начальное значение индикатора}
BackTraceQueen(1,q); {Вызов подпрограммы расстановки ферзей}
if q then {решение найдено}
for i := 1 to 8 do writeln(i:4, Queens[i]:1); {вывод расстановки ферзей}
end.
14.06.2025
163
164.
Полученное решение находит только одно из возможных решений. Анализ показывает, что существует 92 решения, а с учетом симметрии шахматной доски ипозиций ― всего 12 различных решений.
Если ставится задача отыскать все возможные размещения ферзей на доске,
полученную подпрограмму следует изменить так, чтобы выполнение программы
не прекращалось после получения уже первого решения.
Какой элемент подпрограммы отвечает за прекращение анализа?
Цикл прекращается либо после исчерпания всех возможных вариантов на шаге,
либо после того, как переменная q получит значение true, означающее согласно
сделанным соглашениям, что решение найдено. Следовательно, нужно отказаться от использования в подпрограмме параметра-индикатора q. Получение
решений, то есть поиск допустимых вариантов размещения ферзей, нужно продолжать и после достижения предельной глубины рекурсии. Необходимо только
отменять последствия каждого предыдущего выбора.
Однако, возникает ещё один вопрос ― способ фиксации результата. В
имеющемся варианте результат фиксируется в массиве Queens, который
выводится в основной программе после завершения работы подпрограммы,
нашедшей первое решение.
14.06.2025
164
165.
Можно предложить несколько различных вариантов фиксации решения.Например, самый простой ― вывод сформированного решения сразу после его
получения, то есть после выбора допустимого варианта на последнем шаге.
И еще одно замечание, в связи с упрощением условия прекращения цикла, для
его реализации можно использовать форму с параметром.
Итак, получаем следующую схему организации подпрограммы.
for j:=1 to 8 do {Перебор всех вариантов k-го шага}
begin
if <условие допустимости варианта > then
begin
<Фиксация последствий выбора >
if k<N then {Рекурсивный вызов для к+1-го шага}
BackTrace (k+1)
else {терминальная ветвь }
{вывод полученного решения}
<Отмена последствий выбора >
end
end
14.06.2025
165
166.
procedure BackTraceQueen(k:integer;
var q: boolean);
BackTraceQueenAll
(k:integer);
{Рекурсивный алгоритм с возвратом расстановки восьми ферзей, k – номер
шага} q – индикатор результата}
текущего шага,
var j: 1..8; {для перебора полей текущей вертикали}
begin
for j:=1 to 8 do {Перебор всех вариантов k-го шага}
begin
if <условие
H[j] and Ddn[k+j]
допустимости
and Dup[k-j]
варианта
then {выбранное
> then
поле не под ударом}
begin
<Фиксация
последствий
>
Queens [k]:=j;
H[j]:=false; выбора
Ddn[k+j]:=false;
Dup[k-j]:=false;
if k<8
вертикаль
еще
не достигнута}
k<N then
then {последняя
{Рекурсивный
вызов для
к+1-го
шага}
BackTraceQueenAll(k+1)
BackTrace (k+1)
else {терминальная ветвь }
{вывод
решения}
for i := 1полученного
to 8 do writeln(i:4,
Queens[i]:1); {вывод}
<Отмена Ddn[k+j]:=
последствий
выбора
> true
H[j]:=true;
true;
Dup[k-j]:=
end
end
end {конец рекурсивной подпрограммы BackTraceQueenAll};
begin {основная программа}… BackTraceQueenAll(1) end.
14.06.2025
166
167.
Тема 4. Динамические структуры данных. СтекСтек представляет собой динамическую структуру данных, основанную на
линейном однонаправленном списке. У стека для взаимодействия доступна
только один конец структуры ─ вершина стека. И включение нового элемента в
стек и выборка последнего ранее включенного идет через вершину стека. Таким
образом на обслуживание попадает первым элемент, поступивший последним.
Говорят, что стек ─ это структура с дисциплиной обслуживания LIFO (Last In,
First Out) ─ «последним пришёл, первым ушёл».
Описание типов, используемых для работы со стеком:
type
T_info=char; {Зависит от типа информационного поля, может быть любой тип}
T_Stack = ↑T_Elem;
T_Elem = record
body : T_info;
Next : T_Stack
end;
14.06.2025
167
168.
struct Tstack{
char body;
//информационное поле
Tstack *Next;
//указатель на следующий элемент
};
14.06.2025
168
169.
Для работы со стеком обычно создаются стандартные процедуры обеспечивающие выполнение четырёх основных операций над стеком: создание стека,включение в стек нового элемента, выборку элемента из стека, проверку стека
на пустоту.
Под созданием стека понимается создание пустого стека. Подпрограмма
должна вернуть в качестве результата пустой указатель типа T_Stack. Если
подпрограмма реализуется как процедура, то она должна иметь формальный
параметр-переменную.
procedure CreateStack (var: L:T_Stack); {Процедура создания пустого стека}
begin
L := nil
end;
void CreateStack(TStack *&T)
{
T=nullptr;
}
14.06.2025
169
170.
Проверку стека на пустоту лучше всего реализовывать с помощью функциилогического типа. Функция должна иметь в качестве формального параметра
указатель на вершину проверяемого стека
function IsEmptyStack (L:T_Stack): boolean; {Функция проверки стека на пустоту}
begin
result := L=nil
end;
Включение нового элемента в вершину стека эквивалентно включению
элемента в начало линейного однонаправленного списка. Формальные
параметры процедуры ― указатель на вершину изменяемого стека и вставляемый элемент.
Указатель на вершину стека является одновременно входным и выходным
параметром, следовательно, это параметр-переменная.
procedure InStack (var L:T_Stack; E:T_info); {Включение в стек L элемента E}
var q : T_Stack; {Для создания нового элемента}
begin
new(q); {создание нового элемента}
q↑.body:= E; {Заполнение информационного поля созданного элемента}
q↑.next:= L; {Подключение «старых» элементов стека к созданному элементу}
L := q {Объявление созданного элемента новой вершиной стека}
end;
14.06.2025
170
171.
LL
q
E
new(q); {создание нового элемента}
q↑.body:= E; {Заполнение информационного поля созданного элемента}
q↑.next:= L; {Подключение «старых» элементов стека к созданному элементу}
L := q {Объявление созданного элемента новой вершиной стека}
14.06.2025
171
172.
procedure InStack (var L:T_Stack; E:T_info); {Включение в стек L элемента E}var q : T_Stack; {Для создания нового элемента}
begin
new(q); {создание нового элемента}
q↑.body:= E; {Заполнение информационного поля созданного элемента}
q↑.next:= L; {Подключение «старых» элементов стека к созданному элементу}
L := q {Объявление созданного элемента новой вершиной стека}
end;
void InStack(char E, Tstack *&L)
/*Функция включения в стек L элемента E */
{
Tstack *q = new Tstack; //Выделение памяти для нового элемента (создание н.э.)
q->body = E;
//Заполнение информационного поля нового элемента
(*q).body=E;
//Другой способ записи этого присваивания
q->Next = L;
//Подключение «старых» элементов стека к новому элементу
L =q;
}
14.06.2025
//Объявление созданного элемента новой вершиной
172
173.
Выборка (исключение) элемента из стека эквивалентна исключению элементаиз начала линейного однонаправленного списка. Формальные параметры
подпрограммы ― указатель на вершину изменяемого стека и переменная для
запоминания выбранного элемента.
Указатель на вершину стека является одновременно входным и выходным
параметром, следовательно, это параметр-переменная.
Реализовать подпрограмму можно и как процедуру и как функцию.
procedure OutStack (var L:T_Stack; var E:T_info); {Выборка из стека L элемента E}
var q : T_Stack; {Для освобождения памяти, занимавшейся старой вершиной стека
begin
if L<> nil then {Стек не пуст}
begin
q := L; {Сохранение указателя на старую вершину}
E := q↑.body; {выборка из информационного поля вершины}
L := q↑.next; {Новая вершина стека}
dispose(q) {Освобождение памяти}
end
else {Стек пуст} writeln(Выбрать элемент невозможно ― стек пуст)
end;
14.06.2025
173
174.
char OutStack(Tstack *&L)//Функция возвращает выбранное из вершины стека значение
{
char E;
if (L!=nullptr)
{
Tstack *q = L;
//Сохранение указателя на старую вершину
E = q->body;
//Выборка из информационного поля вершины стека
L = q->Next;
//Новая вершина стека
delete q;
// Освобождение памяти
}
return E;
}
14.06.2025
174
175.
Пример 10. Задача о балансе скобок.Дан файл символов, который содержит запись некоторого выражения со скобками (круглыми, квадратными, фигурными). Нужно определить правильность
расстановки скобок.
Пример выражения со скобками: [ (x+y) * (y-z) + 4 ] / { 3- [ 4 + ( 5 – b ) ] }
Идея решения задачи состоит в применении стека для хранения встречающихся в выражении скобок.
Более подробно. Нужно организовать посимвольный просмотр выражения
(слева направо). Если во время просмотра встречается открывающая скобка
(любая), то она записывается в стек (до начала просмотра стек должен быть
пуст). Если во время просмотра встречается закрывающая скобка (любая), то
скобка
выбирается из вершины стека.
После чего встретившаяся
закрывающая и выбранная из стека открывающая сравниваются друг с другом.
14.06.2025
175
176.
([[ (( xx ++ yy )) ** (( yy –– zz )) ++ 44 }] / { 3- [ 4 + ( 5 – b ) ] }
(
L
L=nil
[
Сравнение
]}
НеСоответствуют
соответствуют
Когда нарушается баланс скобок?
Анализ показывает, что баланс скобок оказывается нарушенным, если:
1. Очередная закрывающая скобка из выражения и скобка из вершины стека не
соответствуют друг другу;
2. Если при появлении в выражении закрывающей скобки стек оказывается
пустым ― лишняя закрывающая скобка;
3. Если после завершения просмотра выражения стек оказывается не пустым
― лишняя открывающая скобка.
14.06.2025
176
177.
Из проведённых рассуждений следует, что:нужно организовать считывание элементов из файла;
каждый элемент нужно проверить, является ли он какой-либо
открывающей скобкой;
если да, то записать его в стек;
если нет, то проверить является ли он закрывающей скобкой;
если да и если при этом стек пуст, то фиксируется отсутствие баланса
скобок;
если стек не пуст, то нужно извлечь из него верхний элемент (а это какаялибо открывающая скобка) и сравнить очередной символ выражения с
символом выбранным из стека;
если они не совпадают, то фиксируется отсутствие баланса скобок;
если скобки совпадают, то нужно продолжить анализ.
Очередные символы выражения не совпадающие со скобками (либо открывающими, либо закрывающими) пропускаются, не влияя на результат.
Проведённые рассуждения показывают, что рассматриваемый алгоритм
представляет собой цикл, содержащий ветвление, состоящее из нескольких
ветвей.
14.06.2025
177
178.
Обсуждаемая задача есть задача поиска ― её решение следует прекратитьсразу же после обнаружения первого нарушения баланса скобок.
Подготовка к выполнению обсуждаемых действий состоит в 1)формировании
пустого стека; 2)подготовке файла к считыванию; 3)присваивании значения false
индикатору поиска нарушений баланса flag.
Анализ выражения из файла следует продолжать до тех пор пока не будет
обнаружено отсутствие баланса скобок и при этом файл содержит ещё не
обработанные элементы.
Пусть Sf ― очередной символ файла, а Sst ― символ, выбранный из вершины
стека. Тогда получим следующий набросок программы:
14.06.2025
178
179.
begin{формирование пустого стека}
{подготовка файла к считыванию и считывание первого элемента}
flag := false; {нарушение баланса ещё не обнаружено}
while not eof(f) and not flag do {цикл анализа символов выражения}
begin
{вывод считанного символа}
if Sf in [ ‘(‘, ‘[‘, ‘{‘ ] then {считанный символ – открывающая скобка}
{запись скобки в стек}
else {это не открывающая скобка}
if Sf in [ ‘)‘, ‘]‘, ‘}‘ ] then
{считанный символ – закрывающая скобка}
if <стек пуст> or <не соответствие скобок> then
{нарушение баланса скобок} flag := true ;
{ввод следующего символа}
end;
if flag or <стек не пуст> then {баланса нет} else {баланс есть}
end;
14.06.2025
179
180.
{//формирование пустого стека
//подготовка файла к считыванию и считывание первого элемента
int flag = 0; //нарушение баланса ещё не обнаружено
while (( не конец файла) && (flag ==0 ) //цикл анализа выражения
{
//вывод считанного символа
if (Sf==‘(‘ || Sf== ‘[‘ || Sf == ‘{‘) //считанный символ – открывающая скобка
– запись этой скобки в стек
else // это не открывающая скобка
if (Sf==‘)‘ || Sf== ‘]‘ || Sf == ‘}‘)
// считанный символ – закрывающая скобка
if (<стек пуст> || <не соответствие скобок>)
flag =1 ; //нарушение баланса скобок
//ввод следующего символа
}
if ( flag ==1|| <стек не пуст>) //баланса нет; else //баланс есть;
}
14.06.2025
180
181.
function Match (Sf,Sst:char):boolean;{Сравнение скобок, Sf ― символ из файла, Sst ― сивмол из стека}
begin
case Sf of
‘)’ : result := Sst=‘(‘;
‘]’ : result := Sst=‘[‘;
‘}’ : result := Sst=‘{‘;
end;
end;
int Match(char Sf, char Sst)
//Сравнение скобок, Sf ― символ из файла, Sst ― символ из стека
{
switch (Sf) {
case ‘)’: return Sst==‘(‘; break;
case ‘]’: return Sst==‘[‘; break;
case ‘}’: return Sst==‘{‘; break;
}
}
14.06.2025
181
182.
program Balance_Bracket;{Программа анализа баланса скобок в выражении, находящемся в файле}
var f: file of char; {файл, содержащий выражение}
Sf, Sst : char; {символ из файла и символ из стека}
p : T_stack; {указатель на вершину стека}
flag : boolean; {индикатор поиска}
begin
{Инициализация цикла}
reset (f); if not eof(f) then read (f, Sf); {открытие файла и считывание}
CreateStack(p); {Создание пустого стека}
flag:=false; {<Баланс не нарушен}
while not eof(f) and not flag do {цикл анализа символов выражения}
14.06.2025
182
183.
while not eof(f) and not flag do {цикл анализа символов выражения}begin
write (Sf); {Вывод текущего символа выражения}
if Sf in [ ‘(‘, ‘[‘, ‘{‘ ] then {открывающая скобка} InStack(p,Sf)
else {не открывающая скобка}
if Sf in [ ‘)‘, ‘]‘, ‘}‘ ] then {закрывающая скобка}
begin
OutStack(p, Sst); {Выборка из стека}
if IsEmptyStack(p) or not Match(Sf, Sst) then
{нарушение баланса скобок} flag := true ;
end;
read (f, Sf); {Считывание следующего символа выражения}
end;
if flag or not IsEmptyStack (p) then writeln(‘Баланс скобок нарушен’)
else writeln(‘Баланс скобок не нарушен’)
end.
14.06.2025
183
184.
Замечания:1. Если подпрограмму выборки из стека реализовать как функцию, возвращающую символьное значение, то внутреннее ветвление можно реализовать так:
if Sf in [ ‘)‘, ‘]‘, ‘}‘ ] then {закрывающая скобка}
if IsEmptyStack(p) or not Match(Sf, OutStack (p)) then
{нарушение баланса скобок} flag := true ;
2. Вызов подпрограмм IsEmptyStack(p) и CreateStack(p) можно заменить более
простыми операторами p<>nil и p:=nil соответственно. Однако использование
подпрограмм делает текст более читабельным.
14.06.2025
184
185.
Тема 5. Динамические структуры данных. ДеревьяДеревом называется структура данных, элементы которой называемые вершинами (узлами) связаны отношениями подчиненности, когда одному элементу
может быть подчинено несколько, но при этом сам он может быть подчинен
только одному. В структуре имеется только один элемент, не подчиняющийся
никаким другим. Это элемент называется корнем дерева.
Дерево может рассматриваться как частный случай графа. Тогда можно сказать,
что деревом называется связный ориентированный ациклический граф.
Узлы, находящиеся на верхнем уровне и имеющие подчинённые узлы,
считаются родительскими или порождающими, а узлы, находящиеся на нижнем
уровне, считаются дочерними, потомками или порождёнными. В общем случае
каждый узел дерева может иметь любое количество дочерних узлов.
Узлы, не умеющие потомков, принято называть листьями.
В информатике широко применяются несколько частных случаев, несколько
разновидностей деревьев: бинарные деревья, идеально сбалансированные
деревья, АВЛ деревья, деревья поиска, В-деревья и некоторые другие виды.
14.06.2025
185
186.
Бинарные деревьяБинарными называются деревья, каждая вершина которых может иметь не
более двух дочерних.
Считается, что каждая вершина бинарного дерева имеет два возможно пустых
поддерева левое и правое. Каждое непустое поддерево в свою очередь
является бинарным деревом. Это означает, что бинарное дерево имеет
рекурсивную структуру.
Корень
Левое
поддерево
Правое
поддерево
С каждым узлом дерева обычно связана некоторая полезная информация, для
обработки которой собственно и создается дерево. Эта информация может храниться в отдельном поле узла или может быть связана с узлом ссылкой. Для
удобства обработки каждый узел дерева обычно некоторым образом обозначают и это обозначение принято называть ключом вершины (узла). Чаще всего
для в качестве ключей используются целые числа.
К ключам обычно
предъявляется требование уникальности: один и тот ключ не может быть у двух
и более вершин.
14.06.2025
186
187.
Таким образом вырисовывается следующая структура вершины дерева.Информационное поле внутри узла
ключ
Узел содержит ссылку на информационное поле
полезная
информация
ссылки
левое поддерево
правое поддерево
Типы, описывающие структуру дерева:
type
T_info=char; {Зависит от типа информационного поля, может быть любой тип}
T_Tree = ↑T_Node;
T_Node = record
key : integer;
info : T_info;
info : ↑ T_info;
L_tree,R_tree : T_Tree
end;
14.06.2025
187
188.
struct nodestruct node;
{
typedef node *T_tree;
int key;
struct node
char info;
{
node *L_tree, *R_Tree;
int key;
};
char info;
T_tree L_tree, R_tree;
};
14.06.2025
188
189.
Дерево поискаОдна из наиболее часто встречающихся операций в дереве ― поиск узла с заданным ключом. Чтобы упростить работу с деревом в задачах такого типа используют
особую разновидность бинарного дерева ―дерево поиска.
На ключи узлов дерева поиска накладывается требование: ключ любого родительского узла дерево должен быть больше ключа левого порождённого узла и при
этом меньше ключа правого порождённого узла.
9
7
15
Выполнение этого условия требует специального порядка формирования дерева,
специального порядка включения в дерево новых вершин.
Общая идея алгоритма включения: если в дерево нужно включить новую вершину
с ключом k, то начиная с корня дерева в зависимости от результатов сравнения k с
ключом в каждой очередной вершине выбирается для дальнейшего движения
левое или правое поддерево. Если ключ k меньше ключа узла, то выбирается
левое поддерево, если больше ― правое. Если ключи совпадают, то включение
невозможно. Поиск места включения новой вершины завершается при попадании в
лист.
14.06.2025
189
190.
Пусть ключи вершин поступают для включения в дерево в следующем порядке:70, 60, 85, 87, 90, 45, 86, 30, 35, 20, 88, 82
root
Сравнение ключей
*
nil
70
87>70
―
вправо,
85>70
вправо
86<87
―
влево
90>85
60<70
влево
90>70
―
вправо,
вниз
86>70
―
вправо,
вниз
45<70
―
влево,
вниз
86>85
―
вправо,
вниз
45<60― вправо
влево
87>85
90>87
*
*
60
85
45
3
0
20
*
87
82
86
35
90
88
Структура построенного дерева существенно зависит
поступления новых вершин (точнее их ключей) в дерево!
14.06.2025
от
порядка
190
191.
Построение нового дерева сводится к включению в дерево новых узлов, при этомпервый узел включается в пустое дерево и становится его корнем.
Это может делать стандартная процедура включения нового узла в дерево.
Анализ выполняемых при включении действий показывает, что перед включением
нужно найти место включения нового узла в дерево так, чтобы соблюдалось требуемое соотношение между ключами узлов дерева поиска.
Важное замечание! Нужно помнить о том, что не может быть двух одинаковых
ключей у разных узлов в одном и том же дереве поиска.
Анализ действий, выполняемых при поиске места включения нового узла, показывает, что такой поиск по своей сути аналогичен поиску в дереве узла, имеющего
заданный ключ.
Исходя из двух последних соображений, приходим к выводу о том, что нужно
построить процедуру поиска в дереве узла, имеющего точно такой же ключ, что и
включаемый узел. Если такой узел найдется, то делается вывод о невозможности
включения в дерево узла с этим ключом. Если такого узла не окажется, то поиск
должен привести нас к тому месту в которое следует вставить новый узел.
Исходя из общих соображений, заметим, что такую процедуру можно применять и
как самостоятельную для решения задачи поиска, и в сочетании с процедурой
включения нового узла (построения дерева поиска).
14.06.2025
191
192.
Итак, строим подпрограмму поиска в заданном дереве узла с заданным ключом.Подпрограммы поиска обычно реализуются в виде функции, возвращающей значение логического типа: true ― поиск завершён успешно, false― объект не найден.
Дерево задается указателем L на его вершину типа T_Tree, это параметр входной.
Искомый ключ k ― это входной параметр целого типа.
Стандартным считается возвращение из подпрограммы поиска дополнительной
информации о найденном объекте. В рассматриваемом случае такой информацией может быть указатель P типа T_Tree на узел в дереве, ключ которого
совпадает с искомым ключом k. Этот параметр является выходным.
Для прохождения по дереву потребуется вспомогательный указатель q на текущий
узел дерева. Кроме того, в классическом варианте алгоритма решения задачи
поиска необходим индикатор успешности поиска flag логического типа.
Способ решения задачи поиска в дереве также стандартный. Вначале осуществляется подготовка к перебору узлов дерева. Перебор узлов начинается с корня
дерева. Корме того, подготавливается индикатор поиска показывающий, что
искомый узел ещё не найден.
14.06.2025
192
193.
Поиск продолжается пока искомый узел ещё не найден и при этом ещё имеютсяузлы для просмотра.
Анализ каждого очередного узла (в том числе корня) сводится к сравнению искомого ключа с ключом узла.
Если ключи совпадают, то задача решена и индикатор должен получить значение
true.
Если искомый ключ больше, чем ключ вершины, то следует сместиться в правое
поддерево.
Если искомый ключ меньше, чем ключ вершины, то следует сместиться в левое
поддерево.
Если поддерево, в направлении которого нужно сместиться, пусто, то поиск прекращается с отрицательным ответом. Узел, в котором прекратился поиск, при
необходимости может рассматриваться как место вставки нового узла с ключом
равным искомому.
14.06.2025
193
194.
Итерационный вариант решения.function SearchTree (L: T_Tree; k: integer; var p: T_Tree): boolean;
{Поиск узла с ключом k в дереве L; p ― указатель на найденную вершину}
var q: T_Tree; flag: boolean;
{q ― указатель на текущий узел дерева, flag ― индикатор поиска}
begin
{Инициализация поиска}
q:=L {перебор узлов, начиная с корня};
flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {спуск вправо} q:=q↑.R_tree
else {спуск влево} q:=q↑.L_tree;
result := flag; {возвращаемое функцией значение}
p := q;
{если узел найден, то p показывает на найденный, иначе p=nil }
end;
Что представляет собой тело цикла?
Что будет, если дерево пусто?
14.06.2025
Какое значение возвращает p?
194
195.
int SearchTree (int k, T_tree L, T_tree &p)//Поиск узла с ключом k в дереве L; p ― указатель на найденную вершину
{
// Инициализация поиска
T_tree q=L; // Перебор узлов начинается с корня
bool flag=false;
while(q != nullptr && ! flag) // Есть узлы для просмотра и нужный ещё не найден
if(q->key==k) flag=true; // Ключи совпали
else // Ключи не совпали
if(k>q->key) q=q->R_tree; // Cпуск в правое поддерево
else q=q->R_tree; // Cпуск в левое поддерево
p=q;
return flag;
}
14.06.2025
195
196.
Рекурсивный вариант решения.function SearchTreeR (L: T_Tree; k: integer; var p: T_Tree): boolean;
{Рекурсивный поиск узла с ключом k в дереве L; p ― указатель на найденную
вершину}
begin
if L = nil then {Терм. ветвь } begin result := false; p:= nil end
else if k =L↑.key then {Терм. ветвь } begin result := true; p:= L end
else
if k > L↑.key then {Рекурсивная ветвь}
result := SearchTreeR(L↑.R_tree,k,p)
else {Рекурсивная ветвь}
result := SearchTreeR(L↑.L_tree,k,p)
end;
14.06.2025
196
197.
int SearchTreeR (int k, T_tree L, T_tree &p)/*Рекурсивный поиск узла с ключом k в дереве L; p ― указатель на найденную
вершину*/
{
if (L==nullptr) {p=nullptr; return 0; }// Терминальная ветвь с отрицательным рез.
else
if (k==L->key){p=L; return 1; }// Терминальная ветвь с положит. результатом
else // Рекурсивные ветви
if (k>L->key) return SearchTreeR(k,L->R_tree, p); // Спуск в пр. поддер-во
else
return SearchTreeR(k,L->L_tree, p); // Спуск в левое поддерево
return 0;
}
14.06.2025
197
198.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
result := flag; {возвращаемое функцией значение}
p := q; {если узел найден, то p показывает на найденный, иначе p=nil }
q
flag
70
L
false
k
82
Условие цикла
q=L (≠ nil) и flag=false → true
Сравнение ключей
k=82
q↑.key=70
> q↑.key=70
≠ k=82→
→false
true
result
14.06.2025
20
60
p
45
30
85
82
87
86
35
90
88
198
199.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
result := flag; {возвращаемое функцией значение}
p := q; {если узел найден, то p показывает на найденный, иначе p=nil }
q
flag
70
L
false
k
82
Условие цикла
q→85 (≠ nil) и flag=false→true
Сравнение ключей
q↑.key=85
≠ k=82→
false
k=82
>q↑.key=85
→ false
result
14.06.2025
20
60
p
45
3
0
85
82
87
86
35
90
88
199
200.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
result := flag; {возвращаемое функцией значение}
p := q; {если узел найден, то p показывает на найденный, иначе p=nil }
q
flag
70
L
false
true
k
82
Условие цикла
p
q→82 (≠ nil) и flag=false→true
flag=true→false
60
45
Сравнение ключей
3
0
q↑.key=82 = k=82 → true
result
true
14.06.2025
20
85
82
87
86
35
90
88
200
201.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
result := flag; {возвращаемое функцией значение}
p := q; {если узел найден, то p показывает на найденный, иначе p=nil }
q
flag
70
L
false
k
81
Условие цикла
q=L (≠ nil) и flag=false → true
Сравнение ключей
q↑.key=70
≠ k=81→
k=81
> q↑.key=70
→false
true
result
14.06.2025
20
60
p
45
3
0
85
82
87
86
35
90
88
201
202.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
result := flag; {возвращаемое функцией значение}
p := q; {если узел найден, то p показывает на найденный, иначе p=nil }
q
flag
70
L
false
k
81
Условие цикла
q→85 (≠ nil) и flag=false→true
60
p
45
Сравнение ключей
q↑.key=85
≠ k=81→
k=81 > q↑.key=85
→false
false
result
14.06.2025
20
3
0
85
82
87
86
35
90
88
202
203.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
result := flag; {возвращаемое функцией значение}
p := q; {если узел найден, то p показывает на найденный, иначе p=nil }
q
flag
70
L
false
nil
Условие цикла
60
85
p
k
q→82
и flag=false→true
(q=nil)(≠иnil)
flag=false→false
nil
81
45
82
87
Сравнение ключей
3
q↑.key=82
= k=81 → false
k=81>
q↑.key=82
86
90
0
result
20
35
88
false
14.06.2025
203
204.
Тестирование (трассировка) подпрограммы SearchTree показала, что она хорошо реализует задачу поиска, аналогичным образом можно показать работоспособность подпрограммы SearchTreeR.Однако использовать эти подпрограммы как вспомогательные для решения задачи включения нового узла в дерево невозможно, так как при отрицательном
ответе, то есть если узел с искомым ключом в дереве не обнаружен, подпрограммы возвращают в качестве дополнительной информации пустую ссылку, а
не указатель на узел дерева, к которому нужно прикрепить вставляемый.
Что нужно изменить в построенной подпрограмме, чтобы исключить обнаруженный недостаток?
14.06.2025
204
205.
function SearchTree (L: T_Tree; k: integer; var p: T_Tree): boolean;{Поиск узла с ключом k в дереве L; p ― указатель на найденную вершину}
var q: T_Tree; flag: boolean;
{q ― указатель на текущий узел дерева, flag ― индикатор поиска}
begin
{Инициализация поиска}
q:=L {перебор узлов, начиная с корня};
flag := false {узел ещё не найден};
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
p := q;
{если узел найден, то p показывает на найденный, иначе p=nil }
result := flag; {возвращаемое функцией значение}
end;
14.06.2025
205
206.
function SearchTree(L:(L:
T_Tree;
k: k:
integer;
var
p:p:
T_Tree):
boolean;
SearchTreeM
T_Tree;
integer;
var
T_Tree):
boolean;
{Поиск узла с ключом k в дереве L; p ― указатель на найденную вершину}
var q: T_Tree; flag: boolean;
{q ― указатель на текущий узел дерева, flag ― индикатор поиска}
begin
{Инициализация поиска}
q:=L {перебор узлов, начиная с корня};
flag := false {узел ещё не найден}; p:=nil; {если не будет входа в цикл}
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
begin
p := q;
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
end;
result := flag; {возвращаемое функцией значение}
end; { p всегда показывает на нужный узел }
14.06.2025
206
207.
bool SearchTreeM (int k, T_tree L, T_tree &p)//Поиск узла с ключом k в дереве L; p ― указатель на найденную вершину
{
// Инициализация поиска
T_tree q=L; // Перебор узлов начинается с корня
bool flag=false; p=nullptr;// Если не будет входа в цикл
while(q != nullptr && ! flag) // Есть узлы для просмотра и нужный ещё не найден
{
p=q;
if(q->key==k) flag=true; // Ключи совпали
else // Ключи не совпали
if(k>q->key) q=q->R_tree; // Cпуск в правое поддерево
else q=q->L_tree; // Cпуск в левое поддерево
return flag; // p всегда показывает на нужный узел
}
}
14.06.2025
207
208.
bool SearchTreeMR(int k, Tree *&L, Tree *&p){
if (L==nullptr) {return false;}
else
{
if (L->key==k) {p=L; return true;}
else
{
p=L;
if(k>L->key) SearchTreeMR(k,L->R_Tree, p);else SearchTreeMR(k,L->L_Tree, p);
}
}
return 0;
}
14.06.2025
208
209.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден}; p:=nil;
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
begin p:=q;
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
end;
result := flag; {возвращаемое функцией значение}
q
flag
70
false
k
81
Условие цикла
q=L (≠ nil) и flag=false → true
nil
Сравнение ключей
q↑.key=70
≠ k=81→
k=81
> q↑.key=70
→false
true
result
14.06.2025
60
p
20
45
3
0
L
85
82
87
86
35
90
88
209
210.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден}; p:=nil;
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
begin p:=q;
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
end;
result := flag; {возвращаемое функцией значение}
q
flag
70
L
false
k
81
Условие цикла
q→85 (≠ nil) и flag=false→true
60
p
45
Сравнение ключей
q↑.key=85
≠ k=81→
k=81 > q↑.key=85
→false
false
result
14.06.2025
20
3
0
85
82
87
86
35
90
88
210
211.
q:=L {перебор узлов, начиная с корня};flag := false {узел ещё не найден}; p:= nil;
while (q<>nil) and not flag do {есть узлы для просмотра и искомый не найден}
begin p:=q;
if q↑.key= k then {ключи совпадают} flag:= true {индикатор показывает успех }
else {ключи не совпадают}
if k > q↑.key then {движение вправо} q:=q↑.R_tree
else {движение влево} q:=q↑.L_tree;
end;
result := flag; {возвращаемое функцией значение}
k
81
flag
q
false
nil
Условие цикла
q→82
и flag=false→true
(q=nil)(≠иnil)
flag=false→false
Сравнение ключей
q↑.key=82
= k=81 → false
k=81>
q↑.key=82
result
false
14.06.2025
20
70
60
p
45
3
0
L
85
82
87
86
35
90
88
211
212.
Теперь процедуру SearchTreeM можно использовать как вспомогательную длярешения задачи о включении нового узла в дерево.
Назовем подпрограмму включения InTree. Эту подпрограмму можно реализовать
только как процедуру. Почему?
Формальными параметрами процедуры являются: L ― указатель на изменяемое
дерево, (параметр-переменная, почему?), ключ вставляемого узла k ― параметр-значение целого типа, полезная информация связанная с вставляемым
узлом E ― параметр-значение типа T_info.
Для реализации включения потребуется вспомогательная переменная q типа
T_Tree, с помощью которой создается новый узел дерева, а также фактический
параметр p типа T_Tree для вызова подпрограммы SearchTreeM.
Перед собственно включением нового узла нужно вызвать функцию SearchTreeM
для проверки наличия в заданном дереве узла с ключом k.
Если такой узел обнаружится, то нужно прекратить включение с выдачей
сообщения об ошибке, о невозможности выполнить включение.
Если такого узла нет, то p есть указатель на узел дерева, к которому нужно
прикрепить создаваемый, нужно только выбрать правильно место включения (в
корень, слева или справа).
Новый узел создается стандартным образом, его поля заполняются нужными
значениями, а затем он прикрепляется в выбранное место дерева.
14.06.2025
212
213.
procedure InTree (var L:T_Tree; k:integer; E:T_info);{Включение узла с ключом k и содержимым E в дерево L}
var p,q :T_Tree;
begin
if not SearchTreeM(L, k, p) then { узла с ключом k в дереве L нет}
begin
new
(q); with
q↑ do нового узла}
new(q);
{создание
begin
q↑.key:=k; {заполнение
поля ключа}
key:=k; info:=E;
L_tree:=nil; R_tree:=nil
q↑.info:=E; {заполнение
информационного
поля}
q↑.L_tree:=nil;end;
q↑.R_tree:=nil;{заполнение полей ссылок}
if p = nil then { включение в пустое дерево}
L := q { новая вершина объявляется корнем дерева}
else {присоединение новой вершины к узлу p}
if k<p↑.key then p↑.L_tree := q {слева}
else p↑.R_tree := q{справа}
end
else {в дереве L есть узел с ключом k}
writeln(‘Включение узла с ключом’, k, ‘ невозможно’)
end;
Изменить процедуру для случая второго варианта реализации узла дерева.
14.06.2025
213
214.
void InTree (int k, char E, T_tree &L)// Включение узла с ключом k и содержимым E в дерево L
{T_tree p=nullptr;
if (not SearchTreeM(k, L, p)) // узла с ключом k в дереве L нет
{
T_tree q =new node; // создание нового узла
q key=k; // заполнение поля ключа
q info=E; //заполнение информационного поля
q L_tree=nullptr; q R_tree=nullptr; //заполнение полей ссылок
if (p == nullptr // включение в пустое дерево
L= q; // новая вершина объявляется корнем дерева
else //присоединение новой вершины к узлу p
if ( k<p key) p L_tree = q; //слева
else p R_tree = q; //справа
}
else cout << ‘Включение узла с ключом’<< k<< ‘ невозможно’;
//в дереве L есть узел с ключом k
}
14.06.2025
214
215.
Исполним процедуру при k=81k
q
p
70
81
85
q↑
81
key
info
E
R-tree nil
L-tree nil
key
info
81
R-tree
L-tree
p↑
82
nil
nil
new(q); {создание нового узла}
q↑.key:=k; {заполнение поля ключа}
q↑.info:=E; {заполнение информационного поля}
q↑.L_tree:=nil; q↑.R_tree:=nil;{заполнение полей ссылок}
if k<p↑.key then p↑.L_tree := q {слева}
else p↑.R_tree := q{справа}
14.06.2025
215
216.
Собственно подпрограмма включения нового узла в дерево содержит толькосоздание нового узла и ветвление. В то же время используемая как вспомогательная подпрограмма поиска в дереве содержит цикл. Следовательно, сложность процедуры включения полностью определяется сложностью процедуры
поиска.
Оценку сложности подпрограммы поиска можно получить определив количество
узлов дерева, через которые прошёл путь поиска. Эта величина существенно
зависит от структуры дерева.
Какой случай структуры дерева может рассматриваться как самый плохой?
Когда дерево вырождается в линейный список.
В этом случае сложность поиска оценивается
как O(n), где n ― количество узлов в дереве.
70
Когда дерево может выродиться в линейный
список?
Когда ключи поступают по возрастанию или
убыванию значений.
В качестве критерия качества дерева поиска можно
ввести длину самой длинной ветви, которая, очевидно,
определяет оценку для сложности алгоритма поиска.
14.06.2025
root
85
87
90
216
217.
Для характеристики дерева поиска можно использовать ещё и такой параметркак высота дерева h, которая равна количеству уровней в дереве. Известно, что
высота дерева на единицу меньше длины самой длинной ветви. С точки зрения
поиска «хорошими» являются деревья минимальный высоты, «плохими» ―
деревья максимальной высоты.
Деревья минимальной высоты имеют максимальное количество узлов на одном
уровне. Все узлы кроме листьев имеют ровно 2 порождённых. Такое дерево
называется идеально сбалансированным.
70
root
45
60
85
67
84
87
В идеально сбалансированном дереве количество узлов n связано с высотой
дерева h известным соотношением n=2h-1
Сложность алгоритма поиска в идеально сбалансированном дереве оценивается как O(log2n). Почему?
14.06.2025
217
218.
Удаление узла из дерева поиска.Автором алгоритма удаления узла из дерева поиска является Никлаус Вирт.
Будем считать, что удаляемый узел задается своим ключом, а дерево ― ссылкой на его корень.
Чтобы удалить узел нужно сначала спуститься от корня дерева к удаляемому
узлу, а затем исключить его из структуры дерева.
Спуск к нужному узлу, вообще говоря, можно организовать почти так же как и в
алгоритме решения задачи поиска SearchTree. Однако нужно помнить об
особенностях удаления из динамических структур данных. Например, чтобы
удалить звено из линейного списка нужно скорректировать поле связи у звена, к
которому присоединено удаляемое.
При исключении узла могут встретиться три случая: 1) нужно удалить лист; 2)
нужно удалить узел, который имеет только один порождённый; 3) нужно удалить
узел, который имеет два порождённых.
Удаление в двух первых случаях организуется точно также, как исключается
элемент из линейного однонаправленного списка. Запоминается ссылка на удаляемый узел, корректируется ссылка у родительского узла, а затем освобождается память.
14.06.2025
218
219.
qnil
Пусть нужно удалить узел с ключом 33. Это лист, следовательно, ссылку на
этот узел в родительском узле 36 нужно заменить на пустую ссылку.
Этот процесс эквивалентен исключению из списка последнего элемента.
Пусть теперь нужно удалить узел с ключом 36. Этот узел имеет только один
порождённый. В родительском узле с ключом 31 ссылку на узел 36 нужно заменить ссылкой на узел 33.
Этот процесс эквивалентен исключению из середины линейного списка. Тем не
менее оба варианта можно реализовать одной и той же последовательностью
операторов.
14.06.2025
219
220.
Пусть нужно удалить, например, узел с ключом 50. Так как он имеет двапорожденных узла, то просто изменить одну ссылку, как, например, при
удалении узла 36, невозможно.
Родительский узел с ключом 20 можно связать либо с левым поддеревом узла
50 (ключ 30), но тогда некуда девать правое поддерево.
либо с его правым поддеревом (ключ 55).
но тогда некуда девать левое поддерево.
14.06.2025
220
221.
Понятно, что вместо удаляемого узла нужно поставить какой-то другой узел иприкрепить к нему оба поддерева от удалённого узла. Выбрать подставляемый
узел можно только из остающихся в дереве узлов. Еще более точно: это может
быть только один из узлов из левого или правого поддеревьев удалённого узла. В
нашем примере это узлы с ключами 55, 60, 30, 31, 36, 33 или 20.
Для сохранения необходимого свойства ключей дерева поиска Никлас Вирт
предложил выбирать для замены самый правый узел из левого поддерева (36) или
самый левый узел из правого поддерева (55).
Какими свойствами обладают эти узлы? Самый правый из левого поддерева
является наибольшим в этом поддереве, а самый левый в правом поддереве
является наименьшим в этом поддереве.
14.06.2025
221
222.
Такие узлы: 1)всегда существуют, 2)имеют не более одного порождённого узла.Поэтому их: 1)можно подставить вместо удаляемого с сохранением требуемого
свойства ключей в дереве поиска, 2)их легко убрать, исключить с исходной
позиции в дереве, так как они всегда имеют не более одного потомка.
Отсюда вывод: результат выполнения операции исключения узла из
дерева поиск является неоднозначным, он зависит от выбора заменяющего
узла.
14.06.2025
222
223.
Кроме того, Н.Вирт предложил для выполнения операций по удалению узлаиспользовать не вспомогательную внешнюю, по отношению к дереву ссылку, а
непосредственно поле узла.
В линейных списках используется следующий способ исключения элемента.
Ссылка p показывает на узел, к которому прикреплен удаляемый.
p
q
nil
Затем выполняются следующие действия:
q:=p↑.R_tree; {или q:=p↑.L_tree} {для освобождения памяти}
p↑.R_tree:=q↑.L_tree; {или p↑.R_tree:=q↑.R_tree}
dispose(q);
Внимание! Внешняя ссылка (p) должна показывать на узел родительский по
отношению к удаляемому, так как именно в этом узле нужно изменить поле
ссылки.
14.06.2025
223
224.
Идея Вирта состоит в том, чтобы само поле ссылки узла выступало в качествефактического параметра переменной для рекурсивных процедур поиска удаляемого и заменяющего узлов дерева.
Более подробно. Н. Вирт предложил построить рекурсивную подпрограмму, которая в рекурсивных ветвях осуществляет спуск от корня дерева к удаляемому
узлу. В терминальной ветви этого алгоритма определяется тип удаляемого узла и
в зависимости от этого организуется удаление.
Обсуждаемая подпрограмма может быть реализована только как процедура.
Назовём её DeleteNode. Формальными параметрами этой процедуры являются:
параметр переменная (почему?) L типа T_Tree, указывающий на дерево (поддерево), и параметр значение целого типа k, определяющий ключ удаляемого узла.
Для освобождения памяти потребуется вспомогательная ссылка q типа T_Tree на
удаляемый узел.
14.06.2025
224
225.
procedure DeleteNode (var L:T_Tree; k:integer);{Рекурсивная процедура удаления узла с ключом k из дерева L}
var q:T_Tree; {для освобождения памяти}
begin
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin
{Действия по удалению найденного узла}
end;
end;
14.06.2025
225
226.
void DeleteNode (int k, T_Tree *&L)//Рекурсивная процедура удаления узла с ключом k из дерева L
{
if (L==nullptr) // терминальная ветвь
cout << ‘Удаление невозможно ― узла с таким ключом нет’
else // рекурсивный спуск
if (k<L key) DeleteNode(k, L L_tree); // спуск в левое поддерево
else if (k>L key) //спуск в правое поддерево
DeleteNode(k, L R_tree);
else //узел найден ― терминальная ветвь
{
//Действия по удалению найденного узла
}
}
14.06.2025
226
227.
rootФактический параметр
L
DeleteNode(root,51)
k
Сравнение
51
L= nil → false
k=51<L↑.key=100→true
Формальный параметр
procedure DeleteNode (var L:T_Tree; k:integer); …
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
227
228.
rootL
DeleteNode(L↑.L_tree,51)
k
Сравнение
51
L=nil → false
k=51<L↑.key=20→false
k=51>L↑.key=20→true
procedure DeleteNode (var L:T_Tree; k:integer); …
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
228
229.
rootL
DeleteNode(L↑.R_tree,51)
k
Сравнение
51
k=51<L↑.key=50→false
L=nil → false
k=51>L↑.key=50→true
procedure DeleteNode (var L:T_Tree; k:integer);
…
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
229
230.
rootDeleteNode(L↑.R_tree,51)
L
k
Сравнение
51
L=nil → false
k=51<L↑.key=55→true
procedure DeleteNode (var L:T_Tree; k:integer); …
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
230
231.
rootDeleteNode(L↑.L_tree,51)
k
L
Сравнение
L=nil → true
51
procedure DeleteNode (var L:T_Tree; k:integer);
…
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
231
232.
rootDeleteNode(root,50)
k
Сравнение
50
L= nil → false
k=50<L↑.key=100→true
procedure DeleteNode (var L:T_Tree; k:integer); …
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
232
233.
rootDeleteNode(L↑.L_tree,50)
k
Сравнение
50
L=nil
→ false
k=50>L↑.key=20→true
k=50<L↑.key=20→false
procedure DeleteNode (var L:T_Tree; k:integer); …
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
233
234.
rootDeleteNode(L↑.R_tree,50)
k
Сравнение
50
k=50<L↑.key=50→false
L=nil
→ false
k=50>L↑.key=50→false
procedure DeleteNode (var L:T_Tree; k:integer);
…
if L=nil then {терминальная ветвь}
writeln(‘Удаление невозможно ― узла с таким ключом нет’)
else {рекурсивный спуск}
if k<L↑.key then {спуск в левое поддерево} DeleteNode(L↑.L_tree,k)
else if k>L↑.key then {спуск в правое поддерево}
DeleteNode(L↑.R_tree,k)
else {узел найден ― терминальная ветвь}
begin {Удаление найденного узла}
end;
14.06.2025
end;
234
235.
Удаляемый узел найден, причём формальный параметр L процедуры показываетна найденный узел. L обозначает поле ссылки в родительском узле дерева.
Теперь нужно определить сколько порождённых имеет удаляемый. Если таких
узлов нуль или один, то узел удаляется также как элемент из линейного списка.
Если удаляемый имеет два порождённых, то нужно найти заменяющую вершину.
Предположим, что уже написана рекурсивная процедура ReplaceNode поиска заменяющего узла, в которой такой узел не только находится, но и осуществляется
подмена удаляемого узла заменяющим. Тогда можно закончить подпрограмму
DeleteNode таким фрагментом:
else {узел найден ― терминальная ветвь алгоритма}
begin {Действия по удалению найденного узла}
q:= L; {для освобождения памяти}
{определения количества порождённых}
if q↑.L_tree=nil then {удаляемый не имеет левого поддерева}
L:=L↑.R_tree {Либо лист, либо поддерево только справа}
else {есть поддерево слева}
if q↑.R_tree=nil then {нет правого поддерева}
L:=L↑.L_tree {Поддерево только слева}
else {поддерево есть и слева и справа}
ReplaceNode(L↑.L_Tree); {поиск и замена}
dispose(q)
end;
14.06.2025
235
236.
else //узел найден ― терминальная ветвь алгоритма{ //Действия по удалению найденного узла
T_tree * q= L; // для освобождения памяти
// определения количества порождённых
if (q L_tree==nullptr) //удаляемый не имеет левого поддерева
L=L R_tree; //Либо лист, либо поддерево только справа
else // есть поддерево слева
if (q R_tree==nullptr) //нет правого поддерева
L=L->L_tree; //Поддерево только слева
else // поддерево есть и слева и справа
ReplaceNode(L L_Tree); //поиск и замена
delete q;
}
14.06.2025
236
237.
Теперь нужно разработать процедуру ReplaceNode нахождения заменяющего узла. В соответствии с записанным в основной подпрограмме вызовом этойпроцедуры ReplaceNode (L↑.L_Tree) процедура должна иметь один формальный
параметр-переменную (пусть он называется r), который показывает на корень
левого поддерева удаляемого узла. Кроме того, это должна быть рекурсивная
процедура.
L
ReplaceNode (L↑.L_Tree)
L↑
L↑.L_Tree
* rr
* r
*
Заменяющий
В рекурсивной ветви нужно спускаться по правому поддереву, пока правое поле
ссылки в узле, на который показывает формальный параметр, не окажется пустой
ссылкой. Это и будет означать, что в левом поддереве достигнут самый правый
узел, то есть узел, который может заменить удаляемый.
14.06.2025
237
238.
В терминальной ветви (то есть после определения заменяющего узла) нужно переписать ключ и информационное поле заменяющего узла в соответствующиеполя удаляемого узла.
Для организации такой замены нужно иметь ссылку на заменяющий узел (это
ссылка r , которая найдена в рекурсивной ветви) и ссылку на удаляемый узел (это
ссылка q, найденная в основной процедуре удаления).
После чего следует удалить тот узел, который выступает в роли заменяющего. Для
этого нужно: изменить значение q на значение r (для освобождения памяти) и
скорректировать поле в родительском узле заменяющего.
procedure ReplaceNode (var r :T_Tree):
{Рекурсивный поиск заменяющего узла, r ― обозначение поля ссылки в узле дерева, показывает на заменяющий, q ― показывает на удаляемый узел,
глобальная для процедуры величина}
begin
if r↑.R_tree <> nil then {рекурсивный спуск в правое поддерево}
ReplaceNode(r↑.R_tree)
else {терминальная ветвь}
begin
q↑.key := r↑.key; q↑.info ;= r↑.info; {подмена полей}
q:=r; {освобождение памяти от замещающего}
r:=r↑.R_tree {исключение заменяющего}
end
end;
14.06.2025
238
239.
void ReplaceNode(Tree *&r){
if(r->R_Tree!=nullptr)ReplaceNode(r->R_Tree);
else
{
q->key=r->key; q->info=r->info; //
q=r; //
подмена полей
освобождение
r=r->R_Tree; //исключение заменяющего
}
return;
}
Где должна быть описана q, чтобы она была видима в ReplaceNode
DeleteNode? Как называются такие переменные?
14.06.2025
и в
239
240.
В Delphy как можно объявить q глобальной для процедуры ReplaceNodeвеличиной?
Нужно поместить описание процедуры ReplaceNode внутрь описания процедуры
DeleteNode.
Как ещё можно реализовать работу с указателем q?
Объявить его формальным параметром переменной:
Какой способ лучше?
procedure ReplaceNode(var r,q:T_Tree);
В чем существенное отличие итерационного подхода, использованного в
процедуре SearchTree, от рекурсивного подхода, использованного в
процедурах SearchTreeR, DeleteNode?
В итерационном подходе для спуска по дереву используется внешняя по
отношению к дереву ссылка. В рекурсивном подходе для спуска по дереву
используются поля ссылок, входящие в узлы дерева.
Для удаления узла при использовании внешней ссылки она должна показывать
на родительский узел, а при использовании рекурсивного подхода, корректируется ссылка, уже входящая в родительский узел
Выполнить трассировку процедуры ReplaceNode на примере обсуждавшегося дерева.
14.06.2025
240
241.
Обходы бинарных деревьевСуществует класс задач, в которых для достижения результата нужно посетить
все узлы бинарного дерева. Это, например, задача определения суммы всех информационных элементов, связанных с узлами дерева, задача определения
наибольшего элемента, печать значений всех элементов и т.д.
Такой обход может выполняться в любом бинарном дереве, а не только в дереве
поиска, в котором упорядоченность ключей используется для сокраще-ния пути,
проходимого по дереву и для уменьшения сложности алгоритма.
На практике используется несколько различных схем обхода. К основным, базовым схемам обхода относят прямой (в ширину), обратный (центрированный,
симметричный) и концевой (в глубину) обходы.
Схемы обходов:
Прямой обход: корень, левое поддерево, правое поддерево.
Обратный обход: левое поддерево, корень, правое поддерево.
Концевой обход: левое поддерево, правое поддерево, корень.
Прямой:
14.06.2025
Обратный:
Концевой:
241
242.
*70
root
Прямой обход дает следующий порядок ключей:
70, 60, 45, 67, 85, 84, 87
*
45
*
60
*
85
*
67
*
84
Обратный обход дает следующий порядок ключей:
*
87
45,60, 67, 70, 84, 85,87
Концевой обход дает следующий порядок ключей:
45,67, 60, 84, 87, 85, 70
Как всегда, наиболее просто реализуются рекурсивные алгоритмы обхода.
В качестве примера действия выполняемого в каждом узле дерева выберем вывод ключа и информационного поля узла.
Тогда действия выполняемые при прямом обходе можно описать следующим
образом: зайти в корень текущего поддерева, вывести требуемую информация,
затем рекурсивно посетить его левое поддерево, затем рекурсивно посетить его
правое поддерево.
Рекурсивная ветвь, очевидно, выполняется если дерево не пусто. В терминальной ветви делать ничего не нужно. Отсюда вытекает следующий вид процедуры:
14.06.2025
242
243.
procedure DirectRound(L:T_Tree); {Рекурсивный прямой обход дерева L}begin
if L<>nil then {Рекурсивная ветвь}
begin
writeln (L↑.key, L↑.info); {Обработка корня}
DirectRound (L↑.L_tree); {Рекурсивная обработка левого поддерева}
DirectRound (L↑.R_tree) {Рекурсивная обработка правого поддерева}
end
end;
Где в процедуре терминальная ветвь?
В других видах обходов изменяется только порядок следования операторов
внутри рекурсивной ветви.
procedure BackRound(L:T_Tree); {Рекурсивный обратный обход дерева L}
begin
if L<>nil then
begin
BackRound (L↑.L_tree); {Рекурсивная обработка левого поддерева}
writeln (L↑.key, L↑.info); {Обработка корня}
BackRound (L↑.R_tree) {Рекурсивная обработка правого поддерева}
end
end;
14.06.2025
243
244.
void DirectRound(Tree *L){
if (L!=nullptr)
{
cout<<L->key<<" "<<L->info<<"\n";
DirectRound(L->L_Tree);
DirectRound(L->R_Tree);
}
else
return;
}
14.06.2025
244
245.
procedure EndsRound(L:T_Tree); {Рекурсивный концевой обход дерева L}begin
if L<>nil then
begin
EndsRound (L↑.L_tree); {Рекурсивная обработка левого поддерева}
EndsRound (L↑.R_tree); {Рекурсивная обработка правого поддерева}
writeln (L↑.key, L↑.info) {Обработка корня}
end
end;
Значительно сложнее организуется итерационный обход бинарного дерева.
Если бы каждый узел дерева имел ровно один порождённый, то задача решалась бы просто: для полного обхода нужно спускаться от корня дерева налево
или направо в существующий узел, пока не будет достигнут лист.
Стало быть проблема в возможном наличии у родительского узла двух порождённых.
Эта проблема может быть решена с помощью стека, который используется для
хранения указателя на второй порожденный узел. В этом состоит основная
идея итерационного обхода дерева.
14.06.2025
245
246.
Более подробно. Для организации обхода нужно подготовить пустой стек, в котором можно хранить ссылки на узлы деревьев. Обход начинается с корнядерева.
Каждый текущий узел дерева обрабатывается следующим способом. Выполняется необходимая обработка полей этого узла. Если у него имеется только один
порождённый, то производится спуск в этот узел.
Если текущий узел имеет два порождённых, то ссылка на один из них, например,
правый записывается в стек и осуществляется спуск в левое поддерево.
После достижения листа осуществляется выбор вершины стека и обработка
выбранного поддерева продолжается точно таким же образом.
Завешается обход после того как спуск приведёт в лист и при этом стек окажется
пустым.
Для работы со стеком нужна переменная p типа T_Stack, а для обхода дерева ―
переменная q типа T_Tree. Будем считать, кроме того, что имеется описание type
T_info_Stack= T_Tree; {Информационное поле стека имеет тип T_Tree}
Во время спуска ссылка q показывает на текущий, обрабатываемый узел дерева. Заметим, что после попадания в лист, q показывает на этот лист.
Если стек не пуст, то из его вершины выбирается ссылка на ранее не обработанное поддерево и присваивается в качестве нового значения переменной q.
14.06.2025
246
247.
Если же стек в это время оказался пустым, то это значит, что все узлы деревапросмотрены и можно прекратить обход, присвоив переменной q значение nil.
q
nil
root
↑31
Количество поддеревьев
два
Одно
Лист
↑50
↑55
↑120
Направление спуска
направо
налево
Обработанные узлы
100, 20, 15, 50, 30, 20, 31, 36, 33, 55, 60, 120, 130
14.06.2025
247
248.
procedure RoundIt(L:T_Tree); {Итерационный обход дерева L}var p:T_Stack; q:T_Tree;
begin
CreateStack(p); {Создание стека}
q:=L; {Начало обхода – корень дерева}
while q<> nillptr do {Пока есть необработанные узлы}
begin
writeln (q↑.key, q↑.info); {Обработка корня}
if q↑.L_tree<>nillptr then {есть левое поддерево}
begin {смотреть есть ли правое поддерево}
if q↑.R_tree<>nil then {есть и правое и левое поддерево}
InStack(p,q↑.R_tree) {ссылку в стек};
q:=q↑.L_tree {спуск в левое поддерево}
end
else {левого поддерева нет}
if q↑.R_tree<>nil then {есть правое поддерево и нет левого}
q:=q↑.R_tree {спуск в правое поддерево}
else {поддеревьев нет}
if not IsEmptyStack(p) then {стек не пуст} OutStack(p,q)
else {стек пуст} q:=nil
end
end;
14.06.2025
248
249.
void RoundIt(Tree *L){ Tree *q; Stack *p=new Stack; p=nullptr; q=L;//Обход с корня дерева
while(q!=nullptr)
{
cout<<q->key<<" "<<q->info<<"\n";
if (q->L_Tree!=nullptr)
{
if (q->R_Tree!=nullptr) InStack(q->R_Tree, p);
q=q->L_Tree;
}
else
if(q->R_Tree!=nullptr) q=q->R_Tree;
else
if(p!=nullptr) q=OutStack(p);else q=nullptr;
}
}// Необходимо внести изменения в функции InStack и OutStack по типу параметра
и возвращаемого значения
14.06.2025
249
250.
Примеры использования процедуры обходаЗадача уничтожения дерева.
Уничтожить дерево ― это значит исключить из него (с освобождением памяти) все
узлы, так что в результате останется пустое дерево. Как это можно сделать?
Для этого, конечно, можно использовать процедуру DeleteNode и поодиночке
исключить из дерева все узлы. Но: 1) нужно знать ключи всех узлов; 2)это долго.
Естественный и простой способ уничтожения дерева без знания ключей его узлов
можно организовать на базе процедур обхода.
Какая из процедур обхода лучше всего подойдёт для уничтожения дерева?
procedure DestroyTree (var L:T_Tree); {Уничтожение дерева L}
begin
if L<>nil then
begin
DestroyTree (L↑.L_tree); {Рекурсивное уничтожение левого поддерева}
DestroyTree (L↑.R_tree); {Рекурсивное уничтожение правого поддерева}
dispose(p) {Уничтожение корня}
end
end;
14.06.2025
250
251.
Задача слияния деревьев.Пусть даны два бинарных дерева L1 и L2. Требуется построить бинарное дерево L,
содержащее те и только те его узлы, которые имеются в L1 и в L2. Бинарные
деревья, участвующие в слиянии, могут быть произвольными деревьями или же
деревьями поиска.
L1
L2
L
Самый простой способ слияния ― выбрать подходящий лист (или узел с одним потомком) в первом дереве и подсоединить к нему второе дерево целиком
14.06.2025
251
252.
Важное замечание! Операция слияния деревьев неоднозначна. Результат существенно зависит от способа выполнения слияния.Однако реализация этого способа порождает две проблемы.
Первая проблема касается только любых деревьев. Такое слияние может привести к дублированию ключей у разных узлов внутри одного и того же дерева.
Вторая проблема касается только деревьев поиска. Такое слияние может привести к нарушению основного соотношения между ключами узлов деревьев поиска.
Если позаботиться о том, чтобы не было дублирования ключей в результирующем
дереве, то для слияния произвольных деревьев указанный способ использовать
можно.
А в случае слияния деревьев поиска для исключения этих проблем предлагается
выполнять поузловое включение узлов второго дерева L2 в первое L1, используя
для этого процедуру InTree. Предусмотренные при её написании функции
обеспечивают и необходимое соотношение между ключами и исключают
дублирование.
14.06.2025
252
253.
L1L
L2
Результат такого слияния не содержит двух экземпляров узла с ключом 130.
Остальные узлы второго дерева присоединены в разные места первого в соответствии с требуемым соотношением между ключами
14.06.2025
253
254.
Поскольку существует несколько вариантов способов обхода дерева, следует выбрать наиболее подходящий для решаемой задачи способ.Это выбор можно сделать исходя из следующих рассуждений. Одно из сливаемых
деревьев может быть пустым. Посмотрим к чему приведёт в этом случае процесс
слияния способом поузлового включения.
L1 nil
L2
4
1
Прямой обход
L
2
6
3
5
7
Обратный обход
1
L
4
Концевой обход
L
1
2
3
3
2
6
4
5
2
5
1
3
5
7
4
6
7
14.06.2025
7
6
254
255.
Таким образом, применение обратного обхода дает наихудший результат, так как вэтом случае дерево вырождается в линейный список.
Применение прямого обхода не изменяет структуру не пустого дерева, поэтому
для реализации процедуры слияния следует применять именно прямой обход.
Заметим, что если при слиянии деревьев первое из них пусто, то такую операцию
называют перерисовкой. Из приведённых примеров видно, что результат операции перерисовки неоднозначен и существенно зависит от применяемого способа
обхода.
А что будет результатом слияния, если пусто второе дерево L2?
В этом случае результатом всегда будет дерево L1. Следовательно, операция
слияния некоммутативная ― результат зависит от порядка операндов.
Итак для реализации слияния следует применить схему прямого рекурсивного
(или итерационного) обхода дерева L2, в которой выполняемая над текущим узлом
операция представляет собой включение этого узла в дерево L1.
Результатом выполнения слияния является изменённое дерево L1. Поэтому
процедура слияния должна иметь только два формальных параметра. Первый
параметр ― ссылка на корень дерева L1. Этот параметр является одновременно и
выходным и выходным. Второй параметр ― только входной, это ссылка на дерево
L2. При таком подходе нужно помнить о том, что исходный вариант дерева L1 не
сохраняется.
14.06.2025
255
256.
procedure Merge (var L1:T_Tree; L2:T_Tree);{Слияние деревьев поиска L1 и L2. Результат в изменённом дереве поиска L1}
begin
if L2<>nil then {Рекурсивная ветвь}
begin
InTree(L1, L2↑.key, L2↑.info); {Обработка корня}
Merge (L1, L2↑.L_tree); {Рекурсивное слияние левого поддерева}
Merge (L1, L2↑.R_tree) {Рекурсивное слияние правого поддерева}
end
end;
Как нужно изменить процедуру слияния, чтобы сохранялись оба исходных дерева?
Как нужно изменить процедуру слияния, чтобы сохранялись освобождалась
память от ненужного в дальнейшем дерева?
Нужно включать в результирующее дерево не копию узла из второго, а сам узел.
Для этого очередной включаемый узел нужно присоединить к выбранному месту в
первом дереве, после чего отрезать этот узел от второго.
Можно также после слияния деревьев с помощью процедуры Merge уничтожить
второе дерево с помощью процедуры DestroyTree.
14.06.2025
256
257.
Задача сравнения бинарных деревьев.Пусть даны два бинарных дерева L1 и L2. Требуется выяснить совпадают ли эти
деревья.
В общем случае два дерева совпадают между собой если полностью совпадают их
структуры, и при этом в соответствующих друг другу узлах деревьев совпадают
ключи и информационные поля. Кроме того, можно считать равными друг другу
два пустых дерева.
Рекурсивные рассуждения для построения этой подпрограммы в случае бинарных
деревьев выглядят следующим образом.
Если оба дерева не пустые, то они совпадают если у корней равны ключи и при
этом у корней равны информационные поля, и при этом равны левые и правые
поддеревья. Если оба дерева пустые, то они также считаются равными. Во всех
остальных случаях деревья не совпадают.
14.06.2025
257
258.
function IsEqualTree(L1, L2: T_Tree): boolean;{Сравнение деревьев L1 и L2}
begin
if (L1<>nil) and (L2 <> nil) then {рекурсивная ветвь}
result := (L1↑.key=L2↑.key) {равны ключи корня}
and (L1↑.info=L2↑.info) {равны информац. поля}
and IsEqualTree(L1↑.L_tree, L2↑.L_tree)
and IsEqualTree(L1↑.R_tree, L2↑.R_tree)
else {терминальные ветви}
if (L1=nil) and (L2=nil) then result := true
else result := false
end;
14.06.2025
258
259.
Сбалансированные деревьяДеревья минимальной высоты имеют максимальное количество узлов на каждом
уровне. Все узлы кроме листьев имеют ровно 2 порождённых. Такое дерево
называется идеально сбалансированным.
root
70
45
60
85
67
84
87
В процессе создания идеального дерева подобной «идеальной» ситуации
может не получиться.
Подключение новых вершин к идеально сбалансированному дереву происходит
в соответствии с правилом: заполнение дерева осуществляется по уровням
слева направо и сверху вниз.
Чтобы учесть нарушения, возникающие при включение в дерево новых вершин,
определение идеально сбалансированного дерева нуждается в уточнении.
14.06.2025
259
260.
В идеально сбалансированном дереве количество узлов левого и правогоподдеревьев любого узла дерева отличаются не более, чем на единицу.
Пусть ключи вершин поступают для включения в дерево в следующем порядке:
70, 60, 85, 45, 84, 67, 87
n=1
n=2
n=3
70
70
70
60
60
85
n=4
n=5
n=6
n=7
70
70
70
70
60
45
14.06.2025
85
60
45
85
84
60
45
67
85
84
60
45
67
85
84
260
87
261.
Если нумерацию уровней k начинать с нуля k=0, 1, 2, 3, …, то максимальноеколичество узлов, которые можно разместить на k-ом уровне, равно 2k, при
этом высота дерева h равна количеству уровней k+1.
В идеально сбалансированном дереве максимально возможное количество узлов N связано с высотой дерева h известным соотношением N=2h-1
Для заданного количества узлов идеально сбалансированное дерево имеет
минимальную высоту.
Если заранее известно количество узлов N, из которого должно состоять
идеально сбалансированное дерево, то для его построения можно использовать
следующий рекурсивный алгоритм.
1. Первый узел считается корнем строящегося идеального дерева.
2. Рекурсивно строится левое поддерево с NL=N div 2 узлами.
3. Рекурсивно строится правое поддерево с NR=N-NL-1 узлами.
Подпрограмму построения можно оформить и как процедуру, и как функцию,
которая возвращает ссылку на корень построенного дерева.
14.06.2025
261
262.
Исходя из предыдущих рассуждений, получаем, что такая подпрограмма должна вкачестве параметра иметь количество узлов строящегося дерева.
Для простоты организации подпрограммы будем считать, что ключи узлов и информация, связанная с узлами вводится с консоли во время выполнения подпрограммы.
function BuildIdealBalanceTree(N:integer):T_Tree;
{Построение идеально сбалансированного дерева с N узлами}
var NR,NL: integer; p:T_Tree;
begin
if N>0 then {Рекурсивная ветвь}
begin
new(p); result:=p; NL:= N div 2; NR:=N-NL-1;
with p do
begin
read(key); read(info);
L_tree:= BuildIdealBalanceTree(NL);
R_tree:= BuildIdealBalanceTree(NR);
end
end else {терминальная ветвь} result:= nil
end;
14.06.2025
262
263.
Tree * BBT(int N){ if(N>0)
{ Tree *p=new Tree;
int NL=N/2; int NR=N-NL-1;
int key; char c;
cout<<"Введите ключ и значение"<<"\n";
cin>>key; cin>>c;
p->key=key;p->info=c;
p->L_Tree=BBT(NL);
p->R_Tree=BBT(NR);
return p;
}
else return nullptr;
}
14.06.2025
263
264.
Построить идеально сбалансированное дерево, если ключи узлов поступают вследующем порядке: 8, 9, 11, 15, 19, 20, 21, 7, 3, 2, 1, 5, 6,4, 13,14,10,12,17,16,18
N=21
(5, 4)
8
(10, 10)
9
11
5
(2, 2)
(1, 0)
(1, 0)
(0, 0)
7
15
20
19
3
(1, 0)
12
4
1
(0, 0)
2
21 (0, 0)
6
(2, 1)
13
14
17
10
18
16
(0, 0)
Построить по тем же ключам дерево поиска.
8
7
9
3
2
1
11
5
4
15
10
6
19
13
12
14
16
14.06.2025
20
17
21
18
264
265.
Видно, что высота дерева поиска больше высоты идеально сбалансированногодерева. Но в нем быстрее осуществляется поиск. Почему?
Поиск в идеально сбалансированном дереве может потребовать его полного
обхода, то есть сложность O(N), в дереве поиска минимальная сложность равна
O(log2 N), а максимальная ― O(N).
Пусть N=106=1 000 000. Тогда максимальная сложность оказывается равной 106, а
минимальная ― log2106 = 6 log210 = 6 3,3219 = 19,93.
Хотелось бы иметь одновременно и минимальную высоту, как у идеально
сбалансированного дерева, и возможности поиска, как у дерева поиска.
Создавать и поддерживать (при включении и исключении узлов) у одного и того
же дерева и свойства идеально сбалансированных деревьев и свойства
деревьев поиска очень сложно.
14.06.2025
265
266.
АВЛ-деревьяДеревья поиска могут иметь любую структуру, вплоть до вырожденной в линейный
список. Это приводит к тому, что поиск потребует время O(N), где N ― количество
узлов дерева.
Идеально сбалансированные деревья, имеющие высоту log2N, не имеют необходимого соотношения между ключами, следовательно, нужен полный обход дерева,
что может потребовать также O(N).
Советские учёные Г.М. Адельсон-Вельский и Е.М. Ландис в 1962 году предложили
компромиссный вариант построения деревьев. Впоследствии эти деревья назвали
АВЛ-деревьями.
По определению Г.М. Адельсона-Вельского и Е.М. Ландиса дерево поиска называется сбалансированным тогда и только тогда, когда высоты левого и правого
поддеревьев каждого из узлов дерева отличаются не более, чем на единицу.
root
8
4
hL
2
14.06.2025
10
6
hR
|hL-hR|≤1
266
267.
Сравните определение сбалансированного дерева (просто сбалансированного),данного Г.М. Адельсоном-Вельским и Е.М. Ландисом, с определением идеально
сбалансированного дерева.
Важным моментом в определении сбалансированности (как простой, так и
идеальной) является требование выполнения указанного условия для каждого
узла дерева. Можно построить множество примеров, когда условие выполняется
на многих участках дерева, а целом не выполняется.
Авторы доказали, что в любом сбалансированном дереве (АВЛ-дереве) за время
O(log2 N) можно найти узел с заданным ключом, включить в дерево новый узел,
исключить из дерева узел с заданным ключом.
Это утверждение является следствием доказанной авторами теоремы о том, что
любое сбалансированное дерево по высоте никогда не превышает более чем на
45% идеально сбалансированное дерево.
Таким образом, АВЛ-дерево, сохраняя необходимое соотношение между ключами
узлов, обладает если не минимально возможно высотой, характерной для
идеально сбалансированных деревьев, то достаточно близкой к ней.
14.06.2025
267
268.
Рассмотрим особенности операций включения и исключения для АВЛ-деревьев.Для участка, примыкающего к месту включения нового узла (место включения определяется по правилам выбора места в дереве поиска), до включения может
быть верным одно из трёх соотношений:
1. hL=hR, тогда включение нового узла в любое поддерево не нарушает баланса;
2. hL=hR+1, тогда включение нового узла в левое поддерево
балансировку, а включение в правое поддерево улучшит;
нарушит
3. hR=hL+1 тогда включение нового узла в левое поддерево
балансировку, а включение в правое поддерево нарушит.
улучшит
Аналогичные соотношения можно записать и для случая исключения узла из АВЛдерева.
Восстановление сбалансированности во втором и третьем случаях требует такой
перестройки структуры дерева, чтобы а)добиться нужного соотношения между
высотами поддеревьев, то есть уменьшить высоту либо левого, либо правого
поддерева; б)не нарушить при этом основное соотношение между ключами узлов.
Из этого следует, что при изменении структуры в процессе балансировки узлы
дерева могут смешаться только между уровнями, только по вертикали (вверх
или вниз) и не могут смещаться по горизонтали.
14.06.2025
268
269.
Рассмотрим возможные случаи включения новых узлов, предположив, что hL=hR+1Нарушение баланса в этом случае возникнет только при включении нового узла в
левое поддерево.
а) LL- включение (в левое поддерево левого поддерева)
8
4
hL
10
2
hR
6
1
hL-hR=2
3
б) LR- включение (в правое поддерево левого поддерева)
8
4
hL
2
6
5
14.06.2025
10
hR
7
hL-hR=2
269
270.
Аналогичные случи включения новых узлов существуют и для hR=hL+1Нарушение баланса в этом случае возникнет только при включении нового узла в
правое поддерево.
а) RR- включение (в правое поддерево правого поддерева)
hL
8
4
12
10
hR-hL=2
hR
16
15
17
б) RL- включение (в левое поддерево правого поддерева)
hL
8
4
12
10
hR-hL=2
14.06.2025
9
hR
16
11
270
271.
С точки зрения восстановления сбалансированности после включения нового узлаLL включение эквивалентно RR включению, а LR включение ― RL включению.
Для восстановления сбалансированности после LL и RR включений используется
малый поворот, а для восстановления сбалансированности после LR и RL
включений ― большой поворот.
а) LL-поворот (малый правый поворот).
A
8
4
2
1
10
6
3
Поскольку высота левого поддерева на единицу больше допустимой, её следует
уменьшить. Для этого, очевидно, нужно поднять на один уровень вверх поддерево, в котором произошло нарушение баланса после вставки нового узла.
В данном случае это узел с ключом 4.
14.06.2025
271
272.
Поднятие на один уровень вверх эквивалентно тому, что этот узел становитсякорнем поддерева. А стало быть узел 8, который ранее был корнем рассматриваемого поддерева, должен опуститься на один уровень вниз и стать корнем
правого поддерева узла 4.
A
A
4
8
4
2
1
2
10
6
1
8
3
6
10
3
Но узел 4 уже имеет правый порождённый ― это узел 6. Выход в том, чтобы отрезать старое правое поддерево от нового узла и прицепить его в качестве нового левого поддерева к старому корню.
Преобразование в целом выглядит как правый поворот поддерева вокруг некоторой оси, именно поэтому такое преобразование называют правым поворотом.
14.06.2025
272
273.
Таким образом, схема малого правого поворота сводится к следующим действиям:1. Нужно отрезать правое поддерево у нового корня и прицепить его слева к
старому корню (речь идет о корне рассматриваемого поддерева, а не всего
дерева).
2. Образовать у нового корня поддерева правую ссылку на старый корень.
3. Изменить ссылку на корень, объявив поднятый узел новым корнем.
Общая схема LL (малого правого) поворота
A
hL=hR+2
+1
A
L
R
14.06.2025
hR
A
B
L
B
hR
M
R
M
273
274.
procedure LL_Turn(var A: T_Tree);{Процедура малого правого поворота}
var B:T_Tree;
begin
B:=A↑L_tree; A↑.L_tree:=B↑.R_tree; {пер. прав. поддер.}
B↑.R_tree:=A; {присоединение старого корня к новому}
A := B {объявление нового корня}
end;
void LLTurn(Tree *&A)
{ Tree *B=A->L_Tree;
A->L_Tree=B->R_Tree;
B->R_Tree=A;
A=B;
}
а) LR-поворот (большой правый поворот).
В данной ситуации применение малого поворота не приведет к нужному
результату
4
8
4
2
10
2
14.06.2025
10
6
6
5
8
7
5
7
274
275.
Для балансировки предлагается поднимать вверх узел с ещё более низкогоуровня, и поднимать её не на один уровень, а на два.
A
A
6
8
4
2
6
5
14.06.2025
10
4
2
8
5
7
10
7
275
276.
Общая схема LR (большого правого) поворота+1
hL=hR+2
A
hR
С
B
B
A
С
L
L
14.06.2025
R
R
276
277.
Таким образом, схема большого правого поворота сводитсядействиям:
к следующим
1. В качестве нового корня поддерева выбирается правый узел левого поддерева, в котором нарушается сбалансированность в результате включения
нового узла.
2. Нужно отрезать левое поддерево у нового корня
родительскому узлу нового корня.
и присоединить его к
3. Нужно отрезать правое поддерево у нового корня и присоединить его к
старому корню поддерева.
4. От нового корня образовать ссылку на бывший ранее родительским для него
и на старый корень.
5. Объявить поднятый узел новым корнем.
14.06.2025
277
278.
procedure LR_Turn(var A: T_Tree);{Процедура большого правого поворота}
var B,C:T_Tree;
begin
B:=A↑.L_tree; C:=B↑.R_tree; {формирование ссылки на новый корень}
B↑.R_tree:=C↑.L_tree; {перенос левого поддерева}
A↑.L_tree:=C↑.R_tree; {перенос правого поддерева}
С↑.L_tree:=B; {формирование левого поддерева нового корня}
С↑.R_tree:=A; {формирование правого поддерева нового корня}
A := С {объявление нового корня}
end;
14.06.2025
278
279.
void LR_Turn(T_Tree *&A);// Процедура большого правого поворота
{
T_Tree * B=A->L_tree;
T_Tree * C=B->R_tree; // формирование ссылки на новый корень
B->R_tree=C->L_tree; {перенос левого поддерева}
A->L_tree=C->R_tree; {перенос правого поддерева}
С->L_tree=B; {формирование левого поддерева нового корня}
}
С->R_tree=A; {формирование правого поддерева нового корня}
A= С {объявление нового корня}
Для восстановления сбалансированности в дереве нужно либо каждый раз после
включения или исключения узла определять наличие нарушения сбалансированности, вообще говоря, по всему дереву, либо вести постоянный учёт высот левых
и правых поддеревьев в каждом узле.
Чтобы вести постоянный учёт сбалансированности следует изменить структуру
узла. Предлагается в определении записи, описывающей узел, ввести ещё одно
поле, в котором фиксируется разность высот правого и левого поддеревьев этого
узла, и далее на основании анализа этого поля выполнять ту или иную
балансировку дерева.
14.06.2025
279
280.
typeT_info=char; {Зависит от типа информационного поля, может быть любой тип}
T_Tree = ↑T_Node;
T_Node = record
key : integer;
info : T_info;
info : ↑ T_info;
bal:-1..1;
L_tree,R_tree : T_Tree
end;
Поле bal ― показатель сбалансированности, определяемый как разность между
высотами правого и левого поддеревьев bal=hR-hL. Для всех узлов сбалансированного дерева эта величина может принимать только три разных значения -1, 0
или 1. При включении в дерево нового узла (листа) значение bal задается равным нулю. Значение bal изменяется при включении узла, исключении узла, и выполнении операции балансировка.
14.06.2025
280
281.
84
2
10
6
7
2
8
7
После включения
После поворота
Узел Bal
8
-1
10
0
Узел Bal
Узел
8
10
Bal
0
0
4
2
6
-1
0
0
7
0
4
2
6
6
4
До включения
0
0
0
8
10
4
-2
0
1
2
6
7
0
1
0
10
Фактически значение bal не становятся равными -2 (или 2) , так как при обнаружении значения -1 (или 1) и определении необходимости добавления узла в более
длинное поддерево делается вывод о необходимости проведения соответствующей балансировки.
14.06.2025
281
282.
{Если выросла левая ветвь}case A↑.bal of
1: A↑.bal:=0;
0: A↑.bal:= -1;
-1: begin {нужна балансировка}
B:=A↑L_tree; {Корень левого поддерева}
if B↑bal= -1 then
begin { малый LL поворот}
A↑.L_Tree:=B↑.R_Tree; B↑.R_Tree:=A;
A↑.bal:=0; A:=B;
end
else begin {большой LR поворот}
C:=B↑.R_Tree; B↑.R_tree:=C↑.L_tree; {перенос левого поддерева}
A↑.L_tree:=C↑.R_tree; {перенос правого поддерева}
С↑.L_tree:=B; С↑.R_tree:=A; {форм. поддеревьев нового корня}
A := С {объявление нового корня}
14.06.2025
282
283.
if C↑.bal= -1 then A↑.bal:=1 else A ↑.bal:=0;if C↑.bal=1 then B↑.bal:= -1 else B ↑.bal:=0;
A := С; {объявление нового корня}
С↑.bal:=0 {восстановление сбалансированности}
end;
end;
Таким образом на основе процедуры вставки для обычного дерева поиска и
четырёх процедур балансировки (двух левых и двух правых поворотов) можно
построить процедуру вставки в АВЛ дерево с сохранением свойств
сбалансированности и упорядоченности.
14.06.2025
283
284.
Обзор других разновидностей деревьевПри построении информационных систем кроме рассмотренных выше широко используются некоторые другие частные случаи сбалансированности.
В частности, можно упомянуть так называемые красно-чёрные деревья, которые
как и АВЛ-деревья гарантируют выполнение различных операций в дереве за
время O(log2N) даже в наихудшем случае.
Узлы красно-черных деревьев по сравнению с деревьями поиска обладают дополнительным полем цвета, который может быть либо красным, либо чёрным.
Понятно, что такое поле занимает всего один дополнительный бит памяти.
Бинарное дерево относится к красно-чёрным деревьям, если оно удовлетворяет
следующим условиям:
1. Корень дерева является чёрным.
2. Каждый лист дерева является чёрным.
3. Если родительский узел красный, то оба его дочерних узла ―чёрные.
4. Для каждого узла все пути от него до листьев, являющихся его потомками,
содержат одно и то же количество чёрных узлов.
В соответствии с этим ограничениями, ни один путь в дереве не отличается от
другого по длине более чем в два раза.
14.06.2025
284
285.
Сильно ветвящиеся деревья. В-деревьяЕсли узел дерева может иметь более двух дочерних, то такое дерево принято
называть сильно ветвящимся. Такие деревья на практике возникают достаточно
часто. Примеры: родословное дерево, каталог на дисковом устройстве.
Сложность с отображением структуры этих деревьев на структуры данных состоит
в неопределенности количества порожденных узлов. Если использовать подход,
принятый в реализации бинарных деревьев, то в записи, представляющей узел
дерева, нужно выделить по одному полю для каждой ссылки на порождённый узел.
Вопрос только в том, сколько нужно предусмотреть таких полей?
Выявленную проблему можно решить двумя способами. Первый способ: зафиксировать максимально возможное количество порождённых узлов и в каждом узле
предусматривать столько же полей ссылок.
В чём недостаток этого способа?
Если всё-таки пойти по этому пути, то возникает ещё одна проблема. Для каждого поля ссылки нужно подбирать своё уникальное имя (типа L_tree, R_tree). Это
не очень удобно, если, например, считать что узел может порождать до 256
дочерних.
Какой выход можно предложить?
Вместо большого количества полей ссылок можно использовать одно поле
типа массив ссылок с нужной размерностью.
14.06.2025
285
286.
Необходимо понимать, что применение для указания на порождённые узлымассива ссылок с зафиксированным максимальным количеством элементов
связано с одной важной проблемой ― неэффективным расходованием памяти.
Если выбирать размерность массива относительно маленькой, то велик риск что
некуда будет помещать ссылку на порождённый узел.
Если выбирать размерность массива ссылок относительно большой, то риск что
количество порождённых узлов окажется больше количества элементов в мас-сиве
будет маленьким. Но при этом может оказаться, что у многих родительских узлов,
имеющих небольшое количество дочерних, большинство элементов мас-сива
ссылок не будут задействованы, они будут бесполезно занимать место в памяти.
Второй способ состоит в организации в каждом узле дерева линейного списка
ссылок на порождённые в нём узлы.
В этом случае каждый узел имеет не более двух ссылок: ссылку на линейный
список дочерних узлов и ссылку на порождённый вместе с ним «сестринский»
узел. Следовательно, полученное дерево станет бинарным.
14.06.2025
286
287.
Преобразование сильно ветвящегося дерева в бинарное80
60
40
27
32
90
50
41
47
49
70
55
62
66
100
74
76
95
98
110
80
90
60
4
0
27
50
32
14.06.2025
41
47
49
70
55
62
100
66
74
76
95
98
110
287
288.
Этот способ лишен недостатков предыдущего, но существенно усложняются процедуры упорядочения ключей при обслуживании (включение, исключение узлов)такого дерева.
Поэтому в упорядоченном дереве, каким является дерево поиска, такой способ не
используется. Зато он широко применяется для отображения графов, которые
обычно рассматриваются как неупорядоченные структуры данных.
Вторая сложность, возникающая у сильно ветвящихся деревьев, связана с организацией упорядоченности. Для бинарных деревьев проблема упорядоченности
ключей узлов решается весьма просто на основании естественных отношений
старшинства между ключом родительского и ключами двух порождённых узлов. В
то время как для сильно ветвящихся деревьев нужно вносить упорядоченность в
некоторый набор ключей порожденных узлов, при этом нужно учесть ещё и ключ
родительского узла.
B-дерево
Если рассматриваемое дерево (бинарное или сильно ветвящееся) состоит из
очень большого количества узлов, то может оказаться что его невозможно или
нецелесообразно размещать в оперативной памяти. В этом случае дерево приходится хранить на дисковых носителях и кроме перечисленных выше проблем
возникает ещё один очень неприятный вопрос ― какое количество обращений к
дисковой памяти необходимо для прохождения от корня до нужного узла дерева?
14.06.2025
288
289.
Каждое такое обращение требует огромного по меркам процессора времени исильно тормозит выполнение программы, которая работает с этим деревом.
Для уменьшения количества обращений к внешней памяти, деревья разбиваются
на поддеревья, все узлы которого передаются в оперативную память
одновременно. Совокупность узлов такого поддерева принято называть
страницей. Пример бинарного дерева, разделённого на страницы, каждая из
которых содержит поддерево, состоящее из 7 узлов (3 уровня):
14.06.2025
289
290.
Пусть, например, каждая страница бинарного дерева поиска содержит поддерево,состоящее из 128 узлов (7 уровней). В этом случае для поиска в дереве,
содержащем 106 узлов потребуется не log2106 ≈ 20 обращений к внешней памяти, а
всего log128106 =6/(7log102) ≈ 2,84 ≈ 3 обращения, что обеспечивает весьма
значительную экономию времени.
Следует понимать, что различные поддеревья, каждое из которых занимает ровно
одну страницу, могут содержать разное количество узлов, но все страницы должны иметь один и тот же размер, так как они передаются из внешней памяти в оперативную одним и тем же механизмом обмена.
Разбиение на страницы не гарантирует дереву поиска малую высоту. Например, в
условиях рассмотренной выше ситуации высота дерева в худшем случае может
оказаться равной 106 и, следовательно, потребуется до 106 : 128 ≈ 8 000 обращений к внешней памяти.
Сказанное выше относительно деревьев поиска относится и к разделенным на
страницы сильно ветвящимся деревьям, которые хранятся на дисковых устройствах. В силу этого и для этих деревьев необходимо заботиться о сбалансированности, приводящей к максимально возможному уменьшению высоты дерева.
Как и у бинарных деревьев у сильно ветвящихся деревьев идеальная сбалансированность требует слишком больших временных затрат на её поддержание при
включении и исключении узлов.
14.06.2025
290
291.
Поэтому для хранения данных, организованных в сильно ветвящиеся деревья,особенно если это хранение осуществляется на дисковых устройствах, применяется специальная разновидность сбалансированных деревьев поиска, которые называются B-деревьями.
Критерий сбалансированности для размещаемых на внешних носителях сильно
ветвящихся деревьев и способ их построения предложили в 1970 году Рудольф
Байер и Эдвард Маккрейт.
В соответствии с этим критерием каждая страница сильно ветвящегося дерева
должна содержать не менее чем k и не более чем 2k его узлов (при заданном
фиксированном значении k, которое принято называть порядком B-дерева).
Если состоящее из N узлов дерево удовлетворяет этому критерию, то в самом
худшем случае потребуется logkN обращений к внешней памяти. Кроме того,
коэффициент использования памяти при таком способе заполнения страниц
составляет не менее 50%, поскольку каждая страница заполнена не менее, чем на
половину.
14.06.2025
291
292.
Определение B-дерева k-го порядка :1. каждая страница содержит не более чем 2k ключей;
2. каждая страница кроме корневой содержит не менее k ключей;
3. каждая страница является либо листом, либо имеет ровно m+1 порождённых
страниц-листьев, где m (k ≤ m ≤ 2k) ― количество ключей на странице;
4. внутренние страницы содержат упорядоченные по возрастанию ключи, а также
соответствующие ключам ссылки на порождённые страницы;
5. все страницы-листья находятся на одном уровне, листья не имеют ссылок на
порождённые (все их ссылки пустые).
Из этого определения следует, что у В-дерева роль узлов переходит к страницам,
которые содержат несколько ключей (и соответствующих им информационных
полей), а не один, как у рассматривавшихся выше деревьев.
Упорядоченность ключей на странице и в целом по B-дереву достигается следующими соглашениями:
1. все ключи на странице упорядочены по возрастанию;
2. каждому ключу внутренней страницы соответствует ссылка на порожденную
страницу, содержащую ключи, каждый из которых больше своего родительского
ключа;
3. на странице имеется единственная ссылка на порожденную страницу,
содержащую ключи, меньшие чем минимальный ключ родительской страницы.
14.06.2025
292
293.
Схема страницы и соглашения упорядоченности в B-деревеp0 (k1, p1) (k2, p2)
(km,pm)
m ключей, m+1 ссылка
c1,c2, …(все больше, чем km)
a1, a2, …(все меньше чем к1)
b1, b2, …(все больше чем k1 но меньше, чем k2
Здесь как бы воспроизводится ситуация бинарного дерева. Ключи меньшие, чем
родительский размещаются как бы слева от него (роль «слева» играет ссылка p0).
Ключи большие родительского, размещаются как бы справа от него. На любой
внутренней странице (в том числе и у корневой страницы) может быть только
один «левый» диапазон и до 2k «правых» диапазонов.
14.06.2025
293
294.
Пример B-дерева 2-го порядкаroot
25
10, 20
2, 5, 7, 8
13, 14, 17, 18
30, 40
21, 24
26, 28, 29
32, 33, 36,37
44, 46, 47, 49
B-деревья 2-порядка иногда называют (2, 3, 4)-деревьями. Любая страница (кроме
корневой) такого дерева может содержать от 2 до 4 ключей. При этом любая
внутренняя страница содержит до 5 ссылок на дочерние.
Некоторые авторы рассматривают В-деревья первого порядка, которые иногда
называют (2,3)-деревьями. Страницы этих деревьев содержат не более 2
ключей и до 3 ссылок на порождённые страницы .
На практике чаще всего используются В-деревья с порядками 50-100 и выше.
14.06.2025
294
295.
Типы, описывающие структуру B-дерева:const order = 2; {порядок дерева} order2= 2*order; {размерность массива}
type
T_info=char; {Зависит от типа информационного поля, может быть любой тип}
T_B_Tree = ↑T_Page;
T_item = record {элемент страницы, аналогичный узлу обычных деревьев }
key : integer;
info : T_info;
info : ↑ T_info;
Ptr : T_B_Tree {ссылка на дочернюю страницу элемента}
end;
T_Page = record {запись, описывающая структуру страницы}
Ptr0 : T_B_Tree {ссылка на «левую» дочернюю страницу}
kp: array [1..order2] of T_items {от keys_pointers}
end;
Пусть, например, p это ссылка на некоторую текущую страницу B-дерева. Тогда,
p↑.kp[1].key есть минимальный ключ на странице, p↑.kp[1].Ptr ссылка на связанную с ним порождённую страницу, а p↑.Ptro ― это ссылка на порождённую
страницу, которая содержит ключи, меньшие, чем минимальный на родительской
странице.
14.06.2025
295
296.
struct Page;struct Item
{
int key;
char info;
Page * ptr;
};
struct Page
{
Page * ptr0;
item * KeyPointers[order2];
};
14.06.2025
296
297.
Алгоритм поиск в B-дереве с учётом выявленных его свойств достаточно простой.Пусть x ― искомый ключ, а p ― ссылка на текущую страницу B-дерева. Тогда:
1. перебор страниц начинается с корневой;
2. если x совпадает с одним из ключей p↑.kp[1].key, p↑.kp[2].key, …, p↑.kp[m].key,
находящихся на текущей странице, то задача поиска решена;
3. в противном случае искомый ключ x сравнивается с наименьшим p↑.kp[1].key на
текущей странице, если x < p↑.kp[1].key, то для дальнейшего поиска выбирается страница p↑.Ptr0;
4. если p↑.kp[i].key < x < p↑.kp[i+1].key (1 ≤ i < m), то для дальнейшего поиска
выбирается страница p↑.kp[i].Ptr;
5. если x> p↑.kp[m].key, то для дальнейшего поиска выбирается страница
p↑.kp[m].Ptr;
6. если найденная ссылка имеет значение nil, то поиск заканчивается неудачей.
14.06.2025
297
298.
Включение и исключение элементов в B-дерево не требуют балансировки. Этипроцедуры не очень сложны с идейной стороны, но достаточно громоздки, так как
требуют поддержания в упорядоченном состоянии массива расположенных на
странице ключей. Поэтому рассмотрим только общую схему включения нового
элемента в B-дерево.
Как и при включении в бинарное дерево поиска вначале вызывается процедура
поиска в B-дереве элемента, ключ которого совпадает с включаемым.
Если такой элемент обнаружен, то процедура включения завершается с выдачей
соответствующего сообщения.
Если такого элемента нет, то процедура поиска возвращает указатель на страницу B-дерева, в которой поиск оборвался и, следовательно, в эту страницу нужно включить новый элемент с заданным ключом.
Если найденная страница содержит m<2k элементов, то новый элемент просто
включается в эту страницу с сохранением свойства упорядоченности у массива
ключей.
Если найденная страница уже содержит m=2k элементов, то вместе с
включаемым получается 2k+1 ключ. Поэтому страница разбивается на две
самостоятельные страницы, каждая из которых содержит ровно k элементов, а
средний переносится вверх, в страницу, родительскую для преобразуемой.
14.06.2025
298
299.
При этом в родительской странице может произойти «переполнение», котороеразрешается точно таким же способом. В худшем случае переполнение доберётся
до корневой страницы и тогда у В-дерева высота увеличится на единицу, за счёт
появления новой корневой страницы.
Схема включения нового элемента при «переполнении» страницы
20
20, 30
A
7, 10, 15, 18
26, 30, 35, 40
A
7, 10, 15, 18
22, 26
B
35, 40
Пусть в изображённое на рисунке B-дерево нужно включить элемент с ключом 22
Алгоритм поиска возвращает информацию, о том, что новый элемент должен быть
включён в страницу A.
Так как рассматривается B-дерево второго порядка, то найденная страница заполнена полностью и включить в неё новый элемент невозможно.
Поэтому добавляется новая страница B. Элементы со страницы A вместе с вставляемым распределяются между страницами A, B и их родительской страницей.
14.06.2025
299
300.
Тема 6. Динамические структуры данных. ГрафыНаиболее общей динамической структурой является граф. Графы, в отличие от
деревьев, не имеют иерархической структуры. Поэтому такие понятия, как корень,
родительский узел, порождённый узел к графам не применимы.
Графы имеют очень обширные применения в информационных системах. В
частности, они используются для анализа корректности программ, оптимизации
трансляторов, решения задач, возникающих в компьютерных и нефтегазовых сетях, транспортных коммуникациях и т.д.
Математически строгое определение графа:
Графом называется G(V,E) упорядоченная пара множеств V и E, где V ― непустое
множество элементов произвольной природы, которые называются узлами графа и
E ― множество двухэлементных подмножеств множества V, которые называ-ются
рёбрами графа.
Например, V={1, 2, 3, 4, 5}, E={{1, 2}, {2, 3}, {1, 3}, {3,4}} . Пара (E,V) является
графом. Этот граф можно изобразить задать следующим образом:
1
2
3
5
4
14.06.2025
300
301.
Такое математическое определение является для потребностей информатикиизлишне строгим, так как исключает многие практически важные свойства.
Множества считаются неупорядоченными, поэтому {1, 3} и {3, 1} эквивалентны.
Кроме того, множество не может содержать двух и более одинаковых элементов,
так {1, 1} ― есть одноэлементное множество {1}. Основываясь только на приведённом определении, невозможно сформировать понятие ориентированного графа
или графа с петлями.
Поэтому вводится много других определений. В частности, мы будем исходить из
следующих определений, более подходящих для работы с графами в программах.
Простым (обыкновенным) графом называется множество вершин (узлов), которые могут быть связаны между собой дугами (ребрами). При этом любая вершина графа может быть связана дугой с любой другой вершиной.
Если связанные дугой вершины упорядочены (известно, какая вершина считается
первой, а какая ― второй), то граф называется ориентированным.
Если две вершины графа связаны более чем одной дугой, то такой граф называется мультиграфом.
Если существует дуга от вершины к самой себе, то такой граф называется псевдографом. При этом дуга называется петлей.
14.06.2025
301
302.
В силу этого определения в графе могут существовать вершины, не связанныедугами ни с одной другой вершиной графа (вершина 5 в примере). Такие вершины
называются изолированными. При наличии хотя бы одной изолированной вершины граф называется несвязным, в противном случае граф считается связным.
Связанные дугой вершины графа называются инцидентными или смежными.
С каждой вершиной и дугой графа может быть связана некоторая полезная с точки
зрения решаемой задачи информация. В этом случае граф считается взвешенным, а связанная с вершиной или дугой информация называется весом вершины
или дуги. Например, у графе, представляющего собой схему дорог весами дуг
могут быть расстояния между вершинами ― населёнными пунктами.
14.06.2025
302
303.
Структура данных, используемая для представление графа.Основной особенностью графа по сравнению с деревом является возможность существования большого количества ссылок, связывающих любую из вершин графа
со всеми остальными. В общем случае вершина простого графа, состоящего из N
вершин, может быть связана с N-1 вершиной. Следовательно, в записи, описывающей вершину графа должно быть предусмотрено N-1 поле ссылки.
Получается, что структура данных, описывающая граф с 10 вершинами не подходит для описания графа, содержащего 11 вершин.
Если же рассматривать возможность решения задач, в которых возникают
мультиграфы и псевдографы, то ситуация становиться безнадёжной, так как
количество дуг, выходящих из вершины в таких графа может быть любым.
Следовательно, идти по пути увеличения количества полей записи
бесперспективно.
Возможные пути решения проблемы обсуждались при рассмотрении сильно ветвящихся деревьев. Там же отмечалось, что для графов используется структура,
основанная на линейном списке ссылок, которые связаны с рассматриваемой
вершиной.
Вообще говоря, существуют и другие способы реализации графов, например, основанные на матрице инцидентности. Понятно, что разные способы описания
обладают различными достоинствами и недостатками.
14.06.2025
303
304.
Наиболее гибкие возможности по работе со всеми вариантами графов (мультиграфами, псевдографами, взвешенными графами и т.д.) предоставляет структура,являющаяся линейным списком вершин графа, при этом каждый элемент списка
содержит ссылку на линейный список дуг, выходящих из вершины.
Элементы списка вершин принято называть дескрипторами (описателями) вершин. Каждый дескриптор должен содержать ключ, служащий для идентификации
вершины, информационное поле, служащее для хранения веса вершины, поле
ссылки на следующий элемент списка вершин и поле ссылки на список дуг, исходящих из этой вершины.
Элементы списка дуг принято называть дескрипторами дуг. Каждый дескриптор
дуги должен содержать информационное поле, служащее для хранения веса дуги,
поле ссылки на вершину, к которой идёт дуга и поле ссылки на следующий элемент
списка дуг.
Дескриптор вершины
Дескриптор дуг
key
dataarc
datanode
linknode
nextnode
nextarc
listarc
14.06.2025
304
305.
Пример реализации графа с помощью предложенных дескрипторов2
1
3
5
4
1
2
3
4
5
nil
nil
nil
14.06.2025
nil
nil
305
306.
Для чего нужен список дескрипторов вершин, если есть дуги, связывающие вершины?Основная причина ― возможность появления изолированных вершин. Кроме того,
существенно упрощаются многие алгоритмы, например, полный обход.
Заметим, что список дескрипторов вершин считается неупорядоченным.
Какая разновидность графа представлена полученной структурой данных?
Несвязный, неориентированный взвешенный граф.
Может ли эта структура служить для реализации мультиграфов и псевдографов?
Итак, для представления графа используется линейный список (вершин) линейных
списков (дуг), некоторые из которых могут быть пустыми. Все списки считаются
неупорядоченными.
14.06.2025
306
307.
Типы, описывающие структуру графаtype
T_info_Node=char; {Тип поля веса вершины}
T_info_Arc =char; {Тип поля веса дуги}
T_Ref_Node =↑T_Node; {Ссылка на дескриптор вершины}
T_Ref_Arc = ↑T_Arc;
{Ссылка на дескриптор дуги}
T_Node = record {дескриптор вершины графа}
key :
integer; {ключ вершины}
datanode : T_info_Node; {вес вершины}
nextnode : T_Ref_Node; {ссылка на следующую вершину}
listarc:
T_Ref_Arc {ссылка на список дуг}
end;
T_Arc = record {дескриптор дуги графа}
dataarc : T_info_Arc; {вес дуги}
linknode : T_Ref_Node; {ссылка на связанную дугой вершину}
nextarc:
T_Ref_Arc {ссылка на следующую дугу}
end;
14.06.2025
307
308.
Типы, описывающие структуру графаstruct arc;
struct node
{
int key;
char datanode;
node * nextnode;
arc * refarc;
};
struct arc
{
char dataarc;
node * linknode;
arc * nextarc;
};
14.06.2025
308
309.
Основные процедуры работы с графамиДобавление новой вершины в граф. Создание графа.
Добавление новой вершины в граф эквивалентно включению элемента в линейный однонаправленный список. Поскольку этот список считается неупорядоченным включение удобнее всего проводить в начало списка. Как всегда, добавление в пустой граф считается созданием графа.
Вершины в граф целесообразно включать отдельно от списка дуг. То есть новая
вершина поступает в граф как изолированная. Затем с помощью отдельной процедуры подключается каждая дуга по отдельности.
Формальными параметрами процедуры является ссылка на вершину графа, которая находится в начале списка дескрипторов вершин (корня у графа в отличие от
дерева нет), ключ (идентификатор) новой, включаемой вершины и её вес.
14.06.2025
309
310.
procedure AddNodeGraph (var G:T_Ref_Node; k:integer; x:T_info_Node);{Включение в граф G новой вершины с ключом k и весом x}
var p: T_Ref_Node; {для создания новой вершины}
begin
new(p); {новая вершина}
with p↑ do; {заполнение полей новой вершины}
key := k; datanode:=x;
nextnode:=G; {подключение существующих вершин графа}
listarc:=nil {список дуг пуст}
end;
G:=p {новая вершина в начале списка}
end;
Отметим, что эта процедура не проверяет наличия в графе вершины с ключом k.
Следовательно, при её использовании допускается существование в графе нескольких вершин с одинаковыми ключами.
Что нужно изменить в предложенной процедуре, чтобы избежать дублирования
ключей?
14.06.2025
310
311.
Добавление новой дуги в существующий граф.Добавить новую дугу можно только в уже существующий граф, то есть в граф, в
котором уже имеются хотя бы две вершины (для добавления петли достаточно
только одной вершины).
При написании процедуры будем считать, что соединяемые новой дугой вершины
задаются указателями u и v на эти вершины.
При этом важно понимать, что в одной и той же программе могут рассматриваться
несколько графов. Это означает, что ссылки u и v должны показывать на вершины
из одного и того же графа, иначе получиться не создание новой дуги, а объединение двух графов.
Заметим, что ссылки u и v могут совпадать, следовательно, с помощью такой
процедуры можно создавать псевдографы.
Заметим также, что если не проверять существования в графе дуги между u и v, то
это позволит создавать мультиграфы.
14.06.2025
311
312.
procedure AddArcGraph (u, v :T_Ref_Node; x:T_info_Arc);{Включение в граф новой дуги из вершины u в вершину v с весом x}
var p: T_Ref_Arc; {для создания новой дуги}
begin
new(p); {новая дуга}
with p↑ do; {заполнение полей новой дуги}
dataarc:=x;
linknode:=v; {дуга из u в v}
nextarc:=u↑.listarc {подключение списка старых дуг}
end;
u↑.listarc:=p {новая вершина в начало списка дуг}
end;
Считая, что дуга идет из вершины u в вершину v и создавая единственную дугу,
получаем ориентированный граф.
Для нужно сделать для включения дуги в неориентированный граф?
Вообще говоря, нужно проверять ссылки u и v на не пустоту, а также на их принадлежность к одному и тому же графу.
14.06.2025
312
313.
void AddNodeGraph(int k, char E, node *& G){ //Включение вершины в граф
node * p=new node;
p->key=k;
p->datanode=E;
p->refarc=nullptr;
p->nextnode=G;
G=p;
}
void AddArcGraph(node *u, *v, char E)
{//Включение неориентированной дуги в граф
arc *p=new arc;
p->dataarc=E;
p->linknode=v;
p->nextarc=u->refarc;
u->refarc=p;
}
14.06.2025
313
314.
Удаление вершин и дуг из графаУдаление вершин и дуг из графа также как и включение рекомендуется осуществлять с помощью раздельных процедур.
Поскольку дуги существенно зависят от вершин, а вершины могут не иметь дуг,
вначале следует удалить все дуги, связывающие данную вершину со всеми остальными, и только после этого удаляется сама вершина. Поэтому вначале построим процедуру удаления дуги.
Удаляемая дуга задается ссылками на вершину u↑, из которой дуга выходит, и
вершину v↑, в которую дуга приходит.
С точки зрения используемых для реализации графа структур данных, задача удаления дуги, идущей из u в v, эквивалента задаче исключения заданного элемента
из линейного списка дуг вершины u↑.
Чтобы удалить элемент из списка, сначала нужно в этот список войти.
Где находится указатель на первый элемент этого списка? Как он обозначается?
На начало списка дуг, идущих из вершины u↑, показывает ссылка u↑.listarc
(u listarc).
Необходимо понимать, что если u=nil, то есть если вершина u↑ не существует, то
запись u↑.listarc не имеет смысла и программа завершится аварийно. Поэтому
перед началом анализа списка следует проверить не пуста ли эта ссылка. И если
u=nil, следует выдать соответствующее сообщение о невозможности удалить дугу.
14.06.2025
314
315.
Далее, если ссылка u не пуста, нужно решить задачу поиска удаляемого элементав списке, на который показывает ссылка u↑.listarc.
При решении задачи поиска для перемещения по списку требуется вспомогательная переменная q типа T_Ref_Arc и переменная логического типа flag, которая
служит индикатором успешности поиска.
Если задача поиска будет решена успешно, то переменная q покажет на элемент
списка дуг, в котором поле ссылки на связанную вершину q↑.linknode равно v, то
есть на удаляемый из списка элемент.
Найденный элемент можно стандартным способом исключить из списка.
14.06.2025
315
316.
vu
1
2
3
4
u↑.listarc
q
q↑.linknode →2 (q↑.linknode<> v)
q↑.linknode→ 3 (q↑.linknode= v)
nil
14.06.2025
316
317.
Но для удаления элемента из линейного списка нужно, чтобы указатель показывална предшествующую вершину, так как корректировать поле связи со следующим
элементом нужно именно в предыдущем элементе списка.
Для решения возникшей проблемы предлагается ввести еще один указатель p,
который всегда должен отставать на один элемент списка от того, на который
показывает q, то есть именно на тот, в котором нужно изменить ссылку.
Для этого перед изменением значения q, то есть перед переносом указателя на
следующий элемент списка (q:=q↑.nextarc) старое значение q следует запомнить в
переменной p (p:=q).
14.06.2025
317
318.
vu
1
2
3
4
u↑.listarc
q
q↑.linknode →2 (q↑.linknode<> v)
p
q↑.linknode→ 3 (q↑.linknode= v)
nil
14.06.2025
318
319.
При удалении элемента из списка, нужно учесть ещё одну возможность.Удаляемый элемент может находиться в начале списка дуг. В этом случае следует
изменять ссылку не в предшествующем элементе списка, а в соответствующем поле дескриптора вершины.
v
u
1
2
3
4
u↑.listarc
q
q↑.linknode →2 (q↑.linknode= v)
p
14.06.2025
nil
319
320.
procedure DeleteArcGraph (u, v :T_Ref_Node);{Удаление из графа дуги, идущей из вершины u в вершину v}
var p, q: T_Ref_Arc; {для прохождения по списку дуг} flag : boolean;
begin
if u<> nil then {проверка u на существование}
begin {u существует}
q:=u↑.listarc;{в начало списка дуг} flag:=false; {элемент ещё не найден}
while (q<> nil) and not flag do {цикл поиска}
if q↑.linknode=v then {дуга найдена} flag:=true
else
begin
p:=q; {ссылка на предыдущий элемент}
q:=q↑.nextarc {переход к следующему элементу}
end;
{Если после окончания цикла q=nil ― нужная дуга не найдена}
{иначе q ― ссылка на исключаемый элемент, а p ― на предыдущий}
if q<> nil then begin
end
if q=u↑.listarc then u↑.listarc:=q↑.nextarc
else p↑.nextarc:=q↑.nextarc; dispose(q);
end
else writeln {‘Удаление невозможно ― не существует дуги в v}
14.06.2025
else wrtiteln(‘Удаление невозможно ― вершина
end;
u не существует’)
320
321.
void DeleteArcGraph(node * u, node *v){ arc *p, *q;
if(u!=nullptr)
{ q=u->refarc; bool flag=false;
while(q!=nullptr && ! flag)
{ if(q->linknode==v) flag=true;
else {
p=q; q=q->nextarc;
}
if(q!=nullptr)
{ if(q==u->refarc)u->refarc=q->nextarc;
else p->nextarc=q->nextarc;
delete q;
}
else cout<<"Удаление дуги невозможно - не существует дуги в вершину v"<<"\n";
}
}
else cout<<"Удаление дуги невозможно - не существует вершины u"<<"\n";
}
14.06.2025
321
322.
В подпрограмме удаляется только дуга, которая выходит из u и приходит в v. Дляориентированного графа этого достаточно. Если граф неориентированный, то в
процедуре нужно предусмотреть ещё и удаление дуги, идущей из v в u. Или же
применить процедуру удаления ещё раз, указав первым параметром v, а вторым u.
Ссылки u и v могут совпадать, следовательно, данную процедуру можно применять и для графа с петлёй (псевдографа).
Для обыкновенных графов дуга из u в v может быть только одна. В случае
мультиграфа и мультиграфа с петлями эту процедуру нужно применять несколько
раз, пока не будут удалены все дуги из u в v ( из u в u).
Задание. Реализовать общую процедуру удаления дуги для случая произвольного графа, предусмотрев в качестве входного параметра признак графа (простой ориентированный, простой неориентированный, мультиграф ориентированный, мультиграф неориентированный.
14.06.2025
322
323.
Удаление вершины из графа, в принципе, также сводится к удалению элемента излинейного списка.
Однако, нужно помнить о том, что каждая вершина графа может иметь собственный список дуг и кроме того, из любых других вершин могут идти дуги к удаляемой.
Поэтому перед собственно удалением вершины (как элемента из линейного списка) нужно удалить и связанный с ней список, и все идущие к ней дуги.
Для этого нужно организовать проход по всем элементам списка вершин и в каждой текущей вершине проверить, является ли она удаляемой.
Если текущая есть удаляемая, то нужно зайти в список её дуг и удалить все элементы этого списка, а затем удалить и саму вершину.
Для удаления элементов списков дуг и вершин можно воспользоваться уже
рассмотренным приёмом ведения двух ссылок, одна из которых показывает на
текущий элемент, а вторая на предшествующий ему.
Если текущая вершина не есть удаляемая, то нужно зайти в список её дуг и удалить элемент списка, ссылающийся на удаляемую вершину (для простоты будем
считать граф обыкновенным). Для удаления такой дуги можно воспользоваться
уже имеющей процедурой DeleteArcGraph.
Граф, из которого нужно удалить вершину, задается указателем G на начальный
элемент списка вершин. Удаляемую вершину можно задавать её ключом или же
ссылкой на неё. Для определённости примем, что вершина задается ссылкой u.
14.06.2025
323
324.
procedure DeleteNodeGraph (var G :T_Ref_Node; u: T_Ref_Node);{Удаление из графа G вершины u}
var qn, pn: T_Ref_Node; qa, pa: T_Ref_Arc; {Для прохождения по спискам}
begin
qn:=G; {просмотр графа с начальной вершины списка}
while qn<>nil do {цикл перебора вершин}
begin
if qn<> u then {текущая вершина не совпадает с удаляемой}
begin DeleteArcGraph(qn,u); {удаление дуги}
pn:=qn; {сохранение ссылки} qn:=qn↑.nextnode end
else {удаляется текущая вершина}
begin
qa:=qn↑.listarc; {для удаление списка дуг вершины u↑}
while qa<> nil do {цикл по списку дуг вершины u↑}
begin
pa:=qa; {сохранение ссылки на текущую дугу}
qa:=qa↑.nextarc; {на следующую дугу}
dispose(pa); {освобождение памяти}
end;
qn:=qn↑.nextnode; {на следующую вершину}
if G=u then {уд. нач. вершина} G:=G↑.nextnode
else {не нач. вершина} pn↑.nextnode=qn;
dispose(u)
14.06.2025
324
end
end
end;
325.
void DeleteNodeGraph(node *u, node *& G){//Удаление вершины из графа
node *pn, *qn=G; arc *pa,*qa;
while( qn!=nullptr)
{
if (qn!=u)
{// Текущая вершина не совпадает с удаляемой
DeleteArcGraph(qn,u);
pn=qn; qn=qn->nextnode;
}
else
{//Удаляется текущая вершина
qa=u->refarc;
while(qa!=nullptr) { pa=qa; qa=qa->nextarc; delete pa; }
qn=qn->nextnode;
if(G==u) G=G->nextnode; else pn->nextnode=qn;
delete u;
}
}
}
14.06.2025
325
326.
Gu
1
qn
pn
2
3
4
qn:=G; {просмотр графа с начальной вершины списка}
while qn<>nil do {цикл перебора вершин}
begin
if qn<> u then {текущая вершина не совпадает с удаляемой}
begin DeleteArcGraph(qn,u); {удаление дуги}
pn:=qn; {сохранение ссылки} qn:=qn↑.nextnode end
else {удаляется текущая вершина}
begin
qn:=qn↑.nextnode; {на следующую вершину}
if qn=G then {нач. вершина} G:=G↑.nextnode
else {не нач. вершина} pn.nextnode=qn;
14.06.2025
326
327.
Полный обход (просмотр) графа.Полный обход графа подразумевает посещение всех его вершин (в том числе изолированных), а также посещение всех дуг его и выполнение в процессе такого
обхода некоторых полезных (с точки зрения решаемой задачи) действий (например, подсчет количества вершин и дуг, подсчет сумм весов, печать весов и т.д.).
Считается, что полный обход графа выполняется в случайном порядке. Фактически обход выполняется в порядке поступления вершин и дуг в граф при его создании.
В качестве простого примера рассмотрим задачу определения общего количества
вершин и дуг графа, а также вывода весов всех его вершин и дуг.
В такой постановке задачи граф не претерпевает никаких изменений, следовательно, у процедуры должен быть единственный формальный параметр-значение, указывающий на начальный элемент списка вершин графа.
Для прохода по линейному списку вершин потребуется вспомогательная переменная qn типа T_Ref_Node, а для прохода по спискам дуг ―переменная qa типа
T_Ref_Arc. Для подсчета количеств вершин и дуг ― две целых переменных Nn и
Na.
14.06.2025
327
328.
procedure BrowseGraph (G :T_Ref_Node);{Полный обход графа G}
var qn:T_Ref_Node; qa: T_Ref_Arc; {для прохода по спискам}
Nn, Na: integer; {для подсчёта количеств вершин и дуг}
begin
Nn:=0; Na:=0; qn:=G; {Инициализация цикла прохода по списку вершин}
while qn<>nil do {цикл по списку вершин}
begin
Nn:=Nn+1; {учёт новой вершины}
writeln(‘Вес вершины ‘, qn↑.key, ‘ равен ‘, qn↑.datanode);
writeln(‘Список дуг вершины ‘, qn↑.key, ‘ :’);
qa:=qn↑.listarc; {переход в список дуг}
if qa=nil then {список дуг пуст} writeln (‘пустой’);
while qa<>nil do
begin
Na:=Na+1; {учёт новой дуги}
writeln(‘Дуга к вершине ‘, qa↑.linknode↑.key,‘ её вес ‘, qa↑.dataarc);
qa:=qa↑.nextarc {к следующей дуге}
end;
qn:=qn↑.nextnode {к следующей вершине}
end;
writeln(‘Граф содержит ‘, Nn, ‘ вершин ‘, Na, ‘ дуг’)
14.06.2025
328
end;
329.
void BrowseGraph(node *G){ node *qn=G;
int Nn=0,Na=0;
while (qn!=nullptr)
{ Nn++;
cout<<"Вес вершины "<<qn->key<<" равен "<<qn->datanode<<"\n";
cout<<"Список дуг этой вершины :";
arc *qa=qn->refarc;
if (qa==nullptr)cout<<" пустой";
cout<<"\n";
while(qa!=nullptr)
{ Na++;
cout<<"Дуга к вершине "<<qa->linknode->key<<" её вес равен “
<<qa->dataarc<<"\n";
qa=qa->nextarc;
}
qn=qn->nextnode;
}
cout<<"Граф содержит "<<Nn<<" вершин и "<<Na<<" дуг"<<"\n";
14.06.2025
329
}
330.
Пример применения схемы полного обхода для уничтожения графа.procedure DeleteGraph (var G :T_Ref_Node);
{Уничтожение графа G}
var qn,pn:T_Ref_Node; qa,pa: T_Ref_Arc; {для прохода по спискам}
begin
qn:=G; {Инициализация цикла прохода по списку вершин}
while qn<>nil do {цикл по списку вершин}
begin
qa:=qn↑.listarc; {переход в список дуг}
while qa<>nil do
begin
pa:=qa; {для освобождения памяти}
qa:=qa↑.nextarc {к следующей дуге}
dispose(pa)
end;
pn:=qn; {lдля освобождения памяти}
qn:=qn↑.nextnode; {к следующей вершине}
dispose(pn)
end;
G:=nil
end;
14.06.2025
330
331.
Тема 7. Сортировка и поискОбщая постановка задачи поиска. В заданной совокупности элементов требуется
найти элемент, обладающий заданным набором свойств.
Важнейший частный случай. Задан массив A, нужно определить имеет ли в нем
элемент, совпадающий с заданным числом a. Если такой элемент обнаружен, то в
качестве дополнительной информации следует получить номер совпадающего с
заданным элемента массива
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
55
82
42
94
18
6
63
x
25
Ответ: В рассматриваемом массиве A элемента, совпадающего с
заданным x =25 нет.
x
18
14.06.2025
Ответ: В рассматриваемом массиве A есть элемент, совпадающий с
заданным x=18. Его номер k=6.
331
332.
Типы данных, используемые в задачах поиска и сортировкиN=….
const N=8;
type T_index=1..N; T_Elem=integer;
T_Elem=…;
T_Massiv=array [T_index] of T_Elem;
Достаточно часто в качестве T_Elem используется запись с полем некоторого типа,
напоминающим информационное поле в дереве.
const int N=8;
int A[ ]={6,55,82,42,94,18,43,63};
При использовании стандартных методов сортировки в С-подобных языках, в
которых нумерация элементов массивов начинается с нуля, необходимо следить
за смещением индекса на единицу. Вместо этого можно не использовать нулевой
элемент, сдвинув вправо все элементы массива и увеличив на единицу константу
N.
const int N=9;
int A[ ]={0, 6,55,82,42,94,18,43,63};
vector<int> A={0,6,55,82,42,94,18,43,63};
14.06.2025
332
333.
a)Классический алгоритмПредлагается очевидный подход к решению задачи: последовательное сравнение
каждого очередного элемента массива с заданным. Такой способ называется линейным поиском.
x[1]
x[2]
x[3]
x[4]
x[5]
x[6]
x[7]
x[8]
43
55
82
42
94
18
6
63
a
Ответ
Искомый элемент отсутствует
Не совпадают
25
x[1]
x[2]
x[3]
x[4]
x[5]
x[6]
x[7]
x[8]
43
55
82
42
94
18
6
63
a
18
14.06.2025
Ответ
Не
Совпадают
совпадают
Элемент есть, его номер k=6
333
334.
bool SearchLinear( int *A, char x, int &k){
int i=0; bool flag=false; k=-1;//Поиск с начального элемента, нужный ещё не найден
while ( (i<N) && ! flag)
{
if(A[i]==x)
i++;
{flag=true;k=i;}
}
return flag;
}
В приведённой реализации алгоритма нулевой элемент массива используется.
14.06.2025
334
335.
б)Быстрый алгоритмИдея быстрого алгоритма состоит в том, что логические выражения flag и A[i]==x
эквивалентны. Следовательно, в условии в заголовке цикла вместо ! flag можно
использовать x[i]!=a, и отказаться от использования индикатора flag.
i=0; while ((i<N) && (A[i]!=x)) i++;
// пока номер не превосходит последний и искомый элемент не найден перейти
к следующему элементу
В этом варианте построения цикла имеется опасный фрагмент. Какой?
Является ли цикл
while ((A[i]!=x) && (i<N))
варианту цикла быстрого алгоритма поиска?
i++; эквивалентным первому
Если включен режим сокращенного вычисления логических выражений, то первый
вариант цикла быстрого поиска будет работать правильно.
Если включен режим полного вычисления значений логических выражений, то оба
варианта построения цикла могут привести к исключительной ситуации выход индекса за границы.
14.06.2025
335
336.
в)Алгоритм с барьеромСледующее улучшение состоит в упрощении условия в заголовке цикла. Целевым
является условие A[i]!=x, которое убрать или упростить невозможно. Следовательно, можно рассматривать только условие i<N, обеспечивающие прекращение
просмотра после исчерпания всех элементов цикла. Идея состоит в выставлении в
конце массива «барьера». Для этого в массив добавляется N+1 элемент, значение
которого приравнивается к искомому.
Для использования барьера необходимо внести следующие уточнения в описания используемых типов данных:
const int N=8; const int N1=N+1; int A[N1];
Основной фрагмент алгоритма:
i=0; A[N+1]=x; while (A[i]!=x) i++;
Будет ли данный цикл закончен? Возможно ли возникновение исключительной
ситуации в данном случае?
При обнаружении элемента, совпадающего с заданным нарушится условие A[i]!=x
и выполнение цикла закончится. Такой элемент всегда есть. В худшем случае это
барьерный N+1-й элемент. Исключительная ситуация выхода индекса за границы
не возникает ни при каких обстоятельствах.
14.06.2025
336
337.
Как определить успешность поиска?Можно сравнить i с N. Если i>N, то поиск прошел безуспешно.
Сложность алгоритмов линейного поиска есть O(N).
14.06.2025
337
338.
г)Бинарный поиск.Если данные упорядочены, то поиск можно сделать значительно более эффективным. Если A[i]<=A[i+1], i=1,2,…,N-1, то массив называется отсортированным (упорядоченным) по возрастанию.
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
6
18
42
43
55
63
82
94
x
25
Искомый элемент сравнивается со средним A[m] элементом массива.
Если они совпадают(A[m]==x), то задача уже решена. Так как массив упорядочен,
то при несовпадении элементов, в дальнейшем поиске можно не рассматривать
одну из половин массива.
А именно, если средний элемент массива больше искомого (A[m]>x), то все элементы, расположенные правее его (i > m), также будут больше искомого и дальнейший поиск следует осуществлять в левой половине массива.
В противном случае, если средний элемент массива меньше искомого (A[m]<x), то
все элементы, расположенные левее (i < m), будут также меньше его и дальнейший поиск следует выполнять в правой половине массива.
14.06.2025
338
339.
Итак, во время поиска приходится повторять следующие действия: 1) выбиратьсредний элемент массива; 2) сравнивать его с искомым; 3) при необходимости
уменьшать рассматриваемую часть массива в два раза выбором его правой или
левой половины.
Так как начальный и конечный элементы рассматриваемой части массива при
отбрасывании одной из половин массива будут изменяться, то для записи
алгоритма следует использовать переменные, имеющие смысл номеров
начального (левого) L и конечного (правого) R элементов массива. Поскольку
в начале рассматривается весь массив, то L=1, а R=N. Номер среднего
элемента M можно найти стандартным способом: m=(R+L) / 2.
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
6
18
42
43
55
63
82
94
L
R
m
1
8
4
x
25
В данном случае выбранный элемент массива не совпадает с искомым. Он
больше его. Следовательно для поиска нужно выбрать левую половину массива.
14.06.2025
339
340.
Выбор левой половины массива означает, что его правая границаперемещается к среднему элементу: R=m .
A[1]
A[2]
A[3]
A[4]
6
18
42
43
x
L
R
m
1
8
4
4
25
Но уже известно, что средний элемент не совпадает с искомым, следовательно,
область поиска можно ещё больше сузить и считать правой границей элемент,
стоящий перед средним: R=m-1
x
25
14.06.2025
A[1]
A[2]
A[3]
6
18
42
L
R
m
1
8
3
4
340
341.
Вновь находим средний элемент рассматриваемой части массива:m=(L+R)/2, m=2.
A[1]
A[2]
A[3]
6
18
42
x
25
L
R
m
1
8
3
2
Опять не совпадение среднего элемента с искомым. Так как он меньше искомого
(A[2]=18, x=25), то для дальнейшего поиска следует выбрать правую половину
массива, сместив левую границу L к среднему. Учитывая, предыдущее
соображение относительно выбранного элемента, получим, что нужно взять
следующий за средним L=m+1
A[3]
42
x
25
14.06.2025
L
R
m
1
3
8
3
2
341
342.
Вновь находим средний элемент рассматриваемой части массива:m=(L+R) / 2, m=3.
A[3]
42
x
25
L
R
m
1
3
8
3
2
3
И вновь не совпадение среднего элемента с искомым. Так как выбранный элемент
больше искомого (A[3]=42,x=25), то для дальнейшего поиска следует выбрать
левую половину массива, сместив правую границу R к следующему за выбранным
R=m-1, R=2.
x
25
L
R
m
3
2
3
Пришли к ситуации, когда дальнейший поиск невозможен, так как левая
граница массива стала больше правой L>R ─ массив исчерпан.
14.06.2025
342
343.
Таким образом, повторяющиеся действия состоят в выборе среднего элементамассива m=(L+R)/2 и организации соответствующего рассмотренной ситуации
ветвления. Повторять эти действия следует пока искомый элемент ещё не найден
и при этом левая граница рассматриваемого участка массива не превосходит
правую. Начальные значения L и R уже обсуждались.
bool SearchBinary (int *A, char x, int &k)
// Бинарный поиск элемента x в массиве A. k – номер найденного элемента
{
int L=1; // левая граница области поиска совпадает с 1
Int m, R=N-1; // правая граница области поиска совпадает с N
bool flag=false; k=-1; //элемент еще не найден
while (L<=R && ! flag )
{
m=(L+R)/2; // определение номера среднего элемента
if (A[m]==x) {flag=true; k=m;} //элемент найден
else // элемент не найден
if (A[M]<x) L=m+1; //перенос левой границы отрезка поиска
else R=m-1; // перенос правой границы отрезка поиска
}
return flag;
14.06.2025
343
}
344.
Как можно улучшить эффективность алгоритма?Анализ показывает, что первое проверяемое условие if(A[m]==x) //элемент найден
может быть удовлетворено только один раз, а проверяется для каждого очередного
элемента массива. Следовательно, простая перестановка ветвей условного
оператора уменьшит количество сравнений.
if (A[m]>x) R=m-1; //перенос правой границы отрезка поиска
else if (A[m]<x) L=m+1; //перенос левой границы отрезка поиска
else flag=true; // элемент найден
Кстати, а почему A[m]==x может быть только один раз, разве в массиве
запрещено быть одинаковым элементам?
14.06.2025
344
345.
д)Быстрый бинарный поиск (бинарный поиск с барьером)Следующая идея повышения эффективности поиска состоит в отказе от проверки
на совпадение А[m] и x. Бинарный поиск продолжается до тех пор, пока оба
интервала (A[k]<x, 1≤ k< L) и (A[k]>x, R< k ≤ N) не накроют весь массив.
int L=0; int m; int R=N-1;
while( L<=R)
{
m=(L+R)/2; //определение номера среднего элемента
if (A[m]>x) R=m-1; else L=m+1;
}
Пусть A= (6, 12, 18, 42, 44, 65, 67, 94), x=25
R m
8
A[m]
До цикла
L
1
1)
1
3
4
42
2)
3
3
2
12
3)
4
3
3
18
После
L>R – поиск завершён с отрицательным результатом
14.06.2025
345
346.
int L=1; int R=N; int m;while (L<=R)
{
m=(L+R)/2; // определение номера среднего элемента
if (A[m]>x) R=m-1; else L=m+1;
}
Пусть A= (6, 12, 18, 42, 44, 65, 67, 94), x=12
L
R
m
A[m]
До цикла
1
8
1)
1
3
4
42
2)
3
3
2
12
3)
3
2
3
18
L>R – поиск завершён с отрицательным результатом
Проблема возникла из-за того, что была исключена ветвь с прямой проверкой равенства A[m]=x, при этом средний элемент в предшествующем алгоритме обходился операторами L=m+1 и R=m-1. Следовательно, в таком варианте алгоритма
элемент A[m] вообще исключён из рассмотрения. В одном из этих операторов
нужно восстановить включение A[m] в рассматриваемый отрезок, например, R=m.
14.06.2025
346
347.
int L=1; int R=N; int m;while (L<=R)
{
m=(L+R)/2; //определение номера среднего элемента
If (A[m]>x) R=m; else L=m+1;
}
Пусть A= (6, 12, 18, 42, 44, 65, 67, 94), x=12
L
R
m
A[m]
До цикла
1
8
1)
1
4
4
42
2)
3
4
2
12
3)
3
3
3
18
4)
3
3
3
18
Возник вечный цикл!
14.06.2025
347
348.
Вечный цикл возник из-за условия L<=R в заголовке цикла. Следует оставитьтолько строгое равенство L<R.
Теперь важно определиться с ответом ещё на один вопрос: как отличить
ситуацию успешного поиска от ситуации неуспешного поиска?
Очевидно, после цикла можно добавить проверку среднего элемента на совпадение с искомым.
int L=1; int R=N; int m;
while (L<R)
{
m=(L+R)/2; // определение номера среднего элемента
if (A[m]>x) R=m; else L=m+1;
}
if (A[m]==x) return true; else return false;
Пусть A= (6, 12, 18, 42, 44, 65, 67, 94), x=12
L R m
A[m]
До цикла
1
8
1)
42
1
4 4
3
3 2
2)
12
Цикл завершён, выполнение следующего оператора показывает, что поиск прошёл
успешно.
14.06.2025
348
349.
Оценим максимальное количество операций, которые потребуется выполнить длярешения задачи поиска в алгоритме бинарного поиска.
На первом шаге количество K рассматриваемых элементов массива равно N
После первого шага количество K рассматриваемых элементов массива уменьшается в два раза K=N/2.
После второго шага ─ в четыре раза K=N/22.
Вообще, после шага с номером m: K=N/2m.
В худшем случае процесс поиска закончится после того, как останется один элемент: N/2m=1. Отсюда: m=log2N: сложность алгоритма бинарного поиска O(log2N).
Например, при N=1024 для линейного поиска в худшем случае потребуется 1023
шага, в среднем 512 шагов. А для бинарного поиска ─ в худшем случае 10 шагов.
14.06.2025
349
350.
Задача сортировки элементов массиваСортировкой в информатике называется переупорядочение рассматриваемых
объектов по некоторому признаку или системе признаков. Например, упорядочение слов по алфавиту называется лексикографической сортировкой.
Задача сортировки не менее важна для приложений информатики, поскольку существенно ускоряет поиск, задачу, которая возникает в огромном количестве массовых применений информационных технологий.
Различают два основных случая сортировки: это внутренняя сортировка или
сортировка массивов и внешняя сортировка или сортировка файлов.
Внутренняя сортировка выполняется, когда все рассматриваемые объекты находятся в оперативной памяти, то есть в любой момент времени «видны», доступный любые элементы массива (имеется прямой доступ к сортируемым элементам).
Внешняя сортировка выполняется над объектами, находящимися во внешней памяти. У файла «виден», доступен только один элемент, попавший в буфер файла
(имеется последовательный доступ к сортируемым элементам).
14.06.2025
350
351.
Внутренняя сортировка должна выполняться «на том же самом месте», то естьбез использования вспомогательных массивов. В условиях когда сортируемые
массивы могут иметь огромные размерности, когда нужно отсортировать сотни
миллионов элементов, это требование, собственно говоря, как раз и обеспечивает возможность выполнения внутренней сортировки. В остальных случаях это
требование обеспечивает эффективное использование оперативной памяти.
Ввиду большой важности оценка сложности алгоритмов сортировки выполняется
более детально, чем в обычно.
Для оценки сложности привлекают два параметра C ― количество сравнений и M
― количество пересылок (присваиваний), которые должны быть выполнены для
достижения результата.
Существует большое количество различных методов и соответствующих им алгоритмов сортировки, которые существенно отличаются друг от друга по указанным
параметрам. Причем для разных N и разных сортируемых массивов (упорядоченных в большей или в меньшей степени, по возрастанию или убыванию) оказываются более эффективными разные методы и алгоритмы.
НЕ СУЩЕСТВУЕТ УНИВЕРСАЛЬНОГО, НАИБОЛЕЕ ЭФФЕКТИВНОГО СПОСОБА
СОРТИРОВКИ.
14.06.2025
351
352.
Внутренние сортировки делятся на прямые и улучшенные. Существует трибазовых способа прямых внутренних сортировок: прямым выбором, прямыми
вставками и обменная, а также больше количество их модификаций.
Сортировка прямым выбором
Рассмотрим способ сортировки массива прямым выбором. Идея алгоритма состоит в том, чтобы на каждом шаге переупорядочения выбирать наименьший элемент в массиве и помещать его в начальную позицию с тем, чтобы на следующем
шаге его уже не рассматривать.
Более подробно. На первом шаге ищется минимальный элемент во всем рассматриваемом массиве.
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
82
42
94
18
43
6
63
В данном случае это A[7]=6. Чтобы массив был упорядоченным этот элемент должен стоять на первом месте. Поэтому, совершим обмен значениями между найденным и начальным элементом массива.
14.06.2025
352
353.
A[1]A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
94
18
55
43
6
63
Наименьший элемент уже стоит на месте, поэтому в дальнейшем можно рассматривать уже не весь массив, а только его часть, начинающуюся со второго
элемента.
Итак, на втором шаге ищется минимальный элемент в части массива, начинающейся со второго элемента. В данном примере это A[6]=18. И менять
шестой элемент нужно с начальным элементом рассматриваемого участка
массива, то есть со вторым элементом массива.
Теперь уже два элемента стоят на своих местах.
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
94
18
55
43
6
63
14.06.2025
353
354.
A[1]43
6
A[2]
55
18
A[3]
82
42
A[4]
42
82
A[5]
94
A[6]
A[7]
A[8]
18
55
43
6
63
Третий шаг. Минимальный элемент A[4]=42.
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
42
82
43
94
18
55
43
82
6
63
A[6]
A[7]
A[8]
43
82
6
63
Четвертый шаг. Минимальный элемент A[7]=43
A[1]
43
6
14.06.2025
A[2]
55
18
A[3]
82
42
A[4]
42
43
82
A[5]
94
18
55
354
355.
A[1]A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
42
43
82
94
55
18
55
94
43
82
6
63
Пятый шаг. Минимальный элемент A[6]=55
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
42
43
82
94
55
18
55
94
63
43
82
6
63
94
Шестой шаг. Минимальный элемент A[8]=63
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
42
43
82
94
55
18
55
63
94
43
82
6
63
94
14.06.2025
355
356.
A[1]A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
42
43
82
94
55
18
55
63
94
43
82
6
63
94
Седьмой шаг. Минимальный элемент A[7]=82
A[1]
A[2]
A[3]
A[4]
A[5]
A[6]
A[7]
A[8]
43
6
55
18
82
42
42
43
82
94
55
18
55
63
94
43
82
6
63
94
Массив упорядочен.
В целом можно так описать сущность выполняемых действий. Сортируемый массив разбивается на два участка: уже «готовый», упорядоченный и ещё неупорядоченный. На каждом шаге сортировки путем перебора неупорядоченного участка
выбирается один элемент и включается в конец уже упорядоченного участка.
14.06.2025
356
357.
Набросок алгоритмаПусть массив содержит N элементов и i ─ номер шага переупорядочения. Из
предыдущих рассуждений вытекает, что нужно проделать N-1 шаг и на каждом
шаге с номером i найти минимальный на участке массива от i-го элемента
массива до N-го, а затем поменять его местами с начальным i-м элементом.
for( int i=0; i<N-1; i++) {Перебор шагов сортировки}
{
//Определение номера k наименьшего элемента на участке от i до N
//Обмен значениями между i и k элементами
}
14.06.2025
357
358.
Окончательный вариант алгоритмаvoid SortChoice(int * A) / /сортировка массива A методом прямого выбора
{ int k, c;
for (int i=0;i<N-1;i++) // Перебор шагов сортировки
{
//Определение номера k наименьшего элемента на участке от i до N
k=i; //номер кандидата — первый элемент на участке
for(int j=i+1;j<N;j++) //Перебор элементов на участке
if (A[j]<A[k]) k=j; //замена кандидата
// выполнение обмена значениями между i и k элементами
c=A[k]; A[k]=A[i]; A[i]=c;
}
return;
}
14.06.2025
358
359.
void SortChoiceV(vector<int> &A){//Сортировка выбором
for (unsigned int i=0;i<A.size()-1;i++)
{int k,c;
k=i;
for(unsigned int j=i+1;j<A.size();j++)
{
if(A[j]<A[k]) k=j;
}
c=A[i];A[i]=A[k];A[k]=c;
}
return;
}
14.06.2025
359
360.
Оценим сложность алгоритма прямым выбором. Причём во время оцениванияоперации, связанные с организацией циклов, учитывать не будем.
Сначала подсчитаем количество сравнений С при выполнения сортировки.
Связанные с сортировкой сравнения входят только в условный оператор
if (A[j]<A[k]) k=j; Этот оператор находится внутри вложенного цикла.
Тело внешнего цикла выполняется N-1 раз. В этом цикле имеется вложенный, который, следовательно, также выполняется N-1 раз.
Тело вложенного цикла, в котором имеется ровно одно сравнение, выполняется
для каждого j от i+1 до N, где i ― номер шага.
То есть, на 1-ом шаге (от 2 до N) ― N-1 раз, на 2-ом шаге (от 3 до N) ― N-2 раза и
т.д. На последнем шаге сравнение выполняется 1 раз.
Таким образом, количество сравнений C равно сумме всех сравнений по всем
шагам (удобнее начинать с конца): 1+2+3+…+(N-1)= (a1+aK) k/2
В данном случае: a1=1, aK=N-1, k=N-1. Отсюда C=(1+N-1)(N-1)/2=(N2-N)/2
Аналогичный подсчёт дает для количества пересылок M верхнюю границу
M=(N2-N)/2+4*(N-1). На самом деле, если учесть, что пересылки происходят не
при каждом выполнении внутреннего цикла, то окажется, что M=N2/4+4(N-1).
Итак, сложность алгоритма сортировки прямым выбором O(N2).
14.06.2025
360
361.
Сортировка прямыми вставками (прямым включением)Сущность выполняемых во время сортировки включением действий следующая.
Сортируемый массив разбивается на два участка: уже «готовый», упорядоченный
и ещё неупорядоченный. На каждом шаге берётся первый элемент из неупорядоченной части и вставляется в подходящее место в уже упорядоченной части,
которое подбирается путём перебора её элементов.
В чём принципиальное различие между методом выбора и методом включения?
Способ определения места вставки основан на том, что место ищется в уже упорядоченной части массива. Её элементы, начиная с последнего, по очереди сравниваются с элементом, для которого ищется место. Как только очередной элемент
упорядоченной части оказывается меньше, чем новый элемент (при сортировке в
порядке возрастания), место вставки найдено.
14.06.2025
361
362.
A[1]1 шаг.
Исходное положение:
A[2]
A[3]
A[4]
A[5]
A[7]
A[8]
43
44
55
12
42
94
18
6
67
44
55
12
42
94
18
6
67
Упорядоченная
часть
2 шаг.
A[6]
44
55
Неупорядоченная часть
12
42
94
18
6
67
12
42
94
18
6
67
<?
44
14.06.2025
362
363.
3 шаг.4 шаг.
44
55
12
<?
<?
44
55
12
44
55
<?
12
14.06.2025
44
42
94
18
6
67
42
94
18
6
67
42
94
18
6
67
94
18
6
67
<? <?
55
363
364.
Набросок алгоритмаПусть i ─ номер шага сортировки (i = 2, 3, …, N). Из предыдущих рассуждений
вытекает, что на каждом шаге с номером i нужно взять i-й элемент массива и
вставить его в подходящее место в уже упорядоченной части. То есть, в отличие
от способа выбором ищется не элемент, а место для него.
for (int i=2; i<=N; i++) {Шаги сортировки}
{
c = A[i]; //очередной элемент из неупорядоченной части, для
// которого ищется место вставки
//определение места вставки, номера позиции вставки
}
Для определения места вставки нужно пройти по упорядоченной части от её
конца к началу. Пусть j ― номер очередного элемента упорядоченной части. На iом шаге последний элемент упорядоченной части имеет номер i-1.
Место вставки определяется сравнением очередного элемента упорядоченной
части A[j] с вставляемым элементом c. Перебор выполнятся до тех пор пока
очередной элемент упорядоченной части больше чем вставляемый (A[j]>c) и при
этом в упорядоченной части ещё есть элементы (j>=1).
14.06.2025
364
365.
Каждый раз текущий элемент упорядоченной части перемещается направо(A[j+1]=A[j]) и организуется переход к предыдущему элементу упорядоченной
части (j--).
int j = i-1; //перебор начинается с последнего элемента упорядоченной части
while (A[j]>c && j>=1) // проход по упорядоченной части
{
A[j+1]= A[j]; //сдвиг элемента вправо и освобождение j позиции для вставки
j - - ; //к следующему элементу упорядоченной части
}
Какое неравенство (строгое или нестрогое) следует использовать при определении начала массива?
Всегда ли найдется позиция для вставки? Какой номер она имеет?
Выход из цикла обеспечивается невыполнением неравенства A[j]>c, то есть
нахождением элемента меньшего или равного c (A[j]<=c), следовательно,
вставлять элемент a нужно сразу после A[j] ― на j+1 позицию. Аналогичные
рассуждения показывают, что при невыполнении неравенства j>=1 (то есть если
j=0) вставку нужно выполнять в j+1 позицию.
Вставка выполняется простым присваиванием j+1-му элементу массива значения
c вставляемого элемента A[j+1] =c.
14.06.2025
365
366.
Окончательный вариант алгоритмаvoid SortInsert (int * A) //сортировка массива А простыми вставками
{int c;
for (int i=2; i<=N; i++) //Шаги сортировки
{
c = A[i]; // вставляемый элемент
int j = i-1; //перебор с последнего элемента упорядоченной части
while ((A[j]>c) && (j>=1)) // проход по упорядоченной части
{
A[j+1]= A[j]; //сдвиг элемента вправо
j - -; //к следующему элементу упорядоченной части
}
A[j+1]=c; //вставка
}
return;
}
14.06.2025
366
367.
Как и в алгоритме линейного поиска повысить эффективность алгоритма можноубрав условие проверки достижения начала массива в заголовке внутреннего цикла и выставив соответствующий барьер.
В качестве барьера, очевидно, можно использовать вставляемый элемент а.
Барьер ставиться в конце пути перемещения по массиву. Следовательно, нужно
скорректировать диапазон изменения индекса:
for (i=2; i<=N; i++) //Шаги сортировки
{ c = A[i]; A[0]=с; //вставляемый элемент и выставление барьера
j = i-1; //перебор с последнего элемента упорядоченной части
while (A[j]>c)
((A[j]>c) //проход
&& (j>=1))
по//проход
упорядоченной
по упорядоченной
части
части
{
A[j+1] = A[j];
//сдвиг элемента вправо
j - -; //к следующему элементу упорядоченной части
}
A[j+1]=c; //вставка
}
14.06.2025
367
368.
Оценка количества сравнений и пересылок в худшем случае производиться точнотакже, как в методе прямого выбора.
Худший случай означает, что во время сортировки приходится выполнять максимально возможное количества сравнений и пересылок. Такая ситуация имеет место, например, если в сортируемом массиве элементы расположены в убывающем
порядке (а нужно разместить в возрастающем порядке).
В этом случае приходится сравнивать вставляемый элемента с каждым элементом из упорядоченной части и сдвигом каждого из них слева направо.
Тело внешнего цикла выполняется N-1 раз. На i-ом шаге в упорядоченной части
находится i-1 элемент. Суммируя по всем проходам вновь получаем С=(N2-N)/2 и
M=(N2-N)/2. То есть сложность алгоритма вставками O(N2).
Процесс сортировки вставками устойчивый. Это значит, что присутствующие в
массиве одинаковые элементы в процессе сортировки остаются на своих местах.
Следующий шаг улучшения эффективности метода вставок основывается на том,
что участок вставки уже упорядочен и, следовательно, место вставки можно искать
не линейным, а бинарным поиском.
Этот подход позволит уменьшить количество сравнений. Так как бинарный поиск
имеет сложность O(log2N), то количество сравнений оценивается не как O(N2) а как
O(N*log2N). Количество присваиваний при этом не изменится.
Написать подпрограмму реализующую сортировку бинарными вставками.
14.06.2025
368
369.
Обменная (пузырьковая) сортировкаИдея обменной сортировки основана на сравнении двух расположенных рядом
элементов массива и обмене их местами, если элементы расположены в неправильном порядке.
Для сортировки в порядке возрастания неправильным является порядок, при
котором больший элемент находится перед меньшим: A[j]>A[j+1].
Для сортировки в порядке убывания неправильным является порядок, при котором
меньший элемент находится перед большим: A[j]<A[j+1].
Начинать обмен можно и с первой и с последней пары элементов массива. Для
сортировки в порядке возрастания обмен обычно начинают с последней пары
элементов и двигаются к началу массива.
В случае обменной сортировки для повышения наглядности процесса упорядочения элементы массива принято размещать не горизонтально, а вертикально
14.06.2025
369
370.
4444
6
6
6
55
44
12
12
55
18
18
12
44
42
42
55
44
94
42
55
18
67
67
67
94
94
370
да
55
да
да
12
12
да
да
42
94
18
да
да
42
нет
94
да
18
да
да
6
6
нет
14.06.2025
67
нет
67
371.
Как всегда для осуществления сортировки нужно выполнить несколько шагов,несколько проходов по массиву.
На первом шаге на своем месте оказывается самый маленький элемент. На втором ― следующий по величине и т.д. Вообще, на каждом шаге на «свое место» попадает, по крайней мере, один элемент массива. Следовательно, для полного упорядочения нужно выполнить N-1 шаг сортировки.
Так как при вертикальном расположении массива на каждом проходе в начальную
часть массива, наверх «поднимаются», «всплывают» маленькие, «лёгкие» элементы, то обсуждаемый тип сортировки часто называют «пузырьковой», по аналогии с всплывающими к поверхности воды пузырьками воздуха.
Следует обратить внимание на то, что за один проход в начальную часть массива
(в его уже упорядоченную часть) попадает самый маленький элемент из неупорядоченной части, а самый большой элемент перемещается в конец массива, «опускается вниз» всего на одну позицию.
И ещё одно замечание. В методе обменной сортировки, как и в методе прямого
выбора нужный элемент отыскивается с помощью действий в неупорядоченной
части и найденный элемент добавляется в конец уже упорядоченной части. Отличаются методы способом выбора нужного элемента.
14.06.2025
371
372.
На каждом шаге нужно организовать сравнение двух соседних элементов. Так каксравнения начинают с последней пары элементов, то сначала сравниваются N-1-й
и N-й элементы, затем N-2-й и N-1-й элементы и т.д., последними на первом проходе сравниваются 2 и 1 элементы.
Пару сравниваемых элементов можно задавать меньшим или большим номером
из номеров образующих пару элементов. Для определённости выберем для задания пары меньший номер, номер «верхнего» элемента.
На первом проходе этот номер (пусть это будет j ) изменяется от N-1 до 1, на втором проходе ― от N-1 до 2, на третьем ― от N-1 до 3, и т.д.
Если у сравниваемых элементов A[j] и A[j+1] обнаруживается «неправильный» порядок, то они стандартным способом меняются местами.
14.06.2025
372
373.
void BubleSort (int *A) // пузырьковая сортировка массива A{int c;
for (int i=0; i<N-2; i++) // проходы сортировки
for (int j=N-2; i>=i; i--) //цикл сравнений на проходе
if (A[j]>A[j+1]) // неправильный порядок элементов в паре
{
c= A[j]; A[j]=A[j+1]; A[j+1]=c // обмен местами
}
return;}
Проведя рассуждения тем же самым способом, что и в случае сортировки выбором, можно найти, что в худшем случае количество сравнений C равно (N2-N)/2, а
количество присваиваний M равно 3(N2-N)/2, то есть сложность обменной сортировки оценивается как O(N2).
14.06.2025
373
374.
void SortBubleV(vector<int> &x){//Пузырьковая сортировка
int a;
for(unsigned int i=0; i<x.size()-2; i++)
for(unsigned int j=x.size()-2; j>=i; j - -)
if(x[j]>x[j+1]) {
a=x[j];x[j]=x[j+1];x[j+1]=a; }
return;
}
14.06.2025
374
375.
Повышение эффективности обменной сортировкиВ общем случае для получения полного упорядочения нужно выполнить N-1 проход по элементам неупорядоченной части. Однако, в конкретных случаях, как например, в рассмотренном выше примере, массив может оказаться упорядоченным
раньше, на одном из промежуточных проходов.
Для повышения эффективности алгоритма предлагается обнаружить эту ситуацию, и при её выявлении прекратить проходы.
Как можно находясь на проходе обнаружить, что массив уже упорядочен?
Если за весь проход не было обнаружено ни одной «неправильной» пары, если не
было совершено ни одного обмена, то массив уже упорядочен. В нашем примере,
последние обмены были совершены на четвёртом проходе, а на пятом проходе не
будет выполнено ни одного обмена ― поэтому сортировку можно завершить сразу
после обнаружения отсутствия на проходе обменов, сэкономив тем самым два
прохода (из семи максимально необходимых).
Для обнаружения факта выполнения обмена на проходе можно использовать
индикатор ― переменную логического типа, которая при совершении обмена принимает, например, значение true. Чтобы индикатор смог обнаружить факт обмена
он должен получить это значение внутри составного оператора, в котором совершается обмен.
14.06.2025
375
376.
Если перед текущим проходом такой индикатор получает значение false, а в конце этого прохода он имеет значение true, то обмен на проходе хотя бы один раз нобыл. Если же в конце прохода значение индикатора не изменилось, осталось
равным false значит процесс ни разу не попал внутрь составного оператора,
обменов не было, массив уже упорядочен и проходы можно завершать.
Здесь мы имеем еще одну вариацию задачи поиска. Но в ней ищется не наличие
некоторого объекта или события, а его отсутствие. Поэтому переменная-индикатор используется немного по-другому.
Если после завершения прохода значение переменной-индикатора (пусть это
вновь будет flag) окажется равным true, то проходы следует продолжить, а если
flag останется равным false, то проходы нужно завершить.
В силу этого цикл по проходам следует выполнять пока номер прохода i не больше
N-1 и при этом flag=true , то есть отсутствие обменов ещё не обнаружено:
(i<=N-1) and flag. Чтобы войти в цикл проходам, переменная flag до цикла должна
получить значение true ― до начала проходов отсутствие обменов ещё не обнаружено.
14.06.2025
376
377.
void BubleSortA (int * A);// усовершенствованная пузырьковая сортировка массива x
{
bool flag=true; // отсутствие обменов ещё не обнаружено
int c;int i=0; // инициализация
while (i<=N-2 && flag) // цикл проходов сортировки
{
flag=false; //обменов на проходе ещё не было
for ( int j=N-2; j>=i; j- -) // цикл сравнений на проходе
if (A[j]>A[j+1]) // неправильный порядок элементов в паре
{
c =A[j]; A[j]=A[j+1]; A[j+1]=c; //обмен местами
flag=true; //факт обмен зафиксирован
}
i++;
}
return; }
Конечно, слежение за наличием обменов, присваивание индикатору flag значения
false в начале каждого прохода и true при каждом обмене, вообще говоря, снижает
эффективность подпрограммы. Однако, уменьшение общего количества проходов
во многих случаях значительно превышает издержки, «накладные расходы».
14.06.2025
377
378.
Шейкерная сортировкаКроме возможного уменьшения количества проходов в обменной сортировке можно осуществить ещё ряд усовершенствований.
Для уменьшения количества сравнений предлагается на текущем проходе регистрировать не только факт наличия обмена, но и номер k одного из элементов пары,
которая последней участвовала в обмене.
Это дает возможность на следующем проходе подниматься не до конца неупорядоченной части, а только до элемента с индексом k, поскольку все находящиеся
«выше» пары уже упорядочены.
Ранее отмечалось, что при организации проходов «снизу вверх» за один проход
самый маленький элемент «поднимается» с любой исходной позиции в своё конечное положение, а самый большой ― «опускается» на одну позицию вниз.
Логично предположить, что если организовать проход «сверху вниз», то за один
проход самый большой элемент из любой позиции опуститься в своё конечное
положение, а самый маленький поднимется на одну позицию вниз.
Для улучшения процесса обменной сортировки предлагается за один шаг сортировки выполнять два последовательных прохода: один вверх, а второй вниз. Каждый проход следует выполнять от номера L, характеризующего «верхнюю» (левую) пару элементов, до номера R, определяющего «нижнюю» (правую) пару элементов. Эти номера ограничивают снизу и сверху диапазон индексов элементов,
которые должны участвовать в сортировке на любом проходе.
14.06.2025
378
379.
Проход вверх нужно выполнять от R до L c убыванием номера. На проходе следует зафиксировать номер k «верхнего» элемента пары, которая последний разучаствовала в обмене.
Так как пара, опредёляемая номером k, уже упорядочена (и все вышестоящие
пары также уже упорядочены) , то последующий проход вниз следует начинать со
значения L=k+1.
Внимание! Переменная k получает своё значение во время прохода вверх только
в том случае, если будет выполнен хотя бы один обмен. Если же обменов уже на
первом проходе не окажется (исходный массив упорядочен), то k останется неопределенным. Это вызовет неприятные последствия во время выполнения присваивания L=k+1 после такого прохода вверх.
Поэтому до цикла по проходам нужно задать значение k, которое, во-первых, исключает неопределённость при присваивании, а, во-вторых, учитывает выявленные условия возникновения этой ситуации.
Обсуждаемая ситуация возникнет только в случае применения алгоритма к уже
упорядоченному массиву. Следовательно, переменной k нужно присвоить значение, которое завершает выполнение сортировки. Таким значением может быть
например, k=N, которое больше, чем любое (в том числе и начальное) значение R.
Проход вниз выполняется от L до R с возрастанием номера. Аналогично проходу
вверх следует зафиксировать номер k пары, последний раз участвовавшей в обмене. А после прохода следует заменить значение R (R=k-1), подготовив новую
нижнюю
границу для следующей пары проходов.
14.06.2025
379
380.
До начала проходов необходимо инициализировать переменные L и R значениями, которые покрывают весь массив: L=1; R=N-1.На каждой паре проходов значение L увеличится по крайней мере на единицу, а
значение R уменьшится по крайней мере на единицу.
Поэтому такие пары проходов следует повторять, пока существует не пустой диапазон номеров элементов массива, которые должны участвовать в сортировке, то
есть пока L<R (если L=R, то диапазон содержит не пару, а только один элемент).
Исходя из проведённых рассуждений получаем, что специальный индикатор flag,
который отслеживает необходимость в дальнейшем выполнении проходов, в такой модификации алгоритма не нужен. Также как нет нужды и в счётчике количества проходов i.
Полученная сортировка носит название шейкерной (от shakеr ― сосуд для приготовления коктейля).
14.06.2025
380
381.
void ShakerSort (int * A) //Шейкерная сортировка массива x{
int L=0; int R=N-2; int k=N; int c; // начальный диапазон номеров пар, участ. в
обменах
while (L<R) //повторение пар проходов сортировки
for (int j=R; j>=L; j- -) //проход вверх
if (A[j]>A[j+1]) //неправильный порядок элементов в паре
{ c = A[j]; A[j]=A[j+1]; A[j+1]=c; //обмен местами
k=j; // фиксация номера пары, участвовавшей в обмене
}
L=k+1; //новая граница диапазона сверху
for (j=L; j<=R; i++) // проход вниз
if (A[j]>A[j+1]) //неправильный порядок элементов в паре
{ c = A[j]; A[j]=A[j+1]; A[j+1]=c; //обмен местами
k=j; //фиксация номера пары, участвовавшей в обмене
}
R=k-1; //новая граница диапазона снизу
}
return; }
14.06.2025
381
382.
Анализ показывает, что шейкерная сортировка значительно уменьшает количествосравнений, однако она фактически не влияет на количество присваи-ваний,
которые требуется выполнить для полного упорядочения массива.
Итак, все прямые методы сортировки имеют сложность O(N2). Однако все они
отличаются друг от друга, во-первых, коэффициентами мажоранты, во-вторых, поразному относятся к исходному порядку элементов массива, в третьих, имеют
различные средние оценки количеств сравнений и количеств присваиваний.
14.06.2025
382
383.
Улучшенные внутренние сортировкиВсе рассмотренные варианты прямых сортировок имеют сложность O(N2). Вообще
говоря, это довольно большая сложность, хотя для малых и средних значений N
(порядка 10~1000) эти методы дают вполне приемлемые времена счёта.
Специалисты прилагали много усилий для разработки более эффективных методов сортировки. Их работа привела к созданию различных вариантов улучшенных
(усовершенствованных) методов сортировки. Ниже рассматриваются три разновидности улучшенных сортировок, которые построены на основе трех видов прямых сортировок.
14.06.2025
383
384.
Улучшение сортировки прямыми вставками. Сортировка Шелла.В 1959 году Дональд Шелл предложил улучшенный вариант сортировки прямыми
вставками. Основная идея этой сортировки состоит в выполнении нескольких
предварительных проходов, на каждом из которых методом прямых вставок
сортируются некоторые подпоследовательности элементов массива с заданным
шагом k.
Номера элементов массива:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28…
k=9
k=9
k=9
Пусть, например, k=9, тогда в предварительной сортировке участвуют, например,
элементы с номерами 1, 10, 19, 28, …
Отметим, что в исходной последовательности (исходном массиве) элементов можно выделить несколько различных подпоследовательностей с одним и тем же шагом по номерам. Например, элементы с номерами 2, 11, 20, 29, … также находятся
друг от друга на расстоянии k=9.
Видно, что количество различных подпоследовательностей с шагом k равно k и
каждую из них можно отличать по номеру её первого элемента.
Ещё раз подчеркнём, что в сортировке Шелла элементы каждой из подпоследовательностей упорядочиваются независимо от всех остальных подпоследовательностей.
14.06.2025
384
385.
Разберём возникающие особенности организации сортировки прямыми вставкамина примере подпоследовательности элементов с номерами 1, 10, 19, 28 и т.д.
Первый элемент считается упорядоченным. Действия выполняемые над любым
следующим элементом массива при стандартной сортировке прямыми вставками
имеют вид:
a := x[i]; {вставляемый элемент} x[0]:=a;{выставление барьера}
j := i-1;
i-k; {перебор с последнего элемента упорядоченной части }
while x[j]>a do {проход по упорядоченной части}
begin
x[j+1] := x[j];{сдвиг элемента вправо}
j-1 {к
{к следующему
следующему элементу
элементу упорядоченной
упорядоченной части}
части}
j := j-k
end;
x[j+1]:=a {вставка}
Заметим, что в стандартном случае номера элементов массива увеличиваются с
шагом k=1. Изменим рассматриваемый фрагмент с учётом того, что в рассматриваемой подпоследовательности номера элементов изменяются с шагом k=9.
Во-первых, при определении номера начального элемента упорядоченного участка
и определении места вставки для элемента a[i] номера нужно уменьшать не на
k=1, а на k=9.
14.06.2025
385
386.
x[0]:=a;{выставление барьера}a := x[i]; {вставляемый элемент} x[1-k]:=a;{выставление
барьера}
j := i-k: {перебор с последнего элемента упорядоченной части }
while x[j]>a do {проход по упорядоченной части}
begin
x[j+1] := x[j];{сдвиг элемента вправо}
x[j+k]
j := j-k {к следующему элементу упорядоченной части}
end;
x[j+k]:=a
x[j+1]:=a {вставка}
{вставка}
Во-вторых, нужно определить место положение барьера. В стандартном случае
барьер выставляется перед первым элементом массива в нулевую позицию:
x[0]:=a. В данном случае барьер также должен находиться перед первым элементом подпоследовательности, но на расстоянии не k=1, а k=9 от него, то есть
положение барьера определяется номером 1-k: x[1-k]:=a.
Осталось изменить действия сдвига элемента вправо и вставки. Так как сдвиг при
таком движении вправо происходит на расстояние k, также как и следующий за
найденным элементом подпоследовательности (который меньше чем a) находится
от него на расстоянии k, то индексы j±1 в соответствующих операторах нужно
заменить на индексы j±k.
Организовав цикл для перебора всех элементов подпоследовательности и используя полученный фрагмент как тело этого цикла можно отсортировать всю рассматриваемую подпоследовательность.
14.06.2025
386
387.
Теперь нужно учесть, что исходный массив состоит из k таких подпоследовательностей. Следовательно, нужно организовать ещё один внешний цикл по переборувсех возможных подпоследовательностей с заданным шагом k.
При такой организации сортировки для, например, k=9 вначале упорядочиваются
элементы первой подпоследовательности с номерами 1, 10, 19, 28, 37,… ,затем
элементы второй подпоследовательности с номерами 2, 11, 20, 29, 38, …, далее
третьей с номерами 3, 12, 21, 30, 39, …и т.д. Последними сортируются элементы
девятой подпоследовательности с номерами 9, 18, 27, 36,….
Чтобы уменьшить «накладные расходы» рассмотренного подхода, в котором для
полного перебора всех элементов исходного массива требуется организовать
кратный цикл, Д. Шелл предложил выполнять сортировку всех подпоследовательностей за один проход по сортируемому массиву.
Во время этого прохода номера выбираемых для вставки элементов массива берутся в порядке 10, 11, 12, 13 и т. д. То есть сначала «находит свое место» второй элемент первой подпоследовательности (10), затем второй элемент второй
подпоследовательности (11), далее второй элемент третьей подпоследовательности (12) и т.д.
После того как в сортировке «поучаствует» второй элемент последней девятой
подпоследовательности (18), очередь доходит до третьих элементов подпоследовательностей: 19-го из первой, 20-го из второй, 21-го из третье и т.д.
14.06.2025
387
388.
Такой порядок просмотра позволяет упорядочить все подпоследовательности заодин просмотр массива, одним циклом. Но при этом необходимо внимательно
следить за выставлением барьера.
Дело в том, что барьерный элемент разных подпоследовательностей должен располагаться в разных местах. Выше мы определили, что для первой подпоследовательности, начинающейся элементом с номером 1, барьер должен находится в
позиции 1-k. Аналогичные рассуждения для второй подпоследовательности дадут
положение барьера 2-k и т.д. Общую картину для k=9 даёт следующая таблица:
Положение
барьерного
элемента
14.06.2025
Номер
начального
элемента
Последующие элементы
-8 ← 9 →
1
10, 19, 28, 37, 46, …
-7
2
11, 20, 29, 38, 47, …
-6
3
12, 21, 30, 39, 48, …
-5
4
13, 22, 31, 40, 49, …
-4
5
14, 23, 32, 41, 50, ...
-3
6
15, 24, 33, 42, 51, …
-2
7
16, 25, 34, 43, 52, …
-1
8
17, 26, 35, 44, 53, …
0
9
18, 27, 36, 45, 54, ..
388
389.
К=9-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28…
Барьеры
Начальные элементы
подпоследовательностей
Последующие элементы
подпоследовательностей
Первый упорядочиваемый элемент ― первая подпоследовательность
Второй упорядочиваемый элемент ― вторая подпоследовательность
Третий упорядочиваемый элемент ― третья подпоследовательность
…
Девятый упорядочиваемый элемент ― девятая подпоследовательность
Десятый упорядочиваемый элемент ― первая подпоследовательность
14.06.2025
389
390.
Исходное положение барьера, выставляемого для первой подпоследовательности, s=1-k. При переходе к очередному элементу массива, принадлежащемуследующей подпоследовательности, барьер смещается на соседнюю справа позицию s:=s+1. Однако, после того, как будут обработаны k элементов и s окажется
равным 0, k+1 элемент вновь окажется принадлежащим первой подпоследовательности, для которой s=1-k.
a := x[i]; {вставляемый элемент} x[1-k]:=a;{выставление барьера}
if s=o then s:=1-k else s:=s+1; {Текущее положение барьера}
x[s]:=a; {выставление барьера}
j := i-k: {перебор с последнего элемента упорядоченной части }
while x[j]>a do {проход по упорядоченной части}
begin
x[j+k] := x[j];{сдвиг элемента вправо}
j := j-k {к следующему элементу упорядоченной части}
end;
x[j+k]:=a {вставка}
Полученный фрагмент является телом цикла, который должен быть выполнен для
всех элементов массива, начиная c k+1-го. Нужно только не забыть инициализировать значение s до цикла.
14.06.2025
390
391.
s:=1-k; {начальное положение барьера}for i:=k+1 to N do
begin
a := x[i]; {вставляемый элемент}
if s=o then s:=1-k else s:=s+1; {Текущее положение барьера}
x[s]:=a; {выставление барьера}
j := i-k: {перебор с последнего элемента упорядоченной части }
while x[j]>a do {проход по упорядоченной части}
begin
x[j+k] := x[j];{сдвиг элемента вправо}
j := j-k {к следующему элементу упорядоченной части}
end;
x[j+k]:=a {вставка}
end;
14.06.2025
391
392.
Таким образом получен фрагмент процедуры, который для заданного k обеспечивает раздельное упорядочение всех подпоследовательностей сортируемогомассива.
Однако простейший анализ показывает, что такая сортировка ещё не означает, что
массив в целом окажется отсортированным
Здесь следует вспомнить исходную идею сортировки Д. Шелла: «выполнении нескольких предварительных проходов». То есть сортировка подпоследовательностей ― это только предварительные действия.
Более того, Д. Шелла предложил выполнить несколько таких проходов с разными
шагами. Причем, на последнем проходе шаг обязательно должен быть равным
единице. То есть на последнем шаге необходимо выполнит самую обычную сортировку прямыми вставками.
В первоначально предложенном Д. Шеллом варианте сортировка выполнялась за
четыре прохода с шагами 9, 5, 3 и 1.
14.06.2025
392
393.
В алгоритме сортировки Д. Шелла используется группа барьеров, которые размещаются слева от сортируемых элементов массива, поэтому для его реализациинеобходимо изменить описания используемых типов.
const N=8; {Количество сортируемых элементов}
T=4;{Количество проходов}
Kmax=9; {Максимальный шаг на проходах}
type
T_index=-Kmax..N; T_Elem=integer;
T_Massiv=array [T_index] of T_Elem;
Теперь для реализации всего алгоритма сортировки Шелла нужно задать шаги на
каждом проходе и организовать цикл по проходам.
14.06.2025
393
394.
procedure ShellSort (var x:T_Massiv); {Сортировка Шелла массива x}var i, j, k, s:T_index; a:integer; m: 1..T; {для цикла по проходам}
h: array [1..T] of integer; {массив шагов по проходам}
begin
h[1]:=9; h[2]:=5; h[3]:=3; h[1]:=1; {шаги по проходам}
for m:=1 to T do {цикл по проходам}
begin
k:=h[m]; {шаг текущего прохода } s:=1-k; {начальное положение барьера}
for i:=k+1 to N do
begin
a := x[i]; {вставляемый элемент}
if s=o then s:=1-k else s:=s+1; {Текущее положение барьера}
x[s]:=a; {выставление барьера}
j := i-k: {перебор с последнего элемента упорядоченной части }
while x[j]>a do {проход по упорядоченной части}
begin x[j+k] := x[j]; j := j-k end;
x[j+k]:=a {вставка}
end
end
14.06.2025
end;
394
395.
Несмотря на внешнюю искусственность и кажущееся большими «накладные расходы» проверка работы сортировки Шелла на самых разных массивах показала еёвысокую эффективность.
Оценка сложности этого алгоритма представляет собой весьма непростую математическую задачу. Поэтому приведем только окончательный результат: O(N1,2)
До настоящего времени неизвестно, сколько предварительных проходов нужно
сделать для получения наилучших результатов и какие шаги должны быть для этого выбраны.
Опытным путем подобраны следующие рекомендуемые шаги по проходам:
1, 4, 13, 40, …
1, 3 5, 9, 37, …
1, 3, 7, 15, 31, …
14.06.2025
395
396.
Улучшение сортировки прямым выбором.Пирамидальная сортировка
Пирамидальная сортировка, представляющая собой улучшение метода прямого
выбора, была предложена Джоном Уильямсом в 1964, а затем улучшена Робертом Флойдом.
В сортировке прямым выбором наименьший элемент на рассматриваемом участке
массива фактически отыскивается путём полного просмотра участка, то есть также
как в процедуре линейного поиска.
Идея улучшения этой сортировки состоит в переходе от линейного выбора со
сложностью O(N) к выбору в дереве, с помощью которого можно сохранить и
использовать гораздо больше информации о процессе выбора и уменьшить
сложность до O(log2N).
Замечание. Указанные выше оценки сложности относятся не ко всей сортировке в
целом, а только к одному из её этапов ― выбору наименьшего на некотором
участке массива.
14.06.2025
396
397.
Рассмотрим сначала бытовой аналог пирамидальной сортировки. Допустим проводятся соревнования по какому-либо виду спорта (шахматы, теннис и т.д.) средивосьми участников. Можно провести чемпионат, когда каждый из участников встречается с каждым, но это требует много времени и затрат.
Есть более простой и быстрый способ организации соревнований ― кубковая система. Участников по какому-либо принципу разделяют на пары. Победитель каждой пары выходит в следующий круг, а проигравший выбывает из соревнования.
Шакиров
Шакиров
Борисов
Борисов Волков
14.06.2025
Сивашов
Шакиров
Шакиров Щуров
Сивашов
Тютерев
Бородулин Сивашов
Тютерев Искольный
397
398.
Таким образом очень быстро в три этапа определяется сильнейший игрок. Однако,кубковая система с выбыванием имеет недостаток: сложно определить второго,
третьего и т.д. по силе игрока, в то время как чемпионат распределяет всех по
своим местам.
Шакиров
Шакиров
Борисов
Борисов Волков
Сивашов
Шакиров
Шакиров Щуров
Сивашов
Тютерев
Бородулин Сивашов
Тютерев Искольный
Дело в том, что Сивашов, проигравший в финале Шакирову, совсем не обязательно второй по силам участник соревнований.
Сильнее Сивашова может быть Борисов, сильнее может быть и Щуров, которые
проиграли на ранних этапах Шакирову.
Чтобы выявить второго по силе нужно пройти по дереву соревнования вниз,
выбрать
соперников Шакирова, организовать между ними матч, а 398
затем
14.06.2025
победитель сыграет с Сивашовым.
399.
Видно, что для выявления второго участника потребуется организовать всего двадополнительных матча. Это оказалось возможным за счёт того, что в структуре дерева существует дополнительная информация о выполненных ранее сравнениях и
её использование приведет к уменьшению количества сравнений для выбора второго участника.
Однако построение подобного дерева из массива требует дополнительных затрат
памяти, по крайней мере, за счет дублирования одних и тех же элементов на
разных уровнях дерева: вместо хранения N элементов нужно хранить 2N-1
элемент, что фактически эквивалентно использованию вспомогательного массива.
В основе предложенной Р. Флойдом эффективной реализации сортировки выбором из дерева лежит специальная разновидность бинарного дерева, которую принято называть пирамидальным деревом или просто пирамидой. Иногда такое
дерево называют деревом сортировки.
Пирамидальным называется полное бинарное дерево, у которого ключ корня любого поддерева больше (в более общей трактовке не меньше), чем ключи двух его
дочерних вершин.
В отличие от дерева поиска ключи дочерних вершин пирамидального дерева
считаются неупорядоченными: ключ левой дочерней вершины может быть как
больше, так и меньше ключа правой дочерней вершины.
14.06.2025
399
400.
7028
65
60
45
54
43
Ключ корня 70 больше, чем ключи двух его дочерних узлов 65 и 60. Ключ левого
поддерева 65 больше ключей 28 и 45, также как и ключ правого поддерева 60
больше, чем ключи 54 и 43 их дочерних узлов. Изображённое дерево является
пирамидой.
Для сортировки в порядке убывания используется другой вариант пирамидального
дерева, в котором ключ корня любого поддерева меньше (в более общей трактовке не больше), чем ключи двух его дочерних вершин.
14.06.2025
400
401.
В отличие от рассмотренного ранее идеально сбалансированного дерева, включение новых узлов в пирамидальное дерево осуществляется строго слева направо и только после полного заполнения предшествующего уровня. Заполненнымсчитается уровень дерева, содержащий максимально возможное количество
узлов.
70
28
65
60
45
54
43
Частично незаполненным может быть только самый нижний уровень дерева.
14.06.2025
401
402.
Узлы пирамидального дерева принято нумеровать в соответствии с порядком поступления новых узлов в дерево. Эти номера принято называть индексами узловпирамидального дерева.
1
70
2
65
4
28
60
5
45
3
6
54
7
43
В этой системе нумерации корневой узел всегда имеет индекс 1. Два его дочерних узла имеют индексы 2 и 3, а, например, дочерние для узла с индексом 3 имеют индексы 6 и 7 и т.д. В общем случае для узла с индексом k дочерние узлы
(если они есть) всегда имеют индексы 2k и 2k+1. Для узла с индексом m (m≠1) родительский всегда имеет индекс int(m/2). Эти простые соотношения между индексами родительского и дочерних узлов обеспечивают высокую эффективность
адресной арифметики на машинном уровне.
С использованием индексов свойство ключей узлов пирамидального дерева можно записать в виде (A[k] ≥ A[2k]) ⋀ (A[k] ≥A[2k+1]), k=1, 2, 3,…, int(N/2)
14.06.2025
402
403.
Использовать пирамидальной дерево для сортировки массива можно следующимобразом. Допустим из элементов сортируемого массива {45, 28, 54, 43, 70, 60, 65}
удалось некоторым образом построить рассматриваемое пирамидальное дерево.
1
1
70
43
2
4
28
3
65
60
5
6
45
54
2
7
43
4
28
3
65
60
5
6
45
54
7
70
По основному свойству пирамиды максимальный элемент (70) находится в её корне и имеет индекс 1. При сортировке в порядке возрастания максимальный элемент должен находиться в конце массива, быть последним, поэтому узел с индексом 1 можно поменять местами с последним узлом (43), имеющим индекс 7, после
чего исключить его из дальнейшей сортировки.
14.06.2025
403
404.
11
43
65
2
3
65
4
45
3
43
6
54
65
2
60
5
28
1
7
70
4
60
5
28
45
2
45
6
54
3
7
70
4
60
5
28
43
6
54
7
70
Однако в результате получится бинарное дерево, которое имеет нарушение пирамидальности в корневом узле.
Дерево, у которого свойство упорядоченности (A[k] ≥ A[2k]) ⋀ (A[k] ≥ A[2k+1])
выполняется для всех узлов, кроме корневого называется частично
упорядоченным пирамидальным деревом.
Оказывается, что восстановление пирамидальности выполняется очень простым
способом: нужно поменять местами корень и больший из его двух дочерних узлов,
а затем рекурсивно применить эту процедуру к выбранному поддереву.
В результате такого преобразования вновь получится пирамидальное дерево, в
корне которого находится максимальный ключ.
14.06.2025
404
405.
165
3
4
2
60
5
28
43
60
54
2
45
1
1
45
6
54
7
70
4
43
6
65
3
45
60
5
28
2
3
7
70
4
28
54
5
43
6
65
7
70
Можно сказать, что произошёл выбор наибольшего элемента в неупорядоченной
части массива, который теперь можно присоединить к уже упорядоченной части,
поменяв местами с предпоследним элементом.
Вновь получено частично упорядоченное пирамидальное дерево, которое можно
тем же способом преобразовать в пирамидальное.
Этот процесс следует продолжать до тех пор, пока все элементы массива не окажутся на своих местах.
14.06.2025
405
406.
160
54
5
43
28
Обмен
3
4
54
43
2
45
1
1
2
3
45
6
7
65
70
54
5
4
60
28
6
65
1
54
3
43
5
60
45
5
4
7
70
28
6
65
14.06.2025
6
60
7
65
70
54
2
Обмен
43
5
60
70
43
3
4
7
1
2
Восстановление 28
Обмен
43
45
2
4
3
1
28
45
Восстановление
2
6
65
7
70
3
28
5
4
54
45
60
6
65
7
70
406
407.
11
43
Восстановление
2
3
28
60
6
65
2
Обмен
45
5
4
54
28
7
70
3
43
5
4
54
45
60
6
65
7
70
В результате получена структура, в которой ключи узлов упорядочены по возрастанию.
Но для применения этого способа нужно уметь представлять сортируемый массив
в виде пирамидального дерева.
В принципе, для начального построения дерева из заданного сортируемого массива применяется практически тот же самый подход, что и для восстановления
дерева.
Вначале из заданного массива, исходя из соответствия индексов массива индексам узлов пирамидального дерева, строится дерево, в котором условие пирамидальности ещё не выполняется.
14.06.2025
407
408.
Возьмем для сортировки , например, такой 10-элементный массив: {4, 1, 3, 2, 16, 9,10, 14, 8, 7}. Элементы по одному выбираем из массива и включаем в пирамидальное дерево в соответствии с правилами его заполнения, не обращая при
этом внимания на значения элементов.
Индексы
1
Массив
4 1 3 2 16 9 10 14 8 7
2
3
4
5
6
7
8
9
10
1
4
3
2
1
3
4
5
2
16
8
9
14
6
8
7
9
10
10
7
Получилось бинарное дерево общего вида, ключи узлов которого являются
соответствующими элементами сортируемого массива.
Это дерево не является пирамидальным, но его довольно просто можно преоб14.06.2025
408
разовать
в пирамидальное.
409.
14
3
2
1
3
4
5
2
16
8
9
14
6
8
7
9
10
10
7
Можно считать, что листья этого дерева уже являются пирамидальными поддеревьями. Листья образуют нижний уровень дерева, его нижний слой.
По построению дерева количество листьев всегда равно N-int(N/2). Причём в
массиве они занимают последние позиции: A[i], i=int(N/2)+1,…,N
Процедура преобразования полученного дерева сводится к последовательному
перебору в обратном порядке всех ещё не упорядоченных узлов (в рассматриваемом примере узлов с индексами 5, 4, …,1) и применению описанного выше приёма приведения частично упорядоченного дерева к пирамидальному к совокупности узлов, состоящей из вновь рассматриваемого и уже пирамидальных.
Итак, выбираем узел с индексом 5 и преобразуем поддерево в корне которого он
находится , так чтобы выполнялось свойство пирамидальности.
14.06.2025
409
410.
14
3
2
3
1
4
5
2
16
8
9
14
6
8
7
9
10
10
7
Так как узел 5, содержащий ключ 16, имеет единственный дочерний, ключ которого меньше, чем у узла 5, можно утверждать, что поддерево с корнем 16 уже является пирамидальным.
Следующим по порядку рассматривается узел с индексом 4.
Он имеет два дочерних с ключами 8 и 14. Большим из них является узел с ключом
14 и его нужно поменять местами с корневым.
Следующим по порядку рассматривается узел с индексом 3.
Он имеет два дочерних с ключами 9 и 10. Большим из них является узел с ключом
10 и его нужно поменять местами с корневым.
14.06.2025
410
411.
14
3
2
1
10
4
5
14
16
8
9
2
6
8
7
9
3
10
7
Далее рассматривается узел с индексом 2.
Два его дочерних узла имеют ключи 14 и 16. Больший из них 16 должен поменяться местами с корневым узлом.
Но такой обмен нарушил свойство пирамидальности для поддерева, имеющего в
качестве корня узел с индексом 5.
Следовательно, нужно восстановить пирамидальность, выполнив обмен для нового корня и его дочернего узла с индексом 10.
14.06.2025
411
412.
43
2
16
10
4
5
14
7
8
9
2
6
8
7
9
3
10
1
На последнем этапе выбираем узел с индексом 1
Вначале меняем его местами с большим дочерним (16).
Теперь работаем в поддереве с узлом, имеющим индекс 2. Его нужно поменять
местами с большим дочерним (14).
И последним преобразуется поддерево, имеющее корнем узел с индексом 4. Он
меняется местами с дочерним узлом, с индексом 9.
В результате из сортируемого массива получено пирамидальное дерево, к
которому уже можно применять описанный выше способ сортировки.
Заметим, что это пирамидальное дерево эквивалентно массиву {16, 14, 10, 8, 7, 9,
3, 2, 4, 1}, он существенно отличается от исходного {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}
14.06.2025
412
413.
Фактически для реализации алгоритма пирамидальной сортировки само деревостроить необязательно. И алгоритм построения пирамидального дерева и последующее его преобразование сводятся к перемещениям соответствующих элементов в сортируемом массиве.
Сводя все предыдущие рассуждения вместе получим следующий алгоритм пирамидальной сортировки.
Вначале нужно преобразовать сортируемый массив к виду, эквивалентному пирамидальному дереву. В результате на первое место попадет максимальный по
всему массиву элемент A[1]=max {A[i], i=1,2,…, N}.
Затем нужно выполнить N-1 шаг сортировки.
На первом шаге меняются местами находящийся на первом месте максимальный
и N элементы. После чего последний элемент образует уже упорядоченную часть,
а элементы с 1-го по N-1-й ― неупорядоченную. Получившаяся совокупность элементов неупорядоченной части массива эквивалента частично упорядоченному
пирамидальному дереву, которое восстанавливается до полностью пирамидального. При этом максимальный из неупорядоченной части вновь попадает в начало
массива.
На втором шаге меняются местами 1 и N-1 элементы. После чего на «своих» местах уже находятся N-1-й и N-й элементы, образуя упорядоченную часть. Первые
N-2 элемента, образующие неупорядоченную часть, вновь преобразуются и максимальный из них перемещается на первое место.
14.06.2025
413
414.
Таким образом, на i-ом шаге всегда находящийся на первом месте максимальныйэлемент A[1] меняется местами с последним элементом неупорядоченной части
A[N-i+1], затем из уменьшенной на один элемент неупорядоченная части при восстановлении её пирамидальности выбирается наибольший и перемещается на
первое место в массиве.
В чем сходство и в чём различие между методом пирамидальной сортировки и
сортировки прямым выбором?
Первый набросок подпрограммы пирамидальной сортировки.
{преобразование массива к виду, эквивалентному пирамидальному дереву}
for ( i=1; i<=N-1; i++) // цикл шагов сортировки
{
// обмен местами A[1] и A[N-i+1] элементов
// в нумерации С - (A[0] и A[N-i])
// восстановление пирамидальности для элементов от 1 до N-i
// в нумерации С - от 0 до N-i-1
}
14.06.2025
414
415.
Теперь обсудим алгоритм преобразования исходного массива, соответствующийпостроению пирамидального дерева.
Итак, в состоящем из N элементов сортируемом массиве упорядоченными в смысле пирамидальности считаются все последние элементы с индексами L+1, L+2, …,
N, где L=int(N/2).
Выбирается элемент массива с индексом i=L и переставляются нужным образом
он и элементы, которые соответствуют его поддереву.
Затем выбирается элемент массива с индексом i=L-1 и точно также переупорядочиваются связанные с ним элементы массива.
Последним выбирается элемент массива с номером i=1.
Следовательно, нужно организовать цикл по перебору элементов массива с индесами i=L, L-1, L-2, …, 1. В теле цикла выбирается очередной элемент с=A[i] и
переставляются связанные с ним элементы массива, так чтобы соответствующее
поддерево стало пирамидальным.
14.06.2025
415
416.
Переставляемая совокупность элементов массива эквивалентна пирамидальномуподдереву либо частично упорядоченному поддереву.
Это вытекает из следующих соображений. На каждом шаге к совокупности элементов, которые уже обладают свойством пирамидальности, добавляется только один элемент. Он попадает в начальную позицию новой совокупности, то есть
он становиться корнем некоторого поддерева.
При этом возможен вариант, когда новый элемент больше своих дочерних, тогда
получается готовое пирамидальное поддерево. Если же новый элемент оказывается меньше, чем любой из дочерних, то получается частично упорядоченное поддерево.
Это соображение показывает, что составной частью алгоритма построения пирамидального дерева является алгоритм преобразования частично упорядоченного
поддерева в пирамидальное.
Единственное отличие в том, что в случае построения пирамидального дерева
индекс начального элемента равен не 1, как при выполнении сортировки, а уменьшается от L до 1.
14.06.2025
416
417.
Получаем следующий набросок алгоритма приведения массива к виду эквивалентному пирамидальному дереву.L=N/2;
for ( i=L; i>=1; i - -)
{
// восстановление пирамидальности для элементов от i до N
// в нумерации С от i-1 до N-1
}
Из проведённых рассуждений вытекает, что для реализации алгоритма пирамидальной сортировки целесообразно построить вспомогательную подпрограмму
восстановления пирамидальности для частично упорядоченного дерева, которая
играет центральную роль во всем алгоритме пирамидальной сортировки, так как
используется и при начальном построении дерева и при выполнении собственно
сортировки.
14.06.2025
417
418.
Очевидно, подпрограмму необходимо реализовать так, чтобы её можно было применять и для первоначального построения дерева и для его сортировки.Эти случаи отличаются друг от друга участками массива, элементы которых переставляются. При построении дерева в перестановках участвуют элементы с индексами от i-го по N-й, а при выполнении сортировки ― элементы с 1-го по (N-i)-й.
Пусть L и R ― номера индексов, ограничивающие участок массива, элементы которого участвуют в перестановках, k ― индекс «корневого» элемента преобразуемого «поддерева».
Тогда левый «дочерний» элемент определяется индексом 2k. Правый «дочерний»
имеет индекс 2k+1. «Дочерний» элемент существует если его индекс не превосходит максимальный индекс участка R, то есть если 2k≤R и 2k+1≤R. Заметим, что
ситуация, когда правый «дочерний» элемент существует, а левый не существует
невозможна по принципу построения дерева.
Для восстановления пирамидальности нужно определить индекс m большего из
двух «дочерних» элементов (предварительно убедившись, что элемент существует) и обменять местами «корневой» и выбранный «дочерний».
14.06.2025
418
419.
После такого обмена нужно спуститься на уровень вниз, то есть объявить новым«корневым» тот «дочерний», с которым был произведён обмен. Это значит, что
индекс k должен получить в качестве нового значение m.
Затем нужно вновь вычислить индекс большего «дочернего», поменять его местами с «корневым» и спуститься на уровень вниз.
Этот процесс следует продолжать до тех пор, пока существуют «дочерние» элементы, принадлежащие рассматриваемому диапазону индексов L,…,R.
После завершения цикла преобразуемый участок массива станет эквивалентным
пирамидальному поддереву.
Организуя цикл следует помнить о том, что преобразуемое «поддерево» может
сразу же или на одном из промежуточных уровней оказаться пирамидальным, следовательно, в заголовке цикла нужно не только проверять выход индекса «дочернего узла» за диапазон рассматриваемых индексов, но и сравнивать «корневой»
элемент с=A[k] с максимальным из «дочерних» A[m].
Следовательно, условие заголовка цикла прохода по уровням должно иметь вид:
(m<=R) && (c<A[m-1]) ― проходы повторяются пока «дочерний» элемент больше
«корневого» и его индекс не превосходит индекс последнего.
14.06.2025
419
420.
Перед входом в цикл нужно определить индекс большего «дочернего» (предварительно убедившись в существовании второго «дочернего»).Следовательно, инициализация цикла выглядит следующим образом:
k=L; c=A[k-1]; {индекс корневого и сам корневой} m=2*k; { индекс левого дочернего}
if ((m<R) && (A[m]>A[m-1])) m=m+1; // если правый существует и больше левого
Почему не проверяется существование левого «дочернего»?
Если нет ни одного дочернего, то рассматриваемый элемент «лист», который по
определению не должен участвовать в преобразованиях.
Для уменьшения количества пересылок обмен в теле цикла можно совершать
только частично. То есть в цикле ставить на место «корневого» больший из «дочерних» (A[k-1]=A[m-1]) и только. А бывший «корневой» ставить на «своё» место
(A[m-1]=c) только один раз после завершения цикла прохода по уровням.
В теле цикла после выполнения обмена нужно организовать спуск на один уровень
вниз, взять на нём «корневой» и выбрать для него больший «дочерний» (предварительно проверив существование второго «дочернего»). Спуск организуется заменой «индекса» корневого на индекс «дочернего» k=m и получением индекса
нового левого «дочернего» m=2*k.
14.06.2025
420
421.
void RestoreHeap( int L, int R, int *A)// Вспомогательная процедура восстановления пирамидальности
{
int k=L; int c=A[k]; int m=2*k; // индекс корн. и корн., индекс левого дочернего
if ((m<R) && (A[m]>A[m-1])) m++; // правый существует и больше левого
while ((m<=R) && (c<A[m-1])) // цикл по уровням дерева
{
c=A[k-1];A[k-1]=A[m-1]; A[m-1]=с; // замена корневого дочерним
k=m; m=2*k; // спуск на уровень вниз
if ( (m<R)&&( A[m]>A[m-1])) m++; }// правый сущест. и больше левого
}
return;}
Почему в теле цикла не проверяется существование левого «дочернего»?
14.06.2025
421
422.
Теперь можно записать процедуру пирамидальной сортировки целиком.void HeapSort ( int * A) // Пирамидальная сортировка массива x
{
// Преобразование массива к пирамидальному дереву.
for (int i=N/2; i>=1; i - -)
// восстановление пирамидальности для элементов от i до N
RestoreHeap(i, N, A);
// собственно сортировка
for (int i=1; i<=N-1; i++) // цикл шагов сортировки
{
// обмен местами A[0] и A[N-i] элементов
int c=A[0]; A[0]=A[N-i]; A[N-i]=c;
// восстановление пирамидальности для элементов от 1 до N-i
RestoreHeap(1, N-i, A)
}
return;}
14.06.2025
422
423.
Анализ пирамидальной сортировки показывает, что её сложность O(N*log2N).Эту сортировку (впрочем, как и все улучшенные варианты сортировок) не
рекомендуется применять для небольших массивов, так как, например, для
N=1000 даже прямые вставки окажутся примерно вдвое быстрее пирамидальной.
Сравнение пирамидальной сортировки и сортировки Шелла показывает, что для
малых и средних N более эффективна сортировка Шелла. По мере роста N пирамидальная сортировка начинает работать быстрее сортировки Шелла.
Следует обратить внимание на то, что пирамидальная сортировка даже в худших
случаях имеет сложность O(N*log2N). В то время как у сортировки Шелла оценка
O(N1,2) получена для среднего, а не для худшего случая. В худшем случае у
Шелла O(N2).
Строго говоря сложность как раз и рассматривается только в худшем случае. Поэтому O(N1,2) не может называться сложностью процедуры Шелла.
14.06.2025
423
424.
Улучшение обменной сортировки. Быстрая сортировка Хоара.В 1962 году Чарльз Хоар предложил улучшенный вариант обменной сортировки.
Основная идея улучшения состоит в том, чтобы обменивать не рядом стоящие
элементы массива, а расположенные как можно дальше друг от друга.
Выбор участвующих в обмене элементов массива производится следующим образом. Выбирается один из элементов массива, который должен играть роль своеобразного барьера.
Элементы массива просматриваются с двух концов. При просмотре слева направо
(начиная с первого) выбирается элемент, не меньший чем барьерный. А во время
просмотра справа налево (начиная с последнего) выбирается элемент не больший
чем барьерный. Найденная пара элементов меняется местами, после чего просмотры возобновляются. Завершается проход по массиву после того, как индекс
просмотра слева, станет больше чем индекс просмотра справа.
барьер
43
44
55
Проход направо
14.06.2025
12
42
94
18
6
67
Проход налево
424
425.
Пусть c =42 ― барьерный элемент,i ― индекс элементов при проходе направо: i=1, 2, …
j ― индекс элемента при проходе налево: j=N, N-1, N-2, …
44
55
12
Меньше барьерного
42
94
Обмен
18
66
67
Больше барьерного
Проход слева направо: i=1, A1 (=44) > c (=42).
Проход справа налево: j=7, A7 (=6) < c (=42).
Проход слева направо: i=2, A2 (=55) > c (=42).
Проход справа налево: j=6, A6 (=18) < c (=42).
Проход слева направо: i=4, Достигнут барьер
Проход справа налево: j=4, Достигнут барьер
Как следует поступить далее?
14.06.2025
Можно рекурсивно отсортировать обе
части массива.
425
426.
Следовательно, нужно написать рекурсивную процедуру сортировки, которую можно применять к любому участку массива, начинающему с индекса L и завершающегося индексом R.В это процедуре следует организовать выбор барьерного элемента, а затем цикл, в
котором во время просмотра слева направо и справа налево выбираются
меняющиеся местами элементы. После обнаружения таких элементов поменять
их местами.
Первый набросок процедуры:
void Sort (int L, int R, int *A)
// рекурсивная подпрограмма процедуры быстрой сортировки
{
int i=L; // Проход слева направо с начального элемента L
int j=R; // Проход справа налево с начального элемента R
int d=A[(L+R)/2]; // выбор барьера
while (i<=j) //цикл обменов на проходе
{
// выбор большего на проходе слева направо
// выбор меньшего на проходе справа налево
// обмен
} // проходы завершаются когда левый индекс станет больше правого
// рекурсивные вызовы для левой и правой частей массива
}
14.06.2025
426
427.
Уточним теперь непроработанные фрагменты подпрограммы.Во время просмотра слева направо нужно переходить от текущего элемента к
следующему пока текущий элемент меньше барьерного. Первый встретившийся
элемент больший (либо равный) барьерному приостанавливает просмотр для
обмена. Эти действия можно реализовать следующим циклом:
while (A[i-1]<c) i++;
Какое неравенство строгое (A[i-1]<c)или нестрогое (A[i-1]<=C) нужно применить
в этом цикле?
Применение нестрогого неравенства потенциально опасно, так как в этом случае
барьерный элемент не остановит движение слева направо при просмотре. Следовательно, возникает опасность дальнейшего движения по правой части массива
(если там все элементы меньше барьерного) и последующему выходу индекса за
границы диапазона. Поэтому в заголовке цикла нужно оставить строгое неравенство.
Совершенно аналогично реализуется просмотр справа налево:
while (A[j-1]>c) j - -;
14.06.2025
427
428.
Реализация обменов можно осуществить стандартным способом, однако нужнопомнить, что после обмена просмотры должны быть возобновлены, продолжены с
элементов, которые расположены за участвовавшими в обмене.
Это означает, что после обмена следует увеличить индекс i и уменьшить индекс j
на единицу.
Последний вопрос, который нуждается в уточнении, это рекурсивные вызовы.
Из предыдущих рассуждений следует, что левый участок, для которого нужно рекурсивно вызывать обсуждаемую процедуру, начинается индексом L и завершается индексом j (Sort (L ,j, A)), а правый ― начинается индексом R и завершается
ин-дексом i (Sort (i, R, A)).
Ясно, что по мере выполнения рекурсивной сортировки, эти участки массива
уменьшаются в размерах. Участок, для которого имеет смысл вызывать процедуру, должен содержать не менее двух элементов массива. Поэтому перед вызовом
процедуры для левой и правой частей массива нужно проверить выполнение условий L<i и j<R соответственно.
Какое неравенство (строгое или нестрогое) следует использовать для такой
проверки?
Нестрогое условие, например, L<=i гарантирует наличие только хотя бы одного
элемента, а для имеющего смысл обмена нужно по крайне мере два.
14.06.2025
428
429.
После реализации всех этих фрагментов во вспомогательной рекурсивной подпрограмме в основной процедуре быстрой сортировки останется только осуществить вызов рекурсивной подпрограммы ко всему массиву.void Sort (int L, int R, int *A)
// вспомогательная рекурсивная подпрограмма быстрой сортировки
{ int i=L; // Проход слева направо с начального элемента L
int j=R; // Проход справа налево с начального элемента R
int d:=A[(L+R)/2-1]; // выбор барьера
while (i<=j) // цикл обменов на проходе
{
while( A[i-1]<d) i++; //выбор меньшего на проходе слева направо
while (A[j-1]>d) j - -; //выбор большего на проходе справа налево
int c=A[i-1]; A[i-1]=A[j-1]; A[j-1]=c; // обмен
i++; j - -; //сдвиги индексов
} //проходы завершаются когда левый индекс станет больше правого
if (L<j) Sort(L, j, A); if (i<R) Sort(i, R, A); // рекурсивные вызовы
return; }
void QuickSort (int *A) // Быстрая сортировка массива A
{ Sort(1, N, A); return; } //основная подпрограмма сортировки
14.06.2025
429
430.
Довольно сложный анализ эффективности алгоритма быстрой сортировки Ч. Хоара показал, что в оптимальном случае общее количество сравнений равноC =N*log2N, а общее количество пересылок (присваиваний) M=N*log2N/6.
Оптимальный вариант, при котором достигается самая высокая эффективность и
минимальная сложность сортировки, обеспечивается выбором в качестве барьера так называемого медианного элемента массива.
Медианой массива (медианным элементом) считается такой его элемент, который не меньше одной половины элементов массива и при этом не больше другой
половины (независимо от их взаимного положения, важно лишь общее количество
элементов).
Так для массива состоящего из 7 элементов, нужно выбрать такой элемент, который окажется не больше трёх любых элементов и при этом не меньше трёх других
его элементов. Например, для массива {16, 12, 90, 84, 18, 67, 10} медианой является элемент A5=18, так как он больше A1=16, A2=12 и A7=10, и при этом меньше
чем A3=90, A4=84 и A6=67.
Выбирать медианной элемент дольно сложно, во всяком случае такой выбор представляет собой самостоятельную задачу. Однако самое удивительное свойство
сортировки Хоара состоит в том, что её средняя производительность при случайном выборе (в том числе при выборе среднего) барьерного элемента отличается от
оптимального всего лишь коэффициентом 2*log102.
14.06.2025
430
431.
Сортировка подсчётом.Все рассмотренные выше сортировки имели асимптотическую сложность O(N2)
или O(N logN). Вместе с тем существуют алгоритмы, имеющие линейную
сложность, однако для их применения требуется выполнения некоторых
ограничений на значения элементов сортируемого массива.
Рассмотрим один из простейших алгоритмов этого класса, который называют
«Сортировка подсчётом». Он применим только для целочисленных массивов,
при этом желательно, чтобы диапазон возможных значений был не очень широк.
Предположим, что входной массив состоит из N целых чисел, значения которых
находятся в диапазоне от 0 до k-1. Эти значения рассматриваются как индексы
вспомогательного массива. Организуется цикл прохода по исходному массиву, во
время которого во вспомогательном массиве для каждого индекса прямым
подсчётом накапливается количество элементов основного массива, которые
имеют значение равное индексу вспомогательного.
Затем организуется проход по вспомогательному массива, во время которого
исходный массив перезаписывается последовательными значениями индексов
вспомогательного, которые помещаются в отсортированный несколько раз подряд.
Причём количество записей индекса в отсортированный равно значению
соответствующего элемента вспомогательного массива.
14.06.2025
431
432.
Сортируемый массив:8
6
3
10
6
2
3
5
Вспомогательный массив:
1
2
3
4
5
6
7
8
9
10
0
0
1
0
12
0
1
0
0
1
2
0
1
0
0
0
1
Отсортированный массив
2
14.06.2025
3
3
5
6
6
8
10
432
433.
Вовремя
программной
реализации
массива
необходимо
создать
вспомогательный массив В[0..k - 1], состоящий из нулей, затем последовательно
просмотреть элементы исходного массива A, и для каждого элемента A[i]
увеличить значение В[A[i]] на единицу. Далее достаточно пройти по массиву В,
для каждого его элемента в массив A последовательно записать индекс j ровно
B[j] раз.
void CountingSort(int N, int k, int*& A)
{
int B[k+1] = { 0 }; //Инициализация вспомогательного массива
// Подсчёт появлений элементов сортируемого массива
for (int i = 0; i < N; i++) { B[A[i]]++; }
int b = 0; // Индекс отсортированного массива
for (int i = 0; i < k+1; i++) // Перебор индекса вспомогательного массива
{ for (int j = 0; j < c[i]; j++) { A[b++] = i; }}
}
Оценка асимптотической сложности алгоритма сортировки подсчётом: циклы
имеют сложность O(N) и O(k), соответственно общая сложность: O(N+k)
14.06.2025
433
434.
Возникает несколько вопросов. Что делать, если диапазон значений элементовмассива (min и max) заранее не известен?
Этот вопрос можно решить линейным поиском min и max, что не повлияет на
асимптотику алгоритма.
Что делать, если минимальное значение больше нуля?
Если min больше нуля, то следует при работе с массивом B из A[i] вычитать min, а
при обратной записи прибавлять.
Что делать если в сортируемых данных присутствуют отрицательные числа?
При наличии отрицательных чисел нужно при
B к A[i] прибавлять |min|, а при обратной записи вычитать.
14.06.2025
работе
с
массивом
434
435.
Сравнение внутренних сортировокИтак, большинство рассмотренных методов сортировок имеет квадратичную
сложность O(N2). При этом среднее количество сравнений и пересылок у прямых
методов также пропорционально N2, в то время как среднее количество операций
для пирамидальной и быстрой сортировок пропорционально N*log2N, а для
сортировки Шелла ― N1,2.
Для более наглядной сравнительной оценки различных методов сортировок рассмотрим таблицу времени (в секундах) выполнения сортировки массивов из N=256
и N=2048 элементов разными алгоритмами, приведённую Н. Виртом.
N=256
Сортировка
Упорядочен.
Случайный
Обратный
Прямые вставки
0,02
0,82
1,64
Двоичные вставки
0,12
0,70
1,30
Прямой выбор
0,94
0,96
1,18
Обменная
1,26
2,04
2,80
Шейкерная
0,02
1,56
2,92
Шелла
0,10
0,24
0,28
Пирамидальная
0,20
0,20
0,20
Быстрая
0,08
0,12
0,08
14.06.2025
435
436.
N=2048Сортировка
Упорядочен.
Случайный
Обратный
Прямые вставки
0,22
50,74
103,80
Двоичные вставки
1,18
37,66
76,06
Прямой выбор
58,18
58,34
73,40
Обменная
80,18
128,84
178,66
Шейкерная
0,16
104,44
187,36
Шелла
0,80
7,08
12,34
Пирамидальная
2,32
2,22
2,12
Быстрая
0,72
1,22
0,76
Анализ таблиц показывает, что из прямых методов сортировки самой худшей во
всех вариантах первоначальной неупорядоченности массива и для разных размерностей является обменная сортировка.
Самой лучшей из прямых методов является сортировка вставками. Прямой выбор
по эффективности между вставками и обменной.
Улучшение прямых вставок двоичным поиском места вставки практически не дает
эффекта.
14.06.2025
436
437.
Шейкерная сортировка не дает существенного улучшения по сравнению с обменной.Быстрая сортировка в 2-3 раза лучше пирамидальной, а пирамидальная эффективней сортировки Шелла.
Но у быстрой сортировки могут оказаться случаи, когда её производительность
пропорциональна N2, в то время, как у пирамидальной сортировки производительность в любом случае пропорциональна N*log2N.
Замечание. Следует заметить, что существуют сортировки со сложностью O(N). То
есть сортировки более эффективные, чем быстрые, это, например, поразрядная,
карманная и некоторые другие, но такие сортировки рассчитаны, на специальные
случаи сортируемых массивов, к которым предъявляются довольно жёсткие
требования.
14.06.2025
437
438.
СортировкаСложность Сложность в
в среднем
худшем
Область применения
Выбором
O(N2)
O(N2)
Малые массивы
Вставкой
O(N2)
O(N2)
Малые массивы
Обменная
O(N2)
O(N2)
Малые массивы, если
частично отсортированные, то
O(N)
Шелла
O(N1,2)
O(N2)
Крупные, почти
отсортированные
Пирамидальная
O(N logN)
O(N logN)
Крупные с неизвестным
распределением
Слиянием
O(N logN)
O(N logN)
Крупные с неизвестным
распределением
Быстрая
O(N logN)
O(N2)
Крупные, нет много
дубликатов , часто лучше, чем
пирамидальная и слиянием
Подсчётом
O(N+M)
O(N+M)
Крупные с ограниченным
диапазоном, 1:M ─ диапазон
изменения значений
14.06.2025
438
439.
Основные рекомендации:1. Для массивов небольшого объёма рекомендуется использовать сортировки
выбором и вставками.
2. Если такие массивы частично отсортированы, то обменная сортировка лучше,
чем выбором и вставками.
3. Для крупных массивов с ограниченным диапазоном
эффективной является сортировка подсчётом.
значений
самой
4. Если в крупном массиве нет большого количества дубликатов, то лучше
использовать быструю сортировку.
5. Для крупного частично отсортированного массива подходит сортировка Шелла.
6. Для крупного массива с неизвестным распределением ─ пирамидальная.
7. Для внешних сортировок ─ слиянием, для внутренних – необходима
дополнительная память, так как сортировка выполняется не «на месте».
14.06.2025
439
440.
Внешняя сортировкаЕсли сортируемые данные занимают настолько большой объем памяти, что они
не помещаются в оперативной памяти, то вместо внутренней сортировки применяется внешняя. Это означает, что данные организованы в виде файлов и находятся они на внешних носителях, магнитных лентах или дисках. Внешнюю сортировку иногда называют сортировкой последовательностей.
Принципиальная разница между внутренней и внешней сортировками заключается
не столько во времени доступа к нужному элементу, сколько в том, что для файлов
невозможно выполнение основной операции сортировки ― обмена для двух
выбранных элементов. Дело в том, что при записи в файл приходится переписывать по крайней мере целый сектор диска или некоторую другую часть файла.
Поэтому основными операциями, с помощью которых осуществляется внешняя
сортировка, являются разделение файла на две части, которые записываются в
два разных файла, затем слияние этих частей и запись в единую, но уже частично или полностью упорядоченную последовательность, в исходный файл.
Во время работы с файлом в программе доступен только один элемент, находящийся в буфере файла. Поэтому слияние выполняется с помощью сравнения
буферных элементов и записи большего (или меньшего) в результирующий файл.
14.06.2025
440
441.
Операции разделения и слияния принято называть фазами внешней сортировки.Заметим, что многие авторы считают фазой сортировки последовательность, состоящую из операции разделения и слияния.
Рассмотрим пример. Пусть имеются файл, который нужно отсортировать:
F1:
44, 55, 12, 42, 94, 18, 6, 67
Фаза разделения: файл разбивается на два самостоятельных:
F2:
44, 55, 12, 42
F3 :
94, 18, 6, 67
F1:
44, 94,
94 18, 55, 6, 12
12, 42, 67
Фаза слияния, в которой участвуют по одному элементу из каждого файла: из
сливаемых файлов выбираются и сравниваются между собой буферные элементы, затем они записываются в результирующий файл сначала меньший, а
затем больший.
Заметим, что здесь и в дальнейшем, оборот «выбирается из файла» понимается как чтение из файла с последующим сдвигом его буфера к следующей
позиции.
В результате получится файл, состоящий из упорядоченных пар.
14.06.2025
441
442.
F1:44, 94, 18, 55, 6, 12, 42, 67
Фаза разделения: файл вновь разбивается на два самостоятельных:
F2:
44, 94 18, 55
F3 :
6, 12, 42, 67
F1:
6 12,
6,
12 44,
44 94,
94 18, 42,
42 55,
55 67
Фаза слияния, в которой участвуют чётвёрки, образуемые парами из каждого
файла:
1. сравниваются между собой буферные элементы из F2 и F3, меньший из них
выбирается из своего файла и записывается в результирующий файл;
2. такие сравнения, выборки и записи выполняются до тех пор, пока из одного
из файлов (F2 или F3) не будет выбрано ровно два элемента.
3. оставшиеся в другом файле элементы пары выбираются и записываются в
результирующий файл.
4. описанные действия выполняются для каждой очередной четвёрки.
В результате получится файл, состоящий из упорядоченных четвёрок
14.06.2025
442
443.
F1:6, 12 , 44, 94, 18, 42, 55, 67
Фаза разделения: файл вновь разбивается на два самостоятельных:
F2:
6, 12, 44, 94
F3 :
18, 42, 55, 67
F1:
6 12,
6,
12 18,
18 42,
42 44,
44 55,
55 67
67, 94
Фаза слияния, в которой участвуют по четыре элемента из каждого файла. Слияние выполняется по тем же правилам, что в случае слияния упорядоченных
двоек, за тем исключением что завершается сравнение элементов из буферов
файлов F2 и F3 только после выборки из любого файла 4 (а не 2) элементов.
В результате в данном примере получится полностью упорядоченный файл.
Для больших файлов нужно делать гораздо больше проходов, увеличивая каждый раз количество элементов файлов, участвующих в слиянии в 2 раза. Следовательно, общее количество таких проходов пропорционально log2N, где N ― количество элементов в сортируемом файле.
Такой метод называется двухфазной сбалансированной трехпутевой сортировкой.
Вместо термина «трёхпутевой» часто используется термин «трёленточный».
14.06.2025
443
444.
Отметим, что последовательности элементов файлов, которые участвуют вслиянии на каждом шаге принято называть сериями или отрезками.
Можно отказаться от требования сбалансированности, в соответствии с которым
на каждом шаге выполняется упорядочение серий фиксированной длины (1, 2, 4
и т. д.), и сливать упорядоченный серии любой длины, которые уже имеются в
исходном файле. Поэтому такой способ внешней сортировки принято называть
естественной сортировкой.
Естественными сериями, имеющимися в рассматриваемом примере являются:
F1:
44, 55, 12, 42, 94, 18, 6, 67
Фаза разделения в естественной сортировке выполняется по сериям: первая серия в первый файл, вторая ― во второй, третья ― в первый, четвёртая ― во
второй и т.д. Ясно, что в этом случае, в отличие от сбалансированной сортировки, формируемые файлы не будут содержать одинаковых количеств элементов
Фаза слияния в естественной сортировке также выполняется по сериям: сравнение, выборка и запись выполняются также как в сбалансированной сортировке,
до конца серии в одном из файлов, после чего остаток серии из другого файла
переписывается в результирующий. Отличие только в том, что серии имеют не
фиксированную, а произвольную длину.
14.06.2025
444
445.
F1:44, 55, 12, 42, 94, 18, 6, 67
Фаза разделения:
F2:
44, 55, | 18
F3 :
12, 42, 94, | 6, 67
F1:
12, 42, 44, 55, 94, 6, 18, 67
Фаза слияния:
Фаза выделения серий и разделения:
F2:
12, 42, 44, 55, 94
F3 :
6,
18, 67
Фаза слияния:
F1:
6, 12, 18, 42, 44, 55, 67, 94
Файл упорядочен за два прохода, а не за три. Вывод: учет уже имеющейся в
файле упорядоченности с помощью выделения естественных серий может
уменьшить необходимое количество фаз сортировки.
14.06.2025
445
446.
Основным понятием внешней сортировки является понятие серии (отрезка).Точное определение серии:
Серией называется последовательность подряд расположенных уже упорядоченных элементов файла Ai, Ai+1, …, Ai+k, удовлетворяющих следующим условиям:
Ai ≤ Ai+1 ≤ … ≤ Ai+k, то есть Aj ≤Aj+1, ∀i ≤ j ≤i-k+1;
Ai-1>Ai, i≠1; Ai+k> Ai+k+1, i+k<N
Пример. Сколько серий содержит файл:
11, 14, 8, 9, 51, 15, 85, 98, 13, 4, 6, 10
Ответ: пять серий.
11, 14
8, 9, 51
15, 85, 98
13
4, 6, 10
14.06.2025
446
447.
Файл считается состоящим из серий, количество которых в файле может бытьлюбым.
Если файл содержит ровно одну серию, то он уже упорядочен, если файл
содержит N серий, то каждая серия состоит ровно из 1 элемента.
Задачу сортировки файла можно сформулировать следующим образом: файл
состоящий из m>1 серий преобразовать в файл состоящий из m=1 серии
Формулировка задачи фазы разделения файла в терминах серии выглядит следующим образом: преобразовать файл, состоящий из серий I1, I2, I3, I4, …., Im в
два различных файла I1, I3, I5,… и I2, I4, I6, …. Такое разделение называется
двухпутевым или двухленточным.
В более общей формулировке разделение файла может быть выполнено на p≥2
файлов (путей, лент):
I1, Ip+1, I2p+1,I3p+1 , …
I2, Ip+2, I2p+2,I3p+2 , …
I3, Ip+3, I2p+3,I3p+3 , …
…
Ip, I2p, I3p, I4p , …
Такую сортировку принято называть многопутевой или многоленточной.
14.06.2025
447
448.
Фаза слияния на примере двухпутевого случая выглядит следующим образом:Пусть файл F2 состоит из серий B1, B2, …, Bn, а файл F3 ― из серий C1, C2, …,
Cm. Эти файлы с помощью слияния нужно преобразовать в один файл F1, состоящий из серий S1, S2, …, Sk, k=min(n,m). Причём, для i ≤ k серия Si образуется
слиянием Bi и Сi, а для i>k Si=Bi, если n>m и Si=Ci, если n<m.,
В общих чертах процесс образования (слияния) серии Si из серий Bi и Ci описывается так:
1. выбираются элементы из буферов файлов F2 и F3 и меньший из них записывается в результирующий файл;
2. описанный в п. 1 процесс выборки, сравнения и записи продолжается до тех
пор пока не будет достигнут конец текущей серии или конец одного из файлов;
3. оставшиеся элементы из второго файла переписываются в конец результирующего файла;
4. процесс слияния всех остальных серий файлов выполняется так, как описано
в п.п. 1, 2 и 3.
14.06.2025
448
449.
Общая схема трехленточной сортировки файла F1 выглядит следующим образом:F2
F2
F1
…
F1
F3
F1
F3
Разделение Слияние Разделение
Слияние
Если в вычислительной системе имеется необходимый запас внешней памяти, то
эффективность сортировки можно существенно улучшить соединяя фазу разделения с фазой слияния, но для этого требуется четыре файла (четыре ленты, четыре пути).
В четырёхленточной сортировке сливаемые серии записываются не в один файл,
а в два разных: готовая серия записывается по очереди, то в один, то в другой
файл, с тем чтобы на следующем шаге сразу же можно было приступить к новому
слиянию/разделению. Такая сортировка считается однофазной.
14.06.2025
449
450.
Общая схема четырёхленточной сортировки файла F1 выглядит следующим образом:F2
F1
F2
F1
…
F1
F3
F4
F3
F1
F4
Рассмотренные идеи внешней сортировки были использованы и для реализации
внутренней сортировки слиянием. Оценка сложности этого варианта сортировки
также как и быстрой O(N*log N). Сортировка слиянием очень полезна для
ситуаций, когда сортируемый массив не содержится в ОП полностью, а
вычисляется или переписывается в оперативную память частями. В этом её
преимущество перед быстрой сортировкой.
14.06.2025
450
451.
Для реализации процедур слияния можно использовать, например, следующееописание файлового типа:
type T_f_Int= file of integer;
Из предшествующего обсуждения видно, что в случае трёхленточной сортировки
целесообразно подготовить две вспомогательные подпрограммы: подпрограмму
слияния Merge и подпрограмму разделения Split.
Формальными параметрами этих подпрограмм являются используемые для слияния или разделения файлы F1, F2 и F3. Для процедуры слияния исходными являются файлы F2 и F3, а результирующим ― файл F1, а для процедуры разделения
― наоборот, исходный файл F1, а результирующими являются файлы F2 и F3.
14.06.2025
451
452.
В процедуре Merge нужно подготовить файлы F2 и F3 к считыванию, а файл F1 кзаписи.
В соответствии с общим определением операции слияния каждый из файлов F2 и
F3 состоит из некоторого количества серий, которые нужно слить. Следовательно,
нужно организовать цикл по перебору серий, находящихся в файлах.
В общем случае количество k пар сливаемых серий, находящихся в файлах F2 и
F3 неизвестно, равно как неизвестно и общее количество серий n и m в этих файлах. Поэтому слияние имеющихся в файлах серий продолжается до тех пор пока
не будет достигнут конец файла F2 или F3.
После завершения выполнения цикла слияний конец файла может быть достигнут
либо у одного из файлов, либо у обоих сразу. То есть серии могут остаться только
в одном из файлов (либо их не будет ни в одном из файлов).
Поэтому после завершения слияния пар серий из F2 и F3 нужно переписать в результирующий файл серии из того файла, в котором ещё имеются элементы. Для
этого нужно проверить достижение конца файла в каждом из сливаемых файлов.
Перенос серий, оставшихся в
будет достигнут его конец.
14.06.2025
каком-либо файле, следует выполнять, пока не
452
453.
Первый набросок процедуры слиянияprocedure Merge (var F1, F2, F3:T_f_int);
{процедура слияния файлов F2 и F3 в файл F1}
begin
reset(F2); reset(F3); rewrite(F1); {Подготовка файлов к работе}
while not eof(F2) and not eof(F3) do {цикл прохода по сливаемым сериям}
begin
{Слияние пар серий из файлов F2 и F3}
end;
if not eof(F2) then {Серии остались в файле F2}
while not eof(F2) do begin {перенос оставшихся серий из файла F2} end;
if not eof(F3) then {Серии остались в файле F3}
while not eof(F3) do begin {перенос оставшихся серий из файла F3} end;
close(F1); close(F2); close(F3); {Корректное завершение работы с файлами}
end;
Легко заметить, что при выполнении цикла while not eof(F) do проверяется достижение конца файла, поэтому предварительная проверка if not eof(F) then является
излишней.
14.06.2025
453
454.
Слияние двух отдельных серий Bi и Сi производится с помощью выборки (например, процедурами read(F2,bf2) и read(F3, bf3)) элементов bf2 и bf3 из файлов F2 иF3 и записи меньшего из них в результирующий файл F1.
После выборки меньшего элемента в одном из файлов нужно сравнить второй
элемент из этого же файла и оставшийся головной (то есть находящийся в буфере
файла) элемент из другого файла.
В общем случае, из первого файла может быть выбрано и переписано несколько
элементов, которые окажутся меньше головного элемента из второго файла.
Потом файлы меняются ролями, и из первого файла может быть выбрано один,
два или несколько элементов, меньших головного элемента второго файла.
14.06.2025
454
455.
F2:12, 42, 44, 55, 94, 16,…
F3:
49, 51, 52, 54, 10, …
F1:
12 42,
12,
42 44
Сравнением буферных элементов (12) и (49) из файлов F2 и F3 для записи в F1
выбран элемент 12 из файла F2.
При выборе элемента из файла буфер файла F2 сместился к следующему элементу. Поэтому следующее сравнение происходит для элемента 42 из того же
файла, из которого был выбран меньший, и головной элемент из файла F3.
Второй раз выбран элемент из файла F2 и снова сравнение следующего элемента
из F2 и головного элемента из F3.
Третий раз выбран элемент из файла F2 и опять сравнение следующего элемента
из F2 и головного элемента из F3.
Таким образом, осуществлёна последовательность выборок элементов из файла
F2. При этом головной элемент (49) из файла F3 фактически играет роль барьера
для этих выборок.
После того, как текущий элемент файла F2 станет больше барьерного из F3, файлы как бы поменяются ролями
14.06.2025
455
456.
F2:12, 42, 44, 55, 94, 16,…
F3:
49, 51, 52, 54, 10, …
F1:
12 42,
12,
42 44,
44 49,
49 51
51, 52,
52 54
54, 55
Теперь выбран элемент и переместился буфер в файле F3. Поэтому следующее
сравнение выполняется для очередного элемента из F3 и буферного из F2.
Продолжается выборка из файла F3. При этом буферный элемент (55) из F2 играет роль барьера.
Может сложится впечатление, что после выбора элемента 54 в результирующий
файл должен попасть следующий элемент (10) из файла F3, так как он меньше
«барьерного» (55).
Но здесь нужно быть внимательным: в файле F3 элементом 54 завершается одна
серия, а элементом 10 начинается другая. Это значит, что проход по файлу F3
нужно завершить и закончить процесс слияния текущих серий, переписав в результирующий файл все оставшиеся элементы (в данном примере только один) из
текущей серии файла F2.
Следовательно, при слиянии серий нужно производить выборку элементов из файлов группами, при этом необходимо контролировать достижение конца файла,
достижение
границы серии и превышение текущим элементом барьерного
эле14.06.2025
456
мента из буфера второго файла.
457.
Обозначим текущие буферные элементы файлов F2 и F3 именами bf2 и bf3соответственно.
Если, например, меньший элемент оказался в файле F2, то нужно организовать
цикл выборки элементов из F2. При этом элемент bf3 должен играть для очередного выбранного элемента x_curr роль барьера (x_curr<bf3).
Кроме сравнения с барьером в цикле нужно следить за возможным достижением
конца файла F2 и за достижением конца текущей серии.
Отслеживать достижение конца файла можно с помощью стандартной функции
eof(F2).
А для контроля достижения конца серии необходимо сравнивать значение текущего, только что выбранного элемента файла x_curr с предшествующим, ранее
выбранным элементом x_pred. Если x_curr окажется меньше x_pred, то элемент
x_curr начинает следующую серию, а элемент x_pred завершает текущую.
То есть для контроля за достижением конца серии необходимо следить за двумя
последовательными элементами файла, из которого циклом выбираются
элементы.
Для организации такого слежения перед выборкой из файла очередного элемента
x_curr, необходимо сохранить его значение в x_pred (x_pred:=x_curr).
Кроме того, для организации такого слежения следует использовать индикатор ―
переменную логического типа, которая принимает значение true, если произошёл
14.06.2025
457
переход
к новой серии.
458.
Целесообразно ввести две такие переменные flag2 и flag3, с помощью которыхвнутри цикла можно отслеживать достижение конца серии в каждом из файлов по
отдельности.
После достижения конца серии или конца файла в одном из файлов необходимо
выбрать все оставшиеся элементы текущей серии из другого файла.
Переход к новым сериям в каждом из файлов происходит только после выбора
первых элементов серий, после того, как они попадут в буфер своего файла. При
этом первые элементы серий становятся новыми барьерами для их слияния.
Это означает, что для обработки первых серий следует организовать
инициализацию bf2 и bf3 до цикла, обеспечивающего проход по сливаемым
сериям. Ставить процедуры read(F2,bf2) и read(F3,bf3) в начале цикла слияний
нельзя, так как при любой повторной итерации (кроме первой) эти процедуры
сдвинут буферы в файлах на вторые элементы серий.
Следовательно, переменные bf2 и bf3 необходимо инициализировать до цикла
прохода по сериям. Однако необходимо предварительно убедиться, что
соответствующие файлы не пусты.
Цикл выполняется пока в обоих файлах имеются элементы: not eof(F2) and not
eof(F3)
В цикле организуется выбор меньшего головного элемента и каждой из ветвей
реализуется цикл слияния очередных групп серий.
14.06.2025
458
459.
procedure Merge (var F1, F2, F3:T_f_int);{процедура слияния файлов F2 и F3 в файл F1}
var bf2, bf3, x_curr, x_pred: integer; flag2, flag3:boolean;
begin
reset(F2); reset(F3); rewrite(F1); {Подготовка файлов к работе}
if not eof(F2) and not eof(F3) then begin read(F2,bf2); read(F3,bf3) end; {Инициал.}
while not eof(F2) and not eof(F3) do {цикл прохода по сливаемым сериям}
begin
if bf2<bf3 then
begin {считывание группы из F2}
end
else
begin {считывание группы из F3}
end;
{если серия в одном из файлов завершена, считывание «хвоста»
незавершённой серии}
end;
while not eof(F2) do begin {перенос хвоста файла F2} end;
14.06.2025
while
not eof(F3) do begin {перенос хвоста файла F3} end
end;
459
460.
Уточним реализацию циклов считывания групп.Цикл выполняется пока текущий элемент x_curr файла не превосходит барьерный
из другого файла (x_curr<bf2 или x_curr<bf3) и при этом конец серии еще не
достигнут (not flag2 или not flag3) и при этом не достигнут конец файла (not eof(F2
или not eof(F3)).
Следовательно, перед циклом нужно инициализировать значение текущего элемента (x_curr:=bf2 или x_curr:=bf3) и индикатор достижения конца серии (flag2:=
false или flag3:= false ― конец серии еще не достигнут).
В цикле нужно записать текущий элемент в результирующий файл write(F1, x_curr),
считать следующий элемент файла, предварительно объявив текущий предыдущим (x_pred:=x_curr), затем сравнит два соседних, и при обнаружении конца серии
присвоить соответствующее значение индикатору. Кроме того, нужно обновить
значение барьерного элемента, так как в любой момент возможен переход к новой группе и тогда роль барьера будет играть только что считанный текущий элемент (bf2:=x_curr или bf3:=x_currr).
14.06.2025
460
461.
while not eof(F2) and not eof(F3) do {цикл прохода по сливаемым сериям}begin
if bf2<bf3 then
begin {считывание группы из F2}
x_curr:=bf2; flag2:=false; {инициализация цикла считывания группы из F2}
while (x_curr<bf3) and nof flag2 and not eof(F2) do {цикл считывания группы}
begin
write(F1,x_curr);{запись в результирующий файл}
x_pred:=x_curr;{объявление текущего предыдущим для следующего шага}
read (F2, x_curr); {считывание следующего элемента серии}
if x_pred>x_curr then flag2:=true;{достигнут конец серии}
bf2:=x_curr {объявление нового буферного элемента в F2}
end
end
else
begin {считывание группы из F3}
end;
{если серия в одном из файлов завершена считывание «хвоста»
незавершённой
серии}
14.06.2025
end;
461
462.
Аналогичным образом выглядит вторая часть ветвленияwhile not eof(F2) and not eof(F3) do {цикл прохода по сливаемым сериям}
begin
if bf2<bf3 then
begin {считывание группы из F2}
…
end
else
begin {считывание группы из F3}
x_curr:=bf3; flag3:=false; {инициализация цикла считывания группы из F3}
while (x_curr<bf2) and nof flag3 and not eof(F3) do {цикл считывания группы}
begin
write(F1,x_curr);{запись в результирующий файл}
x_pred:=x_curr;{объявление текущего предыдущим для следующего шага}
read (F3, x_curr); {считывание следующего элемента серии}
if x_pred>x_curr then flag3:=true;{достигнут конец серии}
bf3:=x_curr {объявление нового буферного элемента в F3}
end
end;
{если серия в одном из файлов завершена считывание «хвоста»
незавершённой серии}
end;14.06.2025
462
463.
Теперь займемся организацией считывания «хвоста» незавершенной серии.Прежде всего нужно выяснить, сигнализирует ли индикатор flag2 или flag3 о переходе к другой серии в своём файле. Из того файла, в котором остались элементы текущей серии, их нужно переписать в результирующий файл. Количество
таких элементов неизвестно, поэтому нужно организовать цикл по их перебору.
В принципе этот цикл должен выполнять точно такие же действия, что и только
что рассмотренные циклы. Единственное отличие ― в нём не нужно выполнять
сравнение с буферным из другого файла.
if flag2 or eof(F2) then {конец серии или конец файла в F2}
while not flag3 and not eof(F3) do {выборка «хвоста» серии из F3}
begin
write(F1,x_curr);{запись в результирующий файл}
x_pred:=x_curr;{объявление текущего предыдущим для следующего шага}
read (F3, x_curr); {считывание следующего элемента серии}
if x_pred>x_curr then flag3:=true;{достигнут конец серии}
bf3:=x_curr {объявление нового буферного элемента в F3}
end;
14.06.2025
463
464.
Совершенно аналогично организуется считывание «хвоста» серии из другогофайла.
if flag3 or eof(F3) then {конец серии или конец файла в F3}
while not flag2 and not eof(F2) do {выборка «хвоста» серии из F2}
begin
write(F1,x_curr);{запись в результирующий файл}
x_pred:=x_curr;{объявление текущего предыдущим для следующего шага}
read (F2, x_curr); {считывание следующего элемента серии}
if x_pred>x_curr then flag2:=true;{достигнут конец серии}
bf2:=x_curr {объявление нового буферного элемента в F2}
end;
Цикл по слиянию серий реализован полностью. Осталось сформировать фрагмент процедуры, отвечающий за переписывание серий из того файла, в котором
они остались.
Оставшиеся серии нужно просто переписать в результирующий файл, поэтому
эти действия реализуются очень простыми циклами: нужно считывать текущий
элемент из файла и тут же записывать его в результирующий. Такие считывания/записи выполняются пока не будет достигнут конец соответствующего файла.
14.06.2025
464
465.
while not eof(F2) do begin {перенос хвоста файла F2} end;begin {перенос хвоста файла F2} end;
read(F2, x_curr); write(F1, x_xurr)
end;
while not eof(F3) do begin {перенос хвоста файла F3} end;
begin {перенос хвоста файла F3} end;
read(F3, x_curr); write(F1, x_xurr)
end;
close(F1); close(F2); close(F3);{Корректное завершение работы с файлами}
end;{конец процедуры Merge}
Данный фрагмент завершает процедуру, которая реализует операцию слияния
естественной сортировки.
14.06.2025
465
466.
Теперь займемся процедурой Split, реализующей операцию разделения.Как отмечалось выше, эта процедура также как и процедура Merge имеет три
формальных параметра: разделяемый файл F1 и два итоговых файла F2 и F3.
Кроме того, из определения естественной сортировки следует, что сортировка
заканчивается, когда в итоговом
файле окажется равно одна серия.
Следовательно, процедуре Split нужен ещё один выходной параметр L, который
возвращает количество обнаруженных серий в файле F1.
В начале процедуры разделения файла нужно подготовить файлы к работе:
файл F1 к считыванию, а файлы F2 и F3 к записи.
Разделение на серии выполняется в цикле, который выполняется до тех пор,
пока не будет обнаружен конец файла F1.
Перед циклом нужно инициализировать переменную L для подсчёта количества
серий.
Определение границ серий выполняется также, как в процедуре Merge с
помощью сравнения значений двух последовательных элементов x_curr и x_pred
файла F1. Поэтому перед циклом нужно инициализировать значение x_curr.
14.06.2025
466
467.
Предлагается в общем цикле по формированию серий в файле F1 реализоватьдва последовательных цикла записи двух соседних серий в разные файлы.
procedure Split (var F1, F2, F3:T_f_int; var L:integer);
{разделение файла F1 на файлы F2 и F3, L – количество серий в файле F1}
var x_curr, x_pred: integer; flag:boolean;
begin
reset(F1); rewrite(F2); rewrite(F3); {Подготовка файлов к работе}
if not eof(F1) then read (F1, x_curr); L:=0; {Инициализация цикла прохода по F1}
while not eof(F1) do {Цикла прохода по F1}
begin
{Формирование нечётной серии и запись в F3}
{Формирование чётной серии и запись в F2}
end;
close(F1); close(F2); close(F3); {Корректное завершение работы с файлами}
end;
14.06.2025
467
468.
Перед каждым циклом формирования очередной серии нужно инициализироватьиндикатор, сигнализирующий о переходе к новой серии (flag:=true).
Заметим, что в результате инициализации x_curr перед циклом первый элемент
первой серии при входе во внешний цикл уже окажется считанным и его нужно
записать в файл F3, увеличив при этом значение счетчика серий L.
Заметим также, что после обнаружения границы новой серии, когда окажется что
x_pred > x_curr, уже считанный текущий элемент x_curr принадлежит к новой серии и его нужно записывать в новый файл. При этом нужно увеличить на единицу
текущее значение L.
Следовательно, действия записи x_curr в «текущий» файл и увеличения L на
единицу должны предварять каждый цикл формирования серии.
Циклы формирования серий организуются
«хвосты» серий в Merge
14.06.2025
в точности также, как считывались
468
469.
Таким образом получена следующая структура цикла прохода по F1.while not eof(F1) do {Цикла прохода по F1}
begin
{Формирование нечётной серии и запись в F3}
write(F3, x_curr); L:=L+1; flag:=true; {Инициализация цикла }
while not flag and not eof(F1) do
begin
{Формирование текущей серии}
end;
if not eof(F1) then begin {Файл F1 ещё не пуст}
begin {Формирование чётной серии и запись в F2}
write(F2, x_curr); L:=L+1; flag:=true; {Инициализация цикла }
while not flag and not eof(F1) do
begin
{Формирование текущей серии}
end
end
end;
14.06.2025
469
470.
while not eof(F1) do {Цикла прохода по F1}begin
{Формирование нечётной серии и запись в F3}
write(F3, x_curr); L:=L+1; flag:=true; {Инициализация цикла }
while not flag and not eof(F1) do
begin
x_pred:=x_curr;{объявление текущего предыдущим для следующего шага}
read (F1, x_curr); {считывание следующего элемента серии}
if x_pred>x_curr then flag:=true {достигнут конец серии}
else {принадлежит текущей серии, запись в текущий файл}write(F3, x_curr);
end;
if not eof(F1) then begin {Файл F1 ещё не пуст}
begin {Формирование чётной серии и запись в F2}
write(F2, x_curr); L:=L+1; flag:=true; {Инициализация цикла }
while not flag and not eof(F1) do
begin
x_pred:=x_curr;{объявление тек. предыдущим для следующего шага}
read (F1, x_curr); {считывание следующего элемента серии}
if x_pred>x_curr then flag:=true {достигнут конец серии}
else {принад. текущей серии, запись в текущий файл}write(F2, x_curr);
end
14.06.2025
470
end
end;
471.
Теперь уже реализация процедуры естественной сортировки не вызывает никакихтрудностей.
procedure NatureSort (var F1:T_f_Int);
{Естественная сортировка файла F1}
var F2,F3:T_f_Int; L:integer;
begin
Split(F1, F2, F3, L) {Первое разделение F1}
while L>1 do {Цикл разделений/слияний}
begin
Merge(F1, F2, F3) {Текущее слияние}
Split(F1, F2, F3, L) {Текущее разделение}
end
end;
14.06.2025
471
472. ХЕШ-ТАБЛИЦЫ
Хеш-таблица является обобщением обычного массива. Возможность прямойиндексации элементов обычного массива обеспечивает доступ к произвольной
позиции в массиве за время О(1). Она применима, если можно выделить
массив, размер которого достаточен чтобы для каждого значения ключа
(индекса) имелось место в оперативной памяти
для соответствующего
элемента массива.
Однако в большинстве реальных задач количество возможных записей (строк в
таблице) много меньше, чем количество возможных ключей. Так, если в
качестве ключа используется фамилия, то, даже ограничив длину ключа 10
символами кириллицы, получаем 3310 = 1 531 578 985 264 449 возможных
значений ключа. Даже если ресурсы вычислительной системы и позволят
выделить пространство записей такого размера, то значительная часть этого
пространства будет пустовать, так как в каждом конкретном заполнении
таблицы фактическое используемое множество ключей не будет полностью
покрывать пространство ключей.
14.06.2025
472
473.
В таких случаях эффективной альтернативой массиву с прямой индексацией становитсяхеш-таблица, которая обычно использует массив с размером, пропорциональным
количеству реально хранящихся в нем элементов.
Основная идея: вместо непосредственного использования ключа в качестве
индекса элемента массива (индекс совпадает с ключом) , индекс вычисляется по
значению ключа с помощью специально подобранной хеш-функции.
При этом область значений функции выбирается значительно уже (меньше)
области изменения ключа (аргумента). Такой приём с математических позиций
называется сжимающим отображением.
Cлово хеш происходит от английского «hash», одно из значений которого трактуется как
путаница или мешанина. Это значение довольно точно описывает фактический смысл
этого термина. Применяется ещё и термин «хеширование», который является
производным от английского hashing (рубить, крошить, спутывать и т.п.).
14.06.2025
473
474.
Формально хеш-таблица представляет собой структуру данных, которая реализуетинтерфейс ассоциативного массива: она обеспечивает возможность хранить пары
(ключ, значение) и выполнять над ними три операции: операцию добавления новой
пары, операцию удаления и операцию поиска пары по ключу. Ассоциативные массивы
также называют словарями.
Поскольку значения ключей часто оказываются близкими, хорошие хеш-функции
распределяют их таким образом, чтобы они занимали различные строки в таблице
(соответствовали различным элементам массива).
14.06.2025
474
475.
В общем случае хеш-таблица реализуется с помощью массива H, элементы которогоявляются строками хеш-таблицы. Каждый элемент массива представляет собой пару
ключ-значение (хеш-таблица с открытой адресацией) или список таких пар (хеш-таблица
со списками). Второй случай имеет место когда хеш-функция возвращает одно и то же
значение индекса для разных ключей.
14.06.2025
475
476.
Выполнение операции в хеш-таблице начинается с вычисления хеш-функции отключа. Получающееся хеш-значение i=hash(key) играет роль индекса в массиве H.
Затем выполняемая операция (добавление, удаление или поиск) перенаправляется
объекту, который хранится в соответствующем элементе массива H[i].
Основное свойство хеш-таблиц.
Основные операции с таблицей (добавление, удаление, поиск элемента) в
среднем выполняются за время O(1). Но при этом не гарантируется, что время
выполнения отдельной операции мало.
В среднем
В худшем
Память
О(N)
О(N)
Поиск
O(1)
О(N)
Вставка
O(1)
О(N)
Удаление
O(1)
О(N)
Теоретически хеш-таблицы эффективнее дерева, а дерево, в свою очередь, эффективнее
линейного списка.
14.06.2025
476
477.
Ситуация, когда для различных ключей получается одно и то же хеш-значение,называется коллизией. Например, при вставке в хеш-таблицу размером 365 строк
всего лишь 23 элементов вероятность коллизии уже превысит 50%. Поэтому
механизм разрешения коллизий — важная составляющая построения любой хештаблицы.
Количество элементов, фактически записанных в таблицу, делённое на размер
массива H (количество возможных значений хеш-функции), называется
коэффициентом заполнения хеш-таблицы.
Коэффициент заполнения хеш-таблицы показывает, насколько она загружена
записями. Этот показатель влияет на вероятность возникновения коллизий.
Вероятность коллизий выше, если таблица заполнена на 95%, по сравнению с
заполненностью на 10%.
14.06.2025
477
478.
Со временем хеш-таблица может полностью заполниться или стать настолькополной, что коллизии будут очень вероятны, что скажется на производительности.
В этом случае нужно усовершенствовать алгоритм, чтобы определить, когда и как
изменять размер хеш-таблицы, и увеличить ее.
В некоторых ситуациях может потребоваться уменьшить таблицу, чтобы освободить
неиспользуемое пространство, например, если она рассчитана на 1 миллион записей, а их
только 10.
Самый простой способ изменить размеры хеш-таблицы — это создать новую
таблицу нужного размера и рехешировать (переписать) все элементы из исходной
структуры в новую
Таким образом, для построения хеш-таблицы необходимы:
структура для хранения данных;
хеш-функция для сопоставления ключей с элементами структуры данных;
политика разрешения коллизий, которая определяет, что делать в случае
конфликта ключей.
14.06.2025
478
479.
Ключ в хеш-таблице представляет собой объект произвольной природы, которыйимеет смысл обозначения, служащего для поиска требуемых данных в этой
таблице. Обычно с программной точки зрения ключ это имя, идентификатор для
которого может быть выбран любой тип данных.
Варианты ключей.
Строка фиксированной или произвольной длины.
Целые или вещественные числа. Используются как ключи в случаях, когда
данные могут быть естественным образом индексированы числами;
Сложные структуры данных, которые имеют вид
(экземпляры классов).
объектов программы
Графические объекты (рисунки, фотографии и т.д.).
Хеш-таблица обеспечивает хранение значений, доступ к которым осуществляется
через ключи. Значения также могут быть любого типа, что и обеспечивает
высокую гибкость хеш-таблицы. В общем случае считается, что значение хешфункции представляет собой битовую строку.
14.06.2025
479
480.
Хэш-функцииХеш-функция представляет собой отображение множества ключей в множество
индексов массива, который используется для представления хеш-таблицы.
Другими словами, аргументом хеш-функция является ключ, а значением —
индекс (часто говорят «хеш») в массиве, где хранятся значения.
С математической точки зрения хеш-функция есть отображение из N в N.
Основные свойства хеш-функции:
Детерминированность. При одном и том же входном ключе должно
возвращаться одно и то же хеш-значение.
Быстродействие. Хеш-функция должна обеспечивать константную сложность
O(1) вычисления её значений.
Равномерность распределения ключей
минимизации вероятности коллизий.
14.06.2025
по
массиву.
Необходима
480
для
481.
Способы построения обычных хеш-функций.Очевидно, что количество различных хеш-функций как отображений из N в N
счётно. Однако необходимость обеспечить им требуемые свойства
существенно ограничивает практически применимые варианты.
Чтобы обеспечить высокую эффективность вычисления значений хеш-функций,
они формируются с помощью высокоскоростных операций процессора, таких
как сдвиги, логические операции отрицания, дизъюнкции, конъюнкции и т.д.
Пример примитивной хеш-функции.
int h(const char *key)
{return int(key[0]);}
В этом варианте построения хеш-функции ключи представляют собой строки
символов. Значение получается преобразованием первого символа ключа в целое
число, которое рассматривается как индекс в хеш-таблице.
h("Anna")=65
h(«Ivan")=73
h("Andrey")=65
14.06.2025
481
482.
Более сложные варианты.int h(const char *key)
{return int(key[0]+key[1]);}
int h(const char *key)
{return int((key[0]+key[7])%2);}
Во всех этих вариантах весьма высока вероятность коллизий уже по самому
способу построения функции.
Стандартные способы построения хеш-функций.
Пусть K — количество ключей; k — любой ключ; h(k) — хеш-функция, имеющая
не более M различных значений, ∀k∈[0;K):h(k)<M.
Метод деления: h(k)= k mod M.
int h(int key, int m)
{return key%m;}
14.06.2025
482
483.
Не следует использовать в качестве M степень основания системы счисления, так как хешзначение будет зависеть только от нескольких последних цифр числа, что приведёт к
большому количеству коллизий.
На практике в качестве M обычно выбирают простое число; в большинстве
случаев этот выбор вполне удовлетворителен.
A
h
(
k
)
M
Метод умножения
w k
где: w — машинное слово процессора, то есть максимально возможное для
данного компьютера беззнаковое целое, A — взаимно простое с w целое.
Хеш функции, получаемые по методам деления и умножения эффективны, но не
исключают появления коллизий и не надёжны с точки зрения получения
прообраза. В криптографии применяются более сложные алгоритмы.
14.06.2025
483
484.
Способы разрешение коллизийС теоретической точки зрения появление коллизий в хеш-таблицах
принципиально неизбежно. Это вытекает из самой сути сжимающего
отображения, когда область значений «уже» области определения.
Существует два основных способа построения хеш-таблиц метод цепочек и
открытая адресация, которые обеспечивают разрешение коллизий. Выбор
способа существенно зависит от решаемой задачи.
Метод цепочек. Элементы хеш-таблицы представляют собой линейные списки пар
«ключ-значение». Чтобы найти нужный элемент, необходимо хешировать ключ и
определить, в каком из списков он может содержаться, а затем двигаться по линейному
списку до тех пор, пока не будет достигнут его конец или не обнаружится искомый
элемент.
Чтобы включить элемент в хеш-таблицу, его нужно вначале соотнести со списком с
помощью функции хеширования, а затем вставить новую элемент в начало списка. Каждая
из операций имеет сложность О(1). По определению хеш-таблица не должна содержать
дублированных значений. Если в ней B списков и всего N элементов, которые
распределены достаточно равномерно, то каждый список включает приблизительно N/B
элементов. Таким образом, чтобы проверить, присутствует ли элемент в списке,
понадобится O(N/B) шагов. Это значит, что сложность включения элемента в хеш-таблицу
O(1) + O(N/B) = O(N/B) .
14.06.2025
484
485.
Поиск ключей в хеш-таблице проходит быстрее, если списки содержат ключи вотсортированном порядке. В этом случае
при наличии ключа в списке он не
просматривается до конца. Теоретически сложность составит O(N/B).
Удалить элемент из хеш-таблицы в методе цепочек также несложно: требуется хешировать
ключ элемента, чтобы найти нужный список, и выполнить удаление в связном списке.
Сложность хеширования O(1) непосредственно удаления — O(N/B). Таким образом, общая
сложность также O(N/B).
Хеш-таблица в методе цепочек может расширяться и сжиматься по мере необходимости,
поэтому не нужно специально изменять ее размер. Однако если списки станут слишком
длинными, поиск и удаление элементов займут много времени. В этом случае лучше
увеличить таблицу, чтобы создать больше списков. Поскольку при рехешировании таблицы
не надо проводить поиск дубликатов до конца каждого списка, полностью справиться с
операцией можно за время O(N).
14.06.2025
485
486.
Метод цепочек является хорошим способом разрешения коллизий, но он требуетдополнительных затрат памяти на хранение структуры линейных списков. Если записи
малы (например, целые числа), то затраты памяти сопоставимы с размером самих данных.
Чтобы сократить временные затраты, число списков можно увеличить, но тогда возникает
риск получить ряд пустых списков, которые потребуют места в памяти и не будут
использоваться таблицей.
Когда хеш-таблица основана на применении открытой адресации, все пары ключ-значение
хранятся в самой хеш-таблице, и дополнительная структура данных не нужна.
В разных видах открытой адресации используются различные функции хеширования.
Неодинакова и политика разрешения коллизий, но в общем случае для каждого значения в
массиве подбирается несколько элементов, и если первый уже занят, алгоритм пробует
использовать второй, затем третий и так до тех пор, пока не будет найден свободный
элемент или не будет сделан вывод, что такого элемента нет.
Группа элементов массива, которая перебирается для записи значения, называется
пробной последовательностью. По ее средней длине хорошо оценивать наполненность
хеш-таблицы. В идеале пробная последовательность должна равняться 1 или 2, большие
значения говорят о заполненной таблице.
14.06.2025
486
487.
В массиве H хранятся сами пары ключ-значение. При вставке новой парыэлементы H проверяются в некотором порядке до тех пор, пока не будет найден
первый свободный элемент, в которую записывается это пара.
Последовательность, в которой просматриваются строки хеш-таблицы, это и есть
последовательностью проб. В общем случае, она зависит только от ключа
элемента — это последовательность h0(x), h1(x), …, hn — 1(x), где x — ключ,
а hi(x) — произвольные функции, сопоставляющие каждому ключу строку в хештаблице.
Для успешной работы алгоритмов поиска последовательность проб должна быть
такой, чтобы все строки хеш-таблицы оказались просмотренными ровно по одному
разу.
Алгоритм поиска просматривает строки хеш-таблицы в том же самом порядке, что
и при вставке, до тех пор, пока не найдется либо элемент с искомым ключом, либо
свободная строка , что означает отсутствие элемента в хеш-таблице.
14.06.2025
487
488.
Организовать удаление элементов из такой таблицы немного сложнее. Обычно длявыполнения этой операции каждой строке таблицы сопоставляется индикатор занятости:
логическая переменная имеющая соответствующий смысл. В этом случае удаление
элемента состоит в установке этого индикатора для соответствующей строки хеш-таблицы.
Но в этом случае необходимо модифицировать процедуру поиска существующего элемента
так, чтобы она считала удалённые строки занятыми, а процедуру включения — чтобы она
их считала свободными и сбрасывала значение индикатора при включении.
Типовые способы построения последовательности проб.
Линейное пробирование. Строки хеш-таблицы последовательно просматриваются с
некоторым фиксированным интервалом k между ячейками (обычно k = 1), то есть i-й
элемент последовательности проб — это строка с номером (hash(x) + ik) mod N. Для того,
чтобы все строки оказались просмотренными по одному разу, необходимо,
чтобы k было взаимно простым с размером хеш-таблицы.
Предположим, а хеш-функция определена следующим образом: h(key)=key mod 100. Тогда
линейная пробная последовательность для значения key=3796 проверяет строки 96, 97, 98,
99, 0, 1, 2 и т. д.
14.06.2025
488
489.
Преимущество данного метода в его простоте. Если необходимо, пробнаяпоследовательность пройдет по каждой строке таблицы и вставит элемент в свободное место, если оно еще осталось.
Но есть и недостаток, который принято называть первичной кластеризацией, проявляющийся в образовании больших групп смежных элементов, что приводит к длинным
пробным последовательностям. В результате при добавлении нового элемента и его
хешировании пробная последовательность вынуждена пройти через весь кластер, чтобы
найти свободную ячейку.
Квадратичное пробирование. Для создания пробной последовательности в качестве шага
по индексу берется квадрат количества строк. Другими словами, если в линейном
пробировании выбирается последовательность K, K + 1, K + 2, K + 3, ... то в квадратичном
варианте она так: K, K + 12, K + 22, K + 32, ...
Двойное хеширование. Интервал между строками фиксирован, как при линейном
пробировании, но, его размер вычисляется с помощью второй, вспомогательной хешфункцией, а значит, может быть различным для разных ключей. Значения этой хешфункции должны быть ненулевыми и взаимно-простыми с размером хеш-таблицы.
14.06.2025
489
490.
Хотя двойное хеширование эффективно справляется с кластеризациями, оно можетпропускать неиспользуемые записи.
14.06.2025
490
491.
Примеры применения хеш-таблиц и хеширования.Реализация высокоуровневых структур данных в алгоритмических языках.
Хеш-таблицы лежат в основе структур данных, таких как хеш-карты в Java
(HashMap) и словари в Python и C++. Обеспечивают эффективное хранение пар
ключ-значение и быстрый доступ к значениям по их ключам.
Структура данных set в Python и C++ использует хеш-таблицы для хранения
уникальных элементов и обеспечивает эффективные операции проверки
принадлежности элемента множеству
Кеширование в информационных системах.
Хеш-таблицы используются для реализации кешей, таких как LRU-кеш (Least
Recently Used). Кеш обеспечивает возможность быстро находить и обновлять
данные, что ускоряет доступ к часто используемым элементам.
Web-кеширование. Различные серверы используют хеш-таблицы для
кеширования результатов запросов, что уменьшает нагрузку на сервер и
ускоряет обработку запросов.
14.06.2025
491
492.
Обработка текста и анализ данных.Хеш-таблицы применяются для построения обратных индексов в системах поиска и
анализа текстов, что позволяет быстро находить документы, содержащие
определенные слова или фразы.
В задачах анализа данных хеш-таблицы помогают эффективно собирать и
агрегировать статистические данные, такие как частота появления элементов в
больших наборах данных.
Сетевые приложения.
Таблицы маршрутизации. В сетевых протоколах хеш-таблицы используются для
хранения маршрутов и быстрых операций поиска оптимальных путей для передачи
данных.
Кеширование DNS. Сервисы доменных имен (DNS) используют хеш-таблицы для
кеширования результатов запросов, что ускоряет процесс разрешения доменных имен в
IP-адресах.
14.06.2025
492
493.
Системы управления базами данных.Хеш-таблицы используются для создания индексов в базах данных, а также для
организации данных на дисковых носителях, что значительно ускоряет операции поиска и
выборки данных. Индексы помогают быстро находить записи по заданным значениям
ключей.
Компиляторы.
Компиляторы используют хеш-таблицы для хранения информации в таблицах
символов об именах переменных, констант, функций и об других элементах программы.
Это позволяет быстро находить и проверять их свойства и значения во время
компиляции.
При оптимизации кода компиляторы могут использовать
кеширования промежуточных результатов вычислений.
Хеш-таблицы могут использоваться для управления свободными блоками памяти в
системах управления памятью. Они помогают быстро находить и выделять свободные
блоки нужного размера.
В языках программирования с автоматическим управлением памятью, таких как Java
или C#, хеш-таблицы используются для отслеживания объектов и управления их
жизненным циклом.
14.06.2025
хеш-таблицы
493
для
494.
Криптография.Криптография (от др.-греч. κρυπτός «скрытый» + γράφω «пишу») — наука о
математических методах обеспечения конфиденциальности, целостности данных,
об аутентификации и шифровании.
Криптографические хеш-функции — это выделенный класс хеш-функций, которые
имеют определённые свойства, делающие их пригодными для использования
в криптографии. При разработке современного российского стандарта
ГОСТ Р 34.11-201 были сформулированы все требования к криптографическим
хеш-функциям, которые обеспечивают им необходимые свойства.
Идеальной криптографической хеш-функция является такая криптографическая
хеш-функция, которая обладает следующими пятью основными свойствами:
14.06.2025
494
495.
Детерминированность. При одинаковых входных данных результатвычисления хеш-функции будет одинаковым (одно и то же сообщение всегда
приводит к одному и тому же хешу).
Уникальность. Различные входные данные должны приводить к различным
хеш-кодам. Минимальная вероятность коллизий.
Лавинный эффект. Небольшое изменение в сообщениях должно очень
сильно изменить хеш-значения.
Необратимость. Невозможность сгенерировать исходные данные (сообщение)
из хеш-значения, за исключением полного перебора всех возможных
вариантов.
Эффективность. Высокая скорость вычисления значения хеш-функции для
любого заданного сообщения.
Идеальная криптографическая хеш-функция с длиной аргумента n бит для
вычисления прообраза (ключа, аргумента) требует как минимум 2n операций.
14.06.2025
495
496.
В настоящее время чаще всего применяются хеш-функции (алгоритмы) семействMD — Message Digest (MD5), SHA Secure Hash Algorithm (SHA 256) и ГОСТ
Р 34.11-2012 (Стрибог).
Примеры применения хеш-функций семейства SHA.
Результаты хеширования символа пробел:
14.06.2025
496
497.
Пример лавинного эффекта, когда малое изменение сообщения "The quick brownfox jumps over the lazy dog" приводит к значительным изменениям в значении
хеш-функции.
SHA3-224("The quick brown fox jumps over the lazy dog")
d15dadceaa4d5d7bb3b48f446421d542e08ad8887305e28d58335795
SHA3-224("The quick brown fox jumps over the lazy dog.")
2d0708903833afabdd232a20201176e8b58c5be8a6fe74265ac54db0
SHA3-256("The quick brown fox jumps over the lazy dog")
69070dda01975c8c120c3aada1b282394e7f032fa9cf32f4cb2259a0897dfc04
SHA3-256("The quick brown fox jumps over the lazy dog.")
a80f839cd4f83f6c3dafc87feae470045e4eb0d366397d5c6ce34ba1739f734d
14.06.2025
497
498.
SHA3-384("The quick brown fox jumps over the lazy dog")7063465e08a93bce31cd89d2e3ca8f602498696e253592ed26f07bf7e703cf328581e1471
a7ba7ab119b1a9ebdf8be41
SHA3-384("The quick brown fox jumps over the lazy dog.")
1a34d81695b622df178bc74df7124fe12fac0f64ba5250b78b99c1273d4b080168e106528
94ecad5f1f4d5b965437fb9
SHA3-512("The quick brown fox jumps over the lazy dog")
01dedd5de4ef14642445ba5f5b97c15e47b9ad931326e4b0727cd94cefc44fff23f07bf54
3139939b49128caf436dc1bdee54fcb24023a08d9403f9b4bf0d450
SHA3-512("The quick brown fox jumps over the lazy dog.")
18f4f4bd419603f95538837003d9d254c26c23765565162247483f65c50303597bc9ce4
d289f21d1c2f1f458828e33dc442100331b35e7eb031b5d38ba6460f8
14.06.2025
498
499.
14.06.2025499
500.
УСПЕХОВ НА ЭКЗАМЕНАХ!14.06.2025
500






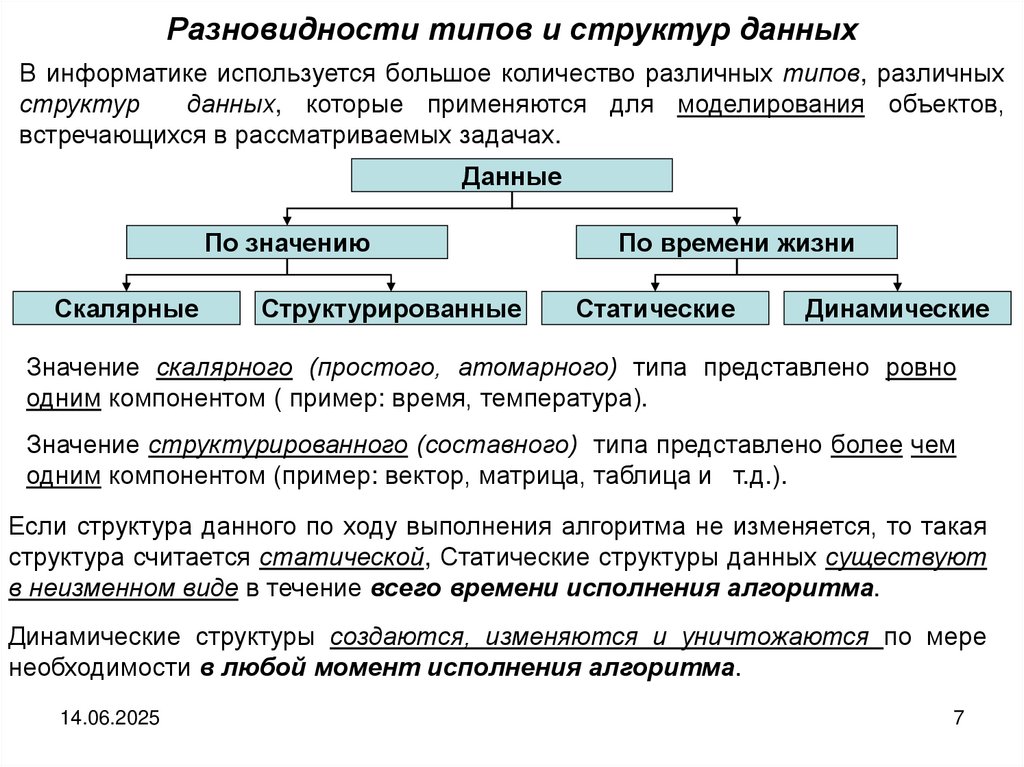



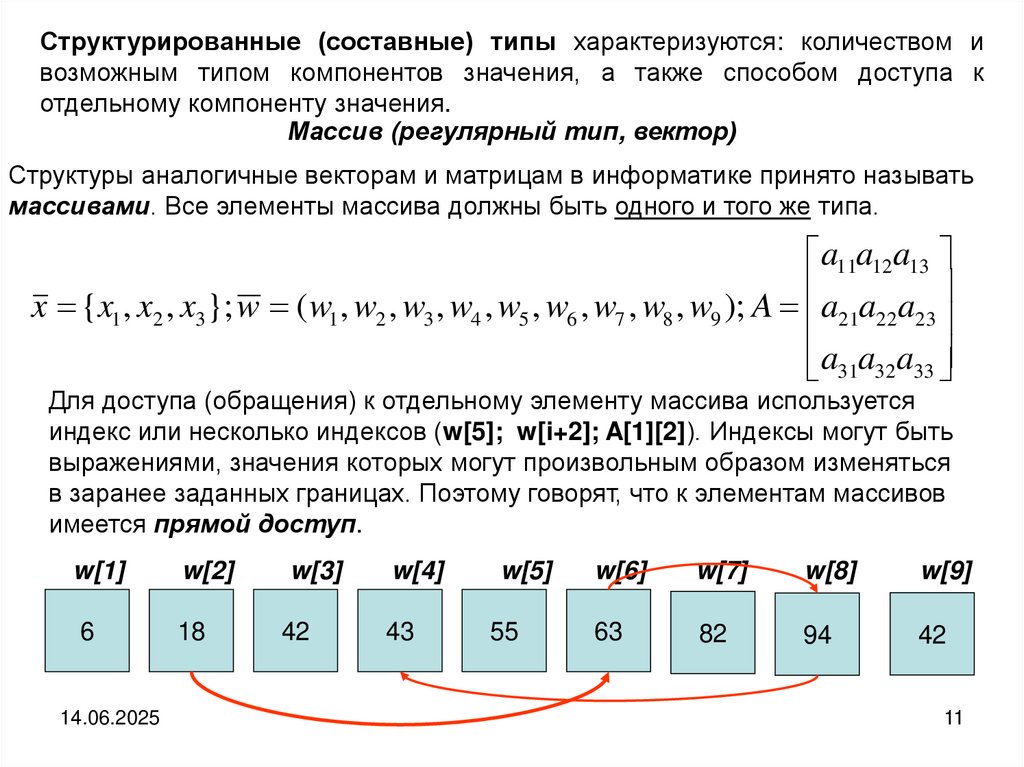
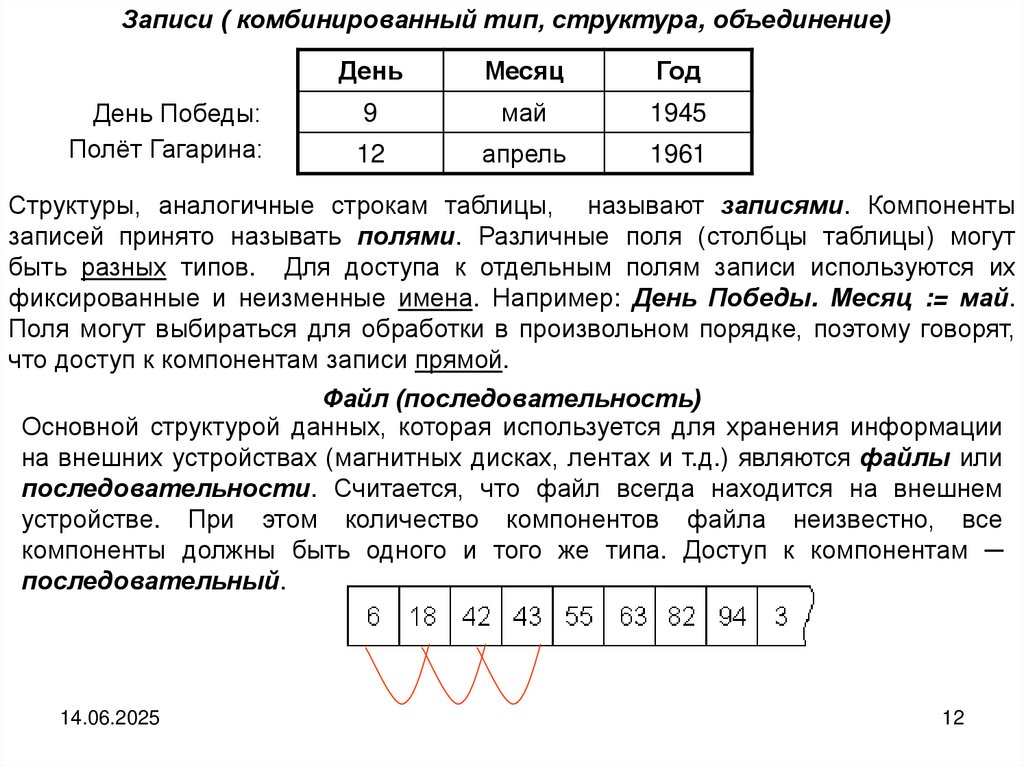
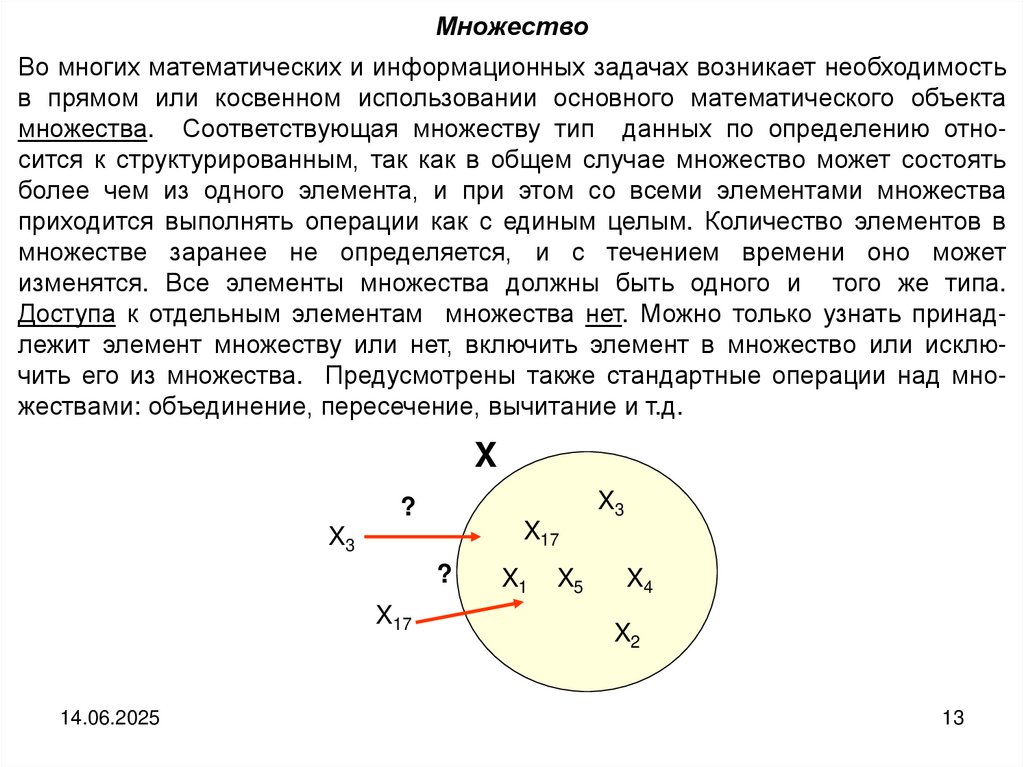

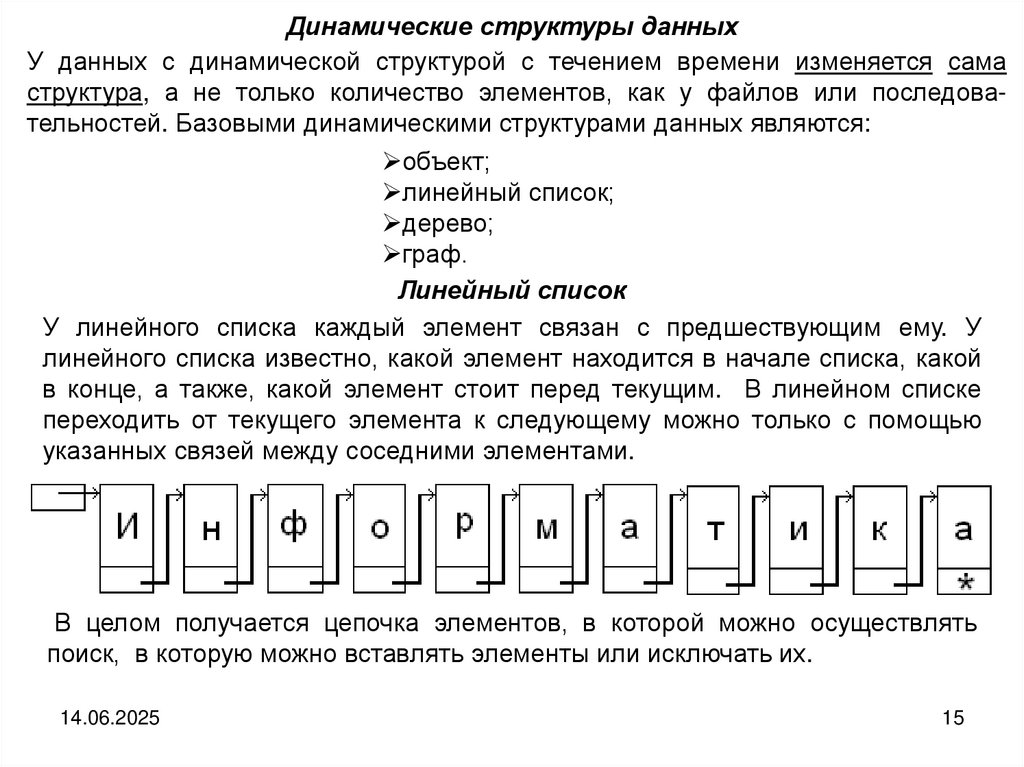
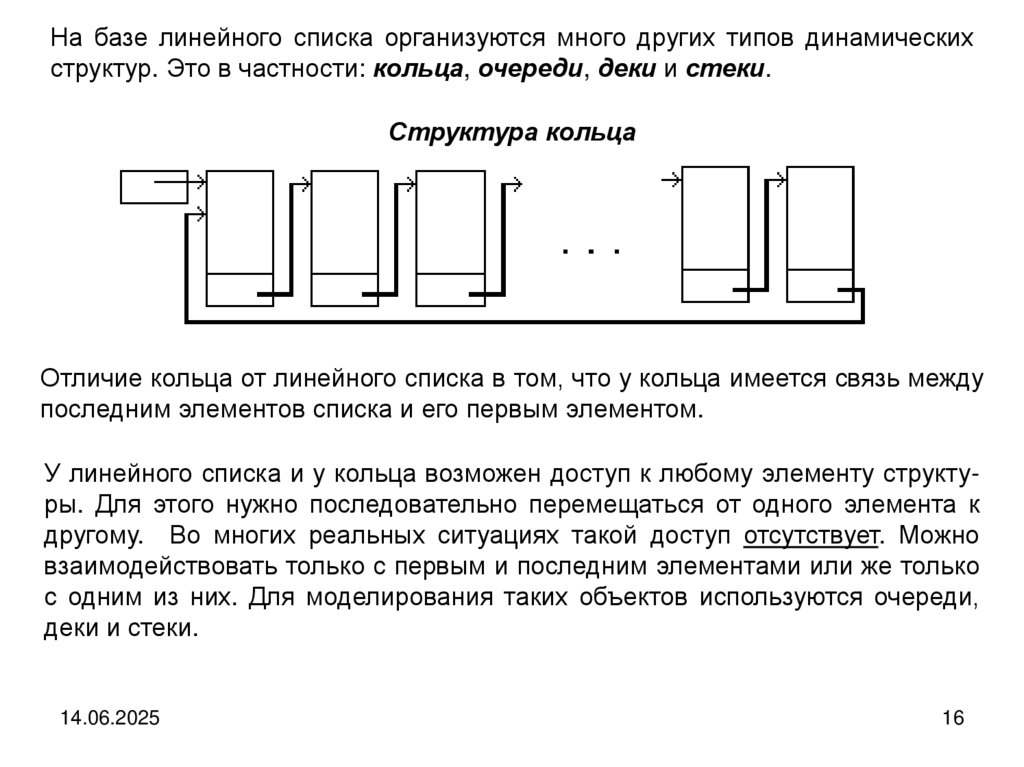
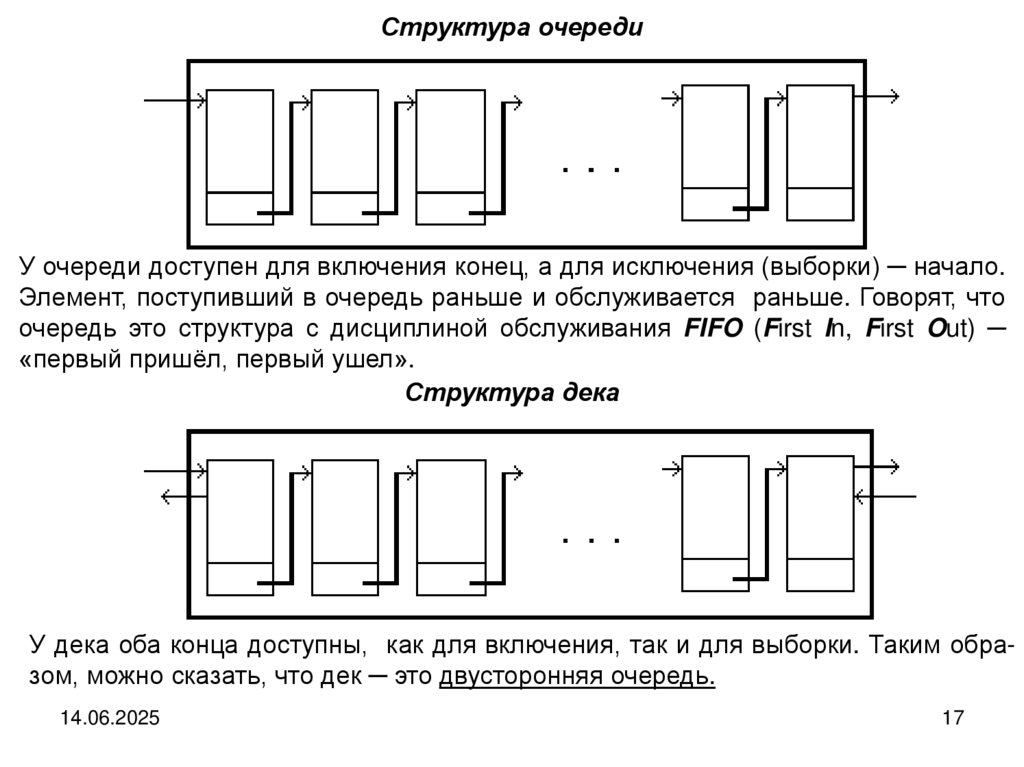
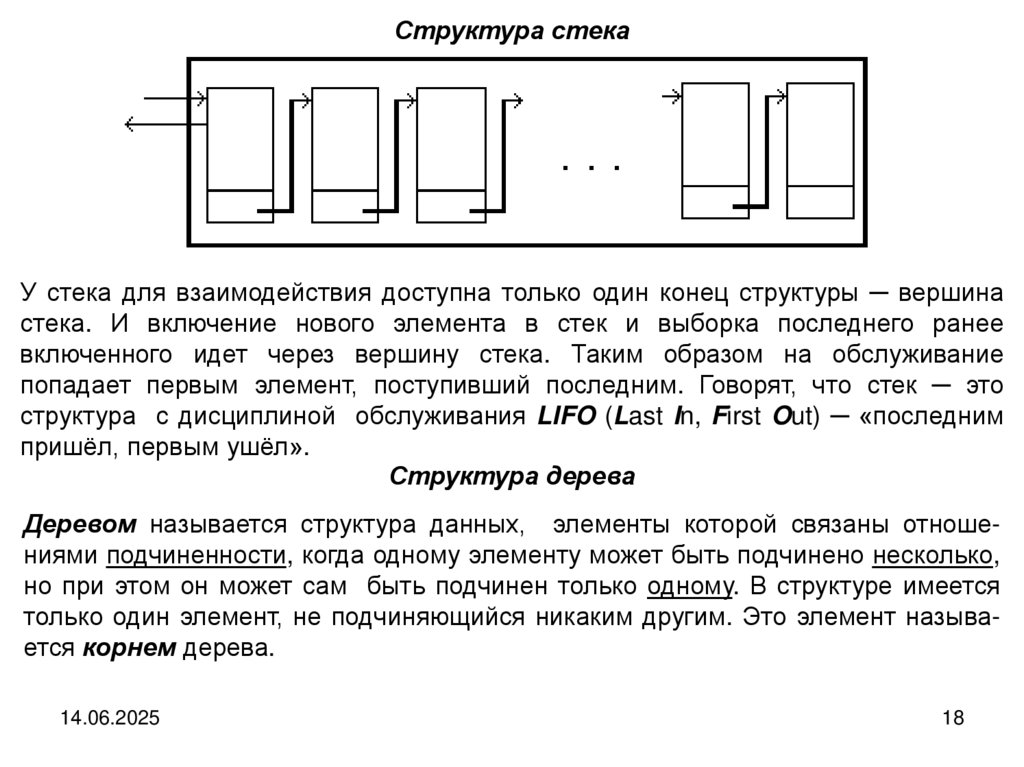
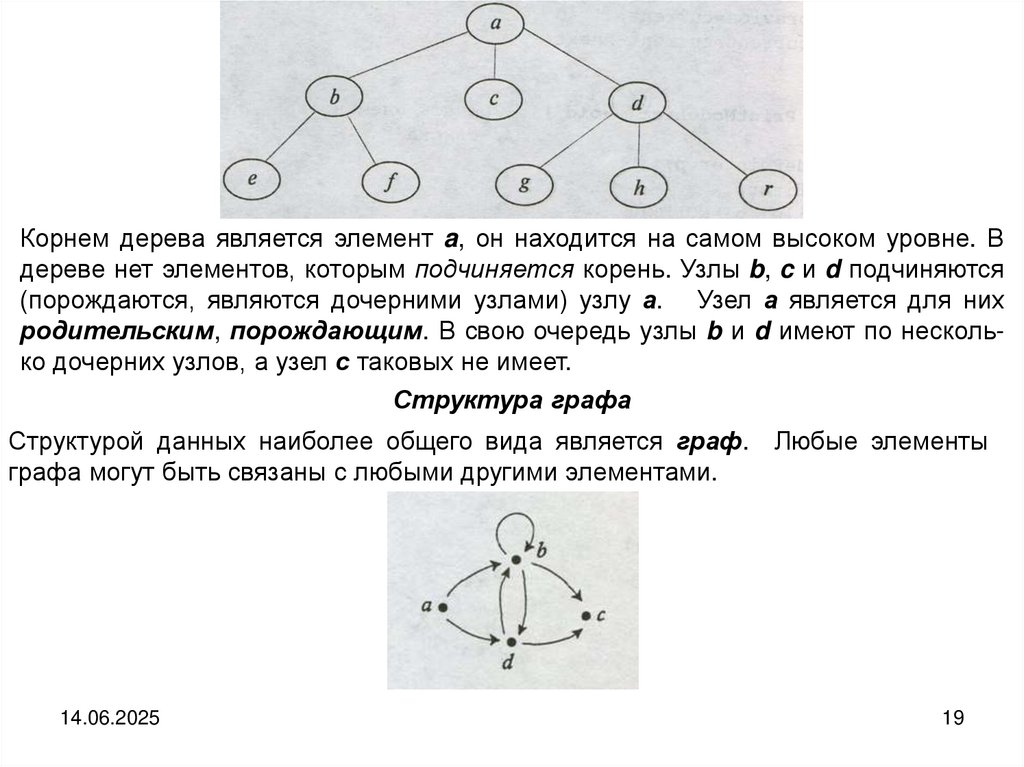

















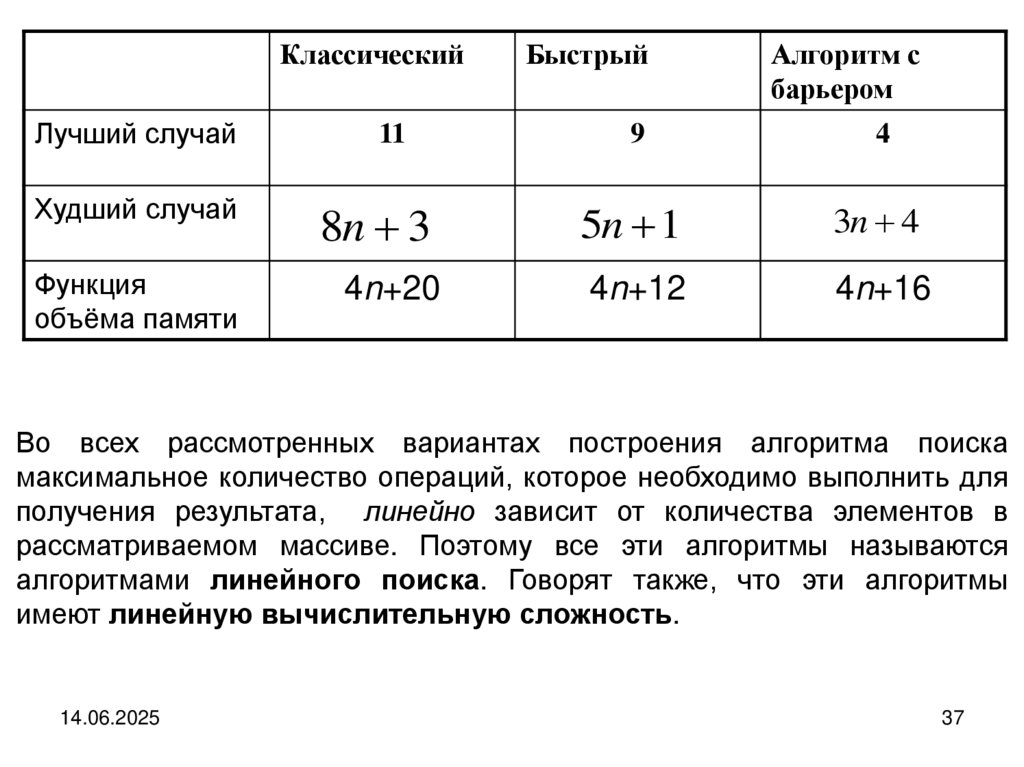













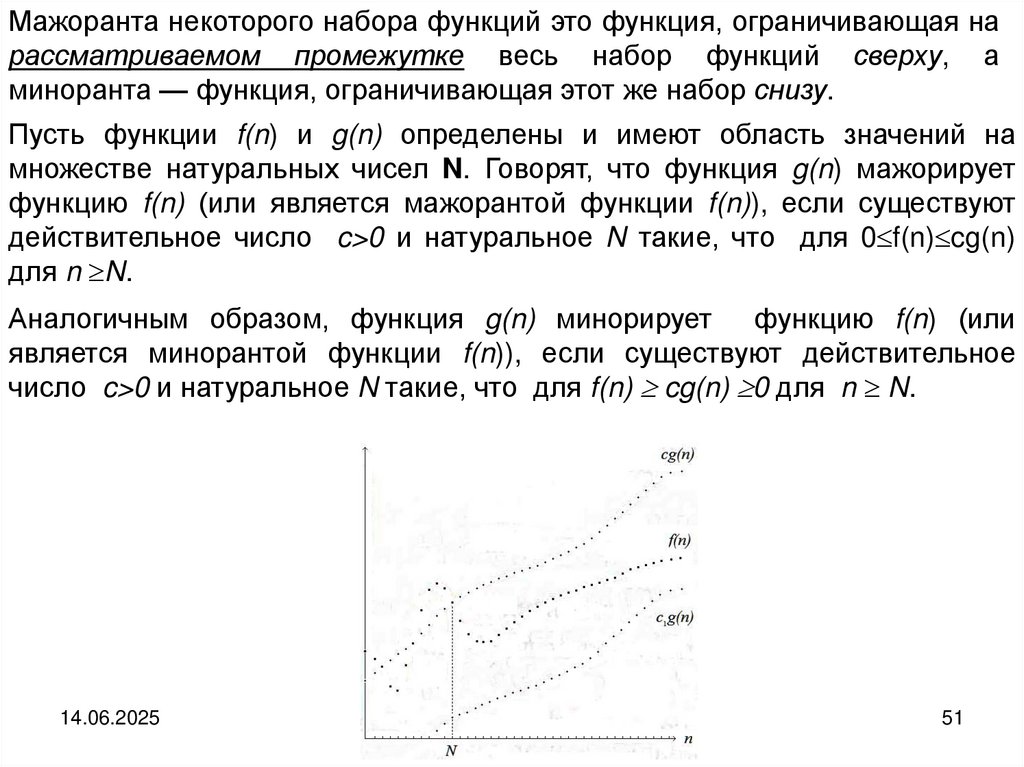






















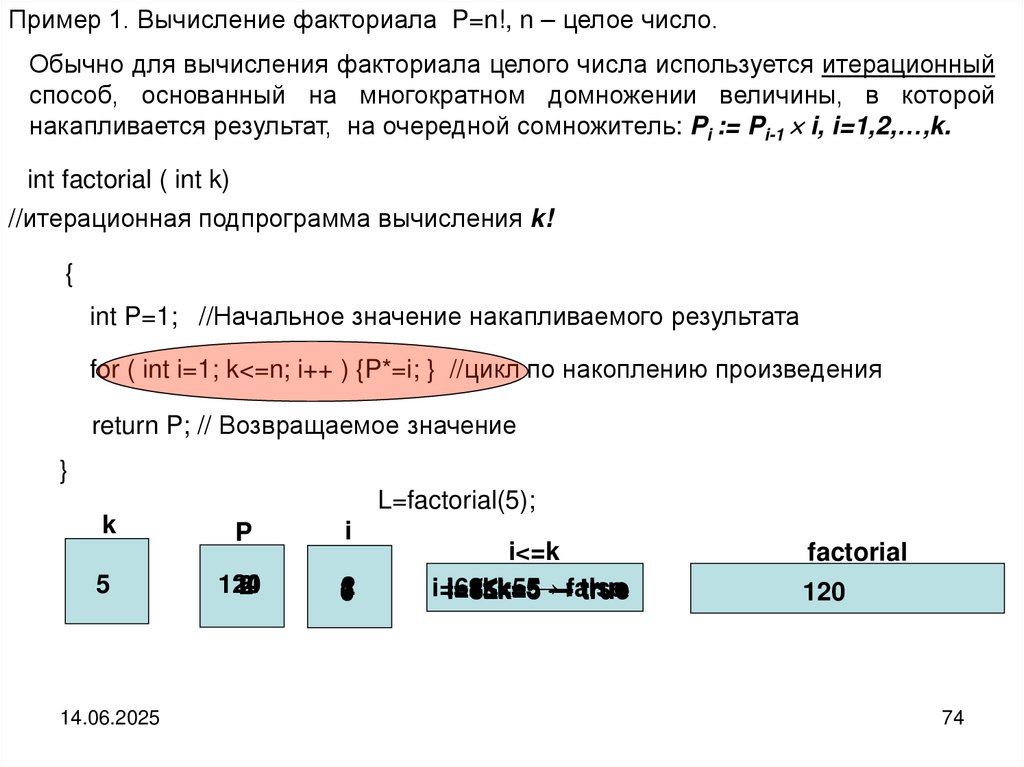



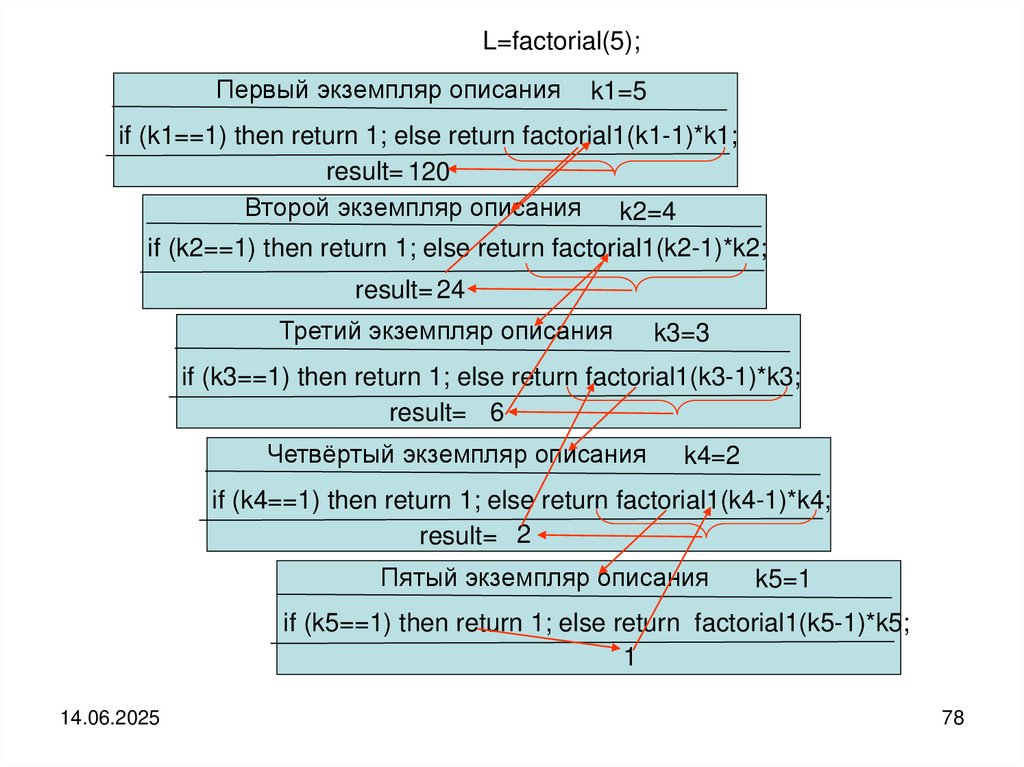







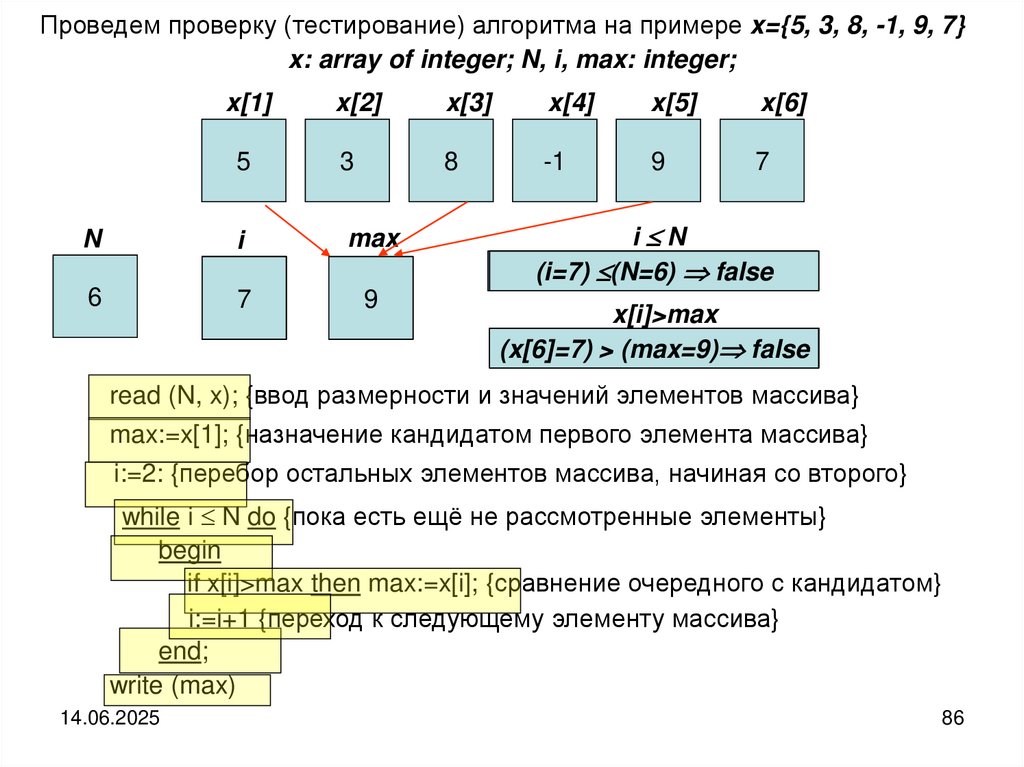







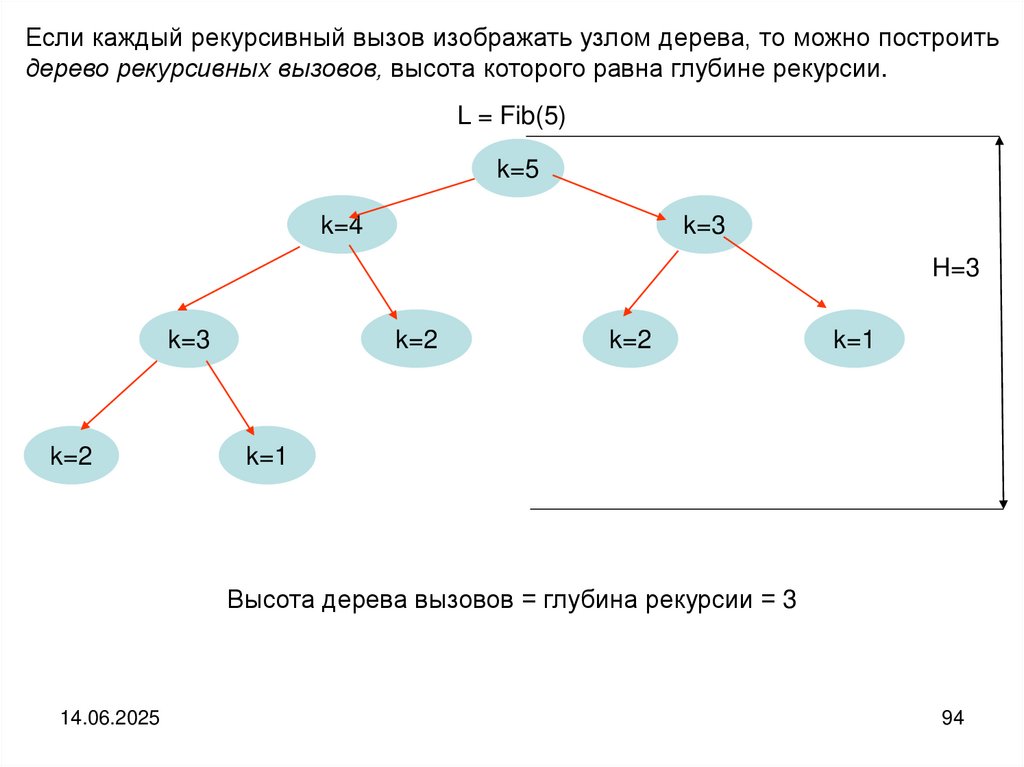


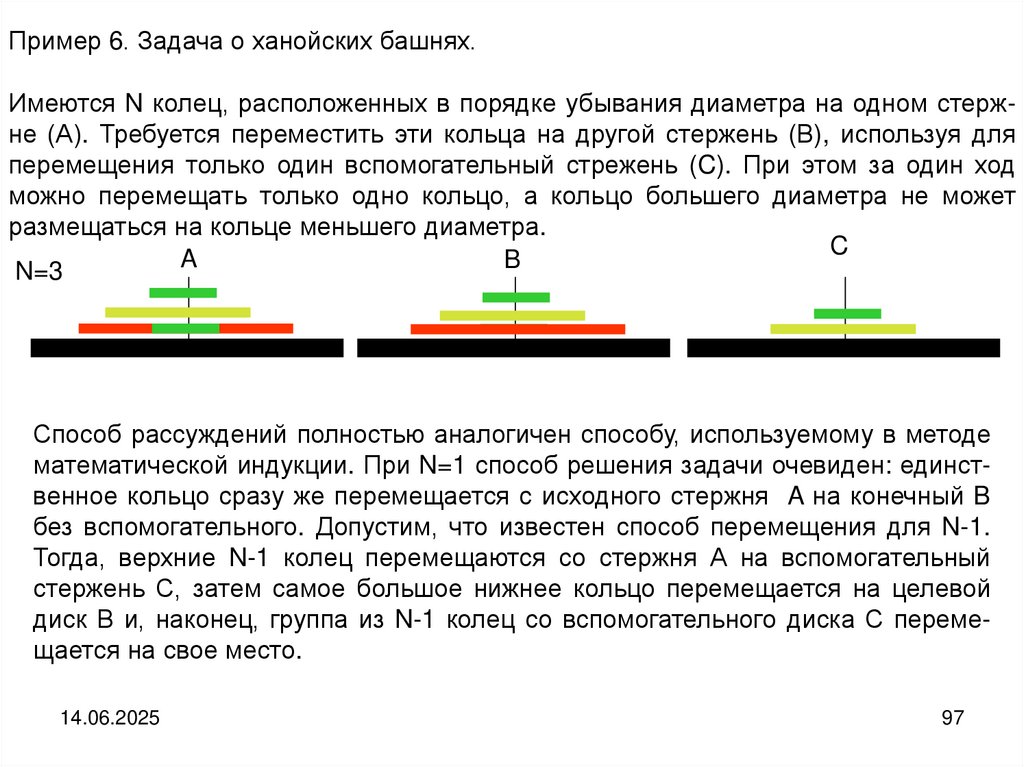
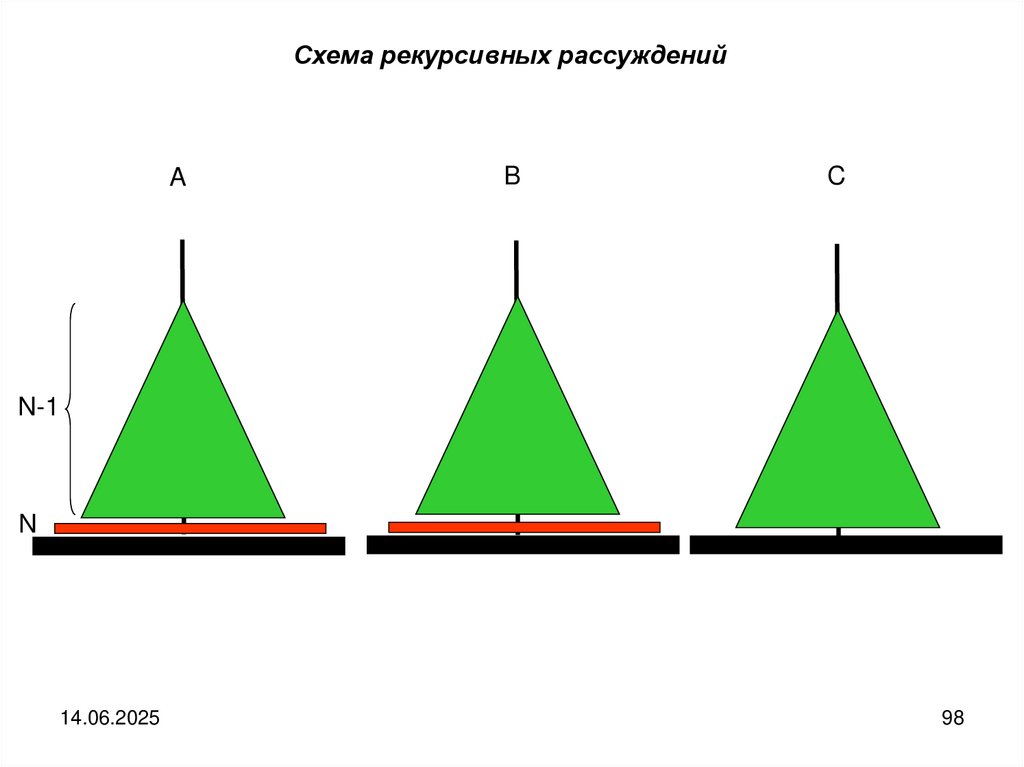













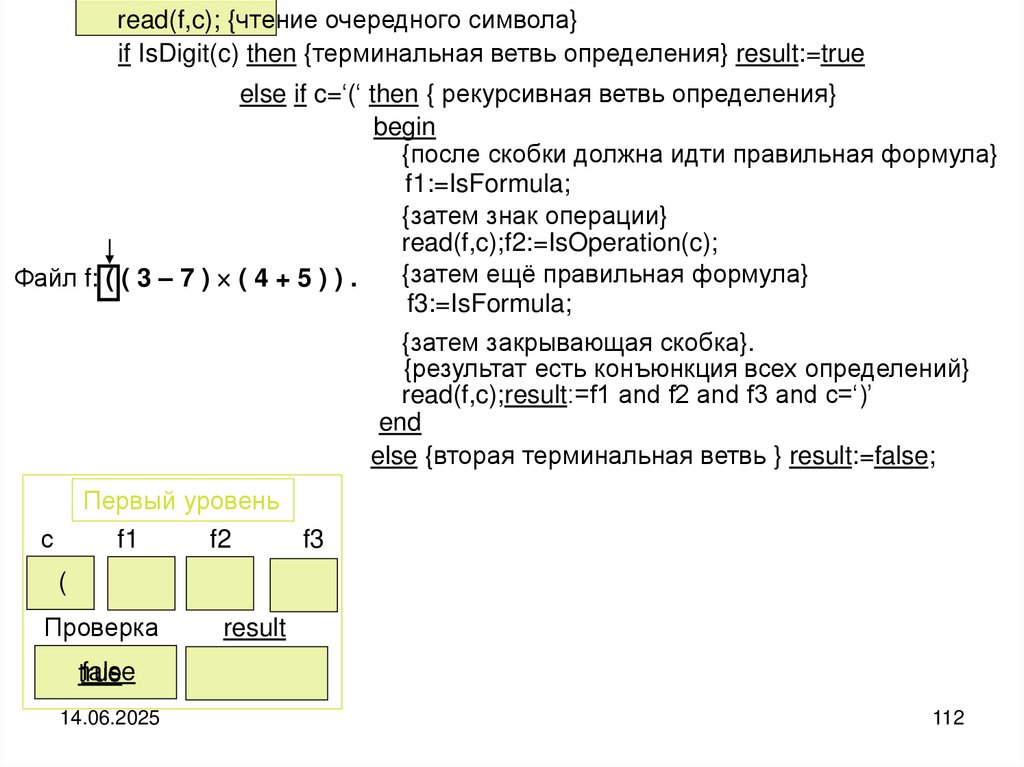
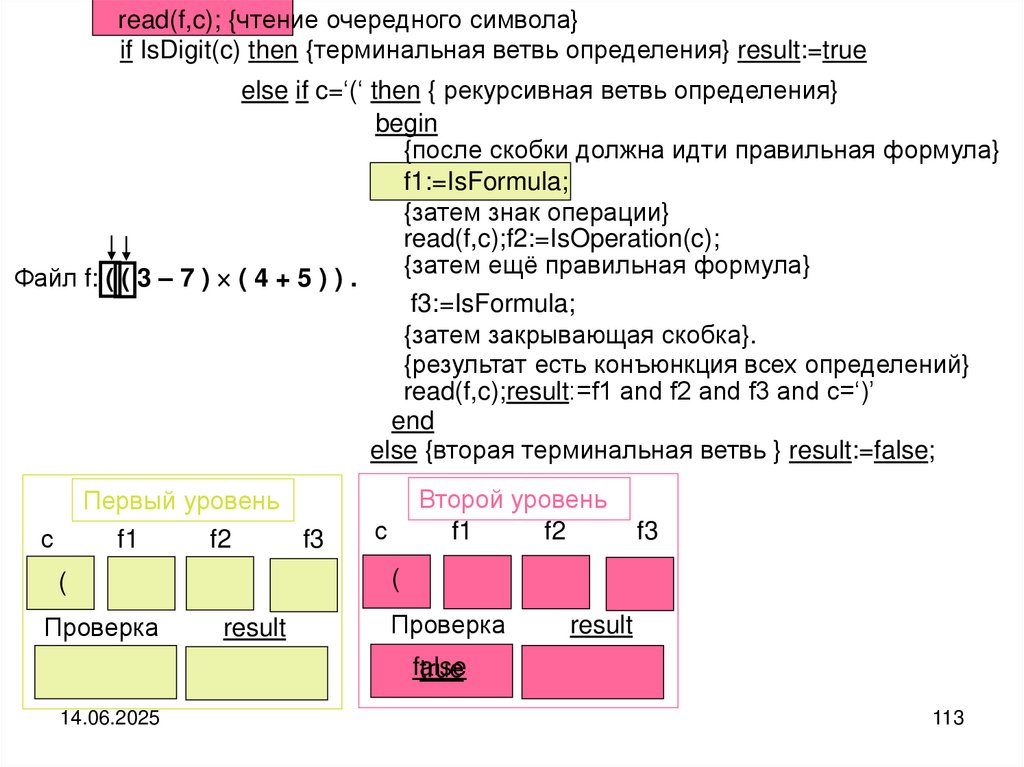
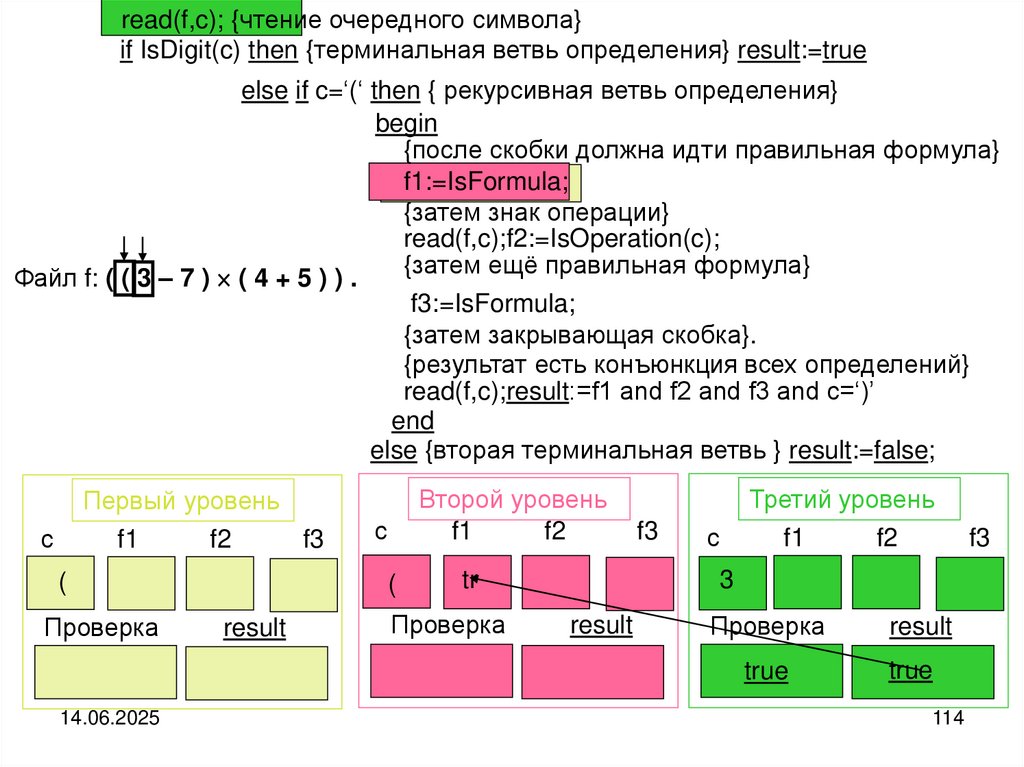
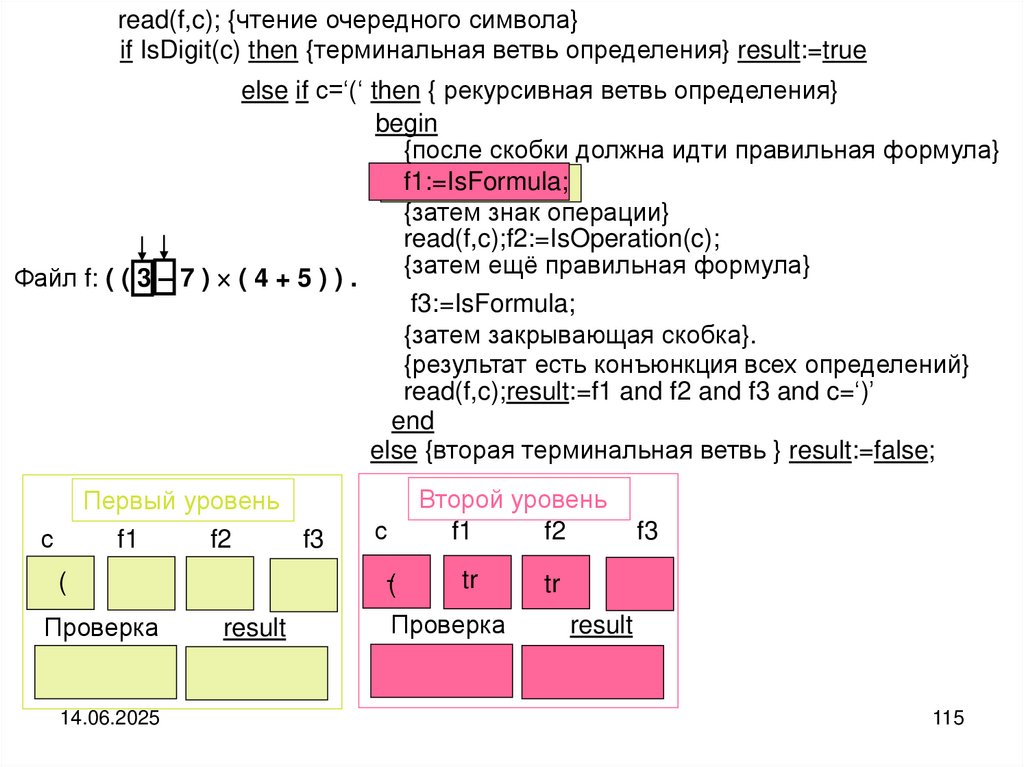
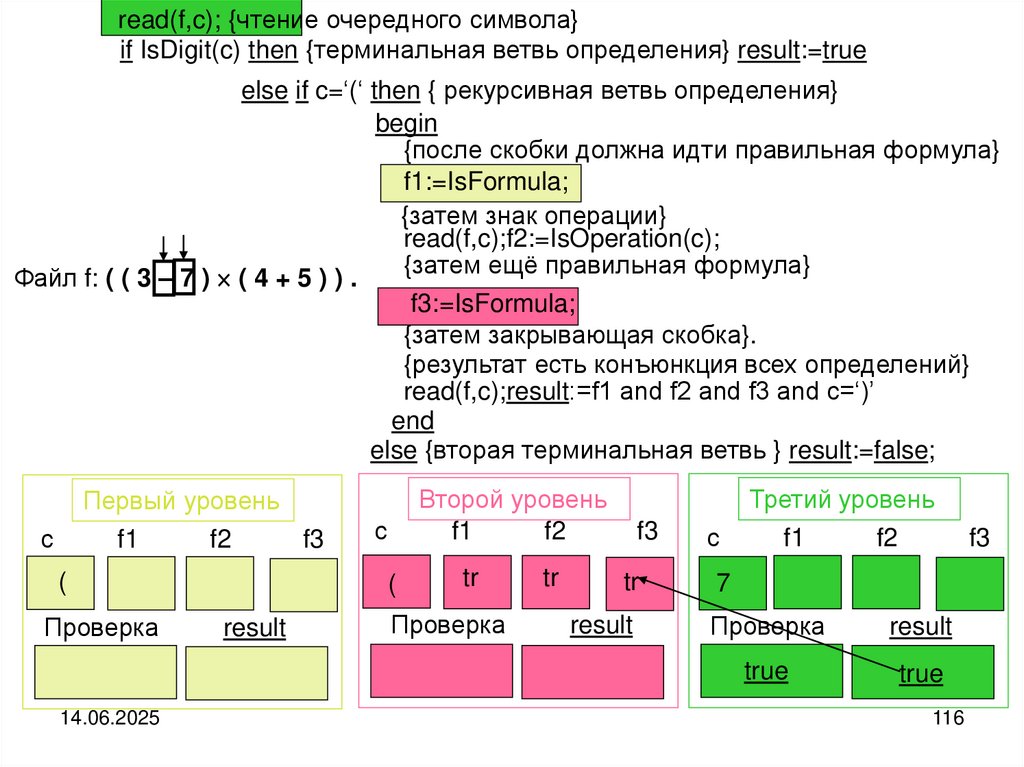
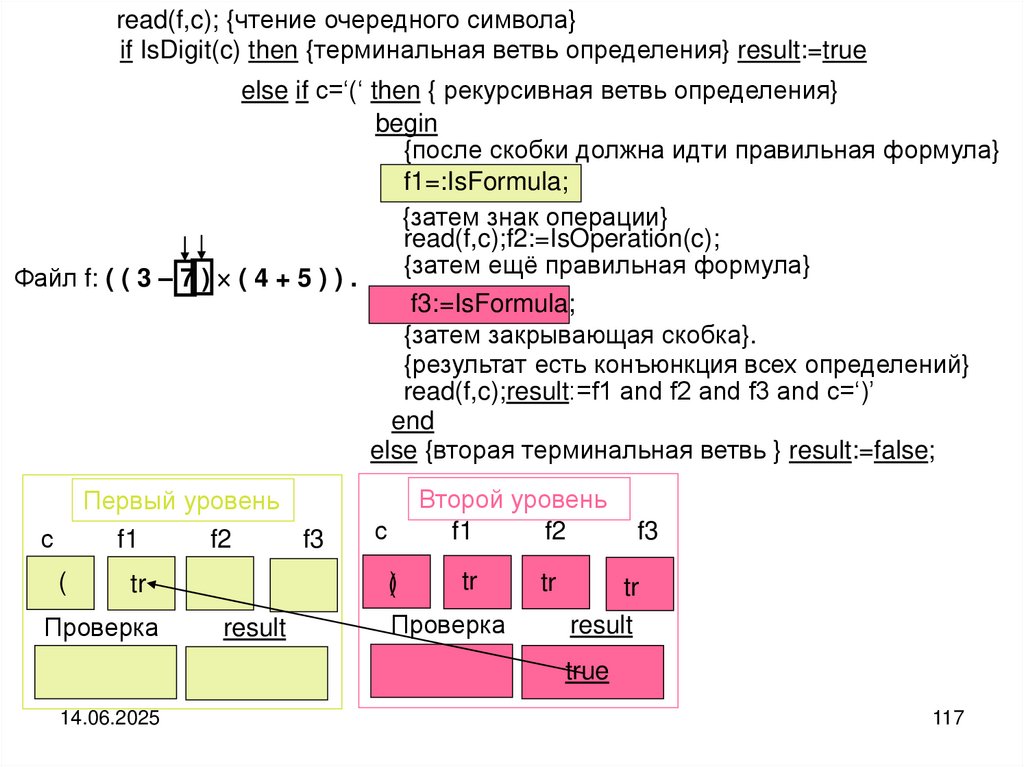
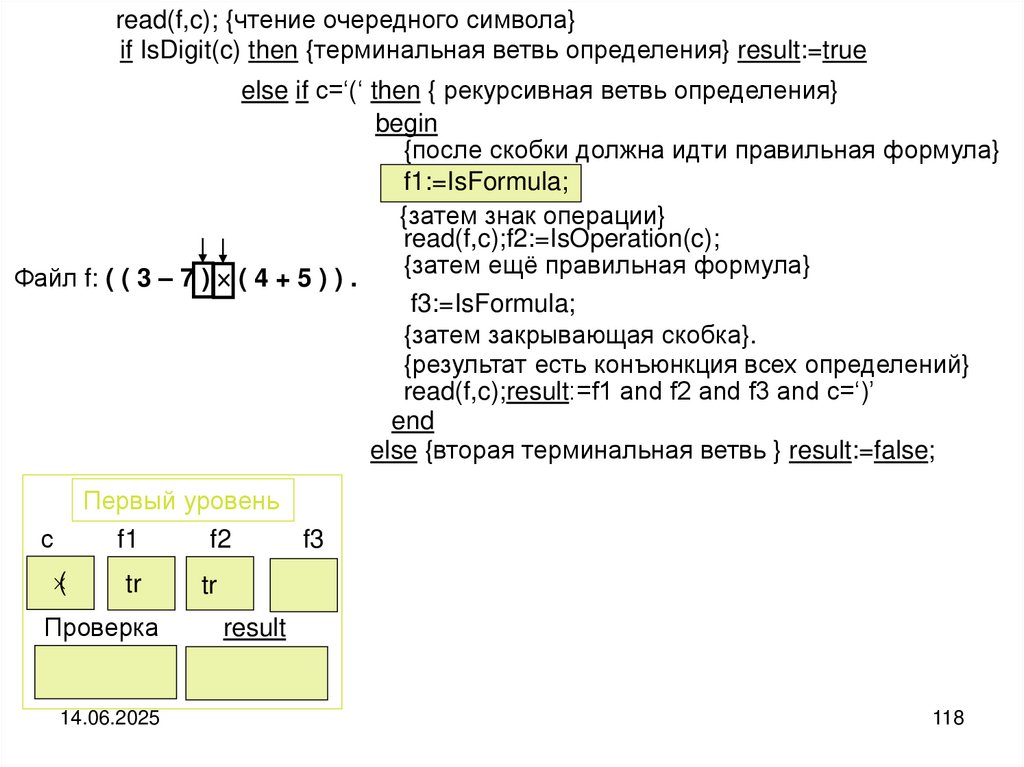
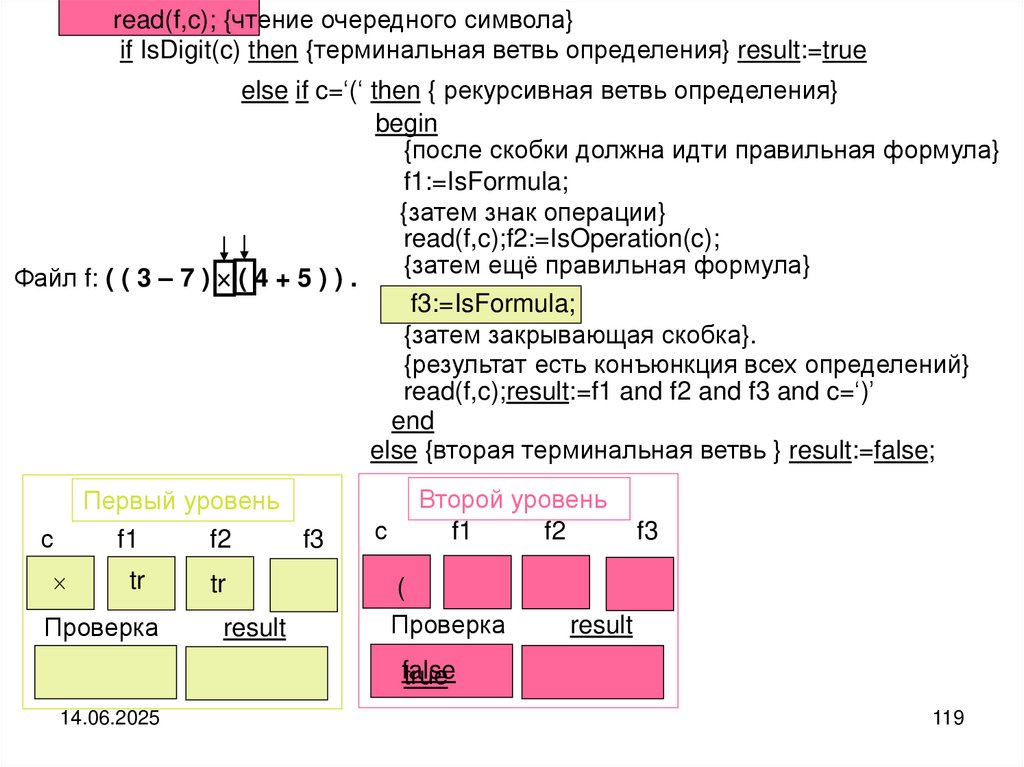
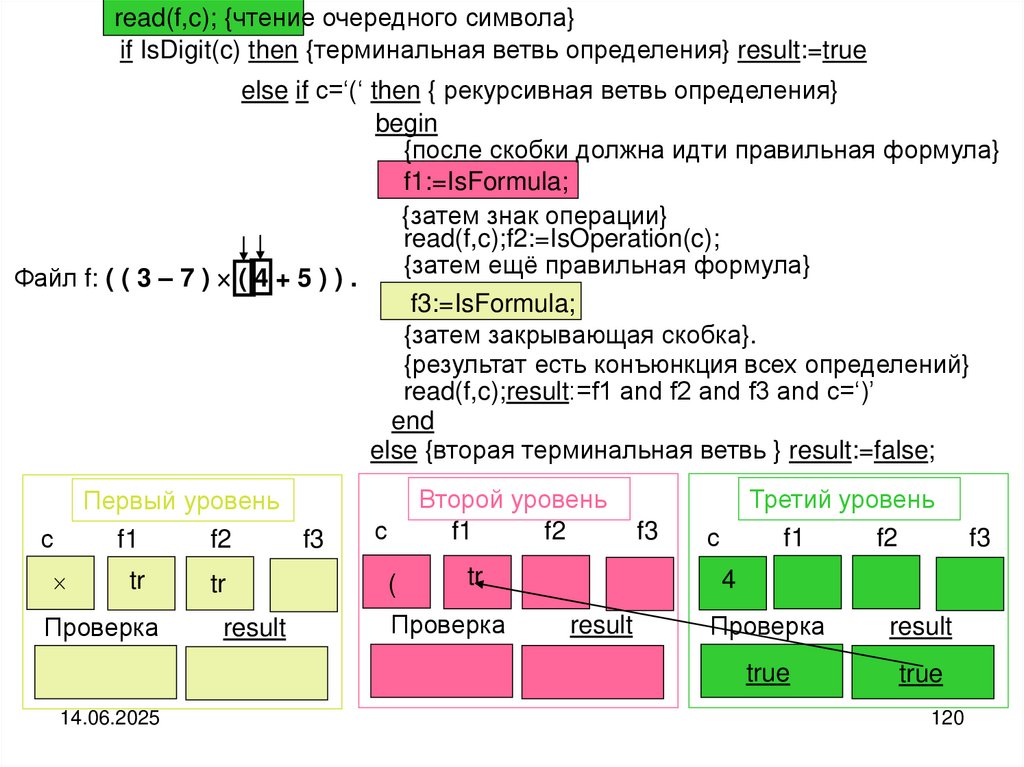
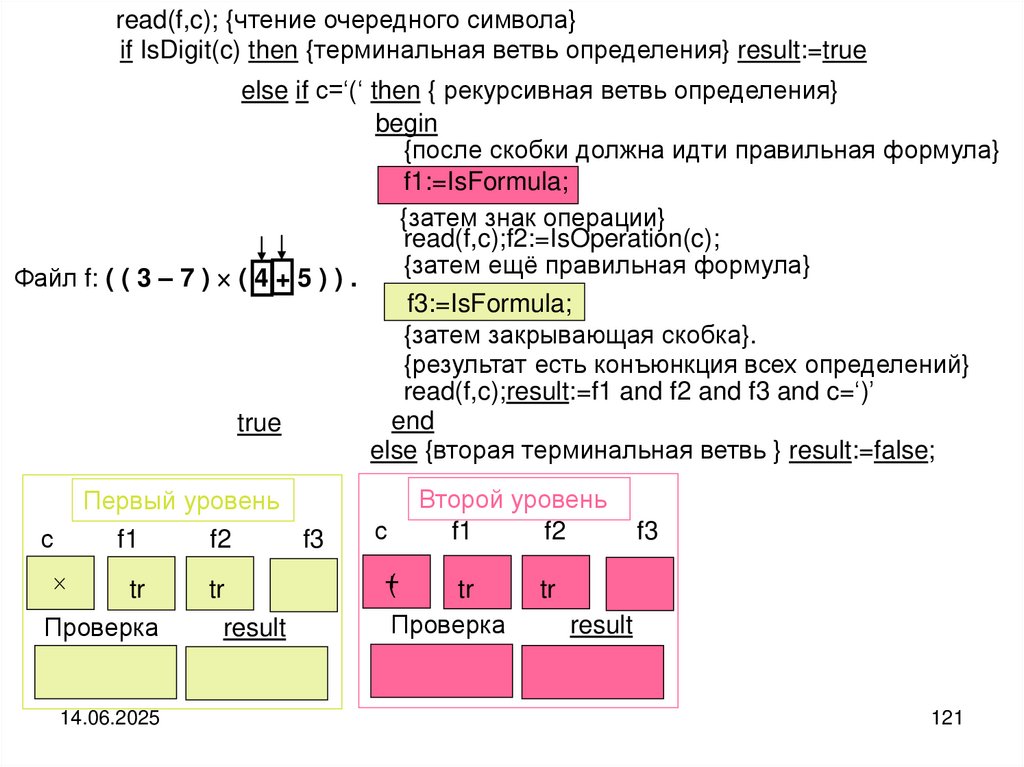
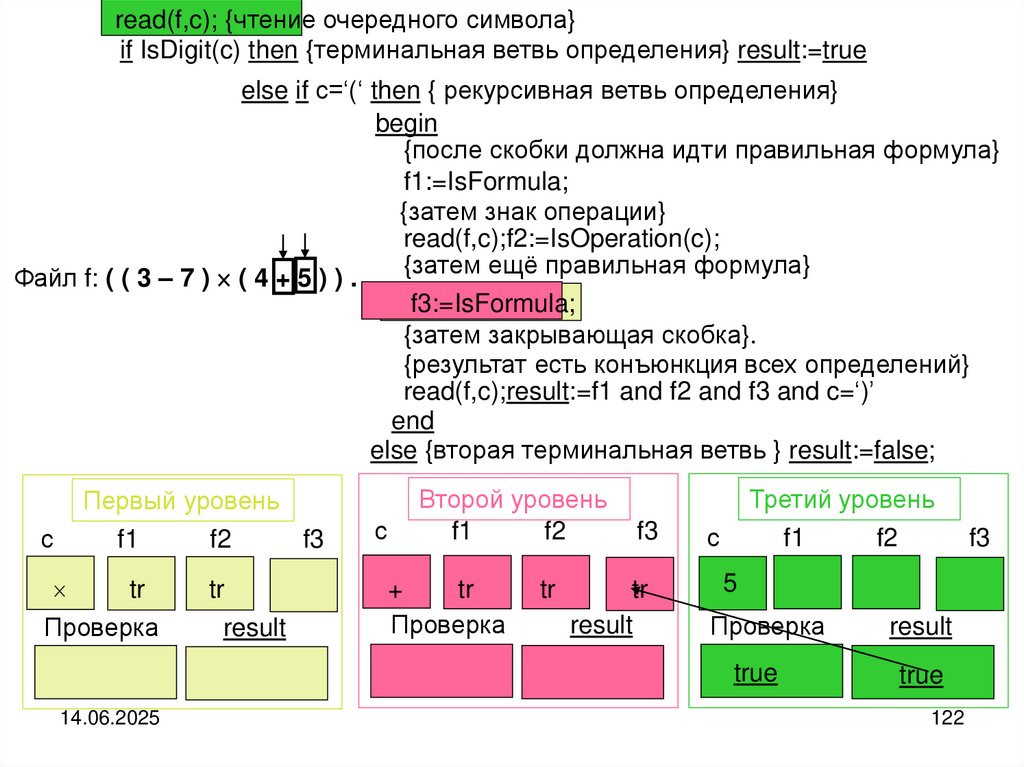
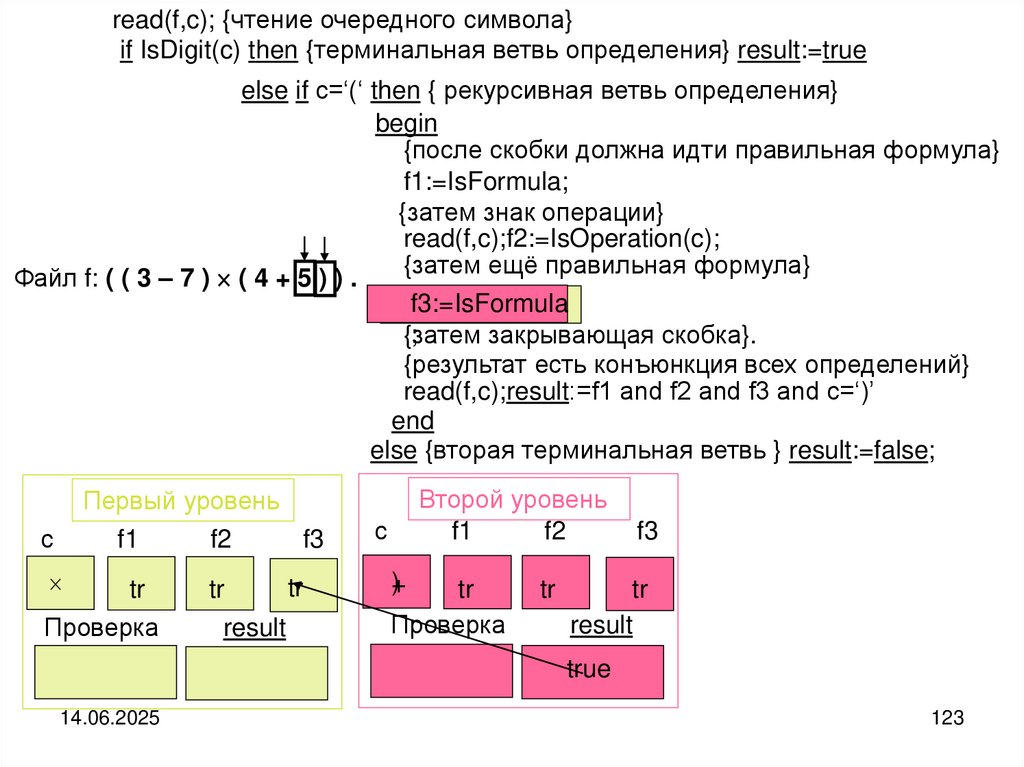
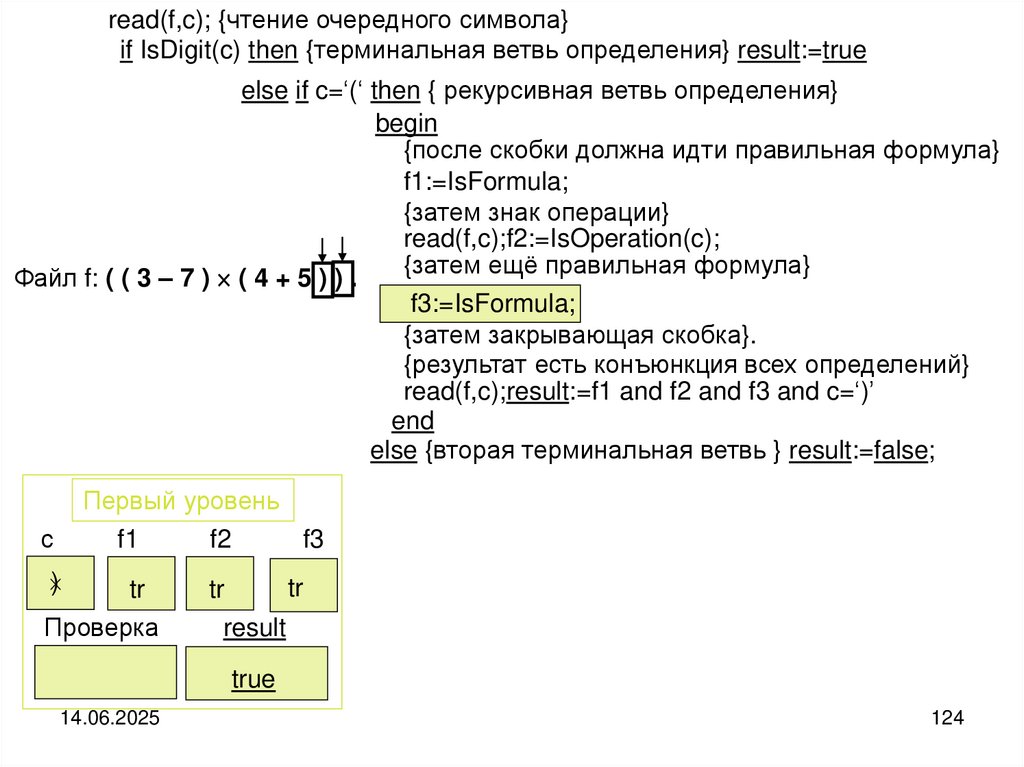







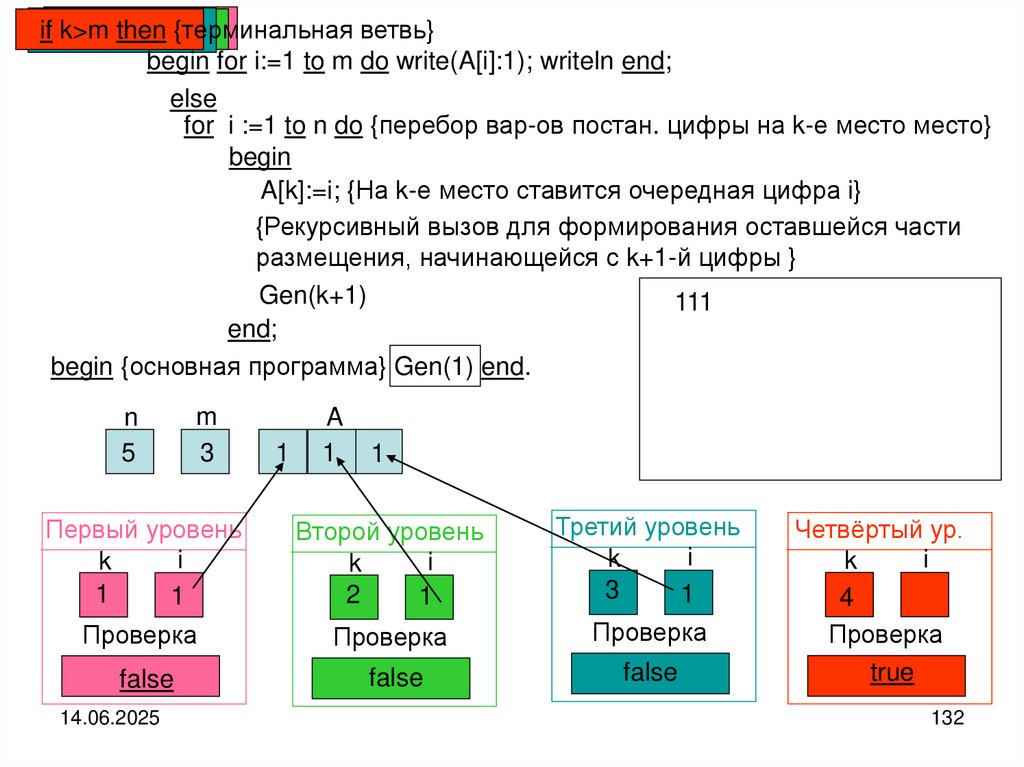
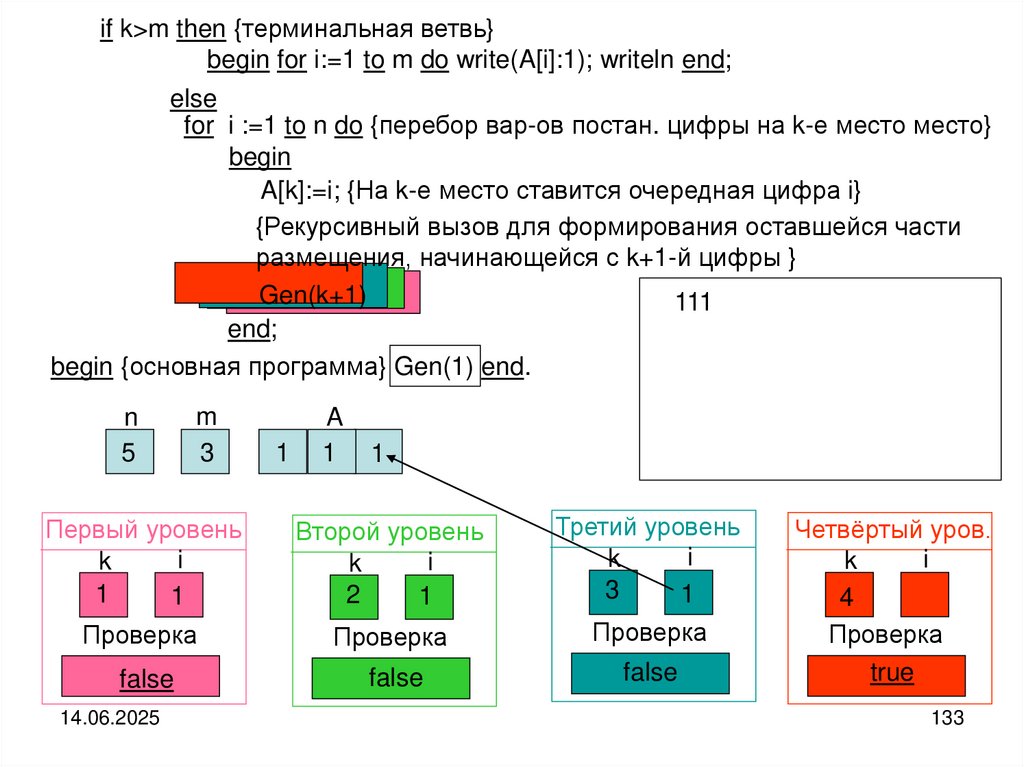
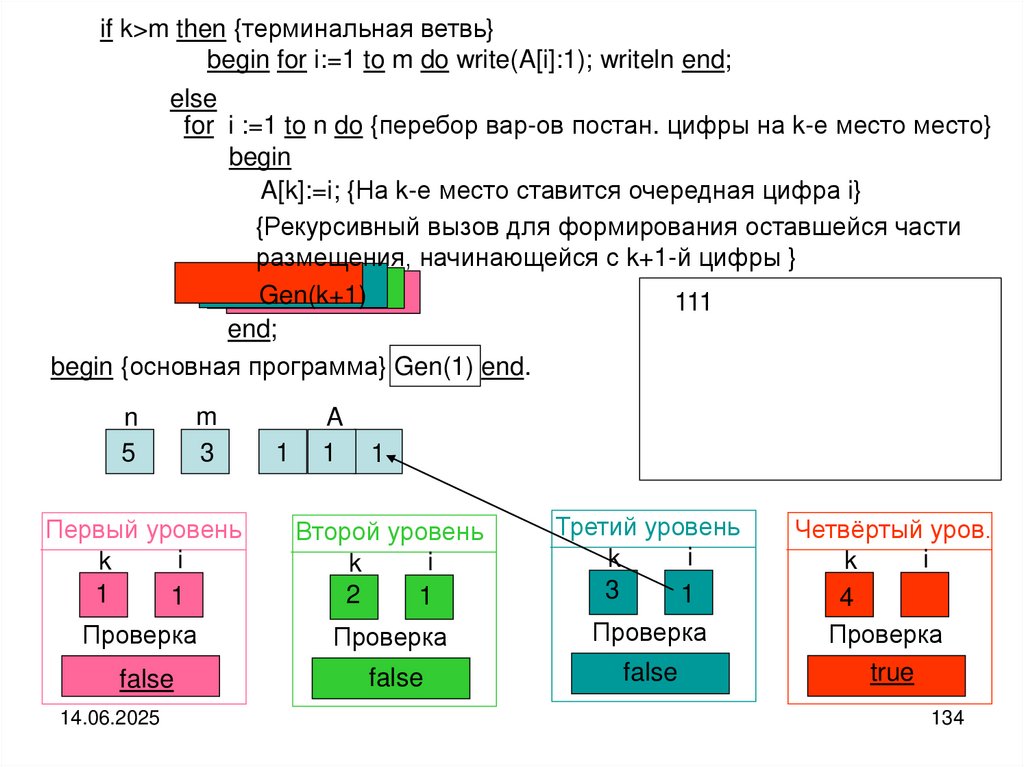

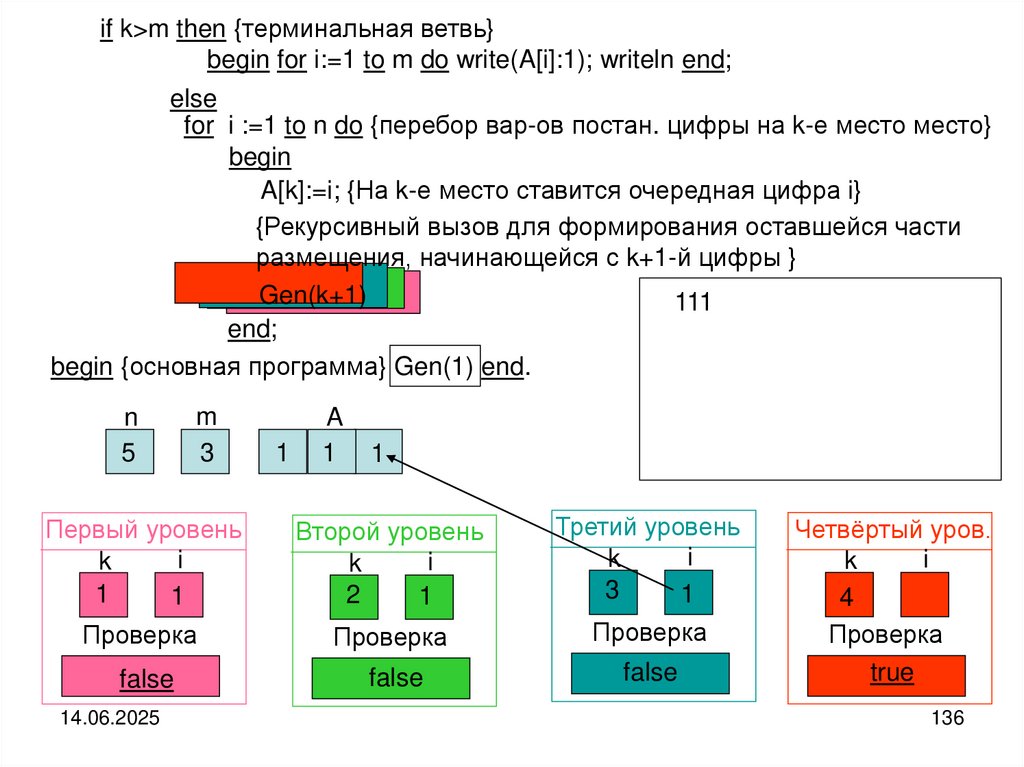
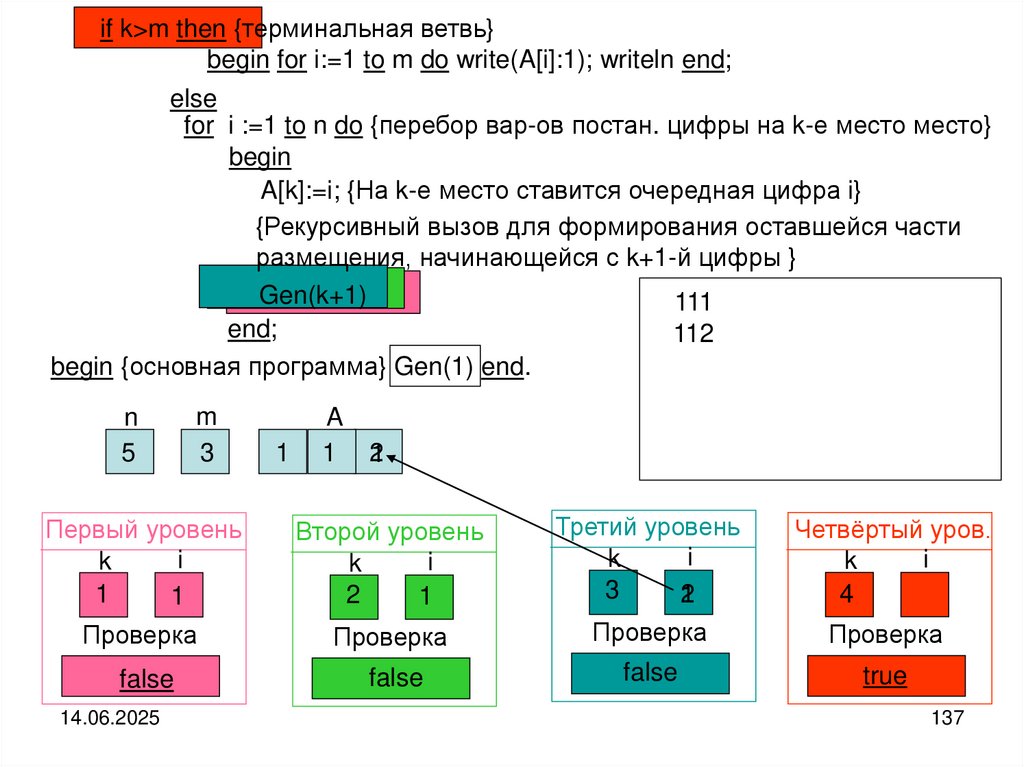

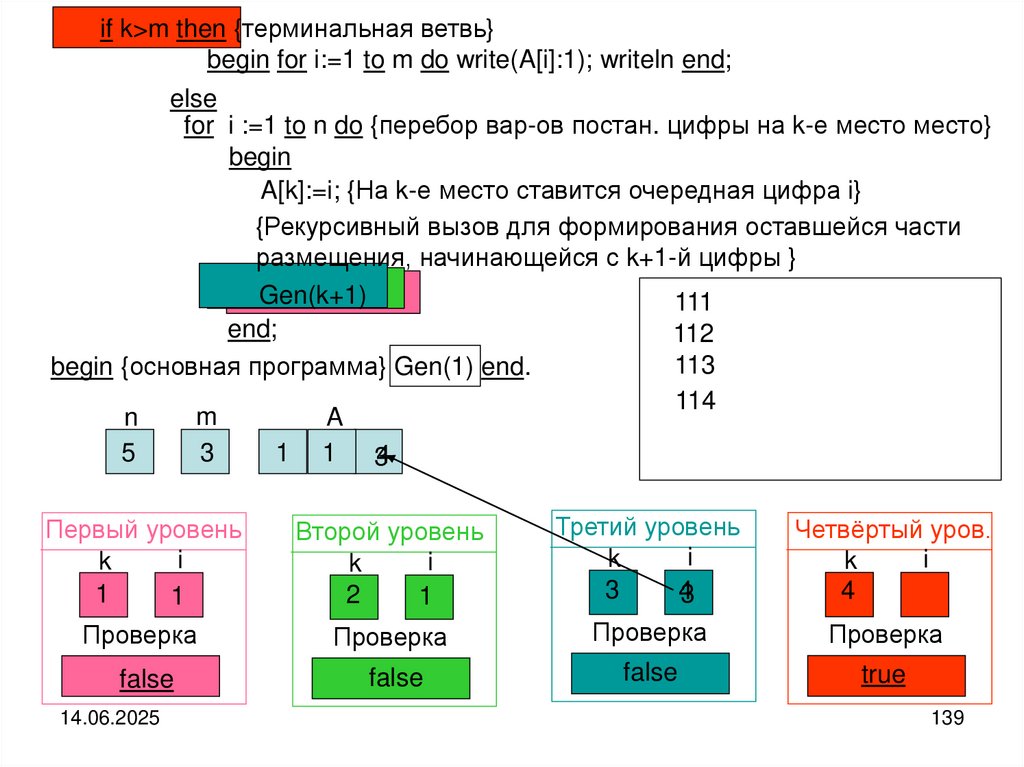
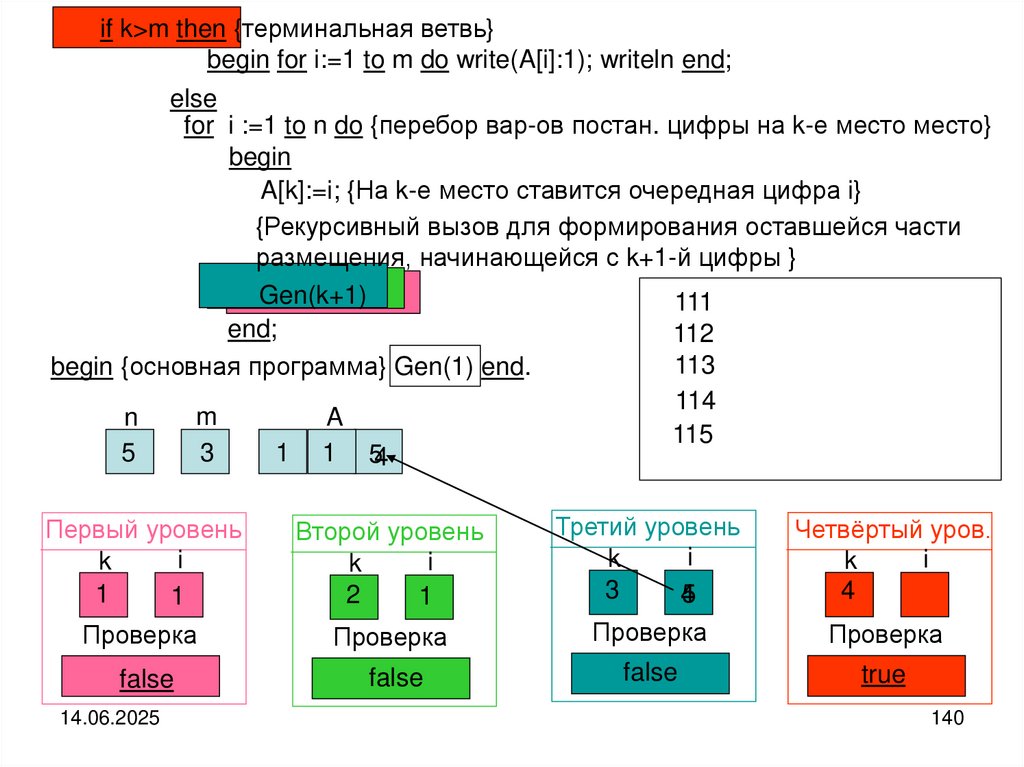
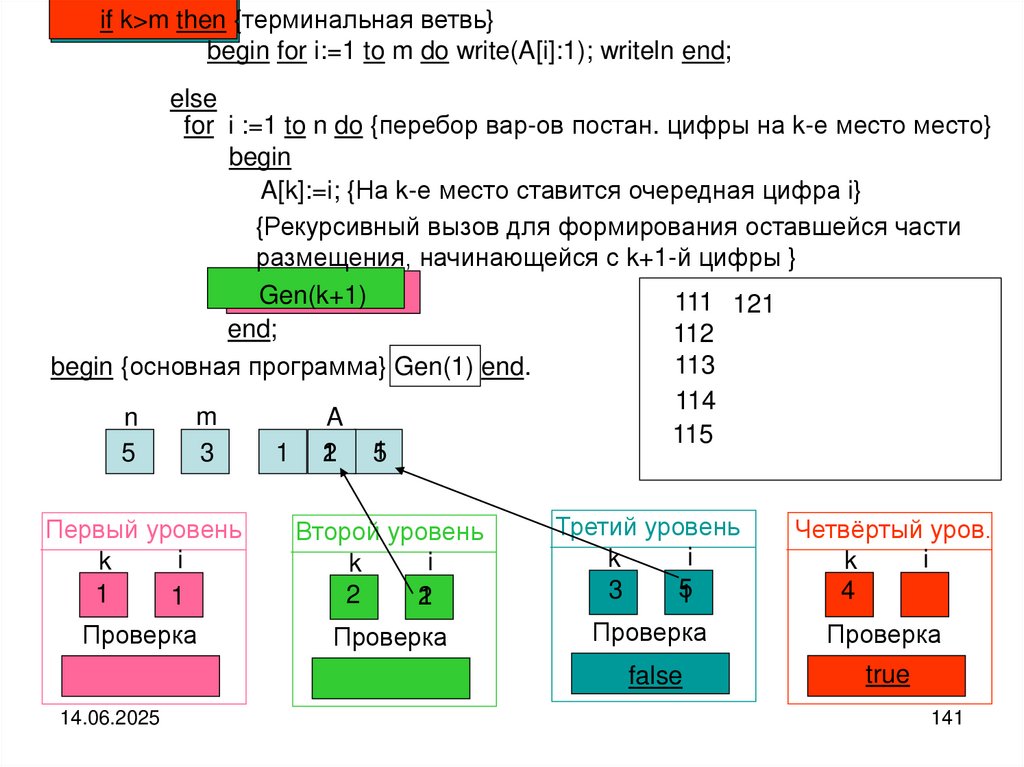




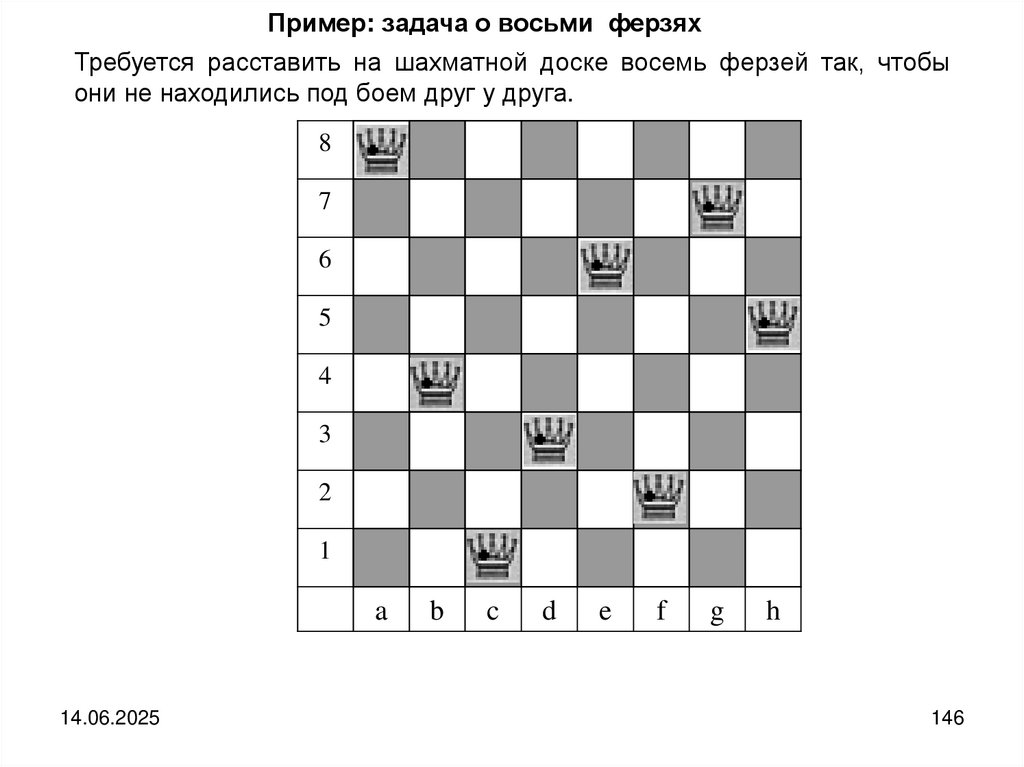
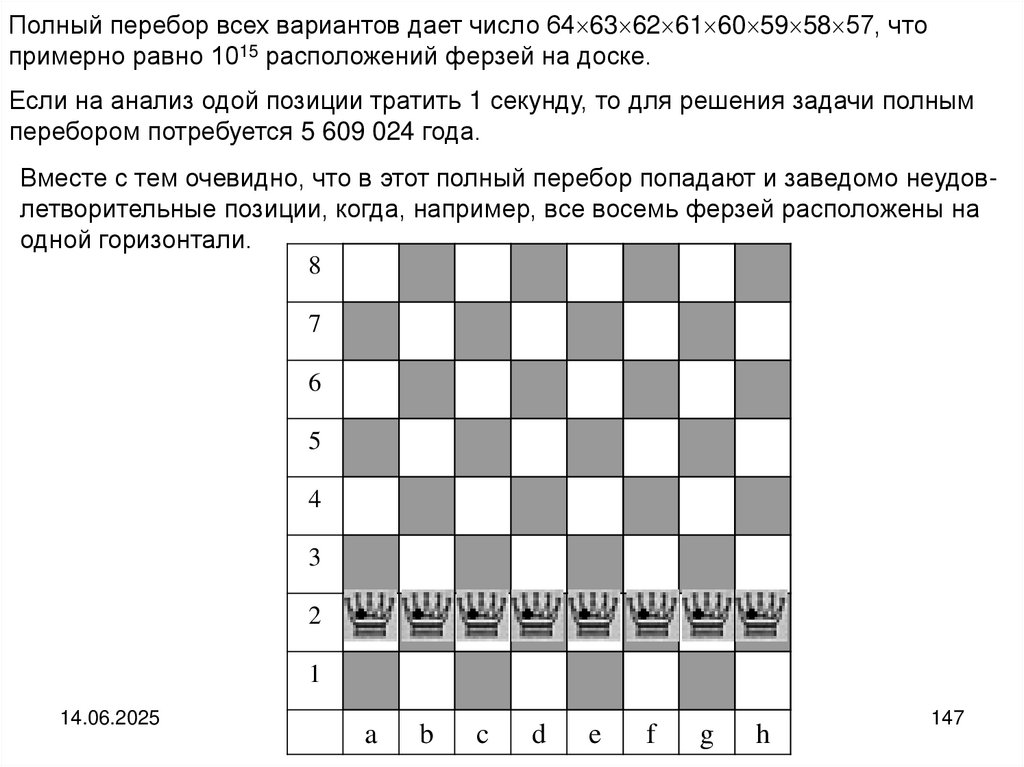

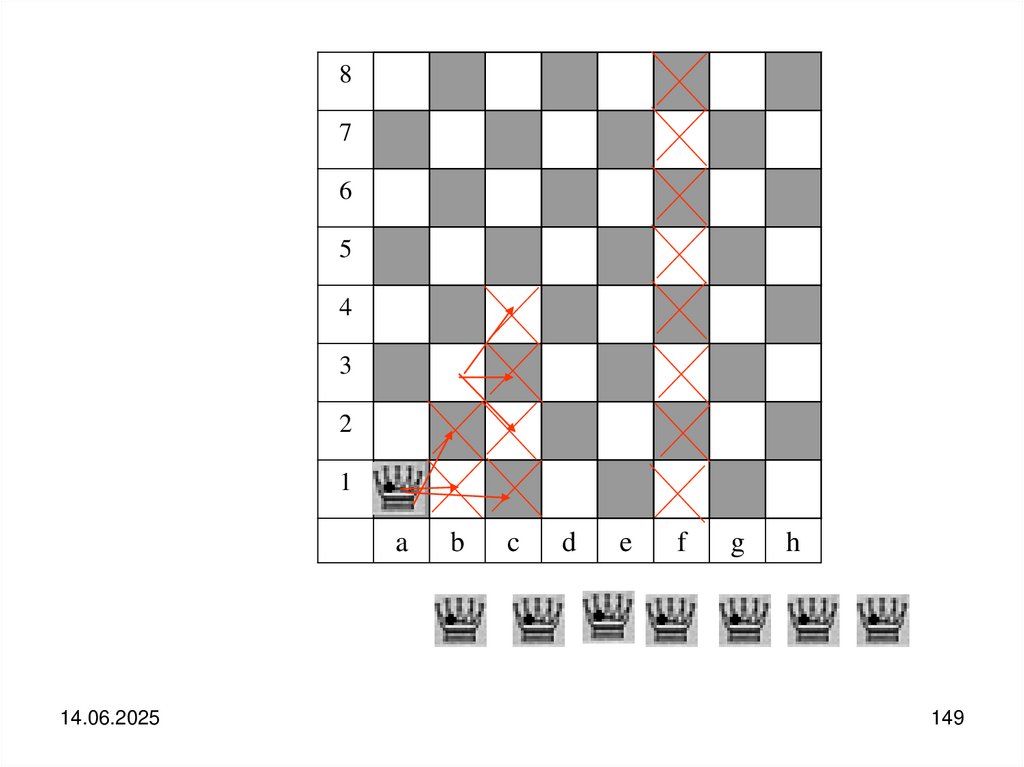
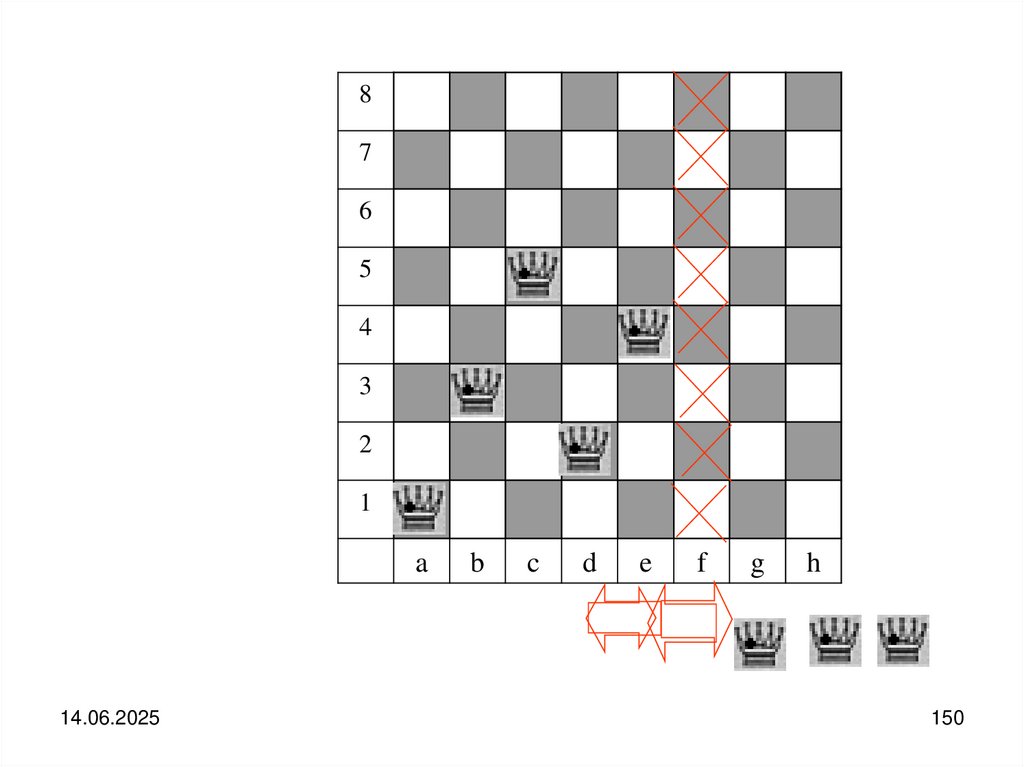







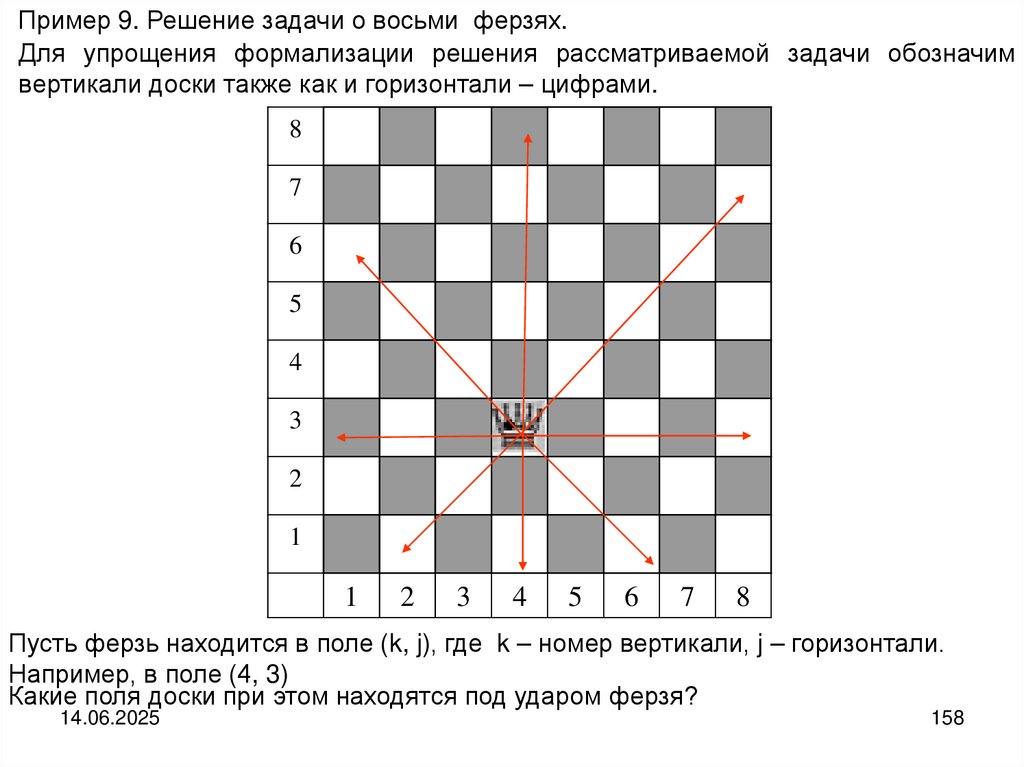








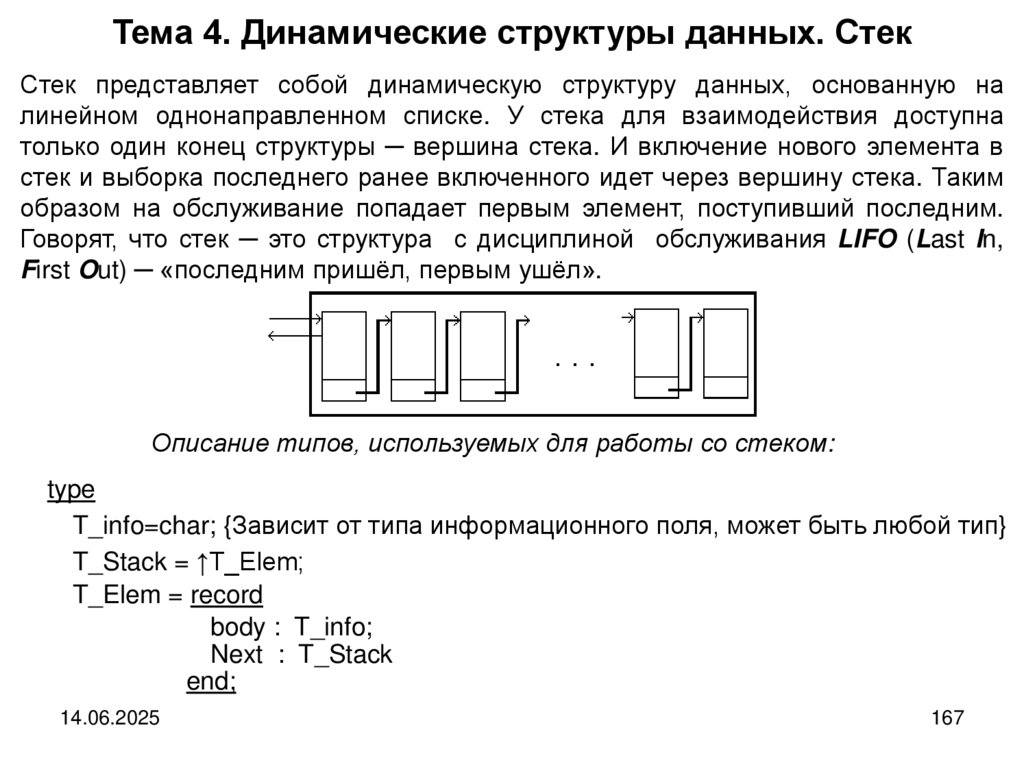



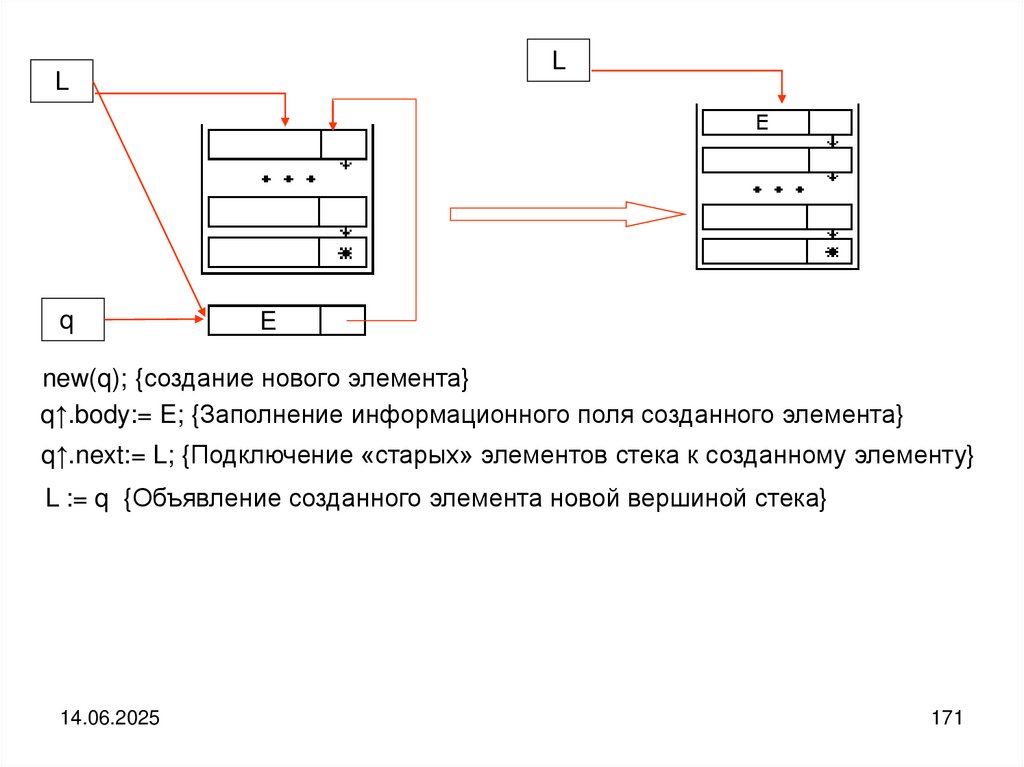














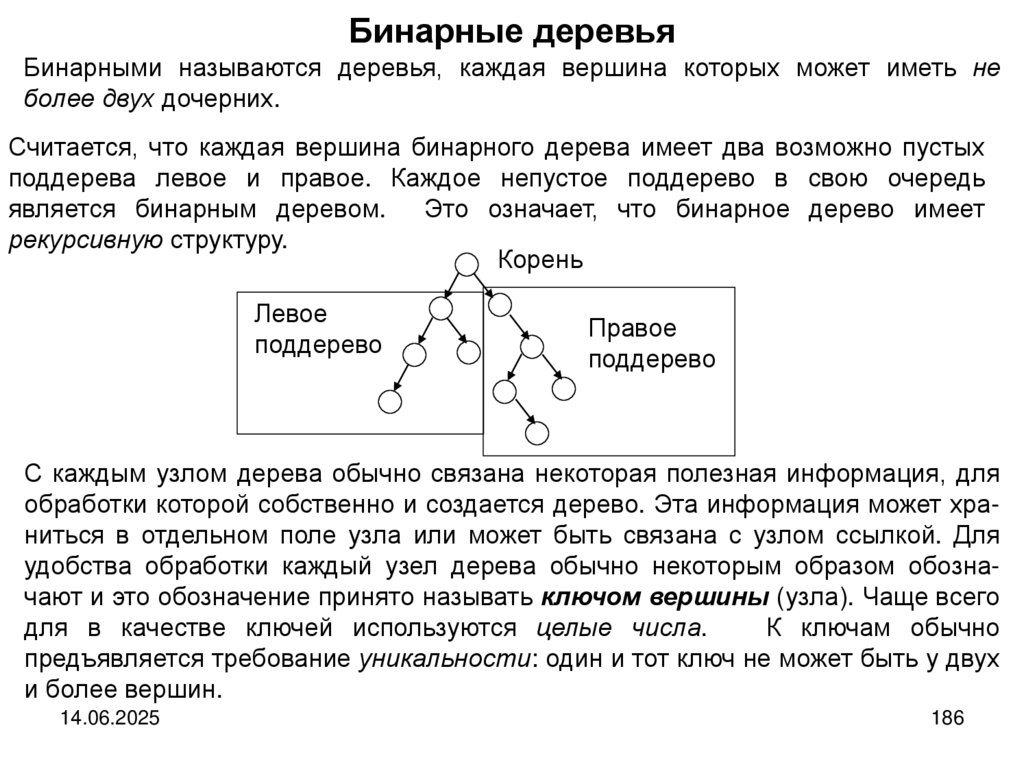
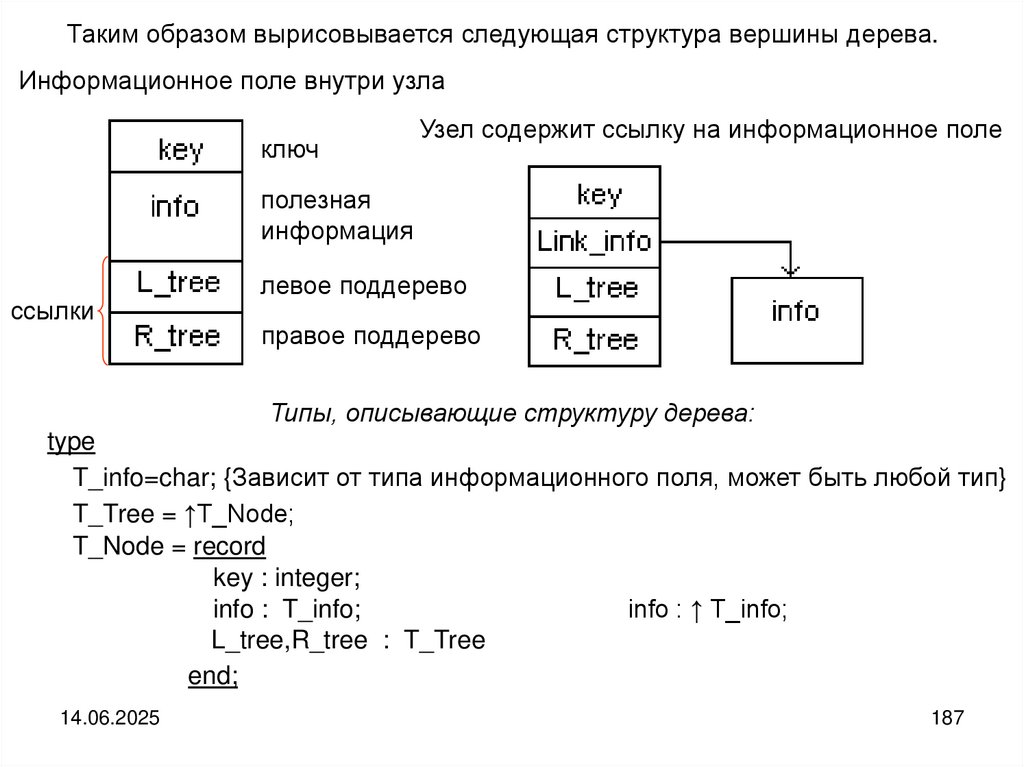


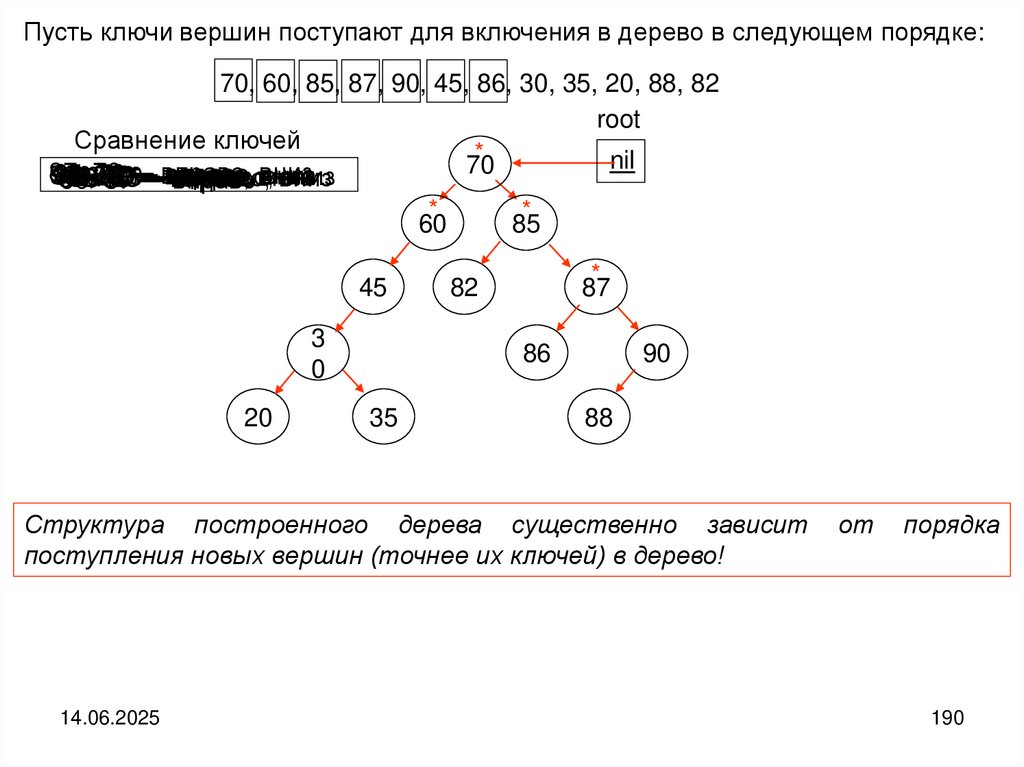







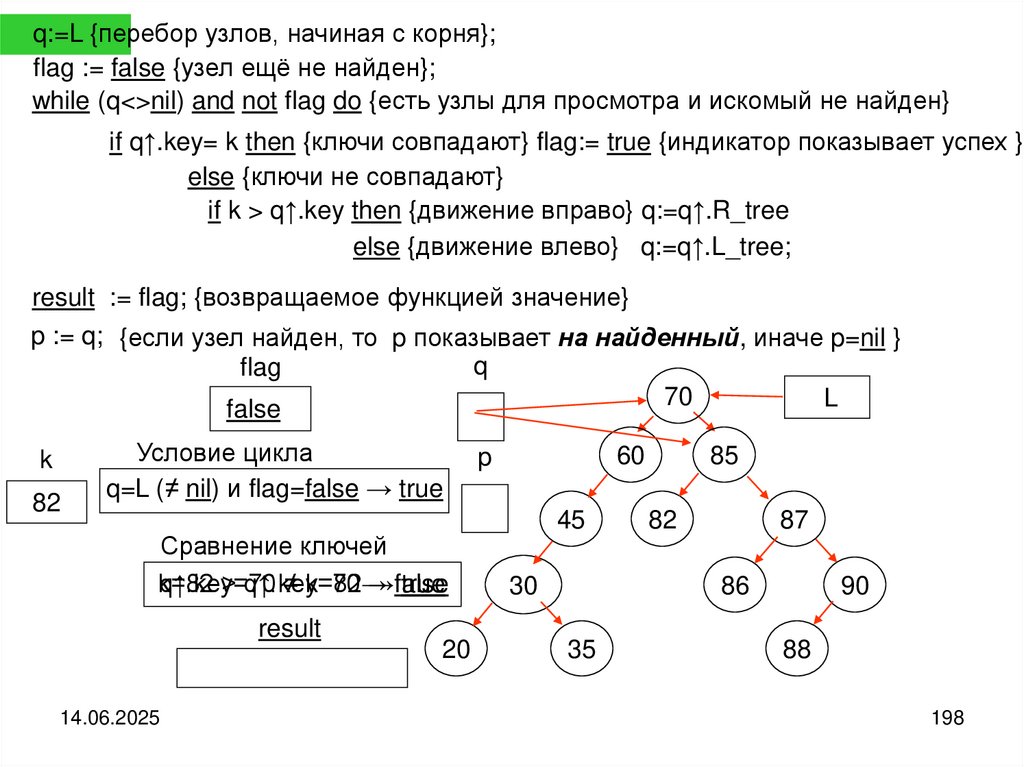

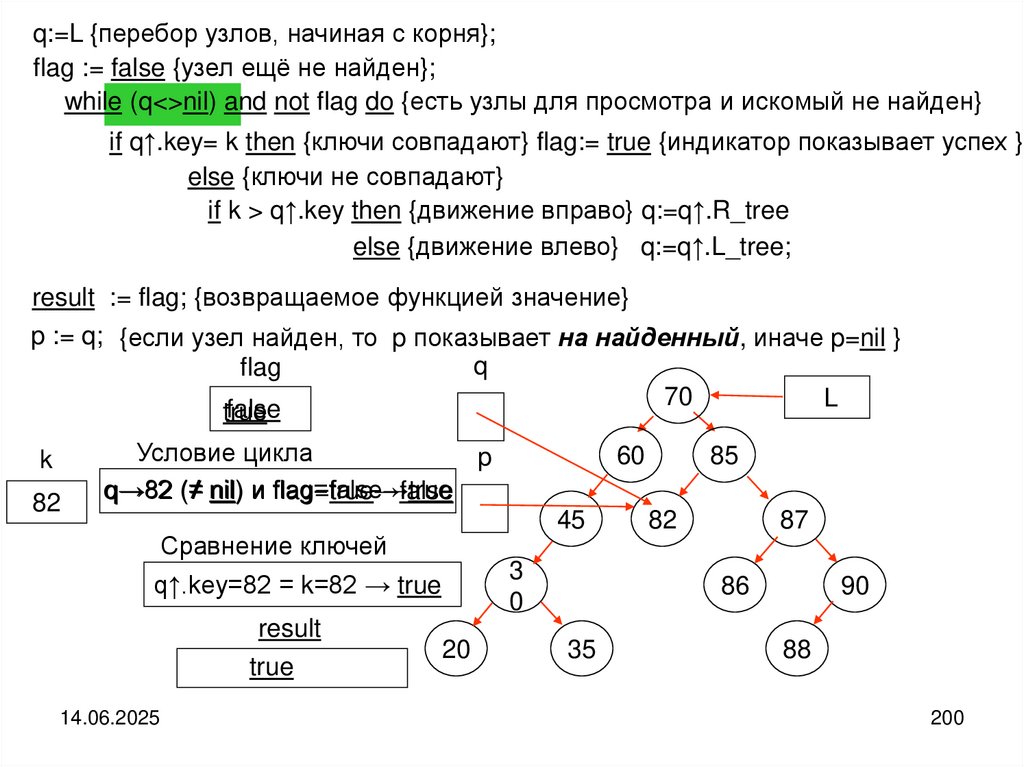
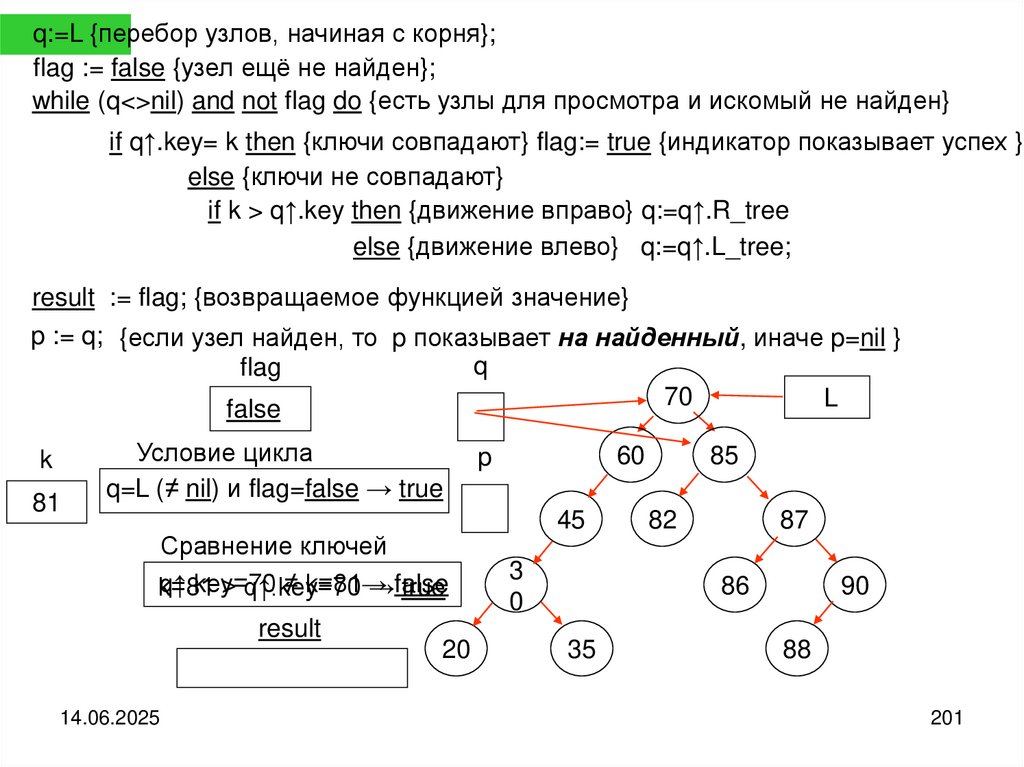
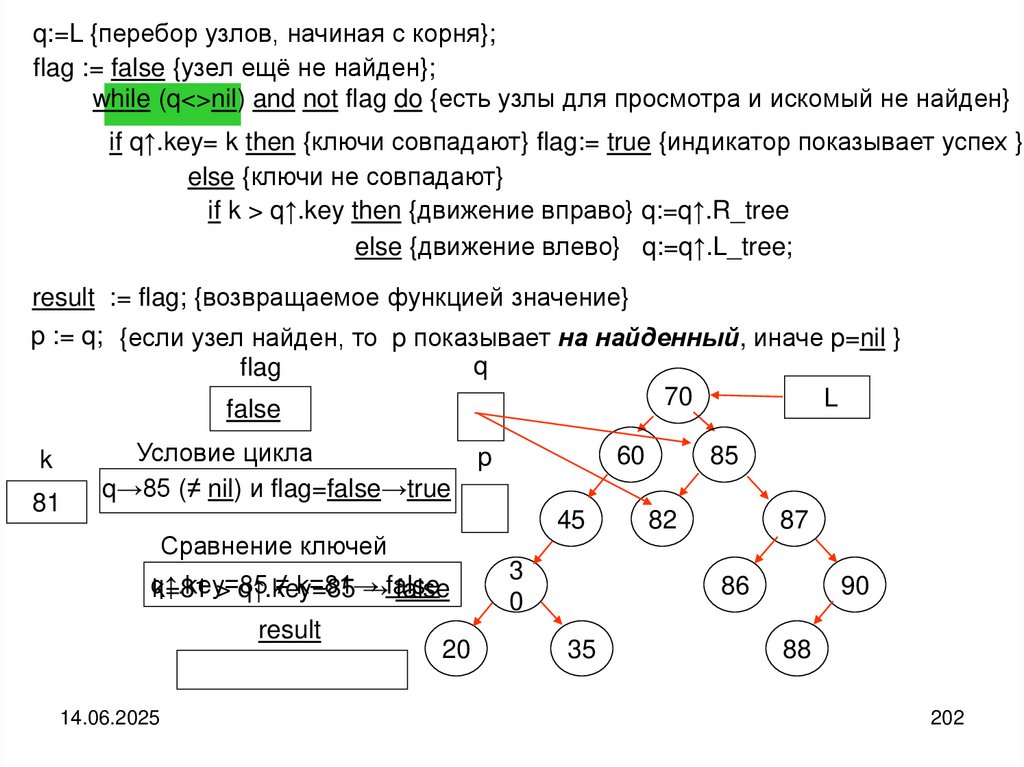
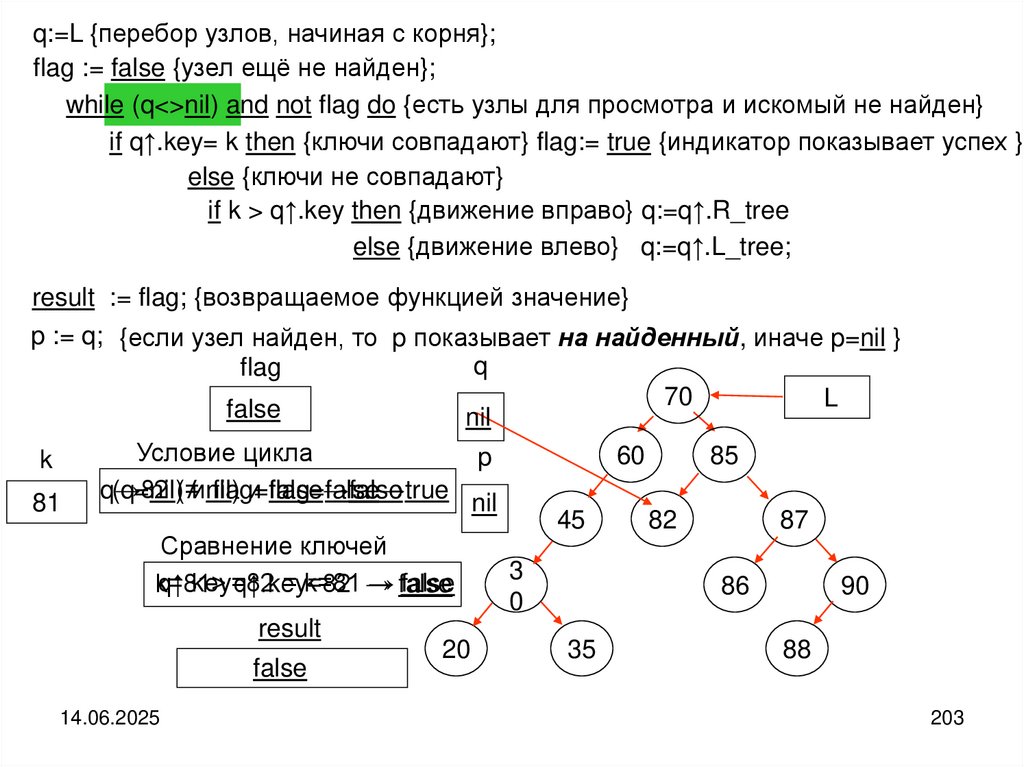





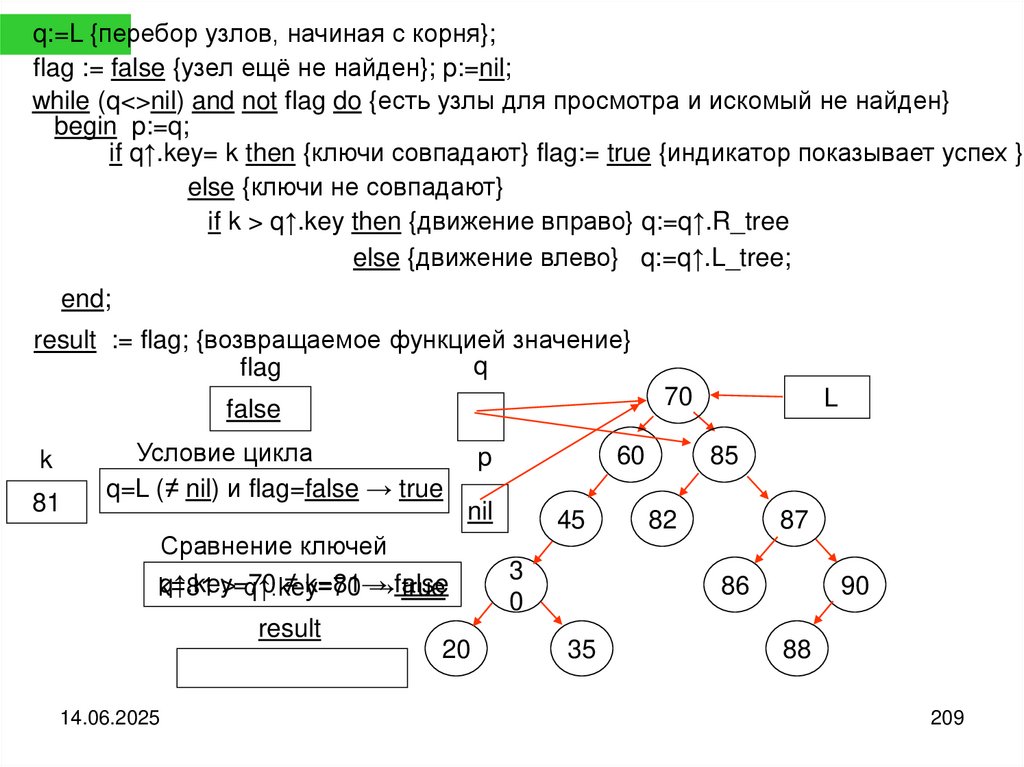
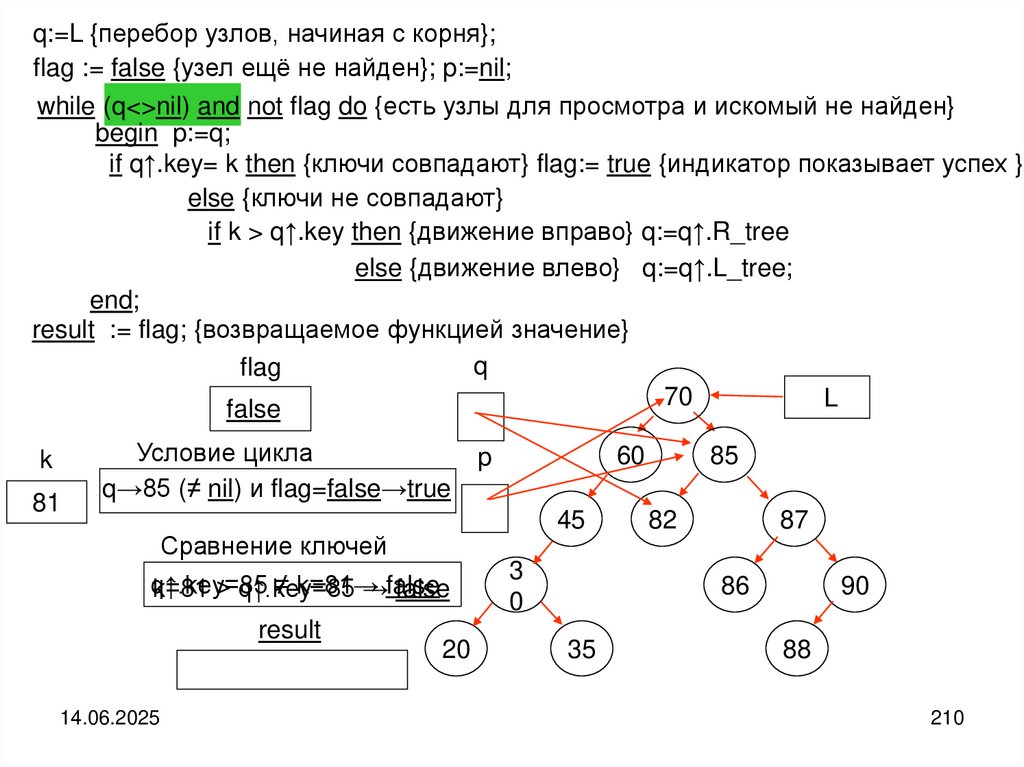




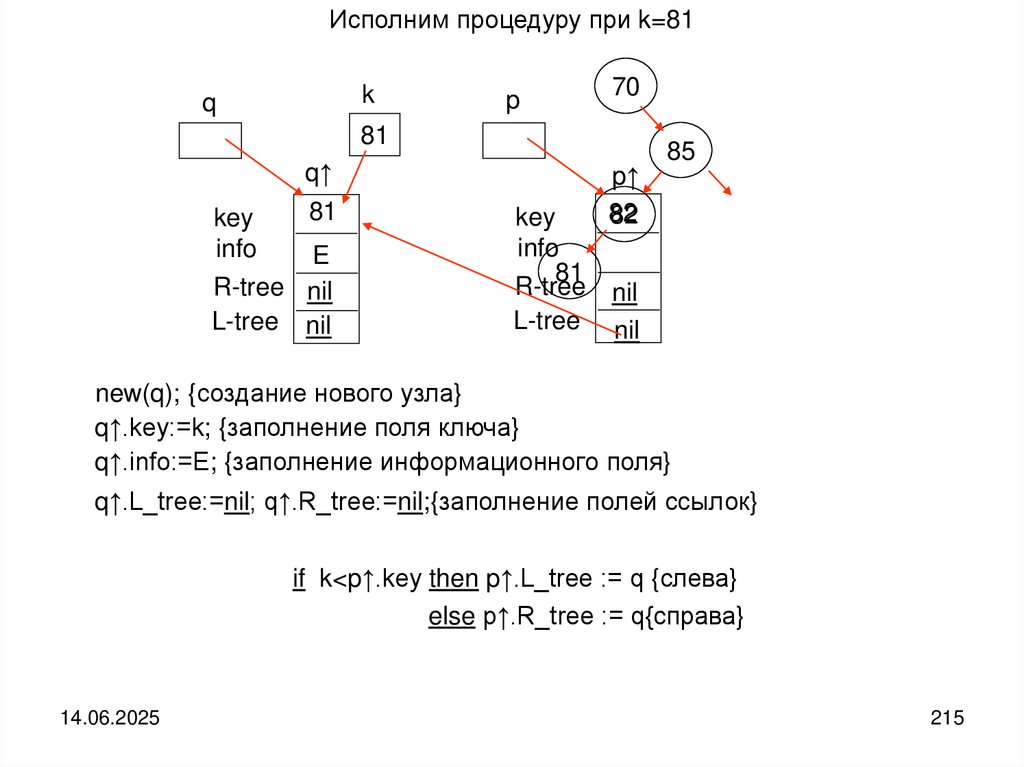
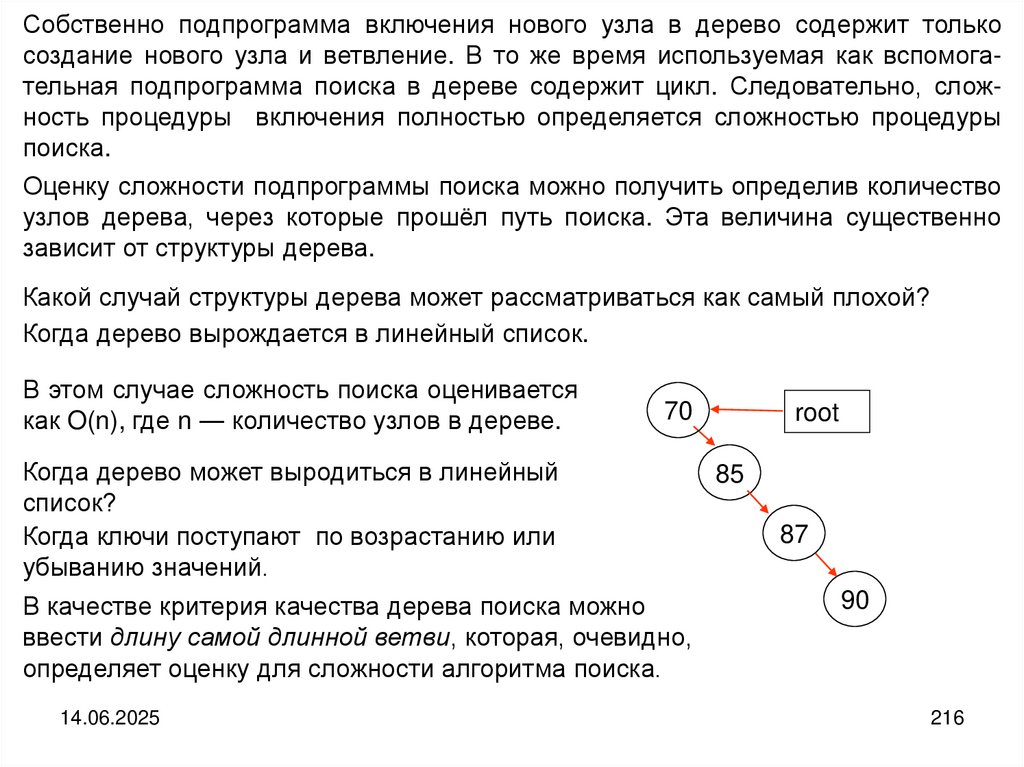


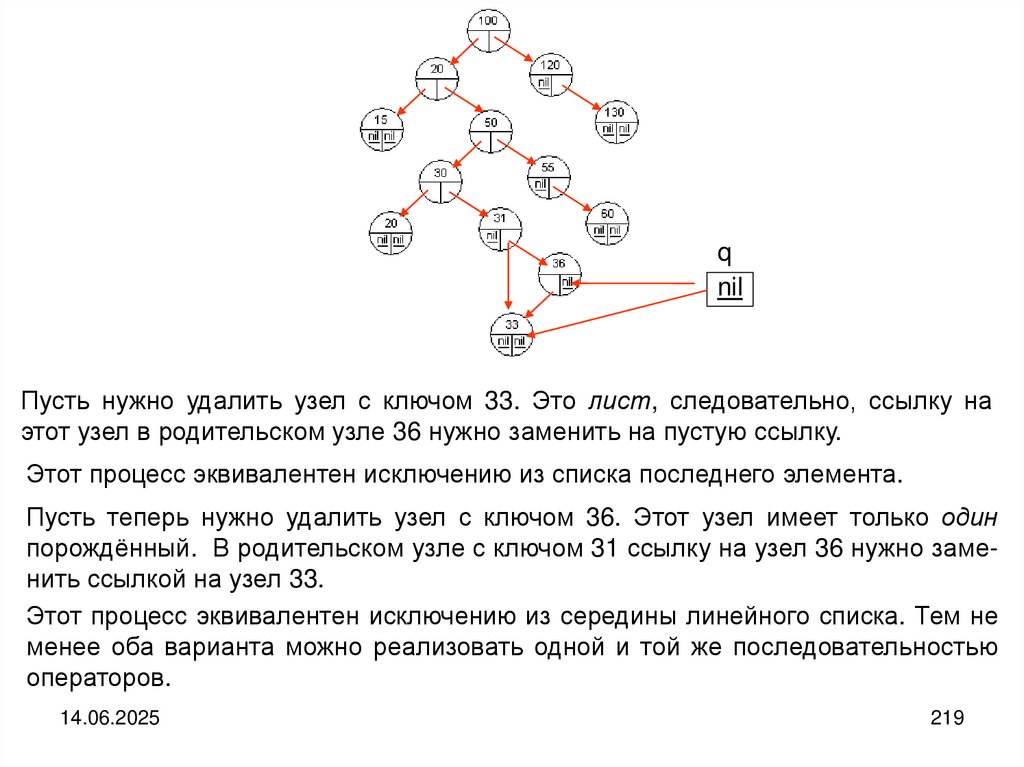
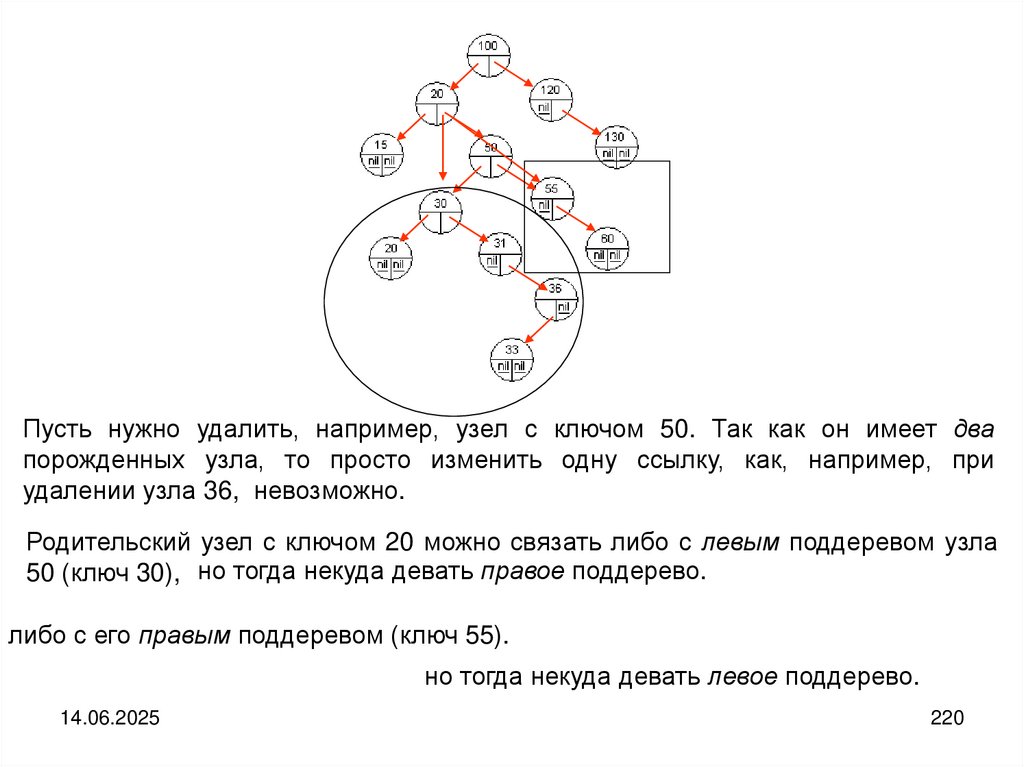
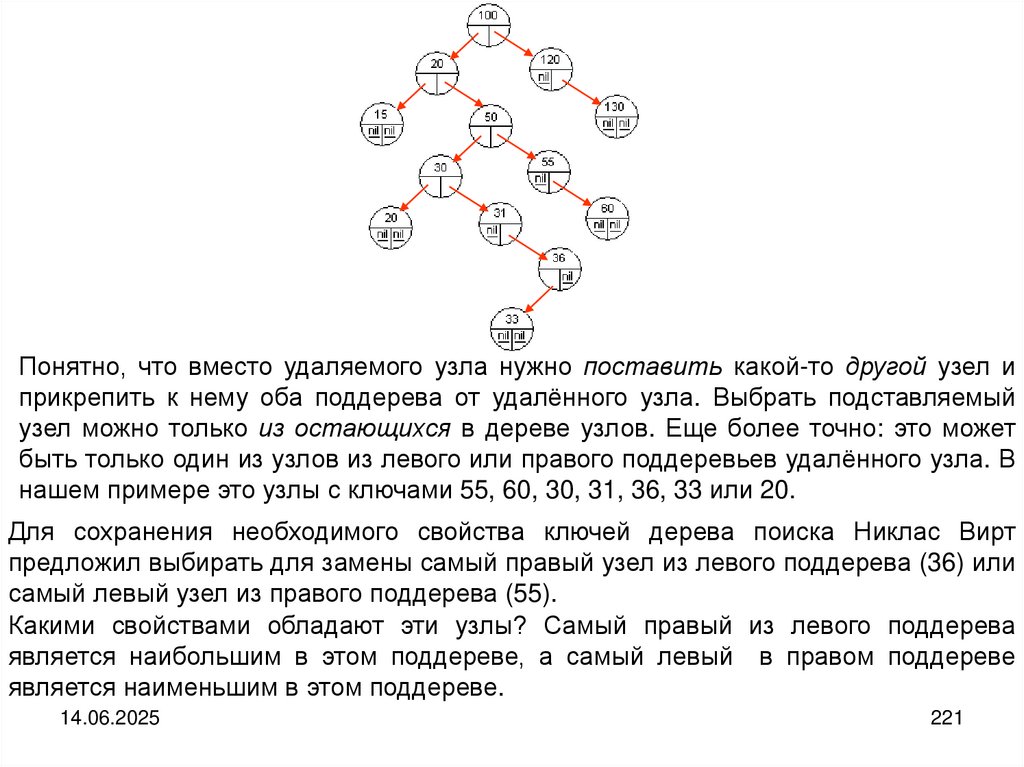
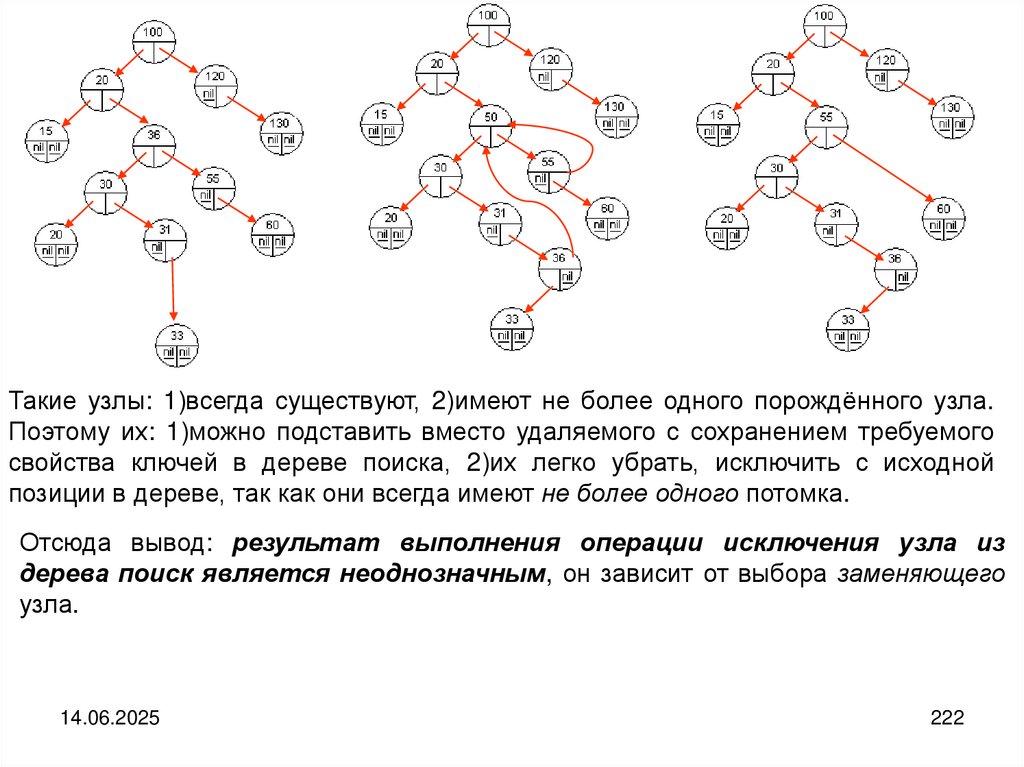
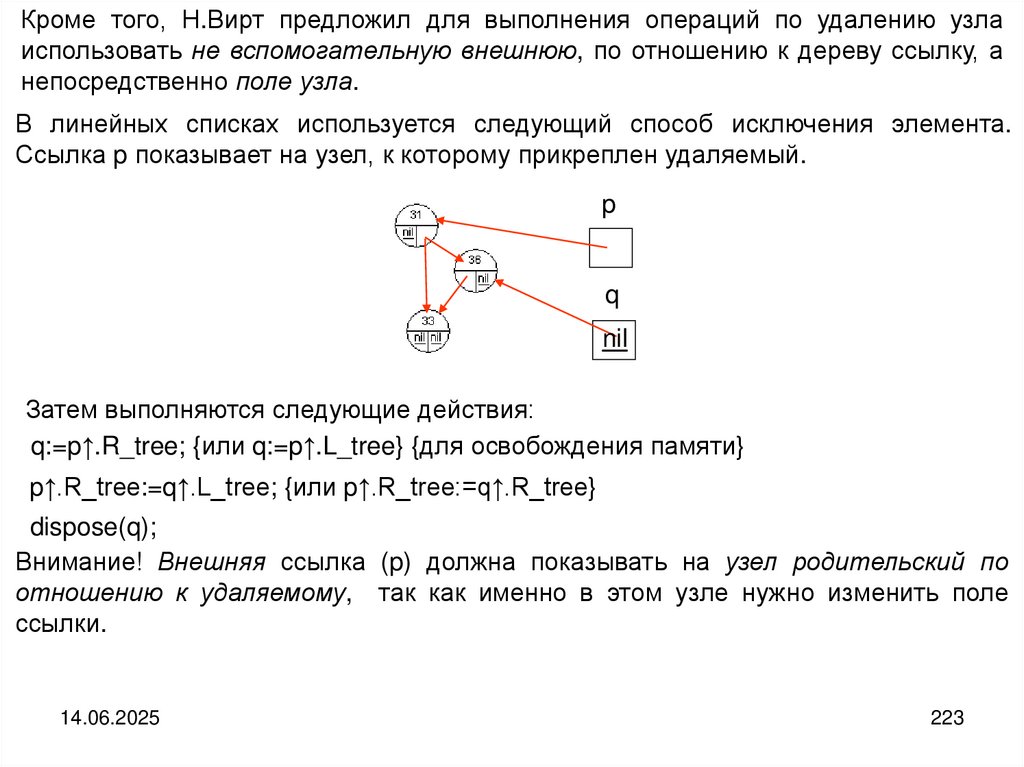




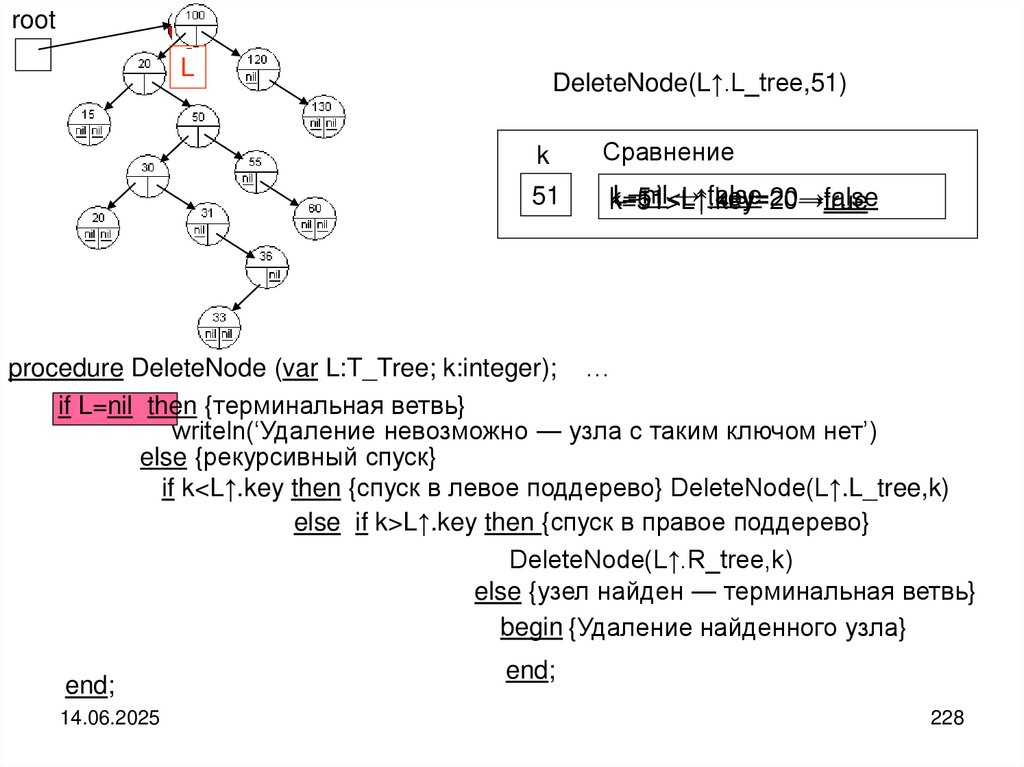
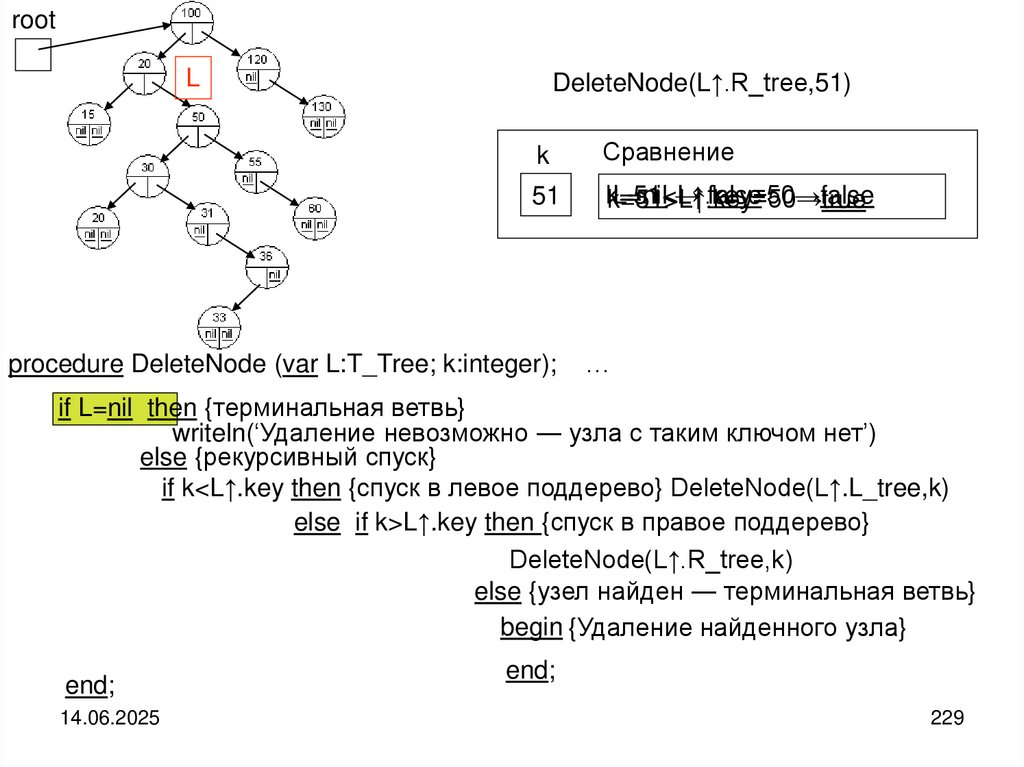
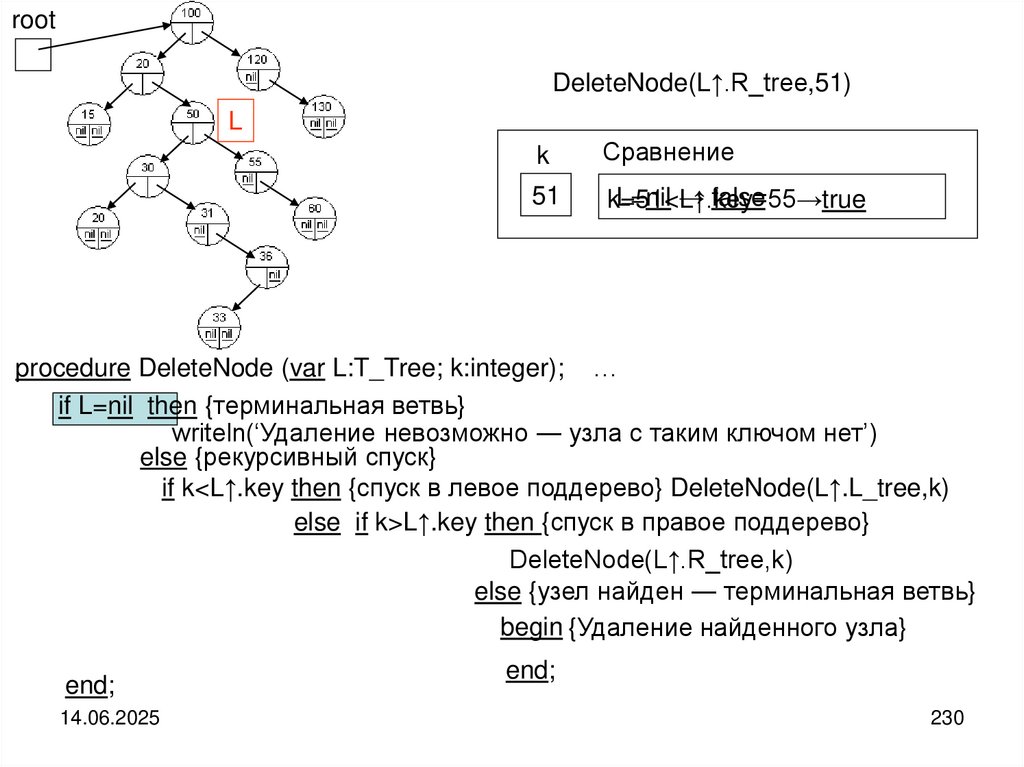
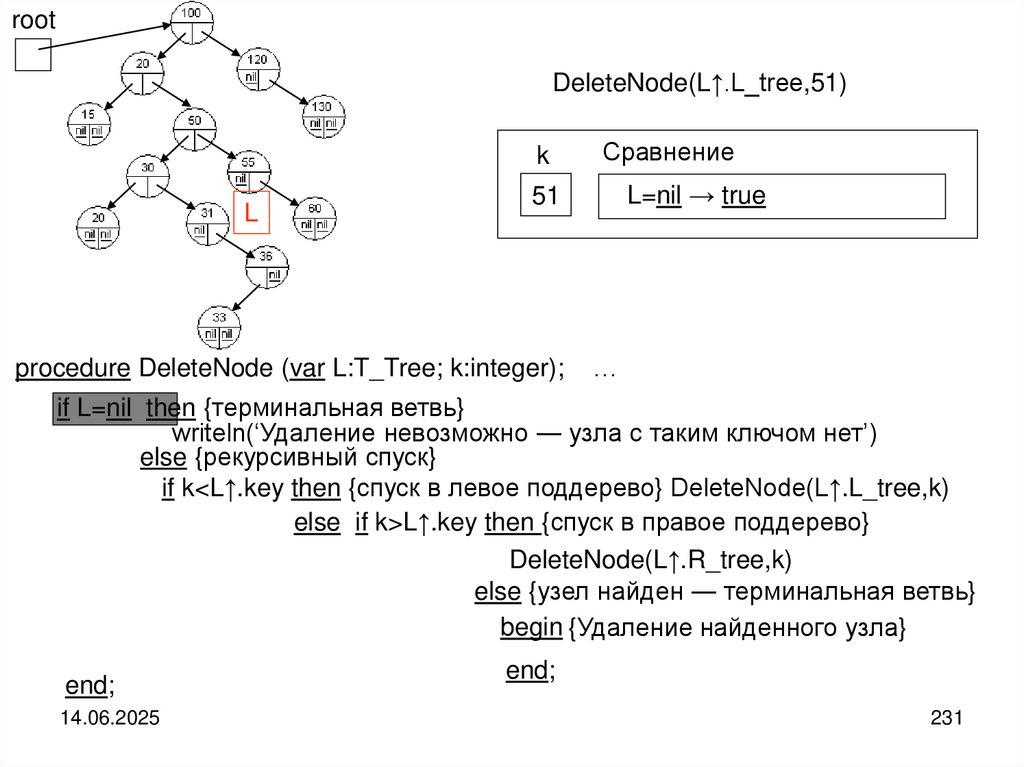
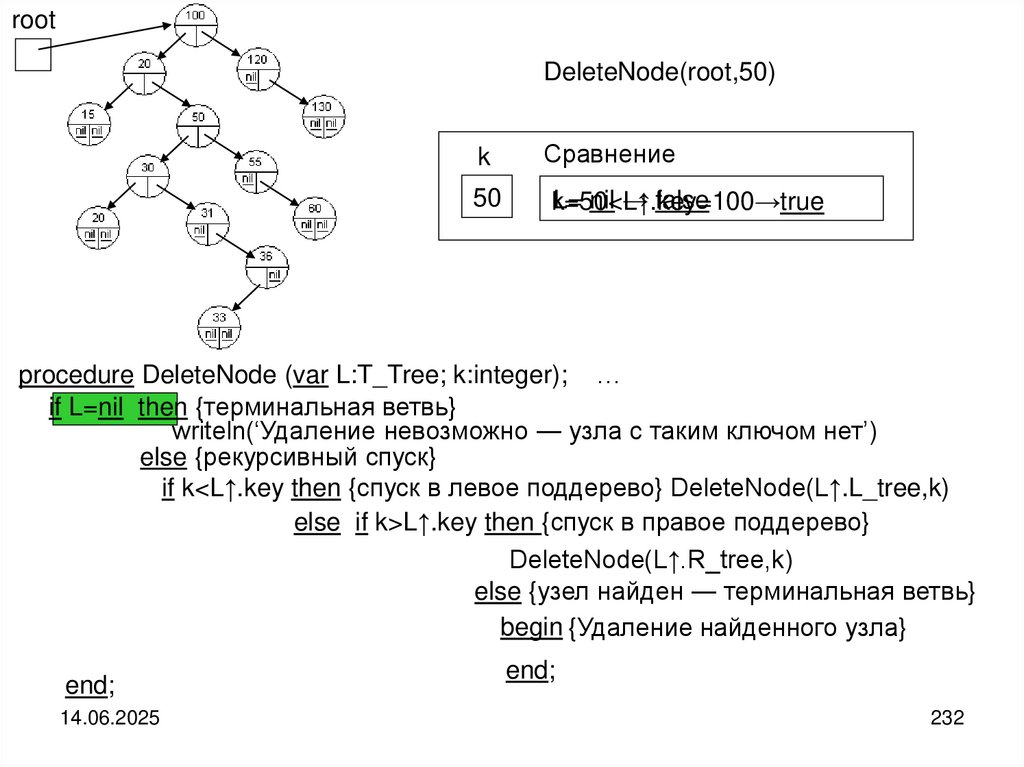
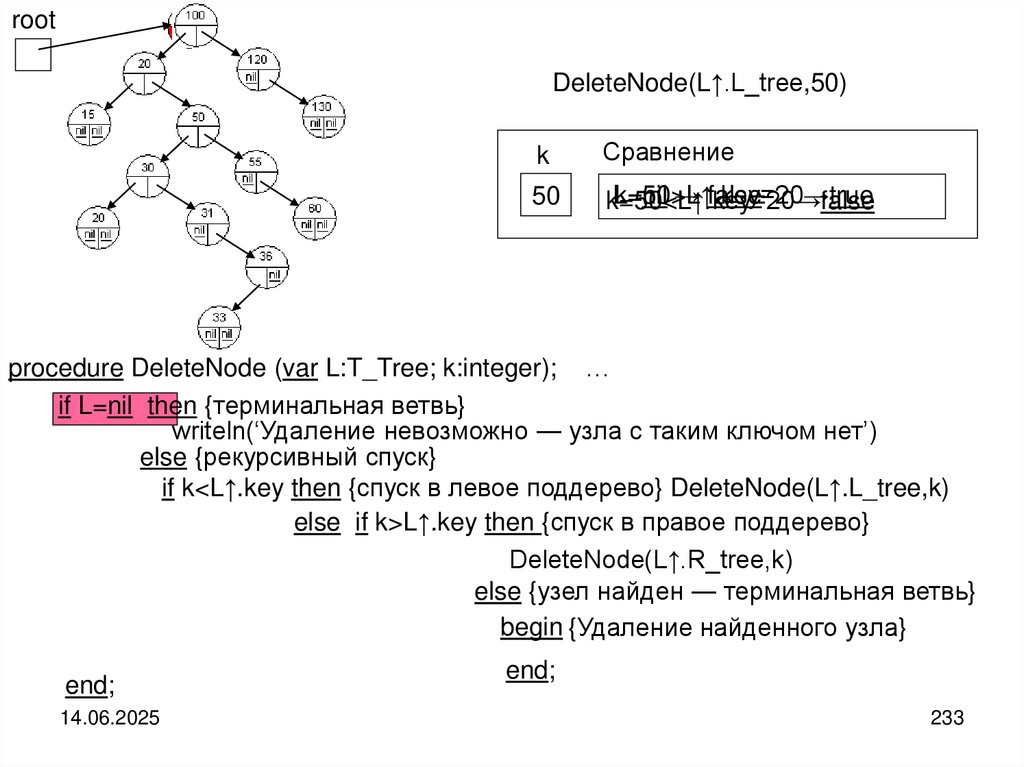
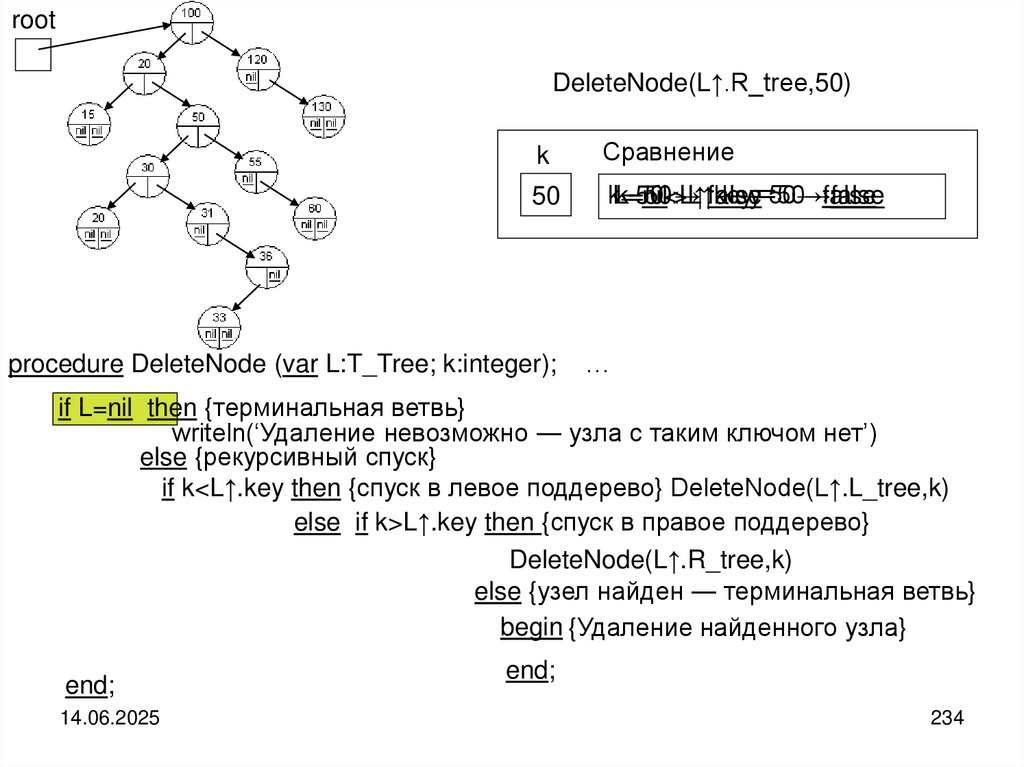


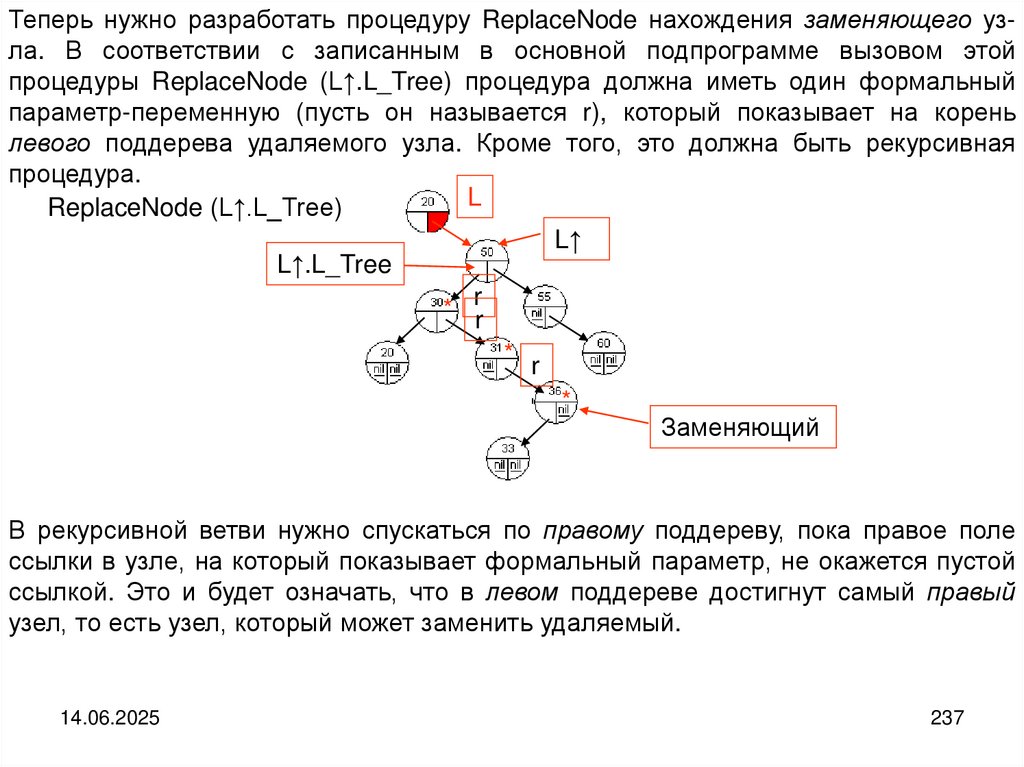



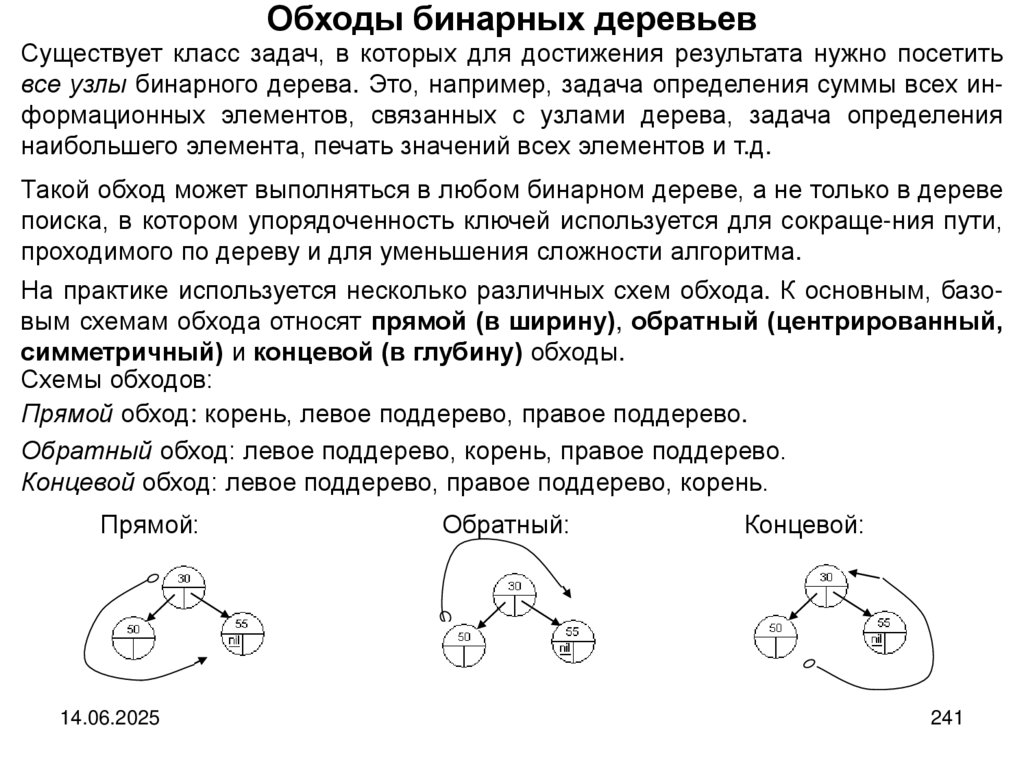
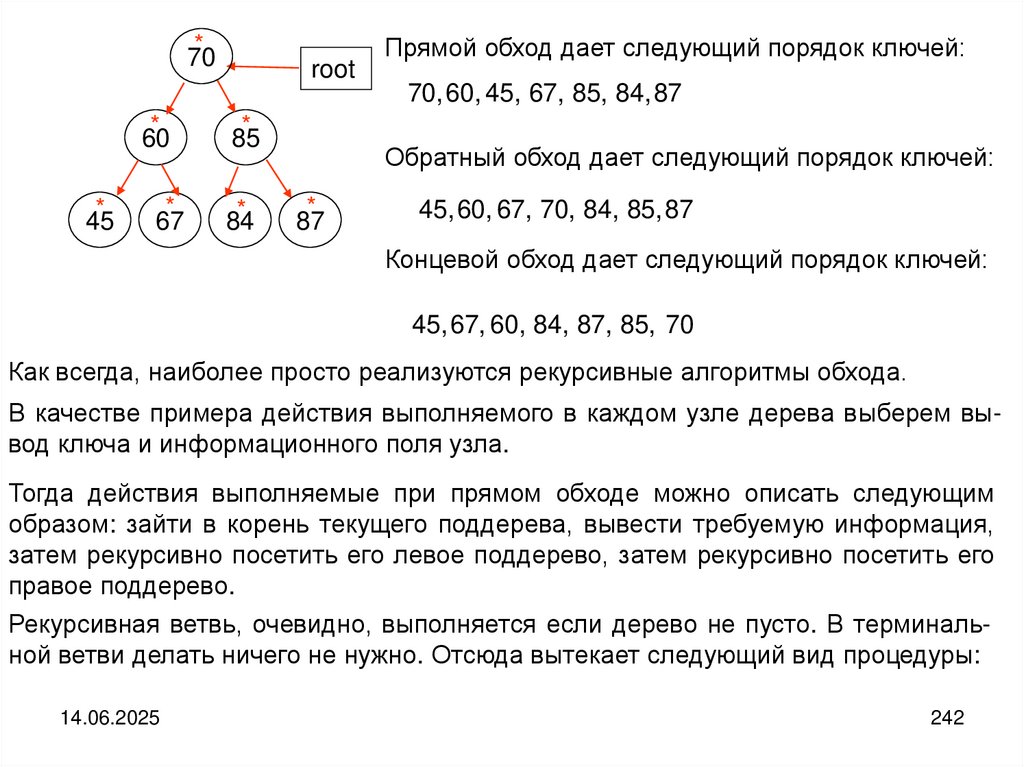




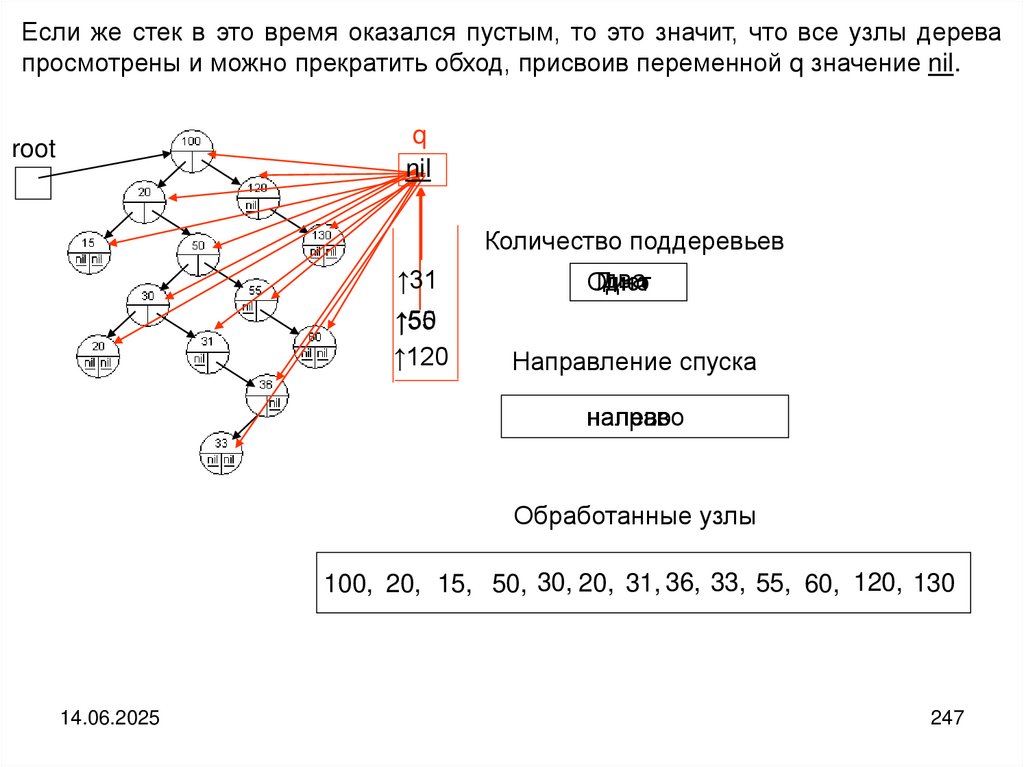



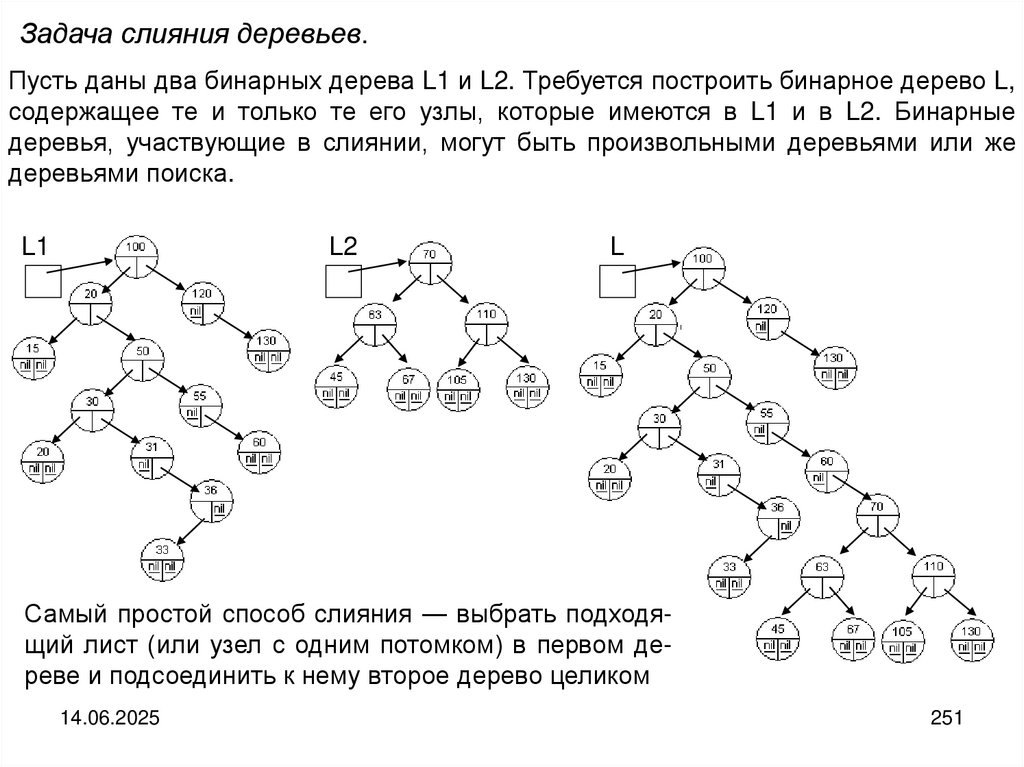

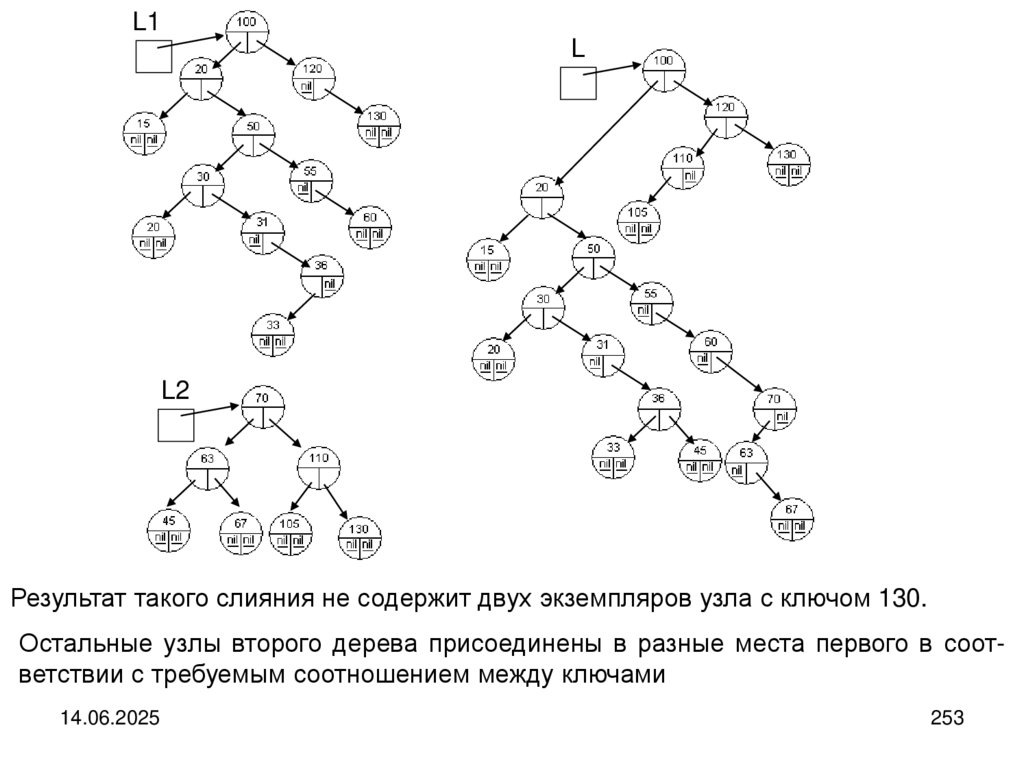
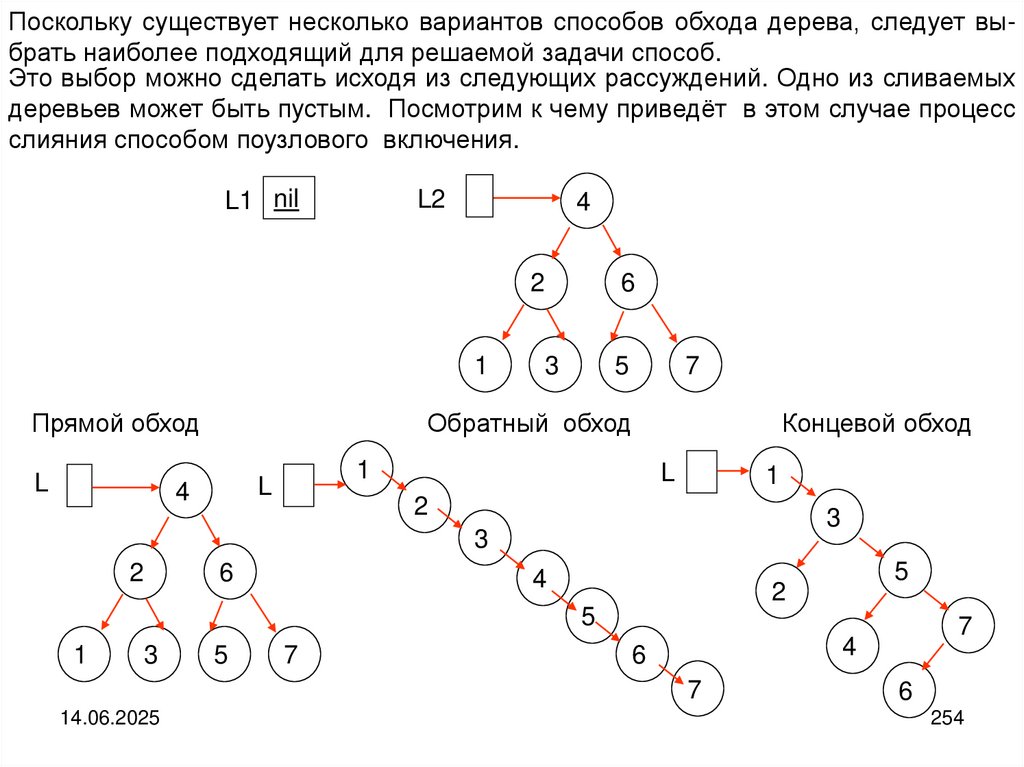




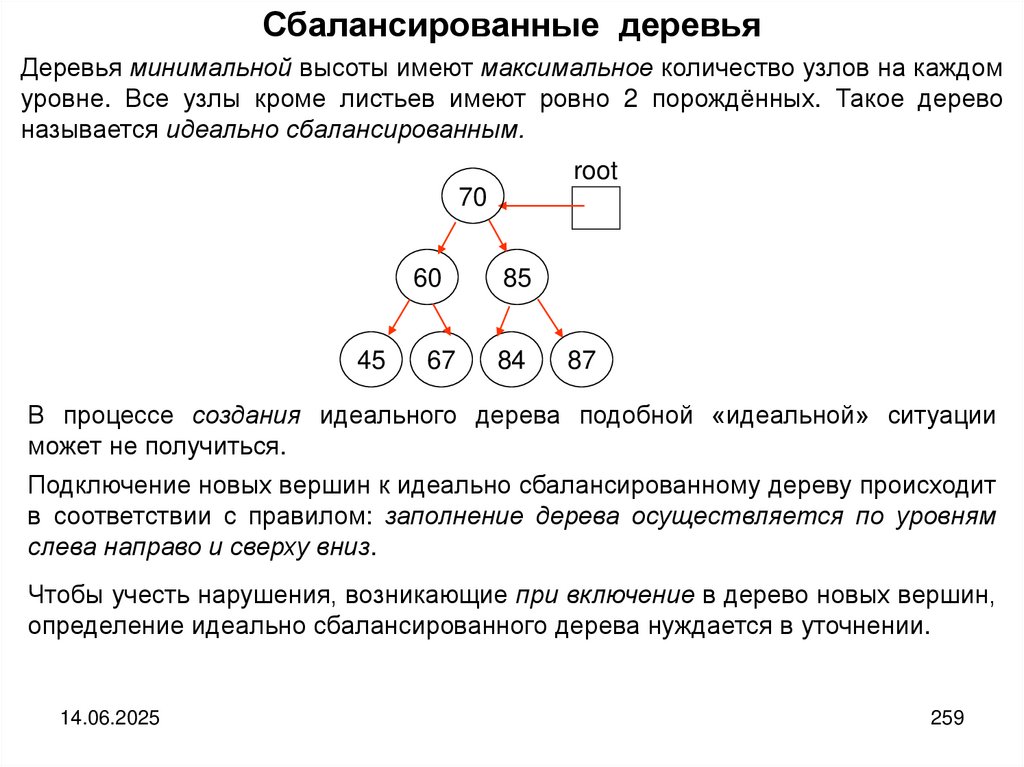
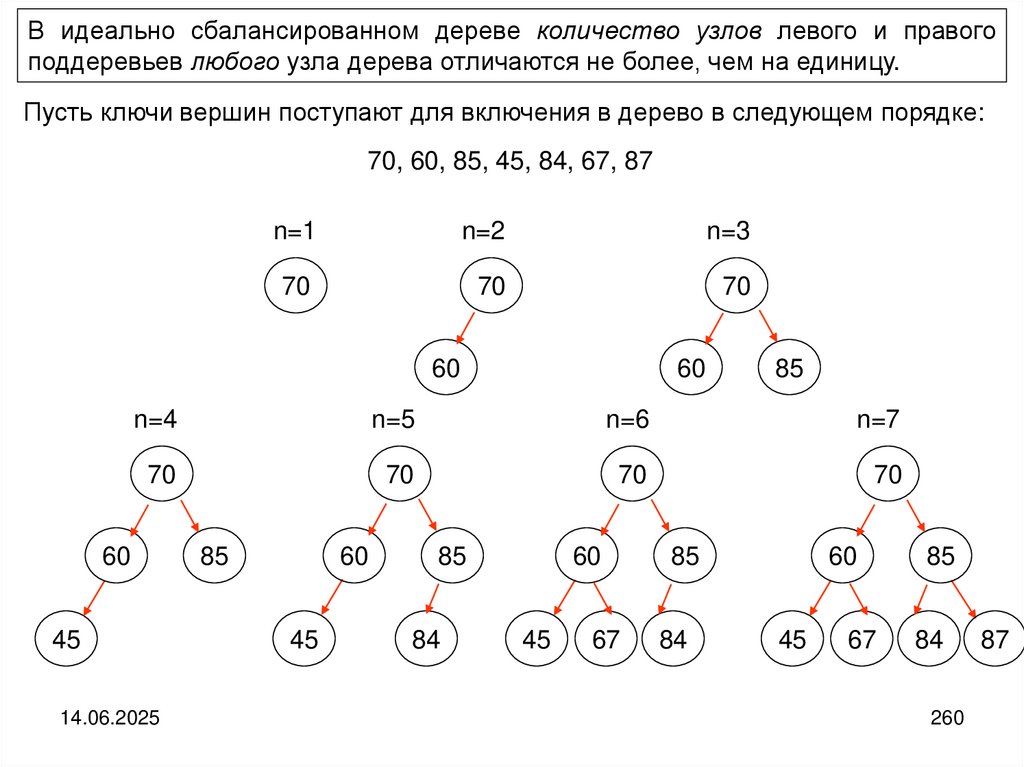



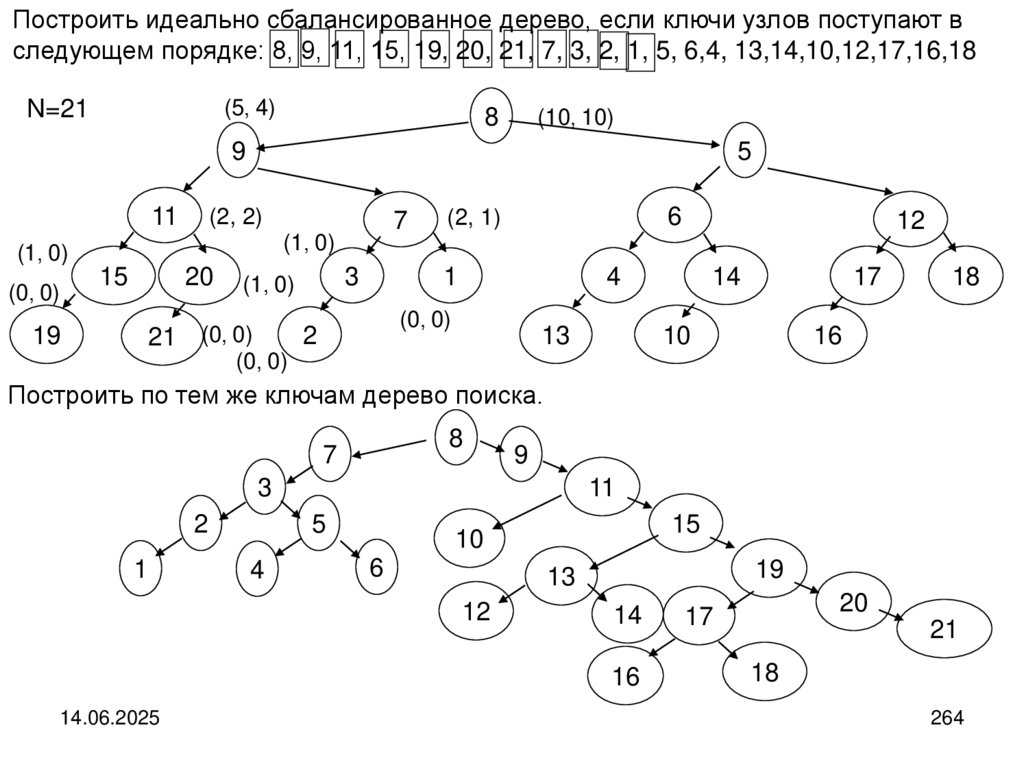

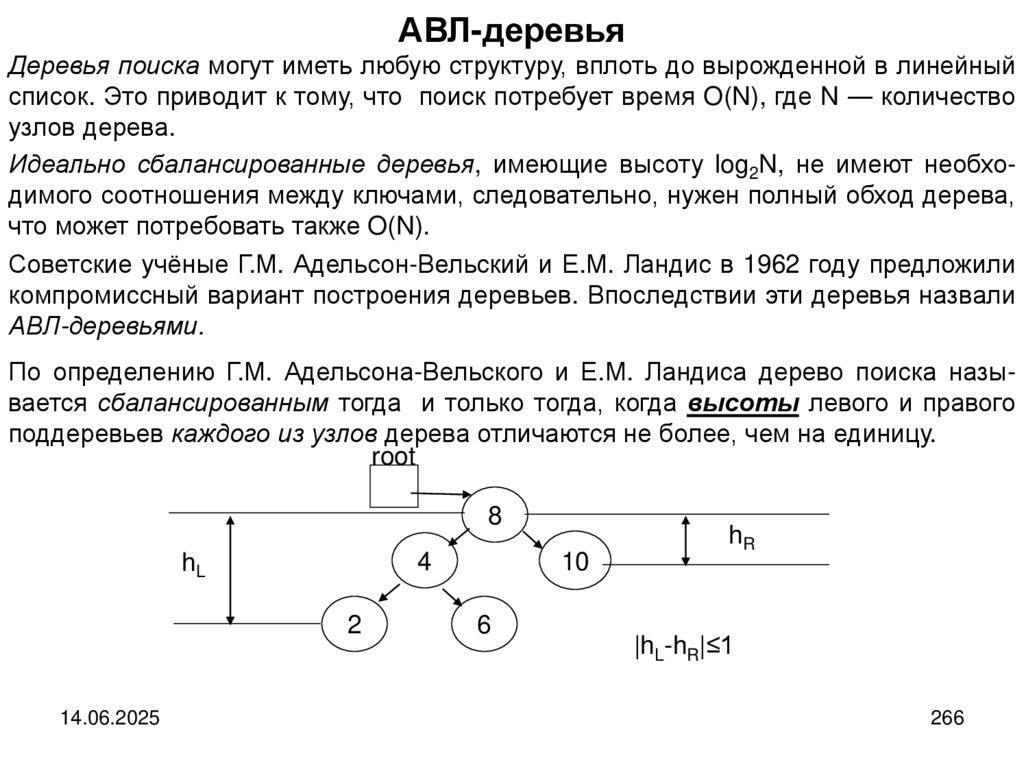


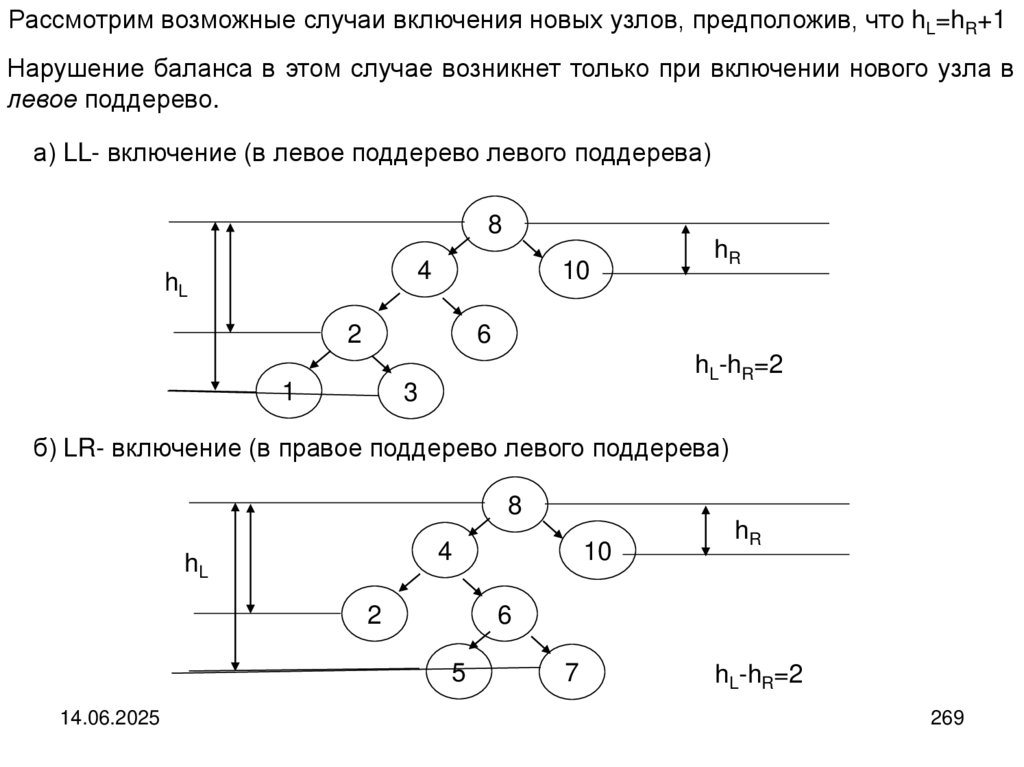
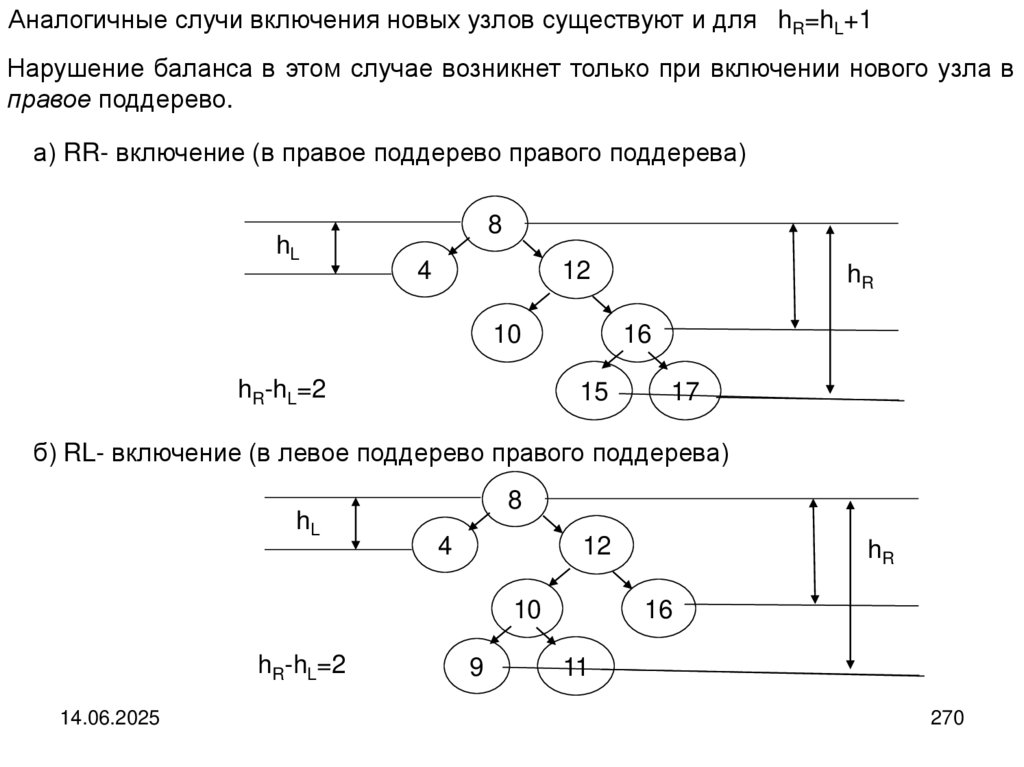
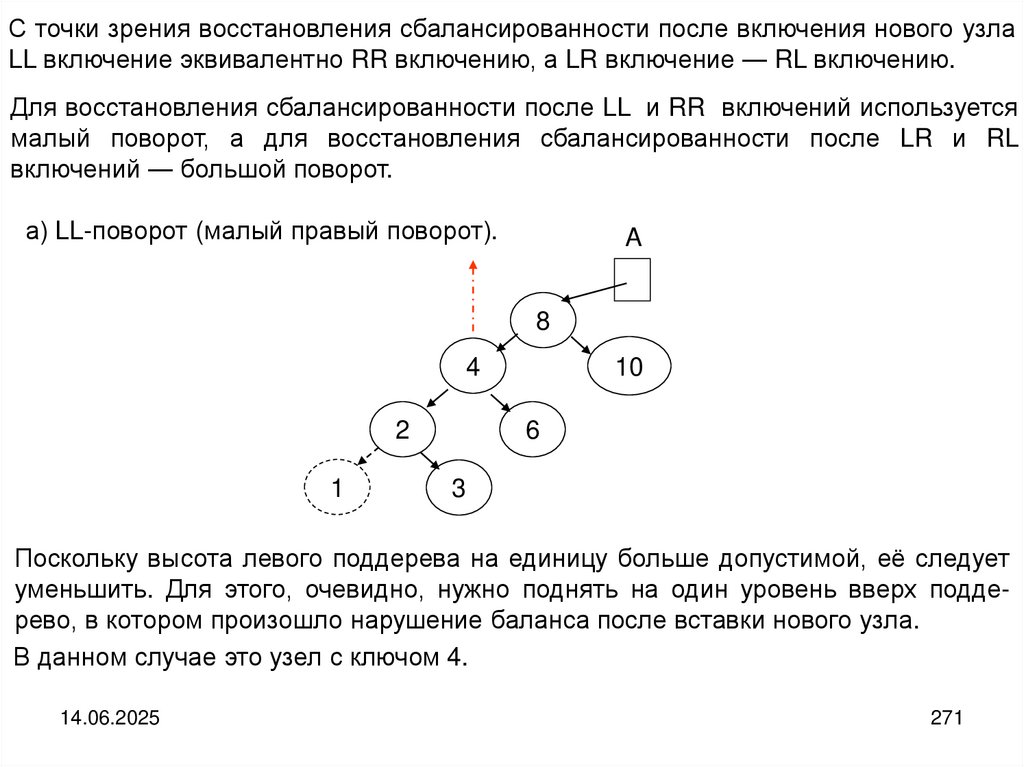
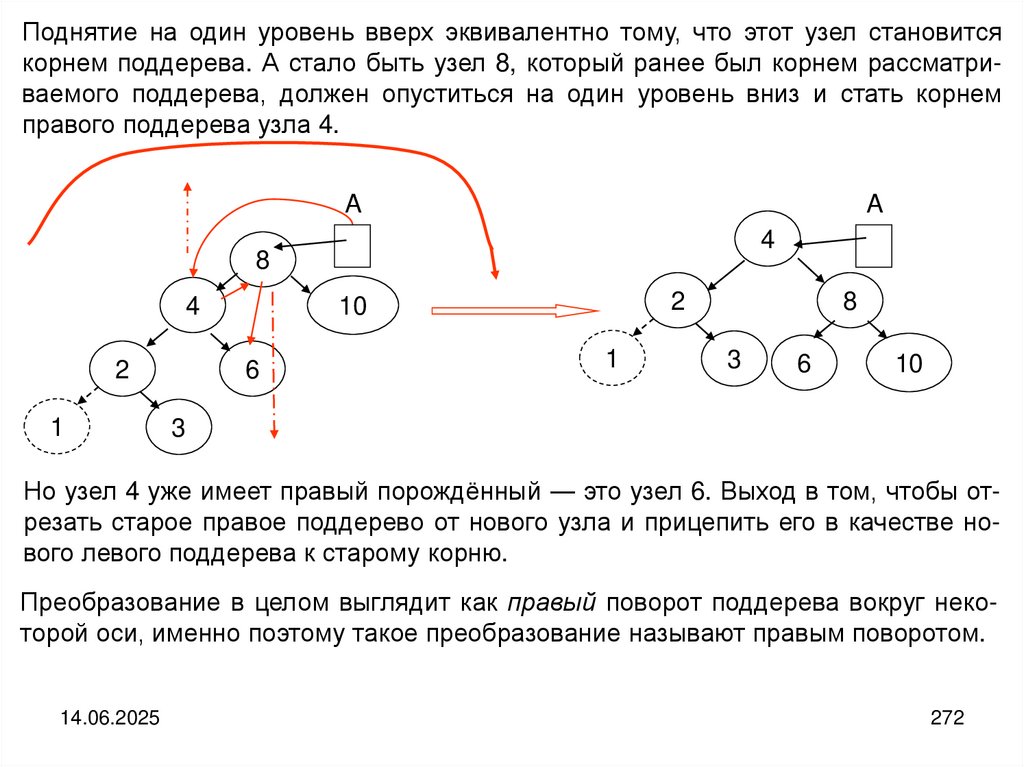
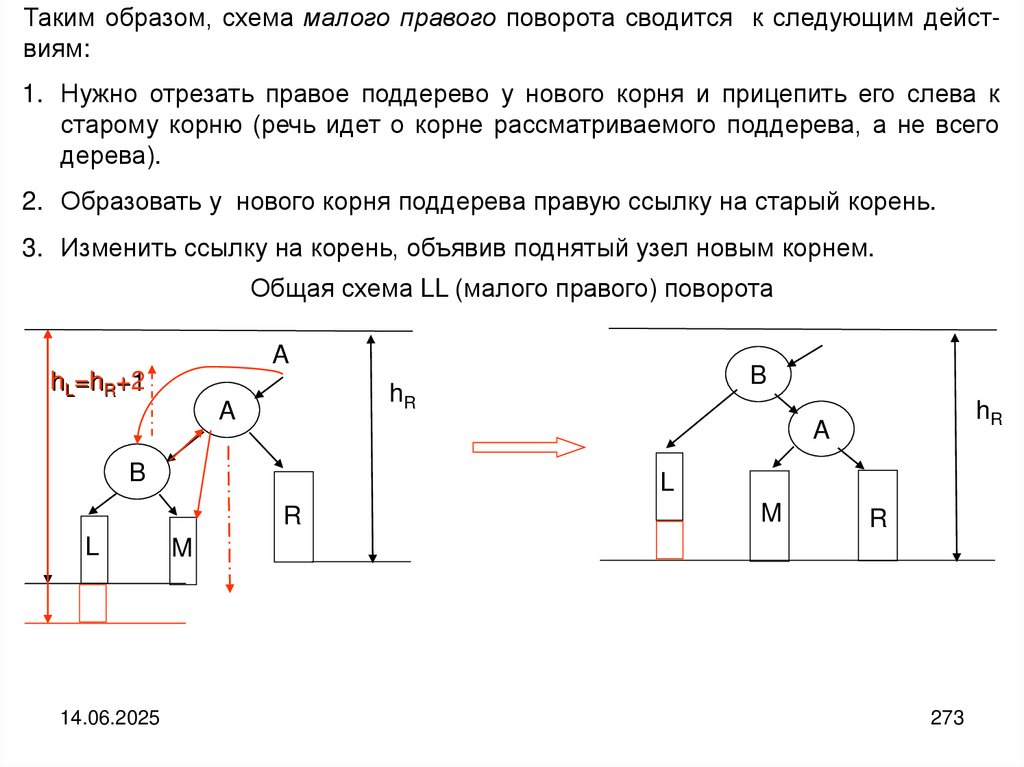
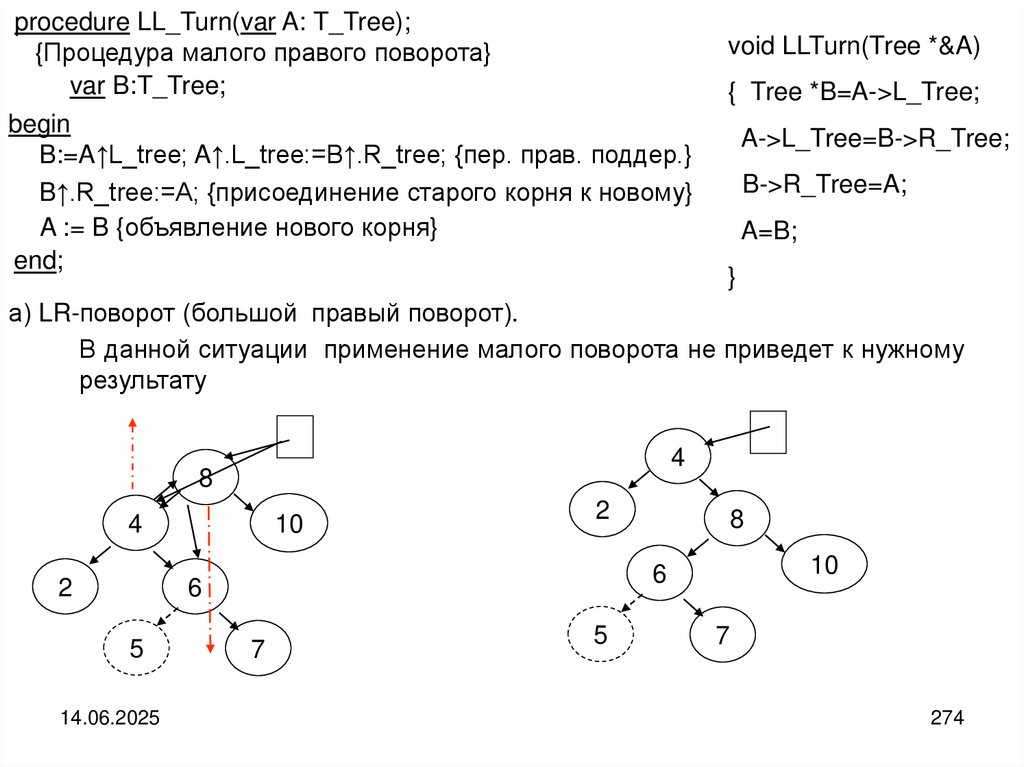
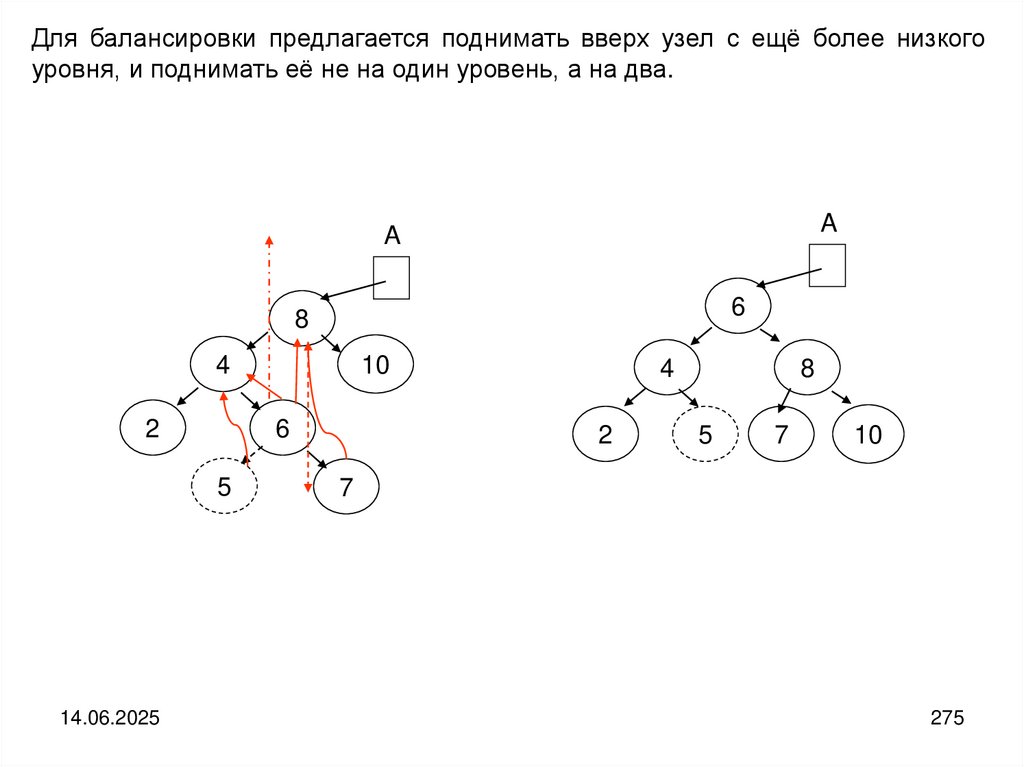
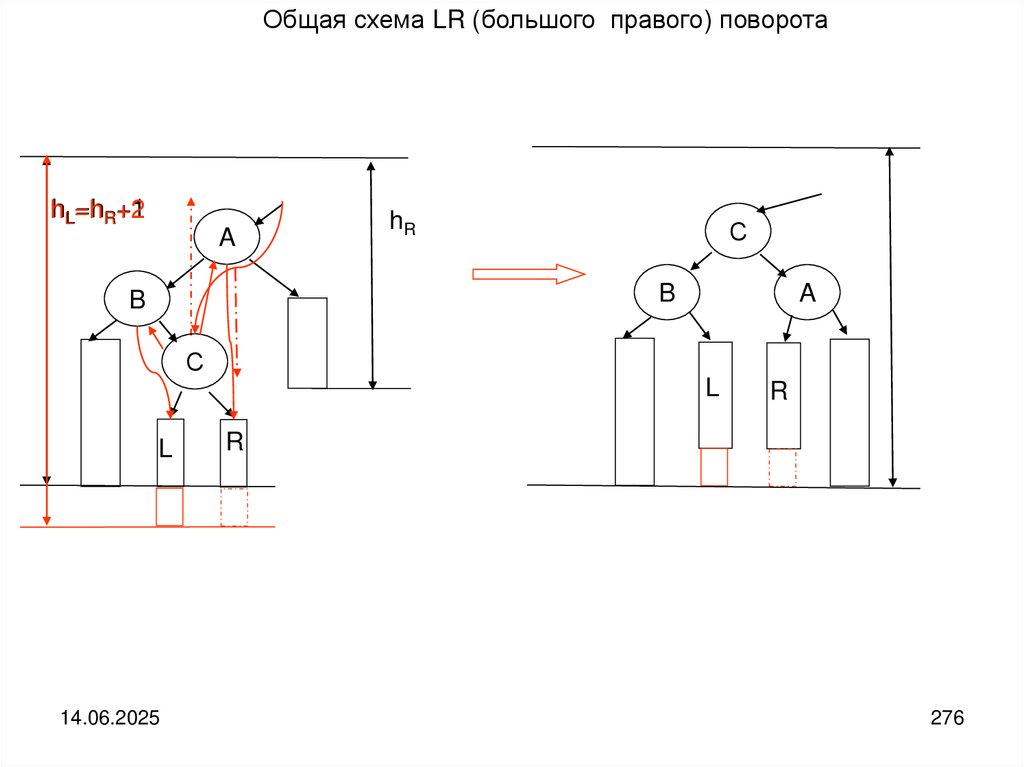




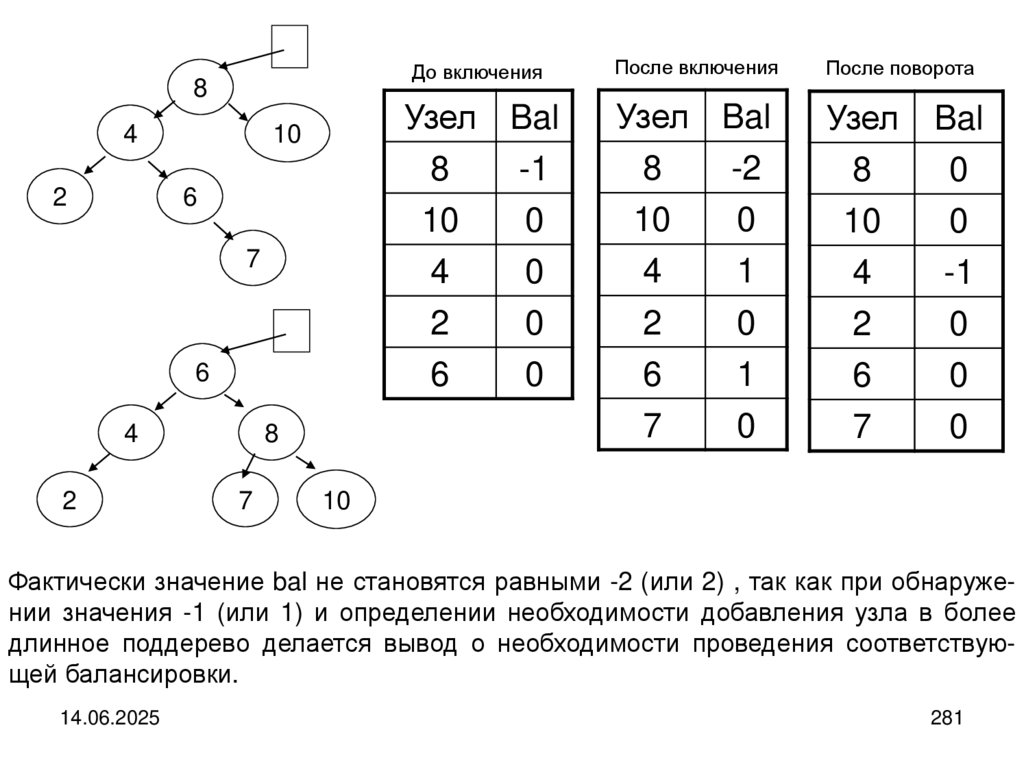





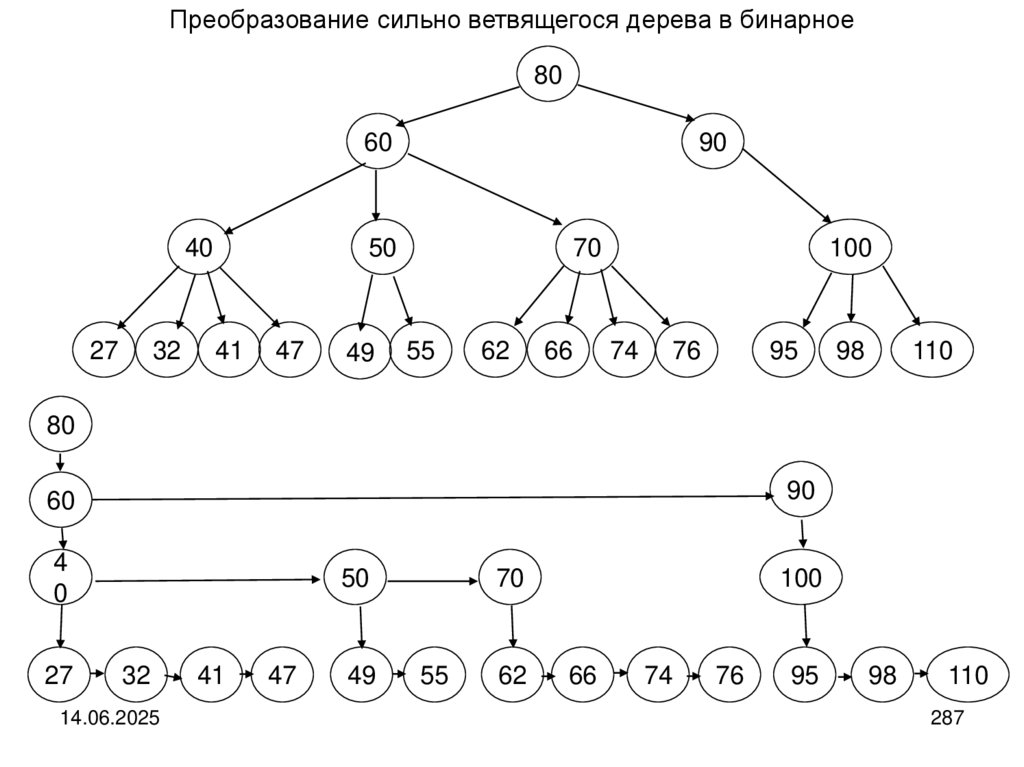

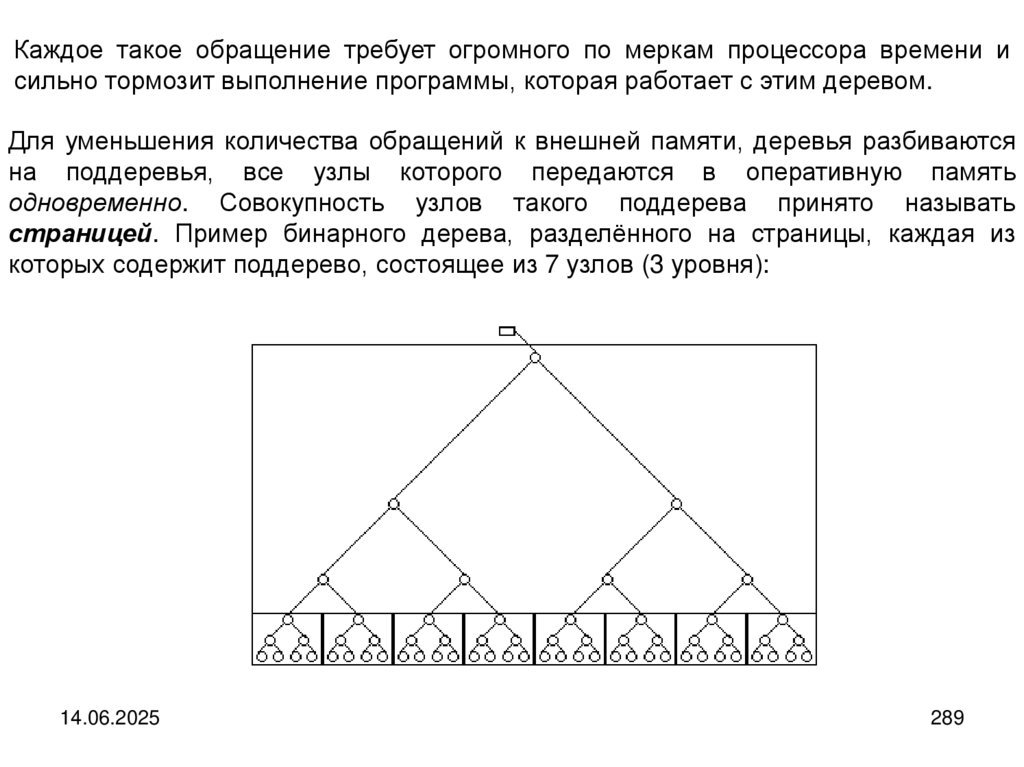



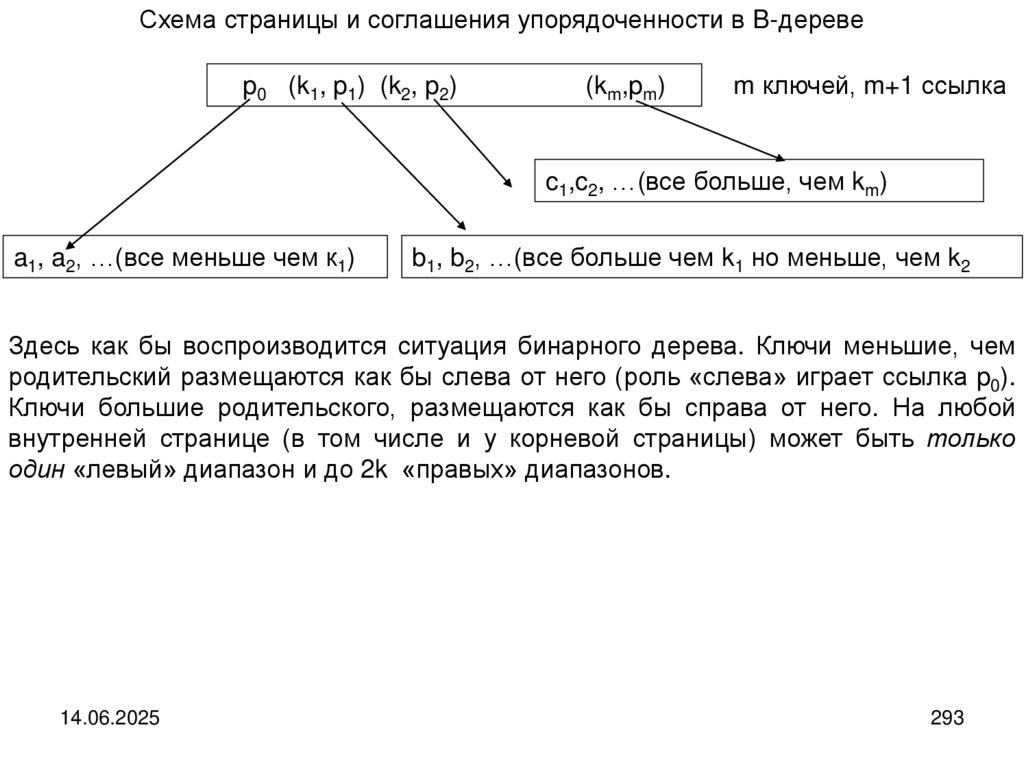
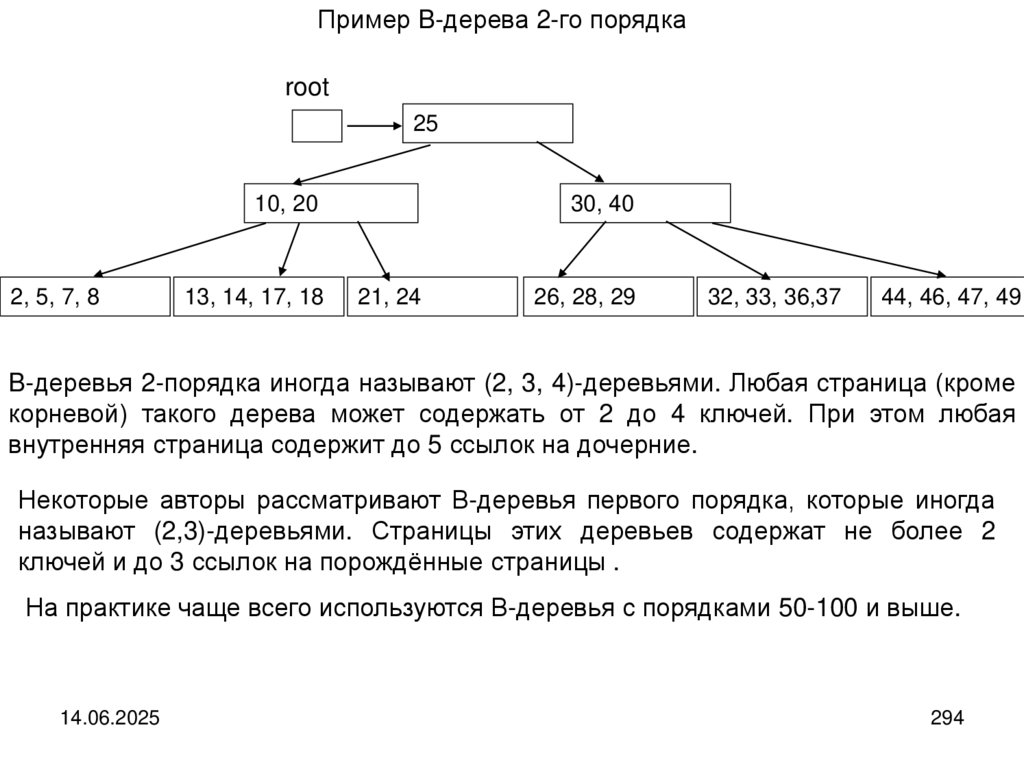




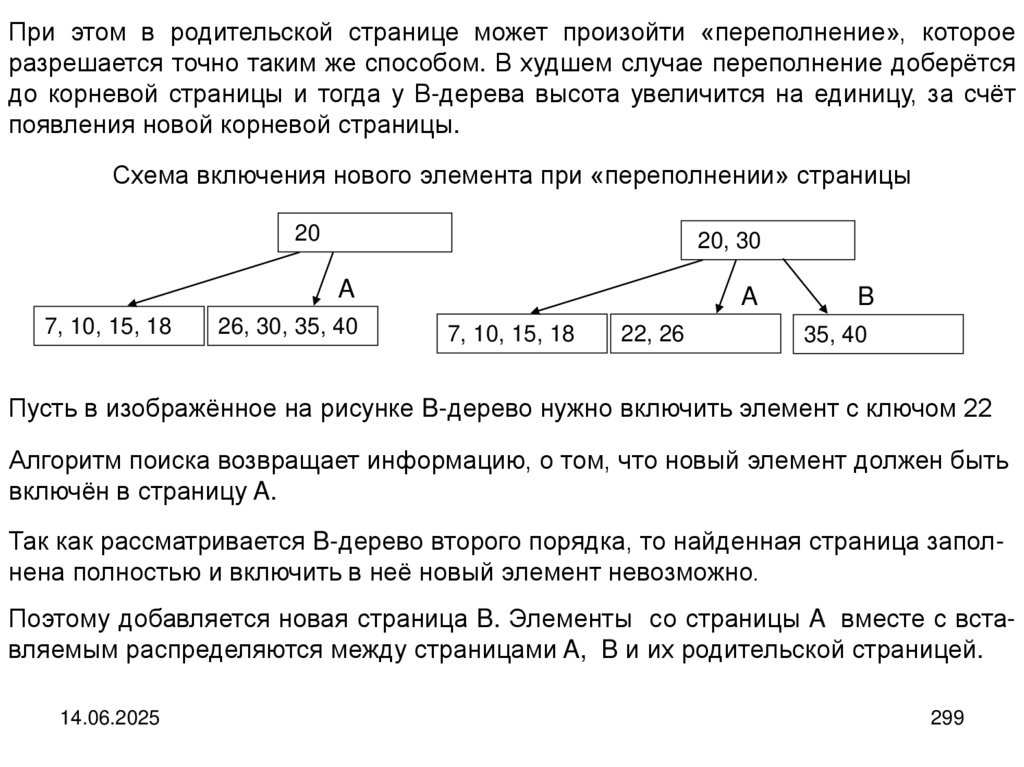
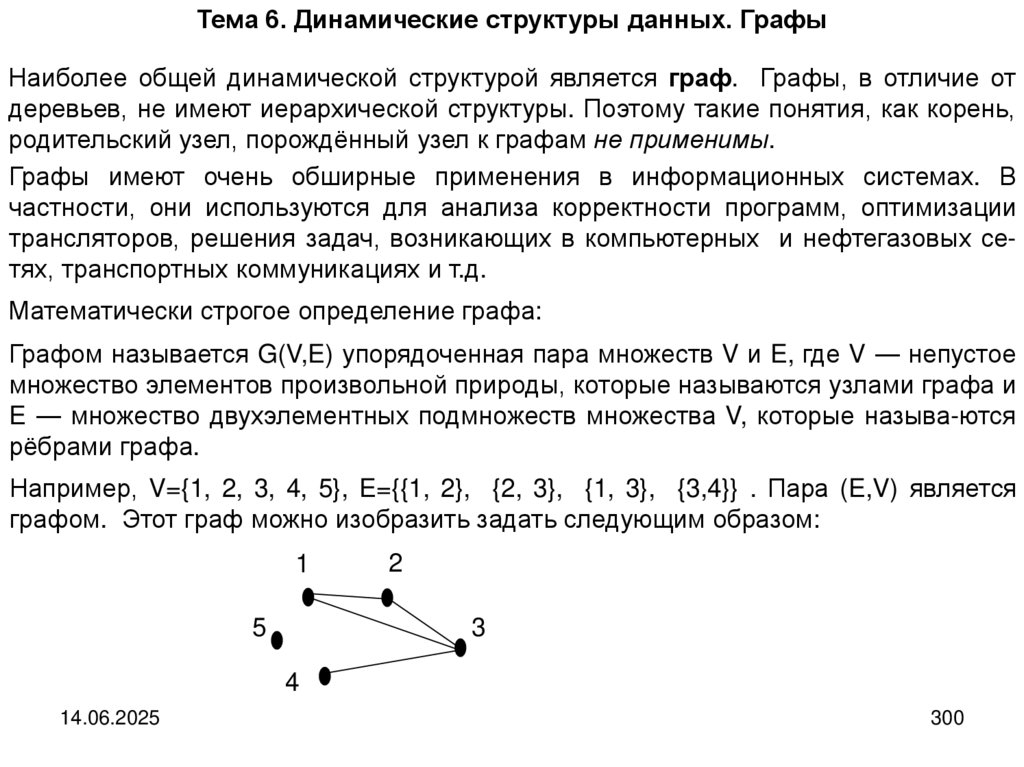




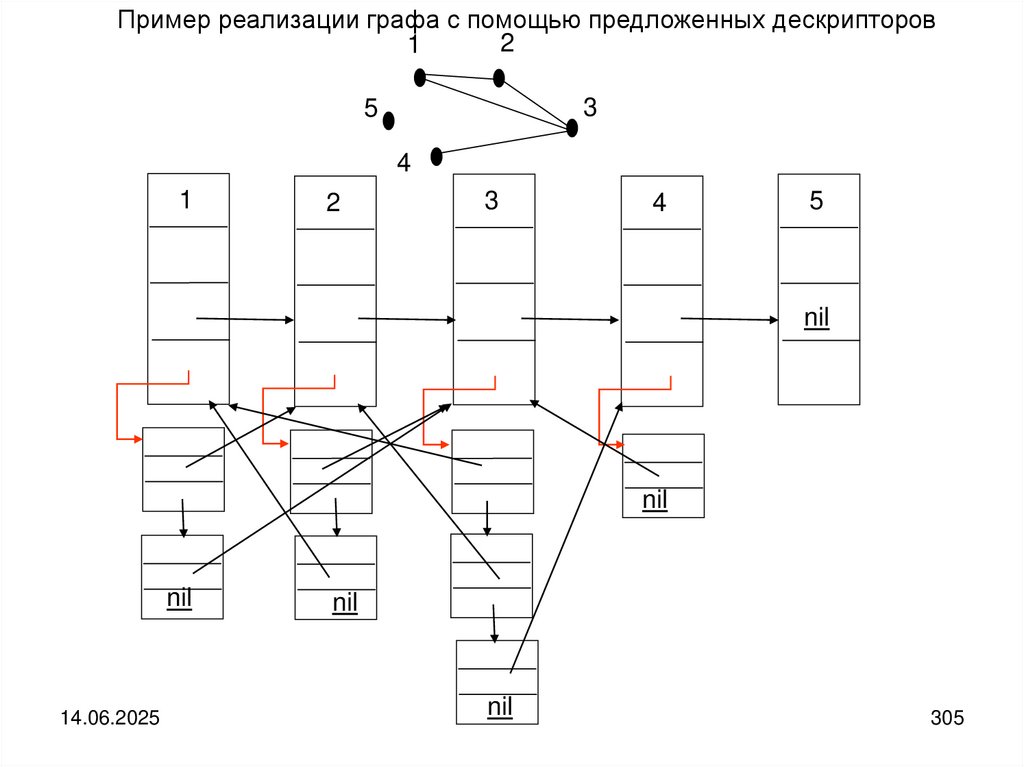










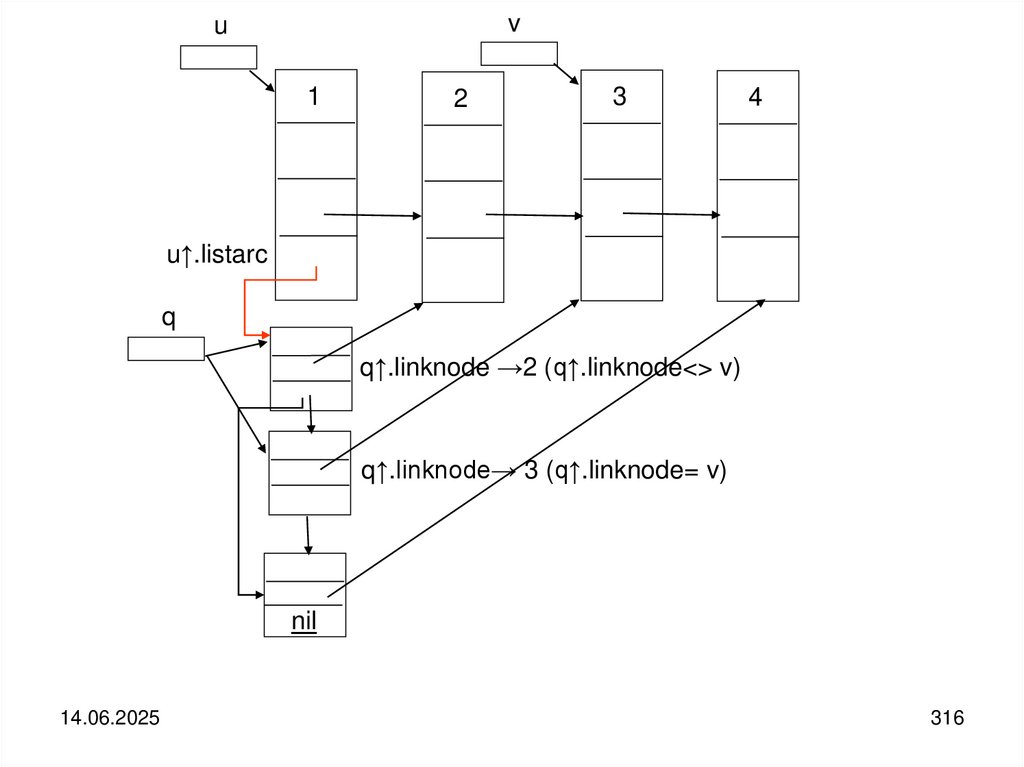

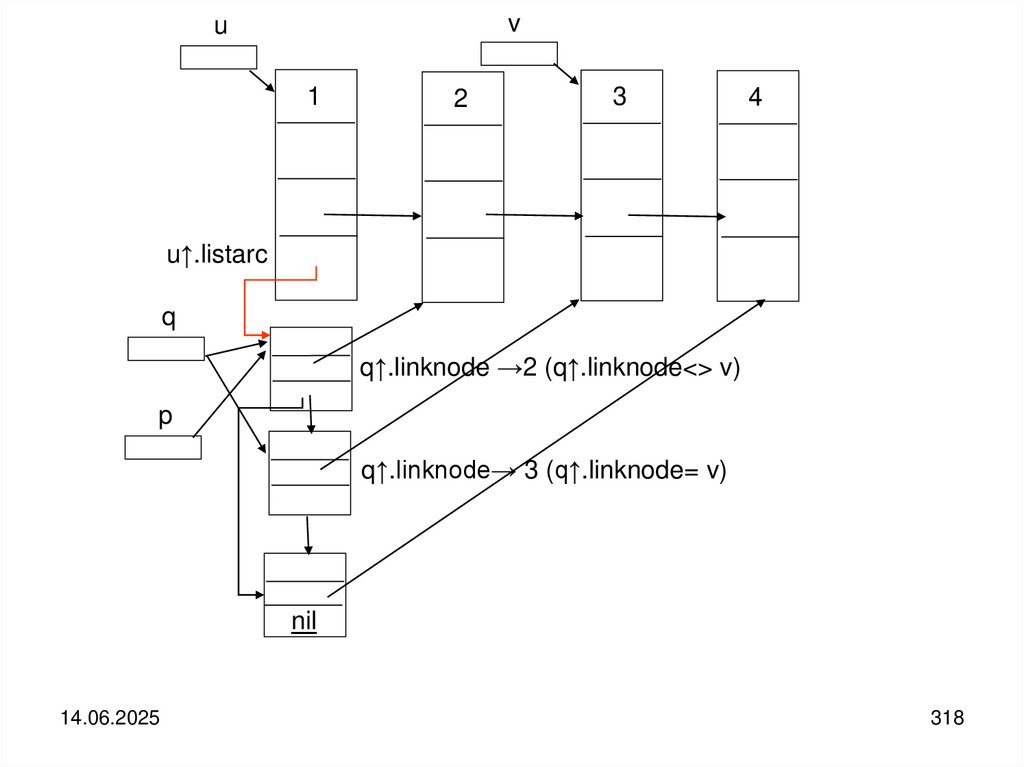
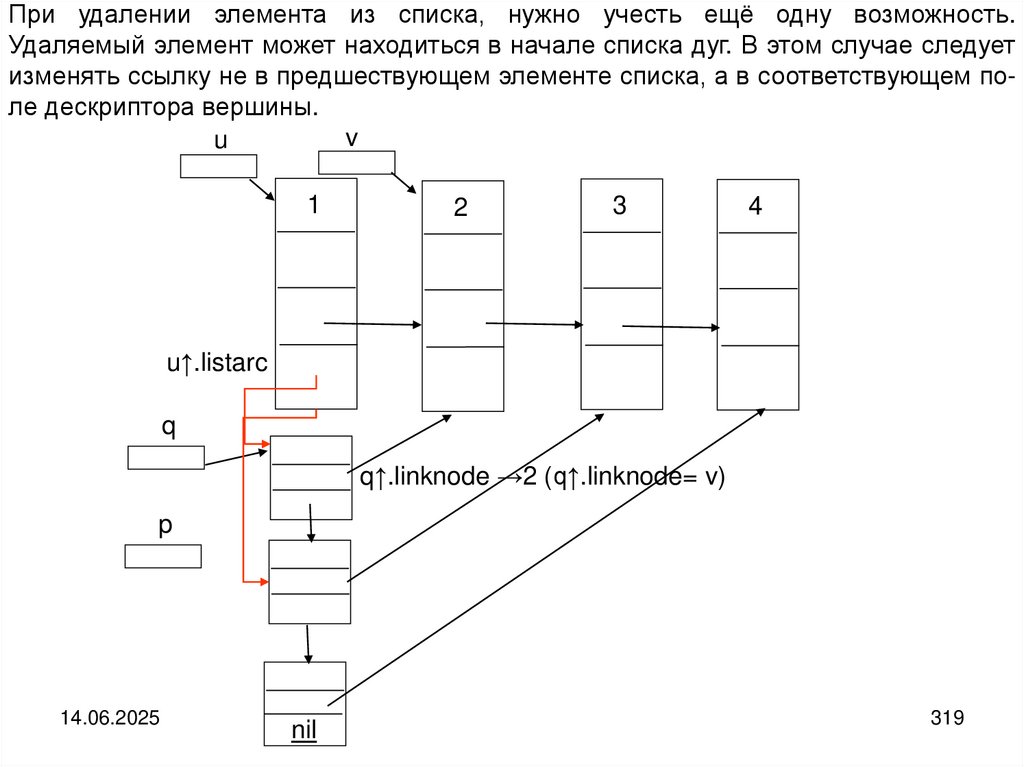






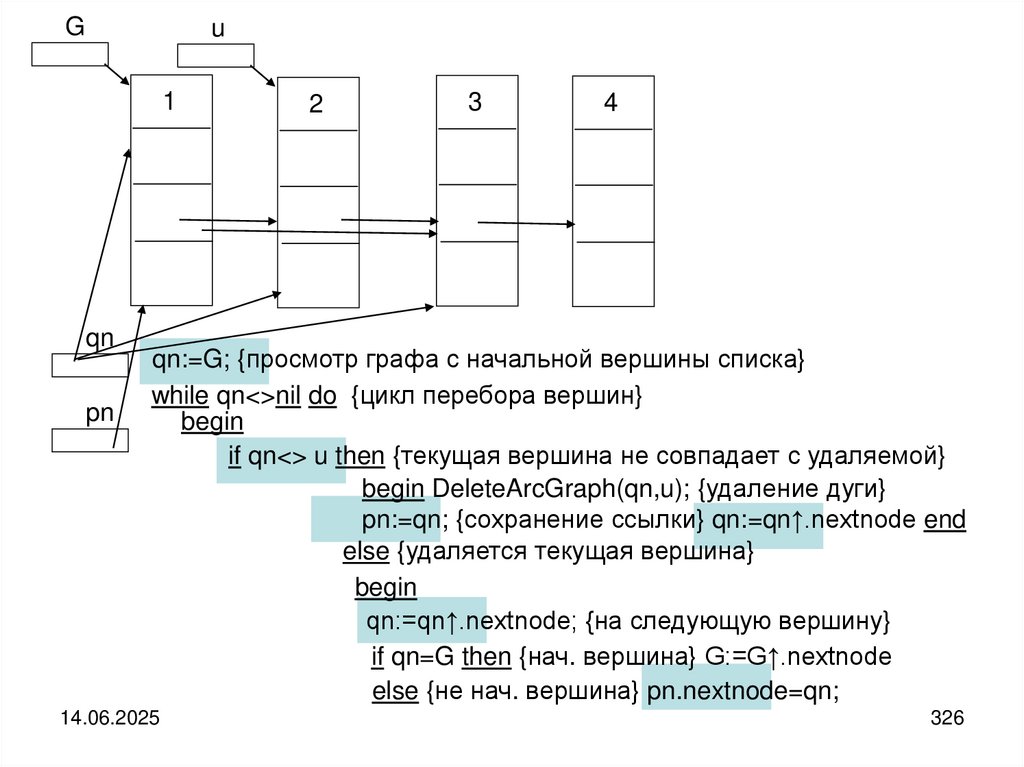






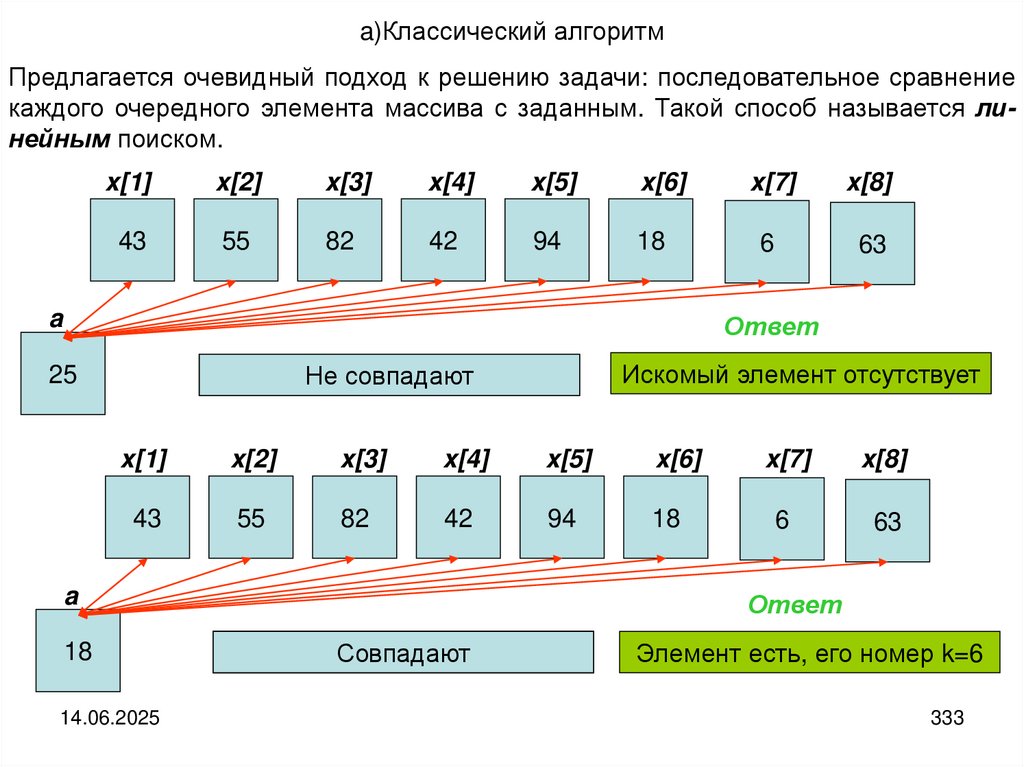





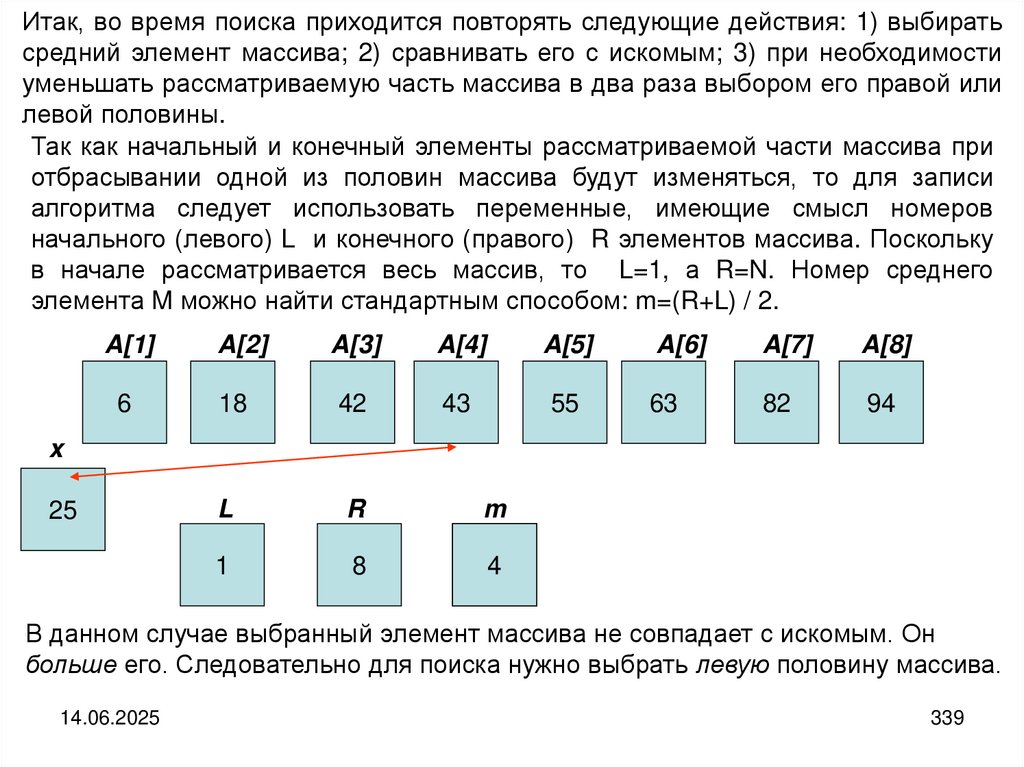
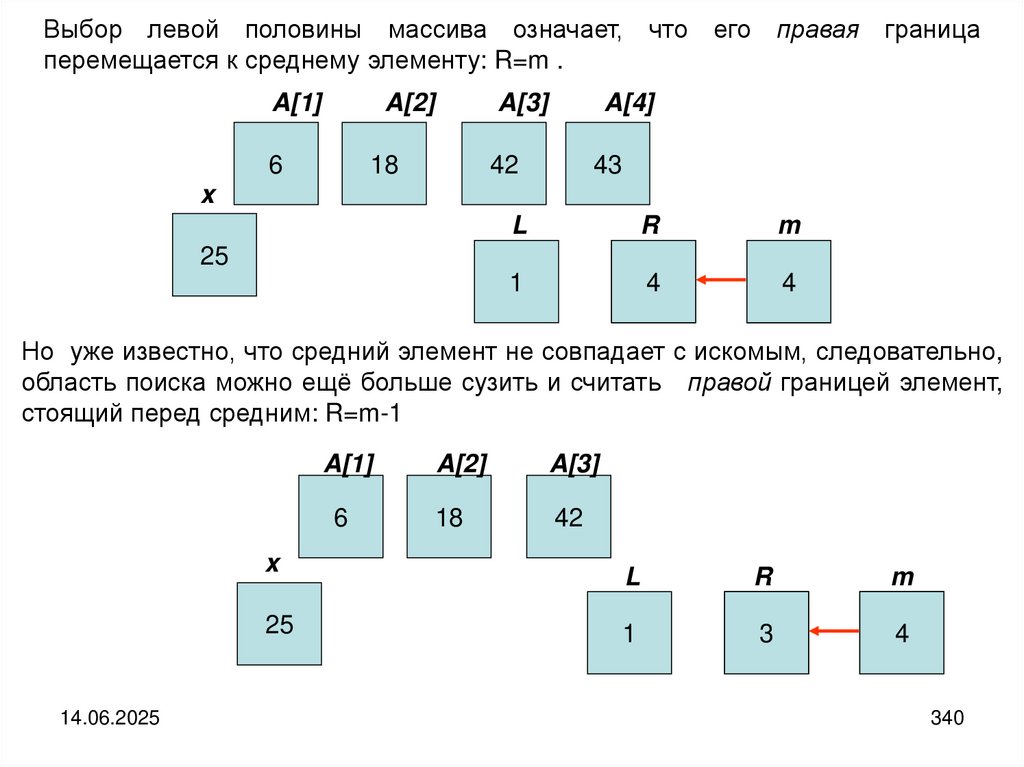
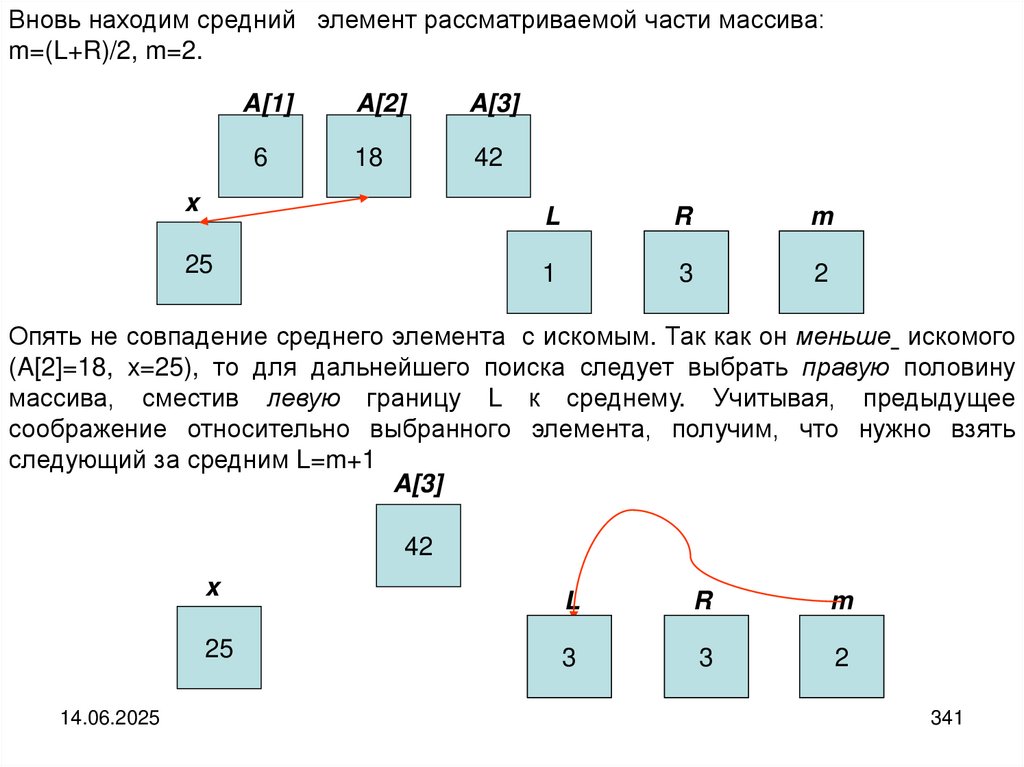
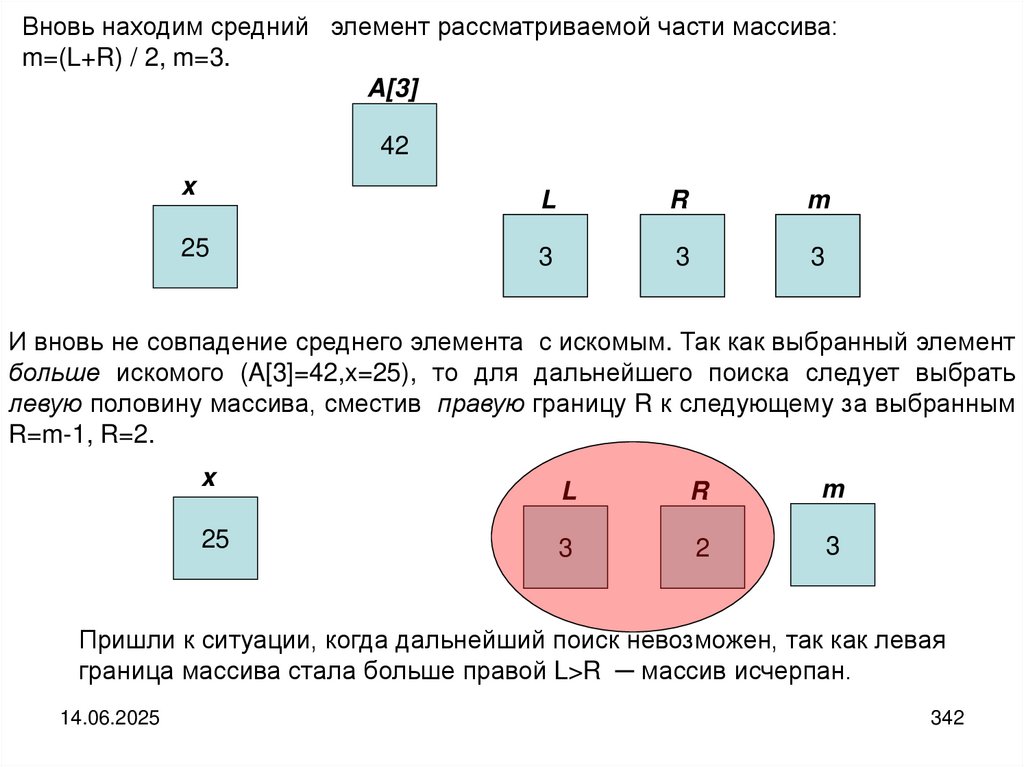










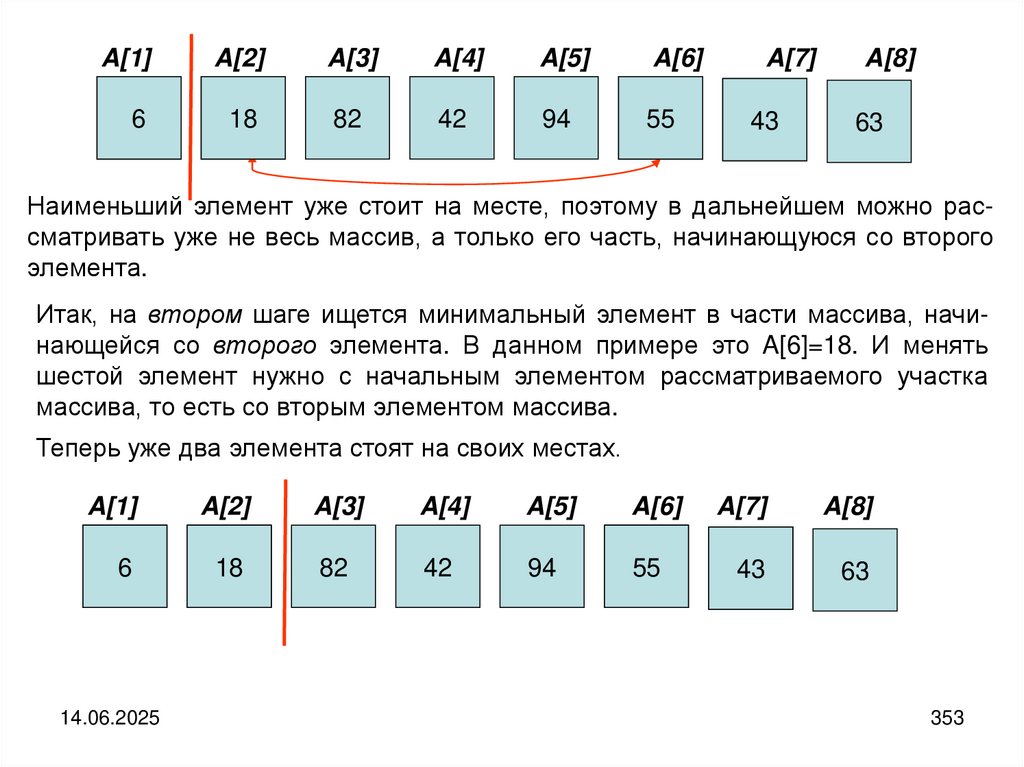
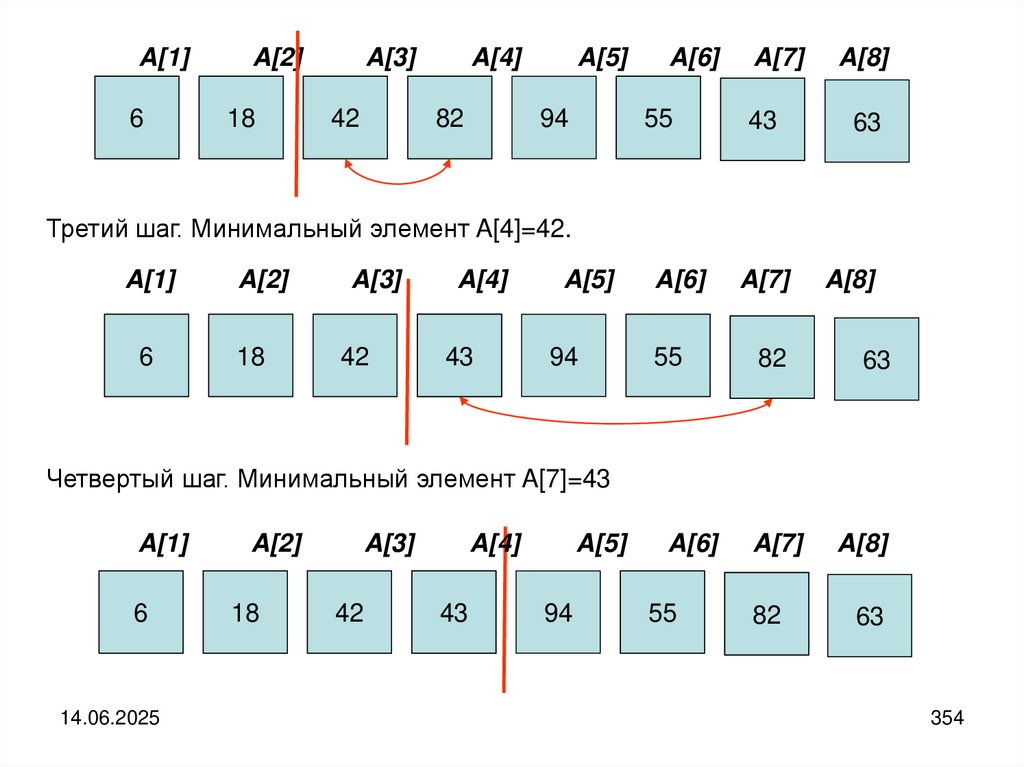
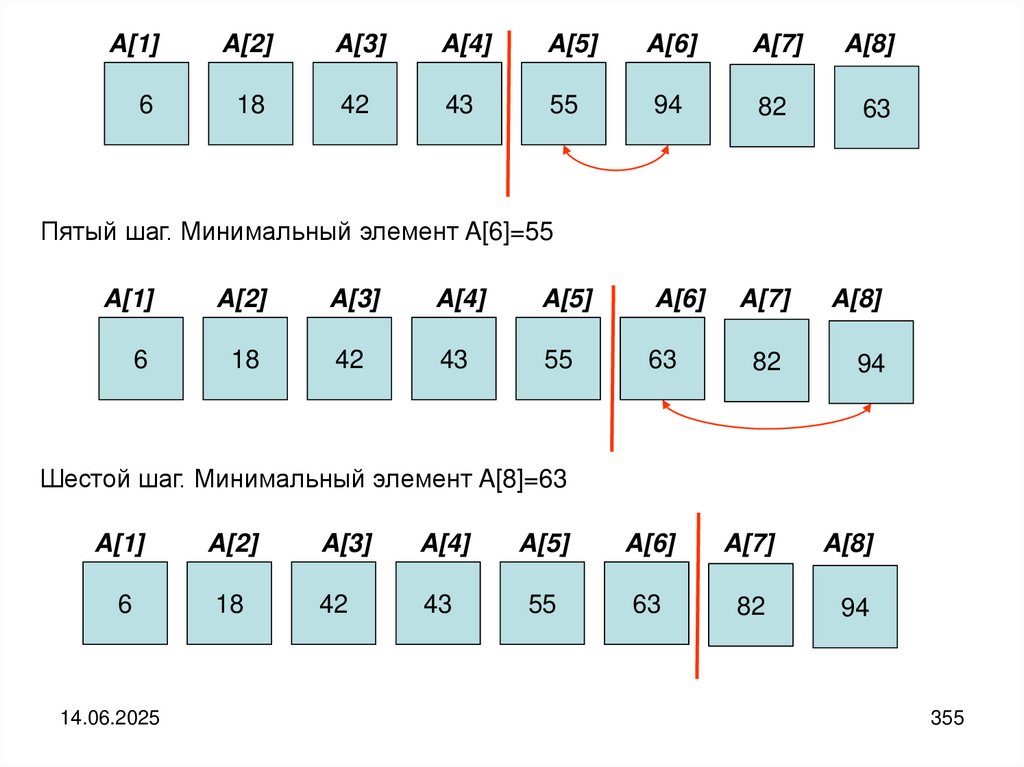






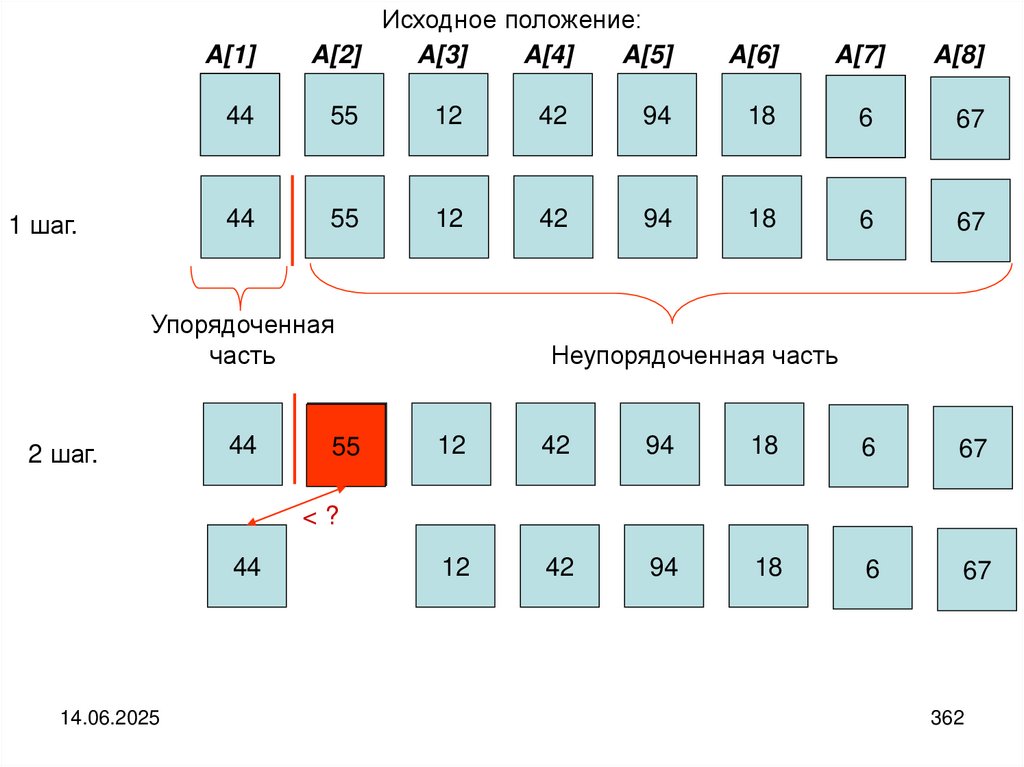







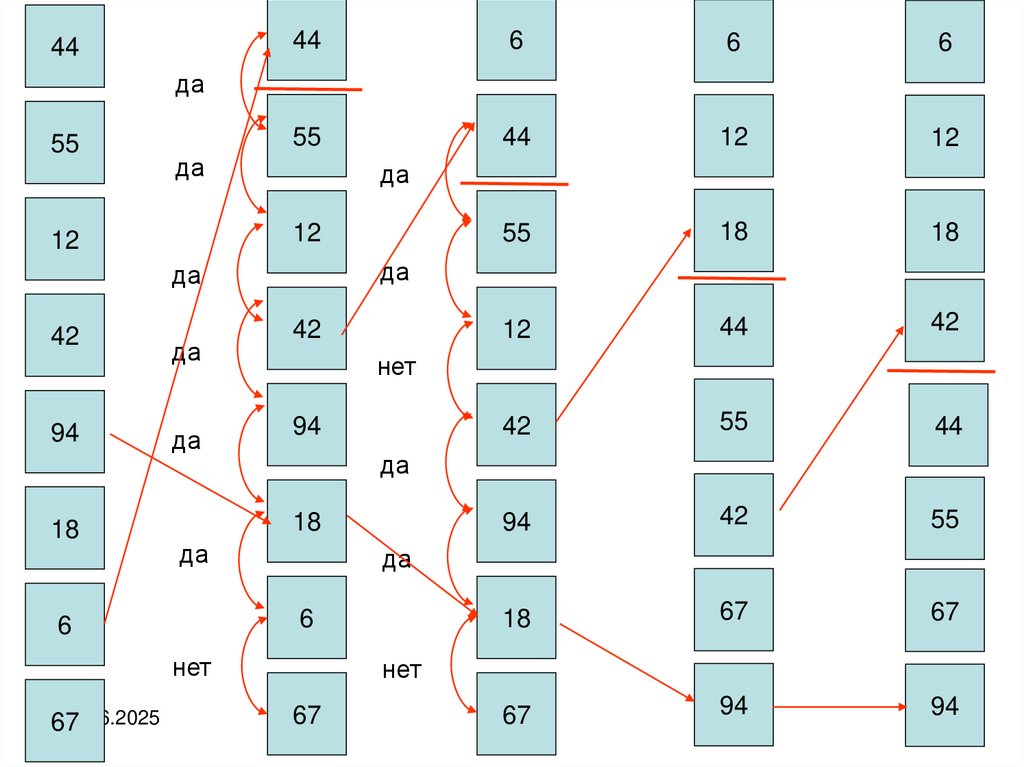

















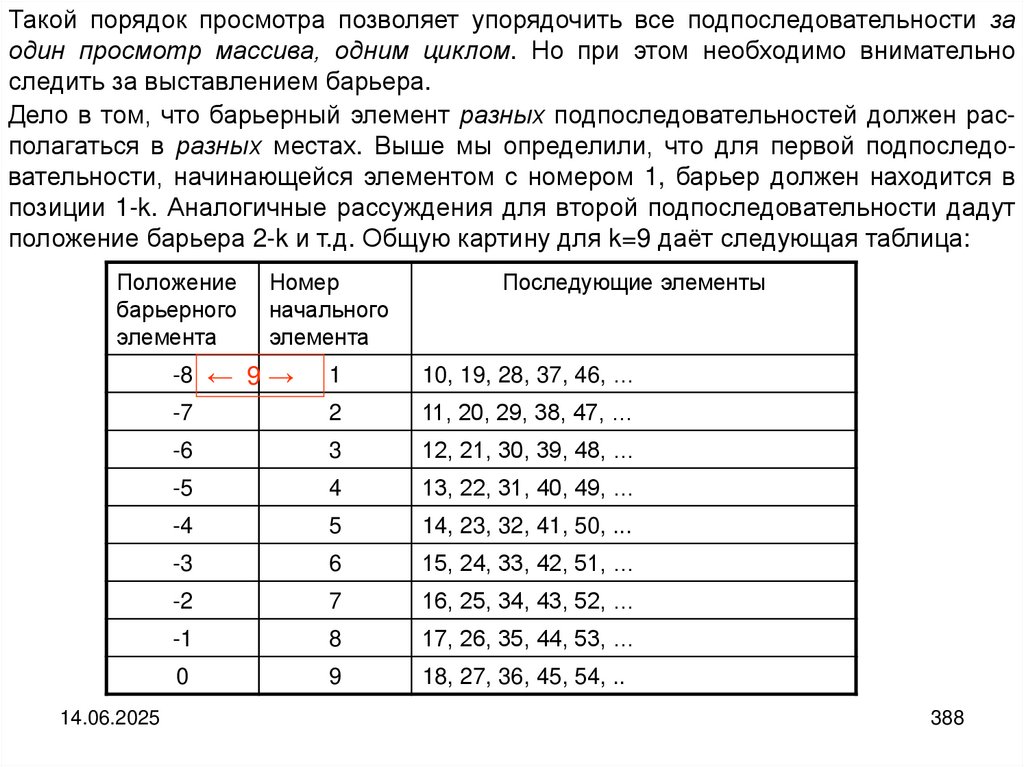
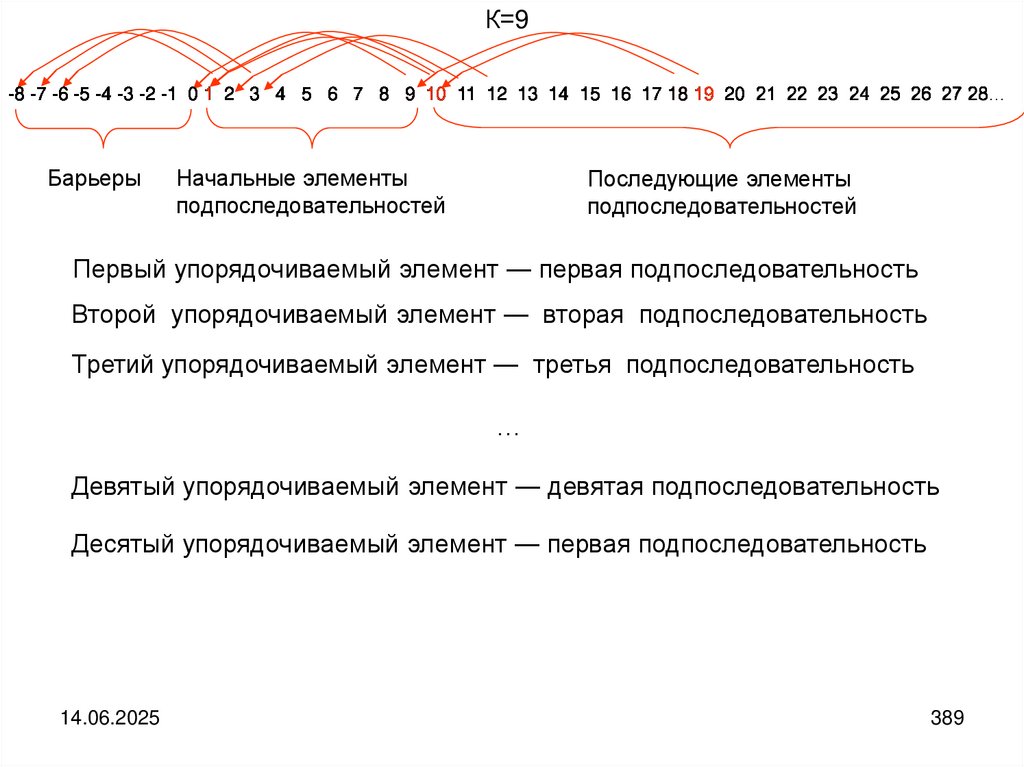










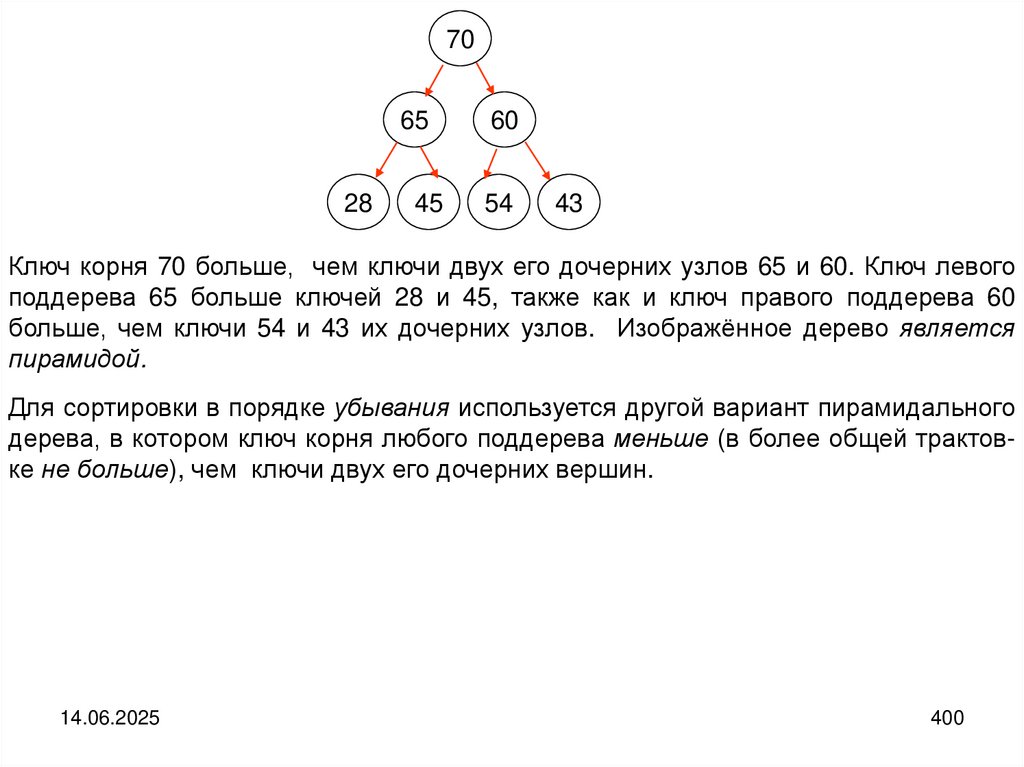
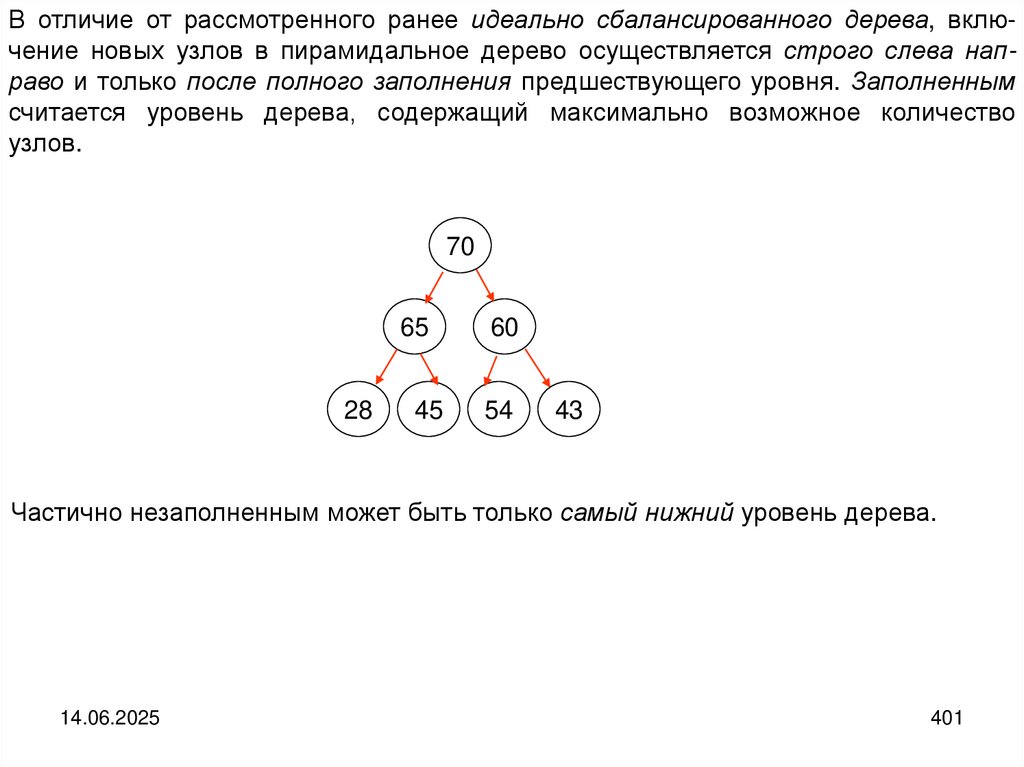
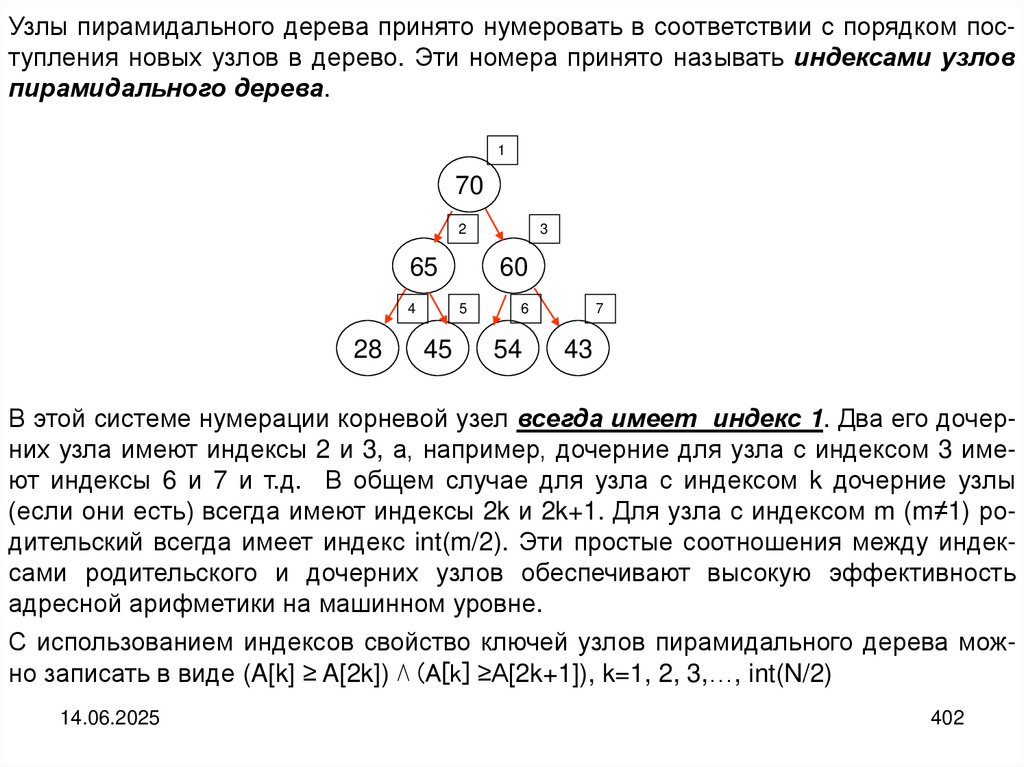
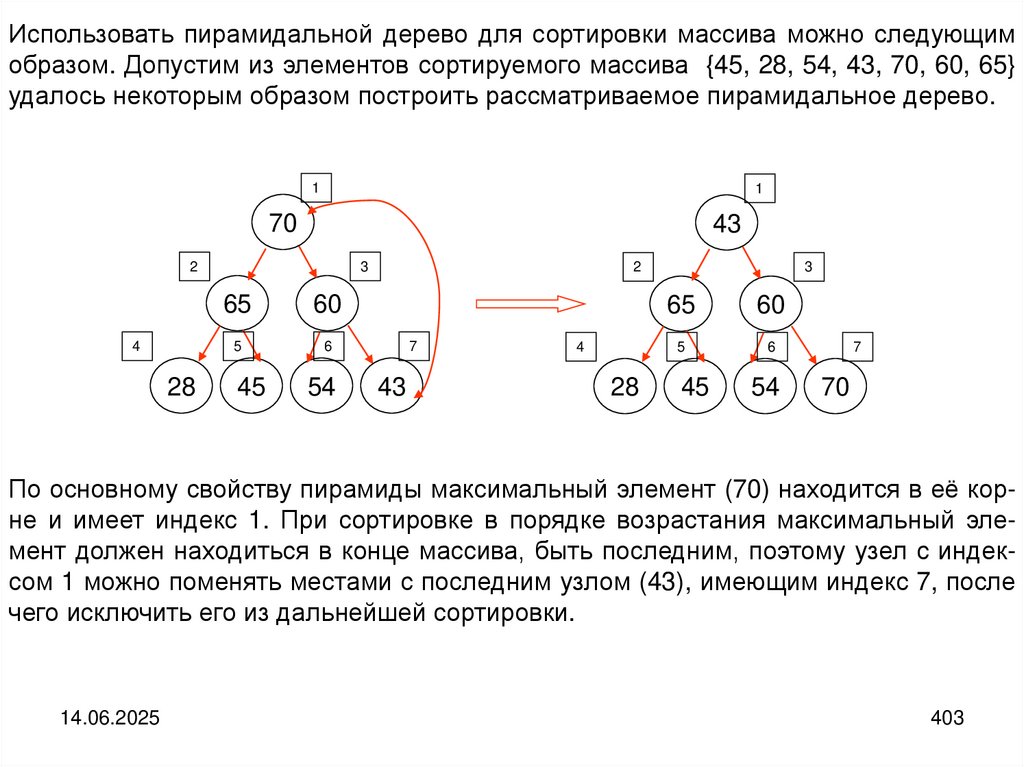
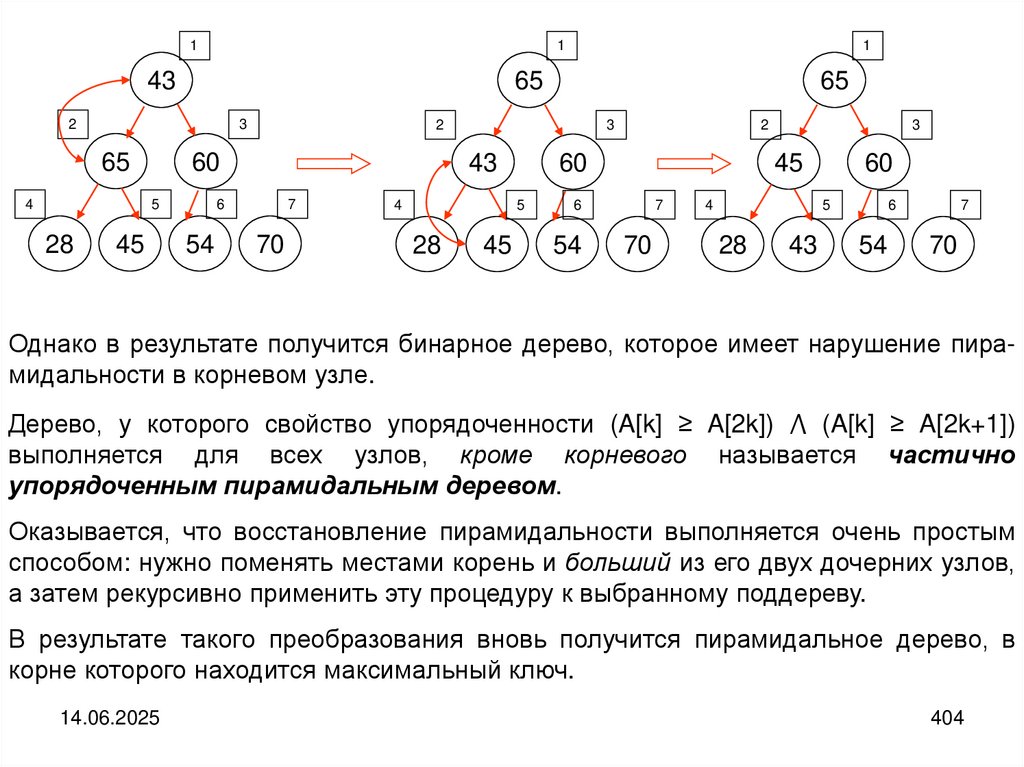
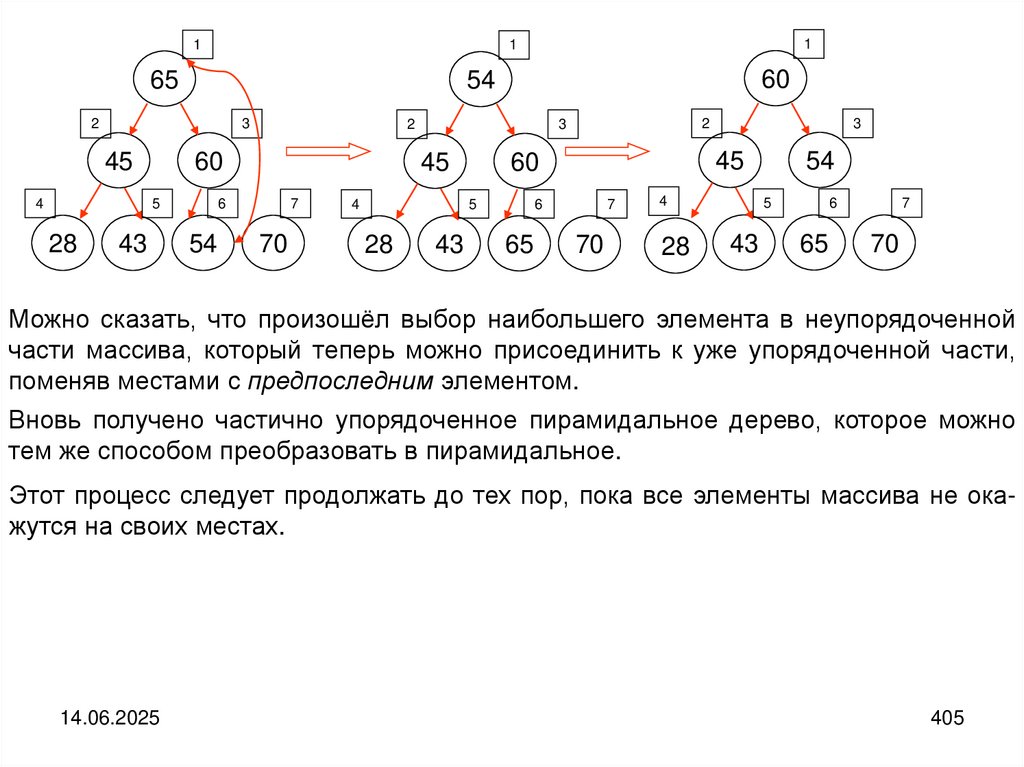
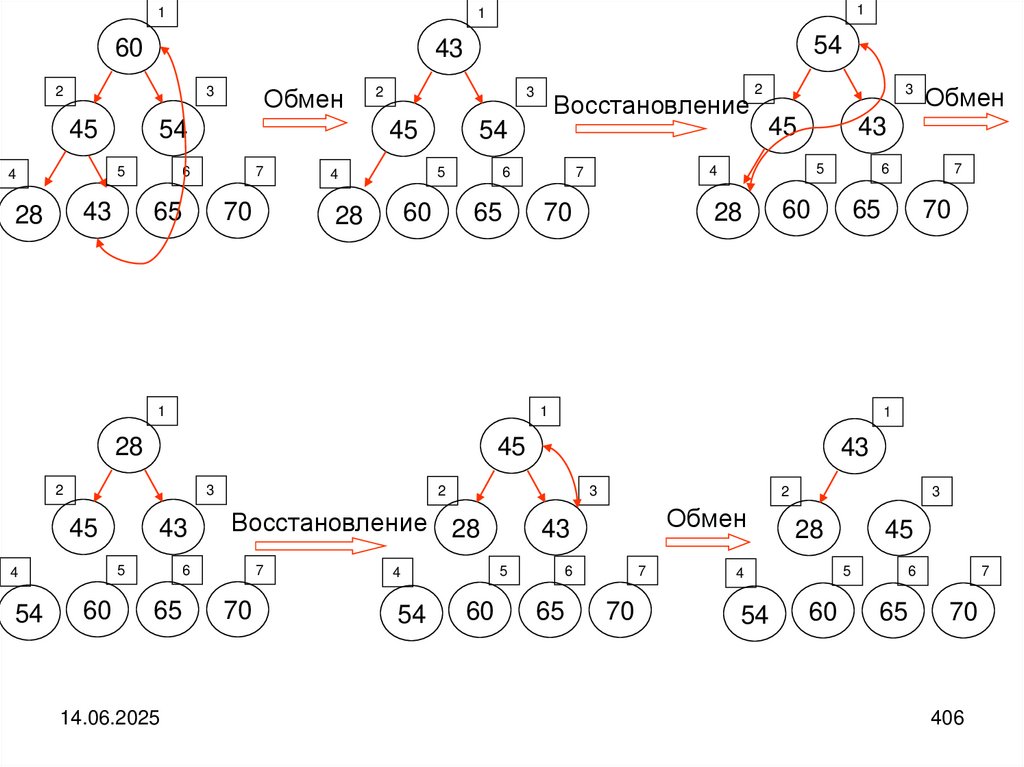
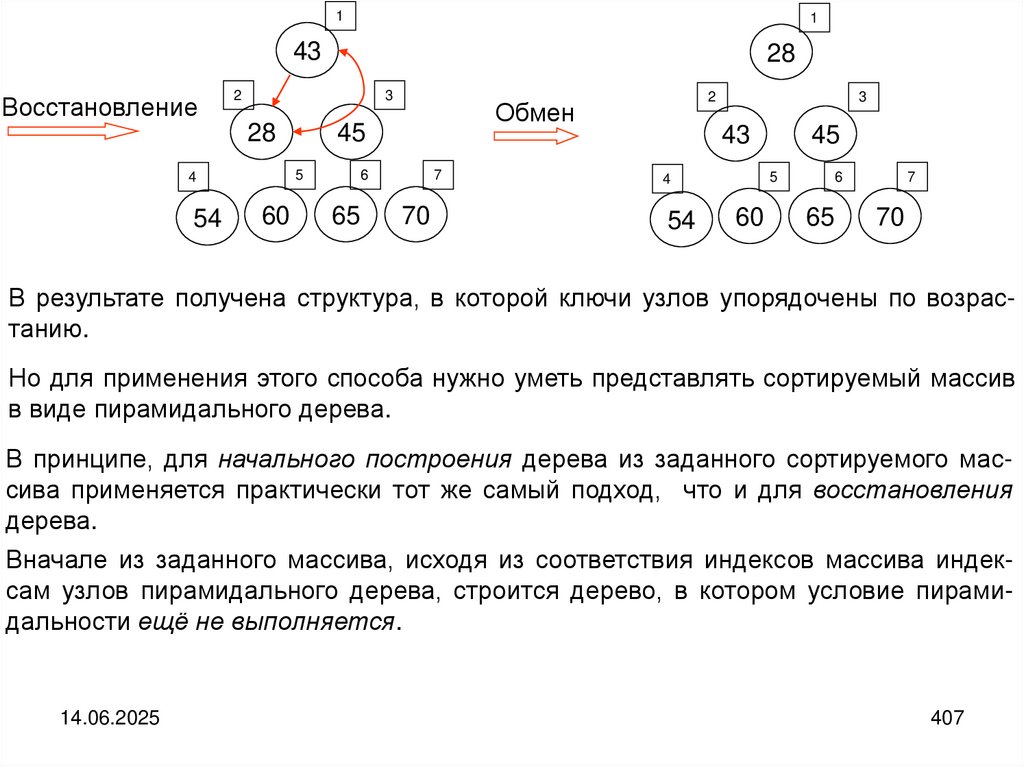
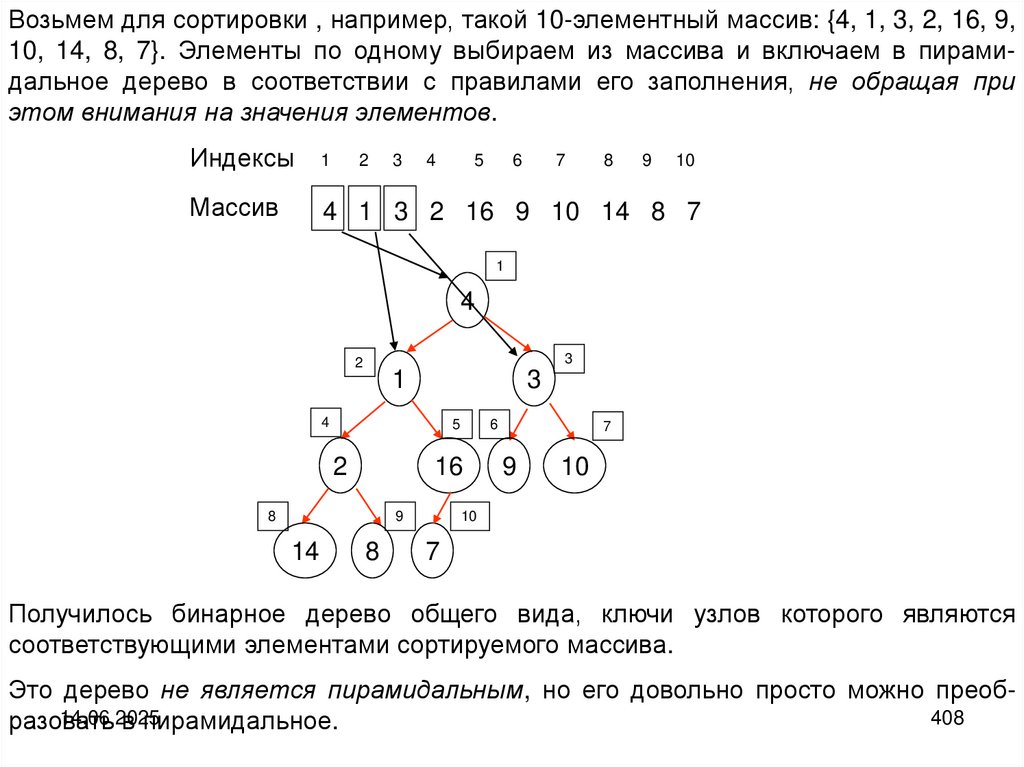
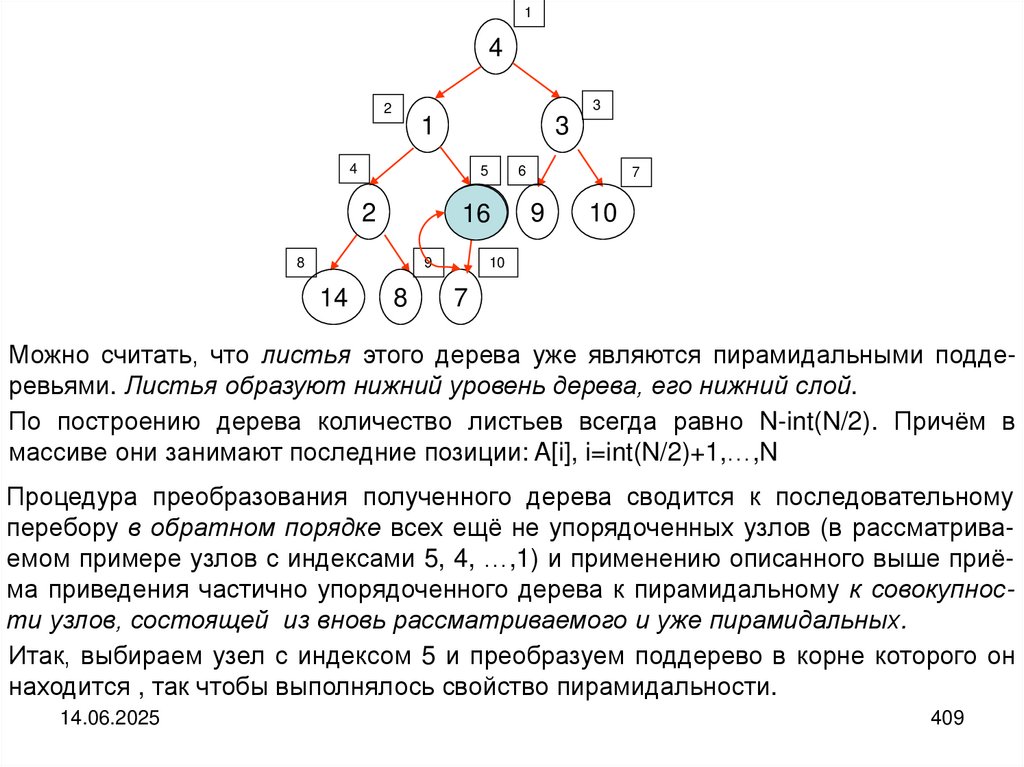
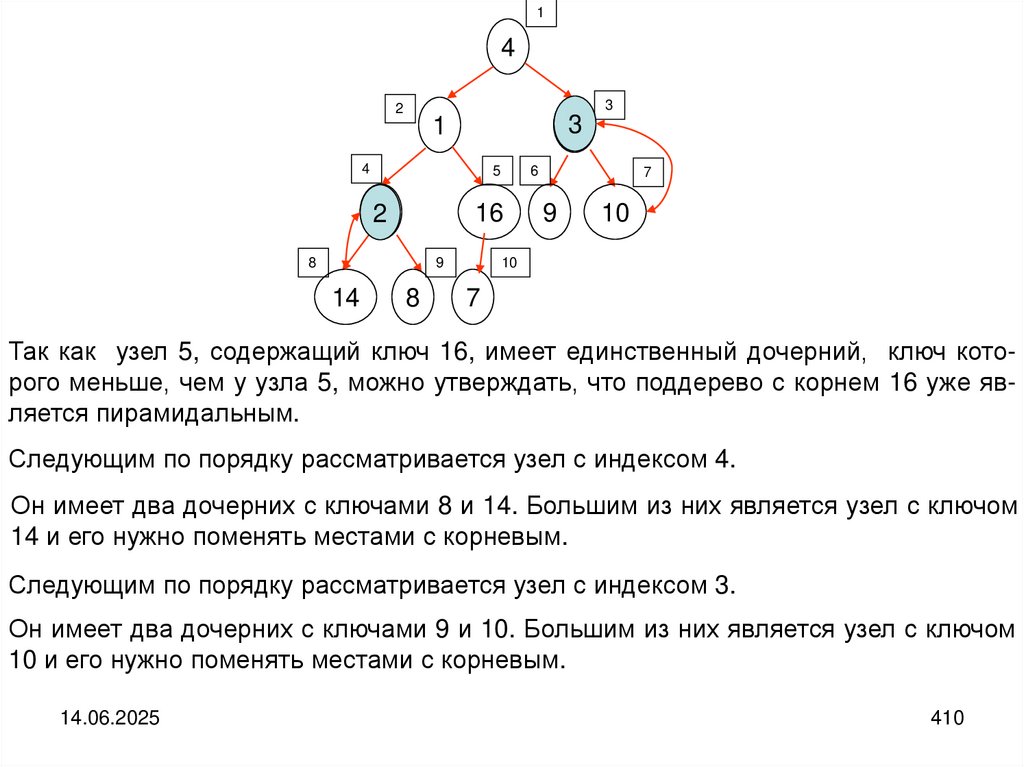
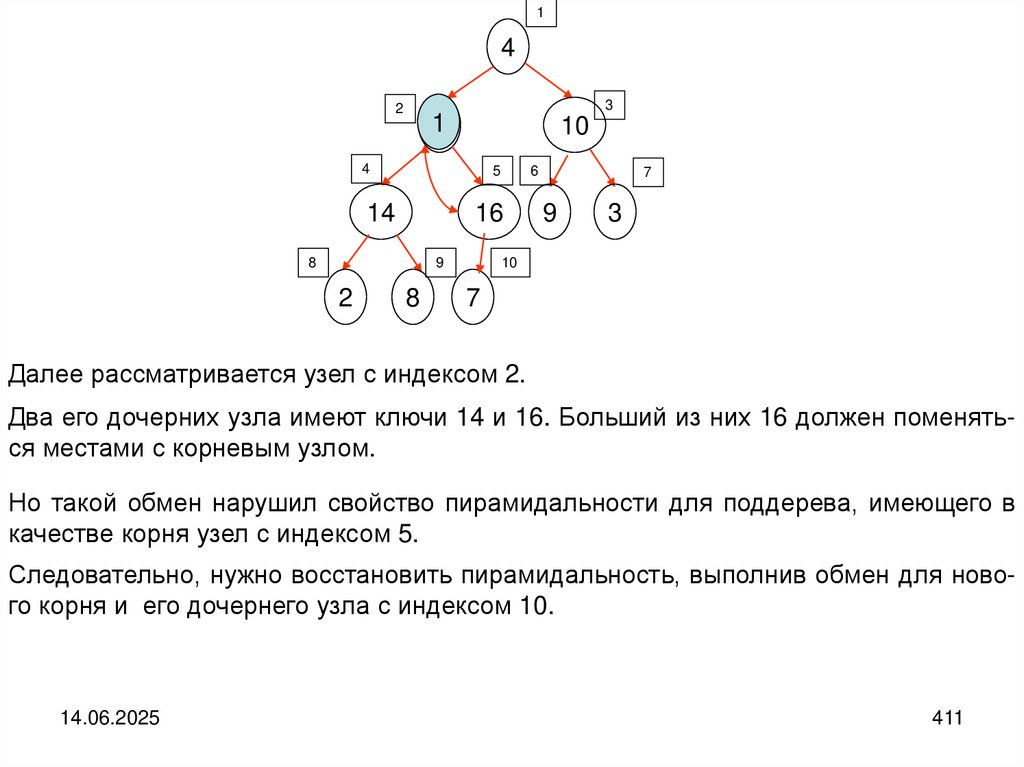
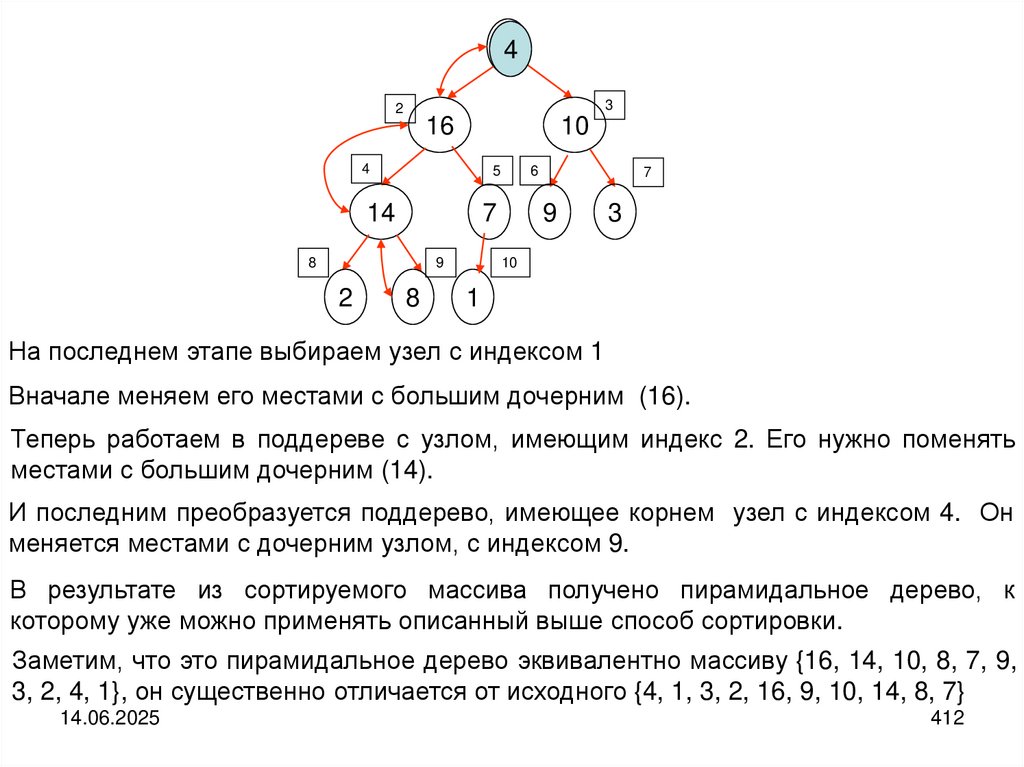











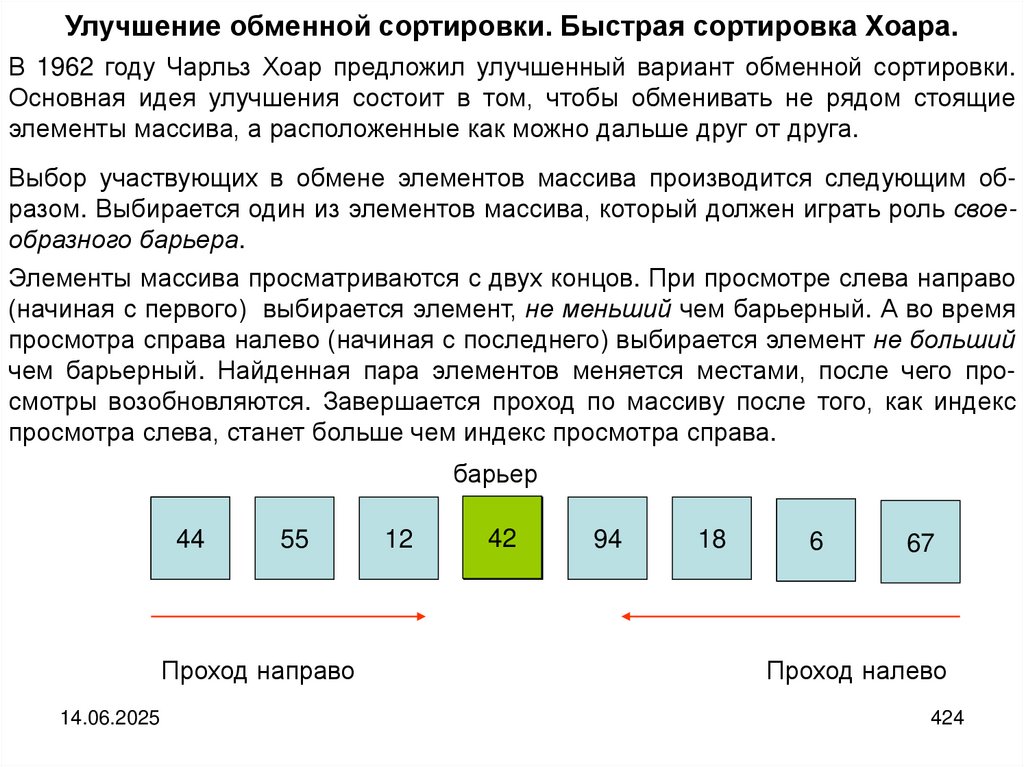







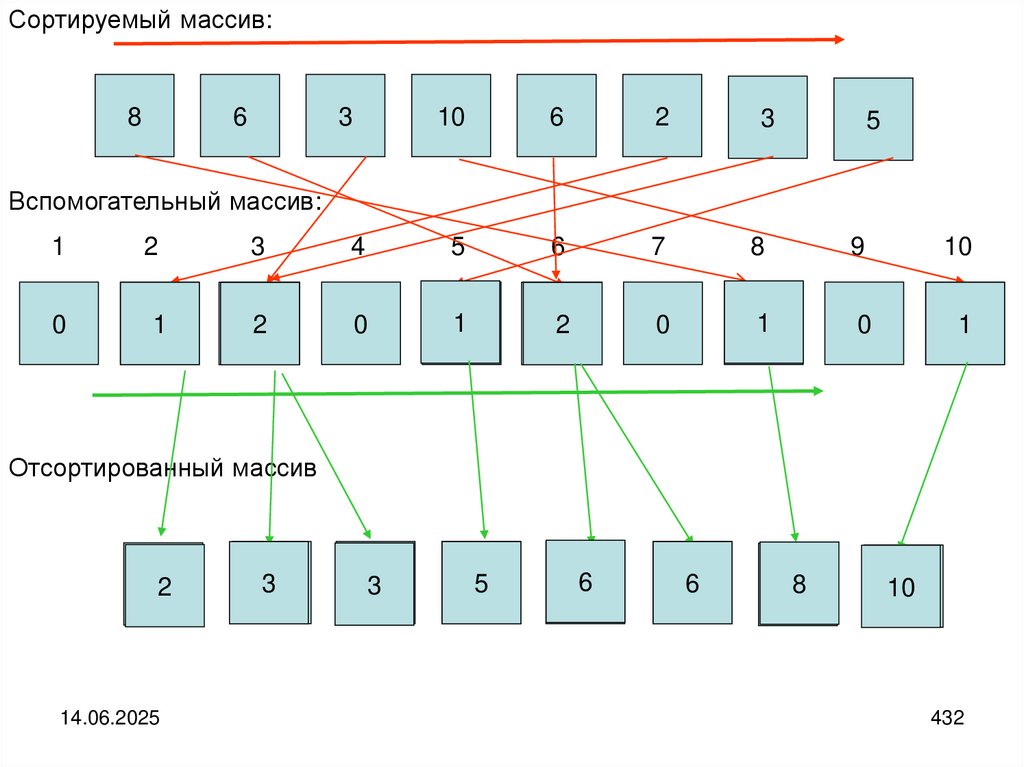



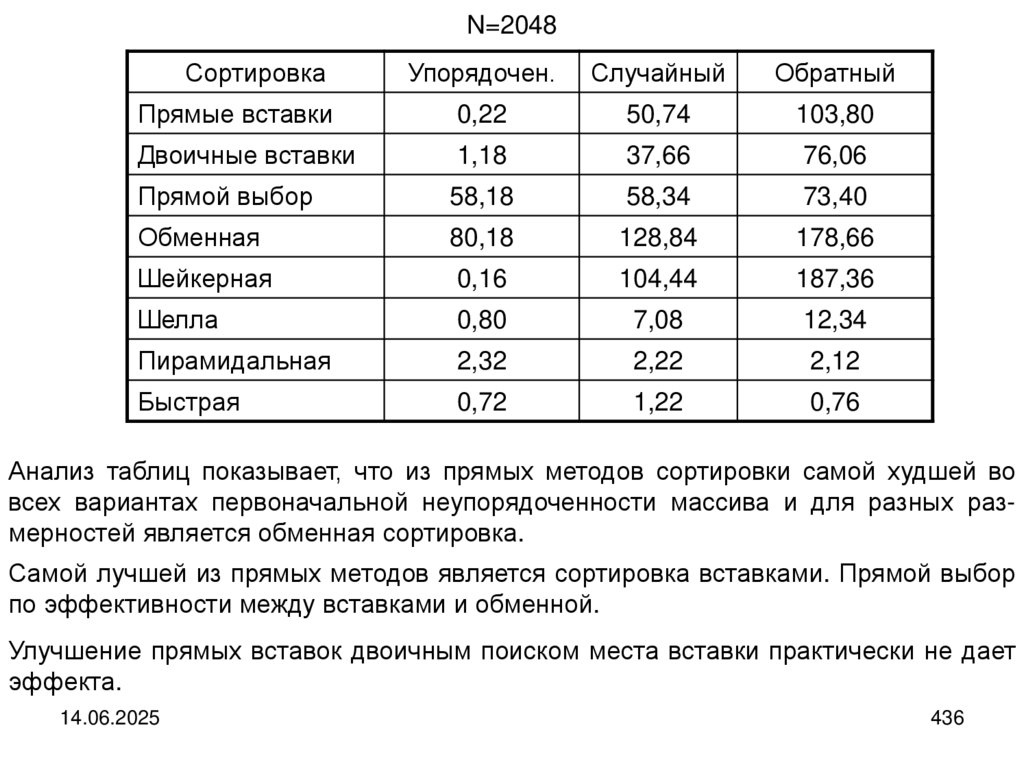

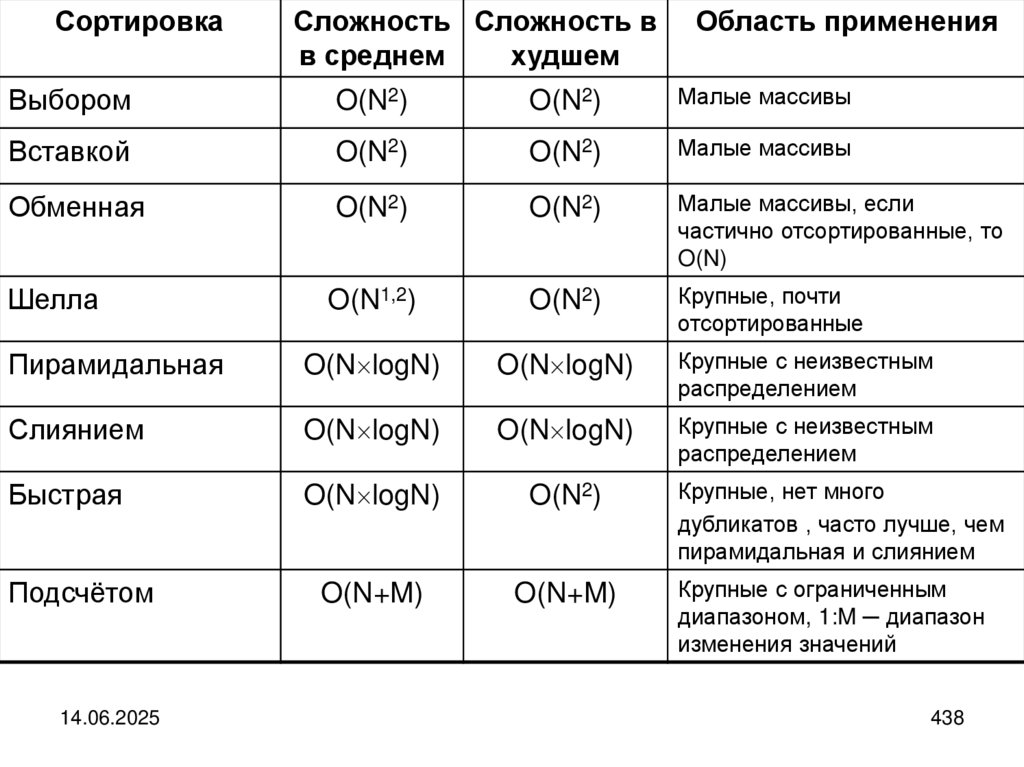










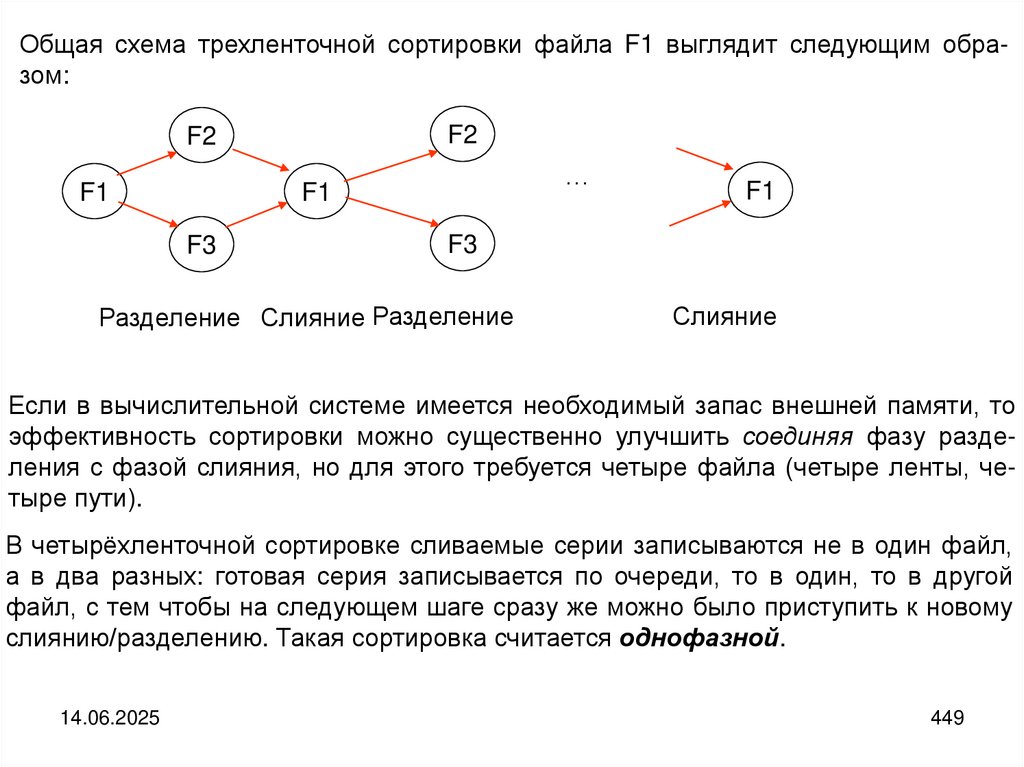
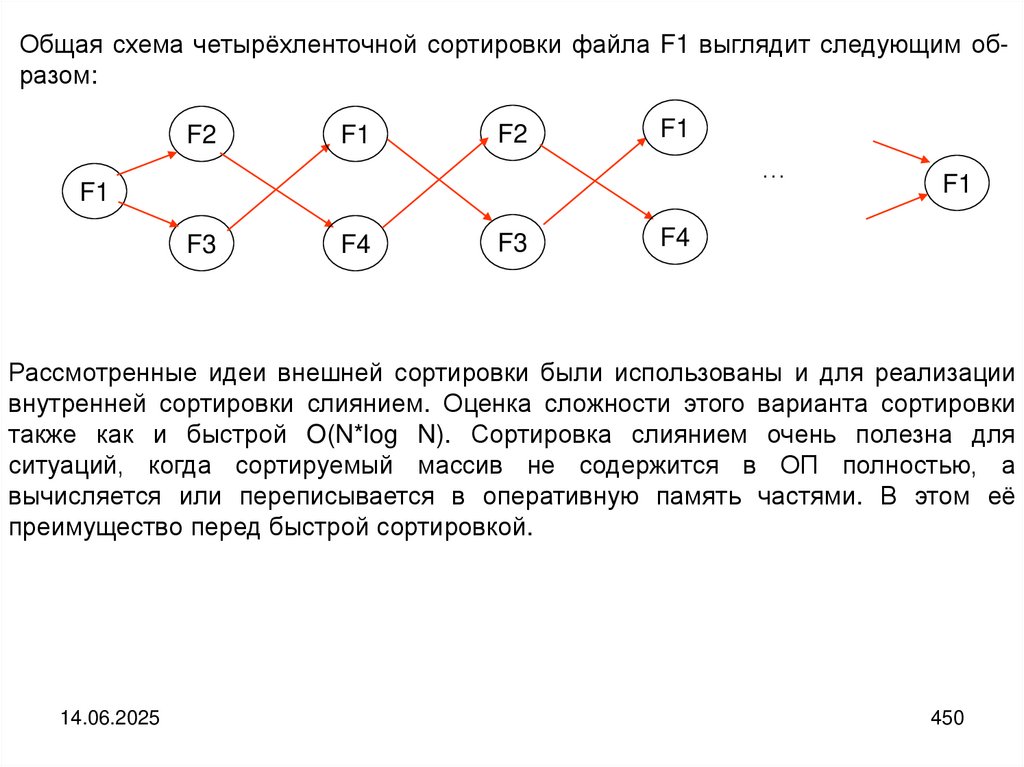























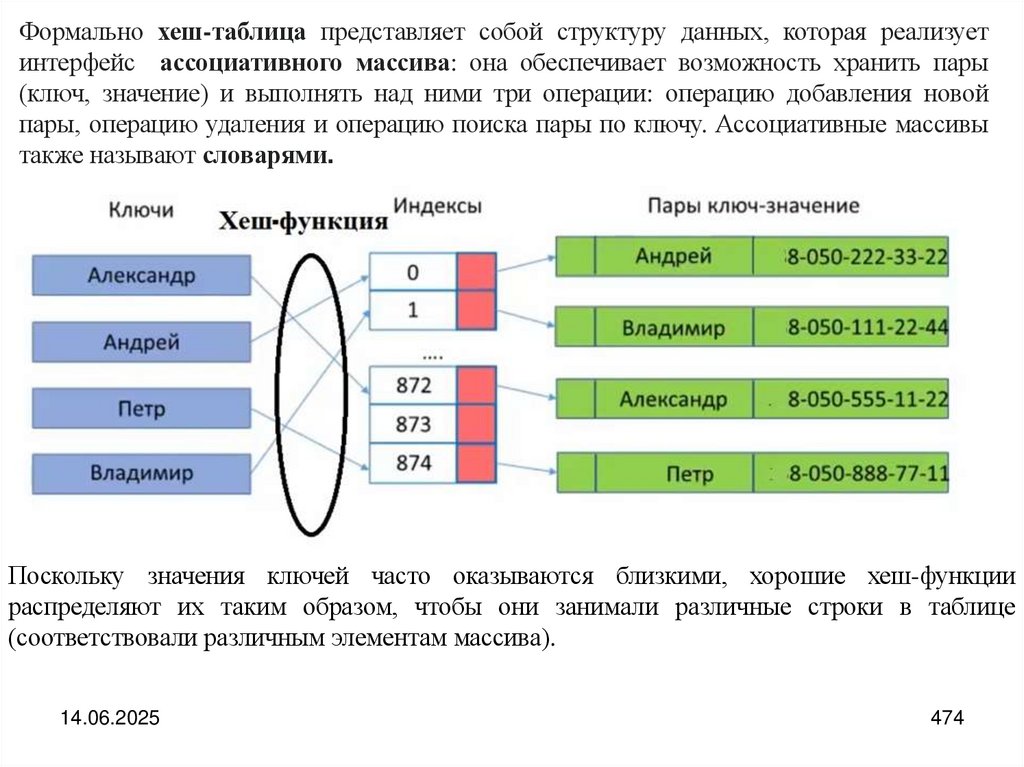
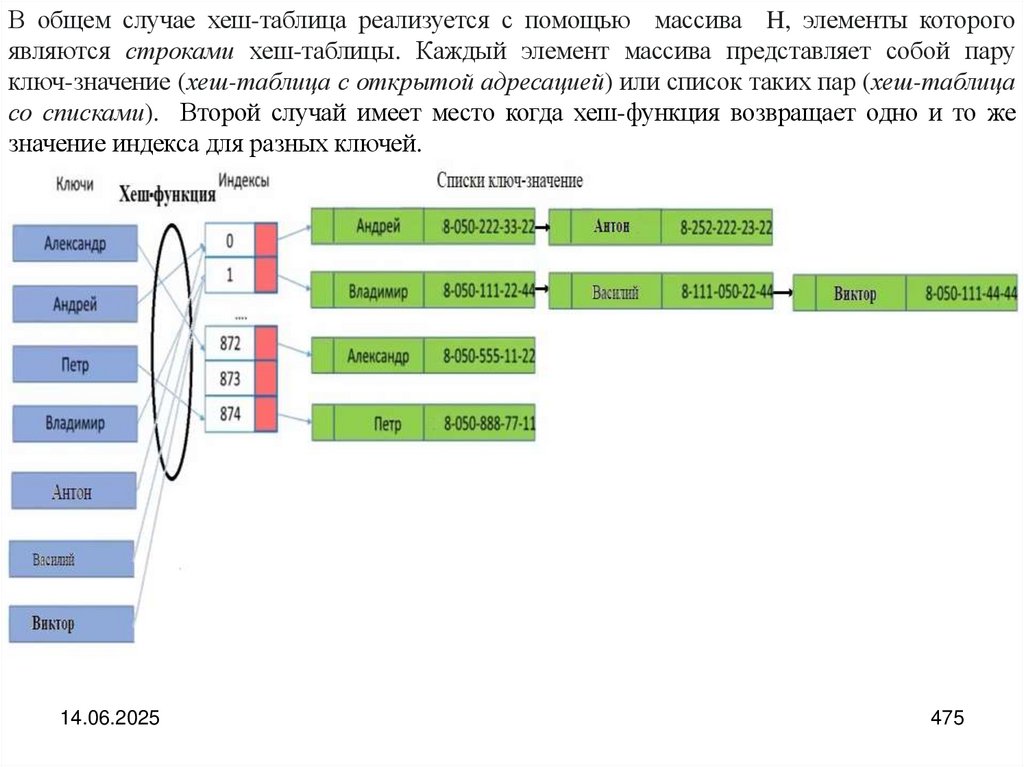
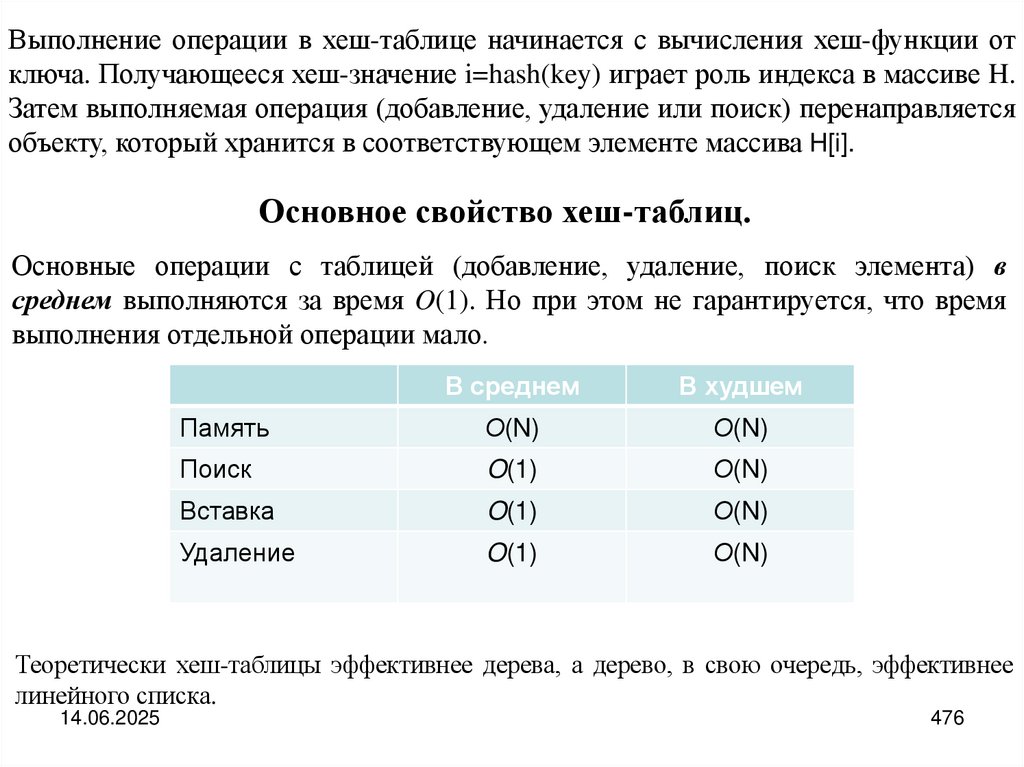
























 programming
programming








