Similar presentations:
электрические заряды
1. Электростатика
2. Содержание
Закон сохранения электрического зарядаЗакон Кулона
Принцип суперпозиции полей
Электростатическое поле
Теорема Гаусса
Применение теоремы Гаусса
Потенциал и разность потенциалов
Связь между силовой и энергетической
характеристиками
Конденсаторы
3. Закон сохранения электрического заряда
• Электрический заряд – величина, характеризующая способностьчастицы вещества к электрическому взаимодействию.
• Электрический заряд изолированной системы остается постоянным
при любых физических процессах, происходящих в системе.
• Положительные и отрицательные заряды в замкнутой системе
могут возникать или исчезать, но при этом их алгебраическая
сумма всегда остается постоянной.
q1 + q2 + q3 + … + qn = const
справедлив для замкнутых систем
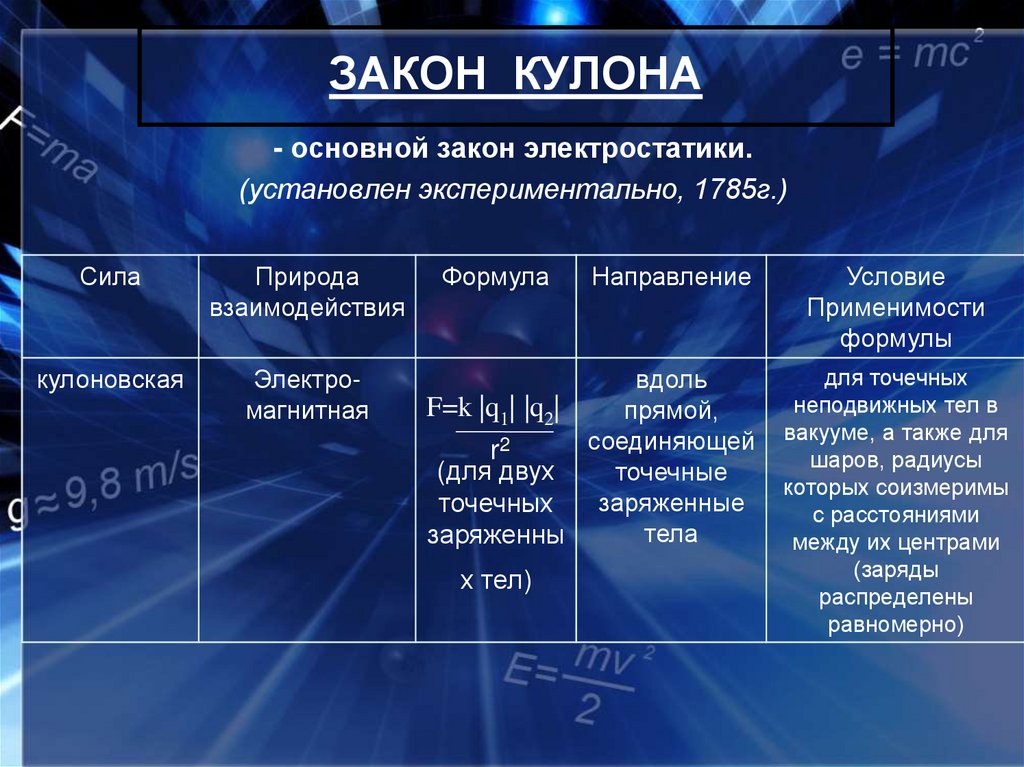
4. ЗАКОН КУЛОНА
- основной закон электростатики.(установлен экспериментально, 1785г.)
Сила
Природа
взаимодействия
кулоновская
Электромагнитная
Формула
Направление
вдоль
F=k |q1| |q2|
прямой,
соединяющей
r2
(для двух
точечные
заряженные
точечных
тела
заряженны
х тел)
Условие
Применимости
формулы
для точечных
неподвижных тел в
вакууме, а также для
шаров, радиусы
которых соизмеримы
с расстояниями
между их центрами
(заряды
распределены
равномерно)
5.
Сила взаимодействия двух точечных неподвижныхзаряженных тел в вакууме прямо пропорциональна
произведению модулей зарядов и обратно пропорциональна
квадрату расстояния между ними.
F=k |q1| |q2|
r2
Н м
9
k= 9*10
Кл 2
1
k=
Заряд электрона е=-1,6*10-19 Кл
4 0
2
0 8,85 10
0
12
Кл2
Н м2
электрическая
постоянная
-
6. Принцип суперпозиции полей
Е = Е1 + Е2 + Е3 + …Для двух зарядов:
E1
E
E2
Е
E1
E2
q1>0
Е = Е 1 + E2
q2>0
q1>0
Е = Е 1 + E2
q2>0
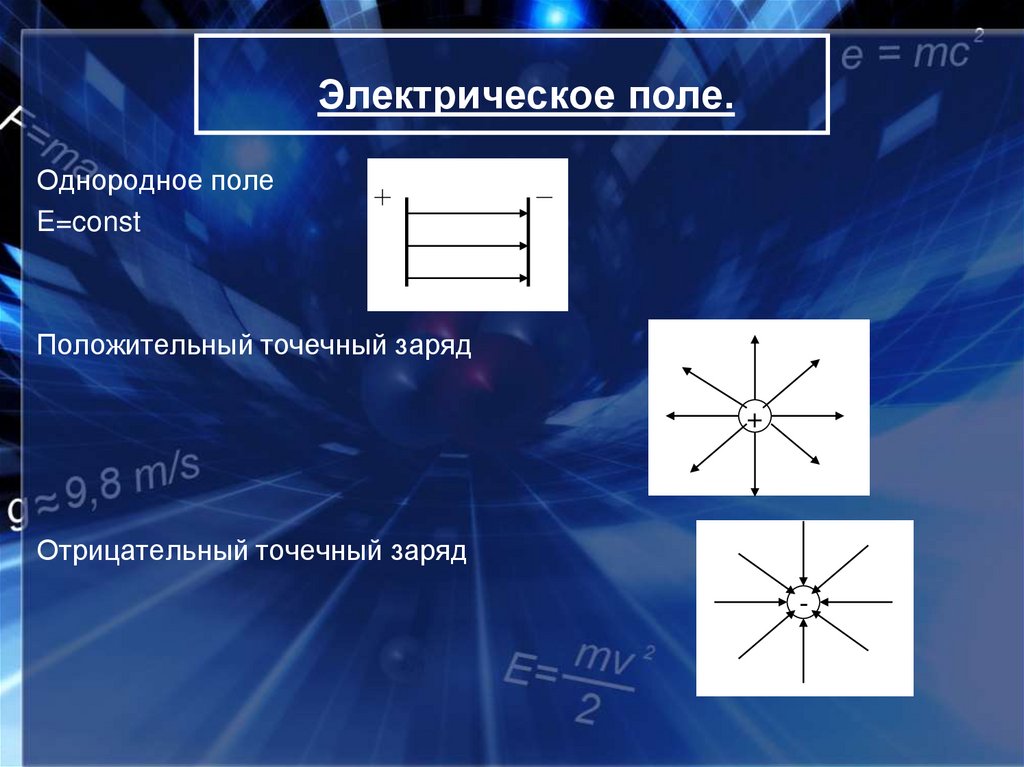
7. Электрическое поле.
Однородное полеE=const
Положительный точечный заряд
+
Отрицательный точечный заряд
-
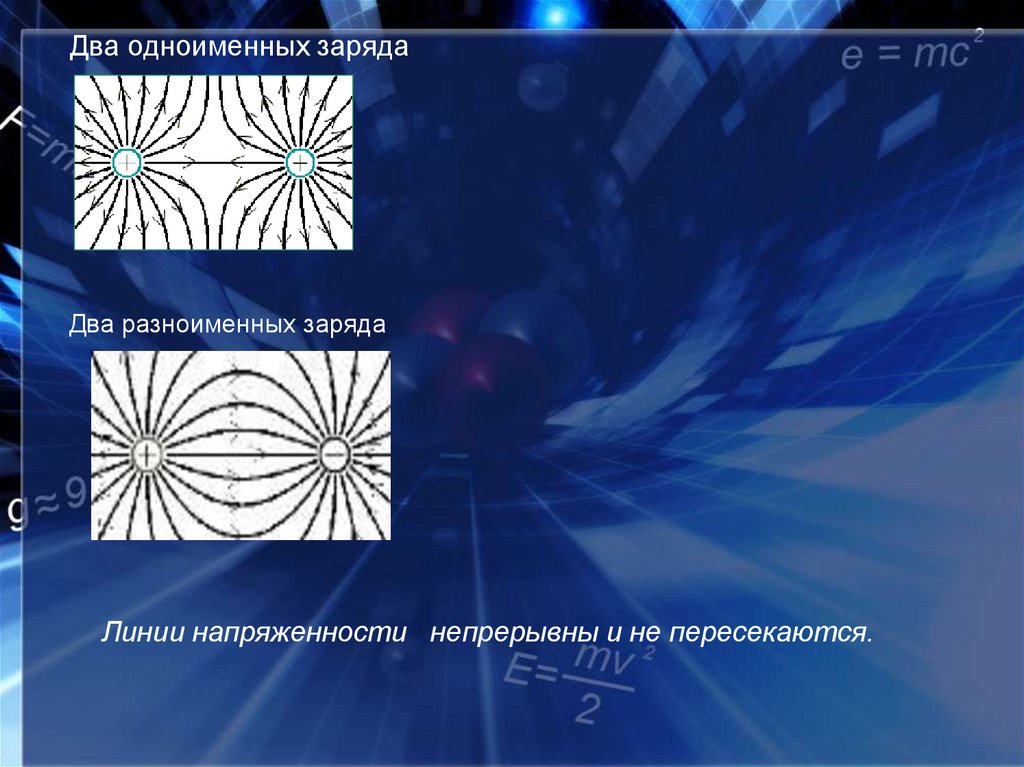
8. Два одноименных заряда
Два разноименных зарядаЛинии напряженности непрерывны и не пересекаются.
9. Теорема Гаусса
Если внутри замкнутой поверхностилюбой формы находятся точечные
электрические заряды q1 ,q2 , … qn , то
общий поток вектора напряженности
электрического поля равен алгебраической
сумме этих зарядов, деленной на
0
(поток)
Ф= Е * S
q
Ф=
0
i
2
Кл
0 8,85 10 12
Н м2
электрическая постоянная
Число линий напряженности через поверхность, перпендикулярную вектору Е
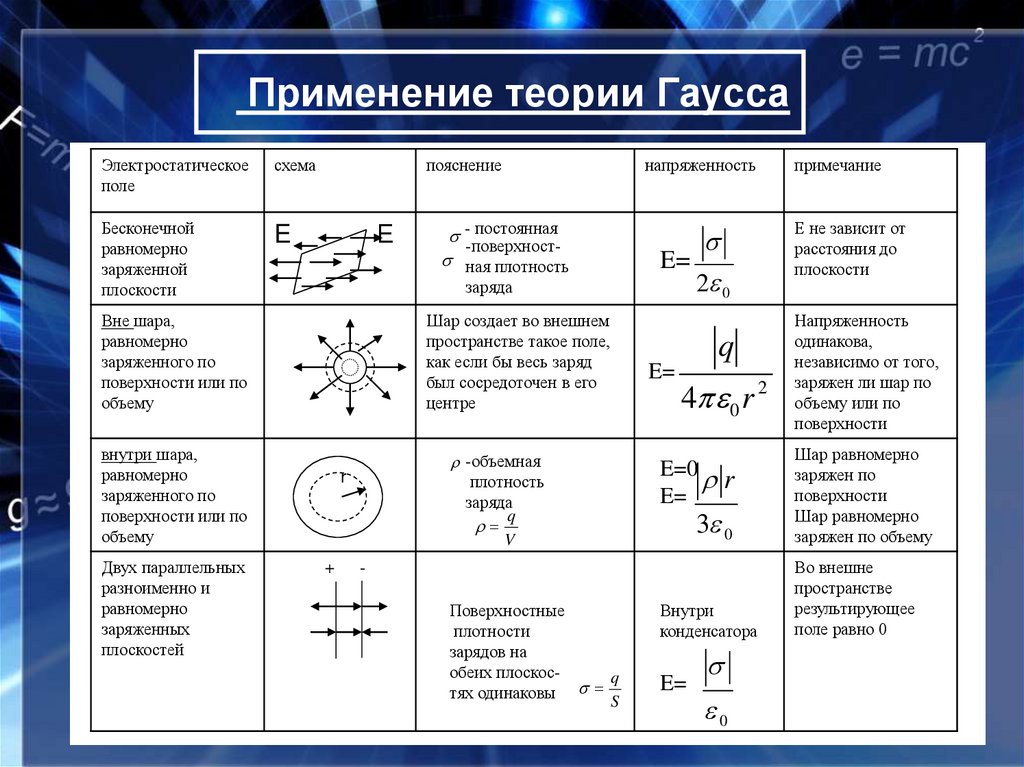
10. Применение теории Гаусса
Электростатическоеполе
схема
Бесконечной
равномерно
заряженной
плоскости
E
пояснение
Е
E=
заряда
Вне шара,
равномерно
заряженного по
поверхности или по
объему
Шар создает во внешнем
пространстве такое поле,
как если бы весь заряд
был сосредоточен в его
центре
внутри шара,
равномерно
заряженного по
поверхности или по
объему
Двух параллельных
разноименно и
равномерно
заряженных
плоскостей
- постоянная
-поверхност ная плотность
напряженность
-объемная
плотность
заряда
q
V
r
+
2 0
q
E=
4 0 r 2
Е не зависит от
расстояния до
плоскости
Напряженность
одинакова,
независимо от того,
заряжен ли шар по
объему или по
поверхности
3 0
Шар равномерно
заряжен по
поверхности
Шар равномерно
заряжен по объему
Внутри
конденсатора
Во внешне
пространстве
результирующее
поле равно 0
E=0
r
E=
Поверхностные
плотности
зарядов на
обеих плоскосq
тях одинаковы
S
примечание
E=
0
11. Потенциал и разность потенциалов
В ДжКл
wp
скаляр
q
Потенциал поля в произвольной точке определяется как алгебраическая
сумма потенциалов, создаваемых отдельными точечными зарядами.
1 2 3 ... n
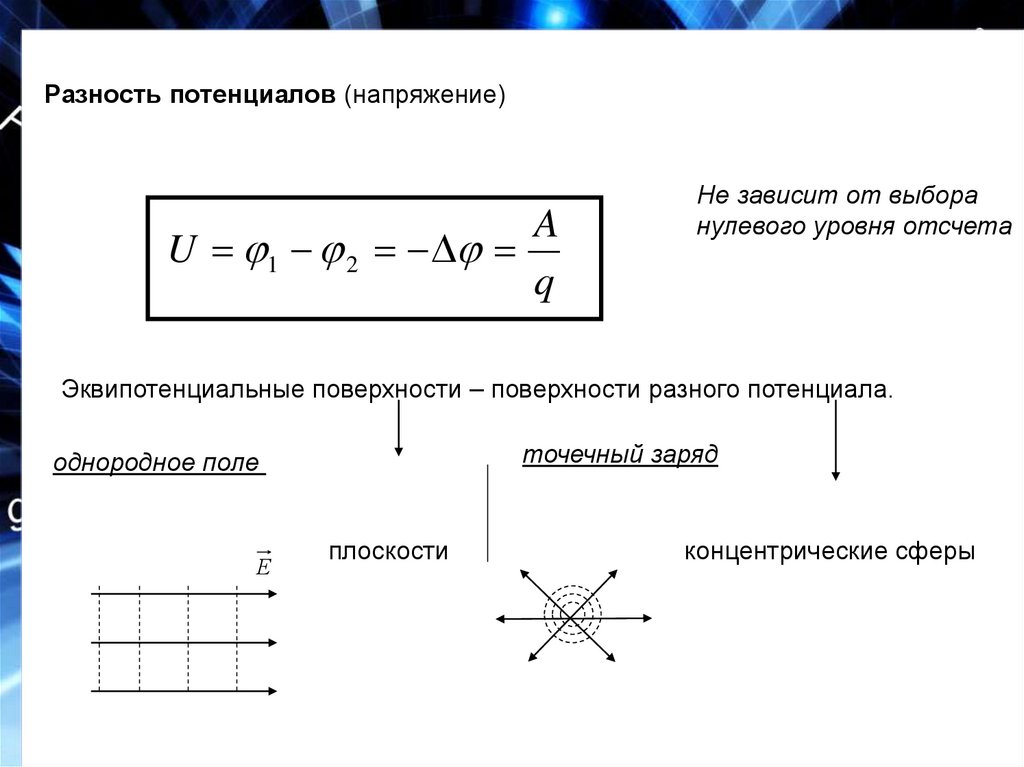
12. Разность потенциалов (напряжение)
AU 1 2
q
Не зависит от выбора
нулевого уровня отсчета
Эквипотенциальные поверхности – поверхности разного потенциала.
точечный заряд
однородное поле
Е
плоскости
концентрические сферы
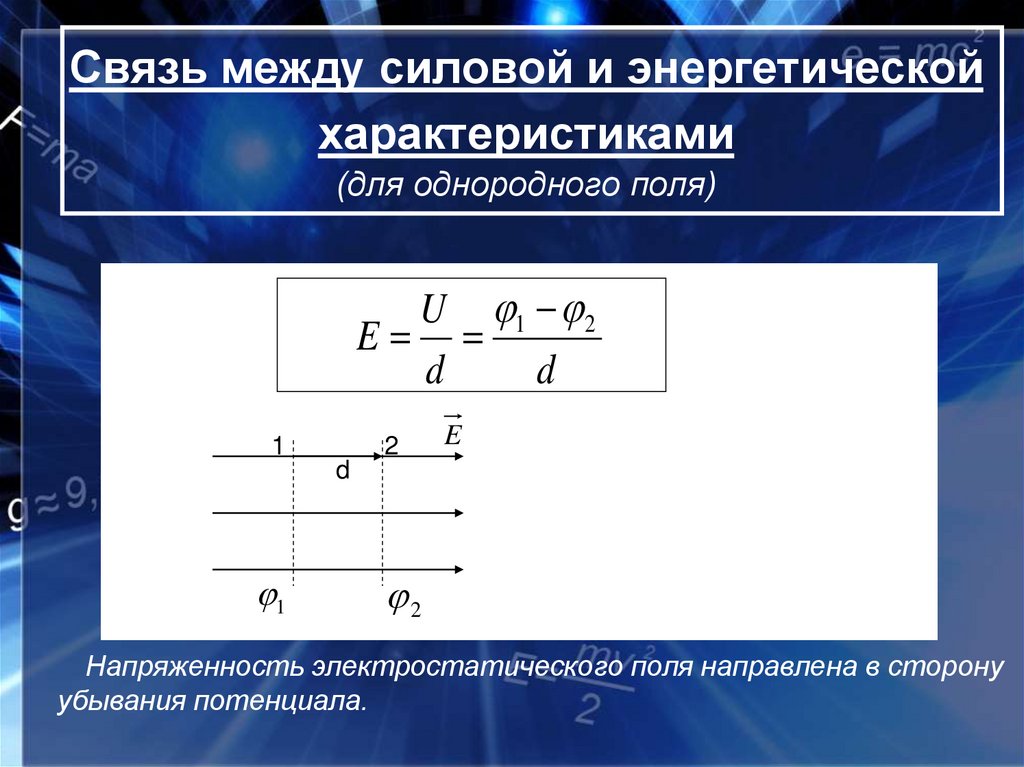
13. Связь между силовой и энергетической характеристиками (для однородного поля)
U 1 2E
d
d
1
2
E
d
1
2
Напряженность электростатического поля направлена в сторону
убывания потенциала.
14. Конденсаторы
Схемаq
конденсатор
q
1
2
Энергия
заряженного
конденсатора
Плотность
энергии
qU
;
2
q2
CU 2 ;
W
W
2C
2
W 0 E 2
p
V
2
W
W
1 2
2
q








 physics
physics








