Лекция 9 Основы электростатики

1. Основы электростатики

Иллюстративный материал к
лекции №8
суббота, 21 июня 2025 г.

2. Электрический заряд

o Электрический
заряд- физическая
величина,
определяющая силу
электромагнитного
взаимодействия
о Существуют два вида
электрических зарядовположительные и
отрицательные.
Заряды не существуют без частиц.
o Единица измеренияКулон(Кл)
о Обозначение- q, Q
Элементарный
элeктрический заряд
e 1,6 10
19
Кл
oЭлектрический заряд
дискретен (квантован)
Q=ne,
где nцелое число.

3. Закон сохранения электрического заряда

• Электрически изолированная система тел-
система тел, через границу которой не проникают
заряды.
• Электрический заряд изолированной системы остается
постоянным при любых физических процессах,
происходящих в системе.
• Положительные и отрицательные заряды в замкнутой
системе могут возникать или исчезать, но при этом их
алгебраическая сумма всегда остается постоянной.
q1 + q2 + q3 + … + qn =
const

4. Электрическое поле

Электрическим полем называют особый вид
материи , передающий силовое воздействие одного
электрического заряда на другой.
Поле, создаваемое неподвижными зарядами, называют
электростатическим.
Свойства электростатического поля:
а)порождается электрическими зарядами;
б)обнаруживается по действию на заряд;
в)действует на заряды с некоторой силой.

5.

Q заряд источника поля
+
В
+
q
FВ
А FА
+
q пробный заряд
Будем изменять q в какое либо число раз. Опыт покажет:
Fn
F1 F2
...
const Е
q1
q2
qn

6.

• Напряженность- силовая
характеристика электрического поля.
F
E
q
• Единица измерения
• Напряженность поля
точечного заряда.
Н В
;
Кл м
E
k q
r
2

7. Сила взаимодействия направлена по прямой, соединяющей заряды, а её направление зависит от знаков зарядов:

Закон Кулона
Сила взаимодействия направлена по прямой, соединяющей
заряды, а её направление зависит от знаков зарядов:
одноимённые заряды- отталкиваются
а разноимённые - притягиваются.
Закон Кулона
F E q

8.

F21 q2
q1 F
12
+
r
F1 2 F 2 1 F k
F k
q1 q 2
r
2
q1 q 2
r
2
Н м
k
9 10
2
4 0
Кл
r – расстояние между зарядами
1
2
9
q 1 q 2 – произведение модулей зарядов
– диэлектрическая проницаемость среды (диэлектрика)

9.

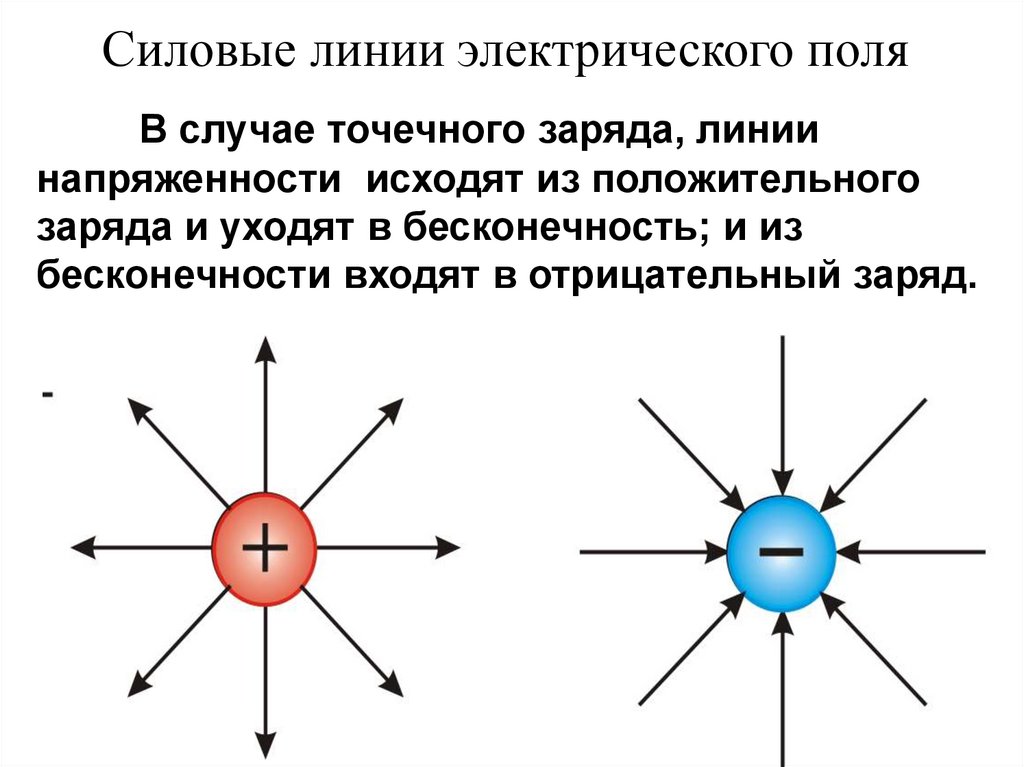
Силовые линии электрического поля
В случае точечного заряда, линии
напряженности исходят из положительного
заряда и уходят в бесконечность; и из
бесконечности входят в отрицательный заряд.

10. Принцип суперпозиции полей

Если в данной точке пространства различные заряженные
частицы создают электрические поля, напряженности
которых Е1,Е2 ,Е3 и т.д., то результирующая напряженность
поля равна:
Е = Е1 + Е2 + Е3 + …
Для двух зарядов:
E
E1
E1
Е
q1>0
Е = Е1 + E2
q2<0
q1>0
Е = Е1 + E2
q2>0

11.

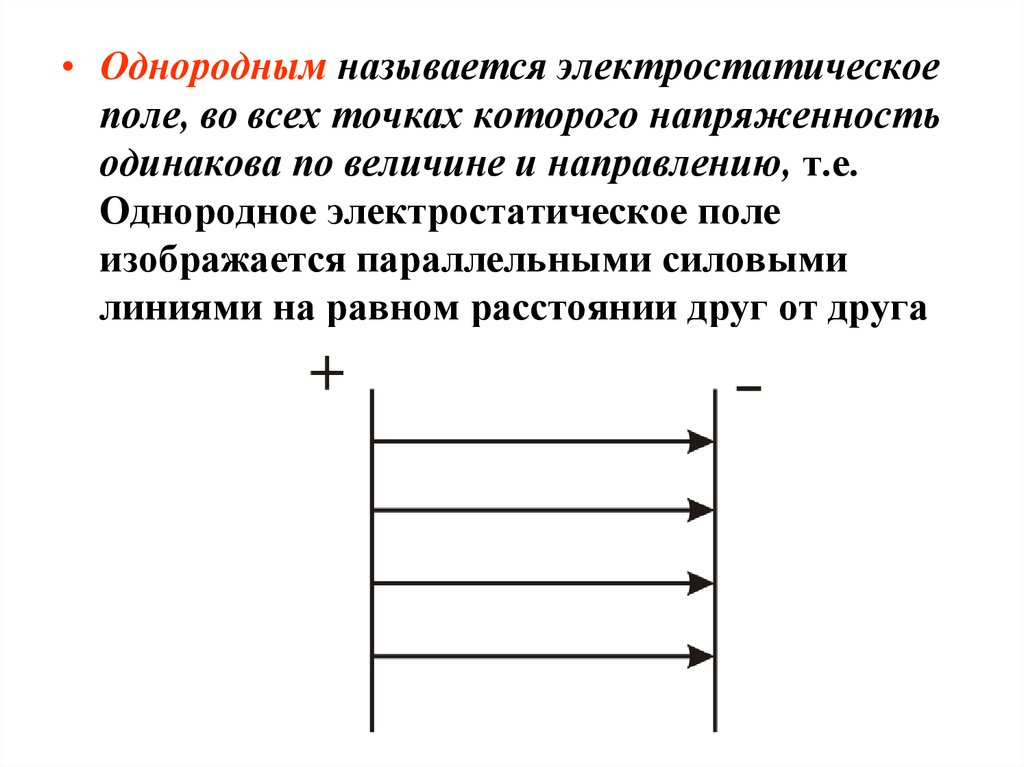
• Однородным называется электростатическое
поле, во всех точках которого напряженность
одинакова по величине и направлению, т.е.
Однородное электростатическое поле
изображается параллельными силовыми
линиями на равном расстоянии друг от друга

12.

Поток вектора
Что такое поток?

13.

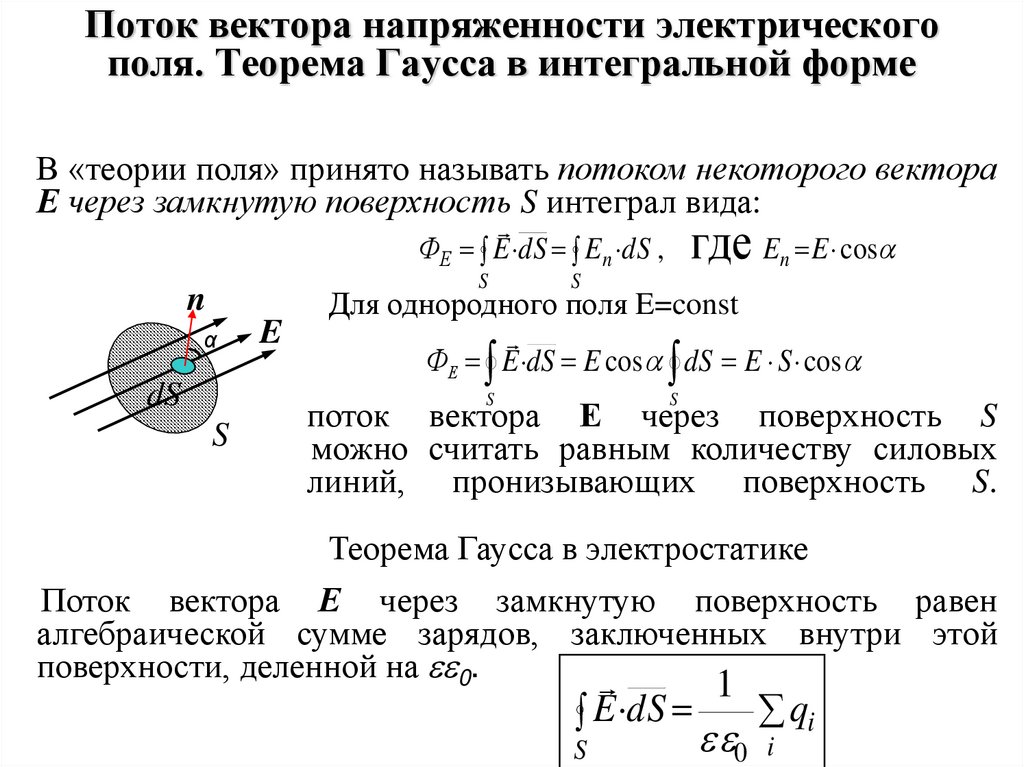
Поток вектора напряженности электрического
поля. Теорема Гаусса в интегральной форме
В «теории поля» принято называть потоком некоторого вектора
Е через замкнутую поверхность S интеграл вида:
ФЕ E dS En dS ,
S
n
α
dS
E
S
Для однородного поля E=const
ФЕ E dS E cos dS E S cos
S
S
где En E cos
S
поток вектора Е через поверхность S
можно считать равным количеству силовых
линий, пронизывающих поверхность S.
Теорема Гаусса в электростатике
Поток вектора Е через замкнутую поверхность равен
алгебраической сумме зарядов, заключенных внутри этой
поверхности, деленной на 0.
1
qi
E dS
0 i
S

14.

Применение теоремы Гаусса для
расчета электростатических полей
• Поле бесконечной равномерно заряженной плоскости
пусть +s – поверхностная плотность заряда
σ
плоскости, Кл/м2
E
E Тогда вектор напряженности направлен так,
∆S причем поле является однородным.
Выделим цилиндрическую поверхность с образующими,
перпендикулярными к плоскости, и основаниями величиной ∆S
Заряд внутри поверхности: σ.∆S
Поток вектора E через боковые поверхности равен нулю (cos =0)
По теореме Гаусса: 2Е.∆S = σ.∆S/ 0 или Е = σ/(2 ε0)

15.

Применение теоремы Гаусса для
расчета электростатических полей
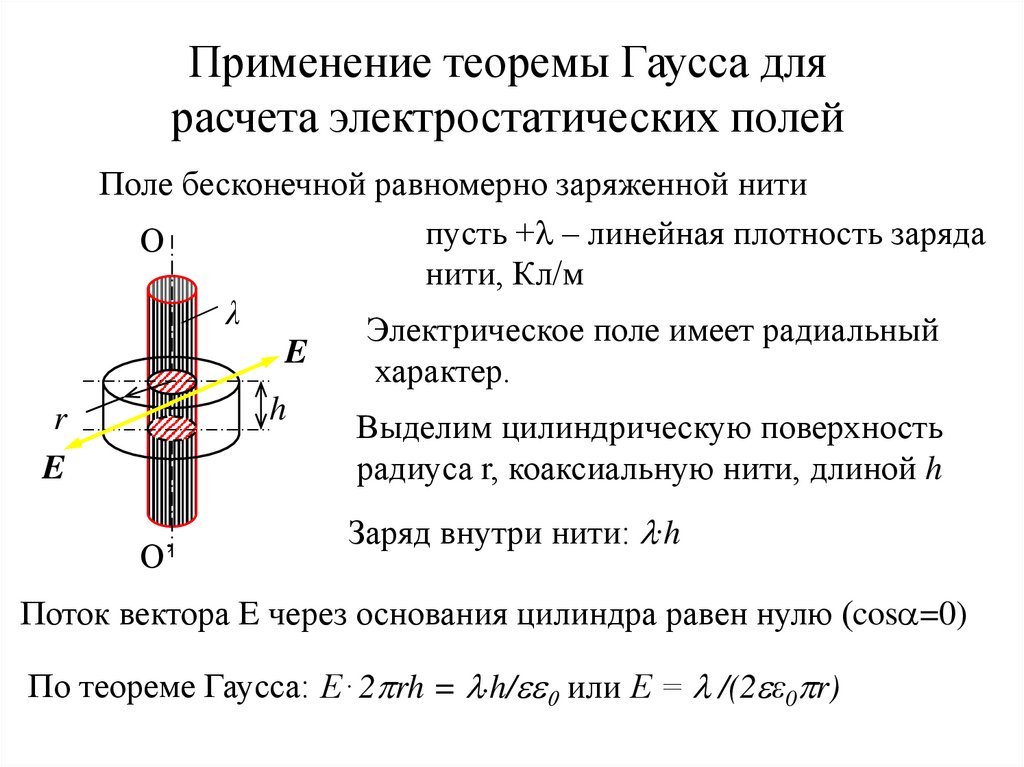
• Поле бесконечной равномерно заряженной нити
пусть +l – линейная плотность заряда
О
нити, Кл/м
λ
Электрическое поле имеет радиальный
E
характер.
h
r
Выделим цилиндрическую поверхность
E
радиуса r, коаксиальную нити, длиной h
О’
Заряд внутри нити: l.h
Поток вектора E через основания цилиндра равен нулю (cos =0)
По теореме Гаусса: Е . 2 rh = l.h/ 0 или Е = l /(2 ε0 r)

16.

Применение теоремы Гаусса для
расчета электростатических полей
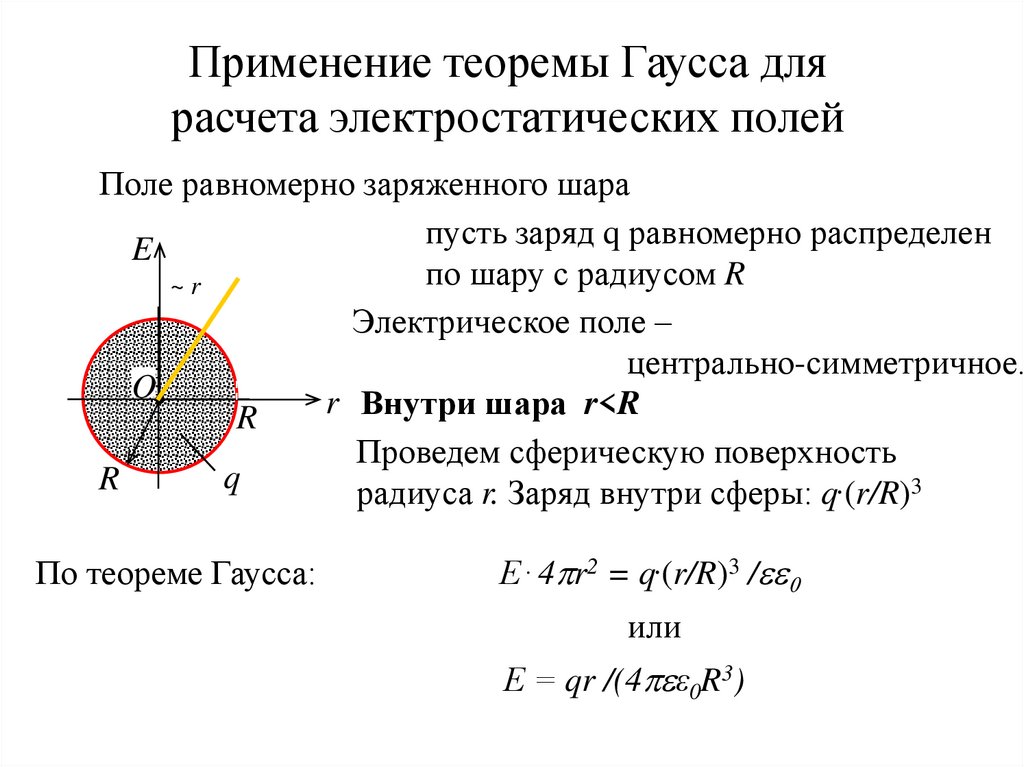
• Поле равномерно заряженного шара
пусть заряд q равномерно распределен
E
по шару с радиусом R
~r
Электрическое поле –
центрально-симметричное.
O
r Внутри шара r<R
R
Проведем сферическую поверхность
q
R
радиуса r. Заряд внутри сферы: q.(r/R)3
По теореме Гаусса:
Е . 4 r2 = q.(r/R)3 / 0
или
Е = qr /(4 ε0R3)

17.

Применение теоремы Гаусса для
расчета электростатических полей
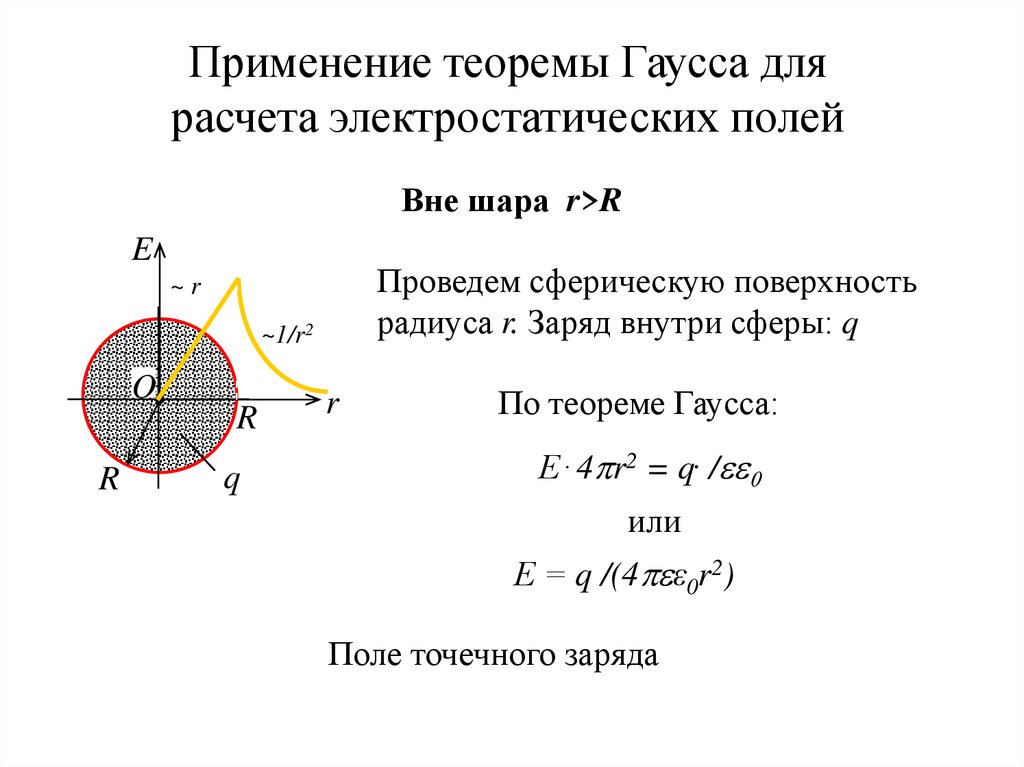
Вне шара r>R
E
Проведем сферическую поверхность
радиуса r. Заряд внутри сферы: q
~r
~1/r2
O
R
R
q
r
По теореме Гаусса:
Е . 4 r2 = q. / 0
или
Е = q /(4 ε0r2)
Поле точечного заряда

18.

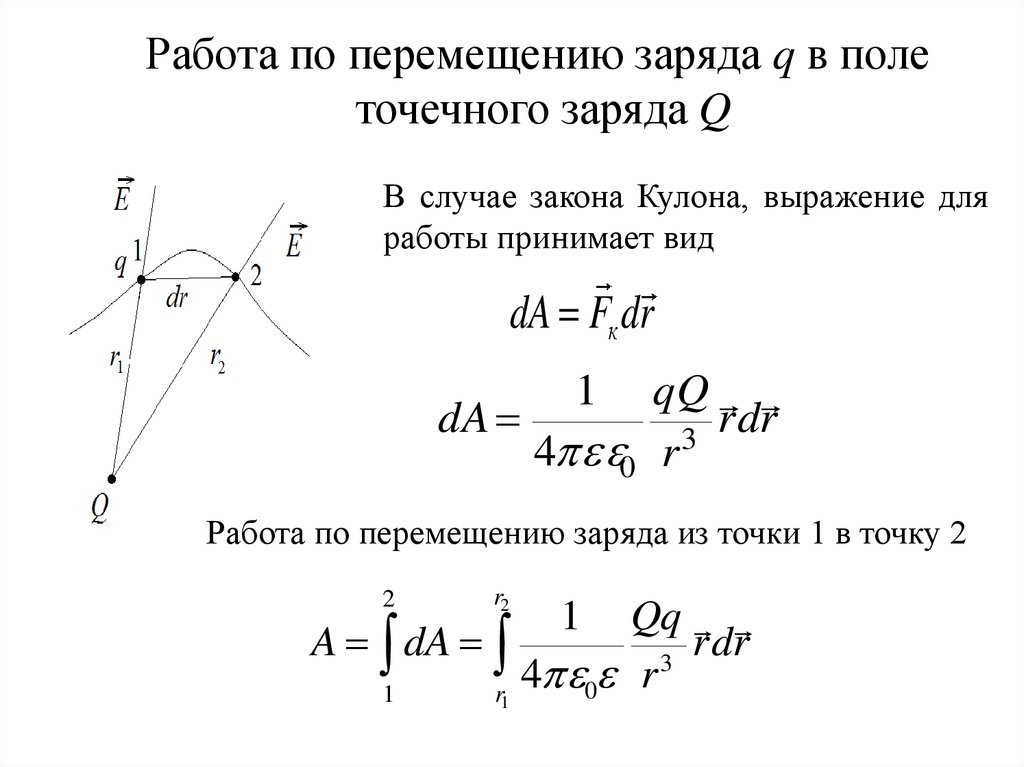
Работа по перемещению заряда q в поле
точечного заряда Q
В случае закона Кулона, выражение для
работы принимает вид
dA Fк dr
qQ
dA
r dr
3
4 0 r
1
Работа по перемещению заряда из точки 1 в точку 2
2
r2
Qq
A dA
r dr
3
4 0 r
1
r1
1

19.

r2
Qq rdr
A
4 0 r1 r 3
При
dr 0
Qq
r2
r dr rdr
r2
r2
rdr
Qq
dr
Qq 1
A
3
2
4 0 r1 r
4 0 r1 r
4 0 r r
1
Получаем
Qq 1 1
A
4 0 r1 r2
Работа сил электрического поля не зависит от траектории
движения, а зависит только от начального и конечного
положения заряда q.

20.

Q заряд источника поля
+
В
q В
W
В
q
+
q
W
A
A
+
q пробный заряд
А
Будем изменять q в какое либо число раз. Опыт покажет:
Wn
W1 W 2
...
const
q1
q2
qn

21. Потенциал и разность потенциалов

Потенциал- это энергетическая характеристика поля.
Потенциалом электростатического поля называют
отношение потенциальной энергии заряда в поле к
этому заряду.
В Дж
Кл
wp
скаляр
q
Потенциал поля в произвольной точке определяется как
алгебраическая сумма потенциалов, создаваемых отдельными
точечными зарядами.
1 2 3 ... n

22.

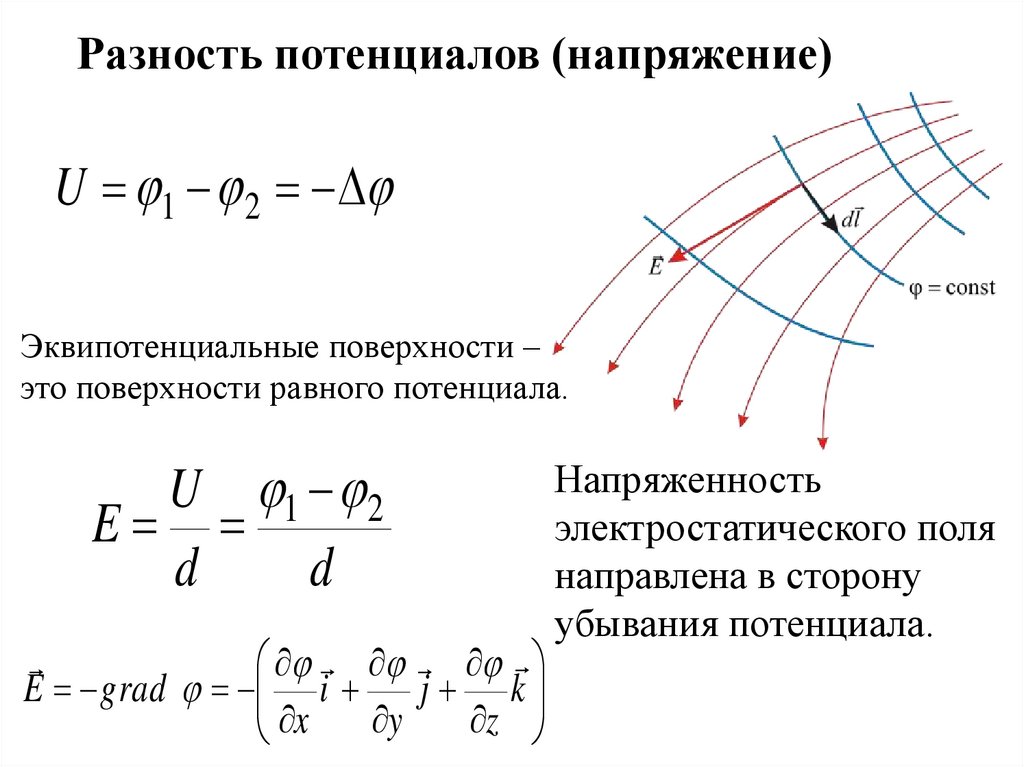
Разность потенциалов (напряжение)
U 1 2
Эквипотенциальные поверхности –
это поверхности равного потенциала.
U 1 2
E
d
d
E grad i j k
y
z
x
Напряженность
электростатического поля
направлена в сторону
убывания потенциала.

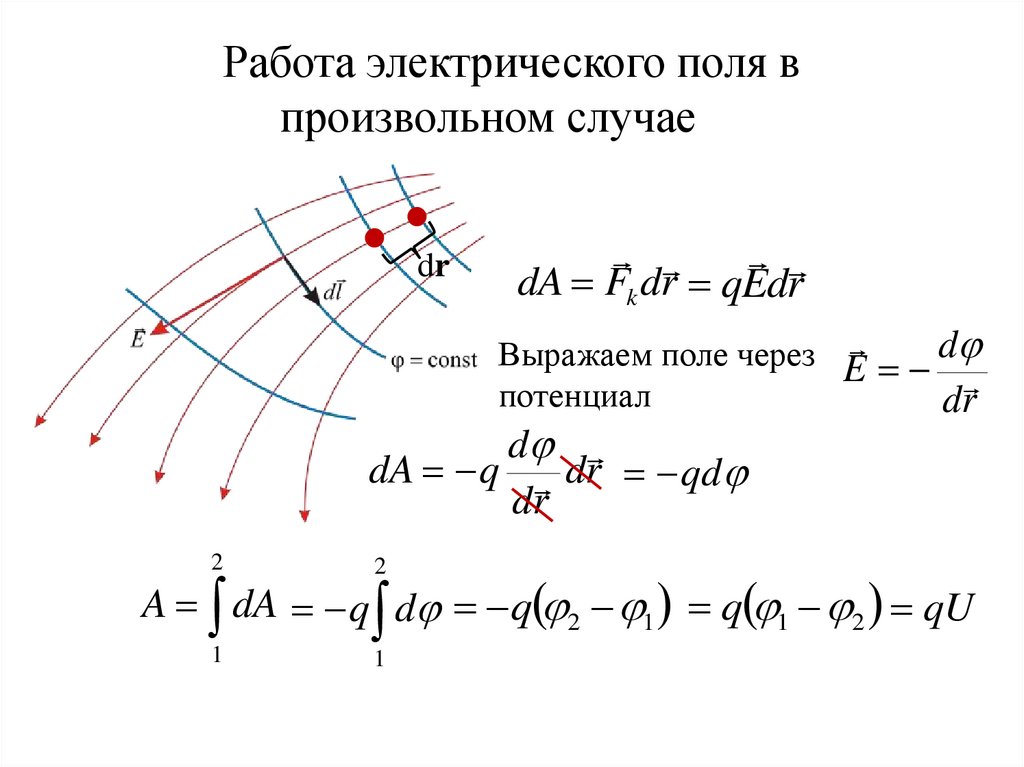
23.

Работа электрического поля в
произвольном случае
dr
dA Fk dr qEdr
Выражаем поле через E d
потенциал
dr
d
dA q dr qd
dr
2
2
1
1
A dA q d q 2 1 q 1 2 qU

24.

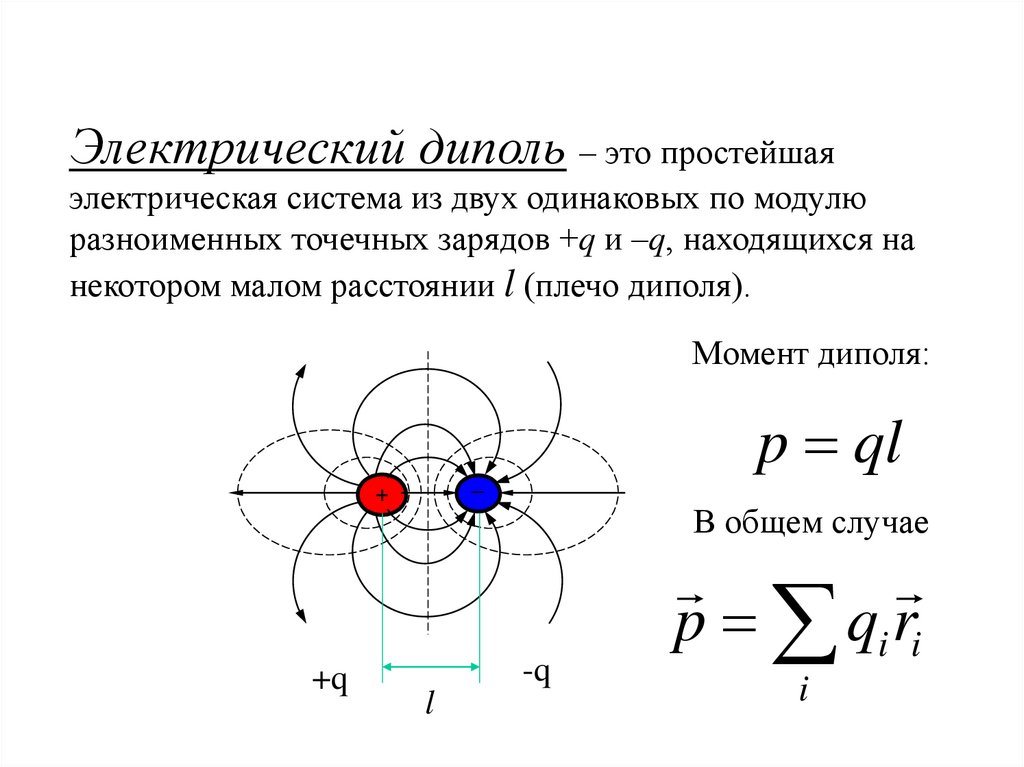
Электрический диполь – это простейшая
электрическая система из двух одинаковых по модулю
разноименных точечных зарядов +q и –q, находящихся на
некотором малом расстоянии l (плечо диполя).
Момент диполя:
p ql
−
+
+q
В общем случае
-q
l
p qi ri
i

25.

Напряженность электрического поля диполя
Е
Еθ
P
r
q−
r−
r+
θ
С l
q+
r>>l
Еr
Результирующее поле:
E
Er2 E 2
Поле на оси (θ=0):
Поле перпендикулярно оси (θ= /2):
Потенциал:
1 p cos
2
4 0 r
1 p
3 1 3 cos2
4 0 r
1 p
E
3
2 0 r
1 p
E
3
4 0 r