Similar presentations:
2_2 Теоремы+
1.
§ 9. Теоремы о дифференцируемыхфункциях
Опр.1.Точка x0 называется точкой локального максимума
(минимума) функции, если существует такая окрестность
точки x0, что для всех точек x ≠ x0 из этой окрестности
выполняется неравенство f (x0) ≥ f (x) (соответственно,
f (x0) ≤ f (x)). Такие точки называются экстремумами. Если
неравенства в этом определении строгие, то и экстремум
называется строгим.
Для графика функции y = f (x) под точкой экстремума
понимается точка (x0, f (x0)).
2.
Замечания. 1. Только в точках экстремума для достаточномалых ∆x приращение функции ∆y = f (x0 + ∆x) – f (x0) не
меняет знак при переходе аргумента через рассматриваемую
точку x0: ∆y ≥ 0 в случае минимума и ∆y ≤ 0 в случае
максимума.
2. Функция может иметь экстремум только во внутренних
точках области определения.
3. Локальные экстремумы следует отличать от глобальных,
относящихся не к точке, а к целому промежутку, и
представляющие соответственно наибольшее (глобальный
максимум) и наименьшее (глобальный минимум) значения
функции на этом промежутке.
3.
ТhФерма.
Пусть
дифференцируемая
функция y= f (x) определена в некотором промежутке и во
внутренней точке этого промежутка x0 имеет локальный экстремум,
то производная этой функции в этой точке обращается в нуль:
f ′(x0) = 0.
Пьер Ферма (17.08.1601 – 12.01.1665)
— французский математик-самоучка,
один из создателей аналитической
геометрии,
математического
анализа, теории вероятностей и теории
чисел. По профессии юрист, с 1631
года — советник парламента в Тулузе.
Один из величайших математиков всех
времён. Блестящий полиглот. Наиболее
известен
формулировкой
Великой
теоремы Ферма, «самой знаменитой
математической загадки всех времён».
Доказана в 1994 году Эндрю Уайлсом
на 130 страницах, за что он в 2016
получил Абелевскую премию.
4.
ТhФерма.
Пусть
дифференцируемая
функция y= f (x) определена в некотором промежутке и во
внутренней точке этого промежутка x0 имеет локальный экстремум,
то производная этой функции в этой точке обращается в нуль:
f ′(x0) = 0.
Геометрическая интерпретация: в точке локального
экстремума касательная к графику функции параллельна оси Ox
(оси абсцисс).
Доказательство.
Пусть для определенности x0 – точка локального максимума, т. е.
∆y ≤ 0.
0 f ( x0 ) f ( x0 ) f ( x0 ) 0.
f ′(x0) = 0. ◄
В доказательстве существенно было использовано предположение,
что x0 является внутренней точкой, так как нам пришлось
рассматривать и точки справа и слева от x0 .
5.
Опасные моменты!1. Во внутренней точке экстремума производная может не
существовать.
2. Точка экстремума функции может не быть внутренней точкой
области определения.
3. Равенство нулю производной является необходимым
условием, но это условие достаточным условием наличия
экстремума не является.
6.
Мишель Ролль21.04.1652 – 08.11.1719
Мишель Ролль французский математик. Родился в
городке Амбер (провинция Овернь). По прибытии в
Париж, в возрасте 23 лет, он в начале добывал себе
средства
к
существованию
перепиской.
Его
математические сведения, обнаружившиеся, между
прочим, в решении трудной задачи, предложенной
Озанамом, открыли ему двери академии. В 1685 году он
стал её членом.
Особенно важны работы Ролля по предмету численного
решения уравнений и особенно найденный им метод
каскадов для определения пределов, заключающих
корень уравнения. Изложение исследований Ролля
находится в его «Алгебраическом трактате» (Париж,
1690).
В «Алгебраическом трактате» обращают на себя
внимание: глава о разыскании общего наибольшего
делителя двух многочленов, составляющих уравнения,
и теорема о числе значений корня n-ой степени.
7.
Тh Ролля. Пусть функция y = f (x) определена и непрерывна наотрезке [a; b], дифференцируема в интервале (a; b) и на концах
промежутка принимает равные значения f (a) = f (b). Тогда
существует хотя бы одна точка c (a; b) такая, что f ′(c) = 0.
Геометрическая интерпретация теоремы Ролля: при
предположениях теоремы на графике функции найдется (по
крайней мере, одна) точка (c; f (c)), касательная к графику
функции в которой параллельна оси Ox (оси абсцисс).
y
f (c)
f (a)=f (b)
0
a
c
b
x
8.
Тh Ролля. Пусть функция y = f (x) определена и непрерывна наотрезке [a; b], дифференцируема в интервале (a; b) и на концах
промежутка принимает равные значения f (a) = f (b). Тогда
существует хотя бы одна точка c (a; b) такая, что f ′(c) = 0.
Доказательство.
Пусть f ( x) const, x [a, b].
f ( x) 0, x (a, b),
любую точку c (a; b) можно взять в качестве искомой.
Пусть f ( x) const, x [a, b].
В силу теоремы Вейерштрасса, непрерывная на [a, b] функция
f (x) достигает на этом промежутке своего наибольшего и
наименьшего значений и хотя бы одно из них достигается
внутри промежутка (т. к. f (a) = f (b) и функция не является
постоянной).
Функция достигает локального экстремума внутри промежутка.
По теореме Ферма внутри (a; b) найдется точка c такая, что
f ′(c) = 0. ◄
9.
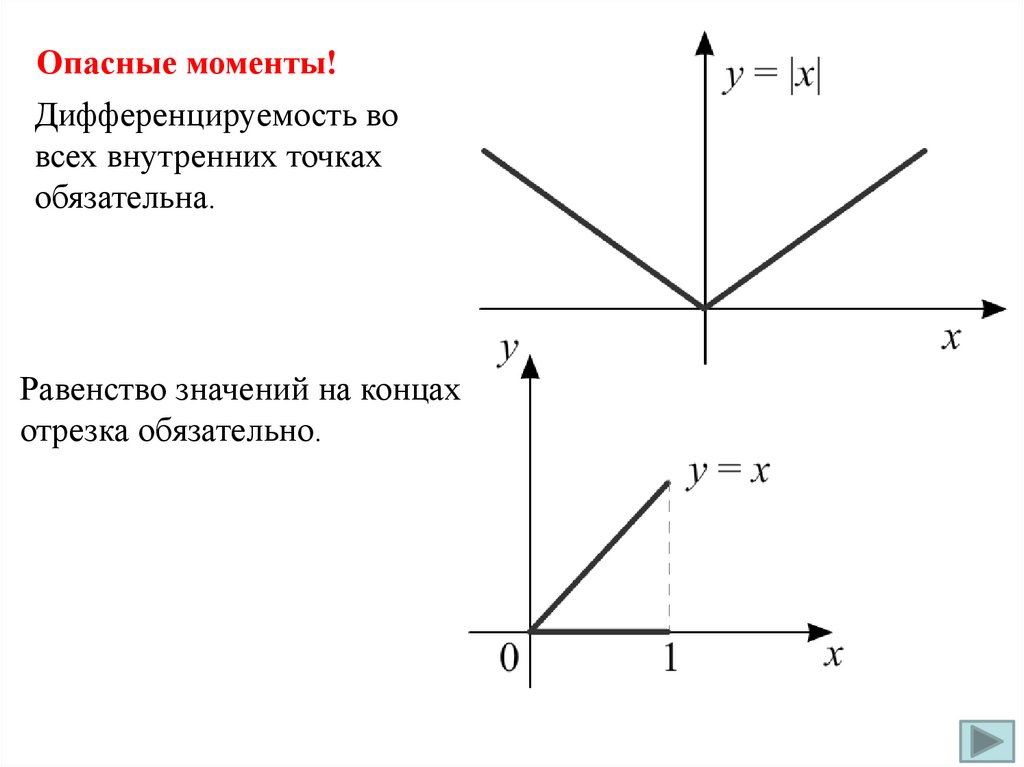
Опасные моменты!Дифференцируемость во
всех внутренних точках
обязательна.
Равенство значений на концах
отрезка обязательно.
10.
Лемма. Пусть функции f (x) и g(x) непрерывны наотрезке [a, b] и дифференцируемы на интервале (a, b).
Тогда внутри (a, b) найдется такая точка c, c (a, b), что
( f (b) – f (a)) g′(c) = ( g(b) – g(a)) f ′(c).
Доказательство.
F(x) = (f (b) – f (a)) ( g(x) – g(a)) – ( g(b) – g(a)) (f (x) – f (a)).
Все предположения теоремы Ролля выполнены, в
частности, F(a) = 0 = F(b).
Поэтому найдется такая точка c, c (a, b), что F′(c) = 0 или
(f (b) – f (a))g′(c) – ( g(b) – g(a))f ′(c)=0,
( f (b) – f (a)) g′(c) = ( g(b) – g(a)) f ′(c). ◄
11.
Тh Лагранжа. Пусть функция y = f (x) определена инепрерывна на отрезке [a; b], дифференцируема в интервале
(a; b). Тогда существует хотя бы одна точка c a; b , что
f (b) – f (a) = f ′(c)(b – a).
Жозеф-Луи Лагранж (25.01.1736 –
10.04.1813).
Французский математик, астроном и
механик
итальянского
происхождения.
Наряду
с
Эйлером
—
крупнейший
математик XVIII века.
Внёс огромный вклад в математический
анализ,
теорию
чисел,
в
теорию
вероятностей
и
численные
методы,
создал вариационное исчисление.
Имя Лагранжа внесено в список 72
величайших учёных Франции, помещённый
на первом этаже Эйфелевой башни.
12.
Французский математик и механик, членПарижской АН (1772). Родился в семье
обедневшего чиновника. Самостоятельно изучал
математику. В 19 лет Лагранж уже стал
профессором в артиллерийской школе Турина. В
1759 избран член Берлинской АН, а в 1766–1787
был её президентом. В 1787 Л. переехал в Париж;
с 1795 профессор Нормальной школы, с 1797 —
Политехнической школы.
Автор классического трактата «Аналитическая
механика», в котором установил
фундаментальный «принцип возможных
перемещений» и завершил математизацию
механики. Внёс большой вклад в развитие
анализа, теории чисел, теорию вероятностей и
численные методы, создал вариационное
исчисление.
13.
14.
Тh Лагранжа. Пусть функция y = f (x) определена инепрерывна на отрезке [a; b], дифференцируема в интервале
(a; b). Тогда существует хотя бы одна точка c a; b , что
f (b) – f (a) = f ′(c)(b – a).
Доказательство. Следует из леммы при g ( x) x, x [a, b].
f (b) – f (a) = f ′(c)(b – a). ◄
Геометрический смысл теоремы
Лагранжа: На графике функции
найдется хотя бы одна точка
С(с; f (c)), в которой касательная
к графику функции параллельна
секущей АВ.
y
B
C
y=f (x)
A
x
a
c
b
15.
ЗамечаниеВозникает вопрос: является ли точка с произвольной точкой
интервала, т. е. можно ли для всякой точки с из интервала (a; b)
указать две другие точки x1 и x2 из этого интервала такие, что
f(x2) − f(x1) = f ′(с)(x2 − x1) (x1 < с < x2)
Ответ на этот вопрос отрицательный.
Рассмотрим функцию f(x) = x3 на отрезке [−1; 1] и точку с = 0.
Производная f ′(x) = 3x2 в точке с = 0 равна нулю. Поэтому
требуемое равенство имеет вид
x23 − x13 = 0·(x2 − x1) = 0,
что выполнено быть не может так как x1 ≠ x2.
16.
Следствие Условие постоянства функцииОпределённая в интервале (a; b) функция f(x) постоянна тогда и
только тогда, когда в этом интервале производная f ′ (x) = 0.
17.
Огюстен Луи Коши21.08.1789 – 23.05.1857
Великий французский математик, член
Парижской академии наук, Лондонского
королевского общества, Петербургской
академии наук и других академий.
Разработал фундамент математического
анализа, внёс огромный вклад в анализ,
алгебру, математическую физику и
многие другие области математики. Его
имя внесено в список величайших
учёных Франции, помещённый на
первом этаже Эйфелевой башни.
18.
Тh Коши. Пусть функции f (x) и g(x) определены инепрерывны на замкнутом промежутке [a; b], дифференцируемы
на (a; b), причем g′(x) ≠ 0 для всех точек интервала. Тогда
найдется такая точка c, c (a; b), что
f (b) f (a) f (c)
.
g (b) g (a) g (c)
Доказательство.
g ( x) 0, x (a, b), g (b) g (a) g c b a 0.
f (b) – f (a) = f ′(c)(b – a).
f (b) f (a) f (c)
. ◄
g (b) g (a) g (c)
Замечание. Геометрическая
интерпретация теоремы Коши
такая же, как и теоремы
Лагранжа, если ее применить к
функции y = y(x), заданной
параметрически: x = g(t), y = f (t).
f
f (b)
f (a)
0
С
B
A
g(a) c
D
g(b)
g
19.
Контрпримерf(x) = x2, g(x) = x3, a = –1, b = 1.
Условия теоремы Коши не выполнены: производная функции
g(x) в интервале (–1; 1) обращается в нуль (в точке x = 0).
20.
Гильом Франсуа де Лопиталь(1661-1704).
Французский математик, автор
первого
учебника
по
математическому
анализу,
маркиз.
Сын богатых родителей, маркиз Лопиталь
поступил сперва в военную службу, но по
слабости зрения вскоре оставил её и посвятил
себя наукам.
Главная заслуга Лопиталя заключается в первом систематическом изложении
математического анализа, данное им в сочинении «Анализ бесконечно
малых» в 1696 г. В этой книге собраны и приведены в стройное целое
отдельные вопросы, разбросанные до того в разных повременных изданиях, а
также приводится Правило Лопиталя.
Лопиталю принадлежит также решение ряда задач, в том числе о кривой
наименьшего времени ската (брахистохрона), о кривой, по которой должен
двигаться груз, прикрепленный к цепи и удерживающий в равновесии
подъёмный мост. Решение этих задач помогло ему стать в один ряд с Ньютоном,
Лейбницем и Якобом Бернулли.
21.
Используемпонятие
производной
для
раскрытия
неопределенностей всех типов. Приводимая ниже теорема в
основном принадлежит Иоганну Бернулли. Содержащееся в ней
правило, однако, обычно называют «правилом Лопиталя», так
как оно впервые было опубликовано именно в книге Лопиталя,
вышедшей в свет в 1696 г.
Теорема 1. Пусть выполнены условия:
1) функции f(x) и g(x) определены и дифференцируемы в
некоторой окрестности точки x0 (кроме, быть может, самой
точки x0 );
3) g′(x) ≠ 0 в указанной проколотой окрестности точки x0.
4) существует (конечный или нет) предел отношения
производных
Тогда и
22.
Доказательство.Так как lim f ( x) lim g ( x) 0, то функции f (x) и g(x) могут иметь
x x0
x x0
не более, чем устранимый разрыв в точке x0, то доопределим
их в этой точке по непрерывности: f (x0) = g(x0) = 0.
Тогда новые функции удовлетворяют всем предположениям
теоремы Коши.
f ( x) f ( x0 ) f (c) , где точка с лежит между x и х.
0
g ( x) g ( x0 ) g (c)
◄
23.
Теорема 2. Пусть выполнены условия:1) функции f(x) и g(x) определены и дифференцируемы на
полупрямой (a;+∞);
3) g′(x) ≠ 0 на полупрямой (a;+∞);
4) существует (конечный или нет) предел отношения
производных
Тогда и
24.
Первоеправило
неопределенность типа
Лопиталя
позволяет
раскрыть
и утверждает, что если существует
f ( x)
предел xlim
отношения производных, то существует предел
x0 g ( x )
f ( x)
отношения функций xlim
и эти пределы совпадают:
x0 g ( x)
f ( x) 0
f ( x)
lim
lim
.
x x0 g ( x)
0 x x0 g ( x)
Однако обратное неверно.
не существует.
25.
Второе правило. Теорема 2. Пусть выполнены условия:1)функции f(x) и g(x) определены и дифференцируемы в
некоторой окрестности точки x0 (кроме, быть может, самой
точки x0 );
f ( x) , lim g ( x) .
2) и xlim
x
x x
3) g′(x) ≠ 0 в указанной проколотой окрестности точки x0.
f ( x)
4) существует (конечный или нет) xlim
x g ( x)
f ( x)
f ( x)
f ( x)
lim
lim
Тогда существует и lim
x x0 g ( x)
x x0 g ( x)
x x0 g ( x)
Доказательство можно свести к доказательству первого
1
правила, если перейти к функциям вида
и 1 .
f ( x)
g ( x)
Замечание 1. Правило справедливо и в случае, когда x → ∞, и
при вычислении односторонних пределов.
Замечание 2. Если функции f ′(x), g′(x), f ″(x), g″(x), …, f (k)(x),
g(k)(x) удовлетворяют условиям теоремы, то правило Лопиталя –
Бернулли можно применять несколько раз:
k
f ( x)
f ( x)
f ( x)
f ( x)
lim
lim
lim
... lim k .
x x0 g ( x )
x x0 g ( x )
x x0 g ( x )
x x0 g
( x)
0
0
0
26.
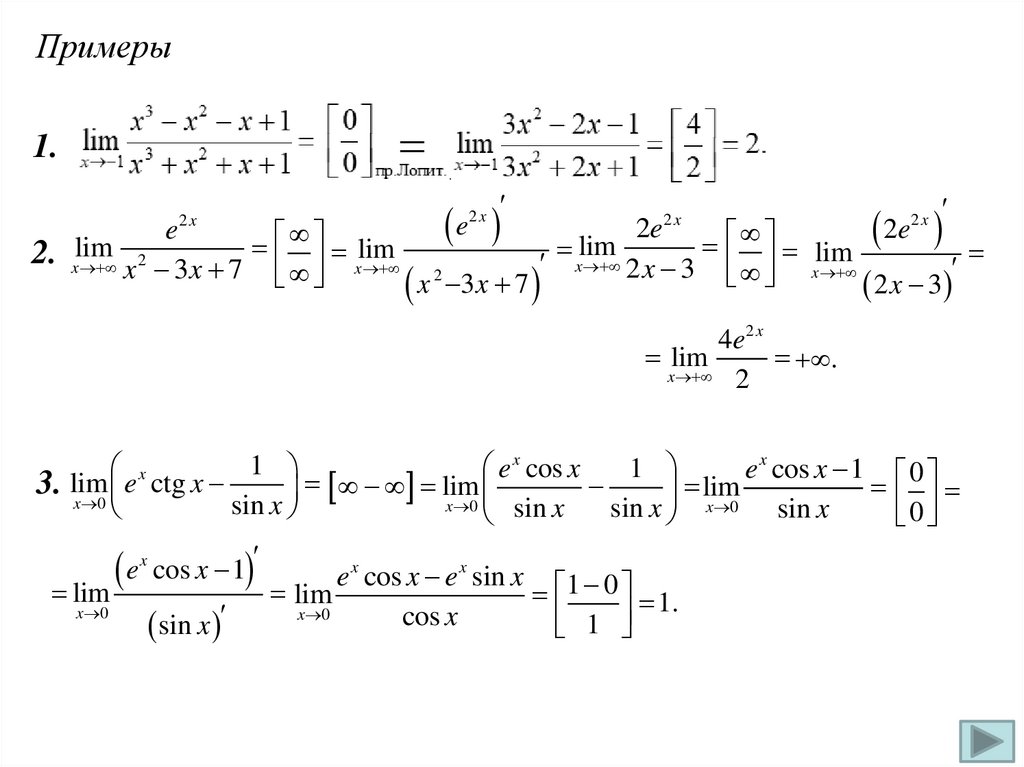
Примеры1.
2x
2x
2
e
2e
e
lim
lim
lim
lim
2. x x 2 3x 7 x
x 2 x 3
x
2
2 x 3
x 3x 7
e
2x
2x
4e2 x
lim
.
x 2
1
e x cos x
x
1
e x cos x 1 0
3. lim
lim
e ctg x
lim
x 0
x
0
x 0
sin x
sin
x
sin
x
sin
x
0
e cos x 1
e cos x e sin x 1 0
lim
lim
x
x 0
x
sin x
x 0
x
cos x
1 1.
27.
2ln x2ln x
ln x
x
3
2
lim
lim
x 0 3
lim
x ln x 0 xlim
4. xlim
0 1
0
x 0 1 x 0 3
x3
x3
x4
3
x
1
2
2 lim ln x 2
x
lim
lim x3 0.
x 0
x 0
x 0 3
9
3
3
1
4
3
x
ln sin x
x
lim
1
x 0
x
lim
x
ln
sin
x
x
ln sin x
0
x
0
x
e
sin x 0 lim e
5. xlim
e
e
0
x 0
ln x
2
2
lim
x 0
1
x
e
e
cos x
lim sin x
x 0 1
ln sin x
x 2
lim
x 0 tg x
x2
e
lim
x 0
e
2x
1
cos2 x e
x2
0
cos x x2
lim
lim
0
x 0 tg x
x 0 sin x
e
e
e
lim 2 x cos 2 x
x 0
e 0 1.
28.
6. Сравнить рост функций y = xn, n N , y = logax, y = bx, a > 0,a ≠ 1, b > 1 при x → +∞.
1
log a x
(log a x) lim x ln a 1 lim 1 0.
lim
x
xlim
n 1
n
x x n
n
n
ln
a
x
n
x
x
(x )
xn
n x n 1
( x n )
lim x lim x lim
x
x b
x
x
ln b b
(b )
применим правило
n!
0.
Лопиталя Бернулли еще xlim
(ln b) n b x
n 1 раз, получим
7.
y
1
y = bx, b > 1
y=x
y = logax, a > 1
0 1
x
29.
§ 10. Формула ТейлораГлавной формулой дифференциального исчисления является
формула Тейлора. Эта формула позволяет значительно
облегчить изучение поведения (гладкой) функции в окрестности
данной точки. Брук Тейлор (18.08.1685 – 29.12.1731).
Брук Тейлор родился в деревне Эдмонтон в графстве
Мидлсекс, в восьми милях от Лондона. В 1701 г. он
поступил в Кембриджский университет, в колледж СентДжон.
Статьи Тейлора были признаны настолько ценными, что в
1712 г. его избрали членом Королевского общества.
В 1718 г. он уходит с поста секретаря Королевского
общества, чтобы освободить время для философской
работы. Он возвращается к увлечениям молодости —
занимается музыкой и живописью.
В 1730 г. от родов умерла жена Тейлора. Правда осталась девочка, но Тейлор
был неутешен в своем горе. Его здоровье резко ухудшалось и больше не
восстанавливалось. 29 декабря 1731 г. он скончался и был погребён в
Лондоне.
30.
Пусть функция имеет в данной точке несколькопоследовательных производных до порядка n включительно.
Рассмотрим задачу о нахождении многочлена степени n,
который имеет те же значения производных
P(a) = f(a), P′(a) = f ′(a), ...,
P(n)(a) = f (n)(a).
Этот многочлен удобно искать в виде следующего разложения
P(x) = c0 + c1(x − a) + c2(x − a)2 + ... + ck(x − a)k + ... + cn(x − a)n.
Последовательно дифференцируя, находим
P′(x) = c1 + 2c2(x − a) + ... + kck(x − a)k−1 + ... + ncn(x − a)n−1.
P″(x) = 2c2 + ... + k(k − 1)ck(x − a)k−2 + ... + n(n − 1)cn(x − a)n−2.
..............................................
31.
P(k)(x) = k(k − 1)(k − 2) ... 3·2ck + ...P(k)(a) = k! ck
n−k
+ n(n − 1)(n − 2) ... (n − k + 1)cn(x − a) .
..............................................
P(n)(x) = n(n − 1)(n − 2) ... 3·2cn.
Полагая во всех полученных равенствах x = a, получаем
P(a) = c0
P(x) = c0 + c1(x − a) + c2(x − a)2 + ... + ck(x − a)k + ... + cn(x − a)n.
Последовательно дифференцируя, находим
P′(x) = c1 + 2c2(x − a) + ... + kck(x − a)k−1 + ... + ncn(x − a)n−1.P′(a) = c1
P″(x) = 2c2 + ... + k(k − 1)ck(x − a)k−2 + ... + n(n − 1)cn(x − a)n−2.
..............................................
32.
Предположим, что функция f (x), определена в окрестноститочки x0 и имеет в этой точке производные до n-го порядка
включительно, тогда для этой функции в точке x0 имеет место
формула Тейлора
n
f x0
f x0
f x0
2
n
f x Pn x Rn x f x0
x x0
x x0 ...
x x0 Rn x
1!
2!
n!
Многочлен Pn(x) называется n-м многочленом Тейлора,
Rn(x) называется n-ым остаточным членом формулы Тейлора.
Числа
называются коэффициентами формулы Тейлора.
33.
Формула Тейлора с остаточным членом в форме Лагранжа.Тh. Если функция f (x) определена в точке x0 и некоторой ее
окрестности и имеет в этой окрестности производные до
(n + 1)-го порядка включительно, то для любого х из этой
окрестности найдется такая точка с, лежащая между x0 и х, что
справедлива формула
где
(остаточный член в форме Лагранжа).
Схема доказательства.
Покажем, что
Фиксируем любое значение x из окрестности точки x0, и по
образцу правой части формулы
заменяя постоянное число x0 на переменную t, составим новую
вспомогательную функцию:
34.
причем независимую переменную t считаем изменяющейся впромежутке (x0,x).
В этом промежутке функция F(t) непрерывна и принимает на
концах его значения: F(x0)=Rn(x), F(x)=0.
Кроме того, в промежутке (x0,x) существует производная
f t f t
f t
f t
2
F t f t
x t
x t
x t ...
1! 2!
1!
1!
n
n 1
f n 1 t
f t
f t
n
n 1
n
x t
x t
x t
n!
n 1 !
n!
заменяя постоянное число x0 на переменную t, составим новую
вспомогательную функцию:
35.
Если взять еще какую-нибудь функцию G(t), непрерывную впромежутке (x0,x) и имеющую в открытом промежутке (x0,x)
производную, не обращающуюся в нуль, например,
Тогда на концах отрезка, она принимает значения
К паре F(t) G(t) можно будет применить формулу Коши:
Окончательно получим:
36.
Формула Тейлора с остаточным членом в форме Лагранжа.n 1
f x0
f x0
f x0
f c
2
n
n 1
f x f x0
x x0
x x0 ...
x x0
x x0
1!
2!
n!
n 1 !
n
В форме
дополнительный член напоминает следующий
очередной член формулы Тейлора, лишь вместо того, чтобы
вычислить (n+1)-ю производную в точке x0, эту производную
берут для некоторого среднего — между x0 и x — значения c.
Формула является прямым обобщением формулы конечных
приращений.
Формула Тейлора с остаточным членом в форме Пеано.
Тh. Если функция f (x) n раз непрерывно дифференцируема в
некоторой окрестности точки x0, то справедлива формула
x x0
f x f x0 f x0 x x0 f x0
2
2!
x
x
n
n
0
f x0
o x x0
n
n!
где o x x0 – бмф более высокого порядка малости, чем (x – x0)
при x → x0.
n
37.
Некоторые записи формулы Тейлора.Формула Тейлора с остаточным членом в форме Лагранжа:
Формула Тейлора с остаточным членом в форме Пеано:
Формула Тейлора с остаточным членом в форме Коши:
При x0=0 формула Тейлора называется формулой Маклорена, в
частности
38.
Формула Тейлора в дифференциалахЕсли заменить в формуле Тейлора
на dx и
, …,
То
Пример. Представить функцию y=x3 в точке x0=2 при n=2 по
формуле Тейлора.
Имеем
Получим
39.
Формула Маклоренаx2
x3
f x f 0 f 0 x f 0 f 0
2!
3!
x
n
f 0
Rn x
n!
n
Некоторые разложения по формуле Маклорена.
1. f (x) = ex, тогда f (n)(x) = ex, при любом n и f (n)(0) = 1, имеем
2
3
n
x
x
x
x
ex 1
...
Rn x
1! 2! 3!
n!
n
(n)
(n)
2. f (x) = sin x,
y (sin x) sin x
, n 0,1,2,...;
2
2n
f 0 sin n 0
n 1
2 n 1
f 0 sin n 1
2
x3 x5
x 2 n 1
n 1
sin x x ... 1
R2 n x
3! 5!
2n 1 !
40.
n3. f (x) = cos x,
f
f 0 1
f
2n
n
x cos x n
2
2 n 1
0 0
2n
x2 x4
n x
cos x 1 ... 1
R2 n 1 x
2! 4!
2n !
4. f (x) = (1 + x)m,
1 x
m
m m 1 2
m m 1 ... m n 1 n
1 mx
x ...
x Rn x
1 2
1 2 3 ... n
41.
5. f (x) = ln(1 + x),n
x 2 x3
n 1 x
ln 1 x x ... 1
Rn x
2 3
n
42.
Связь между ex , sin x и cos xПерепишем формулы Маклорена для ex , sin x и cos x
Связь между ex , sin x и cos x стоит в области комплексных
чисел. Рассмотрим e i x , где i — мнимая единица. Будем
считать, что для любого показателя степени формула
Маклорена верна. Тогда:
43.
Тем самым получаем:eix =cos x+i sin x
Записанная формула так же называется формулой Эйлера.
44.
Некоторые приложения формулы Тейлора.1. Приближенное вычисление значения функции.
x x0
f x f x0 f x0 x x0 f x0
2!
2
Пример 1. Вычислить sin 1 с точностью ε = 0,001.
x3 x5
x 2 n 1
n 1
sin x x ... 1
3! 5!
2n 1 !
1 1
1
1
1
1
,
1 ,
,
3! 6
5! 120
7! 5040
1 1
1
1
101
sin1 1 1
3! 5!
6 120 120
n
x x0
n
f x0
n!
45.
2. Использование формулы Тейлора при раскрытиинеопределенностей.
Пример 2.
0
0





































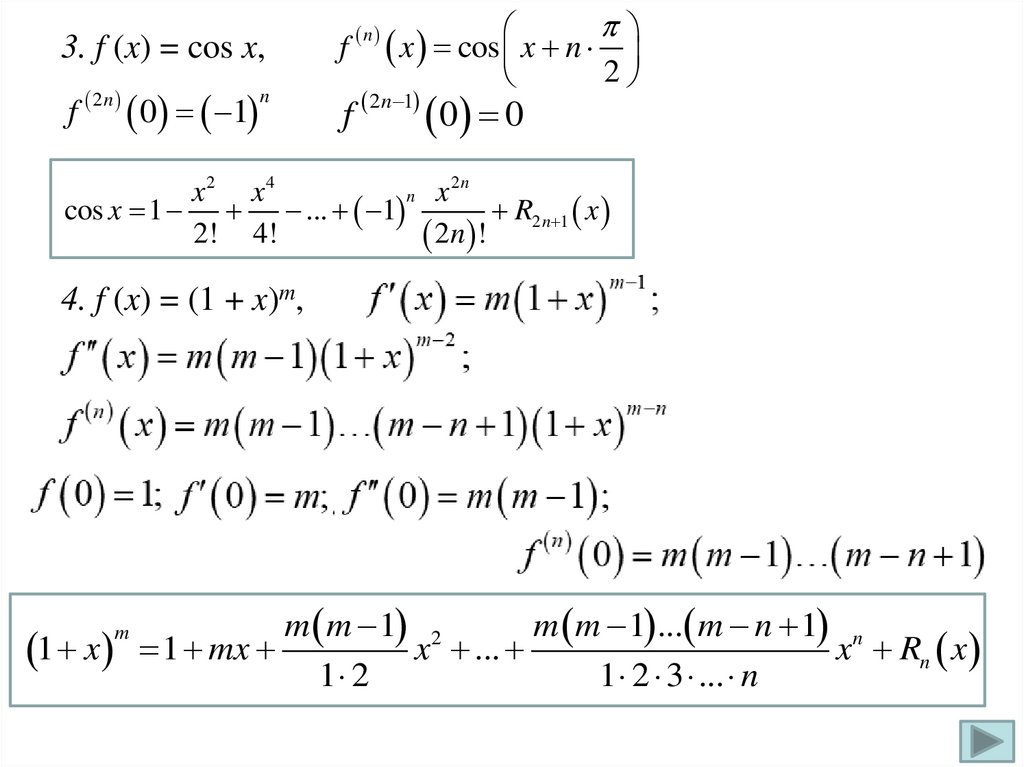
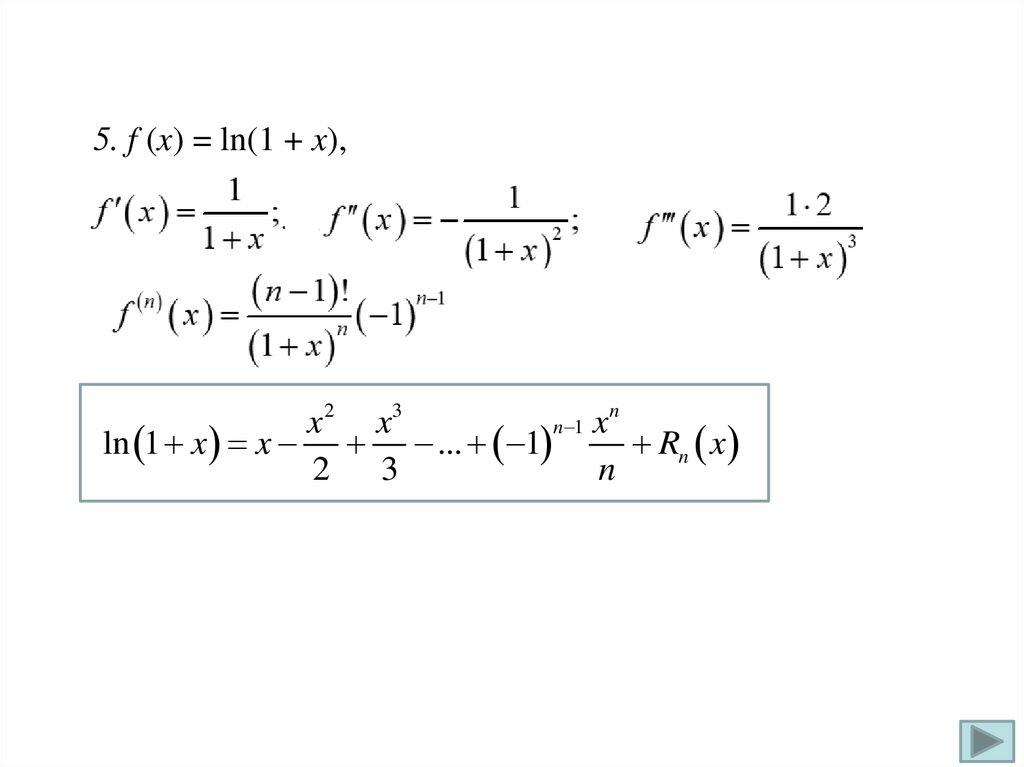




 mathematics
mathematics








