4.76M

Category: $mathematics$ mathematics

06_Основные_теоремы_дифф_исчисления_2025

1.

Лемма Дарбу (достаточное условие строгой монотонности функции).
Если f x0 c и c 0
c 0 , то x x0 – точка возрастания (убывания)
функции f x .
З а м е ч а н и е . Положительность (отрицательность) производной
f x0
не является необходимым условием возрастания (убывания) функции f x
в точке x0 .
1

2.

П р и м е р . Докажем неравенства
1
cos x 1 x 2 ,
2
1
sin x x x3 , x 0 .
6
1 2
f
x
cos
x
1
x .
Рассмотрим функцию
2
f x sin x x
при x 0 функция f возрастает
f x f 0 0 .
1 3
Рассмотрим теперь функцию g x sin x x x .
6
x2
g x cos x 1
f x 0
2
g x возрастает g x g 0 0 .
3

3.

Функция f x имеет:
– локальный минимум (максимум), если в некоторой проколотой окрестности
точки x0 выполняется неравенство f x f x0 ( f x f x0 );
– нестрогий локальный минимум (максимум), если в некоторой проколотой
окрестности точки x0 выполняется неравенство f x f x0 ( f x f x0 ).
Локальный экстремум – общее название локального минимума и локального максимума. Локальный экстремум (минимум, максимум) также называют внутренним
экстремумом (минимумом, максимумом).
Пусть y f x определена на a, b . Тогда f x имеет:
– в точке a краевой минимум (максимум), если найдется правая окрестность
точки a , в пределах которой значение f a – наименьшее (наибольшее) среди всех
других значений,
– в точке b краевой минимум (максимум), если найдется левая окрестность
точкм b , в пределах которой значение f b – наименьшее (наибольшее) среди всех
других значений.
Краевой экстремум – общее название краевого минимума и краевого максимума.
4

4.

Теоремы Ферма, Ролля, Коши и Лагранжа
Теорема Ферма (необходимое условие локального экстремума дифференцируемой функции). Если функция f x дифференцируема в точке x0 и имеет в этой
точке локальный экстремум, то f x0 0 .
Теорема Ролля о нуле производной.
Пусть f x непрерывна на отрезке a, b и дифференцируема внутри него. Тогда
если f a f b c , то x0 a, b f x0 0 .
Теорема Коши, или обобщенная формула конечных приращений.
Пусть f x и g x непрерывны на отрезке a, b и дифференцируемы внутри
него. Тогда если x a, b g x 0 , то x0 a, b
f x0
.
g a g b g x0
f a f b
Следствие (теорема Лагранжа, или формула конечных приращений).
Пусть функция f x непрерывна на отрезке a, b и дифференцируема внутри
него. Тогда x0 a, b f a f b f x0 a b .
5

5.

П р и м е р . Докажем неравенство
x
ln 1 x x , x 0 .
1 x
Рассмотрим функцию y t ln t . На 1, 1 x она дифференцируема,
а значит, и непрерывна. Тогда согласно теореме Лагранжа:
1,1 x ln 1 x ln1 ln t
t
1 x 1
x
.
Так как ln 1 x ln 1 x ln1, то, учитывая диапазон изменения ,
получаем
x
x x
; следовательно,
x 1 1
x
ln 1 x x .
1 x
11

6.

Теорема 6.5. Пусть функция f x непрерывна на x0 , x0 h h 0 и имеет
конечную производную f x для x x0 . Если существует (конечный или бесконечный) предел lim f x S , то такова же будет и правая производная в т. x0 , т.е.
x x0 0
lim f x f x0 .
x x0 0
Аналогичное утверждение справедливо и для левой производной.
З а м е ч а н и е . Наличие предела lim f ( x) ( lim f ( x) ) является достаточным,
x x0 0
x x0 0
но не необходимым условием существования производной f ( x0 ) ( f ( x0 ) ).
Теорема 6.6. Дифференцируемая на a, b функция постоянна на нем тогда и
только тогда, когда x a, b f x 0
Следствие. Если x A f1 x f 2 x , то x A f1 x f 2 x c .
Теорема 6.7. Пусть функция f x дифференцируема на a, b . Тогда
« f x не убывает (не возрастает) на a, b »
x a, b f x 0 f x 0 .
12

7.

8.

Правило Лопиталя. Пусть f x и g x дифференцируемы всюду в некоторой окрестности т. x0 , за исключением, быть может, самой точки x0 , причем всюду
в этой окрестности g x 0 . Тогда, если lim f x lim g x 0 и существует
x x0
x x0
f x
(конечное или бесконечное) предельное значение S lim
, то существует и
x x0 g x
предельное значение lim
x x0
f x
g x
f x
f x
lim
.
x x0 g x
x x0 g x
, причем lim
-------------------------------------------------------------------------
З а м е ч а н и е 1 . Если к условиям теоремы добавить требование непрерывности производных f x и g x в точке x0 , то при условии g x0 0 формула
f x
f x
f x f x0
lim
lim
может быть переписана в виде lim
. .
x x0 g x
x x0 g x
x x0 g x
g x0
19

9.

Правило Лопиталя. Пусть f x и g x дифференцируемы всюду в некоторой окрестности т. x0 , за исключением, быть может, самой точки x0 , причем всюду
в этой окрестности g x 0 . Тогда, если lim f x lim g x 0 и существует
x x0
x x0
f x
(конечное или бесконечное) предельное значение S lim
, то существует и
x x0 g x
предельное значение lim
x x0
f x
g x
f x
f x
lim
.
x x0 g x
x x0 g x
, причем lim
-------------------------------------------------------------------------
З а м е ч а н и е 2 . Теорема верна, если x x0 0 ( x x0 0 ), а функции
f x и g x определены и дифференцируемы всюду в некоторой правой (левой)
окрестности т. x0 .
З а м е ч а н и е 3 . Теорема верна, если x ( x ), а функции определены и дифференцируемы всюду на c, ( , c ), где c .
20

10.

Правило Лопиталя. Пусть f x и g x дифференцируемы всюду в некоторой окрестности т. x0 , за исключением, быть может, самой точки x0 , причем всюду
в этой окрестности g x 0 . Тогда, если lim f x lim g x 0 и существует
x x0
x x0
f x
(конечное или бесконечное) предельное значение S lim
, то существует и
x x0 g x
предельное значение lim
x x0
f x
g x
f x
f x
lim
.
x x0 g x
x x0 g x
, причем lim
------------------------------------------------------------------------З а м е ч а н и е 4 . Если производные удовлетворяют тем же требованиям, что и
сами функции f x и g x , то правило Лопиталя можно применять повторно:
f x
f x
f x
lim
lim
,
x S g x
x S g x
x S g x
lim
S x0 , x0 0, x0 0, , , .
З а м е ч а н и е 5 . Если в теореме заменить условие lim f x lim g x 0
x S
x S
на условие lim f x lim g x или аналогичное условие, в котором вместо
x S
x S
будет или , то теорема остается справедливой.
21

11.

12.

Правило Лопиталя. Пусть f x и g x дифференцируемы всюду в некоторой окрестности т. x0 , за исключением, быть может, самой точки x0 , причем всюду
в этой окрестности g x 0 . Тогда, если lim f x lim g x 0 и существует
x x0
x x0
f x
(конечное или бесконечное) предельное значение S lim
, то существует и
x x0 g x
предельное значение lim
x x0
f x
g x
f x
f x
lim
.
x x0 g x
x x0 g x
, причем lim
-------------------------------------------------------------------------
f x
З а м е ч а н и е 8 . Если предел отношения
при x S существует и
g x
конечен, но при этом не выполнено условие монотонности функции g x , то при
f x
f x
x S предел отношения
может не совпадать с пределом отношения
.
g x
g x
23

13.

ФОРМУЛА ТЕЙЛОРА
Теорема Тейлора. Пусть функция f x имеет в некоторой окрестности точки a
производную порядка n 1 . Пусть x – любое значение аргумента из указанной окрестности, p – произвольное положительное число. Тогда между точками a и x найдется
точка , для которой справедлива следующая формула:
n
f a
f a
f a
n
2
f x f a
x a
x a ...
x a Rn 1 x ,
1!
2!
n!
Остаточный член в форме
x a x
n 1
– Шлемильха-Роша (или в общей форме ): Rn 1 x
f
;
x
n
!
p
a x a , x x a 1 ,
p
n 1
x a f n 1 a x a
– Лагранжа ( p n 1 ): Rn 1 x
;
n 1 !
n 1
n
x a 1 n 1
f
– Коши ( p 1 ): Rn 1 x
a x a ;
n 1
n!
n
– Пеано Rn 1 x o x a , при x a ;
– Rn 1 x O x a
n 1
, при x a .
27

14.

f a
f a
f a
n
2
f x f a
x a
x a ...
x a Rn 1 x
1!
2!
n!
n
---------------------------------------------------Замечания:
1 . Формулу Тейлора с центром a 0 называют формулой Маклорена.
2 . Если f x – произвольная функция, а x, a – ее многочлен Тейлора, то
a, a f a ,
a, a f a ,
,
a, a f a .
n
n
3 . Формула Тейлора позволяет представить любой многочлен по степеням x
в виде многочлена по степеням x a , где a – любое вещественное число.
28

15.

Разложение приращения функции
по степеням приращения независимого аргумента
Если в формуле Тейлора с остаточным членом в форме Лагранжа взять
a : x0 , x a : x , то она примет вид:
f f x f x0
f x0
f x0 2
f x0 n x n 1 n 1
x
x ...
x
f
x0 x
1!
2!
n!
n
1
!
Откуда, учитывая, что
n
(*)
f x0 x df x0 , f x0 x 2 d 2 f x0 , …, f x0 xn d n f x0 ,
получим:
df x0 d 2 f x0
d n f x0
f x0
...
o x n .
1!
2!
n!
З а м е ч а н и е 1 . При n 0 формула (*) дает теорему Лагранжа о конечных приращениях.
З а м е ч а н и е 2 . Формула (*) может быть использована для создания
приближенных формул. Например,
1/ n
x
1/ n
n
x 1 x 1 1 x 1
.
29
n
n

16.

f x sin x , x0 0, x x 1
f x sin x
T1 x x
x3
T3 x x
3!
x3 x5
T5 x x
3! 5!
x3 x5 x 7
T7 x x
3! 5! 7!
x3 x5 x 7 x9
T9 x x
3! 5! 7! 9!
0.841470982
1.
R2 x
– 0.158529015
0.833333333
R4 x
0.008137652
0.841666666
R6 x
– 0.000195682
0.841468254
R8 x
0.000002730
0.841471010
R10 x
– 0.000000028
30

17.

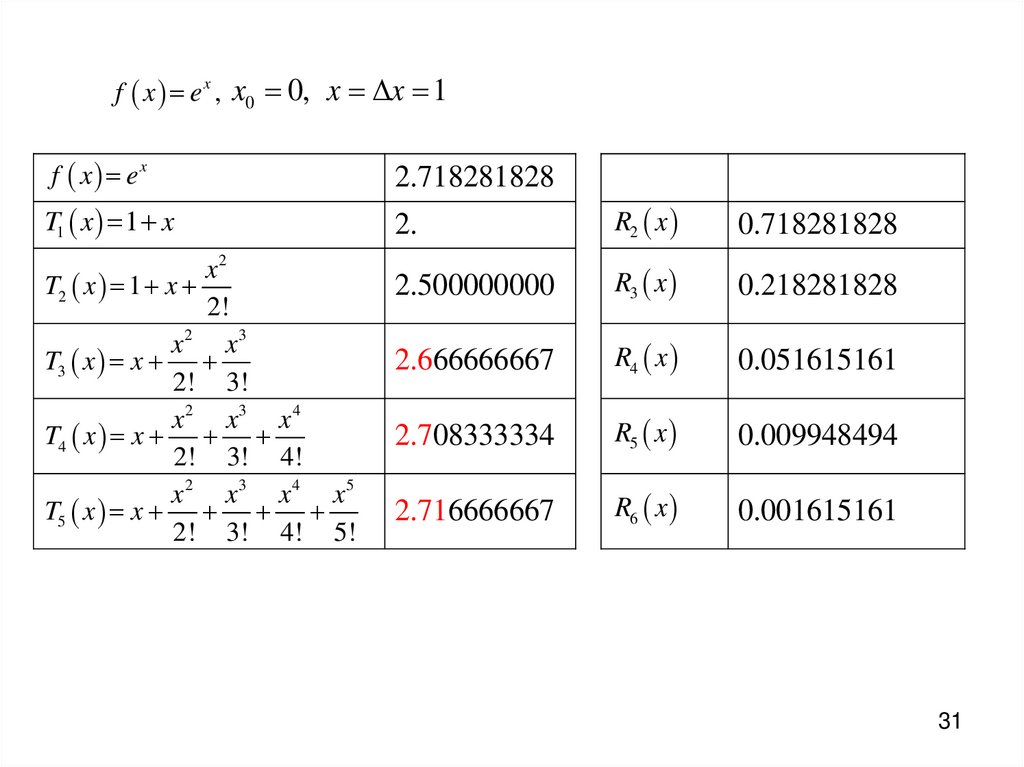
f x e x , x0 0, x x 1
f x ex
2.718281828
T1 x 1 x
2.
R2 x
0.718281828
2.500000000
R3 x
0.218281828
2.666666667
R4 x
0.051615161
2.708333334
R5 x
0.009948494
2.716666667
R6 x
0.001615161
x2
T2 x 1 x
2!
x 2 x3
T3 x x
2! 3!
x 2 x3 x 4
T4 x x
2! 3! 4!
x 2 x3 x 4 x5
T5 x x
2! 3! 4! 5!
31

18.

Теорема 6.10. Пусть f x обладает следующим свойством: существует такое
число M , что для всех номеров n и для всех значений аргумента x из рассматриваемой окрестности точки x a справедливо равенство f x M . Тогда из форn
мулы Тейлора с остаточным членом в форме Лагранжа следует, что
Rn 1 x
x a
n 1
n 1 !
f
n 1
x a
n 1
a x a M n 1 ! .
З а м е ч а н и е . Так как при любом фиксированном x
lim
n
x a
n 1
n 1 !
0,
то, выбирая достаточно большой номер n , можно сделать остаточный член сколь
угодно малым.
32

19.

Многочлен Тейлора как многочлен наилучшего приближения функции
в окрестности данной точки. Пусть f x n раз дифференцируема в т. x a и
представима в виде
f x Pn x o x a , при x a ,
n
где Pn x ck x a
k
n
(*)
– некоторый многочлен степени, меньшей или
k 0
f a
k
равной n . Тогда ck
k!
, т.е. Pn x – многочлен Тейлора.
35

20.

ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИИ
Теорема 6.13. Пусть f x дифференцируема в некоторой окрестности т. x0 и
f x0 0 . Если в пределах этой окрестности
f x 0, x x0 ;
f x 0, x x0 ,
f x 0, x > x0 ;
(*)
f
x
0,
x
x
,
0
то x0 – точка локального максимума (минимума). Если f x имеет один и тот же знак
слева и справа от точки x0 , то экстремума в точке x0 нет.
Следствие 1. Пусть f x дифференцируема всюду в некоторой окрестности т. x0 ,
за исключением, быть может, самой т. x0 , и непрерывна в т. x0 . Если в пределах этой
окрестности для f x выполняются неравенства (*), то f x имеет в т x0 локальный
max ( min ). Если же f x имеет один и тот же знак слева и справа от точки x0 , то
экстремума в точке x0 нет.
Следствие 2. Пусть f x0 0 и f x0 c
имеет в точке x0 локальный max ( min ).
. Тогда, если c 0 ( c 0 ), f x
37

21.

НАПРАВЛЕНИЕ ВЫПУКЛОСТИ ГРАФИКА ФУНКЦИИ
Функция f x называется:
– выпуклой вниз на интервале a, b , если x1 , x2 a, b
0, 1 f x1 1 x2 f x1 1 f x2 ;
– выпуклой вверх на интервале a, b , если x1 , x2 a, b
0, 1
f x 1 x f x 1 f x .
1
2
1
2
Замечания:
1 . Часто выпуклую вниз функцию называют вогнутой, а выпуклую вверх – выпуклой.
2 . Линейная функция является и выпуклой вниз, и выпуклой вверх функцией.
3 . Если в определениях неравенства заменить на строгие неравенства, то получим
определения строго выпуклой вниз (вверх) функции.
4 . График выпуклой вниз (вверх) функции также называют выпуклым вниз (вверх).
40

22.

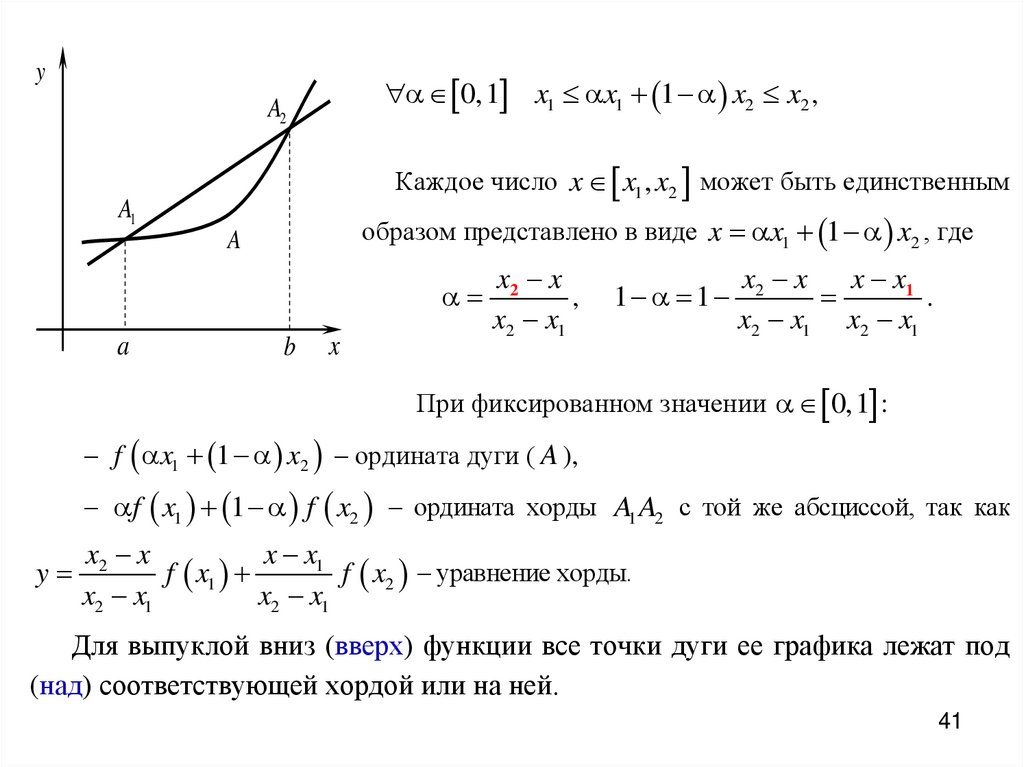
y
0,1 x1 x1 1 x2 x2 ,
A2
Каждое число x x1 , x2 может быть единственным
A1
образом представлено в виде x x1 1 x2 , где
A
a
b
x
x2 x
,
x2 x1
1 1
x2 x
x x1
.
x2 x1 x2 x1
При фиксированном значении 0,1 :
– f x1 1 x2 – ордината дуги ( A ),
– f x1 1 f x2 – ордината хорды A1 A2 с той же абсциссой, так как
y
x2 x
x x1
f x1
f x2 – уравнение хорды.
x2 x1
x2 x1
Для выпуклой вниз (вверх) функции все точки дуги ее графика лежат под
(над) соответствующей хордой или на ней.
41

23.

Теорема 6.14. Пусть f x дифференцируема на a, b . Тогда
« f x – выпукла вниз (вверх)» « f x не убывает (не возрастает)».
Следствие 1. Пусть f x дважды дифференцируема на a, b . Тогда
« f x выпукла вниз (вверх) на a, b » « f x 0 ( f x 0 ) на a, b ».
Следствие 2. Если f x непрерывна и f x0 0 ( f x0 0 ) в т. x0 , то
существует такая окрестность т. x0 , в пределах которой график функции
y f x имеет выпуклость, направленную вниз (вверх).
Теорема 6.15. Пусть f x дифференцируема на a, b . Тогда
« f x выпукла вниз (вверх)»
«график f x всеми точками лежит не
ниже (не выше) любой своей касательной.
42

24.

Основные свойства выпуклых функций
1. Если функция f x выпукла вниз (вверх), то
а) g x f x выпукла вверх (вниз):
б) c 0 g x cf x выпукла вниз (вверх).
2. Сумма двух или нескольких выпуклых вниз (вверх) функций есть
выпуклая вниз (вверх) функция.
47

25.

ТОЧКИ ПЕРЕГИБА ГРАФИКА ФУНКЦИИ
Точку M x0 , f x0 непрерывной кривой называют ее точкой перегиба, если
она отделяет участок графика, где функция f x выпукла вверх, от участка
графика, где она выпукла вниз.
Лемма 6.2. Пусть y f x имеет производную f x , конечную или беско-
нечную, в некоторой окрестности т. x0 . Тогда, если M x0 , f x0 – точка перегиба,
то график функции в этой точке переходит с одной стороны касательной на другую.
Замечания:
1 . Лемму можно переформулировать: «график
функции в точке перегиба пересекается с касательной
в этой точке, если таковая существует».
y
f x
2 . Из того, что график пересекается с касательной,
не следует, что их точка пересечения является точкой
перегиба. Например, на рисунке точка x1 , f x1 не явля-
ется точкой перегиба, хотя f x0 и функция имеет
вертикальную касательную в точке x0 .
x
x0
48

26.

Необходимое условие перегиба дважды дифференцируемой функции
Если функция в точке перегиба имеет вторую производную, то она равна 0.
Докажем от противного. Пусть функция y f x в точке перегиба
M x0 , f x0 имеет ненулевую вторую производную:
f x0 0
2
или f x 0 .
2
0
Тогда, согласно следствию 2 из теоремы 6.14, функция f выпукла вниз
(вверх) в некоторой окрестности т. x0 , что противоречит определению точки
перегиба.
З а м е ч а н и е . На примере функции y x 4 можно доказать, что это условие
не является достаточным.
50

27.

Достаточные условия перегиба дважды дифференцируемой функции
Первое достаточное условие перегиба.
Пусть f x дважды дифференцируема в некоторой окрестности т. x0 и f
2
x0 0 .
x имеет разные знаки слева и справа от т. x0 , то график
функции имеет перегиб в точке M x0 , f x0 .
Если в этой окрестности f
2
Второе достаточное условие перегиба. Если y f x имеет в т. x0 конечную
третью производную и удовлетворяет условиям f
функции имеет перегиб в точке M x0 , f x0 .
2
x0 0 , f 3 x0 0 , то график
Третье достаточное условие экстремума и перегиба. Пусть y f x имеет производную порядка n в некоторой окрестности т. x0 и производную порядка n 1
в самой т. x0 . Пусть далее справедливы отношения:
f x0 f x0
2
3
f x0 0,
n
f
n 1
x0 0 .
(6.23)
Тогда в точке M x0 , f x0 график функции y f x имеет:
1) перегиб, если n четно,
2) локальный экстремум, если n нечетно и f x0 0
( min при f
n 1
x0 0 , max при f n 1 x0 0 ).
51

English Русский Rules