final surface area of sphere

1.

Surface Area:
The Shape of Our World
From packaging to polar bears, exploring why the sphere is nature's
most efficient design.

2.

The Packaging Paradox
Have you ever wondered why milk
cartons are square but water drops
are spherical?

3.

The Packaging Paradox
Have you ever wondered why water drops are spherical?
• Spheres: Hold the maximum volume for the minimum
surface area. Great for saving material.
Think: If we wanted to make an eco-friendly bottle using
the least amount of plastic, what shape should it be?

4.

The Curvature Effect
Why is the Equator Hot?
The Earth is a sphere, so the "Angle of Absorption"
changes.
• Equator: Light hits "head-on" (perpendicular). The
heat concentrates on a small surface area.
• Poles: The surface curves away. The same amount of
light spreads over a large surface area.
Math in Nature: The geometry of the sphere creates our
climate zones!

5.

Future Frontiers
Nanoparticles: The Power of Surface Area
In medicine, scientists make drugs into tiny spheres
(nanoparticles).
Why?
Smaller spheres have a huge surface area compared to
their volume. This allows the drug to dissolve faster and
react better with the body. Understanding surface area
is saving lives!

6.

Defining the Sphere
What is it?
A sphere is a 3D object where every point on the
surface is the exact same distance from the
center.
Key Terms
• Radius (r): Distance from center to edge.
• Surface Area: The total area of the outer
"skin".

7.

Experiment: The Orange Peel
A Juicy Proof
If you peel an orange perfectly and flatten the pieces,
how much space do they take up?
1. Take an orange (sphere) with radius r .
2
.
Draw 4 circles on a paper, each with the same
3
.
Peel the orange and fill the circles.
radius r .
Result: The peel fills exactly 4 circles!

8.

Archimedes' Insight
The Cylinder Projection
Archimedes discovered a "Unique" connection. A
sphere has the same surface area as the curved side
of a cylinder that fits it perfectly.
Cylinder Height (h): 2 r
Cylinder Circumference: 2 π r
Area: h × Circumference
2 r × 2 π r = 4 π r2

9.

The Master Formula
Surface Area of a
Sphere
Just remember: It is exactly equal to the area of 4 circles of the same radius.

10.

Quick Quiz: Level 1
The Question
Find the surface area of a spherical football with
a radius of 10 cm.
(Use π = 3.14 )

11.

Quick Quiz: Level 1
The Solution
The Question
SA = 4 π r 2
Find the surface area of a spherical football with
SA = 4 × 3.14 × 102
a radius of 10 cm.
(Use π = 3.14 )
SA = 4 × 3.14 × 100
SA = 1256 cm 2

12.

Quick Quiz: Level 2
Think About It
If you double the radius of a
sphere, what happens to its
surface area?

13.

Quick Quiz: Level 2
Think About It
The Math
If you double the radius of a
Formula has 4 π r 2
sphere, what happens to its
.
surface area?
If r becomes 2 r , then it
will be 4 π ( 2r) 2
.

14.

Quick Quiz: Level 2
Think About It
The Math
The Answer
4 π ( 2r) (2r)
If you double the radius of a
Formula has 4 π r 2
sphere, what happens to its
.
surface area?
If r becomes 2 r , then it
4* 4 π r2
4 times the original area
will be 4 π ( 2r) 2
.
.

15.

Quick Quiz: Level 3
Working Backwards
The surface area of a sphere is 616 cm 2 .
Find its radius.
(Use π = 22 7 )

16.

Quick Quiz: Level 3
Working Backwards
4 π r 2 = 616
The surface area of a sphere is 616 cm 2 .
4 × 22 / 7 × r 2 = 616
Find its radius.
(Use π = 22 7 )
r2 =
616 × 7
88
r 2 = 49
r = 7 cm

17.

Real World Challenge
The "Ocean Guardian"
Engineers have designed a spherical solar-powered
buoy to detect oil spills. It floats in the ocean and
must be coated with a special Bio-Safe Paint to
prevent algae growth.
Data
:
• Diameter of buoy = 30 cm
• Cost of paint = ₹0.50 per cm
2
Task: Calculate the cost to paint 10 such

18.

The Engineering Solution
Step 1: Surface Area
Diameter = 30 cm, so Radius ( r ) = 15 cm.
SA = 4 π r 2
SA = 4 × 3.14 × 15 2
SA = 4 × 3.14 × 225
Step 2: Total Cost
Area for 10 buoys = 28260 cm 2
Cost = Area × Rate
Cost = 28260 × 0.50
Cost = ₹14,130
SA = 2826 cm 2 (per buoy)
Precision matters in engineering budgets!

19.

Questions?
Thank you for exploring the world of
spheres.

20.

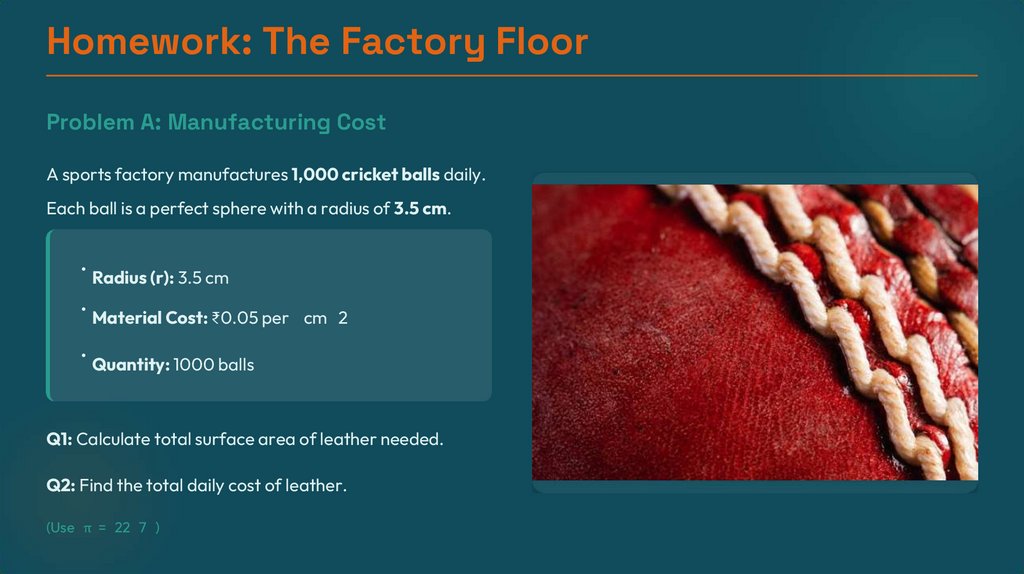
Homework: The Factory Floor
Problem A: Manufacturing Cost
A sports factory manufactures 1,000 cricket balls daily.
Each ball is a perfect sphere with a radius of 3.5 cm.
• Radius (r): 3.5 cm
• Material Cost: ₹0.05 per cm 2
• Quantity: 1000 balls
Q1: Calculate total surface area of leather needed.
Q2: Find the total daily cost of leather.
(Use π = 22 7 )

21.

Homework: Eco-Dome
Problem B: Maintenance
A science museum features a giant spherical glass
dome. It requires a special solar-reflective coating
for summer.
• Dome Diameter: 42 meters
• Paint Coverage: 1 Liter covers 10 m 2
Q1: Calculate the Curved Surface Area (CSA) of the
glass dome. Also find how much paint is required ?