04 Непрерывность 2025

1.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
– непрерывна во внутренней точке x0 X , если выполнено одно
f x : X
из следующих эквивалентных условий:
1) 0 0 x X x x0 f x f x0 ;
2) lim f x f lim x f x0 ;
x x0
x x0
3) f x f x0 x , где x – БМФ при x x0 , x0 0 ;
4) любая -окрестность точки f x0 содержит образ (при отображении f )
некоторой окрестности точки x0 .
f x : X
– непрерывна справа в точке x0 X , если f x0 lim f x f x0
f x : X
– непрерывна слева в точке x0 X , если
x x0
f x0 lim f x f x0
x x0
З а м е ч а н и е . Определения «непрерывна справа» и «непрерывна слева» даны на базе
второго определения непрерывности. Аналогично эти понятия можно дать
на базе любого из трех других определений.
Теорема 4.1.
« f x – непрерывна в точке x0 » « f x в точке x0 непрерывна и справа, и слева»
1

2.

Пусть
y f x определена на a, b ,
x0 a, b .
x – произвольное приращение x такое, что x0 x a, b .
Тогда y f x0 x f x0 – приращение функции y f x в точке x0 ,
соответствующее приращению аргумента x .
Разностная форма условия непрерывности.
« f x непрерывна в точке x0 » lim y lim f x0 x f x0 0 .
x 0
x 0
Замечания:
1 . Аналогично определяется разностная форма непрерывности справа (слева).
2 . Д ля непрерывных функций при бесконечно малом приращении аргумента,
приращение функции также бесконечно мало.
В общем случае судить о величине приращения функции по величине
приращения аргумента нельзя (возможны все три случая:
y o x , x o y , y
x при x 0 ).
2

3.

Свойства непрерывных в точке x0 функций
Пусть f и g – непрерывны в т. x0 , тогда:
1) , f g – непрерывна в т. x0 ;
2) f g – непрерывна в т. x0 ;
f
3)
– непрерывна в т. x0 , если g x0 0 ;
g
4) если f x0 0 , то f x сохраняет знак в некоторой окрестности т. x0 .
5) f x ограничена в некоторой окрестности точки x0 .
Теорема о непрерывности композиции.
Пусть
– y x – непрерывна в точке x x0 и y x0 y0 ,
– x t – непрерывна в точке t t0 и x t0 x0 .
Тогда сложная функция y x t – непрерывна в точке t t0 , т.е.
если lim x t x0
t t0
и lim y x y0 , то lim y x t y0 lim y x .
x x0
t t0
x x0
3

4.

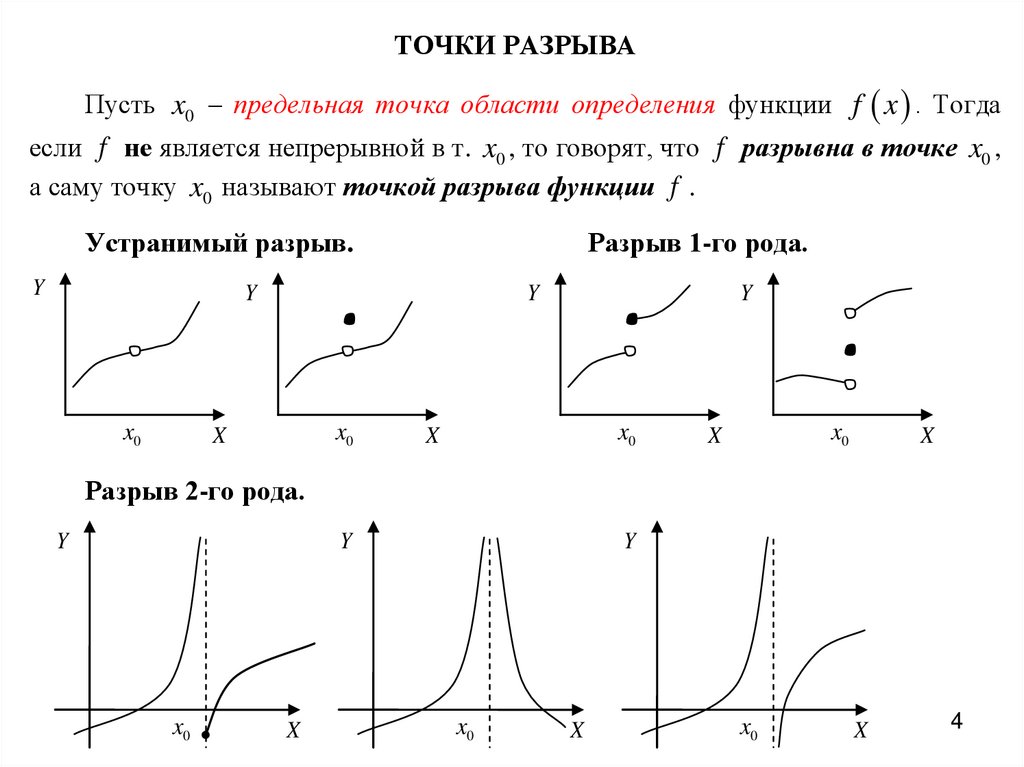
ТОЧКИ РАЗРЫВА
Пусть x0 – предельная точка области определения функции f x . Тогда
если f не является непрерывной в т. x0 , то говорят, что f разрывна в точке x0 ,
а саму точку x0 называют точкой разрыва функции f .
Устранимый разрыв.
Y
Разрыв 1-го рода.
Y
x0
Y
x0
X
Y
x0
X
x0
X
X
Разрыв 2-го рода.
Y
Y
x0
X
Y
x0
X
x0
X
4

5.

Теорема об односторонних пределах монотонной функции.
Пусть функция определена и монотонна в некоторой окрестности
точки x0 . Тогда в этой точке существуют конечные односторонние
пределы.
Теорема о разрывах монотонной функции.
Пусть функция f x определена и монотонна в некоторой
окрестности точки x0 , а в самой точке x0 терпит разрыв. Тогда этот
разрыв либо устранимый, либо I рода. Причем если f x определена
в точке x0 , то разрыв может быть только I рода.
Следствие. Множество точек разрыва всюду определенной монотонной функции не более чем счетно.
5

6.

НЕПРЕРЫВНОСТЬ ФУНКЦИИ НА МНОЖЕСТВЕ
Функция f x непрерывна на множестве A , если она непрерывна
во всех точках этого множества A .
З а м е ч а н и е . Если не все точки множества A входят в него с некоторой
окрестностью, то это определение меняется. Например, функция называется
непрерывной на a, b , если она непрерывна во всех точках интервала a, b
(или, что то же самое, во всех внутренних точках отрезка a, b ), а также
непрерывна справа в точке a и непрерывна слева в точке b .
Функция f x – кусочно-непрерывна на множестве A , если она
непрерывна на множестве A , за исключением, быть может, конечного числа
точек, в которых она имеет устранимый разрыв или разрыв 1-го рода.
11

7.

Теорема Больцано-Коши об обращении функции в нуль. Если f x
непрерывна на a, b и f a f b 0 , то x0 a, b f x0 0 .
Теорема Больцано-Коши о промежуточном значении непрерывной
функции. Пусть функция f x непрерывна на a, b , f a , f b ,
и пусть c – любое число, удовлетворяющее условию
c , если ;
c , если .
Тогда существует точка x0 a, b такая, что f x0 c .
Критерий непрерывности монотонной функции
Пусть f x определена и монотонна на a, b . Тогда для непрерывности ее
на a, b необходимо и достаточно, чтобы
– для неубывающей функции
l f a , f b x0 a, b f x0 l ,
– для невозрастающей функции
l f b , f a x0 a, b f x0 l .
12

8.

Лемма о существовании обратной функции
Функция
f x : X Y
имеет
обратную
функцию
g y : Y X тогда и только тогда, когда она строго монотонна.
При этом характер монотонности функций f x и g y совпадает.
Теорема о непрерывности обратной функции
Пусть функция f x : X Y непрерывна на области определе-
ния X и имеет обратную функцию g y : Y X . Тогда g y непрерывна на Y .

9.

Теорема Вейерштрасса об ограниченности непрерывной функции.
Функция, непрерывная на отрезке a, b , ограничена на нем.
Теорема Вейерштрасса о достижении непрерывной функцией
точных верхней и нижней граней.
Функция, непрерывная на отрезке, достигает своей точной верхней
грани и точной нижней грани, т.е.
x1 a, b такое, что sup f x f x1 ,
x a ,b
x2 a, b такое, что inf f x f x2 .
x a ,b
17