phpviFcjc_Prezentaciya--Natematicheskoe-modelirovanie

1.

2.

Задача Пуассона
Самая древняя из
задач на переливание –
задача Пуассона.
Знаменитый
французский
математик,
механик и физик Симеон
Дени Пуассон (1781 –
1840) решил эту задачу в
юности и впоследствии
говорил, что именно она
побудила
его
стать
математиком.

3.

Задача Пуассона
Один человек имеет
в бочонке 12 пинт вина
(пинта
–
старинная
французская мера объема,
1 пинта ≈ 0,568 л) и хочет
подарить половину вина,
но у него нет сосуда в 6
пинт, однако имеются два
пустых сосуда объемом 8
пинт и 5 пинт. Как с их
помощью отлить ровно 6
пинт вина?

4.

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НА
ПЕРЕЛИВАНИЯ
метод рассуждений;
метод проб и ошибок;
табличный;
метод блок – схем;
метод математического бильярда.

5.

• Задача 1. Летом Винни - Пух сделал запас мёда на
зиму и решил разделить его пополам, чтобы
съесть половину до Нового Года, а другую
половину - после Нового Года. Весь мёд находится
в ведре, которое вмещает 6 литров.
• У него есть 2 пустые банки – 5-литровая и 1литровая.
• Может ли он разделить мёд так, как задумал?

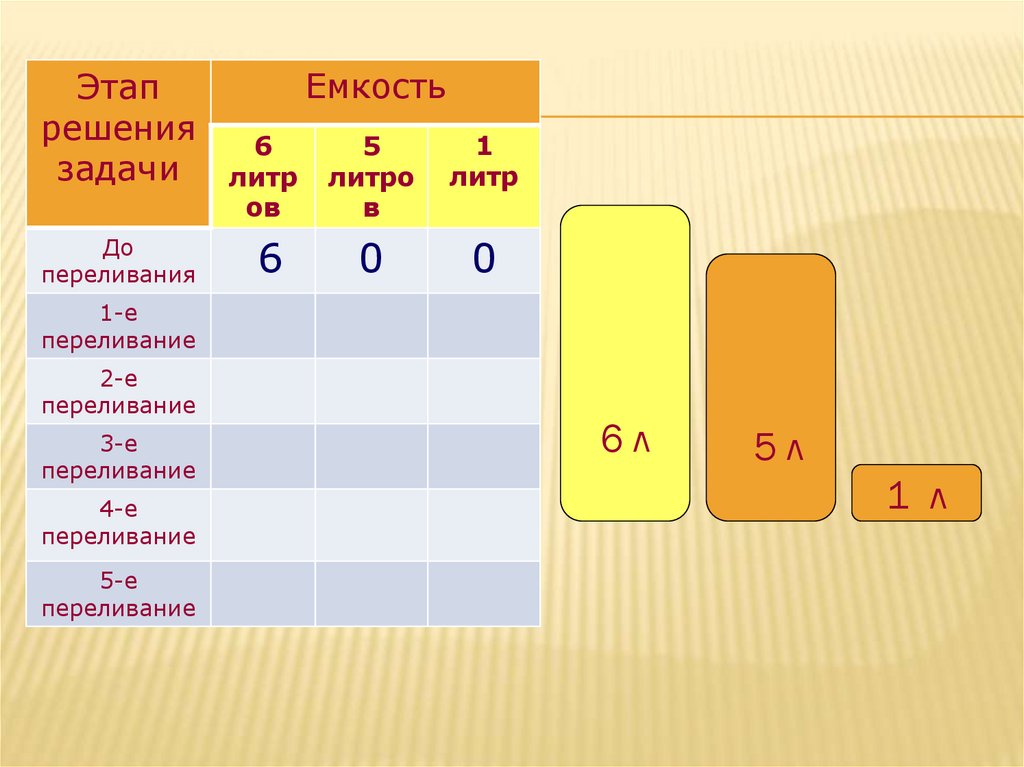
6.

Этап
решения
задачи
До
переливания
Емкость
6
литр
ов
5
литро
в
1
литр
6
0
0
1-е
переливание
2-е
переливание
3-е
переливание
4-е
переливание
5-е
переливание
6л
5л
1 л

7.

Этап
решения
задачи
Емкость
6
литр
ов
5
литро
в
1
литр
До
переливания
6
0
0
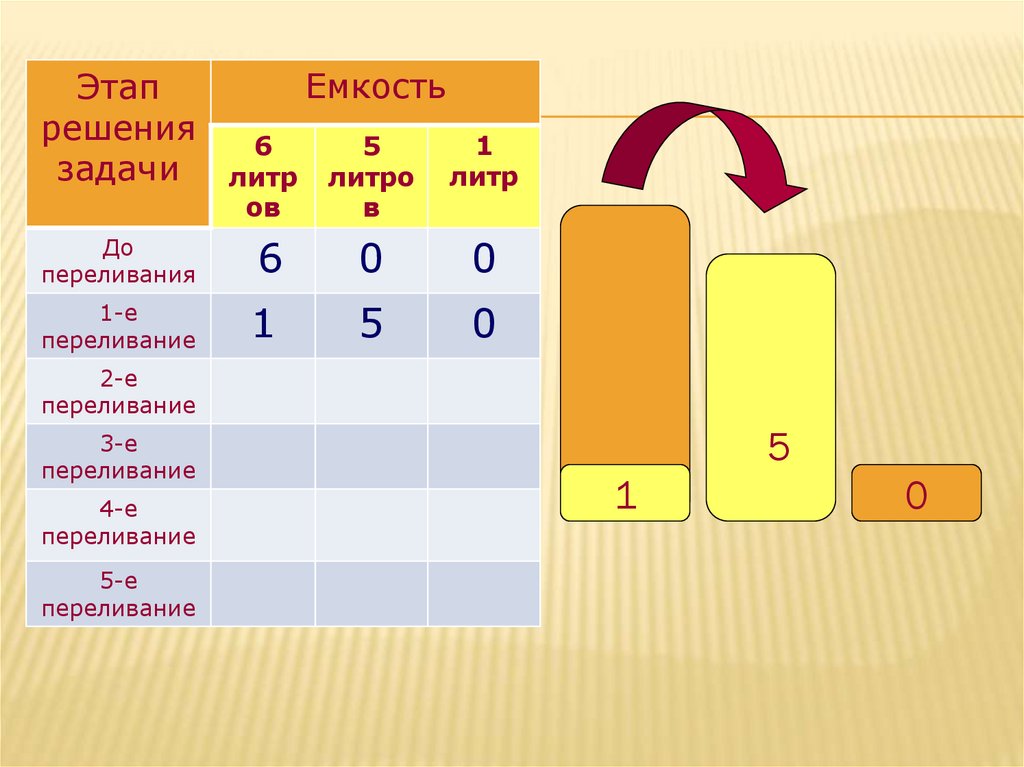
1-е
переливание
1
5
0
2-е
переливание
3-е
переливание
4-е
переливание
5-е
переливание
5
1
0

8.

Этап
решения
задачи
Емкость
6
литр
ов
5
литро
в
1
литр
До
переливания
6
0
0
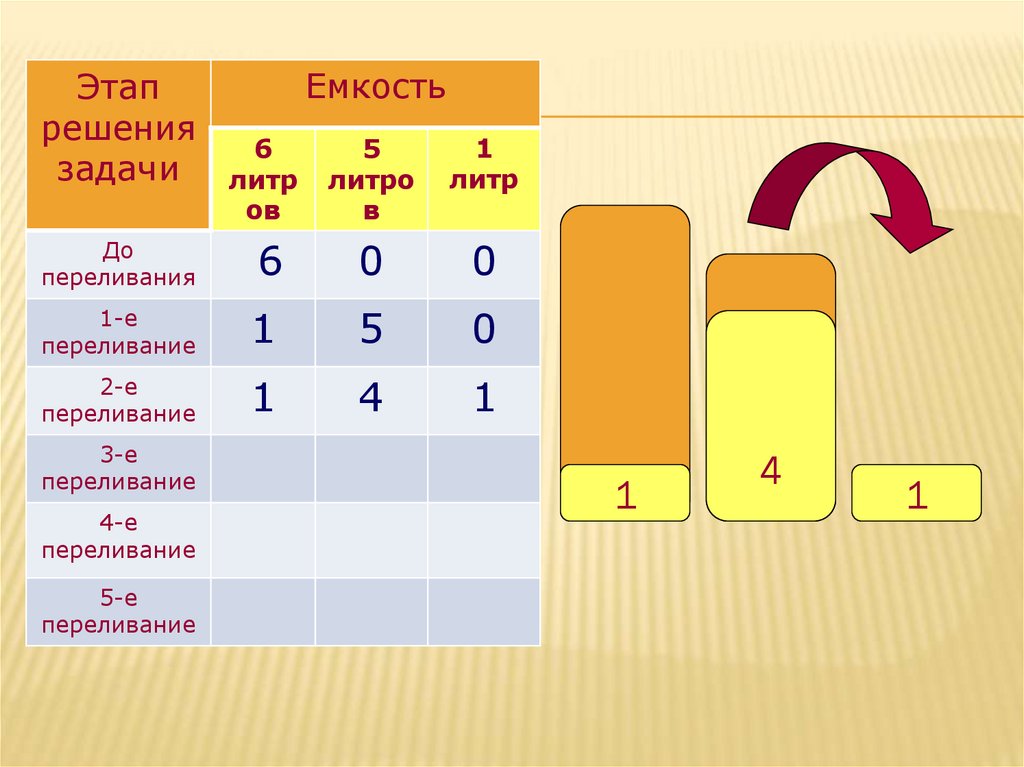
1-е
переливание
1
5
0
2-е
переливание
1
4
1
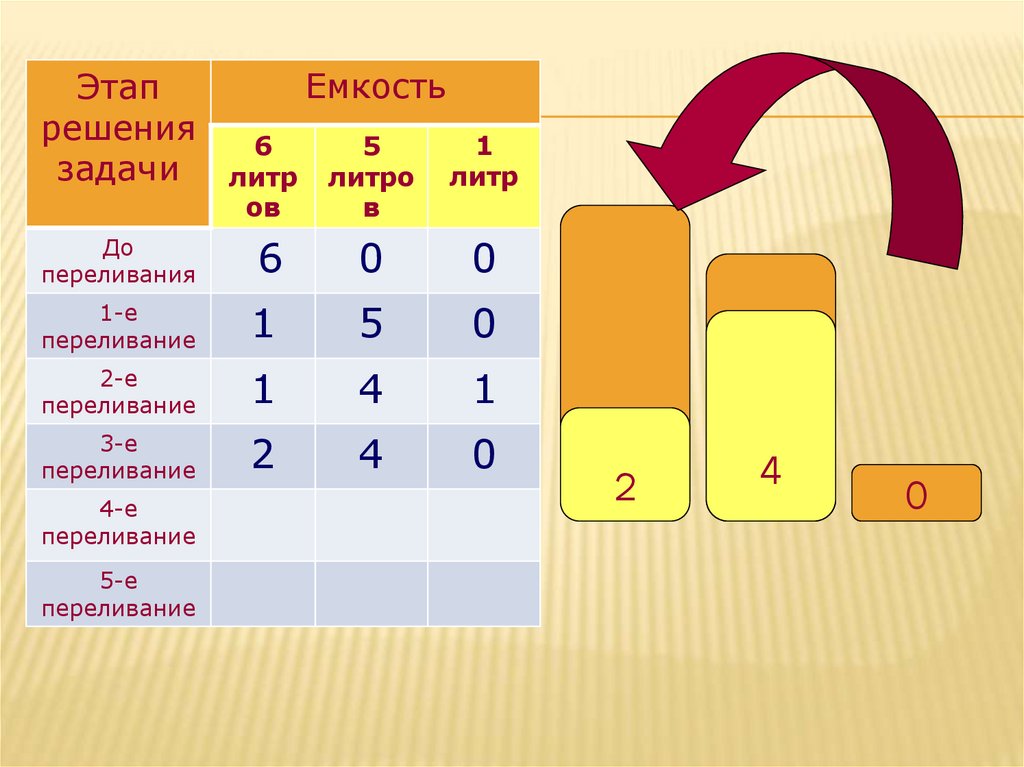
3-е
переливание
4-е
переливание
5-е
переливание
1
4
1

9.

Этап
решения
задачи
Емкость
6
литр
ов
5
литро
в
1
литр
До
переливания
6
0
0
1-е
переливание
1
5
0
2-е
переливание
1
4
1
3-е
переливание
2
4
0
4-е
переливание
5-е
переливание
2
4
0

10.

Этап
решения
задачи
Емкость
6
литр
ов
5
литро
в
1
литр
До
переливания
6
0
0
1-е
переливание
1
5
0
2-е
переливание
1
4
1
3-е
переливание
2
4
0
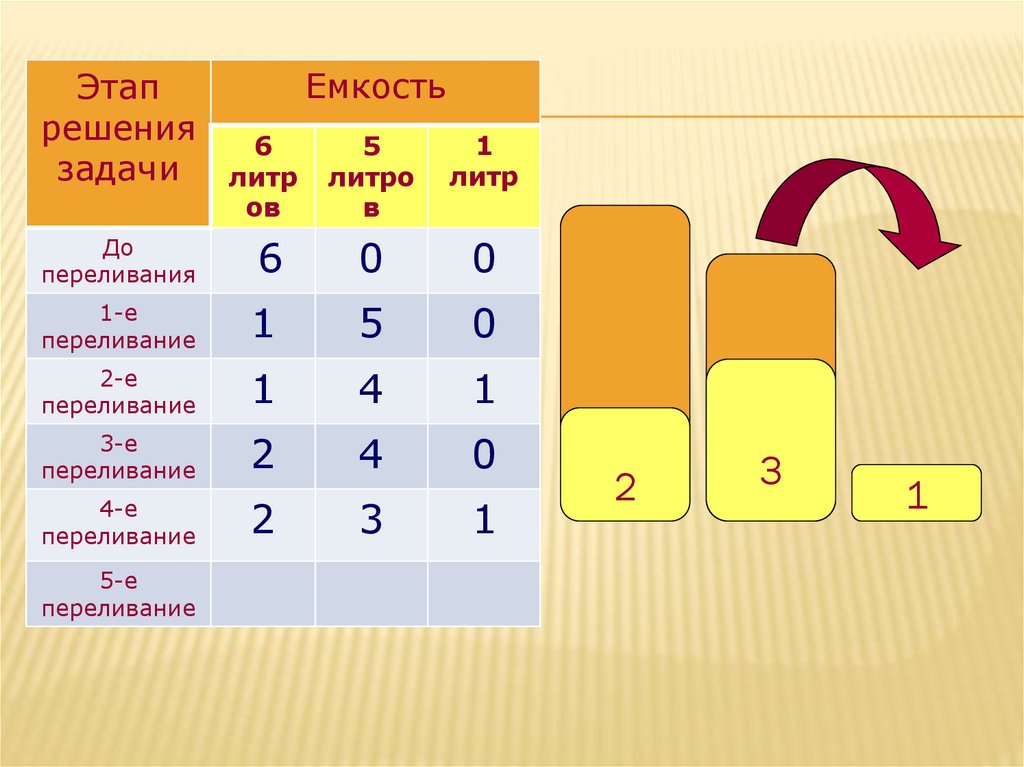
4-е
переливание
2
3
1
5-е
переливание
2
3
1

11.

Этап
решения
задачи
Ёмкость
6
литр
ов
5
литро
в
1
литр
До
переливания
6
0
0
1-е
переливание
1
5
0
2-е
переливание
1
4
1
3-е
переливание
2
4
0
4-е
переливание
2
3
1
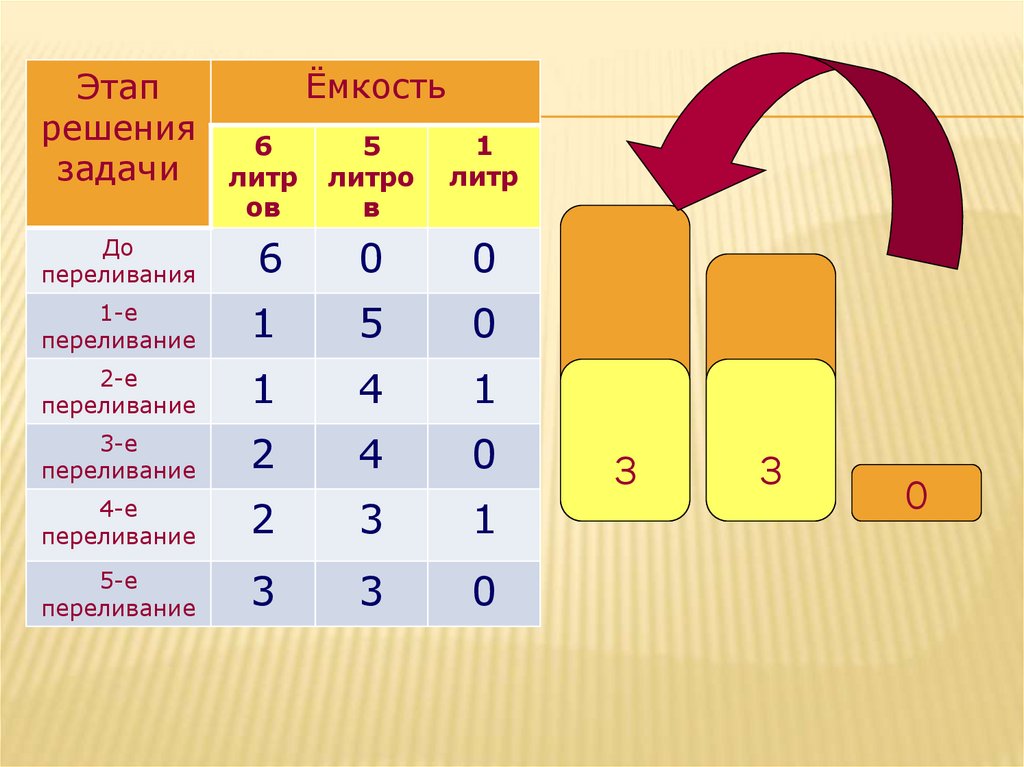
5-е
переливание
3
3
0
3
3
0

12.

Вывод: за 5 переливаний Винни – Пух может
разделить 6 л мёда пополам, используя ёмкости 5 л
и 1 л.

13.

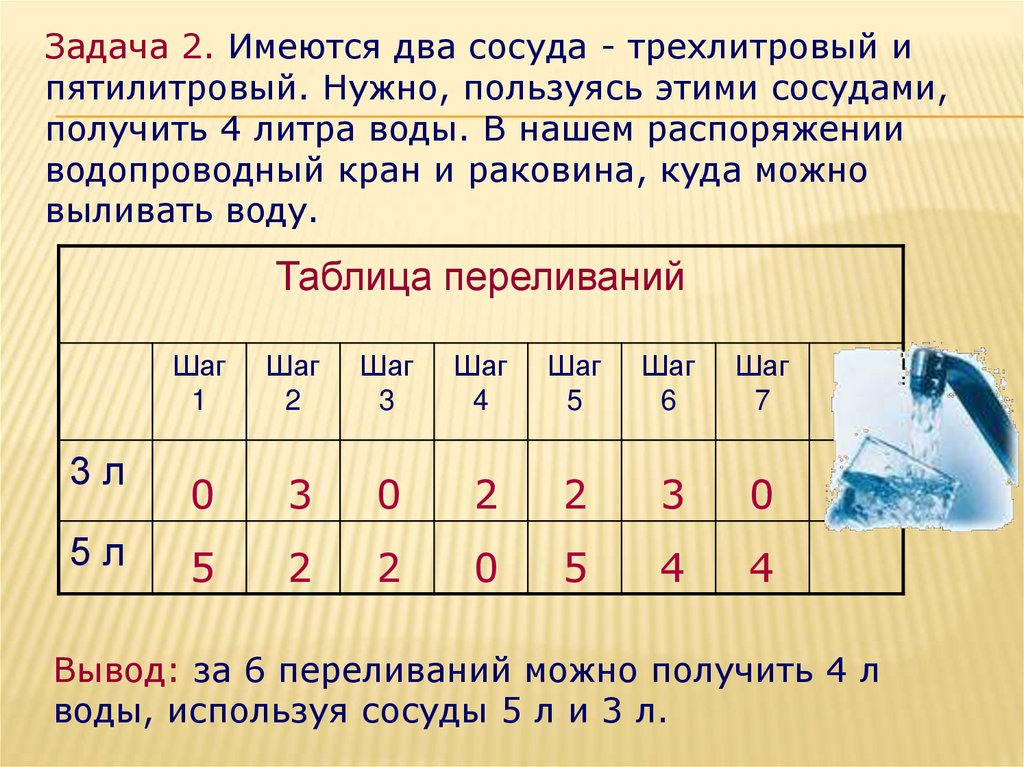
Задача 2. Имеются два сосуда - трехлитровый и
пятилитровый. Нужно, пользуясь этими сосудами,
получить 4 литра воды. В нашем распоряжении
водопроводный кран и раковина, куда можно
выливать воду.
Таблица переливаний
3л
5л
Шаг
1
Шаг
2
Шаг
3
Шаг
4
Шаг
5
Шаг
6
Шаг
7
0
3
0
2
2
3
0
5
2
2
0
5
4
4
Вывод: за 6 переливаний можно получить 4 л
воды, используя сосуды 5 л и 3 л.

14.

Задача
В бидоне не
менее
10
литров
молока.
Как отлить из
него ровно 6 литров
с помощью пустых
девятилитрового
и
пятилитрового
бидонов.

15.

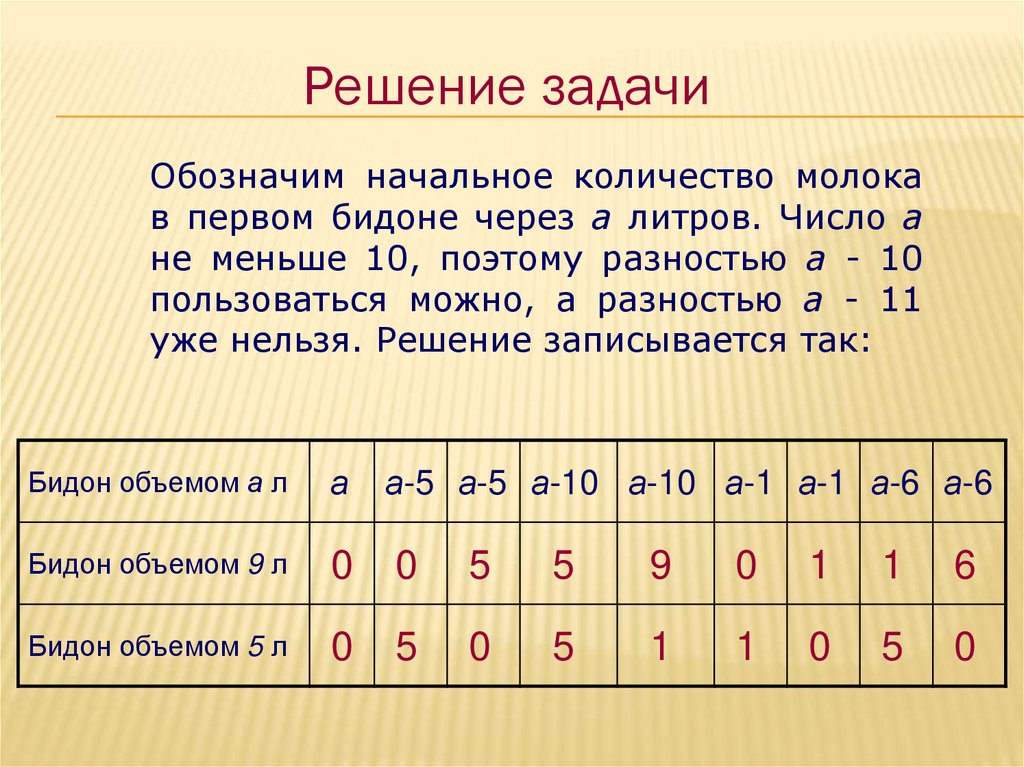
Решение задачи
Обозначим начальное количество молока
в первом бидоне через а литров. Число а
не меньше 10, поэтому разностью а - 10
пользоваться можно, а разностью а - 11
уже нельзя. Решение записывается так:
Бидон объемом а л
а
а-5 а-5 а-10 а-10 а-1 а-1 а-6 а-6
Бидон объемом 9 л
0
0
5
5
9
0
1
1
6
Бидон объемом 5 л
0
5
0
5
1
1
0
5
0