Методика изучения объёма фигуры в начальных классах

1.

«Владимирский государственный университет имени Александра
Григорьевича и Николая Григорьевича Столетовых»
(ВлГУ)
Кафедра педагогики и психологии дошкольного и начального
образования.
Презентация
по дисциплине: «Методика преподавания математики »
на тему : «Методика изучения объёма фигуры»
Выполнила: студентка 2 курса очной
формы обучения группы НОЛ-119
Ёлкина С.Ю.
([email protected])
Проверил: старший преподаватель
Болотова Т.В.
2020 г.

2.

Введение
Когда речь идет о чем-нибудь очень простом, понятном, мы часто
говорим: « Дело ясно, как дважды два - четыре!».
А ведь прежде чем додуматься до того, что дважды два – это четыре,
людям пришлось учиться много тысяч лет. Конечно, это учение шло не
за партой. Человек постепенно учился жить: строить жилища, находить
дорогу в дальних походах, обрабатывать землю. И одновременно он
учился считать. Потому что даже в самые далекие времена, когда люди
жили в пещерах и одевались в звериные шкуры, они не могли обойтись
без счета и меры.
Человеку необходимо было измерять сыпучие физические величины и
жидкости. Для этого он начал использовать все то, что имелось у него в
быту (ведра, сосуды и другие емкости). Таким образом, люди научились
измерять объемы.
Объем – вместимость геометрического тела, т. е. части пространства,
ограниченной одним или несколькими замкнутыми поверхностями.

3.

История возникновения различных мер емкости
сосудов и объема фигур.
1.Международная система единиц
В настоящее время международно-признанной является система СИ —
международная десятичная система единиц, основанная на использовании метра
и килограмма.СИ является наиболее широко используемой системой единиц в
мире, как в повседневной жизни, так и в науке и технике. При некоторых
различиях в деталях, элементы системы
одинаковы во всем мире. Но так было не
На примере Древней Руси и Западной Европы
рассмотрим, какие меры измерения объема
применялись до возникновения СИ.

4.

2.Древняя Русь
Первым письменным упоминанием о мерах, применявшихся на Руси, является
Устав князя Владимира, относящийся к 996 году. Устав предписывал: "извесы и
мерила блюсти без пакости, ни умалити, ни умножити". Первые эталоны на Руси
хранились в церквах, в храмах. Надзор поручали представителям духовенства и
особым лицам - "весцам". Весовщики должны были "крест целовать" - давать
клятвенное обещание в том, что будут взвешивать товары без обмана. Со
временем на весах и гирях появились специальные «печати» - клейма,
удостоверявшие законность весовых мер. В Московском государстве весовое
хозяйство стало «на поток», и надзор начал принимать государственные
масштабы. В таможнях и на гостиных дворах были устроены «важни» помещения с верными весами и «орлеными» гирями.

5.

В Древней Руси, как и во многих других странах, меры объема
имели две области применения: для сыпучих тел и для жидкостей.
Для мер жидкости чаще всего употреблялись бочка, ведро, корчага.
Наибольшее распространение получило ведро, практически очень
удобная мера, сохранившаяся до XX века. По приближенным
подсчетам ведро вмещало около 24 фунтов воды (9,8кг).

6.

Старинные меры объёма:
Ведро = 1/40 бочки = 10 кружек = 30
фунтов воды = 100 чарок = 200 шкаликов =
12 литров. Деление на более мелкие меры
проводилось по двоичному принципу: ведро
делили на 2 полуведра или на 4 четверти
ведра или на 8 получетвертей, а также на
кружки и чарки.
Древнейшая "международная" мера
объёма - «горсть».
В торговое ведро вмещалось 8 кружек.
Значение ведра было переменным, а
значение кружки неизменным, в 3 фунта
воды (1228,5 грамма). Объем ведра был
равен 134,297 кубических вершков.

7.

Бочка, как мера жидкостей, равнялась 40 ведрам
(492 л).Чаще всего в крестьянском быту
использовались небольшие бочки и бочонки от 5-и
до 120-и литров.
В житейском обиходе и в торговле употребляли
разнообразные хозяйственные сосуды: котлы,
жбаны, корчаги, братины, ендовы. Значение таких
бытовых мер в разных местах было различно:
например, емкость котлов колебалась от полуведра
до 20 ведер.
В XVII в. была введена система кубических
единиц на основе 7-футовой сажени, а также
введён термин кубический (или "кубичный").
Кубическая сажень содержала 27 кубических
аршин или 343 кубических фута; кубический
аршин — 4096 кубических вершков или 21952
кубических дюймов.

8.

Кружка – сосуд в форме стакана с ручкой.
Кружка (слово означает - 'для пития по кругу') = 10
чаркам = 1,23 л.
Современный граненый стакан раньше назывался
"досканом" ("строганые доски"), состоящим из
обвязанных
верёвкой
ладов-дощечек,
вокруг
деревянного донца.

9.

Чарка- сосуд для питья крепких напитков, маленькая
чара, иногда имеющая поддон или шаровидную
ножку. Многообразные формы чарок, украшавшиеся
чернью, эмалями или чеканкой, были характерны для
русского быта XVII- XVIII вв.
Чарка- русская единица измерения объёма жидкости,
применявшаяся до введения метрической системы
мер и иначе называвшаяся соткой. 1 чарка= 1/100
ведра= 2 шкаликам. В пересчёте на математическую
систему 1 чарка= 0,1299 литра.

10.

Шкалик – старинная русская единица объёма
жидкостей, равная 61,5 мл или 1/200 ведра .
Шкалик(народное название - «косушка», от слова
«косить», по характерному движению руки) = ½ чарки
= 0,06 л.
Штоф – старинная русская единица объёма жидкостей,
равная 1, 2299 литра, 3 фунтам , или 1/10 ведра, или двум
водочным бутылкам, или 10 чаркам.

11.

Бурдюк (от азерб. burduk) — кожаный
мешок из цельной шкуры животного (козы,
лошади, овцы и др.), предназначен для
хранения вина, кумыса и других жидкостей
Кожаный мешок (бурдюк)вмещает до 60 л
Корчага – глиняный сосуд больших размеров. Он
использовался для нагревания воды, варки кваса,
браги, кипячения белья со щелоком. Корчагами(12
кг) меряли мёд и воск

12.

Ушат- большая деревянная кадка с двумя
выступающими друг против друга боковыми
дощечками- ушами, с прорезанными в них
круглыми
отверстиями,
сквозь
которые
продевается палка для ношения. Высота посудины
– 30-35 сантиметров, диаметр – 40 сантиметров,
объем – 2 ведра или 22-25 л.
Балакирь – глиняный сосуд для хранения и
подачи молока на стол. Характерной
особенностью кринки является высокое,
довольно широкое горло, плавно переходящее
в округлое тулово. Форма горла, его диаметр и
высота рассчитаны на обхват рукой. Балакирь
— 1/4—1/5, ведра.

13.

В житейском обиходе и в торговле употребляли разнообразные
хозяйственные сосуды: котлы, жбаны, братины, ендовы. Значение
таких бытовых мер в разных местах было различно : например,
ёмкость котлов колебалась от полуведра до 20 вёдер. В XVII в. была
введена система кубических единиц на основе 7- футовой сажени, а
также введён термин кубический ( или «кубичный»).
Котёл
Братина
Ендова
Жбан

14.

3. Западная Европа
В Западной Европе бытовали свои собственные меры объемов.
К ним относятся баррель, бушель, галлон, драхма, кварта,
пинта, унция. Рассмотрим, что означала каждая мера объема.
Баррель – мера вместимости и объема,
применяемая в США, Англии и ряде стран,
использующих английскую систему мер. В США
различают Баррель сухой, равный 115,628 дм3, и
Баррель нефтяной, равный 158,988 дм3.
Английский Баррель (мера вместимости для
сыпучих веществ) равен 163,65 дм3.

15.

Бу́шель (англ. bushel) — единица объёма, используемая в английской системе
мер. Применяется для измерения сыпучих товаров, в основном
сельскохозяйственных, но не для жидкостей. Сокращённо обозначается bsh. или
bu. В британской имперской системе мер для сыпучих тел: 1 бушель = 4 пекам =
8 галлонам = 32 сухим квартам = 64 сухим пинтам = 1,032 американским
бушелям = 2219,36 кубическим дюймам = 36,36872 л (дм³) = 3 вёдрам.
В американской системе мер для сыпучих тел: 1 бушель = 0,9689 английских
бушеля = 35,2393 л; по другим данным: 1 бушель = 35,23907017 л = 9,309177489
американских галлонов.
Кроме того, бушелем называют тару для хранения и транспортировки яблок. В
международной торговле под бушелем, как правило, понимается коробка весом
38,691 кг.

16.

Галлон (англ. gallon) — мера объёма в английской системе мер, которая
обычно используется для жидкостей, в редких случаях — для твёрдых тел.
Американский галлон равен 3,785411784 литра. Британский галлон - 4,5461
литра. Изначально галлонами измеряли пшеницу. И один галлон был равен 8
фунтам пшеницы. Позже в галлонах стали мерить и другие продукты. Там уже
были свои галлоны.

17.

Кварта – единица объема (емкости, вместимости),
применяемая в США, Великобритании и др. странах. 1 Кварта
= 1/4 галлона или 2 пинтам. Американская Кварта для
жидкостей = 0,9463 дм3, для сыпучих веществ = 1,1012 дм3.
Английская имперская Кварта= 1,1365 дм3. Прежняя русская
мера жидкостей – кружка – также иногда называлась Кварта; в
Польше Кварта = 1 л
Пинта – единица объема (вместимости) жидкостей и сыпучих
веществ, применяемая в странах, использующих английские меры.
В Великобритании 1 Пинта = 1/8 галлона = 0,568261 дм3. В США
различают жидкую Пинту, равную 1/8 американского галлона =
0,473179 дм3, и сухую Пинту, равную 1/64 американского бушеля =
0,550614 дм3. Пинта применялась также в др. странах до введения
в них метрической системы мер, напр. во Франции 1 Пинта =
0,931389 дм3, в Нидерландах 1 Пинта = 0,6063 дм3.

18.

4. Интересные факты о мерах объема
Сидарб. Люди, побывавшие в Австралии, возможно, сталкивались с этой
таинственной единицей, которая появляется в официальных документах и при
обычном разговоре. Получившая странное название Сидарб, — эта единица
используется для грубого измерения большого объема воды. Она названа в честь
Сиднейской Гавани.
Один Сидарб — это примерное количество воды в области гавани Сиднея —
около 562 000 мегалитров во время прилива. Неудивительно, что эта единица не
приобрела популярности за пределами Австралии.
Все мы - дети, большинство времени проводим в школе, Окружающая среда
влияет на нашу работоспособность, на восприятие и усвоения учебного материала.
Поэтому к состоянию классов предъявляются особые требования называющиеся
СанПиН. Все школьные учреждения обязаны выполнять эти требования. Во время
урока в кабинете возрастает концентрация углекислого газа и падает содержание
кислорода. По требованиям СанПиН* на одного учащегося требуется не менее 4
квадратных метров воздуха.

19.

Каждое государство (а их было множество) имело свою систему
мер, что становилось «тормозом» для торговли (включая
таможенные сборы), развития ремесел и промышленности и т.п.
В этой обстановке и стали рождаться идеи разработки единой,
межгосударственной системы мер.
В настоящее время СИ принята в качестве основной
системы единиц большинством стран мира и почти всегда
используется в области техники, даже в тех странах, в которых в
повседневной жизни используются традиционные единицы.
Метрические единицы широко используются по всему миру,
как в научных целях, так и в повседневной жизни.
В СИ основная единица измерения объема – кубический метр.
Применяются также производные от неё: кубический сантиметр,
литр (кубический* дециметр) и т.д.

20.

Обучение измерению величин.
В начальных классах рассматриваются величины : длина, площадь, масса,
емкость, время и др. Учащиеся должны получить конкретные представления об
этих величинах, ознакомиться с единицами их измерения, овладеть умениями
измерять величины, научиться выражать результаты измерения в различных
единицах,
выполнять
арифметические
действия
над
величинами.
Время
Масса
Объём
Длина
Площадь

21.

Изучение величин имеет большое значение, так как понятие
величины является важнейшим понятием математики. Каждая
изучаемая величина — это некоторое обобщенное свойство
реальных объектов окружающего мира. Упражнения в
измерениях развивают пространственные представления,
вооружают учащихся важными практическими навыками,
которые широко применяются в жизни.
Следовательно, изучение величин - это одно из
средств связи обучения с жизнью. Величины
рассматриваются в тесной связи с изучением
натуральных чисел и дробей; обучение измерению
связывается с обучением счету; новые единицы
измерения
вводятся
вслед
за
введением
соответствующих счетных единиц; арифметические
действия выполняются над натуральными числами и
над величинами. Измерительные и графические
работы как наглядное средство используются при
решения задач. Таим образом, изучение величин
способствует усвоению многих вопросов курса
математики.

22.

В методике выделяют следующие этапы изучения этих
величин:
1. Ознакомление с величиной, на основе уточнения жизненных
представлений учащихся;
2. Сравнение величин разными способами:
А – С помощью ощущений или на глаз
Б - С помощью приемов наложения или приложения
В - С помощью различных мерок
3. Введения единой меры измерения и измерительного прибора,
формирование измерительных навыков;
4. Сложение и вычитание величин, выраженных в одной единицы
измерения;
5. Введение других единиц измерения величины. Перевод из
одной единицы измерения в другую;
6. Сложение и вычитание величин, выраженных в единицы двух
наименований;
7. Умножение и деление величины на число.

23.

Методика изучения объёма фигуры.
Пользуясь подходами изучения величин, рассмотрим методику
формирование представлений об объёме (емкости) предмета.
С этой величиной детей знакомят в различных программах по-разному.
1 Этап. Введение понятия с опорой на жизненные ситуации.
Цель данного этапа – сформировать у учащихся представление о том, что
все окружающие нас объекты обладают свойствами или признаками.
По программе М.И. Моро, С.И. Волковой, С.В. Степановой УМК
«Школа Россия» термин объём не вводят, а используют понятие
«ёмкость сосуда».
Так как в начальных классах не вводится понятие объема, то следует
ограничиться ознакомлением учащихся с процессом измерения
вместимости некоторых предметов . Целесообразно показать сравнение
емкостей, выявить, какая из них больше и показать необходимость
использования единой меры - литра.

24.

На самый первый урок по изучению
величины
«ёмкость»
учитель
приносит
различные сосуды: стакан, ведро, банку. Дети
сравнивают их и при сопоставлении размера,
учитель сообщает, что в математике, говоря о
размере сосудов, мы подразумеваем их
вместимость или ёмкость.(слово ёмкость
должно записано на доске)Например, ёмкость
одного сосуда меньше (больше/равна) ёмкости
другого сосуда.
М1М ч 2. стр. 38.

25.

На примере упражнения 291 по программе
А.Л.Чекина УМК «Перспективная начальная
школа» у детей формируется представление об
объёме предметов. Учитель вместе с учениками
разбирают это задание, используя такие термины ,
как вместимость молочного пакета больше
вместимости стакана, также учитель говорит о
том, что нельзя определить объём стакана, как это
сделал Мише, говоря о высоте предмета или
ширине, так как эти термины используются для
измерении другой величины.
М4Ч 1ч. 86с.

26.

Из программы А.Л.Чекина УМК
«Перспективная начальная школа»
можем
ещё
использовать
304
упражнение для формирования у
детей представления о вместимости
стакана и чашки. Оказалось, что
ёмкость стакана равна ёмкости
чашки. Это означает, что жидкость
заполняющая стакан, имеет такой же
ОБЪЁМ,
как
и
жидкость
,
заполняющая чашку.
М4Ч 1ч. 89с.

27.

В программе Т.Е. Демидовой, С.А.
Козловой, А.П. Тонких УМК «Школа
2100» изучение величины – «Объём»
рассмотрим задание 3, которое помогает
сформировать у детей знания о величине –
«объём», который можно измерить и
результат измерения записать с помощью
числа. Учитель говорит ,что объём 1
бочонка больше объёма 1 ведра, потому что
в 1 бочонок может вместиться 5 вёдер с
водой. ( 1 бочонок= 5 вёдер)
М1Демидова 2ч. 44с.

28.

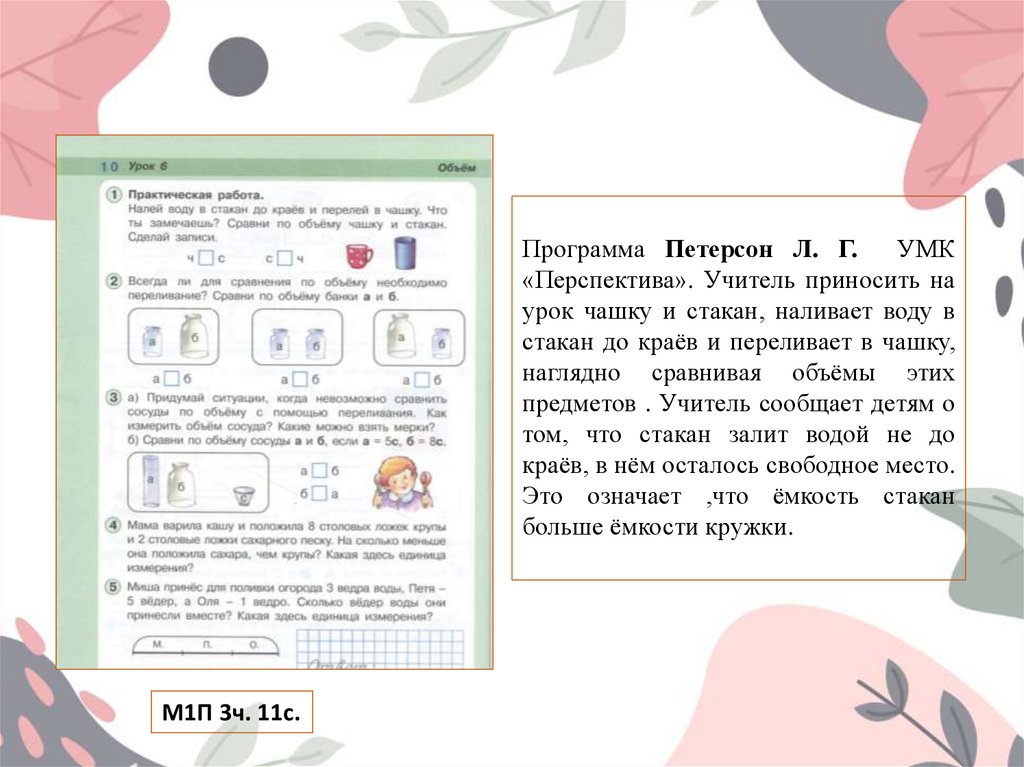
Программа Петерсон Л. Г.
УМК
«Перспектива». Учитель приносить на
урок чашку и стакан, наливает воду в
стакан до краёв и переливает в чашку,
наглядно сравнивая объёмы этих
предметов . Учитель сообщает детям о
том, что стакан залит водой не до
краёв, в нём осталось свободное место.
Это означает ,что ёмкость стакан
больше ёмкости кружки.
М1П 3ч. 11с.

29.

По программе Г.В. Дорофеева, Т.Н.
Мираковой, Т.Б. Бука УМК «Перспектива»
формирование представления об ёмкости
предметов наблюдаем в упражнении 2.
Чтобы решить эту задачу , ученики должны
выполнить вычислительные действия. Если
в оранжевую кастрюлю налили 5л воды, а в
синюю на 3л воды больше, то нужно к
5л+3л= 8л ( в синей кастрюле). Далее
учитель говорит, что 8>5 и так как в синюю
кастрюлю вместило больше литров воды,
значит и объём синей кастрюли будет
больше оранжевой.
М1Дорофеев 2ч. 44с.

30.

По программе И.И. Аргинской УМК
«Система развивающегося обучения
Занкова» формирование представления об
овместимости предметов можем проследить
только в 4 классе . До этого класса автор не
описывает изучение величины – «объём»
М4А 2ч. 11с.

31.

2 Этап. Сравнение сосудов по ёмкости разными способами:
Цель данного этапа – сформировать у учащихся представление о том,
что величины можно сравнивать, устанавливая отношение порядка (как
правило, нестрогого, ибо величины могут быть и равны) на множестве
однородных величин.
В методике изучения объёма фигуры выделяются 3 способа сравнения
ёмкости предметов.
А) « на глаз» Показываем сосуды, контрастные по объему (стакан и
ведро…). Учим правильно формулировать вывод с помощью термина;

32.

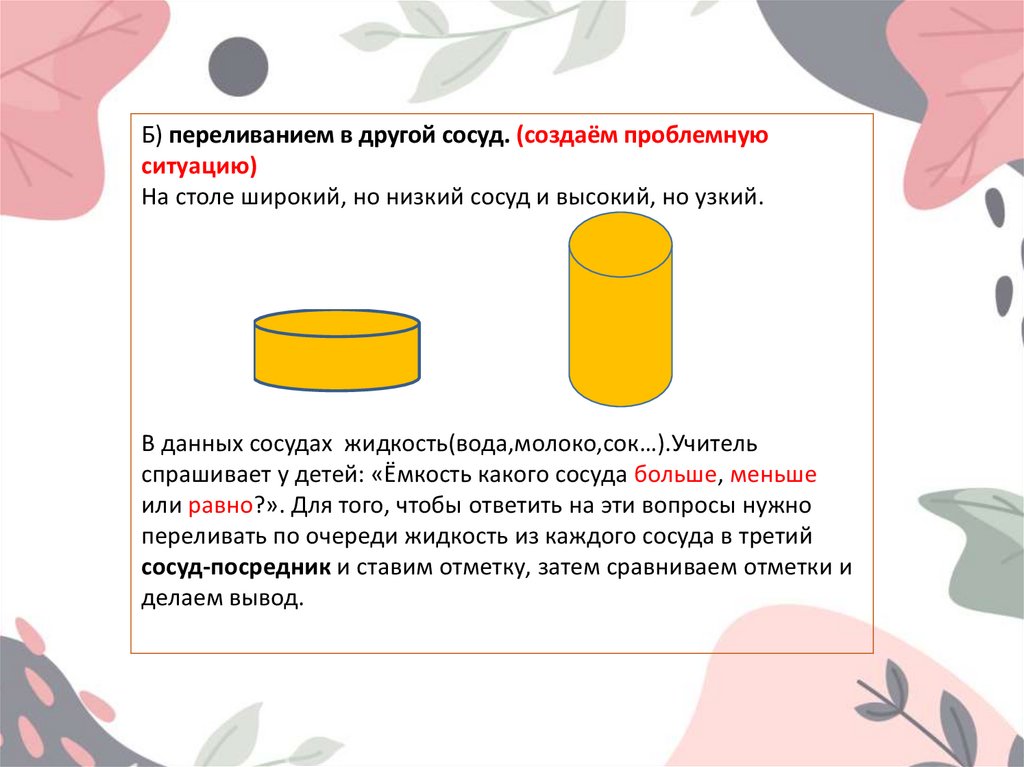
Б) переливанием в другой сосуд. (создаём проблемную
ситуацию)
На столе широкий, но низкий сосуд и высокий, но узкий.
В данных сосудах жидкость(вода,молоко,сок…).Учитель
спрашивает у детей: «Ёмкость какого сосуда больше, меньше
или равно?». Для того, чтобы ответить на эти вопросы нужно
переливать по очереди жидкость из каждого сосуда в третий
сосуд-посредник и ставим отметку, затем сравниваем отметки и
делаем вывод.

33.

В) использование мерок.
Ещё в ДОУ детей знакомят с этим способом. В качестве мерок
используют маленькие чашечки. Проводим несколько опытов
измерения емкости различными мерками. Например, емкость
банки равна 4 чашкам.
Для примера использования мерок для измерения ёмкости
предмета можно взять дидактическую игру «поварята».

34.

Изучение объёма жидкостей и сыпучих тел.
Дидактическая игра «Поварята».
Образовательная область: «Познавательное развитие»; формирование
элементарных математических представлений.
Педагогическая цель: учить измерять сыпучие вещества с помощью
условной мерки; упражнять в счете в пределах 5; развивать логическое
мышление.
Виды деятельности: игровая, двигательная, познавательноисследовательская, музыкальная, коммуникативная,
Средства реализации: мерные стаканчики, песок, мелкие камешки, крупы
(гречневая, рис)
Организационная структура игрового занятия:
Этапы деятельности:
1.Мотивационно-побудительный
Воспитатель предлагает разгадать загадку:
Скажи, кто так вкусно
Готовит щи капустные,
Пахучие котлеты,
Салаты, винегреты,
Все завтраки, обеды? (Повар).

35.

- Наши поварята не могут приготовить обед, так как не знают, как
измерить
молоко и крупу. Давайте им поможем.
Этап деятельности Организационно-поисковый:
Учитель проводит дидактическую игру «Поварята». Дети стоят перед
столом, на котором находится мешочек с рисом, пакет с молоком, 1
стакан,чайная ложка и кастрюлька, накрытые салфеткой.
- Две подруги, Маша и Катя, часто разговаривают по телефону. Однажды
Маша захотела сварить рисовую кашу и купила пакет молока, потом
позвонила Кате, чтобы узнать, как сварить кашу. Катя рассказала свой
рецепт. Нужно взять 1 стакан риса, 2 стакана молока, 1 чайную ложку соли
и 2 чайные ложки сахара. У Маши молоко находится в пакете, и она не
знает, как его измерить, хватит ли ей молока.

36.

-Чем мы уже умеем измерять? Линейкой, метром, меркой, веревочкой …
-Можно этими инструментами измерить молоко? Вспомните рецепт каши.
Чем мы будем измерять молоко?
Дети выполняют практическую работу по очереди отмеряют стаканом
молоко, рис, чайными ложками отмеряют соль и сахар.
Учитель предлагает провести эксперимент, выполнить измерения объёма
разными по высоте и по объёму мерками.
Подводит детей к пониманию того, что: чем мерка меньше, тем их
количество больше.
- Измерьте объем воды в кувшине с помощью стаканов, затем с помощью
кукольных чашечек, с помощью ложек.
- Сколько воды получилось в стаканах? Сколько воды получилось в
чашечках?
Сколько воды получилось в ложках?
- В каких мерках воды больше?
- Какая мерка самая маленькая?
- Значит, объем зависит от объема выбранной мерки.

37.

Воспитатель
проводит
дидактическую
игру
- Что вы видите в банках? В одной - рисовая крупа, в другой – пшенная. Как
вы думаете какой крупы больше: риса или пшена? Как это проверить?
- Правильно, надо измерить объем риса и объем пшена, результаты
измерения
сравнить.
- Что необходимо для измерения? Верно, надо выбрать мерку.
- Можно ли объем крупы измерить полоской или квадратиком?
Почему нельзя?Чем удобнее измерять крупу: стаканом или ложкой? В
банке очень много крупы, поэтому её лучше измерить более крупной
меркой - стаканом. Ложкой нам придется очень долго измерять. Чем будет
служить
стакан?
- Сначала мы с вами измерим объем пшена. До каких пор надо продолжать
измерение?Пока
не
будет
измерено
все
пшено,
Аналогично
измеряется
объем
риса,
- Сколько стаканов пшена получилось? Сколько стаканов риса?
Какой крупы казалось больше, а какой меньше? Почему вы так думаете?
Что надо сделать для того, чтобы что-нибудь измерить?

38.

3 Этап. Введение единой меры емкости.
Цель данного этапа – познакомить учащихся с единой мерой для
определения объёма.
Учитель должен объяснить ученикам , что не всегда удобно
использовать способы определения объёма. Например, при
определении объёма воды в реках , озёрах, морях. Это очень трудно ,
поэтому существует общепринятая мерка для измерения емкости –
литр.
Учитель показывает на доске обще-принятую сокращённую запись
литра в математике (л.).
Вводят литр. Показываем литровую банку и затем проводим
практическую работу по определению ёмкости сосудов в литрах
(например 3л, 5л, 7 л). Для этого приносят такие сосуды в класс, как
банки, ведра…. Практически доказываем, что 5 стаканов составляют
1 литр.

39.

Рассмотрим различные учебники по математике, и проанализируем
в каком классе впервые вводится понятие «литр».
Так по программе М.И. Моро С, И.
Волкова, С. В. Степанова УМК «Школа
Россия» термин объём не вводят, а
используют понятие «ёмкость сосуда».
На самый первый урок по изучению
величины «ёмкость» учитель приносит
различные сосуды: стакан, ведро, банку.
Дети сравнивают их и при сопоставлении
размера,
учитель
сообщает,
что
в
математике, говоря о размере сосудов, мы
подразумеваем
их
вместимость
или
ёмкость.(слово ёмкость должно записано на
доске)Например, ёмкость одного сосуда
меньше (больше/равна) ёмкости другого
сосуда.
М1М ч 2. стр. 38

40.

Фрагмент урока
Класс: 1
Предмет: математика
Учебник: УМК: «Школа России»; М.И. Моро , С.И. Волкова ,С.В.
Степанова; ч.1 с.38.
Тема урока: «Ёмкость. Литр».
Цель: формирования представлений у обучающихся о понятие
«емкость» с единицей её измерения «литр».
Задачи урока:
1) Формирование представлений об использовании приёмов при
сравнении ёмкостей.
2) Введение единой меры измерения объёма – литра.
3) Закрепление новых знаний при решении задач.
Оборудование:
Для учителя – конспект урока, учебник
Для детей – учебник..

41.

Ход урока:
1) Формирование представлений об использовании приёмов при
сравнении ёмкостей.
Учитель предлагает сравнить однородные величины на глаз.
У: Ребята, давайте сейчас с вами попробуем сравнить кастрюлю и
кружку.
Что больше по размеру(объёму)?
Д: Кастрюлю.
У: Верно.
На столе стоит кувшин , стакан и кружка.
У:Ребята , давайте проверим во все ли эти предметы помещается
одинаковое количество жидкости?
Учитель берёт кружку с водой и переливает содержимое в кувшин. Вода
поместилось вся в кувшине, и ещё осталось свободное место :

42.

У: Ребята, мы можем сделать вывод, что воды в кружке меньше, чем в
кувшине.
Теперь учитель возвращает воду в кружку и переливает её в стакан.
Вода поместилась в стакан, и место всё заполнено.
У: Ребята, можем сделать вывод ,что количество воды в кружке и
стакане одинаково(равно).
У:Ребята, сейчас мы с вами сравнили объёмы трёх предметов.
Запоминаем ,что объём –величина ,которая характеризует вместимость
сосудов ,показывает, какое количество жидкости в них войдёт.
Наше сравнение можно записать с помощью знаков (> < =).
Учитель выписывает знаки на доске.

43.

У: Ребята, но не всегда удобно измерить объём предмета с помощью
переливания жидкости. В этом случае используем мерки.
У: В качестве мерки у нас будет стакан.
У: В кастрюлю вмещается 10 стаканов воды, а в ведро 15 стаканов.
У: Измерив таким способов объёмы предметов, можно сделать вывод:
Т.к. 15>10 , то объём ведра больше объёма кастрюли или объёма
кастрюли меньше объём ведра .

44.

2) Введение единой меры измерения объёма – литра.
У: Ребята , не всегда удобно использовать способы определения объёма.
Например, при определении объёма воды в реках , озёрах, морях. Это
очень трудно , поэтому существует общепринятая мерка для измерения
емкости – литр.
Учитель показывает на доске обще-принятую сокращённую запись
литра в математике (л.).
3)Закрепление новых знаний при решении задач.
У:Ребята, открываем страницу 38 учебника номер 2.
Учитель просит Катю прочитать вслух задание. (Катя прочла задание).
У: Ребята, кто-то уже догадался , какое будет решение?
Четверо учеников поднимают руки.
У: Хорошо , ребята , сейчас мы все вместе решим эту задачу. Что нам
дано в условии ?
Д: В ведро входит 10л воды.
У : Правильно. А что нужно найти? Найдите в задании и прочитайте.
Д : (Ваня) читает.

45.

У : Так как нам определить , сколько литров воды можно долить ведро
,если в нём 6 л? Мы должны из 10л вычесть 6л.Сколько получится (л)?
Д: 4л.
У: Верно.
Учитель записывает это выражение на доске 10л -6л =4л.
Далее дети по аналогии доделывают задание письменно в тетради.
У: Ребята, следующее задание выполняем 3. Читаем его , определяем
условие и что нам нужно найти.
Каждый учащийся выполняет это устно и самостоятельно.
У : Ребята ,так что нам дано в задаче?
Д : (Коля) отвечает : в банке – 3л молока , в бидоне на 4л молока
больше.
У: Аня, как мы найдём ,сколько литров молока в бидоне?
Д: Аня говорит , все остальные записывают: 3л+ 4л=7(л) молока в
бидоне.
У: Правильно. А как найти общее количество литров в бидоне и в
банке? Ребята , ответ запишите самостоятельно в тетради.
У : Сколько получилось литров молока , Федя, пожалуйста ,скажите.
Ф: Я к 3л + 7л и получилось 10 л.
У : Ребята, кто согласен с Федей поднимите руки.
Дети поднимают руки.
У : Молодцы.
Записываем домашнее задание: упр.1,4 на странице 38.

46.

По программе Г.В. Дорофеева, Т.Н.
Мираковой,
Т.Б.
Бука
УМК
«Перспектива»
формирование
представления об ёмкости предметы
происходит в 1 классе. На первом уроке
информирует учащихся о том, что
вместимость сосудов можно измерять в
литрах. Литр- единая мера объёма
предмета. Также преподаватель показывает
сокращённую запись слова литр.
М1Дорофеев 2ч. 44с.

47.

В программе Т.Е. Демидовой, С.А.
Козловой, А.П. Тонких УМК
«Школа 2100» изучение величины –
«Объём» начинается с 1 класса.
Детей знакомят с понятием литр,
формируя знания об вместимости
(ёмкости) предмета.
М1Демидова 3ч. 4с.

48.

По программе Т.Е. Демидовой, С.А.
Козловой, А.П. Тонких УМК «Школа
2100» понятие единой меры объёмов
вводится в 1 классе. Учитель должен
донести до учеников информацию о
том, что меры объёмов, измеренных
одинаковыми единицами измерения,
можно сравнивать , а также складывать
и вычитать.
1литр(1 л) – одна из единиц измерения
объёма.
М1Демидова ч.3 с.5

49.

По программе Петерсон Л. Г.
УМК «Перспектива» изучают
величину – «объём» начинают в
1 классе .
М1П 3ч. 10- 11с

50.

В
некоторых
других
программах,
например,
Н.Б.Истоминой
УМК «Гармония» или И.И.
Аргинской УМК «Система развивающегося обучения
Занкова» , учащихся не знакомят с понятием « литр ».
Авторы данных программ включают изучение величины
– «Объём » только в 4 классе. Поэтому учитель должен
сам подготовить материал по единой мере ёмкости и
донести до учащихся.

51.

Приведем примеры ситуаций, которые можно использовать на уроке по
теме "Литр" (разработка Истоминой Н.Б.).
Ситуация 1.
Предлагаются два сосуда с водой. Один узкий, другой широкий. Уровень
воды в обоих сосудах одинаков. Кроме того, на столе стоят два стаканчика
различной емкости (обозначим их 1 и 2). Учитель предлагает выяснить с
помощью мерки 1, в каком сосуде больше. Учащиеся практически
убеждаются, что в широком сосуде таких мерок 7, а в узком 5. 7 > 5.
Делается вывод. Затем используется мерка 2. В широком сосуде их 4, а в
узком 2. 4 > 2. Делается вывод. Затем учитель предлагает измерить
количество воды в широком сосуде меркой 2, а в узкой меркой 1.
Обсуждение результатов приводит к выводу, что для сравнения количества
воды в сосудах необходимо пользоваться единой меркой.

52.

Ситуация 2.
Два сосуда: один широкий, другой узкий. В одном и другом налита
вода. Уровень воды в узком сосуде выше, чем в широком сосуде.
Учитель задает вопрос: В каком сосуде воды больше? Ответы
противоречивы. Нужно решить проблемы – как убедиться, в каком
же сосуде воды больше? После того как было разобрана первая
ситуация, учащиеся сами предложат использовать для этой цели
третий сосуд, который будет выполнять функцию мерки. Данное
задание будет более занимательным, если в одном и другом сосудах
налито воды одинаковое количество. Учитель подводит итог:
сравнение емкостей не всегда можно провести на глаз, точнее делать
это измерением.

53.

После того как введена единица измерения емкости, решаются
различные практические задачи.
Например: "В одном сосуде 5 л, а в другом 3 л. Как сделать, чтобы в
сосудах было поровну?" (Из первого сосуда отлить 2 л воды, тогда в
каждом сосуде будет по 3 л, или из первого сосуда перелить во второй 1 л
воды). Задача решается практически. "В одном сосуде 3 л воды, а в
другом на 2 л больше. Что можно сделать, чтобы во втором сосуде воды
было больше только на 1 л?" Задача решается практически, но требует от
ученика проведения рассуждений, которые должны предопределить,
предугадать практический результат. Полезно рассмотреть различные
способы решения данной задачи:
1) Учащиеся могут предложить долить в первый сосуд 1 л воды. Если такой способ
предложен, он проверяется практически. Проверку, которая связана с умением
непосредственно измерять емкость с помощью единицы измерения, может
выполнить любой ученик.
2) Можно из второго сосуда отлить 1 л, тогда во втором сосуде будет не на 2 л
больше, а на 1 л.
3) Возможны и такие предложения: долить в первый сосуд 2 л воды, а во второй 1 л.
Собственно все задания связаны с практической проверкой предполагаемого
результата, но они даны в виде задачи, а поэтому вызывают больший интерес, чем
простое измерение количества воды с помощью банки в 1 л.

54.

4 Этап. Сложение и вычитание величин, выраженных в литрах
Цель данного этапа- сформировать умения решать задачи на сложение
и вычитание величин, выраженных в литрах.
Например: В банке 3 л молока, а в ведре на 4 л больше. Сколько в
ведре?
3л+4л=7л.
Прежде чем, приступим к описанию данного этапа в методике
изучения величин , нужно упомянуть о Международная система
единиц измерения (СИ).

55.

Международная система единиц измерения
Общие сведения о системе СИ
Система СИ была принята XI Генеральной конференцией по мерам и
весам, некоторые последующие конференции внесли в СИ ряд
изменений.
Система СИ определяет семь основных и производные единицы
измерения, а также набор приставок. Установлены стандартные
сокращённые обозначения для единиц измерения и правила записи
производных единиц.
В России действует ГОСТ 8.417-2002, предписывающий обязательное
использование системы СИ. В нем перечислены единицы измерения,
приведены их русские и международные названия и установлены
правила их применения. По этим правилам в международных
документах и на шкалах приборов допускается использовать только
международные обозначения. Во внутренних документах и
публикациях можно использовать либо международные либо русские
обозначения (но не те и другие одновременно).

56.

Основные единицы системы СИ: килограмм, метр, секунда, ампер,
кельвин, моль и кандела. В рамках системы СИ считается, что эти
единицы имеют независимую размерность, т. е. ни одна из основных
единиц
не
может
быть
получена
из
других.
Производные единицы получаются из основных с помощью
алгебраических действий, таких как умножение и деление. Некоторым из
производных единиц в Системе СИ присвоены собственные названия.
Приставки можно использовать перед названиями единиц измерения; они
означают, что единицу измерения нужно умножить или разделить на
определенное целое число, степень числа 10. Например приставка «кило»
означает умножение на 1000 (километр = 1000 метров). Приставки СИ
называют
также
десятичными
приставками.

57.

История
Система СИ основана на метрической системе мер, которая была
создана французскими учеными и впервые была широко внедрена после
Великой Французской революции. До введения метрической системы,
единицы измерения выбирались случайно и независимо друг от друга.
Поэтому пересчет из одной единицы измерения в другую был сложным. К
тому же в разных местах применялись разные единицы измерения, иногда
с одинаковыми названиями. Метрическая система должна была стать
удобной и единой системой мер и весов.
В 1799 г. были утверждены два эталона — для единицы измерения длины
( метр) и для единицы измерения веса ( килограмм).
В 1874 г. была введена система СГС, основанная на трех единицах
измерения - сантиметр, грамм и секунда. Были также введены десятичные
приставки от микро до мега.

58.

В 1889 г. 1-ая Генеральная конференция по мерам и весам приняла
систему мер, сходную с СГС, но основанную на метре, килограмме и
секунде, т. к. эти единицы были признаны более удобными для
практического использования.
В последующем были введены базовые единицы для измерения
физических величин в области электричества и оптики.
В 1960 г. XI Генеральная конференция по мерам и весам приняла
стандарт, который впервые получил название «Международная система
единиц (СИ)».
В 1971 г. IV Генеральная конференция по мерам и весам внесла
изменения в СИ, добавив, в частности, единицу измерения количества
вещества ( моль).
В настоящее время система СИ принята в качестве законной системы
единиц измерения большинством стран мира и почти всегда
используется в области науки (даже в тех странах, которые не приняли
СИ)

59.

60.

Теперь приступаем к описанию 4 Этапа.
М1П 3ч. 37с
Сложение и вычитание величин,
выраженных в одной единицы измерения в
программе Петерсон Л. Г. УМК
«Перспектива» .
М1П 3ч. 11с
М1П 3ч. 12 с

61.

М1М ч.2 с. 68
М1М ч.2 с. 38.
М1М ч.2 с. 66
В программе М.И. Моро С, И. Волкова, С.
В. Степанова УМК «Школа Росси» учитель
может использовать следующие упражнения
на сложение и вычитание единицы объёмалитр.

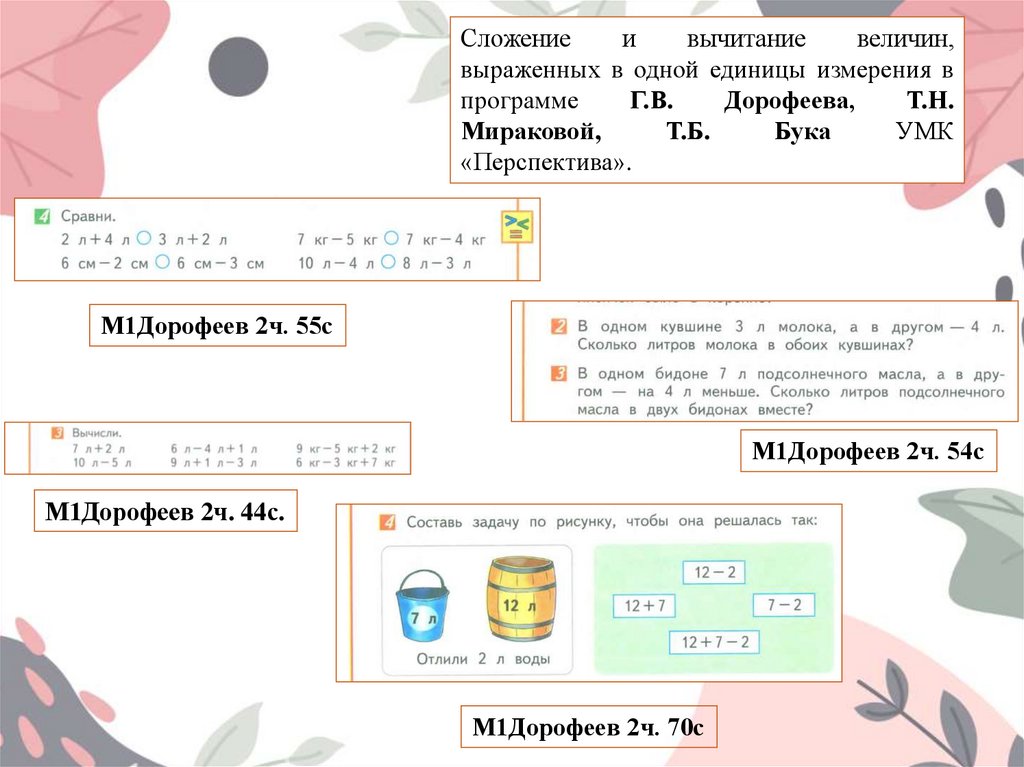
62.

Сложение
и
вычитание
величин,
выраженных в одной единицы измерения в
программе
Г.В.
Дорофеева,
Т.Н.
Мираковой,
Т.Б.
Бука
УМК
«Перспектива».
М1Дорофеев 2ч. 55с
М1Дорофеев 2ч. 54с
М1Дорофеев 2ч. 44с.
М1Дорофеев 2ч. 70с

63.

М1Демидова 3ч. 6с
По обучающей программе Т.Е. Демидовой,
С.А. Козловой, А.П. Тонких УМК «Школа
2100»
учитель
может
использовать
следующие упражнения на сложение и
вычитание единицы объёма- литр.
М1Демидова 3ч. 5с.
М1Демидова 3ч. 7с.

64.

5 Этап. Введение других единиц измерения величины.
Цель данного этапа - формирование знаний о других единицах
измерения величины «объём».
По некоторым другим программам, например, Н.Б.Истоминой или И.И.
Аргинской, учащихся знакомят с понятием «Объём фигуры» при
изучении трёхмерных геометрических фигур. Например,
рассматривая кубы и прямоугольные параллелепипеды,
сравнивают их по размеру и подводят к понятию «Объём
фигуры». Анализируя куб и прямоугольный параллелепипед,
говорят о единицах измерения объема. Например, по программе
Истоминой Н.Б. это 1 см3, 1 дм3
М4И ч.2 с.32-33-34

65.

По программе Аргинской И.И
УМК «Система развивающегося
обучения
Занкова»
первое
упоминание о величине объём
наблюдается при изучении курса
математики в 4 классе.
М4А ч.2 с.16
М4А ч.2 с.26

66.

По программе Аргинской И.И. УМК «Система
развивающегося обучения Занкова» выводят правило
нахождения объёма куба и прямоугольного
параллелепипеда.
М4А 2ч. 20-21 с.

67.

По программаме И.И. Аргинской учащихся знакомят с понятием
«Объём фигуры» при изучении трёхмерных геометрических фигур.
Например, рассматривая кубы и прямоугольные параллелепипеды,
сравнивают их по размеру и подводят к понятию «Объём фигуры».
Вариант беседы ознакомления учащихся с понятием « Объём
фигуры» :
У: Ребята, прежде чем мы с вами перейдём к изучению новой темы,
давайте вспомним , какие единицы измерения уже были изучены на
предыдущих уроках.
Д:Мы изучили единицы измерения длины (мм, см, дм, м…) и площади
(см2, мм2, м2, км2…).
У: Правильно, ребята! Открываем страницу 16 учебника и выполняем
упражнение 306 (1).
Дети самостоятельно в тетрадях выполняют задание!

68.

У: Ребята , давайте проверим задания. Катя, какая связь между
данными единицами измерения? Запиши на доске
К: 1 мм2 = 1мм * 1 мм
1 см2 = 1см * 1 см
1 дм2 = 1дм * 1 дм
1 м2 = 1м * 1 м
1 км2 = 1км * 1 км
У: Верно. Ребята, кто согласен с Катей , поднимите руку.
Дети поднимают руки.
У: Теперь мы с вами переходим к изучению «Объёма фигуры».
Объём измеряют кубическими миллиметрами, кубическими
сантиметрами, кубическими дециметрами, кубическими метрами и
даже кубическими километрами.
На примере разберём упражнение 306 (3).
У: Ребята , на рисунке изображён куб , который показывает такую
единицу измерения объёма , как кубический сантиметр. (Учитель
показывает запись 1 см3 на доске).
У: Ребята , запоминаем ,что 1 см3 = 1см* 1см* 1см.
У: Домашнее задание упражнение 306 (4,5).

69.

М4А ч.2 с.20

70.

Фрагмент урока по математике.
Класс: 4
Предмет: математика
Учебник: УМК: «Система Занкова»; И.И. Аргинская, Е.И. Ивановская,
С.Н. Кормишина ; ч.2 с.26.
Тема урока: «Объём куба».
Цель: формирование представлений о измерении объёма ,выведение
формулы объёма куба.
Задачи урока:
1)Повторение изученного материала
2) Формирование представлений о измерении объёма;
3) Выведение формулы объёма куба.
Оборудование:
Для учителя – конспект урока, учебник
Для детей – учебник..

71.

Ход урока:
1)Повторение изученного материала:
У: Ребята, кто может мне может сказать в чём измеряют объём?
Д:Объём измеряют кубическими миллиметрами, кубическими
сантиметрами, кубическими дециметрами, кубическими метрами и
даже кубическими километрами.
У: Ребята, правильно. А кто может показать на доске запись?
( Коля выходит к доске и записывает : 1 см3, 1дм3, 1м3, 1 км3).
2) Формирование представлений о измерении объёма:
У: Ребята , открываем страницу 26 упражнение 323 (2). На данном
рисунке изображён чертёж коробки .Кто-то знает на какую
геометрическую фигуру он похож?
Д: Нет или на куб.(Проблемная ситуация)
У: Ребята, кто мне скажет определения куба?
Д: Куб – это фигура, у которой все стороны равны!(Отвечает Катя)
У: Катя , неточный ответ. Кто может дать другое определение?
Д: Куб- многогранник ,у которого все стороны равны.
У: Верно. Куб-это прямоугольный параллелепипед , у которого все три
измерения равны. А на рисунке на 26 с. У фигуры все три измерения
разные.

72.

У: Чертёж коробки похож на прямоугольную призму. Чтобы ответить
на вопрос задачи ,давайте вспомним ,как можно разложить 1см3?
Д: Аня отвечает: 1см3 = 1см*1см*1см
У:Верно. Ребята, смотрим все на рисунок . Что нам известно?
Д: Длина( 4см) , ширина (2см), высота(3см).
У: Правильно. Что же у нас получиться, если найти произведение
длины, ширины и высоты коробки?
Д: Нужно длину умножить на ширину и на длину.
У: Что получиться, Федя?
Ф: 4*2*3=24
У : Ребята , поднимите руки ,кто согласен с Федей.
Дети поднимают все руки.
У: Все – молодцы.
У: Сделаем вывод ,что прямоугольной призмы равен значению
произведения её длины, ширины, высоты ! Ребята, это нужно
запомнить.

73.

3) Выведение формулы объёма куба:
У: Ребята , смотрим на упражнение 323 (4).
Формула , по которой можно найти объём прямоугольной призмы
выглядит так :
Домашнее задание упражнение 323(4) вы будете выполнять с
помощью формулы нахождения объёма прямоугольной призмы.

74.

По программе Петерсон Л.Г. УМК
«Перспектива» рассматривают – см3,
дм3, м3. Показывают эти единицы
измерения (кубики). 1 см3- это куб с
ребром 1 см. 1 дм3 – это куб с ребром
1
дм.
М2П ч.3 с.41
М2П ч.3 с.42

75.

По программе Петерсон Л.Г. УМК
«Перспектива» рассматривают
прямоугольный
параллелепипед,который имеет 6
граней, 8 вершин, 12 рёбер.
Куб также является прямоугольным
параллелепипедом, но особым у него
все рёбра равны.
М2П ч.2 с.46

76.

Чекин А.Л. УМК «Перспективная начальная школа»
По этой программе учеников знакомят с такими единицами
измерения объёмы фигуры, как:
Кубический сантиметр и измерение объёмастр.92-93
Кубический дециметр и кубический сантиметрстр.94-95
Кубический дециметр и литр стр. 96
Учитель подводит учеников к знакомству с единицами измерения
объёма, вспоминая и повторяя единицы измерения площади: «Чему
равна площадь квадрата со стороной 1 см? (1 см2)Давайте
догадаемся, а чему равен объём куба с ребром 1 см? (1 см3)А далее
используются различные упражнения на нахождение объёма и
перевод из одной единицы в другую.

77.

М4Ч 1ч. 92-93

78.

М4Ч 1ч. 94-95

79.

По программе Т.Е. Демидовой,
С.А. Козловой, А.П. Тонких УМК
«Школа 2100» детей знакомят с
такими единицами измерения
объёма, как:
Кубический дециметр. (дм^3)
Кубический метр. (м^3)
М3Демидова 1 ч. 28

80.

По программе Т.Е. Демидовой, С.А.
Козловой, А.П. Тонких УМК «Школа
2100» детей знакомят с такими
единицами измерения объёма, как:
Кубический сантиметр. (см^3)
М3Демидова 1 ч. 26

81.

По программе Т.Е. Демидовой, С.А.
Козловой, А.П. Тонких УМК «Школа
2100» на странице 27вводят формулу
нахождения объёма прямоугольного
параллелепипеда.
М3Демидова 1 ч. 27

82.

По программе
Т.Е.
Демидовой,
С.А. Козловой, А.П. Тонких
УМК «Школа 2100»
на
странице 4даётся соотношение
между единицами измерения
объёма .
М4Демидова 2 ч. 4с.

83.

По программе М.И. Моро С, И. Волкова, С. В.
Степанова УМК «Школа Россия» не вводят тему
«объём фигур» , не знакомят учащихся с единицами
измерения объёма . В данной программе мы можем
увидеть введение единой меры измерения ёмкости –
«литр».
По программе Г.В. Дорофеева, Т.Н. Мираковой, Т.Б.
Бука УМК «Перспектива» так же не вводят изучение
единиц измерения величины – «объём». Авторы данной
программы описывают формирование представления у
детей об единой мере измерения объёма – литре.

84.

6 Этап. Сложение и вычитание величин, выраженных в единицы
двух наименований
Цель данного этапа – развитие вычислительных умений и навыков,
формирование представлений о свойствах величин, формирование у
учащихся способности к преобразованию, сравнению, сложению,
вычитанию, умножению и делению величин, выраженных в единицах
сначала одного, затем разных наименований.
Здесь важно, чтобы учащиеся осознали, что для выполнения действий с
именованными числами, их нужно выразить в единицах одного
наименования. Так же нужно обратить внимание учащихся на связь
между действиями с отвлеченными. Числами и именованными (за
исключением именованных чисел, выраженных в единицах времени).

85.

Программа Аргинской И.И. УМК «Система
развивающегося обучения Занкова» .
М4А 2 ч. 20-21 с №314

86.

Программа Т.Е. Демидовой,
С.А. Козловой, А.П. Тонких УМК «Школа
2100»
М4Демидова 3ч. 69с.

87.

Программа Петерсон Л.Г. УМК «Перспектива»
М2П ч.2 с.47
М2П ч.3 с.42

88.

Программа Петерсон Л.Г. УМК «Перспектива»
М2П ч.3 с.39
М1Ч ч.1 с.94
Программа Чекин А. Л. УМК
«Перспективная начальная школа.»

89.

7 Этап. Умножение и деление величины на число
Умножение и деление
Умножение и деление чисел, полученных от измерения величин на
отвлеченное число включает в себя следующие случаи.
1. Умножение и деление числа с одной единицей измерения без замены
единиц измерения в произведении и в частном:
2. Умножение числа с одной единицей измерения с заменой единиц
измерения в произведении.
3. Деление числа с одной единицей измерения на однозначное число.
4. Умножение и деление чисел с двумя единицами измерения на
однозначное число.
5. Умножение и деление чисел, полученных от измерения, на двузначное
число:
Число с одним наименованием мер умножается на двузначное число по
правилу умножения целых чисел. Если необходимо, в ответе
выполняется преобразование.
6. Умножение и деление чисел с двумя наименованиями мер
производятся путем предварительного выражения их числом с одним
наименованием мер.

90.

Программа Т.Е. Демидовой,
С.А. Козловой, А.П. Тонких УМК «Школа
2100»
М4Демидова 2ч . 13с.
М4Демидова 2ч . 6с.

91.

Программа Аргинской И.И. УМК «Система
развивающегося обучения Занкова» .
М4А 2 ч. 62-63 с

92.

Программа Чекин А. Л. УМК «Перспективная
начальная школа.»
М4Ч ч.2 с.25

93.

Список литературы
1.
2.
3.
4.
5.
6.
Интернет
ресурс
https://nsportal.ru/ap/library/drugoe/2018/11/03/issledovatelskayarabota-mezhdunarodnye-mery-obema-istoriya-mer-obema .
Бантова, М. А. Методика преподавания математики в начальных
С
классах: Учебное
пособие для учащихся школ. отд-ний пед. уч-щ /
С
М. А. Бантова, Г. В. Бельтюкова. - М. : Просвещение, 1984. – 335 с.
Демидова, Т.Е. Д30 : учеб. для организаций, осуществляющих
образовательную деятельность. В 3 ч. Ч. 3 / Т.Е. Демидова, С.А.
Козлова, А.П. Тонких. – Изд. 3-е, испр. – М. : Баласс, 2016. – 64 с. :
ил. (Образовательная система «Школа 2100»).
Моро М. И. Учеб. для общеобразоват. организаций. В 2 ч.
Ч. 2 / М. И. Моро, С, И. Волкова, С. В. Степанова. - 6-е изд. — М. :
Просвещение, 2015. – 112 с.
Истомина Н. Б. Математика: учебник для общеобразовательных
учреждений. В двух частях. Часть 2 / Н. Б. Истомина. - 13-е изд. —
Смоленске. Ассоциация XI век, 2013. – 120 с.
Чекин, А. Л. Математика : в 2 ч. Ч. 1 : учебник / А. Л. Чекин; под
ред. Р.Г. Чураковой. – М. : Академкнига/Учебник, 2014.160 с.

94.

Список литературы
7.
Аргинская И.И., Бененсон Е.П., Итина Л.С., Кормиина С. Н.
Математика : в 2 ч. – 2-е изд., стер. – Самара : Издательство
«Учебная литература»: Издательский дом «Федороп», 2012
Часть 2 - 128 с.
8. Петерсон Л. Г. СМатематика. Часть 1. / Л. Г. Петерсон - М.: Ювента, 2012
С
- 112 с.
9. Дорофеев Г. В. Математика. Учеб. для общеобразоват. организаций с
прил.на электрон. носителе, в 2 ч. Ч. 1 / Г. В. Дорофеев, Т. Н. Миракова, Т.
Б. Бука - М.: Просвещение, 2015. – 123 с.
10. Дидактическая игра «Поварята».
https://www.maam.ru/detskijsad/konspekt-zanjatija-tema-izmerenieobema-zhidkostei-i-sypuchih-veschestv-didakticheskaja-igra-povarjata.html
11. Овчинникова М.В. Методика изучения темы «Величины» на уроках
математики в начальных классах: Методические рекомендации для
студентов факультета «Начальное обучение. Дошкольное воспитание».
12. СИ https://metrob.ru/html/ed_izmer/Sist_SI.html