Similar presentations:
Меры объема. Методика преподавания математики
1.
Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное учреждение высшего
образования «Владимирский государственный университет имени Александра
Григорьевича и Николая Григорьевича Столетовых» (ВлГУ)
Кафедра педагогики и психологии дошкольного и начального образования
Презентация по дисциплине «Методика преподавания математики»
На тему: «Объем»
Выполнила: студентка 2 курса группы НОЛ-119
Козлова Олеся
2.
• Первыми мерами объема являлись обычные дляхозяйственной практики сосуды и другие
вместилища, которые после достижения
некоторого единства объемов стали
употребляться в качестве мерила количества
зерна, вина и пр. при операциях товарообмена.
3.
• Меры объема имели двеобласти применения для
сыпучих тел и для
жидкостей. В древней
Руси основная система
мер для сыпучих тел
выражалась следующей
схемой:
• 1 кадь = 2 половникам =
4 четвертям = 8
осминам.
4.
• Для мер жидкости чаще всего употреблялись бочка, ведро,корчага.
• Значение и соотношение древнерусских мер жидкостей бочки, ведра, корчаги неизвестны.
• Одна бочка содержала 10 ведер.
• Корчага - 1 1/2 - 1 3/4 ведра (вмещавшего 30 фунтов чистой
воды).
5.
• Кадь вмещала 14 пудов ржи(пуд XVI - XVII вв.) т.е.
229,32 кг, отсюда половник
равен 7 пудам ржи, четверть
- 3 1/2 пуда ржи, осьмина - 1
3/4 пуда ржи.
• Кадь и ее доли
употреблялись в эпоху
Киевской Руси повсеместно.
В "Русской правде"
упоминаются головажня,
лукно, уборок как меры
объема. Вместимость уборка
была невелика, а лукно
являлось большой мерой.
6.
• Наибольшеераспространение
получило ведро,
практически очень
удобная мера,
сохранившаяся до XX
века. По приближенным
подсчетам ведро вмещало
около 24 фунтов воды (=
9,8 кг.). Более крупные
меры для меда, вина и т.п.
упоминаются в
летописных источниках провара (вара).
7.
• Наряду с системными мерами существовали и бытовые. Впериод феодальной раздробленности Руси появился ряд
местных мер. К таким мерам сыпучих тел относились:
• Новгородская коробья = 4 четверткам = 16 четверикам или
четверникам (вмещала в себя 7 пудов ржи).
• Псковская зобница = 2 позобеньям = 4 четверткам
(заключала в себе 9 1/3, а затем 14 пудов ржи).
• Северодвинский пуз (1 1/2 пуда ржи).
• Вятская куница = 3 московским четвертям.
• Старорусский луб (мера для соли).
• Новгородская мера для жидкостей - "насадка" (2 1/2ведра).
8.
• Сборщики налогов не всегда измеряли вустановленных мерах содержимое той или иной тары:
за единицу обложения принимали именно тару
(мешок, куль, ящик), воз товара, нагруженную ладью
и т.д., а также некоторые орудия производства например, црен (чан для солеварения) или невод.
Использование таких мер объема было легализовано
официальными княжескими актами.
9.
• К концу XVI века меры объема составляли стройнуюсистему с коэффициентом 2", связывающим кратные
и дольные меры. Практически применялась в
основном четверть, равная 2 осьминам, осьмина (2
полосмины), полосьмины (2 четверика) и четверик.
Эта система была дополнена последующим делением
на 3, т.е. четверть = 3 третям (третникам) = 6
полтретям = 12 пол-полтретям = 24 пол-полполтретям и т.д.
10.
• Значение четвертиизменилось с течением
времени: в XVI веке
хлебная четверть вмещала
4 пуда ржи, а в XVII веке 6 пудов ржи (5 пудов
муки). В конце XVII века
фигурирует уже
"московская
осьмипудовая четверть".
За короткое время
значение четверти
увеличилось в два раза.
11.
• Изменение значения четверти соответственно отразилось назначениях дольных мер.
• Наиболее важным правительственным мероприятием,
направленным на унификацию мер объема, было устранение
расхождения значении мер, отраженное в царских грамотах
1680 г. В одной из них содержится предписание не только в
отношении сыпучих тел, но и жидкостей: "На Москве и в
городах... для приему и отдачи стрелецкого хлеба... учинить
меры вновь... а были б на Москве и в городах те указные
приимочные заорленые одны меры... Вино, пиво и мед
принимать в приемное заорленое ведро, каково учитено на
перед сего и продавать и в расход давать в то же приимочное
заорленое ведро, чтоб на Москве и в городах везде меры были
одны и ровны."
12.
• Совокупность мер объемажидкости в Московском
государстве представляла
собой достаточно
стройную систему.
Основной мерой являлось
ведро. Деление на более
мелкие меры проводилось
по двоичному принципу:
ведро делили на 2
полуведра или на 4
четверти ведра или на 8
полу четвертей, а также на
кружки и чарки.
13.
• До середины XVII в. в ведре содержалось 12 кружек,во второй половине XVII в. так называемое казенное
ведро содержало 10 кружек, а в кружке - 10 чарок, так
что в ведро входило 100 чарок. Затем, по указу 1652
года чарки сделали втрое больше по сравнению с
прежними ("чарки в три чарки "). В торговое ведро
вмещалось 8 кружек. Значение ведра было
переменным, а значение кружки неизменным, в 3
фунта воды. На основании различных исследований и
расчетов было установлено, что ведро вмещало 30,3
фунта воды, т.е. его объем равен 134,297 кубического
вершка.
14.
• Бочка, как мера жидкостейприменялась в основном в
процессе торговли с
иностранцами, которым
запрещалось вести
розничную торговлю
вином на малые меры.
15.
• Местные меры оказалисьдовольно живучи. В XV в. еще
были распространены
голважня, лукно и уборок. В
XVI-XVII вв. наряду с довольно
распространенными коробьей и
пузом часто встречается вятская
хлебная мера куница, пермская
сапца (мера соли и хлеба),
старорусские луб и пошев.
Вятская куница считалась
равной трем московским
четвертям, сапца вмещала 6
пудов соли и приблизительно 3
пуда ржи, луб - 5 пудов соли,
пошев - около 15 пудов соли.
16.
• Бытовые меры объемажидкостей были весьма
разнообразны и широко
использовались даже в
конце XVII в.:
"смоленская бочка",
"бочка-селедовка" (8
пудов сельдей; в полтора
раза меньше смоленской).
• Известная мерная бочка
"... из краю в край полтора
аршина, а поперек-аршин,
а мерить вверх, как
ведетца, поларшина".
17.
• В житейском обиходе ив торговле употребляли
разнообразные
хозяйственные сосуды:
котлы, жбаны, корчаги,
братины, ендовы.
Значение таких бытовых
мер в разных местах
было различно:
например, емкость
"котлов" колебалась от
полуведра до 20 ведер.
18.
• В XVIII в. была усвоена система кубическихединиц на основе 7-футовой сажени, а также
введен термин "кубический" (или "кубичный").
Кубическая сажень содержала 27 кубических
аршин или 343 кубических фута; кубический
аршин - 4096 кубических вершков или 21952
кубических дюймов.
19.
• В торговой практике и в быту по-прежнемуупотреблялись особые меры объема сыпучих
тел и жидкостей. У Л.Ф. Магницкого указаны
следующие меры сыпучих тел ("хлебные
меры"): ласт - 12 четвертей, четверть,
осьмина, полосьмина и четверик; меры
жидкостей ("винные меры"): бочка(40 ведер),
ведро, полведра, четверть ведра, "осмуха" и
"крушка" (1/16 ведра).
20.
• Во второй половине XVIIIвека в систему русских
мер жидкостей была
введена новая мера бутылка (значение которой
было твердо
зафиксировано). Указом
Сената от 16 сентября
1744 года в ведре должно
было содержаться 13 1/3
бутылок, т.е. бутылка
составляла 3/40 ведра.
21.
• Меры объема сыпучих тел и жидкостей, унаследованныеот XVII в. не претерпели никаких изменений. В 1736 г. по
поручению Комиссии о весах и мерах учеными было
установлено, что в четверике содержится 286,42, а в ведре
- 136,297 кубических вершков. Таким образом была
установлена связь четверика и ведра с кубическими
мерами. Для того, чтобы округлить до целых линейные
меры размеров ведра и четверика, Комиссией был
предложен "Регламент". В этом документе зафиксировано
отношение объемов равное 2:1, т.е. для четверика
8*6*6=288 кубических вершков, для ведра 9*4*4=144
кубических вершка.
22.
• На протяжении XVIII века правительственные органыпроводили ряд мероприятий, направленных на установление
единства измерений объема.
• В 1745 г. был издан указ об изготовлении образцовых медных
хлебных мер (осьмин, полуосьмин и четвериков). В 70-х годах
было опубликовано несколько указов, касавшихся мер объема
жидкостей. Сначала об изготовлении образцов ведер, затем
бутылок и, наконец, о кубическом измерении объемов кружки и
четверика для изготовления образцов из чугунного литья. Если
Комиссия 1736 г. ставила своей задачей воспроизвести наиболее
вероятные объемные значения употребляемых в XVII - начале
XVIII в. четверика и ведра, то Комиссия 1827, на основании
работ которой был составлен указ 1835 г, встала на путь
установления значения мер объема в зависимости от весовых
количеств вмещаемой ими воды.
23.
• "Указом 1835 г. были легализованы следующие системымер:
• сыпучих тел - четверть = 2 получетвертям = 8 четверикам
= 64 гарнцам;
• жидкостей - ведро = 2 полуведрам = 10 кружкам (штофам)
= 20 полукружкам.
• Четверик был определен как объем перегнанной воды
весом 24 фунта или равный 1601,22 кубического дюйма;
• ведро - объем, вмещающий 30 фунтов перегнанной воды
(750,57 кубического дюйма).
• Были изготовлены исходные образцы новых четверика и
ведра.
24.
• В 1899 г. на основе Положения о мерах и весах система меробъема жидкостей имела следующий вид:
• ведро = 10 штофам (кружкам) = 16 винтим бутылкам = 20
пивным бутылкам = 100 чаркам = 200 шкаликам.
• Было предусмотрено изготовление, поверка и клеймение
следующих мер: пол-ведра, четверть ведра, 1/32 ведра, 1/40
ведра.
• В качестве основных мер объема сыпучих тел осталось прежнее
соотношения:
• четверть = 8 четверикам ("мерам") = 64 гарнцам.
• Гарнец определен как объем, вмещавший 8 фунтов перегнанной
очищенной воды. Дополнительно были указаны осьмина (1/2
четверти), полуосьмина и полугарнец.
25.
• Положением былиузаконены кубические
меры (без их
перечисления).
• В 1902 г. значение
четверика и ведра
были выражены в
метрических мерах:
• четверик = 26,239л.,
• ведро = 12,299л.
26.
• Положением о мерах и весах от 27 июня 1916 г. изметрических мер были узаконены для измерения
объемов жидкостей и сыпучих тел: литр, декалитр,
гектолитр; кубические: километр, метр, сантиметр,
дециметр, миллиметр. (Литр определен как объем
1 килограмма химически чистой воды при
температуре 4° по стоградусному международному
водородному термометру). Для кубического метра
было легализовано наименование "стер", а для 10
кубических метров - "декастер"
27.
Западная Европа• В Западной Европе бытовали свои собственные
меры объемов. К ним относятся баррель, бушель,
галлон, драхма, кварта, пинта, унция. Рассмотрим,
что означала каждая мера объема.
28.
• – Баррель – меравместимости и объема,
применяемая в США,
Англии. В США различают
Баррель сухой, равный
115,628 дм3, и Баррель
нефтяной, равный 158,988
дм3. Английский Баррель
(мера вместимости для
сыпучих веществ) равен
163,65 дм3.
• – Бушель – мера объема
жидкостей и сыпучих
веществ в Англии и США. 1
Бушель = 36,3687 л; 1
Бушель (США) = 35,2393 л.
29.
• – Галлон – единица объема(емкости, вместимости) в
системе английских мер,
применяется в Англии, США
и др. странах для измерений
объема жидких и сыпучих
тел. Английский и
американский Галлон
отличаются друг от друга по
своим размерам. Английский
Галлон = 4,54609 дм3.
Американский Галлон для
жидкости = 3,78543 дм3 и
для сыпучих тел = 4,405 дм3.
30.
• – Кварта – единица объема (емкости,вместимости), применяемая в США,
Великобритании и др. странах. 1 Кварта = 1/4
галлона или 2 пинтам. Американская Кварта для
жидкостей = 0,9463 дм3, для сыпучих веществ =
1,1012 дм3. Английская имперская Кварта= 1,1365
дм3. Прежняя русская мера жидкостей – кружка –
также иногда называлась Кварта; в Польше
Кварта = 1 л.
31.
• – Пинта – единица объема (вместимости)жидкостей и сыпучих веществ, применяемая в
странах, использующих английские меры. В
Великобритании 1 Пинта = 1/8 галлона = 0,568261
дм3. В США различают жидкую Пинту, равную
1/8 американского галлона = 0,473179 дм3, и
сухую Пинту, равную 1/64 американского бушеля
= 0,550614 дм3. Пинта применялась также в др.
странах до введения в них метрической системы
мер, напр. во Франции 1 Пинта = 0,931389 дм3, в
Нидерландах 1 Пинта = 0,6063 дм3.
32.
• Еще в детском саду, развивая количественныепредставления учащихся, дети учились измерять
количество сыпучих и жидких веществ ложками,
формочками, выясняли, в какую формочку песка
входит меньше (больше).
33.
• Далее знакомство с величинамипроисходит в начальных классах.
Там величина наряду с числом
является ведущим понятием.
34.
• Величины - это особыесвойства реальных объектов
или явлений. Обычно
изучаются основные величины:
длина, стоимость, площадь,
объём, масса, скорость, время.
Занятия по данной теме
способствуют формированию
обобщений,
совершенствованию,
целенаправленности и точности
выполнения действий,
воспитанию умения доводить
любую работу до конца,
формированию навыков
самоконтроля.
35.
• В ходе формирования практическихумений и навыков развиваются
внимание, память, наблюдательность,
совершенствуется моторика,
тактильные и зрительные восприятия
и ощущения. Все это служит решению
задач коррекции как познавательной
деятельности, так личностных качеств
детей.
36.
• Знакомство с величинами, единицами ихизмерения имеет не только практическое
значение: оно предоставляет большие
возможности для формирования умения
видеть проблему и находить пути ее
решения, тем самым способствуя развитию
познавательных способностей учащихся.
37.
ПЕРВЫЙ ЭТАП.• С целью
формирования
представлений о
разного рода
величинах проводятся
практические работы,
используются
упражнения,
применяются
демонстрационные и
индивидуальные
наглядные средства,
при этом варьируются
коллективные,
индивидуальные и
групповые формы
работы на уроке.
38.
• Учитель выясняет, знают ли учащиеся,какими мерами измеряют молоко,
бензин, растительное масло, вообще
жидкости.
39.
• Выявляя имеющийся у учащихся опыт, учительпредлагает им стандартные банки вместимостью
1л, 2л, 3л. Некоторые ребята знают вместимость
этих банок, некоторые же не имеют о ней никакого
представления.
40.
• Дети сравнивают их и при сравнении размера, учительсообщает, что в математике, говоря о размере сосудов, мы
подразумеваем их вместимость или ёмкость.
• С этой величиной детей знакомят по-разному в разных
программах. Так по программе М.И. Моро термин объём
не вводят, а используют понятие «ёмкость сосуда».
• Например, ёмкость одного сосуда меньше (больше/равна)
ёмкости другого сосуда. М1М ч 2. стр. 38.
41.
ВТОРОЙ ЭТАП.• Сравнение
однородных величин:
• А) « на глаз»
• Показываем сосуды,
контрастные по
объему (стакан и
ведро…). Учим
правильно
формулировать вывод
с помощью термина;
42.
• Б) переливанием в другой сосуд.• Два сосуда: один широкий, другой узкий. В одном и
другом налита вода. Уровень воды в узком сосуде выше,
чем в широком сосуде. Учитель задает вопрос: В каком
сосуде воды больше? Ответы противоречивы. Нужно
решить проблему – как убедиться, в каком же сосуде воды
больше? После того как было разобрана первая ситуация,
учащиеся сами предложат использовать для этой цели
третий сосуд, который будет выполнять функцию мерки.
Данное задание будет более занимательным, если в одном
и другом сосудах налито воды одинаковое количество.
Учитель подводит итог: сравнение емкостей не всегда
можно провести на глаз, точнее делать это измерением.
43.
• Затем он показывает детям литровую кружку, а затемпоочередно переливает воду из неё в бутылку, а затем в
банку. Так учащиеся подводятся к выводу, что в банку
вмещается столько же воды сколько и в кружку, и столько
же, сколько в бутылку, т.е. равное количество воды – 1 л.
Чтобы этот вывод был понятен учащимся, необходимо,
чтобы каждый ученик проделал эту несложную работу
сам. Важно, чтобы дети запомнили это новое слово,
научились его правильно произносить и записывать при
числах. Учащиеся должны уметь отыскивать среди других
сосудов сосуд емкостью в 1л.
44.
• В) использование мерок.• Ещё в ДОУ детей знакомят с этим способом. В
качестве мерок используют маленькие чашечки.
Проводим несколько опытов измерения емкости
различными мерками. Например, емкость банки равна
4 чашкам.
45.
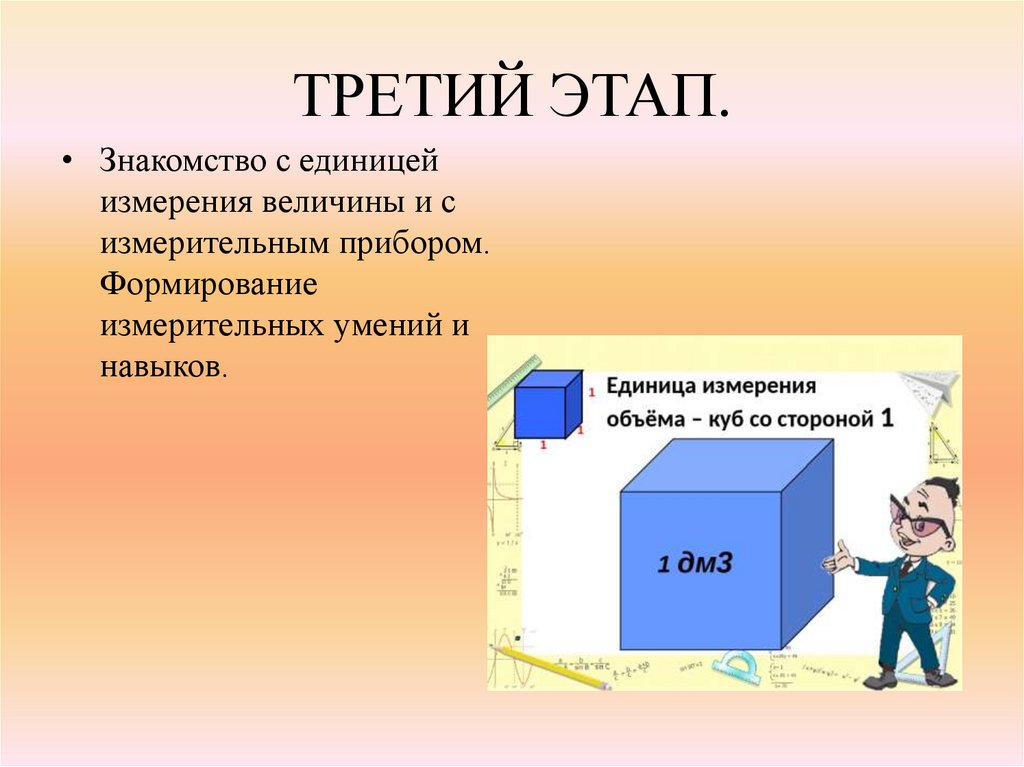
ТРЕТИЙ ЭТАП.• Знакомство с единицей
измерения величины и с
измерительным прибором.
Формирование
измерительных умений и
навыков.
46.
• Далее учащиеся учатся измерять вместимость сосудов иотмеривать заданное количество в литре. Они определяют,
наполняя водой, емкость банок, небольших баллонов,
кастрюль, ведер. Важно развивать глазомер учащихся, т.е.
умение определить емкость сосудов на глаз. Учащиеся
должны запомнить емкость стандартных наиболее часто
встречающихся в быту сосудов: банки емкостью 1л, 2л, 3л,
5л; бидоны емкостью 1л, 2л, 3л, 5л, 10л, 20л, 40л, ведра
емкость 8л, 10л, 12л. Главный упор делается на
практическую работу.
47.
• Кроме литровой банки детям можно показать кубик «тысячи» изарифметического ящика, ведь объем 1 л соответствует 1 куб.дм. Дети
часто не верят, что в литровую банку и этот кубик помещается
одинаковое количество воды или сыпучих продуктов. Можно склеить 1
куб. дм из плотной бумаги и быстро вылить в него воду или пересыпать
сыпучие продукты объемом 1 л.
48.
• V = a ∙b ∙c• Для вывода этого
правила
рассматриваем модель
прямоугольного
параллелепипеда.
Можно её сложить из
кубиков, принимая,
что 1 кубик = 1
единице объёма,
например 1 дм3.
49.
• Задание:• Например, прямоугольный параллелепипед размером
3х4х5.
• Уточняем: сколько всего кубиков в модели, т. е. сколько
единиц измерения объёма, в этом прямоугольном
параллелепипеде? Сначала подсчитываем, сколько
кубиков потребовалось для одного уровня. Дети умеют
находить S прямоугольника, следовательно, ответят 3∙4
=12. Уточняем, что обозначают числа 3 и 4? Это числовые
значения длины и ширины. Таких уровней в нашем
параллелепипеде 5, следовательно, всего 3∙4∙5 кубиков, где
5 – это числовое значение высоты, следовательно,
• V параллелепипеда = произведению длины, ширины и
высоты.
50.
ЧЕТВЕРТЫЙ ЭТАП.• Сложение и вычитание величин, выраженных в единицах
одного наименования.
• Действия над числами, полученными в результате
измерения величин, подчиняются тем же законам, что и
действия над числами в пределах 100, 1000 и
многозначными числами. Действия над числами,
полученные от измерения величин - опираются на знание
учащимися единиц измерений и их соотношения, а также
умения выразить одни меры другими.
51.
• Демонстрируется емкость сосуда в 1 л, проводитсяпрактическая работа по измерению вместимости сосудов:
устанавливают, что в банке 3 л, в ведре – 10 л. Решают
задачи, связанные с составом числа: «В одну банку входит
3 л, в другую – 5 л. Как с их помощью отмерить 2 л, 8 л, 13
л?»
52.
• Полезно рассмотреть различные способы решенияданной задачи:
• 1) Учащиеся могут предложить долить в первый
сосуд 1 л воды. Если такой способ предложен, он
проверяется практически. Проверку, которая
связана с умением непосредственно измерять
емкость с помощью единицы измерения, может
выполнить любой ученик.
• 2) Можно из второго сосуда отлить 1 л, тогда во
втором сосуде будет не на 2 л больше, а на 1 л.
• 3) Возможны и такие предложения: долить в
первый сосуд 2 л воды, а во второй 1 л.
53.
• После того как введена единица измерения емкости,решаются различные практические задачи.
• Например: "В одном сосуде 5 л, а в другом 3 л. Как
сделать, чтобы в сосудах было поровну?" (Из первого
сосуда отлить 2 л воды, тогда в каждом сосуде будет по 3
л, или из первого сосуда перелить во второй 1 л воды).
Задача решается практически. "В одном сосуде 3 л воды, а
в другом на 2 л больше. Что можно сделать, чтобы во
втором сосуде воды было больше только на 1 л?"
54.
• Собственно все заданиясвязаны с практической
проверкой
предполагаемого
результата, но они даны
в виде задачи, а поэтому
вызывают больший
интерес, чем простое
измерение количества
воды с помощью банки
в 1 л.
55.
ПЯТЫЙ ЭТАП.• Перевод величин,
выраженных в единицах
одних наименований, в
однородные величины,
выраженные в единицах
других наименований
56.
• Интересно знать!• В английской системе мер единицей площади является 1
акр:
• 1 акр = 4046,86 м3;
• единицей объема — 1 баррель:
• 1 баррель = 163,65 дм3 = 0,16 м3.
• В США различают сухой баррель:
• 1 сухой баррель = 115,628 дм3
и нефтяной баррель:
• 1 нефтяной баррель = 158,988 дм3 = 0,159 м3.
• Теперь вам будет понятно, о каком объеме нефти идет
речь, когда обсуждается цена за 1 баррель нефти.
57.
• Какая из мензурокпозволит определить
объем куска пластилина
наиболее точно
58.
• А как измерить объем теланеправильной формы,
например гири? Здесь
наиболее удобный способ
— опустить тело (гирю) в
мензурку с водой и
определить объем
вытесненной им воды. Он
будет равен объему тела.
На рисунке объем гири
равен:
• V = 49 мл - 21 мл = 28
мл = 28 см3.
59.
• Определите объем кускапластилина. Выразите
этот объем в кубических
дециметрах (дм3),
кубических сантиметрах
(см3), кубических
миллиметрах (мм3).
60.
ШЕСТОЙ ЭТАП.• Сложение и вычитание однородных величин, выраженных
в единицах различных наименований.
• Затем, рассматриваются действия над числами с разными
единицами измерения. Выполнять действия над ними
можно разными способами:
61.
• а) заменить крупные мерымелкими, т.е. выразить
компоненты действия в
одних и тех же единицах;
• б) показать, что при
сложении, например двух
кубов объемом
соответственно 5 дм3 и 4
см3 в сумме получится
фигура объемом 5 дм3 4
см3
62.
СЕДЬМОЙ ЭТАП.• Умножение и деление величины на число. Деление
однородных величин.
• Дети изучают только умножение и деление чисел,
полученных от измерения величин, на отвлеченное число.
Умножение и деление этих чисел необходимо
сопоставлять соответствующими действиями с
отвлеченными числами.
63.
• Последовательность и приемы выполнениядействий следующее:
• 1. Умножение и деление числа с одной единицей
измерения без замены единиц измерения и
произведения в частном.
64.
• 2. Умножение числа с одной единицей измерения сзаменой единиц измерения в произведении.
• 3. Деление числа с одной единицей измерения на
однозначное число. При решении таких примеров делимое
надо выразить в более мелких мерах.
65.
• 4. Умножение и деление чисел с двумяединицами измерения на однозначное число:
• Когда учащиеся овладевают приемами
умножения и деления, тогда и можно
показать, что в отдельных случаях находить
результат быстрее (можно даже устно), если
умножать или делить число, выраженное
только на крупных мерах или только в
мелких.
66.
• 5. Умножение и деление чисел, получить от измерения надвухзначное число.
• 6. Умножение и деление чисел с двумя наименованиями
мер проводится путем предварительного выражения их
числом с одним наименованием мер.
67.
• Учащиеся для лучшего запоминания последовательности(алгоритма) выполнения действий можно предположить
заметку приблизительно такого содержания:
• 1. Прочитай пример;
• 2. Определи одно или два наименования в числе, которое
нужно умножать.
• 3. Если множимое (делимое) - число с двумя
наименованиями мер, то надо установить единица каких
разрядов равна 0.
• 4. Выразим множимое делимое число с одним
наименованием мер.
• 5. Выполни умножение (делимое).
• Выполни преобразования в ответе.
• При выполнении действий с числами, полученными от
измерений не надо забывать о решении примеров с
неизвестными компонентами действий.
68.
Петерсон Л. Г.УМК «Перспектива»
• В этой программе тему
«объем» дают во 2 классе,
в 3 части учебника.
69.
• Сразу даётся формуланахождения объёма
прямоугольного
параллелепипеда.
• ( стр. 40)
70.
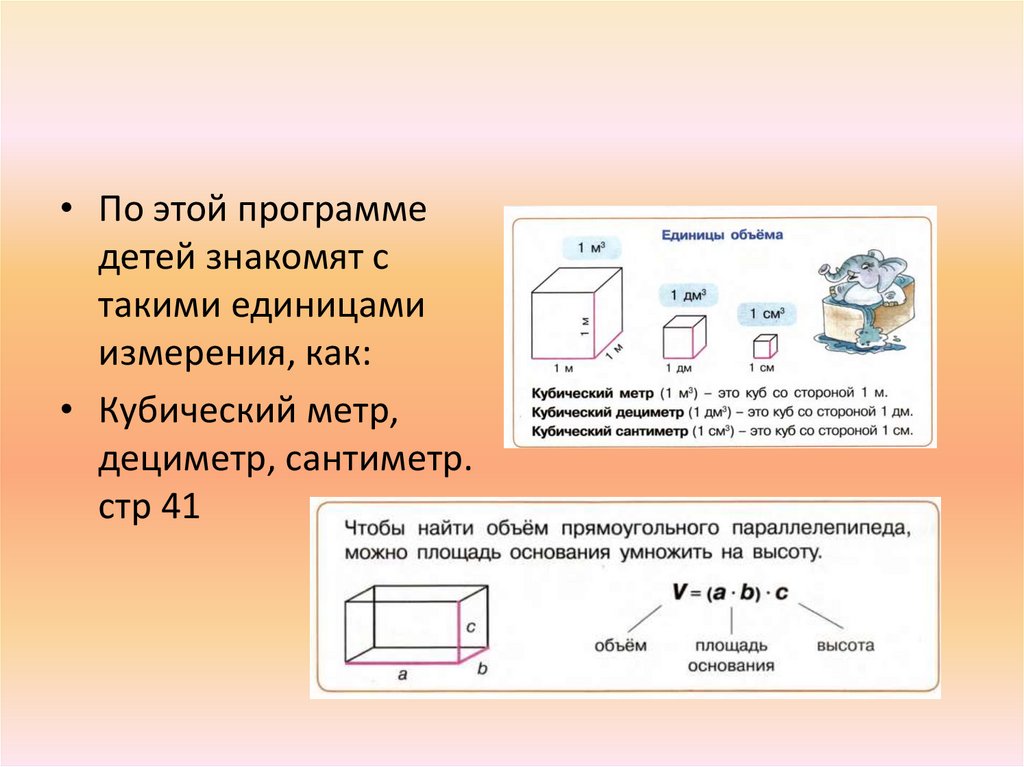
• По этой программедетей знакомят с
такими единицами
измерения, как:
• Кубический метр,
дециметр, сантиметр.
стр 41
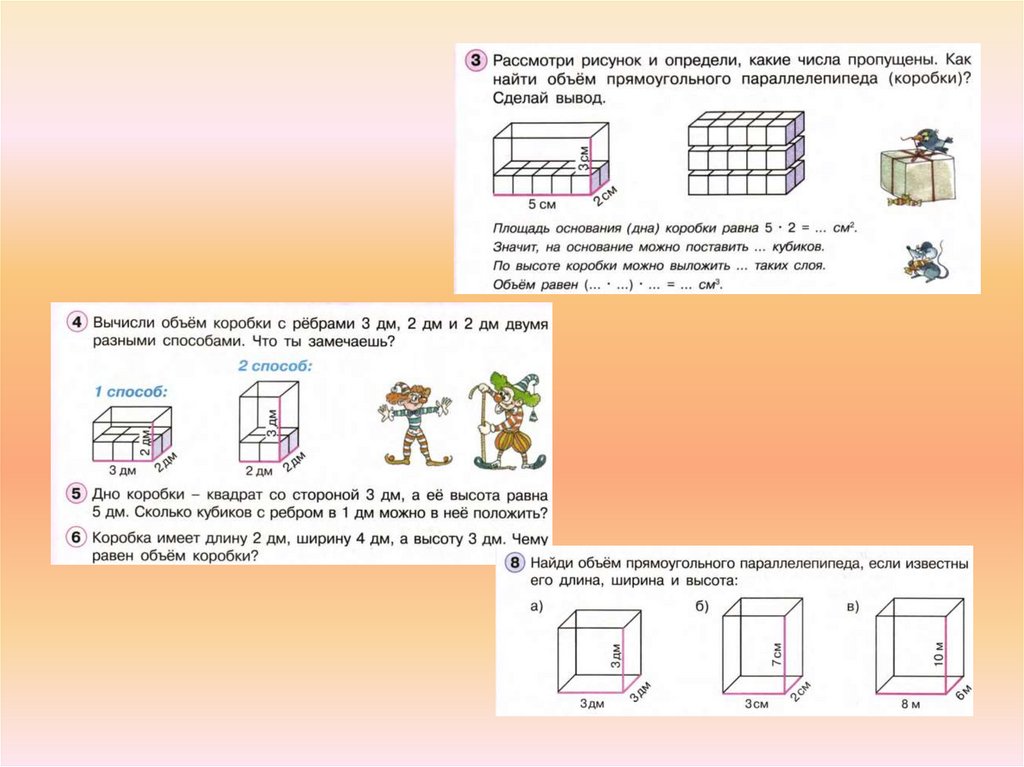
71.
72.
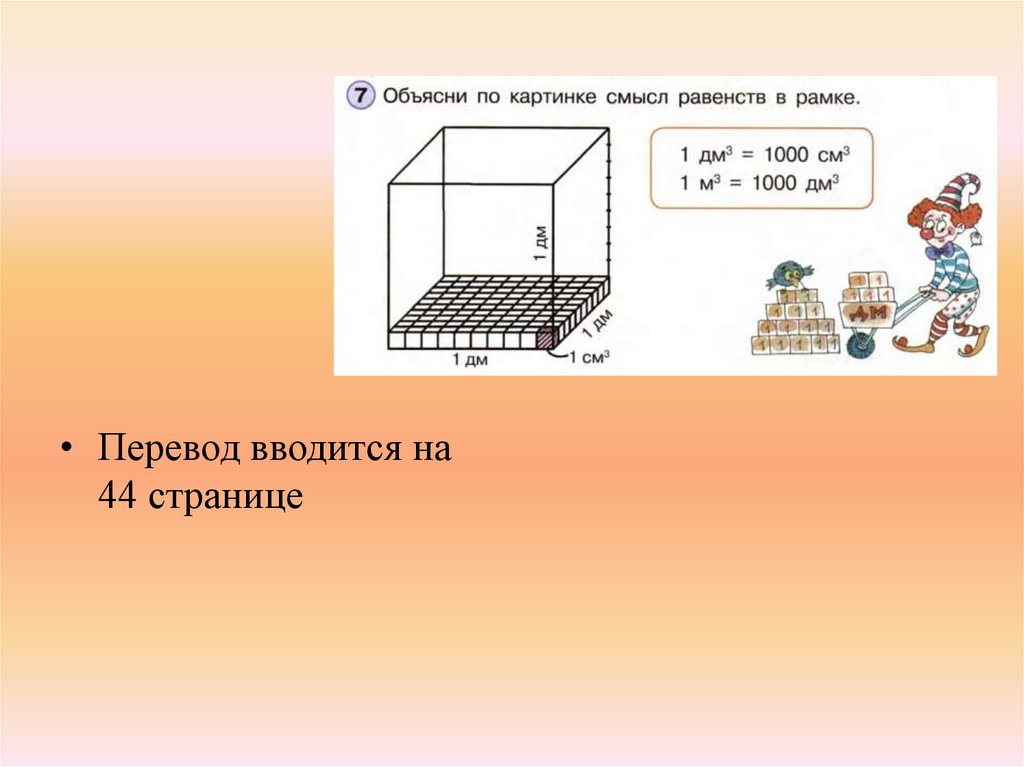
• Перевод вводится на44 странице
73.
• 51 страница• 58 страница
74.
• Умножение на 49странице
75.
Т. Е. Демидова, С. А. Козлова,А. Л. Тонких
УМК «Школа 2100»
• М3ДКТ часть 1
• По этой программе
детей знакомят с
такими единицами
измерения объёма,
как:
76.
• Сначала вводятсяопределения
параллелепипеда и
куба(стр. 24)
• Задание со страницы 25
77.
• Кубическийсантиметр.
стр. 26
78.
• Понятие«объем»
вводится на 27
странице.
79.
• Затем, на 28 страницерассматривается
кубический дециметр и
кубический метр.
80.
• Задача на сложение даетсяна 37 странице.
81.
Чекин А.Л.УМК «Перспективная начальная школа»
• Чекин вводит тему
объема в 4 классе в
первой части учебника.
82.
• Начинает эту темус вместимости
сосудов (стр.84-89)
83.
• Кубический сантиметр иизмерение объёма стр.
92-93
84.
• На 95 странице вводитсяперевод из кубического
дециметра в кубический
сантиметр.
85.
• На 96 страницеобъясняется, что 1 литр
равен 1 кубическому
дециметру.
86.
• На 100-101 страницахсравниваются разные
фигуры с помощью мерки.
87.
• Также, задания на объемдаются во второй части
учебника (стр.82-83; 8889)
88.
Р.И. Аргинская, Е.И. Ивановская,С.Н. Кормишина
УМК«Система развивающего обучения Л.В.
Занкова»
Эти авторы вводят тему
объема в 4 классе во
второй части учебника.
89.
• Тема начинается супражнений на 11,13 и
14страницах
90.
• По этой программедетей знакомят с
такими единицами
измерения объёма,
как:
• кубический
миллиметр,
сантиметр, дециметр,
метр, и даже
кубический километр.
• (стр. 16)
91.
• Приводятся задания настраницах 18, 20, 21.
92.
• А на странице 26 вводятформулу нахождения
объема прямоугольной
призмы.
93.
• На 28 странице вводитсяперевод в другие единицы
измерения объема.
94.
Также даны задания настраницах 32-33, 36.
95.
• На страницах 38 – 39рассказывается про
измерение объема.
96.
• Работа на сложение ивычитание величин
начинается на 43
странице.
97.
Дорофеев Г.В.УМК «Перспектива»
• По этой программе не
вводят тему «объём
фигур» и
соответственно не
знакомят учащихся с
единицами измерения
объёма.
98.
Список литературы:• Бантова М. А., Бельтюкова Г. В. Методика преподавания математики в
начальных классах.
Москва. "Просвещение". 1984г.
• И.И. Аргинская, Е.П. Бененсон, Л.С. Итина, С.Н. Кормишина.
Математика 1-4 класс. Издательство «Учебная литература».
• Т.Е. Демидова, С.А. Козлова, А.П. Тонких. Математика 1-4 класс.
Издательство «Баласс».
• Г.В. Дорофеев, Т.Н. Миракова. Математика 1-4 класс. Издательство
«Просвещение».
• Н.Б. Истомина. Математика 1-4 класс. Издательство «Ассоциация XXI
века».
• М.И. Моро, С.И. Волкова, С.В. Степанова. Математика 1-4 класс.
Издательство «Просвещение».
• Л.Г. Петерсон. Математика 1-4 класс. Издательство «ЮВЕНТА».
• А.Л. Чекин. Математика 1-4 класс. Издательство «Академкнига».
• https://studwood.ru/2108650/tovarovedenie/mery_obema































































































 mathematics
mathematics pedagogy
pedagogy








