Лекция 8 Проекции с числовыми отметками

1. Лекция Тема: Проекции с числовыми отметками

ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
Лекция
Тема: Проекции с числовыми отметками

2.

ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ (ПЧО)
Проекции с числовыми отметками применяются при
проектировании и изображении зданий и инженерных сооружений,
расположенных на топографической поверхности.
Метод проекций с числовыми отметками
– это ортогональное проецирование на одну горизонтальную
плоскость: высота точек (координата z) проставляется на
горизонтальной проекции в виде чисел (высотных отметок)

3.

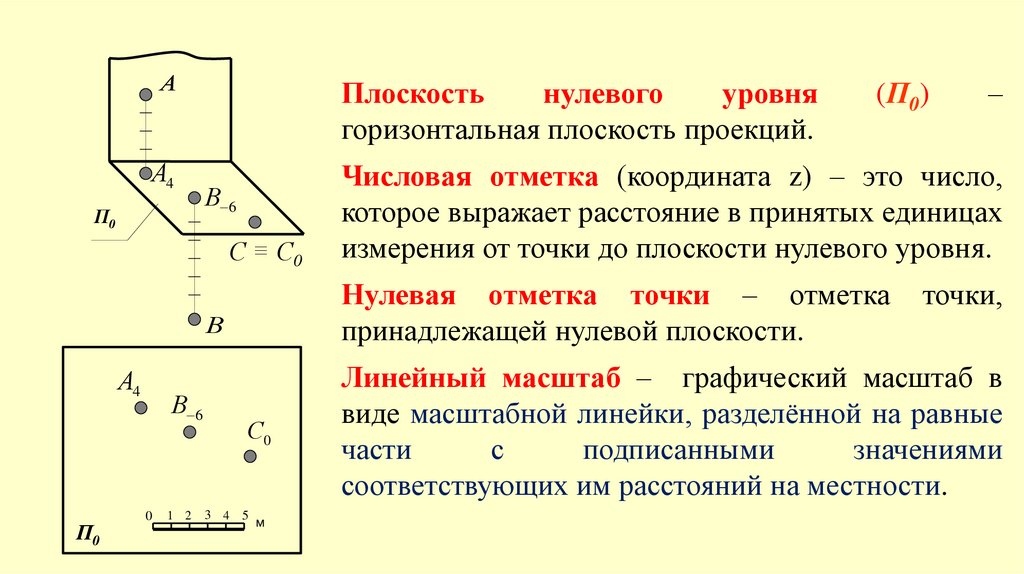
А
Плоскость
нулевого
уровня
горизонтальная плоскость проекций.
А4
Числовая отметка (координата z) – это число,
которое выражает расстояние в принятых единицах
измерения от точки до плоскости нулевого уровня.
П0
В 6
С ≡ С0
Нулевая отметка точки – отметка
принадлежащей нулевой плоскости.
В
А4
П0
В 6
0
1 2
(П0)
С0
3 4 5
м
–
точки,
Линейный масштаб – графический масштаб в
виде масштабной линейки, разделённой на равные
части
с
подписанными
значениями
соответствующих им расстояний на местности.

4. ЛИНИИ В проекциях с числовыми отметками

ЛИНИИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
А
h
4
h3
А5
N0
В-3
О-5
d-5
П0
В
О d
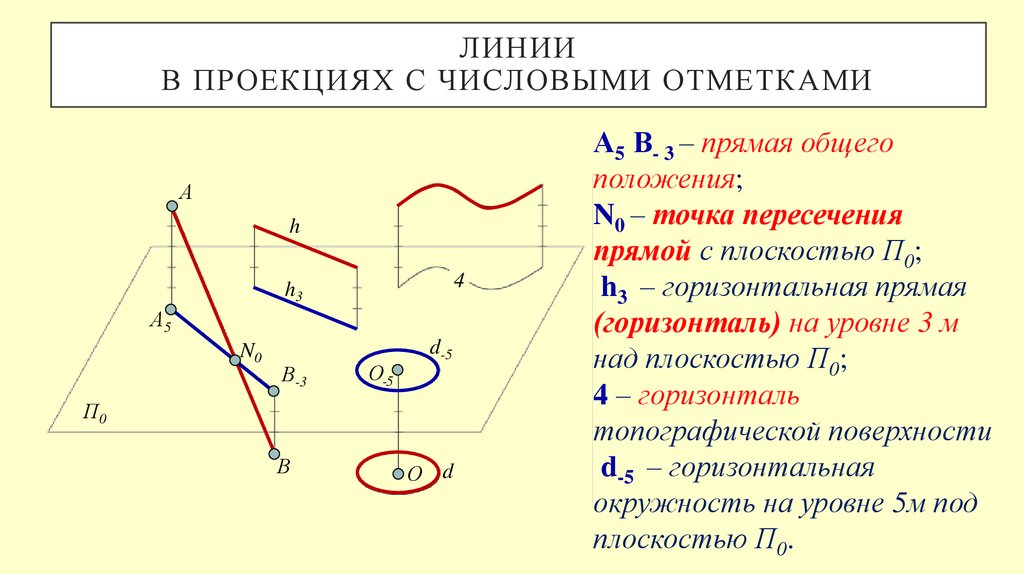
А5 В- 3 – прямая общего
положения;
N0 – точка пересечения
прямой с плоскостью П0;
h3 – горизонтальная прямая
(горизонталь) на уровне 3 м
над плоскостью П0;
4 – горизонталь
топографической поверхности
d-5 – горизонтальная
окружность на уровне 5м под
плоскостью П0.

5. ЛИНИИ В проекциях с числовыми отметками

ЛИНИИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
А
Превышение H
hА
П0
А6
Заложение L
В
hВ
В2
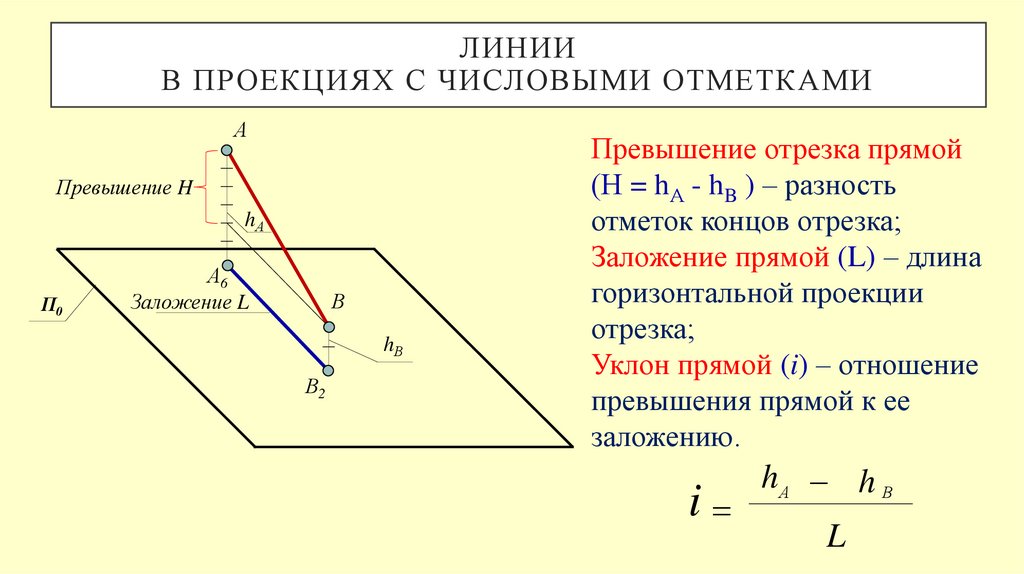
Превышение отрезка прямой
(Н = hА - hB ) – разность
отметок концов отрезка;
Заложение прямой (L) – длина
горизонтальной проекции
отрезка;
Уклон прямой (i) – отношение
превышения прямой к ее
заложению.
i=
hА h В
L

6. ЛИНИИ в проекциях с числовыми отметками

ЛИНИИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
А
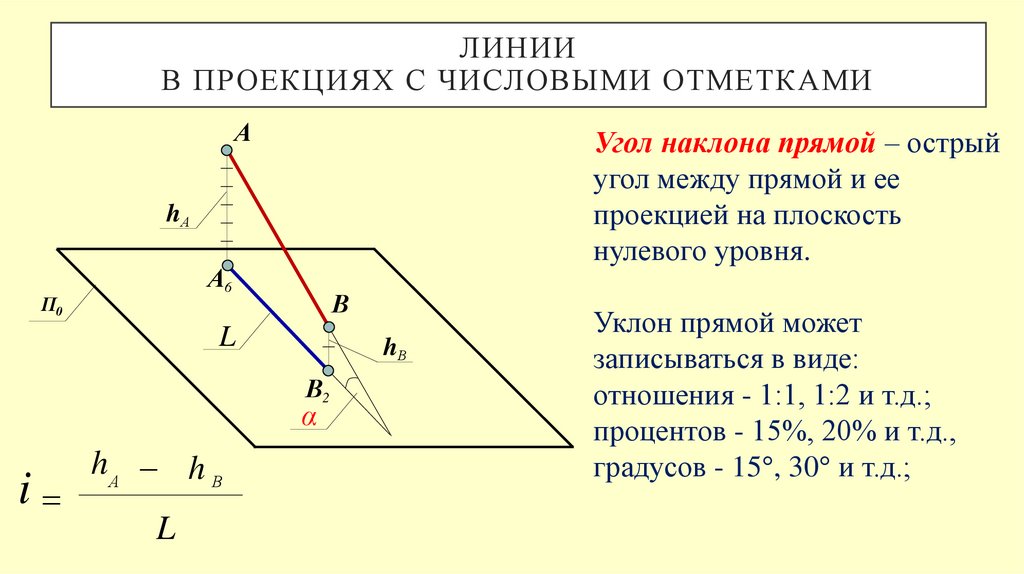
Угол наклона прямой – острый
угол между прямой и ее
проекцией на плоскость
нулевого уровня.
hА
А6
П0
В
L
hВ
В2
α
i=
hА h В
L
Уклон прямой может
записываться в виде:
отношения - 1:1, 1:2 и т.д.;
процентов - 15%, 20% и т.д.,
градусов - 15 , 30 и т.д.;

7. ЛИНИИ в проекциях с числовыми отметками

ЛИНИИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
А
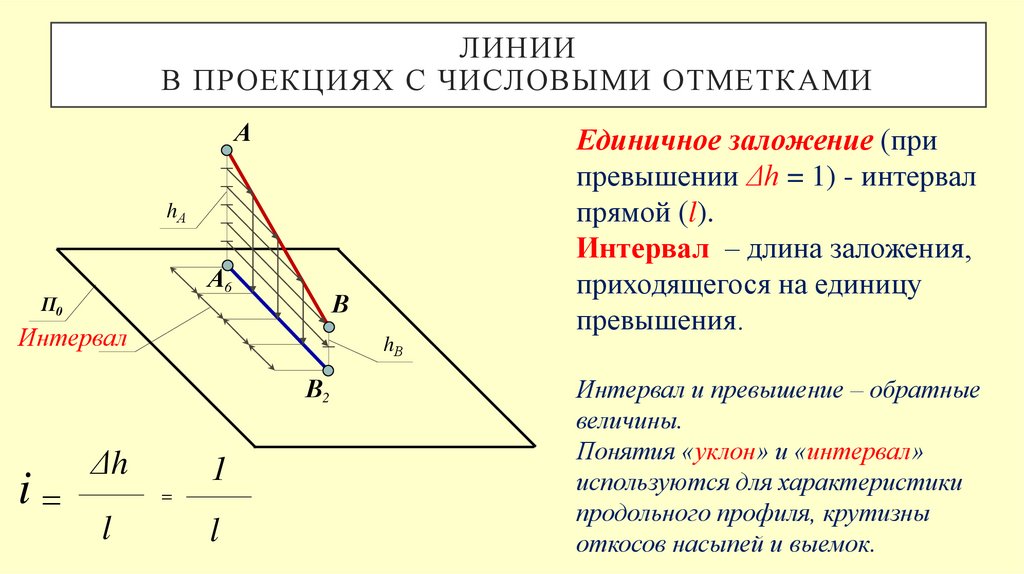
Единичное заложение (при
превышении Δh = 1) - интервал
прямой (l).
Интервал – длина заложения,
приходящегося на единицу
превышения.
hА
А6
П0
В
Интервал
hВ
В2
i=
Δh
=
l
1
l
Интервал и превышение – обратные
величины.
Понятия «уклон» и «интервал»
используются для характеристики
продольного профиля, крутизны
откосов насыпей и выемок.

8. ЛИНИИ в проекциях с числовыми отметками

ЛИНИИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
Прямая может быть задана:
B8
В5
i=1
:4
A2
0 1
2 3 4 5м
- двумя точками
i%=1 А 6
5 :4
i=1
B8
0 1
3 4 5м
20 31 42 5м
%
5
1
i=
0 1
А6
2 3 4 5м
- точкой и направлением уклона

9.

МЕТРИЧЕСКИЕ ЗАДАЧИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
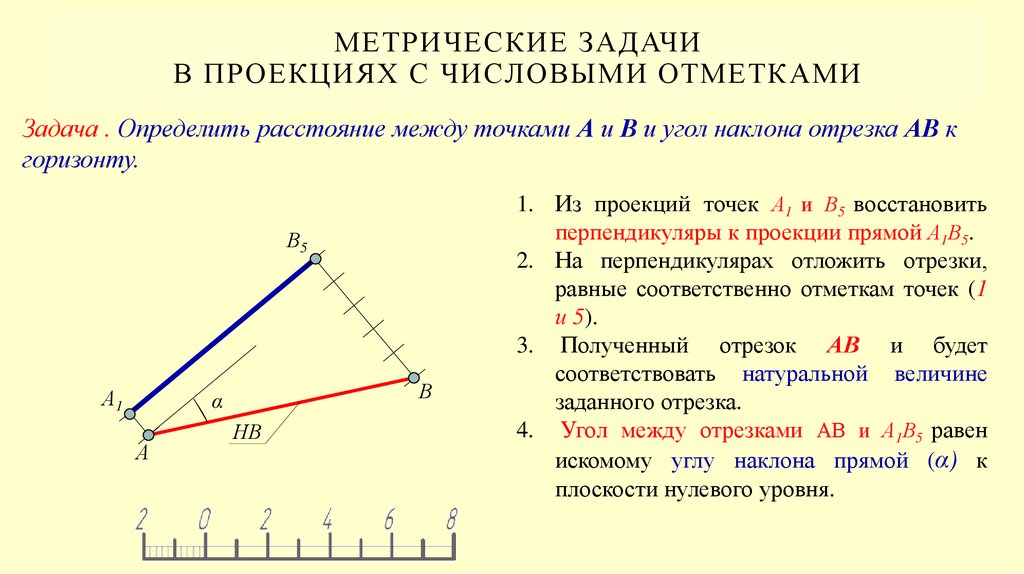
Задача . Определить расстояние между точками А и В и угол наклона отрезка АВ к
горизонту.
В5
А1
В
α
А
НВ
1. Из проекций точек А1 и В5 восстановить
перпендикуляры к проекции прямой А1В5.
2. На перпендикулярах отложить отрезки,
равные соответственно отметкам точек (1
и 5).
3. Полученный отрезок АВ и будет
соответствовать натуральной величине
заданного отрезка.
4. Угол между отрезками АВ и А1В5 равен
искомому углу наклона прямой (α) к
плоскости нулевого уровня.

10.

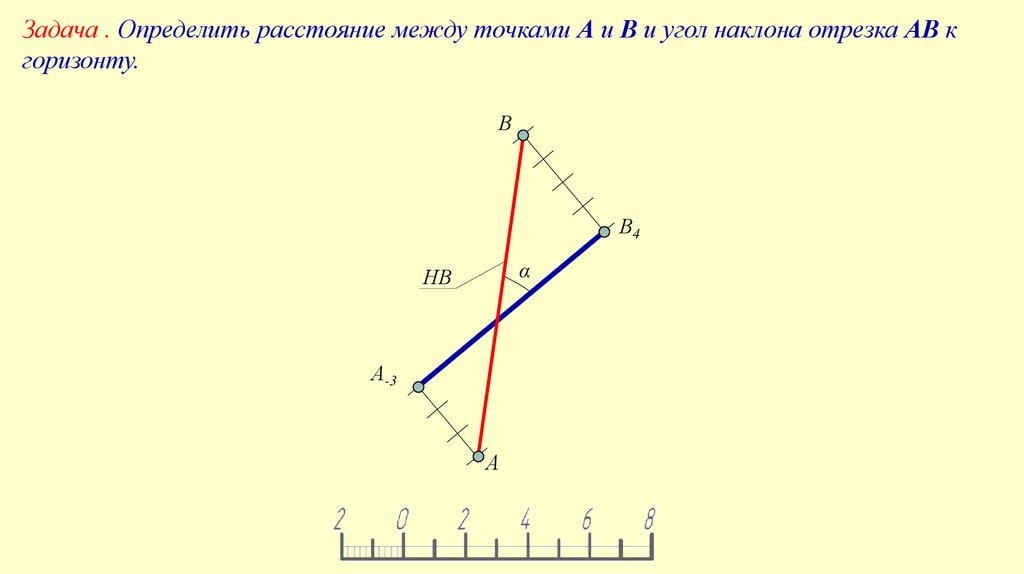
Задача . Определить расстояние между точками А и В и угол наклона отрезка АВ к
горизонту.
В
В4
α
НВ
А-3
А

11. Градуирование прямой ЛИНИИ

ГРАДУИРОВАНИЕ ПРЯМОЙ ЛИНИИ
Градуирование прямой (интерполирование) – процесс определения
на горизонтальной проекции прямой линии точек с целочисленными
отметками, разность между которыми равна единице.
Способы градуирования:
1) Пропорциональное деление заданного отрезка (с использованием теоремы
Фалеса) - определение точек с целочисленными отметками, разность между
которыми равна единице.
2) Нахождение натуральной величины и проекций интервалов.

12.

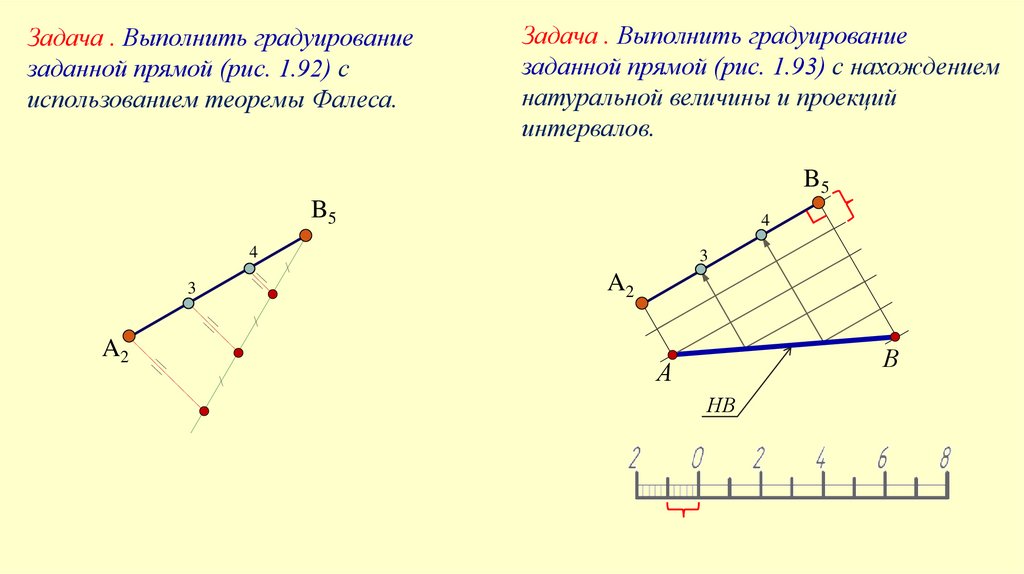
Задача . Выполнить градуирование
заданной прямой (рис. 1.92) с
использованием теоремы Фалеса.
Задача . Выполнить градуирование
заданной прямой (рис. 1.93) с нахождением
натуральной величины и проекций
интервалов.
B5
B5
4
4
3
A2
3
A2
В
А
НВ

13.

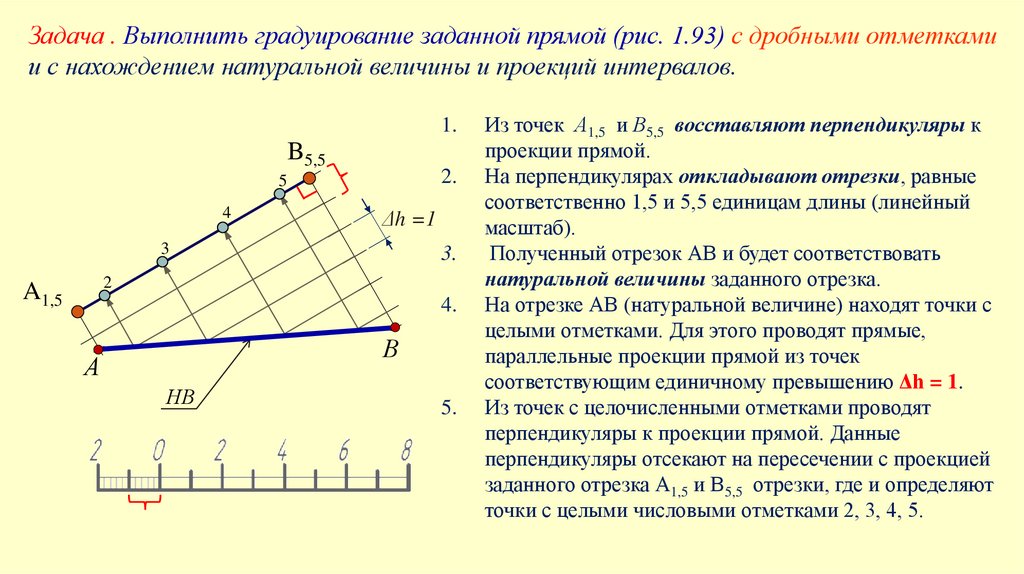
Задача . Выполнить градуирование заданной прямой (рис. 1.93) с дробными отметками
и с нахождением натуральной величины и проекций интервалов.
1.
B5,5
2.
5
4
Δh =1
3
3.
2
A1,5
4.
В
А
НВ
5.
Из точек А1,5 и В5,5 восставляют перпендикуляры к
проекции прямой.
На перпендикулярах откладывают отрезки, равные
соответственно 1,5 и 5,5 единицам длины (линейный
масштаб).
Полученный отрезок АВ и будет соответствовать
натуральной величины заданного отрезка.
На отрезке АВ (натуральной величине) находят точки с
целыми отметками. Для этого проводят прямые,
параллельные проекции прямой из точек
соответствующим единичному превышению Δh = 1.
Из точек с целочисленными отметками проводят
перпендикуляры к проекции прямой. Данные
перпендикуляры отсекают на пересечении с проекцией
заданного отрезка А1,5 и В5,5 отрезки, где и определяют
точки с целыми числовыми отметками 2, 3, 4, 5.

14. Положение прямых В проекциях с числовыми отметками

ПОЛОЖЕНИЕ ПРЯМЫХ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
Прямая, не перпендикулярная и не параллельная
плоскости проекций, называется наклонной прямой.
Если прямая параллельна плоскости нулевого уровня
(АВ // П0), то прямая называется горизонталью.
Концы отрезка имеют одинаковые отметки и горизонталь
проецируется в натуральную величину на П0 (АВ =А5В5).
Если прямая перпендикулярна плоскости уровня
(CD ┴ П0 ), то проекция прямой на горизонтальную
плоскость проекций – точка, и такая прямая называется
вертикальной прямой.
N3
М7
B5
A5
НВ
C2 ≡ D5

15. Положение прямых В проекциях с числовыми отметками

ПОЛОЖЕНИЕ ПРЯМЫХ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
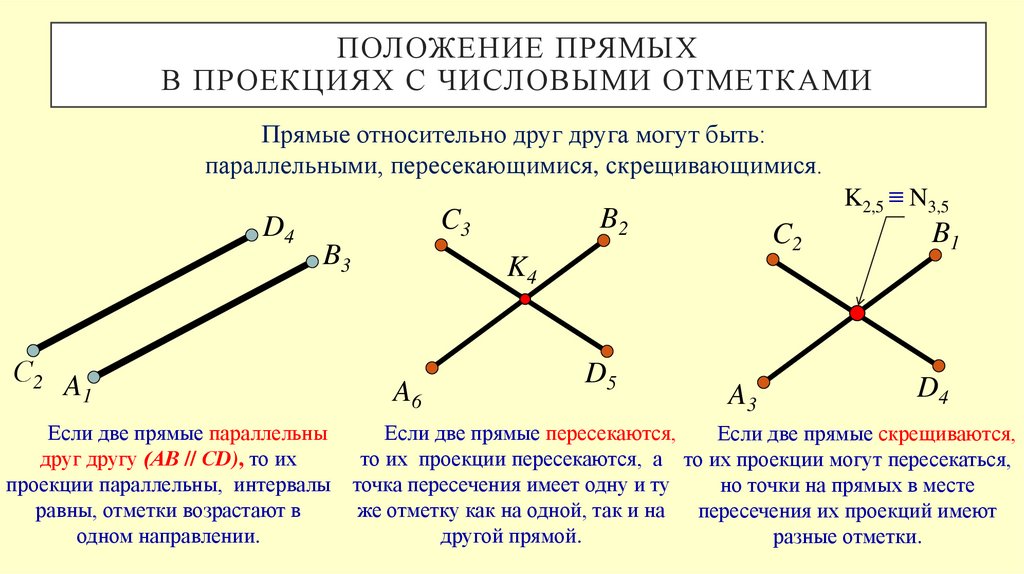
Прямые относительно друг друга могут быть:
параллельными, пересекающимися, скрещивающимися.
D4
B2
C3
B3
С2 A
1
Если две прямые параллельны
друг другу (АВ // СD), то их
проекции параллельны, интервалы
равны, отметки возрастают в
одном направлении.
K2,5 ≡ N3,5
C2
B1
K4
A6
D5
A3
D4
Если две прямые пересекаются,
Если две прямые скрещиваются,
то их проекции пересекаются, а то их проекции могут пересекаться,
точка пересечения имеет одну и ту
но точки на прямых в месте
же отметку как на одной, так и на
пересечения их проекций имеют
другой прямой.
разные отметки.

16. Плоскости В проекциях с числовыми отметками

ПЛОСКОСТИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
А
С0
γ
α
α3
П0
А4
N0
К0
В- 4
В
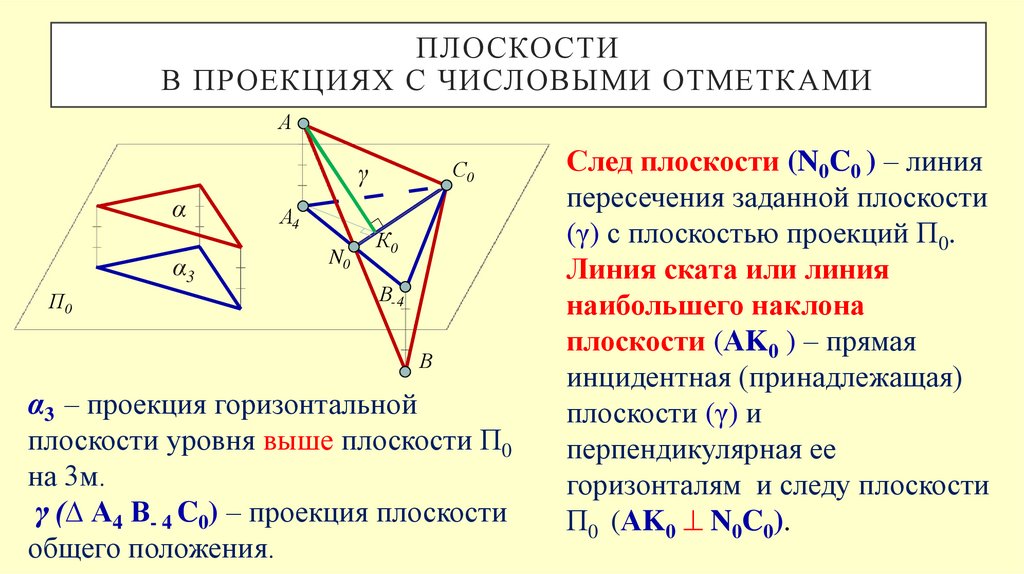
α3 – проекция горизонтальной
плоскости уровня выше плоскости П0
на 3м.
γ (∆ А4 В- 4 C0) – проекция плоскости
общего положения.
След плоскости (N0C0 ) – линия
пересечения заданной плоскости
(γ) с плоскостью проекций П0.
Линия ската или линия
наибольшего наклона
плоскости (АK0 ) – прямая
инцидентная (принадлежащая)
плоскости (γ) и
перпендикулярная ее
горизонталям и следу плоскости
П0 (АK0 N0C0).

17. Плоскости В проекциях с числовыми отметками

ПЛОСКОСТИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
Плоскость в проекциях с числовыми отметками можно задать теми же
способами, что и в ортогональных проекциях. Но удобнее задавать
положение плоскости в пространстве масштабом уклона (падения).
Масштабом уклона (падения) плоскости называется проекция линии
наибольшего наклона (ската) плоскости, на которой показываются
отметки точек (градуированная проекция линии наклона плоскости,
отображается двумя линиями разной толщины).
Масштаб уклона плоскости всегда перпендикулярен проекциям
горизонталей плоскости.

18. Плоскости в проекциях с числовыми отметками

ПЛОСКОСТИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
Линия
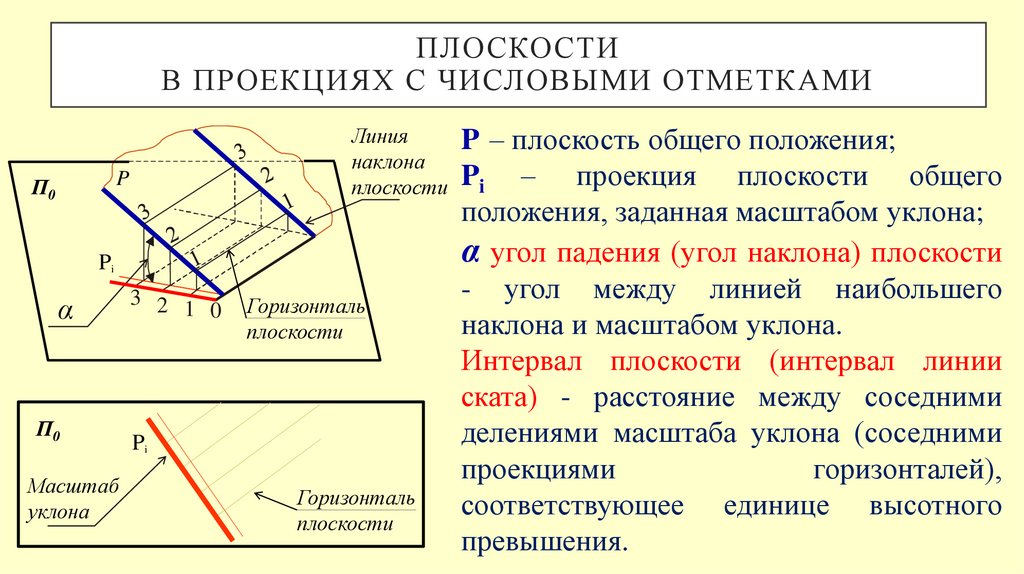
P – плоскость общего положения;
наклона
– проекция плоскости общего
плоскости Pi
P
П0
Pi
α
П0
Масштаб
уклона
3 2
1 0
Горизонталь
плоскости
Pi
Горизонталь
плоскости
положения, заданная масштабом уклона;
α угол падения (угол наклона) плоскости
- угол между линией наибольшего
наклона и масштабом уклона.
Интервал плоскости (интервал линии
ската) - расстояние между соседними
делениями масштаба уклона (соседними
проекциями
горизонталей),
соответствующее единице высотного
превышения.

19. Взаимное расположение двух Плоскостей в проекциях с числовыми отметками

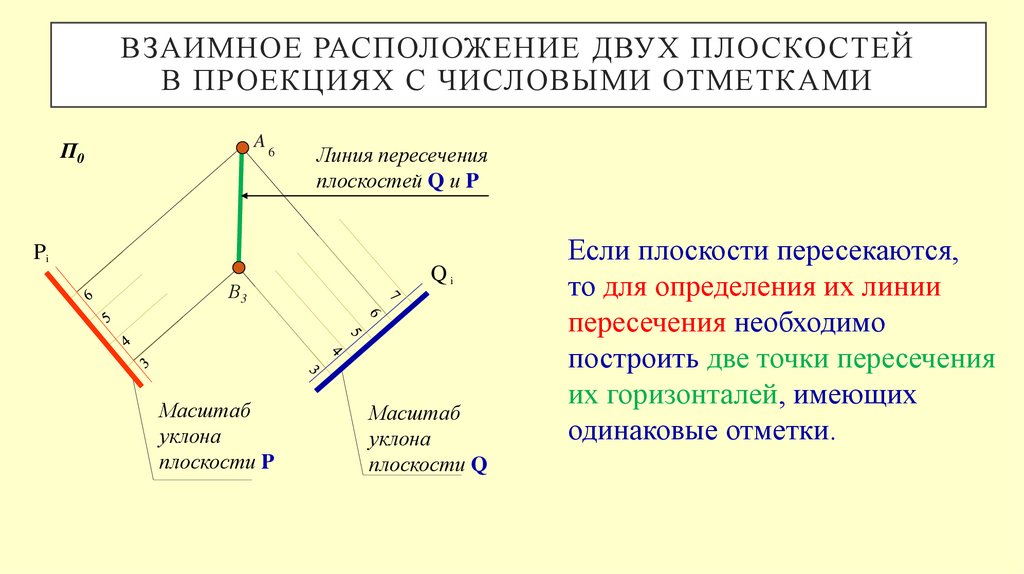
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКАМИ
A6
П0
Линия пересечения
плоскостей Q и P
Pi
В3
Масштаб
уклона
плоскости P
Qi
Масштаб
уклона
плоскости Q
Если плоскости пересекаются,
то для определения их линии
пересечения необходимо
построить две точки пересечения
их горизонталей, имеющих
одинаковые отметки.

20. Поверхности в проекциях с числовыми отметками

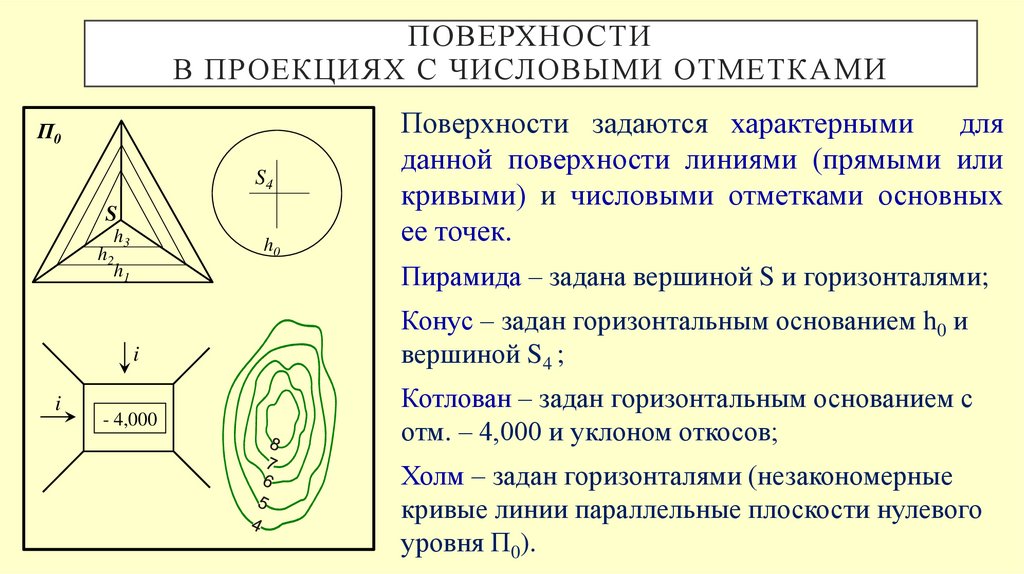
ПОВЕРХНОСТИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКА МИ
П0
S4
S
h3
h0
h2
Пирамида – задана вершиной S и горизонталями;
h1
i
i
Поверхности задаются характерными
для
данной поверхности линиями (прямыми или
кривыми) и числовыми отметками основных
ее точек.
- 4,000
Конус – задан горизонтальным основанием h0 и
вершиной S4 ;
Котлован – задан горизонтальным основанием с
отм. – 4,000 и уклоном откосов;
Холм – задан горизонталями (незакономерные
кривые линии параллельные плоскости нулевого
уровня П0).

21. Поверхности в проекциях с числовыми отметками

ПОВЕРХНОСТИ
В ПРОЕКЦИЯХ С ЧИСЛОВЫМИ ОТМЕТКА МИ
Земная
поверхность
топографическая поверхность.
–
На
чертежах
топографическую
поверхность
изображают
совокупностью расположенных на
ней линий – горизонталей, по
которым
она
пересекается
горизонтальными плоскостями.
Горизонтали
соединяют
точки
топографической поверхности с
одинаковыми числовыми отметками.

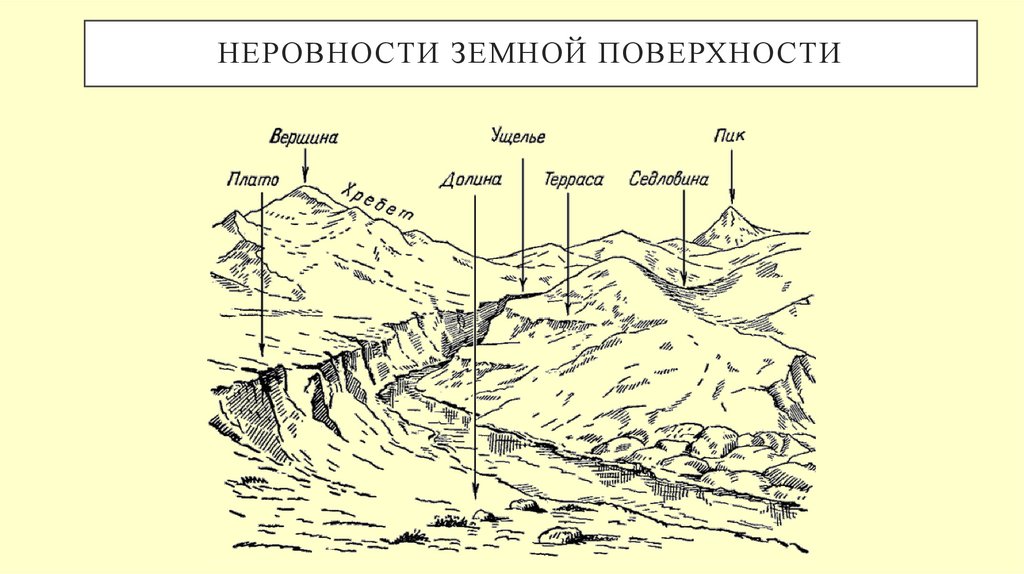
22. Неровности земной поверхности

НЕРОВНОСТИ ЗЕМНОЙ ПОВЕРХНОСТИ

23.

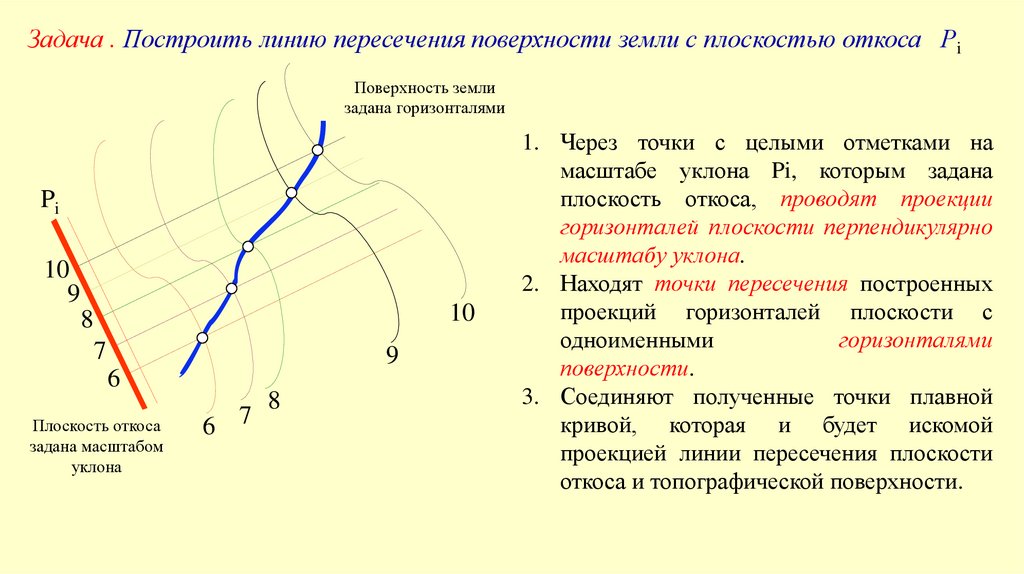
Задача . Построить линию пересечения поверхности земли с плоскостью откоса Рi
Поверхность земли
задана горизонталями
Pi
10
9
10
8
7
9
6
Плоскость откоса
задана масштабом
уклона
6 7
8
1. Через точки с целыми отметками на
масштабе уклона Pi, которым задана
плоскость откоса, проводят проекции
горизонталей плоскости перпендикулярно
масштабу уклона.
2. Находят точки пересечения построенных
проекций горизонталей плоскости с
одноименными
горизонталями
поверхности.
3. Соединяют полученные точки плавной
кривой, которая и будет искомой
проекцией линии пересечения плоскости
откоса и топографической поверхности.

24.

Вертикальная планировка участка
– это инженерная подготовка по искусственному изменению
существующего рельефа местности путем срезки и подсыпки
грунта, смягчения уклонов с целью оптимального
приспособления участка застройки для строительства объекта.
Результатом разработки грунта является земляное сооружение,
представляющее собой инженерное сооружение, устраиваемое из
грунта в грунтовом массиве или возводимое на поверхности грунта.
Земляные сооружения разделяют:
по отношению к поверхности грунта - выемки, насыпи, обратные
засыпки;
по функциональному назначению - котлованы, траншеи, ямы,
скважины, отвалы, плотины, дамбы, дорожные полотна, туннели,
планировочные площадки и пр.

25.

Для решения практических задач вертикальной планировки
решается вопрос пересечения топографической поверхности
(поверхности земли) с откосами проектируемой горизонтальной
площадки или дороги.
Откос – это плоскости и поверхности, ограничивающие
строительную площадку со всех сторон и соединяющие ее с
поверхностью местности.
Откосы всегда проектируются с определённым уклоном к плоскости
нулевого уровня, исходя из условий эксплуатации.
Граница откоса - линия пересечения откосов выемок и насыпей с
топографической поверхностью земли → граница земляных работ.
Определение границ земляных работ необходимо для
подсчета баланса земляных работ.

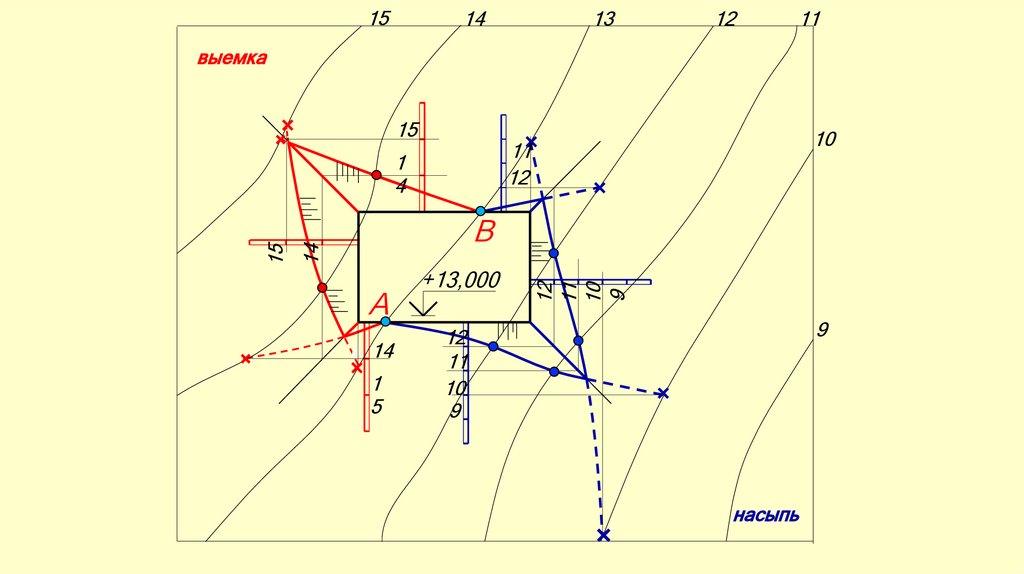
26. ОПРЕДЕЛЕНИЕ ГРАНИЦ ЗЕМЛЯНЫХ РАБОТ СТРОИТЕЛЬНОЙ ПЛОЩАДКИ

Задача: М 1:200
Задана топографическая поверхность и земляное сооружение (строительная
площадка).
На заданной топографической поверхности построить линию пересечения
откосов насыпи и выемки горизонтальной строительной площадки с
топографической поверхностью.
Уклон откосов выемок - 1:1,5;
Уклон откосов насыпей - 1:1.
Высотная отметка строительной площадки - +13.000
lн
lв

27.

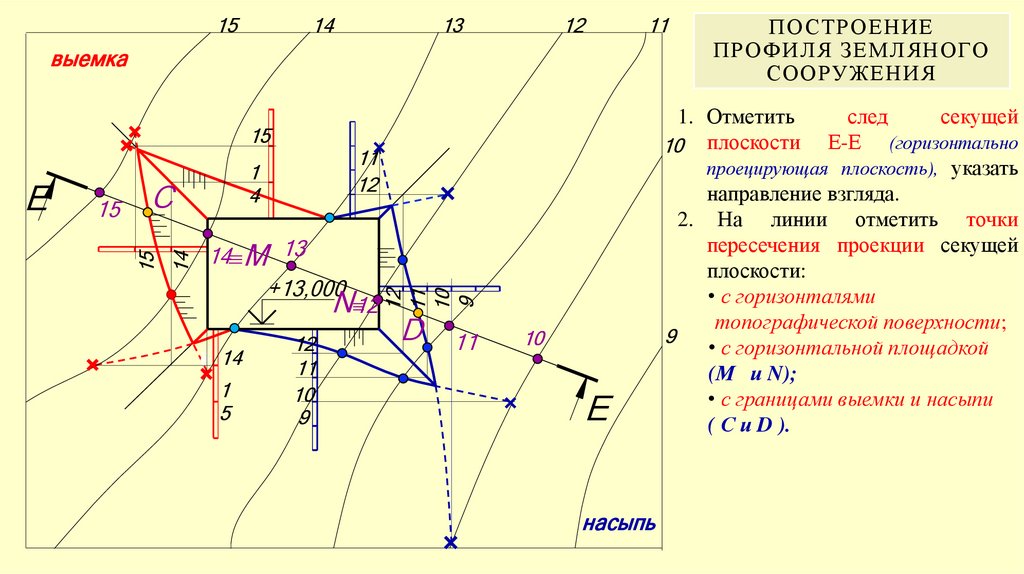
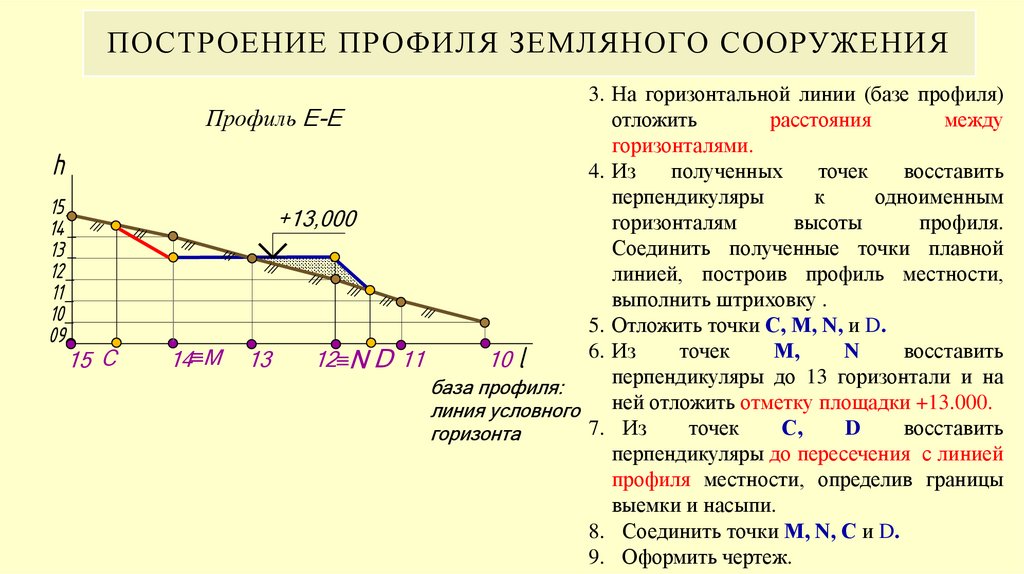
28. Порядок построения

ПОРЯДОК ПОСТРОЕНИЯ
1. Рассчитать величины интервалов