раздел_3, Л_1,2 (5,6)

1.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение
высшего профессионального образования
И.П. БОЛОДУРИНА,
Ю.П. ИВАНОВА
«Оренбургский
государственный
университет»
Кафедра прикладнойкурс
математики
Мультимедийный
лекций
по дисциплине «Математика»
Мультимедийный курс лекций по дисциплине «Математика» (МКЛМ) предназначен для
изучения теоретических основ математики студентами направлений подготовки не
имеющих математический уклон. МКЛМ содержит 13 теоретических тем, включающих
разделы линейной алгебры, элементов аналитической геометрии, математического
анализа, теории вероятностей, а также практические демонстративные примеры по
каждой теме. Возможности МКЛМ позволяют эффективно организовать как аудиторную,
так и самостоятельную работу студентов. Достоинствами МКЛМ являются комплексность
и последовательность в изложении материала курса. Четкая структуризация учебного
материала, его наглядное и компактное представление способствуют наиболее
эффективному восприятию и усвоению его содержания.
Оренбург, 2014

2. Раздел 3 Элементы векторной алгебры и аналитической геометрии

Лекции 3.1, 3.2(5,6)
Основные понятия векторной алгебры
3.1.1 Определения основных объектов векторной
алгебры. Геометрическая модель вектора
3.1.2 Проекция вектора на ось.
Аналитическая модель вектора
3.1.3 Линейные операции над геометрическими и
аналитическими векторами, их свойства
3.1.4 Нелинейные операции над геометрическими и
аналитическими векторами, их свойства

3. 3.1.1 Определения основных объектов векторной алгебры

Вектором называется направленный отрезок
Обозначение вектора:
АВ, a
АВ , a - длина вектора
Вектор, длина которого равна единице
называется единичным вектором

4. 3.1.1 Определения основных объектов векторной алгебры

Единичный вектор, направление которого
совпадает с направлением вектора a называется
ортом вектора a и обозначается a 0
a a a
0
Три вектора в пространстве называются
компланарными, если они лежат в одной плоскости
или в параллельных плоскостях
коллинеарных векторов
a // b 0 : a b

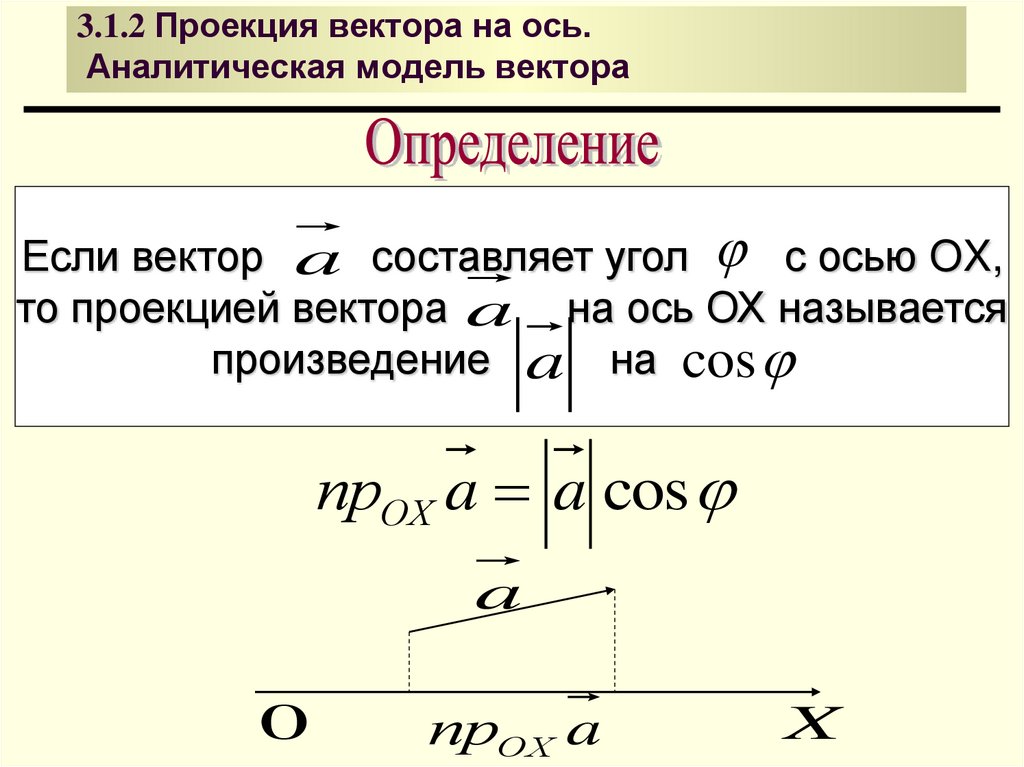
5. 3.1.2 Проекция вектора на ось. Аналитическая модель вектора

Если вектор a составляет угол с осью OX,
то проекцией вектора a на ось ОХ называется
произведение a на cos
прОХ a a cos
a
0
прОХ a
X

6. 3.1.2 Проекция вектора на ось. Аналитическая модель вектора

Рассмотрим в 3-х-мерном пространстве
прямоугольную систему координат Oxyz.
Пусть i, j , k- единичные векторы, направление
которых совпадает с положительными
направлениями координатных осей OX, OY, OZ
соответственно
Углы, образованные
вектором a с
осями координат
обозначим:
, ,

7. 3.1.2 Проекция вектора на ось. Аналитическая модель вектора

Проекции вектора a на оси координат
x a cos y a cos z a cos
Вектор a имеет координаты x, y, z, то есть
a ( x, y, z ) в прямоугольной системе
координат ОXYZ или a xi y j z k , где
i, j , k - единичные векторы координатных осей
a x y z - длина вектора a
cos , cos , cos - направляющие косинусы
вектора a : cos 2 cos 2 cos 2 1
2
2
2

8. 3.1.3 Линейные операции над геометрическими и аналитическими векторами, их свойства

Действия сложения векторов a b
и
умножения вектора на число a называются
линейными операциями над векторами

9. 3.2.1 Скалярное произведение векторов

Скалярным произведением геометрических
векторов называется число, равное произведению
длин этих векторов на косинус угла между ними
a, b a b cos(a, b) a Пр b b Пр a
a
b

10. 3.2.1 Скалярное произведение векторов

Свойства скалярного произведения векторов

11. 3.2.1 Скалярное произведение векторов Скалярное произведение аналитических векторов

a,b x x y y z z .
1
2
1
2
1
2

12. 3.2.1 Скалярное произведение векторов Приложения скалярного произведения векторов

Геометрическая модель
вектора
Аналитическая модель
вектора

13. 3.2.2 Векторное произведение векторов

Векторным произведением векторов a и b
называется новый вектор E a b , который:
1. ортогонален векторам a и b
2. имеет длину, численно равную площади
параллелограмма, построенного на векторах a
и b как на сторонах: E a b sin где (a, b)
3. E направлен так, что если смотреть с его
конца, то поворот от a к b по кратчайшему
углу виден против часовой стрелки

14. 3.2.2 Векторное произведение векторов

Обозначение векторного произведения
a
,
b
a b или
Свойства векторного произведения
a b b a
a b 0 a // b
a, b,
a b a b a b
a b c a c b c

15. 3.2.2 Векторное произведение векторов

Соотношения между ортами
i j k
j i k
j j 0
k i j
k j i
i k j
j k i
k k 0
i i 0

16. 3.2.2 Векторное произведение векторов

Пусть заданы два вектора
a ax i a y j az k
b bx i by j bz k
Выражение векторного произведения
через координаты
a b ax i a y j az k bx i by j bz k
ay
by
az
ax
i
bz
bx
i
a b ax
bx
j
ay
by
ax
az
j
bz
bx
k
az
bz
ay
k
by

17. 3.2.2 Векторное произведение векторов

i
j
a // b a b 0 a x a y
bx b y
k
ax a y az
az 0
bx by bz
bz
S a b
- площадь параллелограмма
1
S a b
2
- площадь треугольника

18. 3.2.3 Смешанное произведение векторов

Рассмотрим произведение векторов a, b и
составленное следующим образом:
c,
a b c a b c
Первые два вектора a, b перемножаются векторно,
а их результат скалярно умножается на вектор c
Такое произведение называется
смешанным произведением векторов
ОБОЗНАЧЕНИЕ
a b c
В результате смешанного произведения получается
число

19. 3.2.3 Смешанное произведение векторов Геометрический смысл смешанного произведения векторов

a b c E c E пр c V
E
пар да
Смешанное произведение трех векторов равно объему
параллелепипеда, построенного на этих векторах
Vпар да a b c

20. 3.2.3 Смешанное произведение векторов Свойства смешанного произведения векторов

Смешанное произведение не меняется при
циклической перестановке его сомножителей
a b c c a b b c a
Смешанное произведение не меняется при
перемене местами скалярного умножения
a b c a b c

21. 3.2.3 Смешанное произведение векторов Свойства смешанного произведения векторов

Если
a b c 0 , то a, b, c - компланарны
Выражение смешанного произведения
через координаты векторов - сомножителей
ax
a b c bx
cx
ay
by
cy
az
bz
cz

22. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1) Что представляют собой геометрическая и аналитическая
модели вектора?
2) Определить линейные операции над векторами и
сформулировать их свойства.
3) Дать определение линейно зависимых / независимых векторов.
4) Дать определение скалярного произведения векторов,
сформулировать
свойства
скалярного
произведения
геометрических и аналитических векторов.
5) Дать определение векторного произведения двух векторов,
сформулировать его свойства и координатное представление.
6) Дать определение смешанного произведения векторов,
сформулировать его свойства и координатное представление.