Similar presentations:
080_Рекурсия
1. РЕКУРСИВНЫЕ АЛГОРИТМЫ
12.
Рекурсивные определения□ Рекурсивными определениями называют
определения объектов, которые содержат в
себе ссылку на сам определяемый объект.
□ Рекурсия - это способ определения
объектов (понятий), при котором определение
объекта строится, опираясь на само понятие
объекта.
2
3.
Рекурсия в различных областях творчестваПримеры из литературы
стихи
проза
афоризмы
Стихи про попа и собаку,
У попа была собака,
Он ее любил.
Она съела кусок мяса,
Он ее убил!
В землю закопал,
Надпись написал, что:
"У попа была собака,
Он ее любил,
Она съела кусок мяса,
Он ее убил….".
В каждой шутке есть доля шутки
Стихи про негритят.
Десять негритят решили пообедать,
Один вдруг поперхнулся — их осталось девять.
Девять негритят, поев, клевали носом,
Один не смог проснуться — их осталось восемь.
Восемь негритят в Девон ушли пото́ м,
Один не возвратился — остались всемером.
Семь негритят дрова рубили вместе,
Зарубил один себя — и осталось шесть их.
Шесть негритят пошли на пасеку гулять,
Одного ужалил шмель — их осталось пять.
Пять негритят судейство учинили,
Засудили одного, осталось их четыре.
Четыре негритёнка пошли купаться в море,
Один попался на приманку — их осталось трое.
Трое негритят в зверинце оказались,
Одного схватил медведь — и вдвоём остались.
Двое негритят легли на солнцепёке,
Один сгорел — и вот один, несчастный, одинокий.
Последний негритёнок поглядел устало,
пошёл повесился, и никого не стало.
3
4.
Рекурсия в различных областях творчестваПримеры из изобразительного искусства
Картины
Эшера
(M.C.Escher)
4
5.
Рекурсия в различных областях творчестваПримеры из изобразительного искусства
Картины Hokusai
5
6.
Рекурсия в различных областях творчестваПримеры из изобразительного искусства
Рекламные плакаты и
постеры
6
7.
Рекурсия в различных областях творчестваПримеры из изобразительного искусства
Русские матрешки
7
8.
Рекурсия в физике8
9.
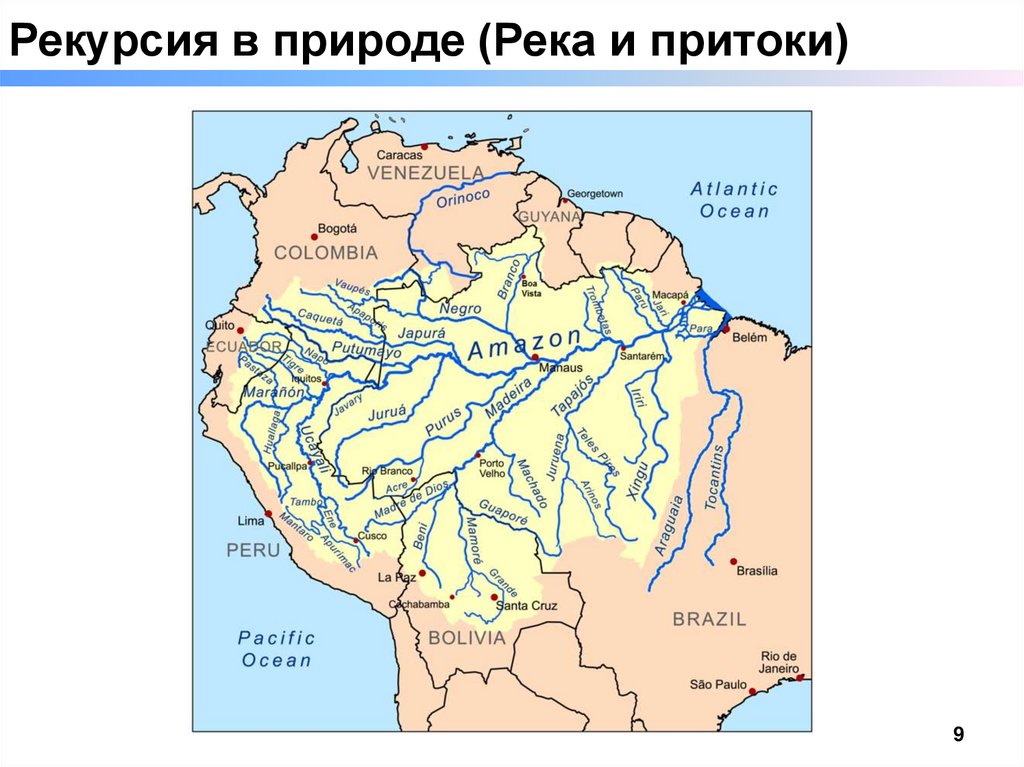
Рекурсия в природе (Река и притоки)9
10.
Рекурсия в природе (дерево его ветви)10
11.
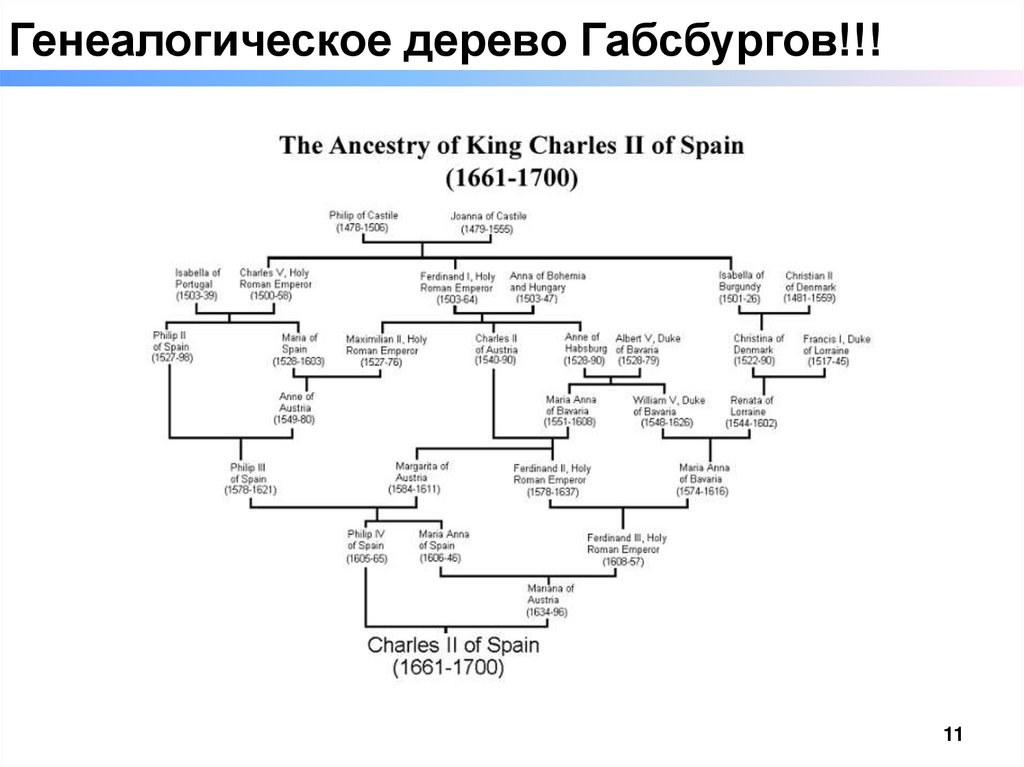
Генеалогическое дерево Габсбургов!!!11
12.
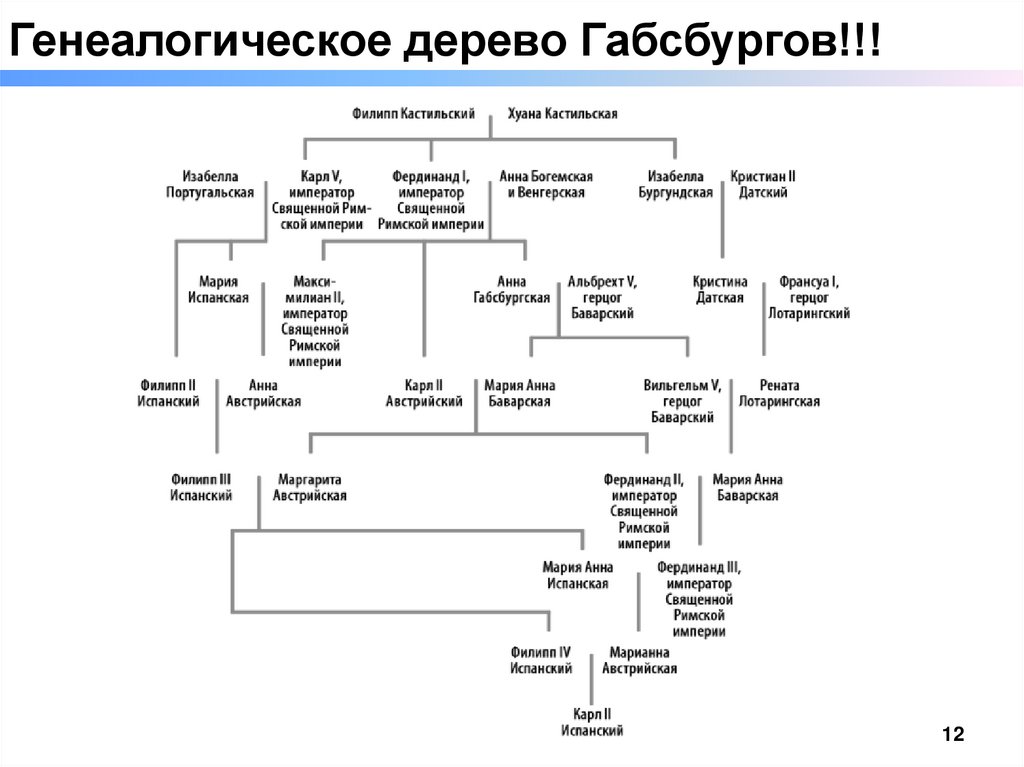
Генеалогическое дерево Габсбургов!!!12
13.
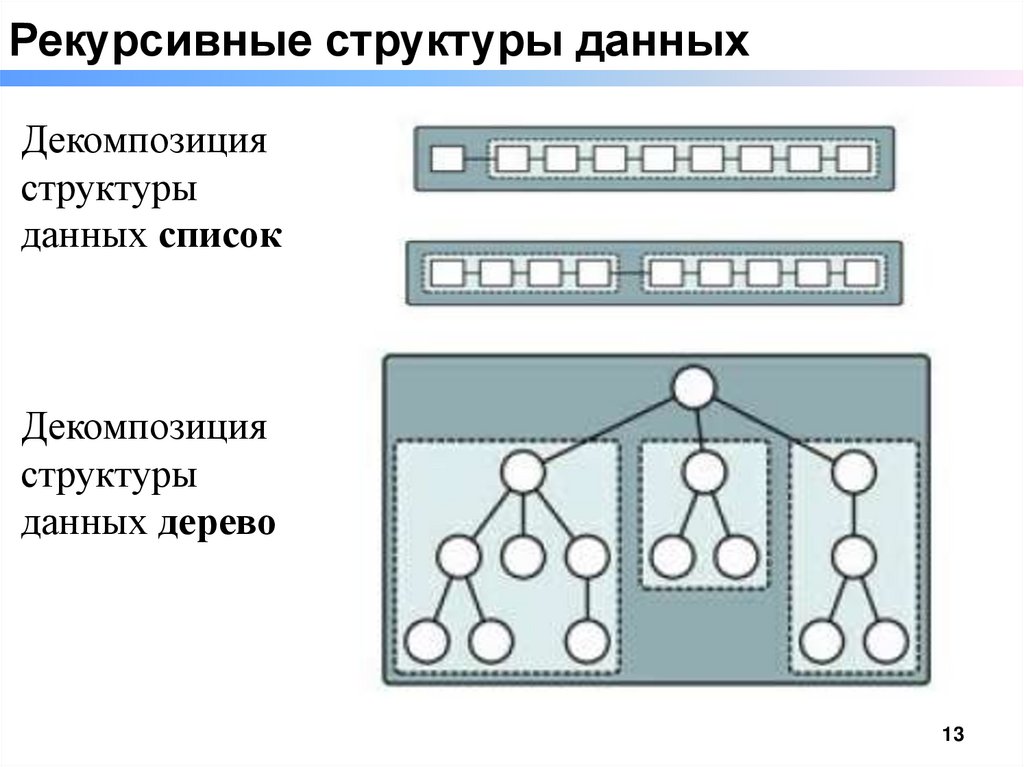
Рекурсивные структуры данныхДекомпозиция
структуры
данных список
Декомпозиция
структуры
данных дерево
13
14.
Рекурсия в математикеРекурсивное определение факториала
1, n 0
f ( n)
n f(n - 1), n 0
Рекурсивное определение чисел Фибоначчи
0, n 0
f (n) 1, n 1
f (n 1) f (n 2), n 2
Рекурсивное определение простых чисел
- 2, наименьшее простое;
- каждое положительное число, которые не делится ни на
одно из простых меньше себя.
14
15.
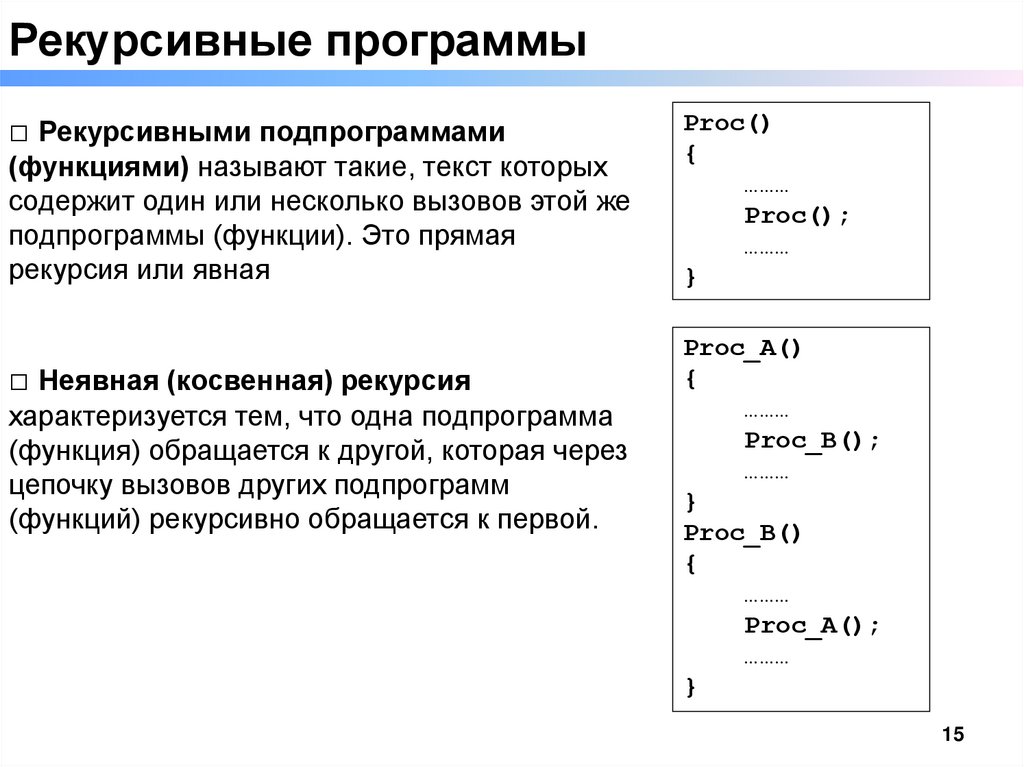
Рекурсивные программы□ Рекурсивными подпрограммами
(функциями) называют такие, текст которых
содержит один или несколько вызовов этой же
подпрограммы (функции). Это прямая
рекурсия или явная
□ Неявная (косвенная) рекурсия
характеризуется тем, что одна подпрограмма
(функция) обращается к другой, которая через
цепочку вызовов других подпрограмм
(функций) рекурсивно обращается к первой.
Proc()
{
………
Proc();
………
}
Proc_A()
{
………
Proc_B();
………
}
Proc_B()
{
………
Proc_A();
………
}
15
16.
Рекурсивные программы□ Пример. Вычисление факториала
int FACT(int K)
{
IF( K > 1 ) THEN RETURN (K*FACT(K-1)); - рекурсивная ветвь
ELSE RETURN (1); - не рекурсивная ветвь (самая глубокая)
};
□ Пример. Вычисление чисел Фиббоначи
INT FIBON(INT K)
{
IF (K==0)||( K==1 ) RETURN 1; - не рекурсивная ветвь
RETURN FIBON(K-2)+FIBON(K-1); - рекурсивная ветвь
}
16
17.
Методика решения рекурсивной задачи□ Параметризация задачи: выделяются все элементы, от которых
зависит решение, и в частности размерность задачи.
□ Поиск тривиального случая и его решение. Тривиальный случай –
ключевой этап, который может быть решён без рекурсии. При этом
размерность задачи в большинстве случаев равна 1 или 0.
□ Декомпозиция общего случая, имеющая целью свести его к одному
из нескольких более простых случаев (меньшей размерности).
17
18.
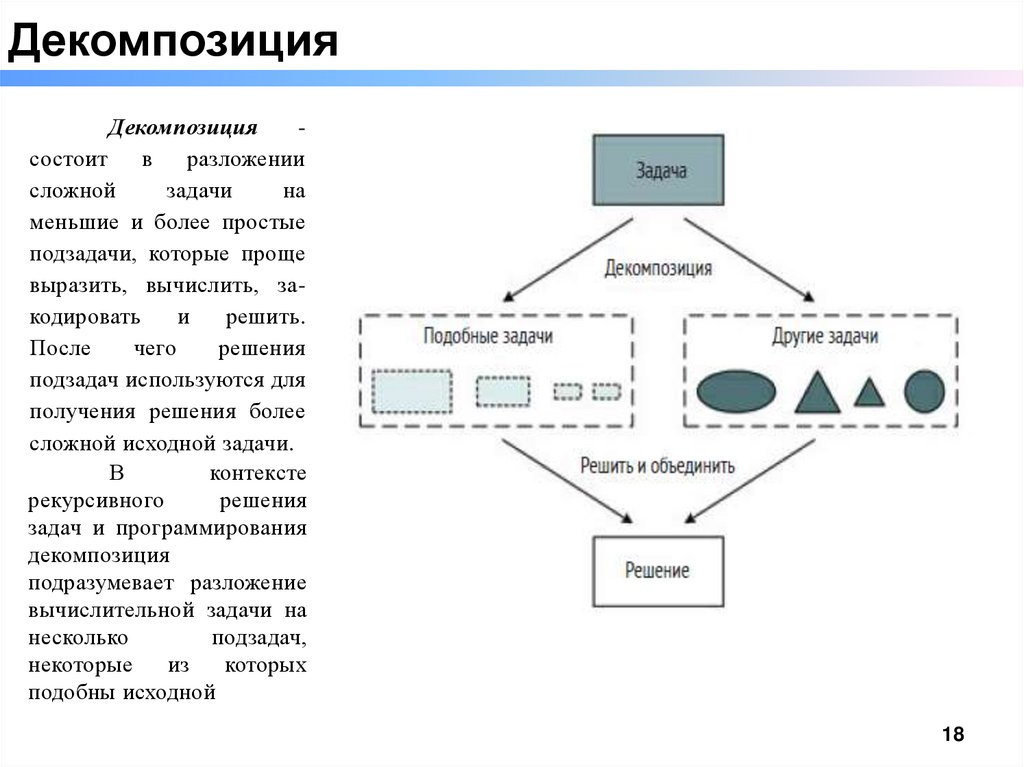
ДекомпозицияДекомпозиция
состоит
в
разложении
сложной
задачи
на
меньшие и более простые
подзадачи, которые проще
выразить, вычислить, закодировать
и
решить.
После
чего
решения
подзадач используются для
получения решения более
сложной исходной задачи.
В
контексте
рекурсивного
решения
задач и программирования
декомпозиция
подразумевает разложение
вычислительной задачи на
несколько
подзадач,
некоторые
из
которых
подобны исходной
18
19.
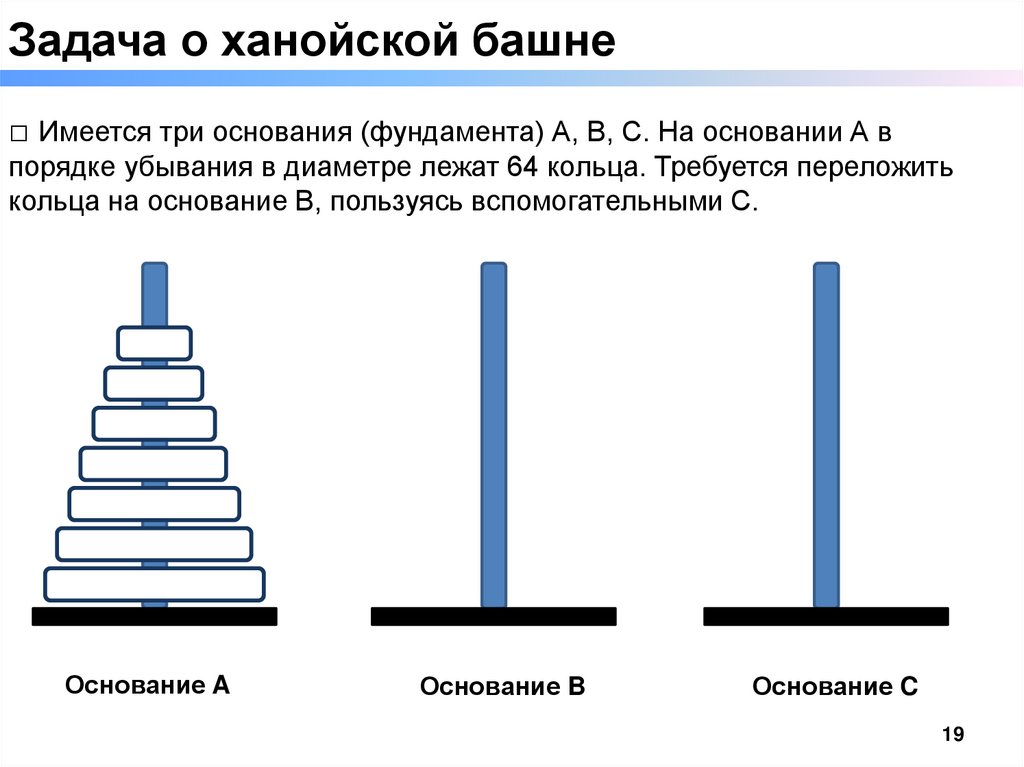
Задача о ханойской башне□ Имеется три основания (фундамента) А, В, С. На основании А в
порядке убывания в диаметре лежат 64 кольца. Требуется переложить
кольца на основание В, пользуясь вспомогательными С.
Основание A
Основание B
Основание C
19
20.
Задача о ханойской башне1
2
3
4
A B C
Этап 1
1
2
4 3
A B C
Этап 9
2
3
4
1
A B C
Этап 2
1 2
4 3
A B C
Этап 10
3
4 2 1
A B C
Этап 3
1
2 4 3
A B C
Этап 11
3 1
4 2
A B C
Этап 4
1
4 2 3
A B C
Этап 5
1
2 4 3
A B C
Этап 12
1
4 2 3
A B C
Этап 6
1 3
2 4
A B C
Этап 13
1
2
4
3
A B C
Этап 7
3
2 4 1
A B C
Этап 14
1
2
4
3
A B C
Этап 8
1
2
4 3
A B C
Этап 9
2
3
4 1
A B C
Этап 15
1
2
3
4
A B C
Этап 16
20
21.
Задача о ханойской башне□ Пусть требуется написать программу, решающую задачу о
ханойской башне. Решение выдается в виде списка
инструкций:
→
▬ «A
B» – пересылка верхнего кольца с основания A на
основание B.
21
22.
Задача о ханойской башне□ Первый этап – «Параметризация»:
22
23.
Задача о ханойской башне□ Первый этап – «Параметризация»:
HANOY (n, x, y, z)
▬ «n» – количество колец, которые надо перенести.
▬ «x» – начальное основание.
▬ «y» – конечное основание.
▬ «z» – вспомогательное основание.
23
24.
Задача о ханойской башне□ Первый этап – «Параметризация»:
HANOY (n, x, y, z)
▬ «n» – количество колец, которые надо перенести.
▬ «x» – начальное основание.
▬ «y» – конечное основание.
▬ «z» – вспомогательное основание.
□ Второй этап – «Поиск тривиального случая»:
24
25.
Задача о ханойской башне□ Первый этап – «Параметризация»:
HANOY (n, x, y, z)
▬ «n» – количество колец, которые надо перенести.
▬ «x» – начальное основание.
▬ «y» – конечное основание.
▬ «z» – вспомогательное основание.
□ Второй этап – «Поиск тривиального случая»:
▬ «n = 0» – ничего делать не надо.
▬ «n = 1» – выводим инструкцию x → y.
25
26.
Задача о ханойской башне□ Первый этап – «Параметризация»:
HANOY (n, x, y, z)
▬ «n» – количество колец, которые надо перенести.
▬ «x» – начальное основание.
▬ «y» – конечное основание.
▬ «z» – вспомогательное основание.
□ Второй этап – «Поиск тривиального случая»:
▬ «n = 0» – ничего делать не надо.
▬ «n = 1» – выводим инструкцию x → y.
□ Третий этап – «Редукция»:
26
27.
Задача о ханойской башне□ Первый этап – «Параметризация»:
HANOY (n, x, y, z)
▬ «n» – количество колец, которые надо перенести.
▬ «x» – начальное основание.
▬ «y» – конечное основание.
▬ «z» – вспомогательное основание.
□ Второй этап – «Поиск тривиального случая»:
▬ «n = 0» – ничего делать не надо.
▬ «n = 1» – выводим инструкцию x → y.
□ Третий этап – «Редукция»:
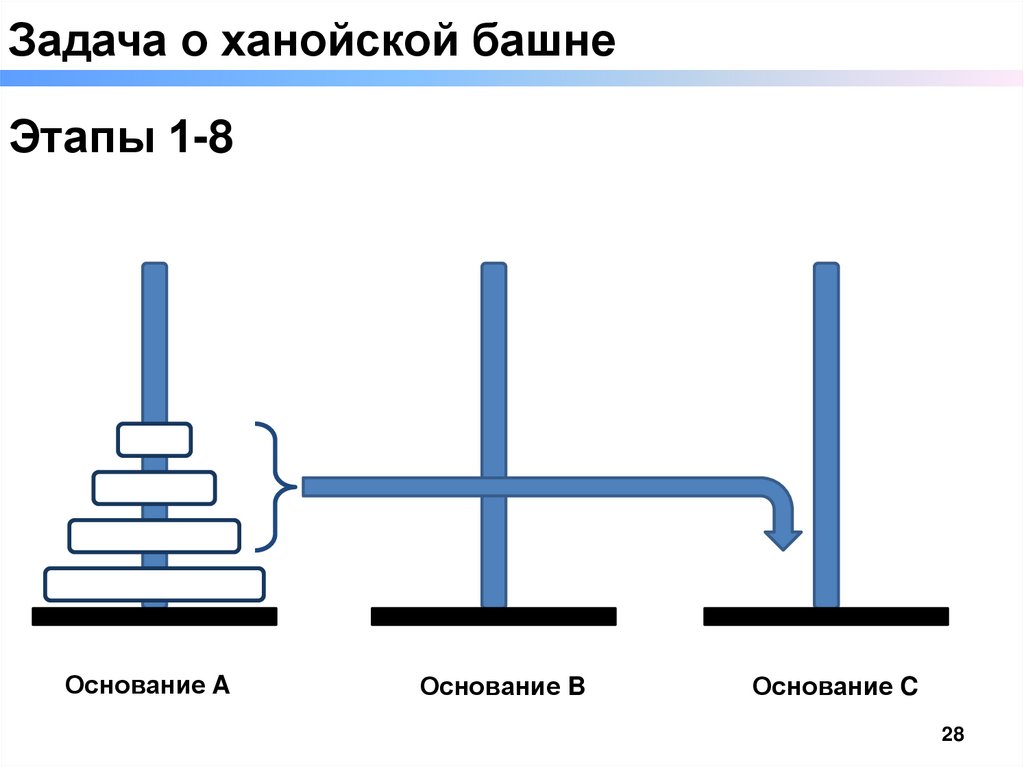
▬ переложить «n -1» кольцо с основания x на основание z. Этап «1 - 8»
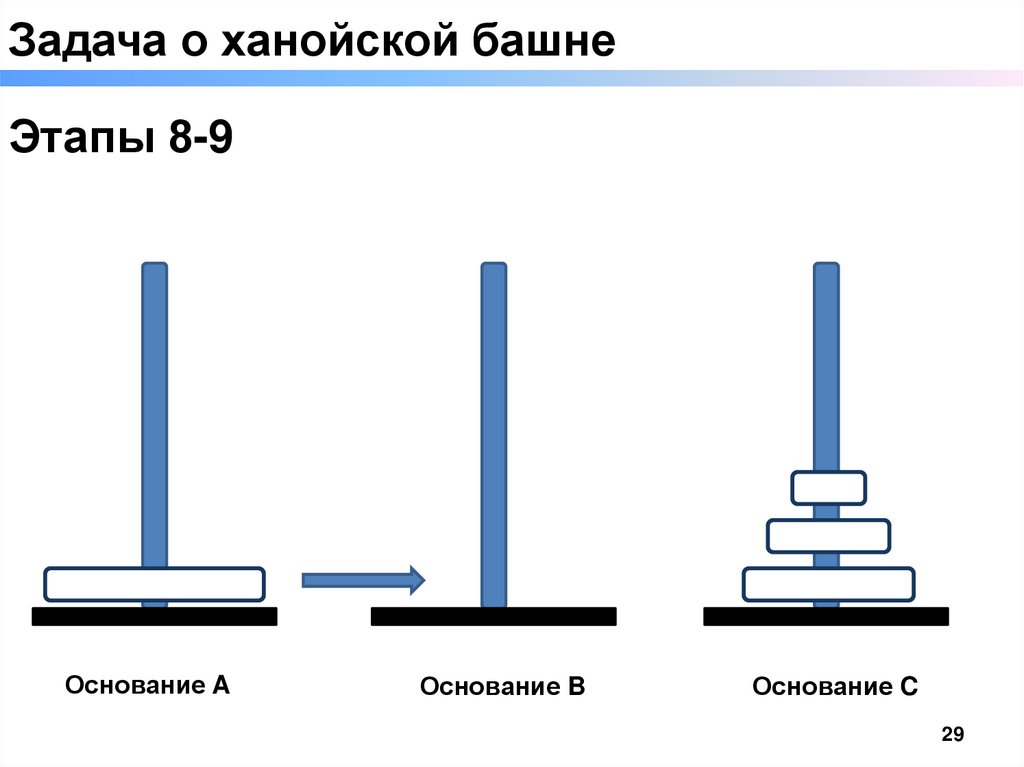
▬ переложить «1» кольцо с основания x на основание y. Этап «8 - 9»
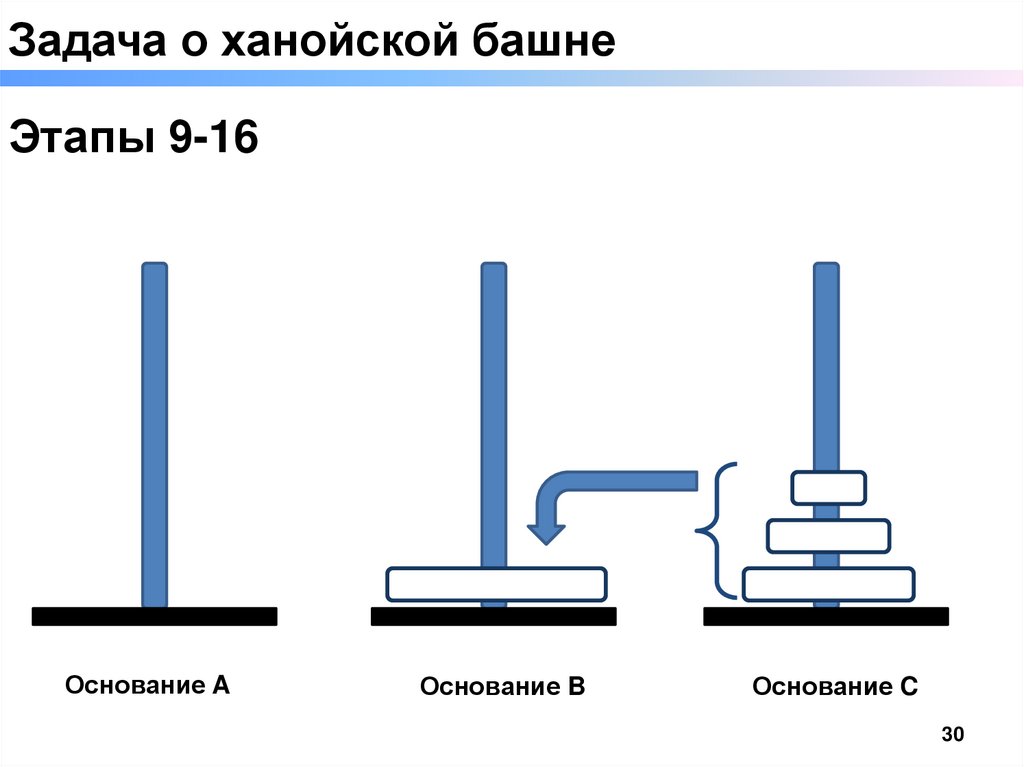
▬ переложить «n -1» кольцо с основания z на основание y. Этап «9 - 16»
27
28.
Задача о ханойской башнеЭтапы 1-8
Основание A
Основание B
Основание C
28
29.
Задача о ханойской башнеЭтапы 8-9
Основание A
Основание B
Основание C
29
30.
Задача о ханойской башнеЭтапы 9-16
Основание A
Основание B
Основание C
30
31.
Задача о ханойской башнеАлгоритм
HANOY (n, x, y, z)
{
if (n > 0) then
{
HANOY (n-1, x, z, y)
print(x, “->”, y)
HANOY (n-1, z, y, x)
}
else return;
}
31
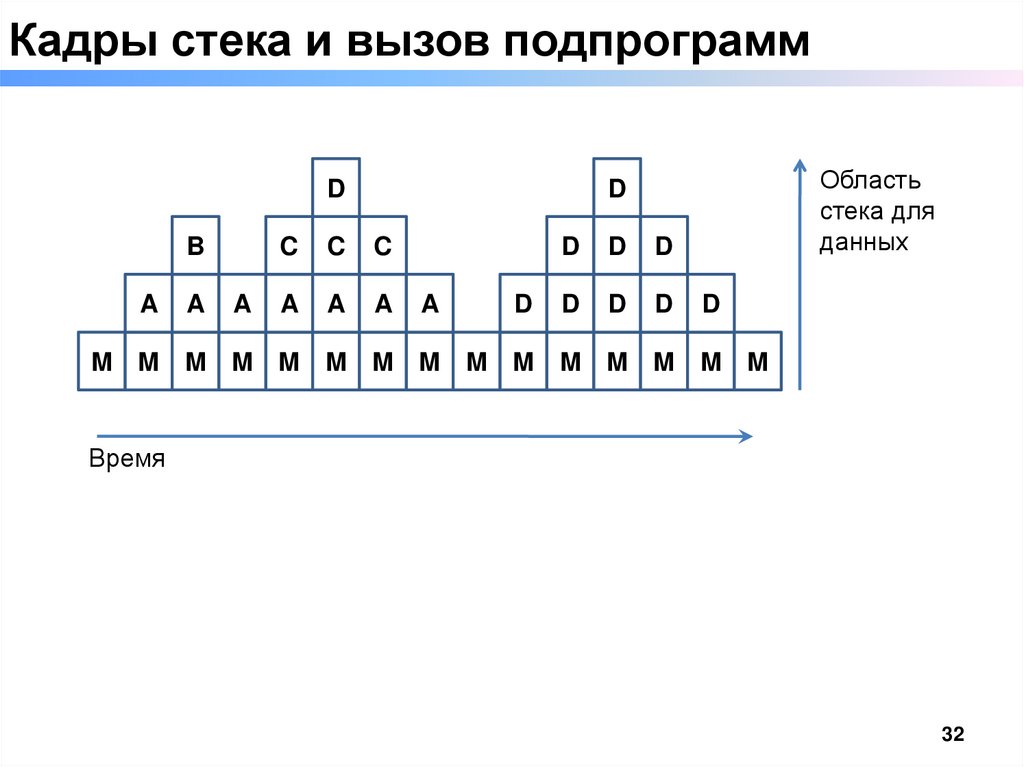
32.
Кадры стека и вызов подпрограммD
B
A
A
A
Область
стека для
данных
D
C
C
C
A
A
A
A
D
D
D
D
D
D
D
D
M M M M M M M M M M M M M M M
Время
32
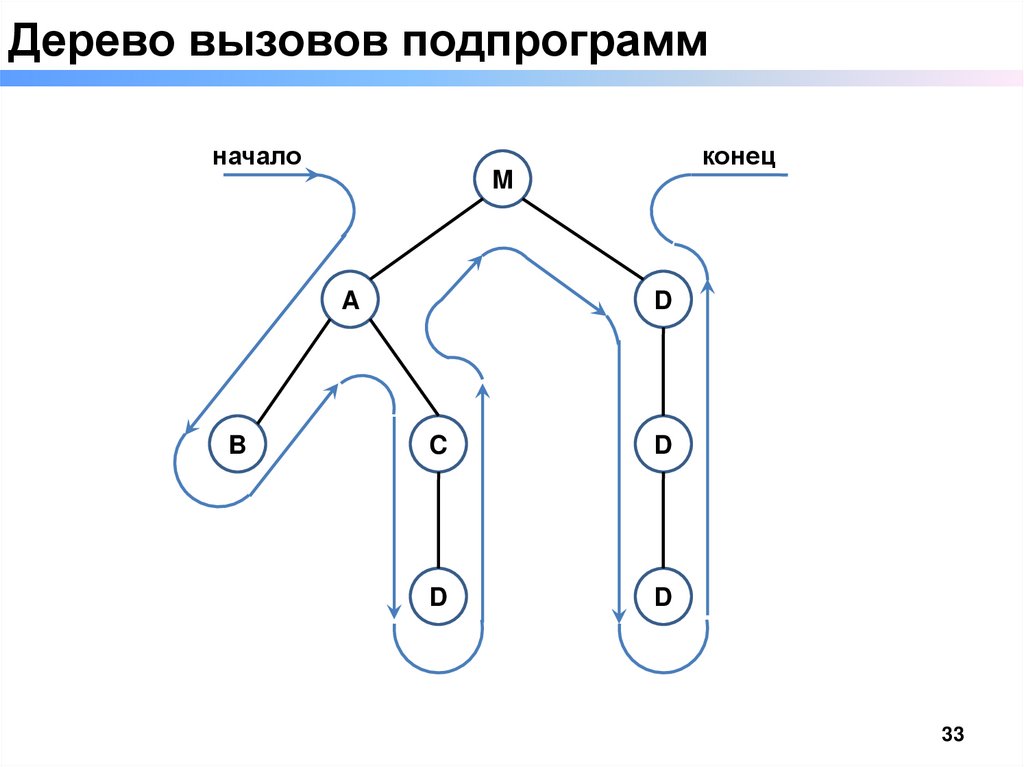
33.
Дерево вызовов подпрограммначало
M
A
B
конец
D
C
D
D
D
33
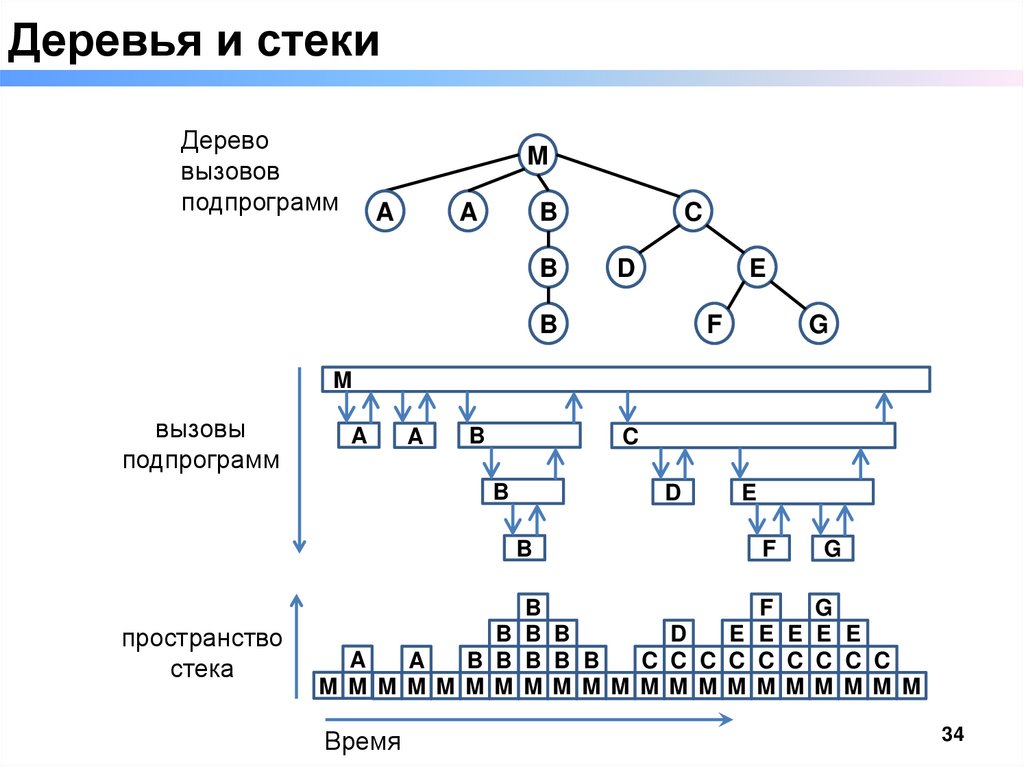
34.
Деревья и стекиДерево
вызовов
подпрограмм
M
A
A
B
B
C
D
E
B
F
G
M
вызовы
подпрограмм
A
A
B
C
B
D
B
пространство
стека
E
F
G
B
F
G
B B B
D
E E E E E
A
C C C C C C C C C
A
B B B B B
M M M M M M M M M M M M M M M M M M M M M
Время
34
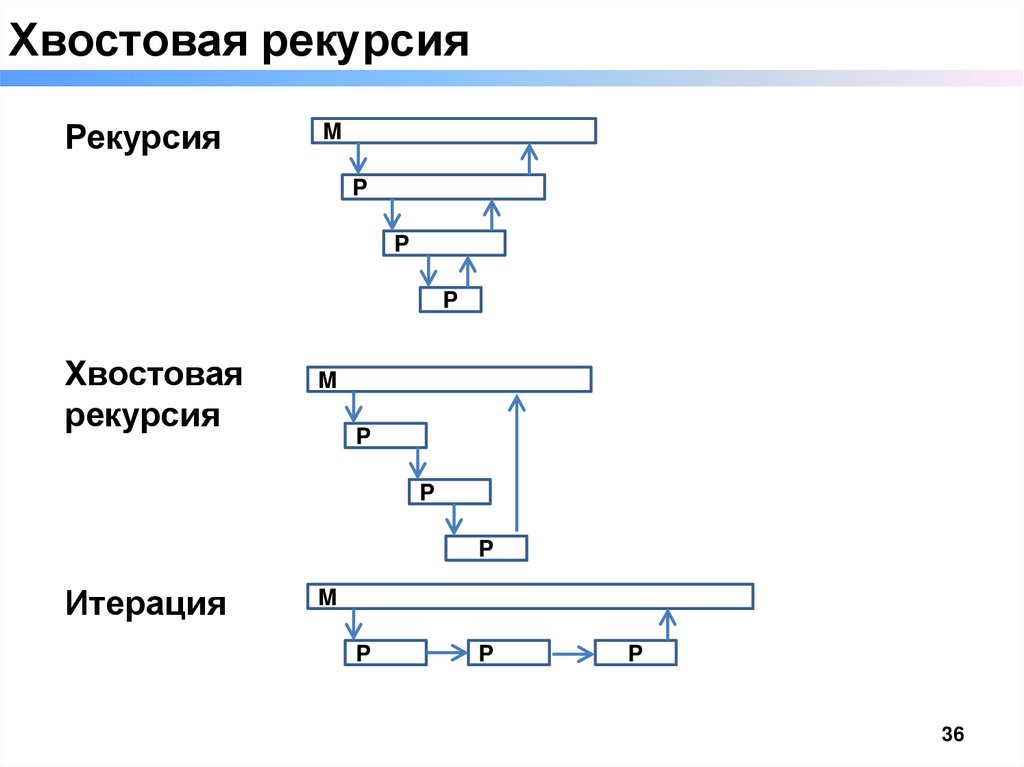
35.
Хвостовая рекурсия□ Хвостовая рекурсия — специальный случай рекурсии, при котором
рекурсивный вызов функцией самой себя является её последней
операцией.
int FACT(int K)
{
IF( K > 1 ) THEN RETURN (K*FACT(K-1));
ELSE RETURN (1);
};
int FACT(int K)
{
rez = 1;
for(i = K ; i > 1 ; i--)
{
rez = rez * i;
}
return rez;
};
35
36.
Хвостовая рекурсияРекурсия
M
P
P
P
Хвостовая
рекурсия
M
P
P
P
Итерация
M
P
P
P
36
37.
Рекурсия и прохождение деревьев□ Любой алгоритм, оперирующий с данными, явно или не
явно, организованными в виде дерева совершает обход
вершин этого дерева, начиная с корня в некотором порядке.
□ Алгоритмы прохождения деревьев делятся на 2 вида:
- прохождение дерева в глубину
- прохождение дерева в ширину
37
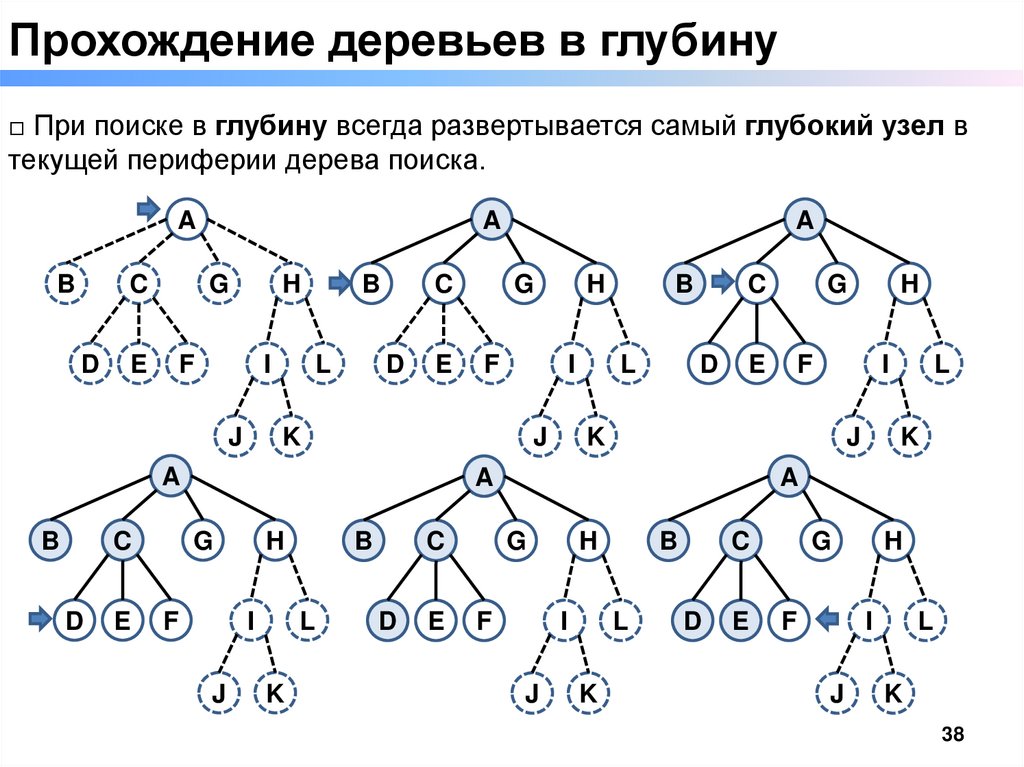
38.
Прохождение деревьев в глубину□ При поиске в глубину всегда развертывается самый глубокий узел в
текущей периферии дерева поиска.
A
B
C
D
A
G
E
H
F
I
J
B
L
C
D
E
C
D
E
G
H
F
I
K
J
A
B
A
B
L
C
D
E
F
H
I
J
B
L
K
C
D
E
H
F
I
K
J
A
G
G
L
K
A
G
F
H
I
J
B
L
K
C
D
E
G
F
H
I
J
L
K
38
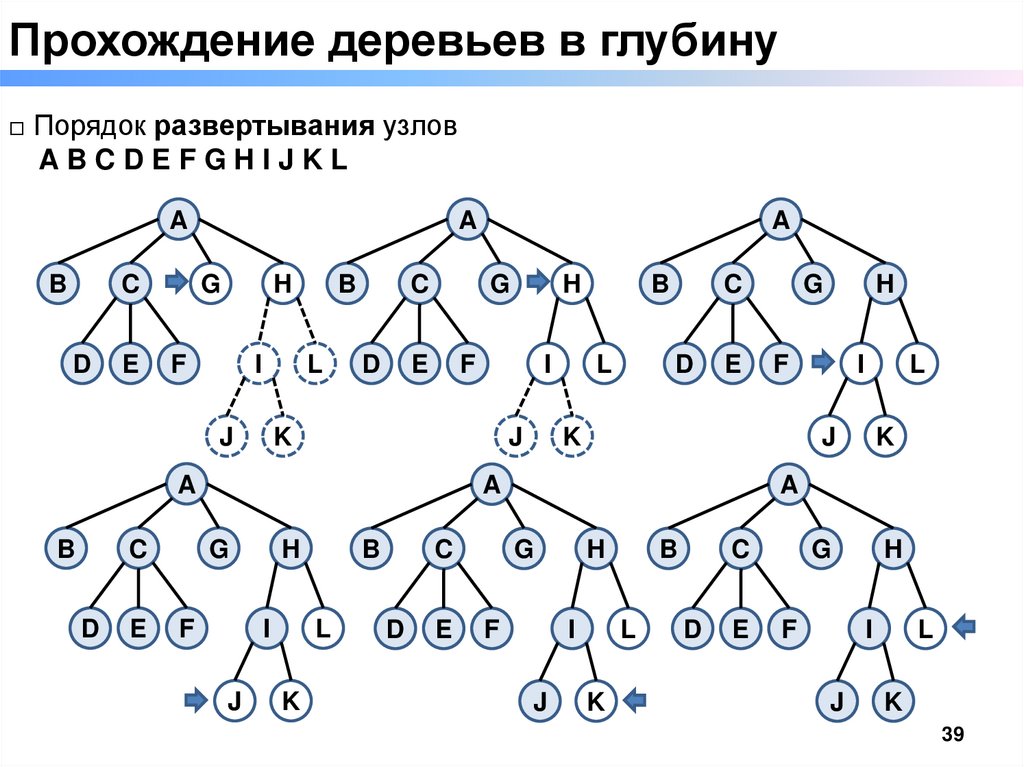
39.
Прохождение деревьев в глубину□ Порядок развертывания узлов
ABCDEFGHIJKL
A
B
C
D
E
A
G
H
F
I
B
L
J
C
D
G
E
C
D
E
H
F
I
K
J
A
B
A
B
L
C
D
E
F
H
I
J
B
L
K
C
D
E
H
F
K
A
G
G
I
L
J
K
G
H
A
G
F
H
I
J
B
L
K
C
D
E
F
I
J
L
K
39
40.
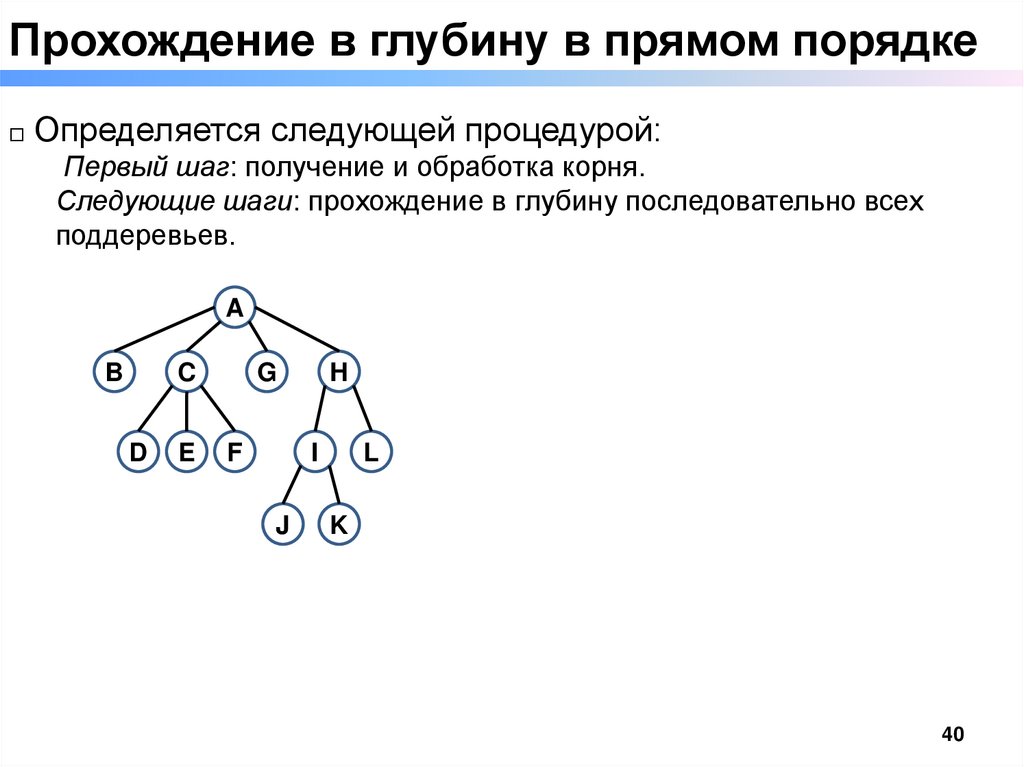
Прохождение в глубину в прямом порядке□ Определяется следующей процедурой:
Первый шаг: получение и обработка корня.
Следующие шаги: прохождение в глубину последовательно всех
поддеревьев.
A
B
C
D
E
G
F
H
I
J
L
K
40
41.
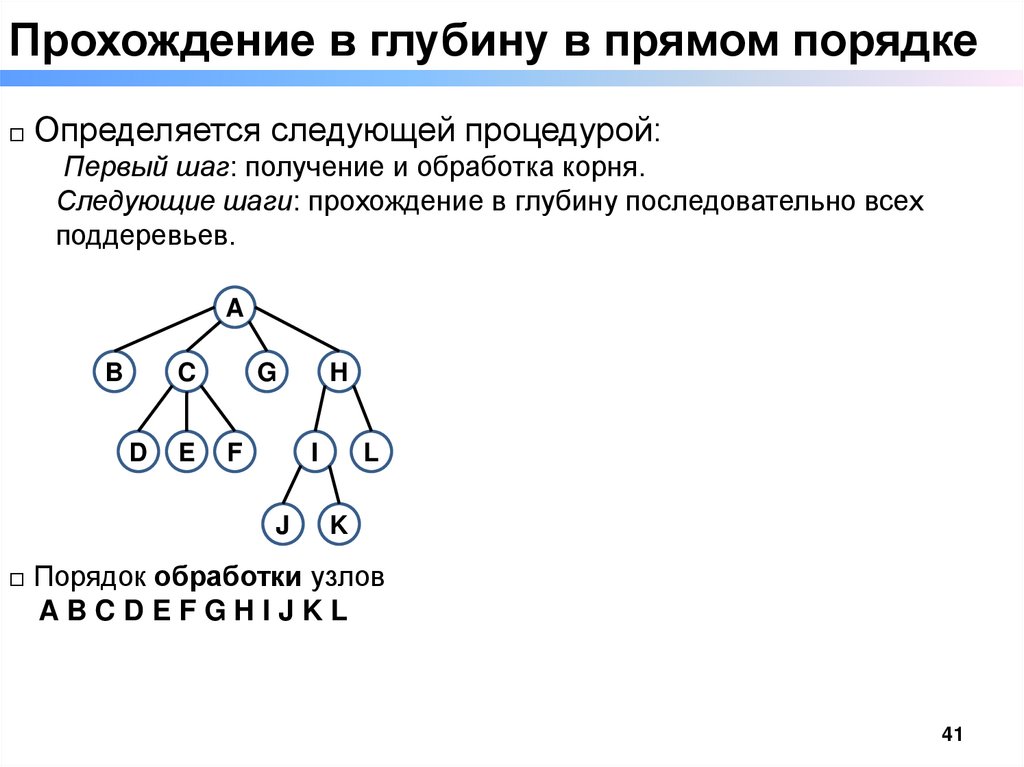
Прохождение в глубину в прямом порядке□ Определяется следующей процедурой:
Первый шаг: получение и обработка корня.
Следующие шаги: прохождение в глубину последовательно всех
поддеревьев.
A
B
C
D
E
G
F
H
I
J
L
K
□ Порядок обработки узлов
ABCDEFGHIJKL
41
42.
Прохождение в глубину в обратном порядке□ Прохождение в глубину в обратном порядке.
Начальные шаги: пройти в глубину последовательно все поддеревья.
Последний шаг: посетить корень и его обработать.
42
43.
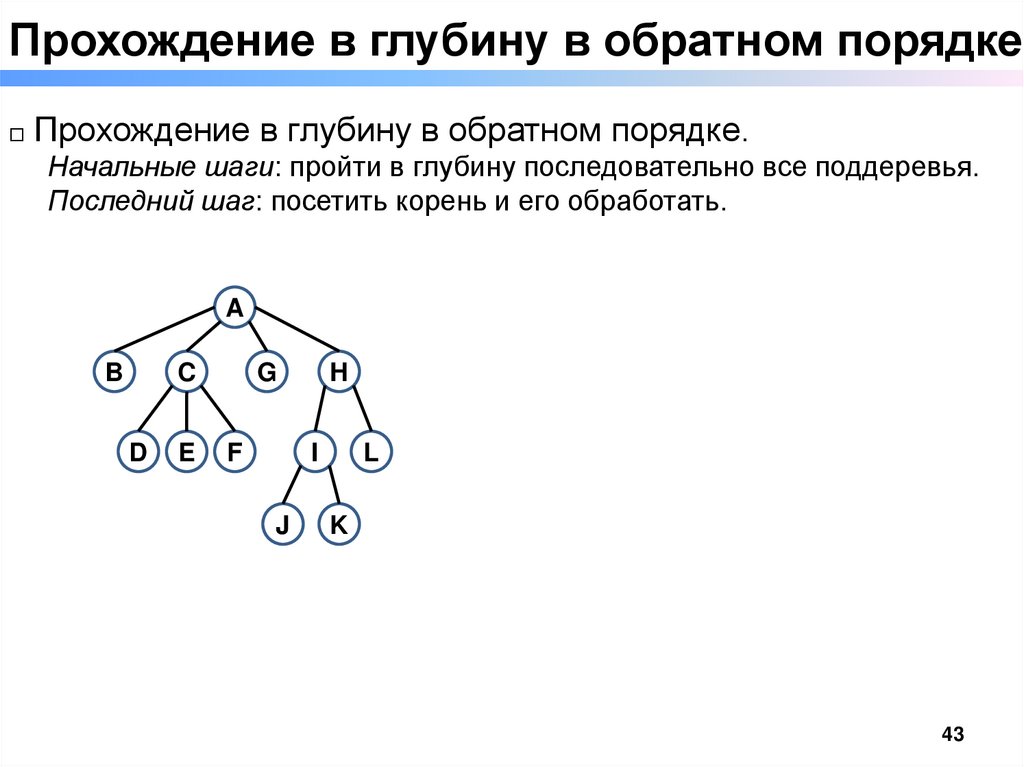
Прохождение в глубину в обратном порядке□ Прохождение в глубину в обратном порядке.
Начальные шаги: пройти в глубину последовательно все поддеревья.
Последний шаг: посетить корень и его обработать.
A
B
C
D
E
G
F
H
I
J
L
K
43
44.
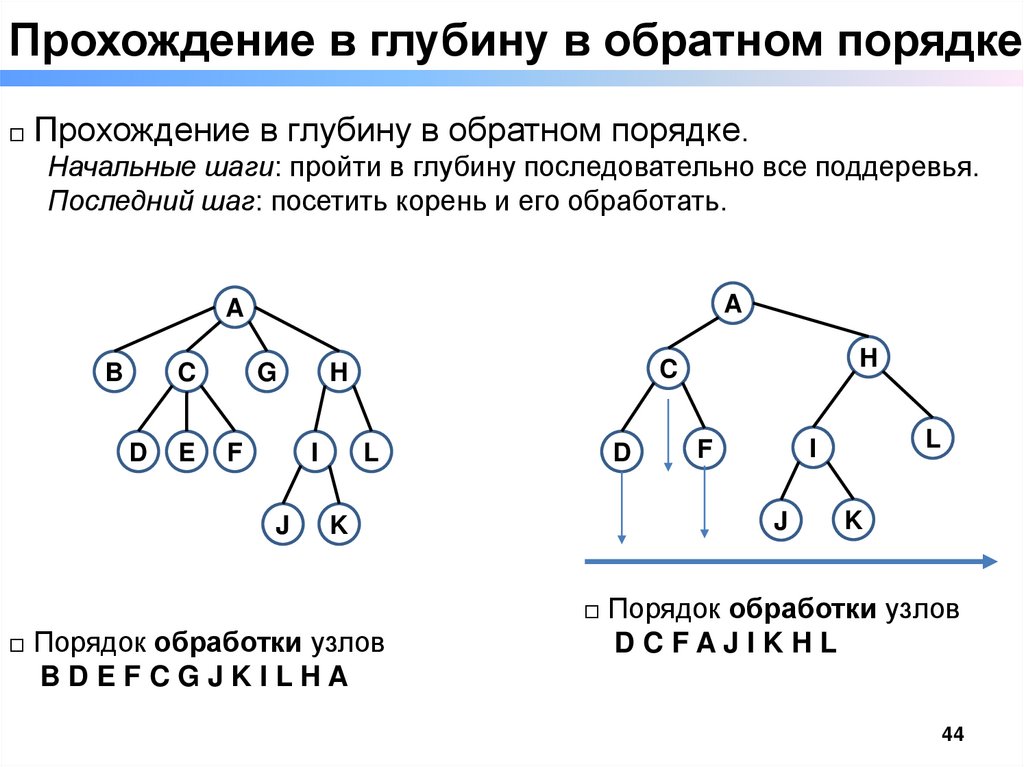
Прохождение в глубину в обратном порядке□ Прохождение в глубину в обратном порядке.
Начальные шаги: пройти в глубину последовательно все поддеревья.
Последний шаг: посетить корень и его обработать.
A
A
B
C
D
E
G
F
I
J
H
C
H
L
K
□ Порядок обработки узлов
BDEFCGJKILHA
D
L
I
F
J
K
□ Порядок обработки узлов
DCFAJIKHL
44
45.
Алгоритмы похождения в глубину□ Алгоритм. Прохождение в глубину бинарного дерева в
прямом порядке
prgl(P)
{
<посещение P и её обработка>
if (P.l≠λ)
prgl(P.l);
if (P.r≠λ)
prgl(P.r);
}
45
46.
Алгоритмы похождения в глубину□ Алгоритм. Прохождение в глубину бинарного дерева в
обратном порядке
prgl(P)
{
if (P.l≠λ)
prgl(P.l);
if (P.r≠λ)
prgl(P.r);
<посещение P и её обработка>
}
46
47.
Алгоритмы похождения в глубину□ Алгоритм. Прохождение в глубину бинарного дерева в
симметричном порядке
prgl(P)
{
if (P.l≠λ)
prgl(P.l);
<посещение P и её обработка>
if (P.r≠λ)
prgl(P.r);
}
47
48.
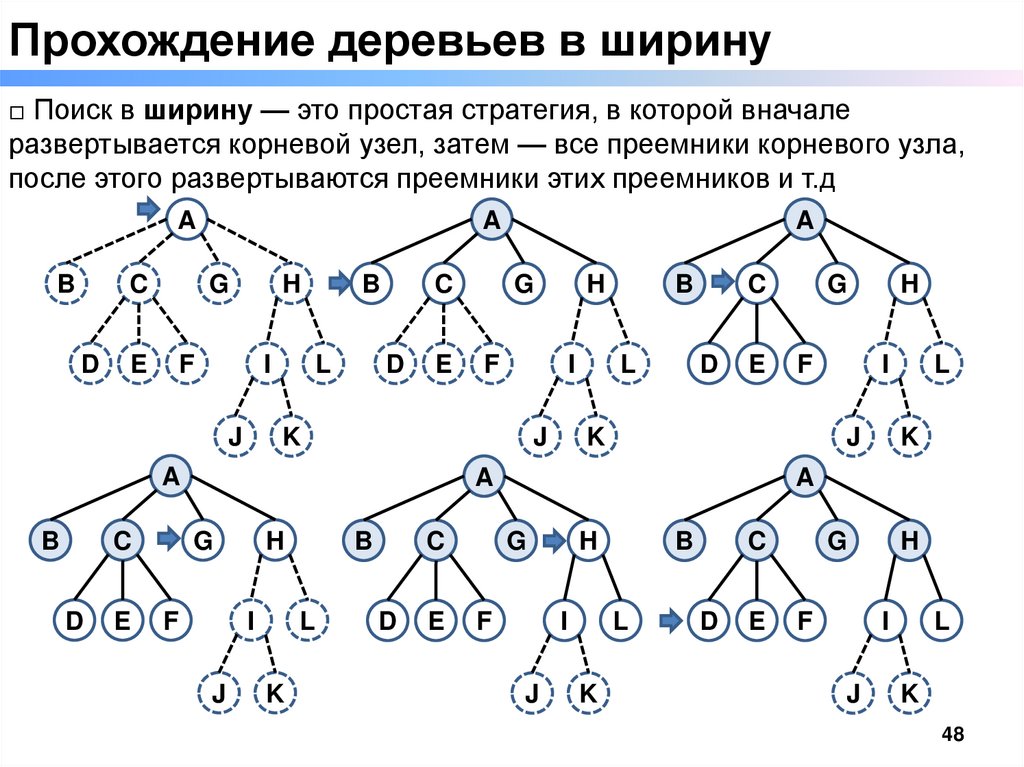
Прохождение деревьев в ширину□ Поиск в ширину — это простая стратегия, в которой вначале
развертывается корневой узел, затем — все преемники корневого узла,
после этого развертываются преемники этих преемников и т.д
A
B
C
D
A
G
E
H
F
I
J
B
L
C
D
E
C
D
E
G
H
F
I
K
J
A
B
A
B
L
C
D
E
F
H
I
J
B
L
K
C
D
E
F
K
A
G
G
H
I
L
J
K
G
H
A
G
F
H
I
J
B
L
K
C
D
E
F
I
J
L
K
48
49.
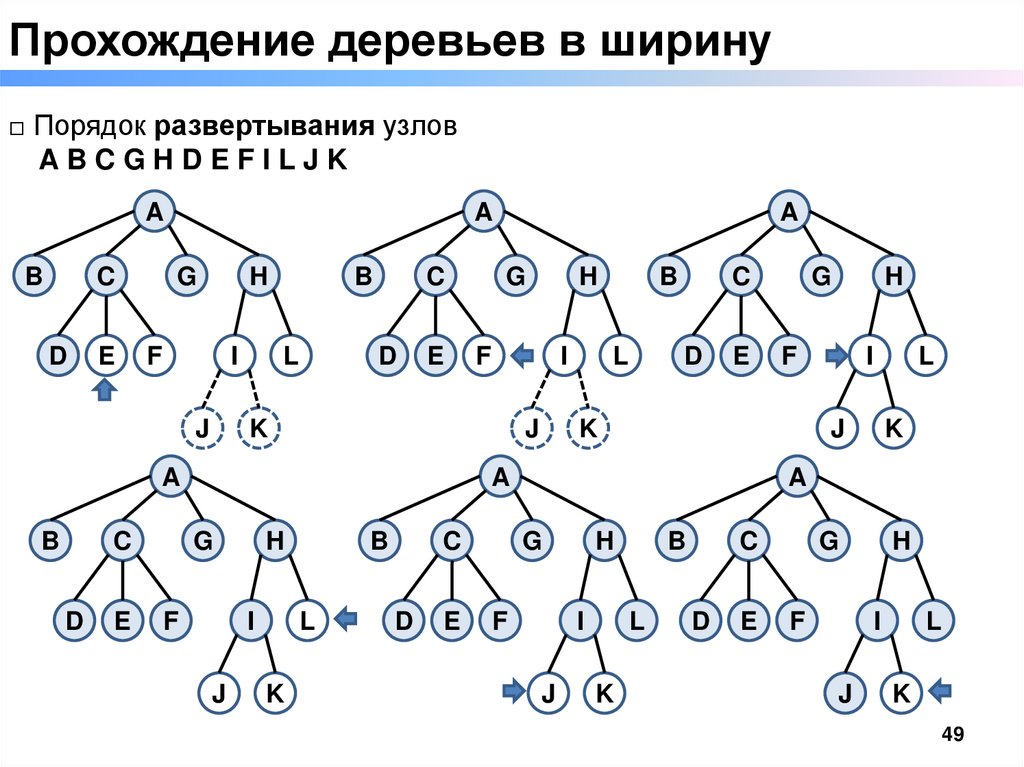
Прохождение деревьев в ширину□ Порядок развертывания узлов
ABCGHDEFILJK
A
B
C
D
E
A
G
H
F
I
J
B
L
C
D
E
C
D
E
G
H
F
I
K
J
A
B
A
B
L
C
D
E
F
H
I
J
B
L
K
C
D
E
H
F
K
A
G
G
I
L
J
K
G
H
A
G
F
H
I
J
B
L
K
C
D
E
F
I
J
L
K
49
50.
Алгоритмы похождения в ширину□ Алгоритм. Прохождение в глубину бинарного дерева в
симметричном порядке
Взять пустую очеpедь O1.
Поместить коpень в очеpедь O1.
WHILE (очередь O1 не пуста) DO
{
0.Пусть p - узел, находящийся в голове очеpеди O1.
1.Посетить (обработать) веpшину p.
2.Поместить всех сыновей веpшины p в конец очеpеди О1,
начиная со стаpшего сына
3.Удалить вершину p из очеpеди O1.
}
50
51.
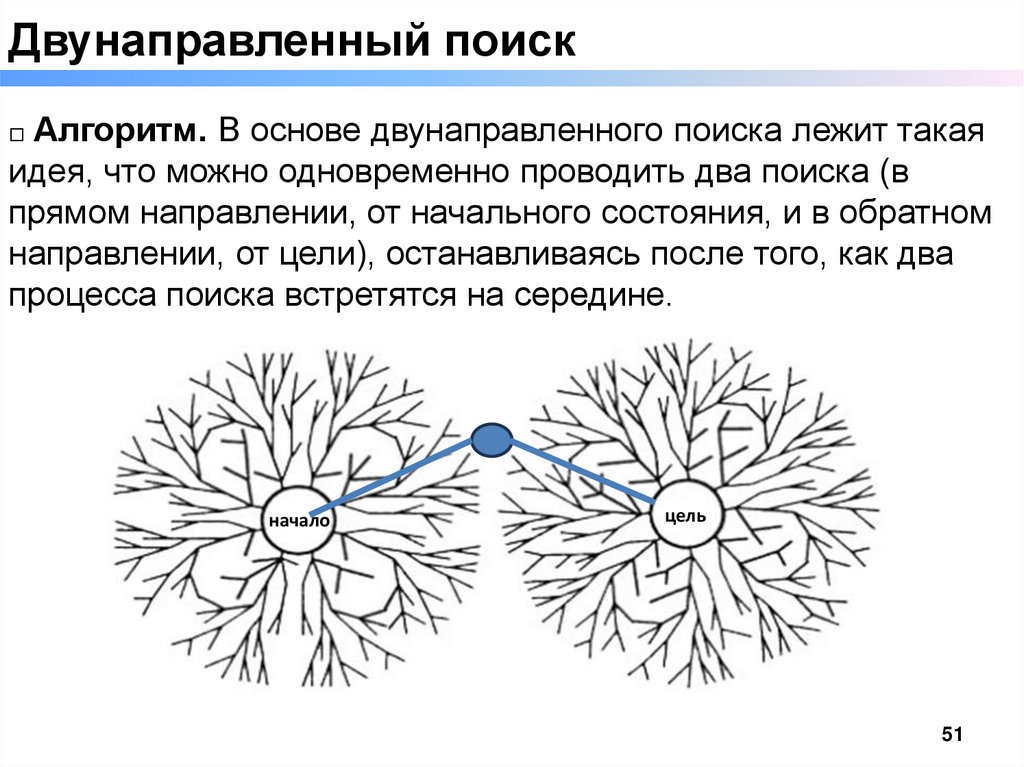
Двунаправленный поиск□ Алгоритм. В основе двунаправленного поиска лежит такая
идея, что можно одновременно проводить два поиска (в
прямом направлении, от начального состояния, и в обратном
направлении, от цели), останавливаясь после того, как два
процесса поиска встретятся на середине.
начало
цель
51
52.
Рекурсивные алгоритмы – задачи!!!Задача 1 – ый ряд.
Дано бинарное дерево. Найти все поддеревья, структура которых совпадает с
заданной.
Задача 2 – ой ряд.
Дано бинарное дерево. Каждая вершина имеет цвет и значение. Цвет может
быть черным или белым. Сместить все черные вершины ближе к корню.
(У белых верши не могут быть черные сыновья)
Задача 3 – ой ряд.
На каждом уровне бинарного дерева найти максимальный элемент
Задача*.
Дано N – дерево. У каждой вершины есть номер. У каждого листа есть номер и
значение. Поставить остальным вершинам значения по следующему правилу:
значение вершины равно сумме значений четных сыновей за вычетом суммы
значений нечетных сыновей
52
53.
Рекурсивные графические алгоритмы53
54.
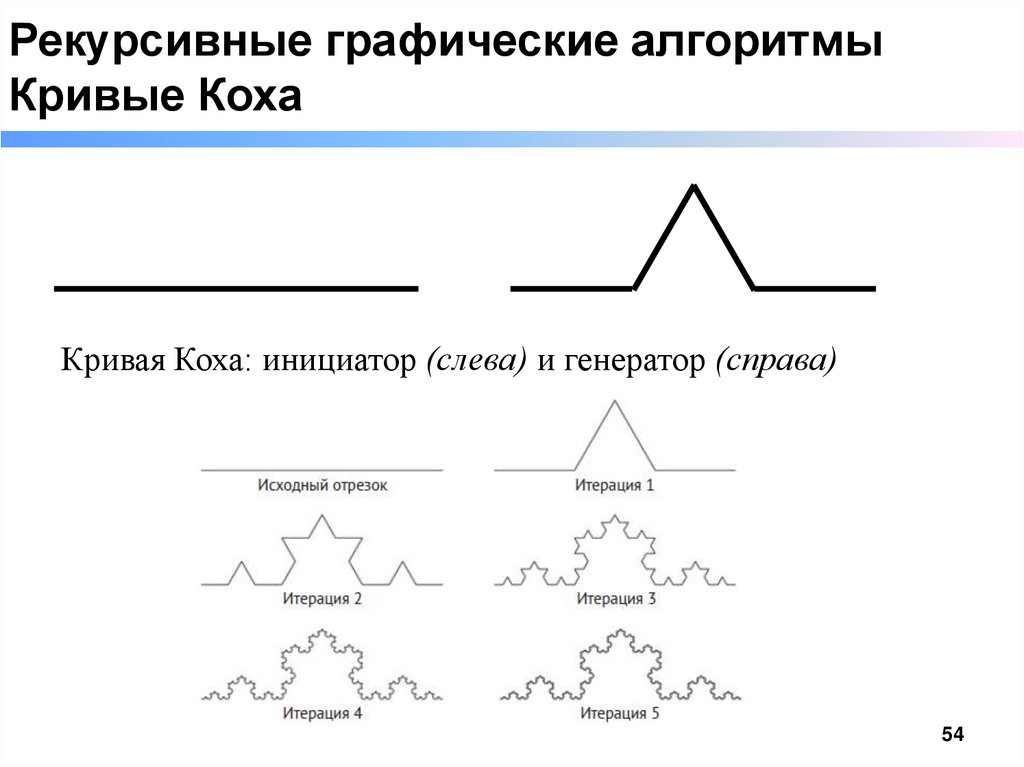
Рекурсивные графические алгоритмыКривые Коха
Кривая Коха: инициатор (слева) и генератор (справа)
54
55.
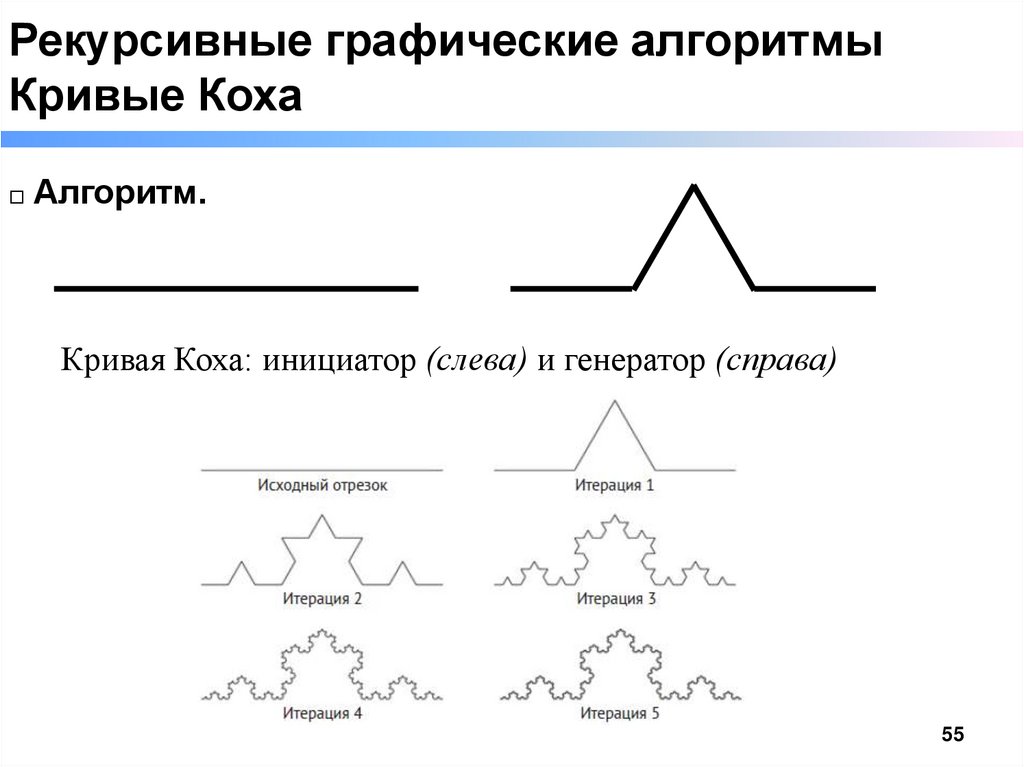
Рекурсивные графические алгоритмыКривые Коха
□ Алгоритм.
Кривая Коха: инициатор (слева) и генератор (справа)
55
56.
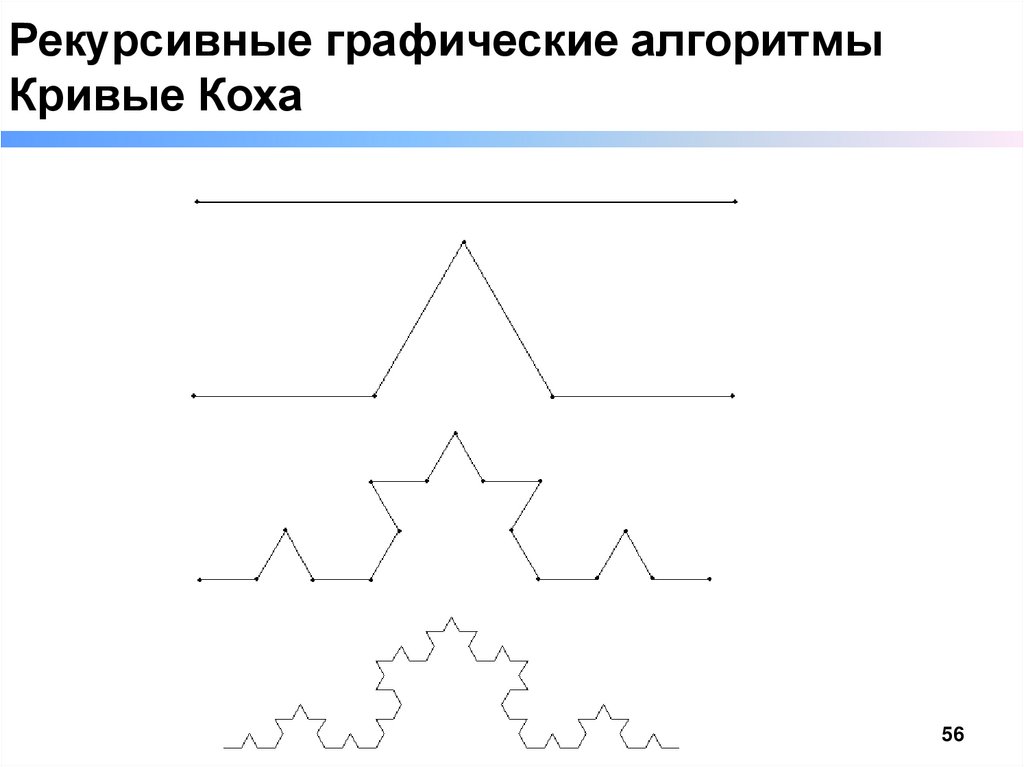
Рекурсивные графические алгоритмыКривые Коха
56
57.
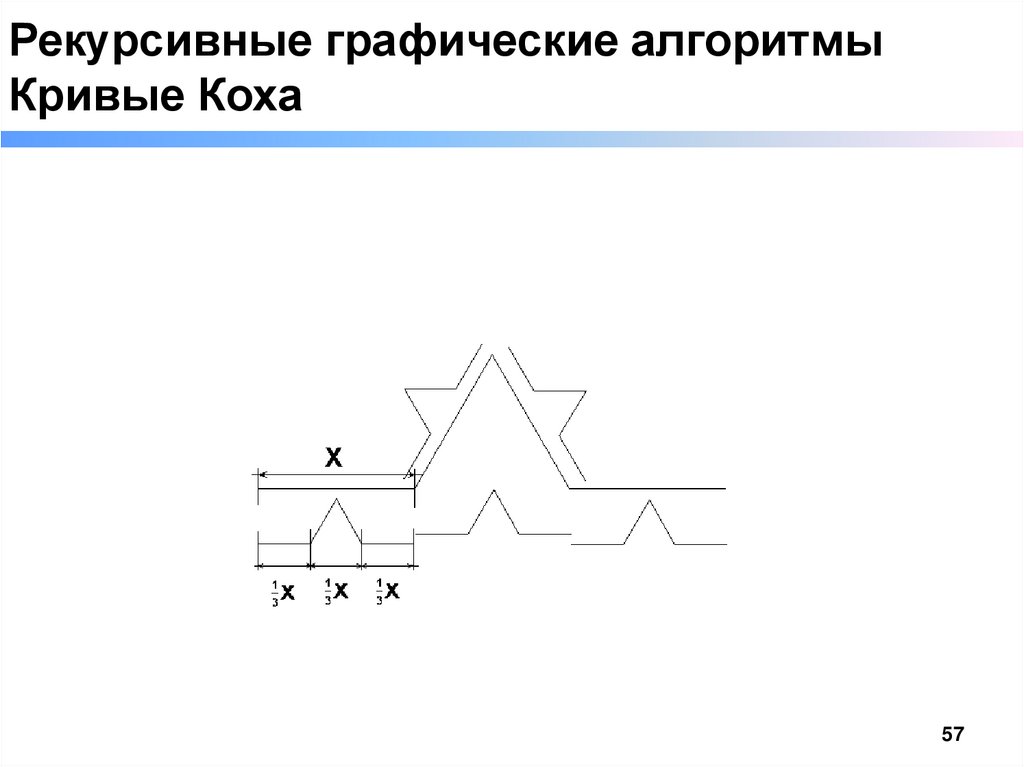
Рекурсивные графические алгоритмыКривые Коха
57
58.
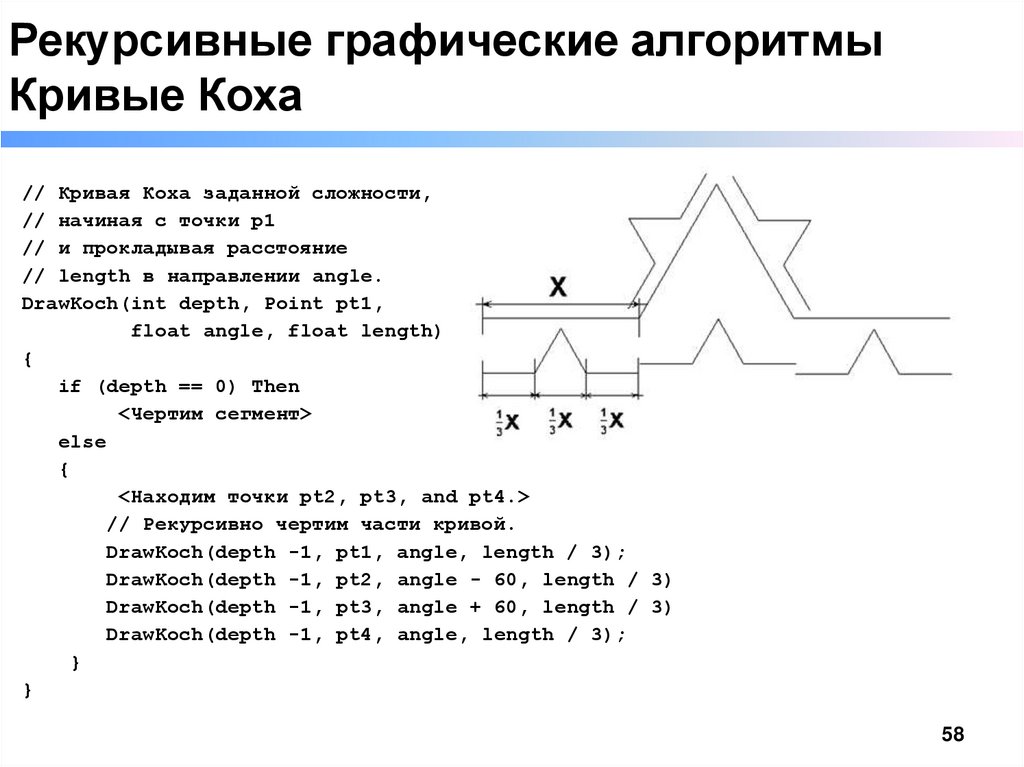
Рекурсивные графические алгоритмыКривые Коха
// Кривая Коха заданной сложности,
// начиная с точки p1
// и прокладывая расстояние
// length в направлении angle.
DrawKoch(int depth, Point pt1,
float angle, float length)
{
if (depth == 0) Then
<Чертим сегмент>
else
{
<Находим точки pt2, pt3, and pt4.>
// Рекурсивно чертим части кривой.
DrawKoch(depth -1, pt1, angle, length / 3);
DrawKoch(depth -1, pt2, angle - 60, length / 3)
DrawKoch(depth -1, pt3, angle + 60, length / 3)
DrawKoch(depth -1, pt4, angle, length / 3);
}
}
58
59.
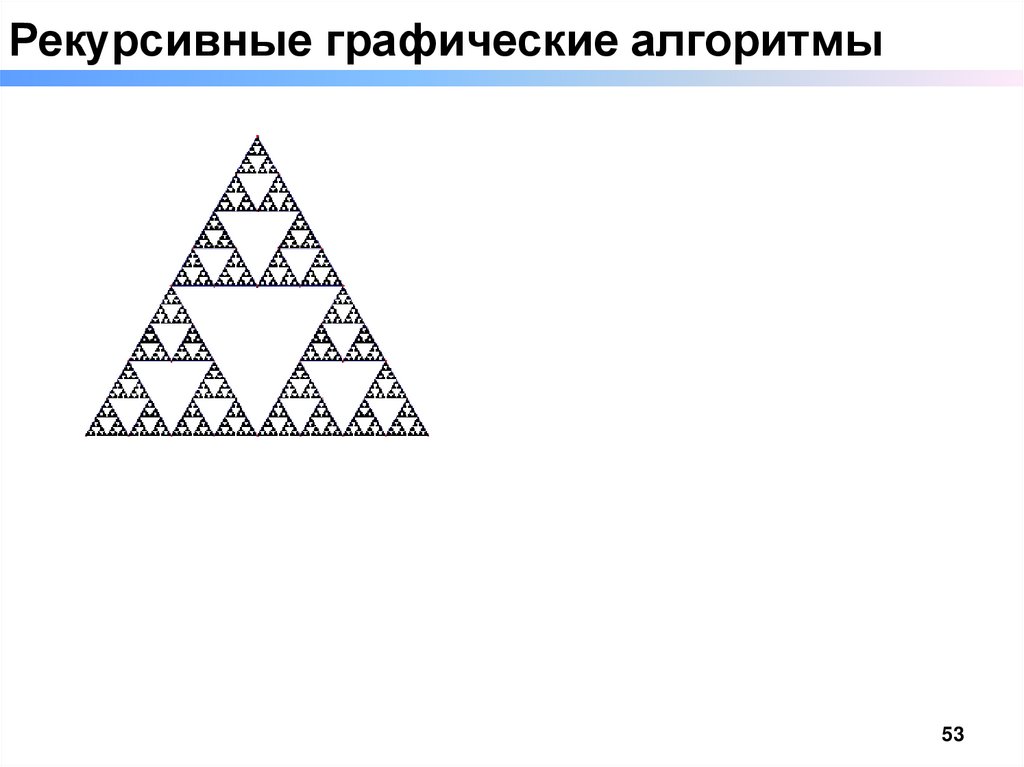
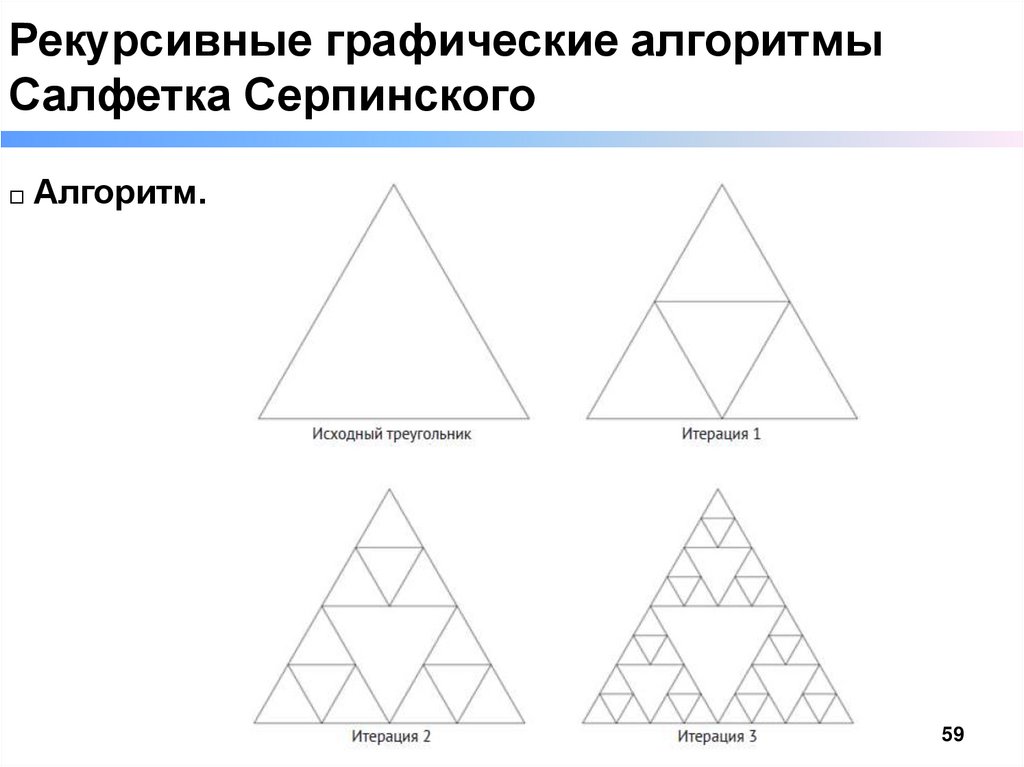
Рекурсивные графические алгоритмыСалфетка Серпинского
□ Алгоритм.
59
60.
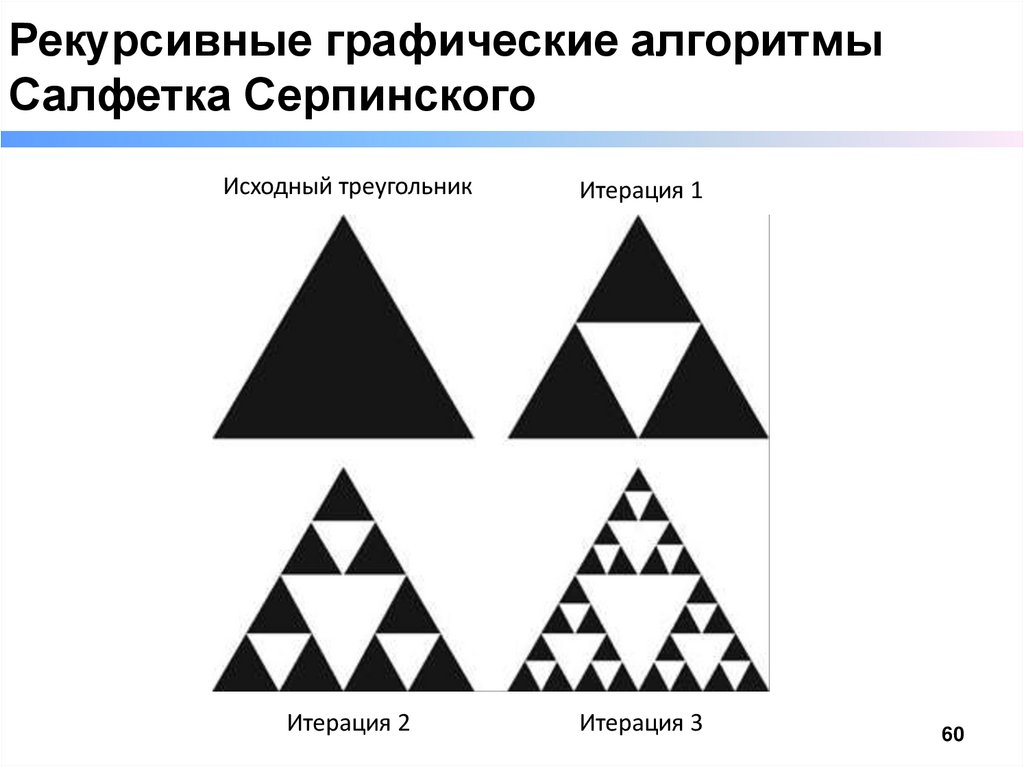
Рекурсивные графические алгоритмыСалфетка Серпинского
Исходный треугольник
Итерация 1
Итерация 2
Итерация 3
60
61.
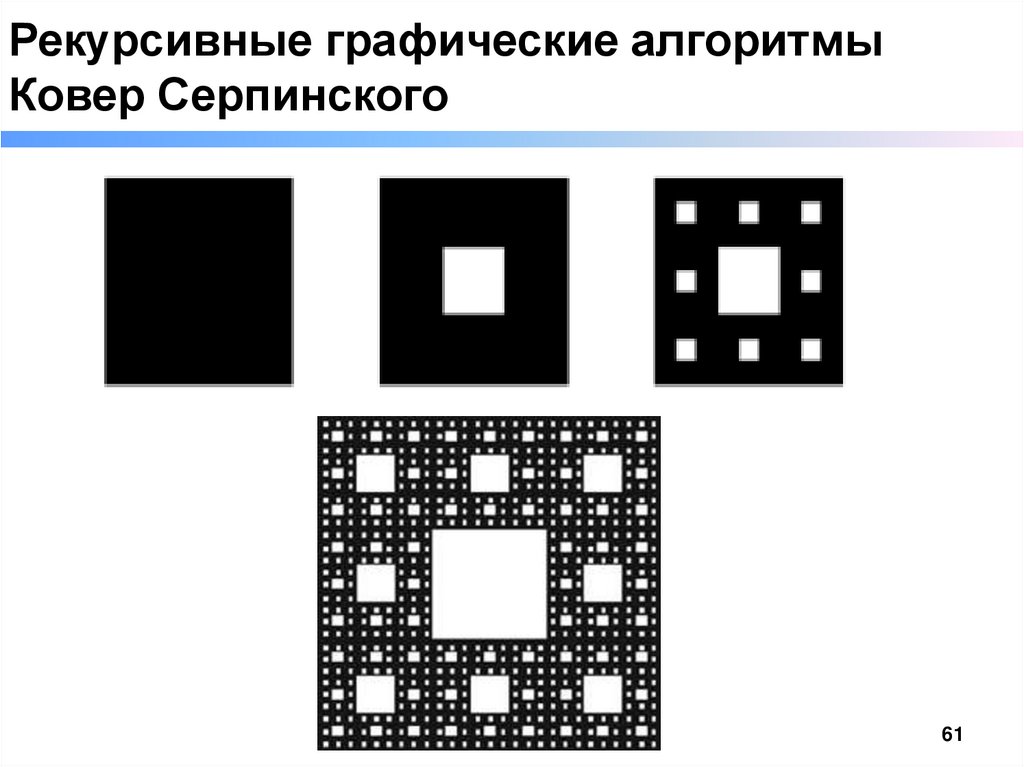
Рекурсивные графические алгоритмыКовер Серпинского
61
62.
Рекурсивные графические алгоритмыКривая Гильберта
□ Алгоритм.
62
63.
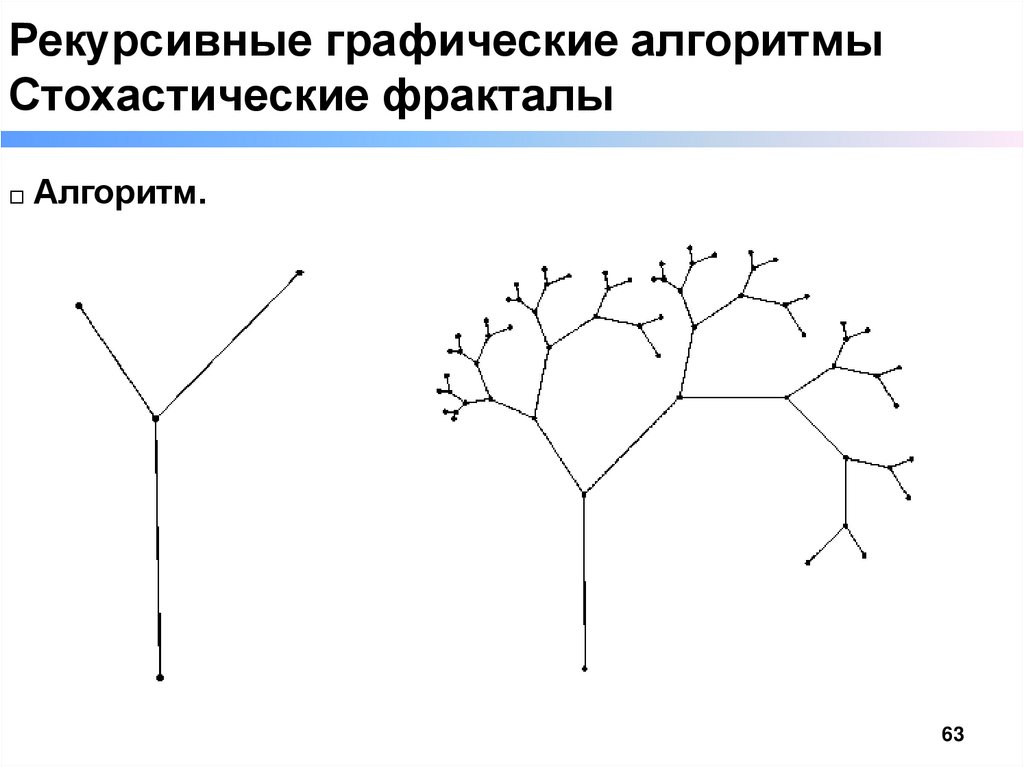
Рекурсивные графические алгоритмыСтохастические фракталы
□ Алгоритм.
63
64.
Рекурсивные графические алгоритмыСтохастические фракталы (+ случайность)
□ Алгоритм.
64
65.
Алгоритмы AI-поискаArtificial intelligence search algorithms
□ Задачи удовлетворения ограничений (constraintsatisfaction problems).
□ Задачи поиска пути одним действующим лицом
(single-agent pathtinding problems)
□ Игры двух игроков (two-player games)
65
66.
Алгоритмы AI-поискаОсновные понятия и определения
□ Начальное состояние, из которого AI-программа приступает к работе.
□ Описание возможных действий (операций operation), доступных AIпрограмме, которые переводят задачу из одного состояния в другое.
□ Проверка цели, позволяющая определить, является ли данное
конкретное состояние целевым состоянием
□ Функция стоимости пути, которая назначает числовое значение
стоимости каждому пути.
66
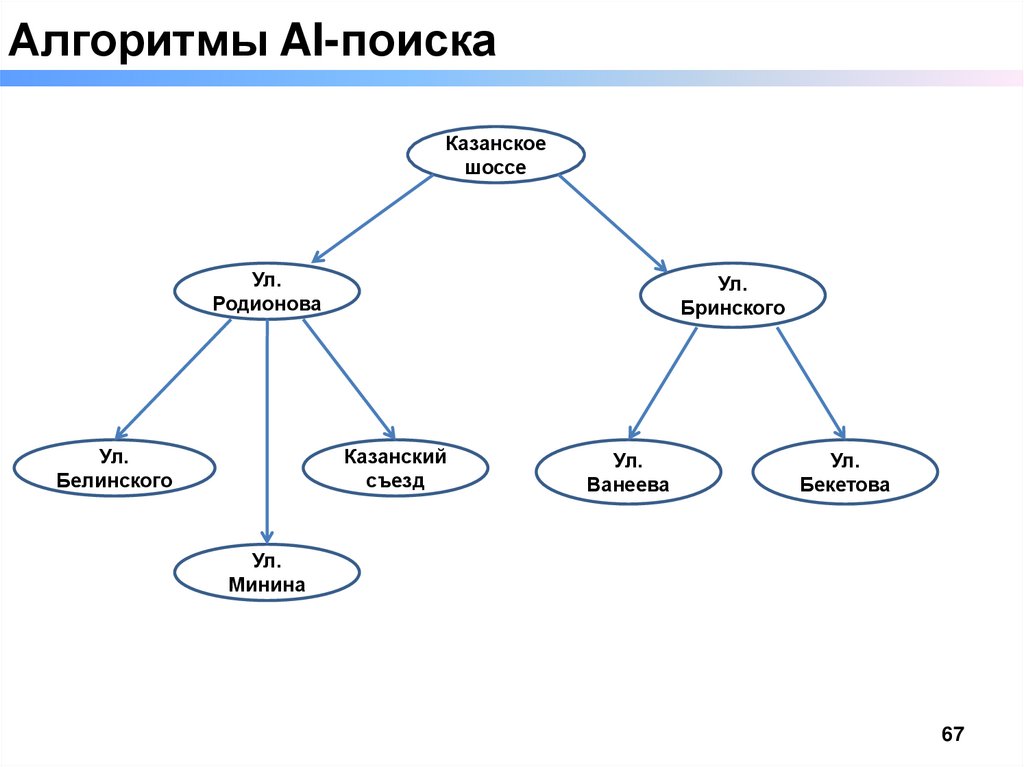
67.
Алгоритмы AI-поискаКазанское
шоссе
Ул.
Родионова
Ул.
Белинского
Ул.
Бринского
Казанский
съезд
Ул.
Ванеева
Ул.
Бекетова
Ул.
Минина
67
68.
Алгоритмы AI-поиска5 компонент узла
□ State. Состояние в пространстве состояний, которому соответствует
данный узел.
□ Parent-Node. Узел в дереве поиска, применявшийся для формирования
данного узла (родительский узел).
□ Action. Действие, которое было применено к родительскому узлу для
формирования данного узла
□ Cost. Стоимость (может быть стоимость пути от начального состояния
до данного узла).
□ Depth. Количество этапов пути от начального состояния, называемое
также глубиной.
68
69.
Алгоритмы AI-поискаПример с улицами
□ State. – место где мы находимся.
□ Parent-Node. – место от куда мы свернули.
□ Action. поворот на улицу.
□ Cost. сколько километров было пройдено (времени затрачено).
□ Depth. сколько улиц проехали.
69
70.
Алгоритмы AI-поискаПример с улицами
□ State. – место где мы находимся.
□ Parent-Node. – место от куда мы свернули.
□ Action. поворот на улицу.
□ Cost. сколько километров было пройдено (времени затрачено).
□ Depth. сколько улиц проехали.
70
71.
Измерения производительности□ Полнота.
□ Оптимальность.
□ Временнáя сложность.
□ Пространственная сложность.
71
72.
Рекурсия и задачи удовлетворения ограниченийЗадачи о N ферзях
□ Цель задачи с восемью ферзями состоит в размещении N ферзей на
шахматной доске N × N таким образом, чтобы ни один ферзь не нападал
на любого другого.
72
73.
Задачи о N ферзяхПервая инкрементная формулировка
□ Состояния. Состоянием является любое расположение ферзей на доске в
количестве от 0 до N.
□ Начальное состояние. Отсутствие ферзей на доске.
□ Функция определения преемника. Установка ферзя на любой пустой клетке.
□ Проверка цели. На доске находится все N ферзей, и ни один из них не атакован.
Вторая инкрементная формулировка
□ Состояния. Состояниями являются расположения с n ферзями (0<n<=N), по
одному ферзю в каждой из находящихся слева n вертикалей (или n верхних
горизонталей), притом что ни один ферзь не нападает на другого.
□ Начальное состояние. Отсутствие ферзей на доске.
□ Функция определения преемника. Установка ферзя на любой клетке в
находящейся слева пустой вертикали таким образом, чтобы он не был атакован
каким-либо другим ферзем.
□ Проверка цели. На доске находится все N ферзей, и ни один из них не атакован.
73
74.
Алгоритм решения задачи о N ферзейQueens(cur_pos,depth)
{
if (not Is_Valid(cur_pos))
{
// позиция недопустима
// выполняем соответствующие действия
return;
}
if (depth == 0)
{
// решение найдено
// если есть необходимость, то сохраняем решение
// если есть необходимость, то сравниваем текущее решение
// с ранее полученными и выбираем оптимальное
return;
}
succ = Successors(cur_pos);
// получение возможных ходов
Save(cur_pos);
// сохраняем позицию
// здесь её можно опустить
while (not Empty(succ))
{
pos = cur_pos + RemoveOne(succ);
// выбираем следующую позицию
Queens (pos, depth-1);
Restore (cur_pos);
// восстанавливаем позицию
// здесь её можно опустить
}
return;
}
74
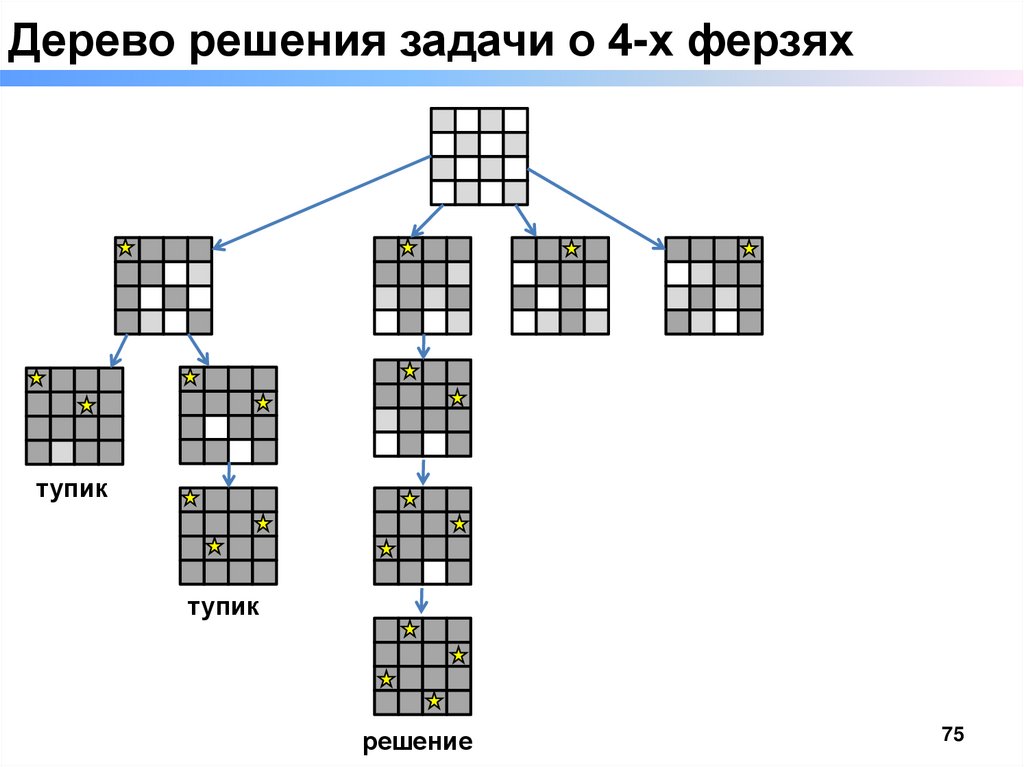
75.
Дерево решения задачи о 4-х ферзяхтупик
тупик
решение
75
76.
Рекурсия и головоломкиРекурсия как метод очень удобна для решения
различного рода головоломок
□ Игра в 15. В квадратной коробке лежат 15 пронумерованных кубиков,
перемешанных некоторым образом. Требуется, двигая по одному кубику за
раз, добиться следующего расположения.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
76
77.
Ирга в 151) Состояния. Описание состояния определяет местонахождение каждой из этих
восьми фишек и пустого участка на одном из девяти квадратов.
2) Начальное состояние. В качестве начального может быть определено любое
состояние.).
3) Функция определения преемника. Эта функция формирует допустимые
состояния, которые являются результатом попыток осуществления указанных
четырех действий (теоретически возможных ходов Left, Right, Up или Down).
4) Проверка цели. Она позволяет определить, соответствует ли данное состояние
целевой конфигурации, показанной на предыдущем слайде. (Возможны также
другие целевые конфигурации.)
5) Стоимость пути. Каждый этап имеет стоимость 1, поэтому стоимость пути
равна количеству этапов в пути.
77
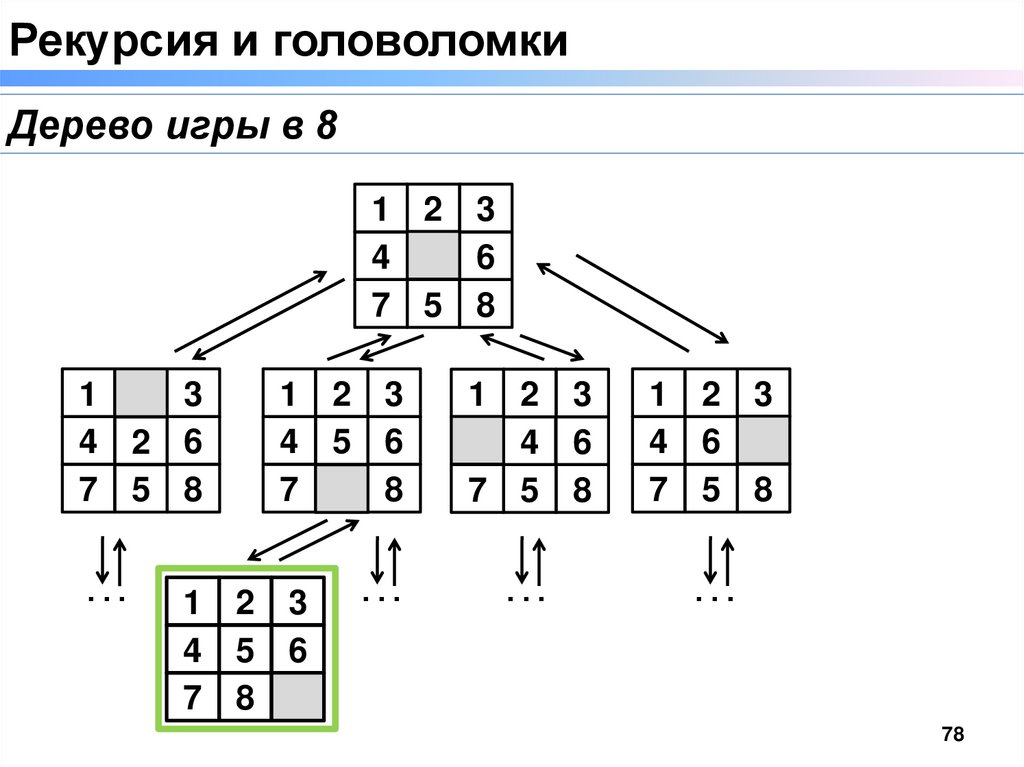
78.
Рекурсия и головоломкиДерево игры в 8
1 2 3
4
6
7 5 8
1
3
4 2 6
7 5 8
...
1 2 3
4 5 6
7
8
1 2 3
4 5 6
7 8
...
1 2 3
4 6
7 5 8
1 2 3
4 6
7 5 8
...
...
78
79.
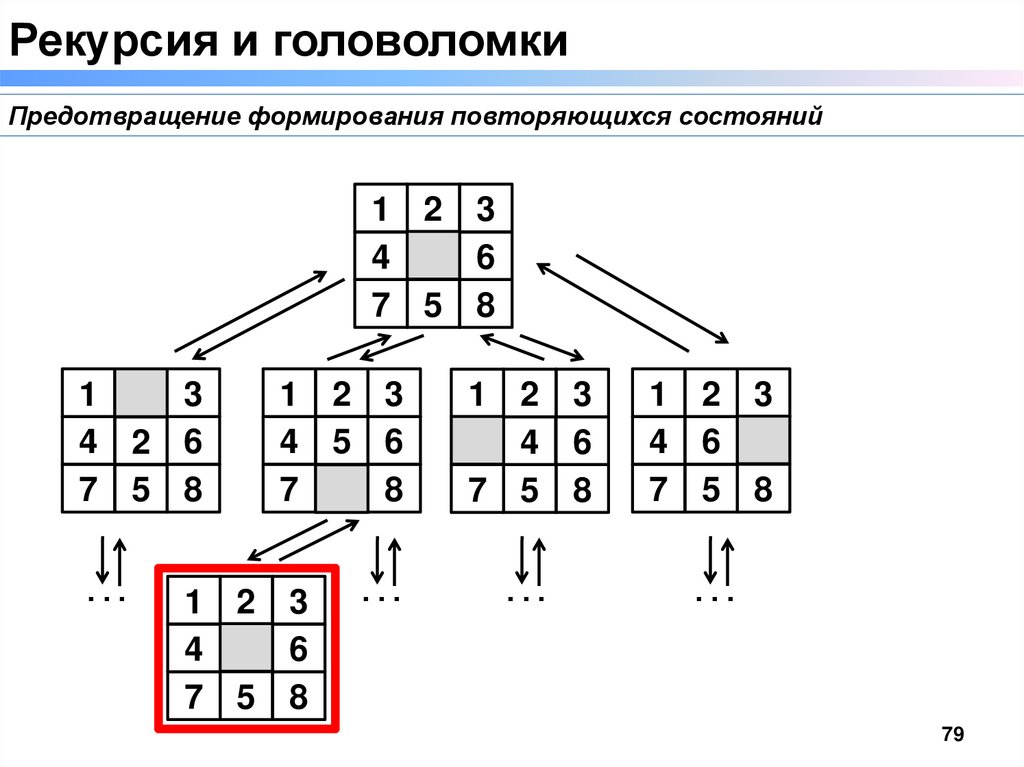
Рекурсия и головоломкиПредотвращение формирования повторяющихся состояний
1 2 3
4
6
7 5 8
1
3
4 2 6
7 5 8
...
1 2 3
4 5 6
7
8
1 2 3
4
6
7 5 8
...
1 2 3
4 6
7 5 8
1 2 3
4 6
7 5 8
...
...
79
80.
Алгоритм решения головоломокGame_15(cur_pos,depth)
{
if (not Is_Valid(cur_pos)) return; // позиция недопустима
if (IsWin())
{
// решение найдено
return;
// если есть необходимость, то сохраняем решение
// если есть необходимость, то сравниваем текущее решение
// с ранее полученными и выбираем оптимальное
}
if (IsLoss()) return ;
// дополнительная проверка на выход из рекурсии
// позиция допустима, но она тупиковая
if (FindPrevPos(cur_pos)) return ;
else Insert_Pos(cur_pos);
// проверяем было ли это состояние раньше
// если было то return;
// чтобы не было зацикливания
// если не было то сохраняем текущее состояние
next_pos = Successors(cur_pos);
// получение возможных ходов
// в нашем случае это (лево право верх вниз)
while (not Empty(next_pos))
{
next_pos = GetNextPosition(next_pos);
Game_15(next_pos, depth-1);
}
Delete_Pos(cur_pos);
return;
// удаляем текущую позицию из списка позиций
}
80
81.
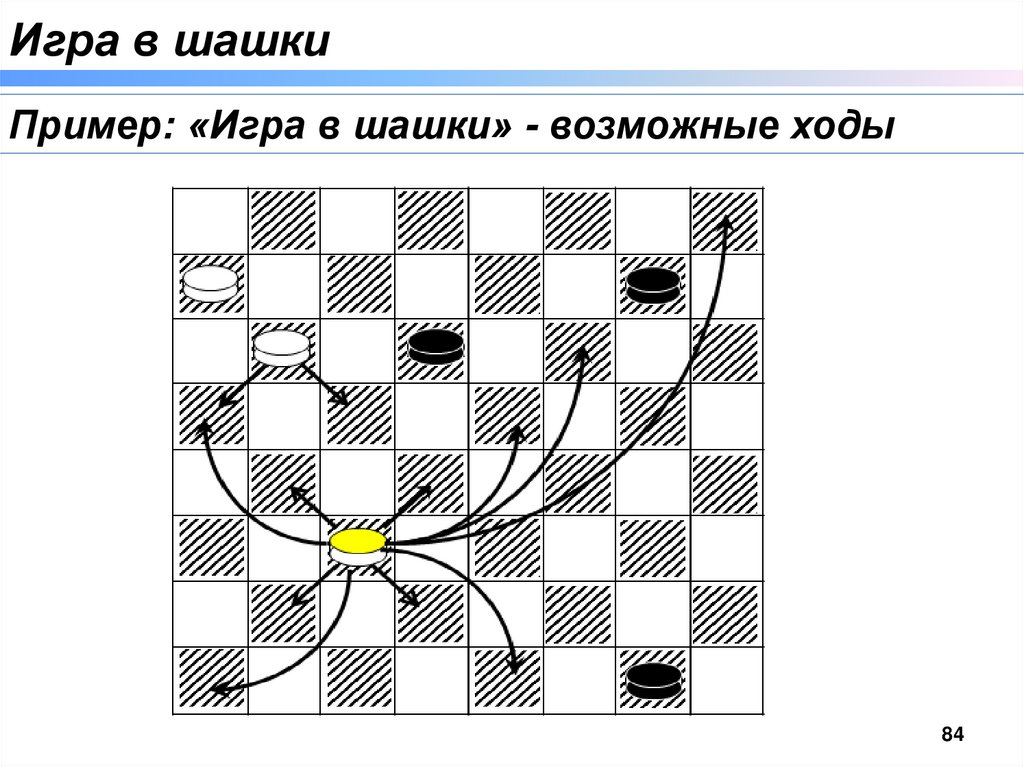
Рекурсия и «Игры двух игроков»Пример: Игра в шашки
□ Наша задача заключается в построении алгоритма, который бы искал
наилучший из возможных ходов, исходя из текущего состояния для
заданного игрока.
□ Состояние S – это описание игры на какой-то момент (клетки заняты
различными фигурами, поле игры некоторым образом заполнено
крестиками и ноликами и т.д.).
□ Тип игрок может иметь два состояния – “компьютер” и “человек”.
81
82.
Рекурсия и «Игры двух игроков»□ Наша задача заключается в построении алгоритма, который бы искал
наилучший из возможных ходов, исходя из текущего состояния для
заданного игрока.
□ Состояние S – это описание игры на какой-то момент (клетки заняты
различными фигурами, поле игры некоторым образом заполнено
крестиками и ноликами и т.д.).
□ Тип игрок может иметь два состояния – “компьютер” и “человек”.
82
83.
Рекурсия и «Игры двух игроков»Алгоритм
□ Алгоритм должен найти оптимальный ход из любой
игровой ситуации. Он должен “вообразить” возможное
развёртывание игры для каждого допустимого хода:
- если нет ни одного допустимого хода, то игра проиграна;
- если возможны n ходов, то исследуются новые состояния
s1,s2,…,sn, вытекающие из этих ходов.
83
84.
Игра в шашкиПример: «Игра в шашки» - возможные ходы
84
85.
Рекурсия и «Игры двух игроков»Алгоритм
□ Для каждого из этих ситуаций алгоритм проверяет
возможные ответы воображаемого противника:
- если у него нет возможного ход, то рассматривается состояние
выигрышное или ничейное;
- в противном случае необходимо рассмотреть различные
возможные ходы для противника.
85
86.
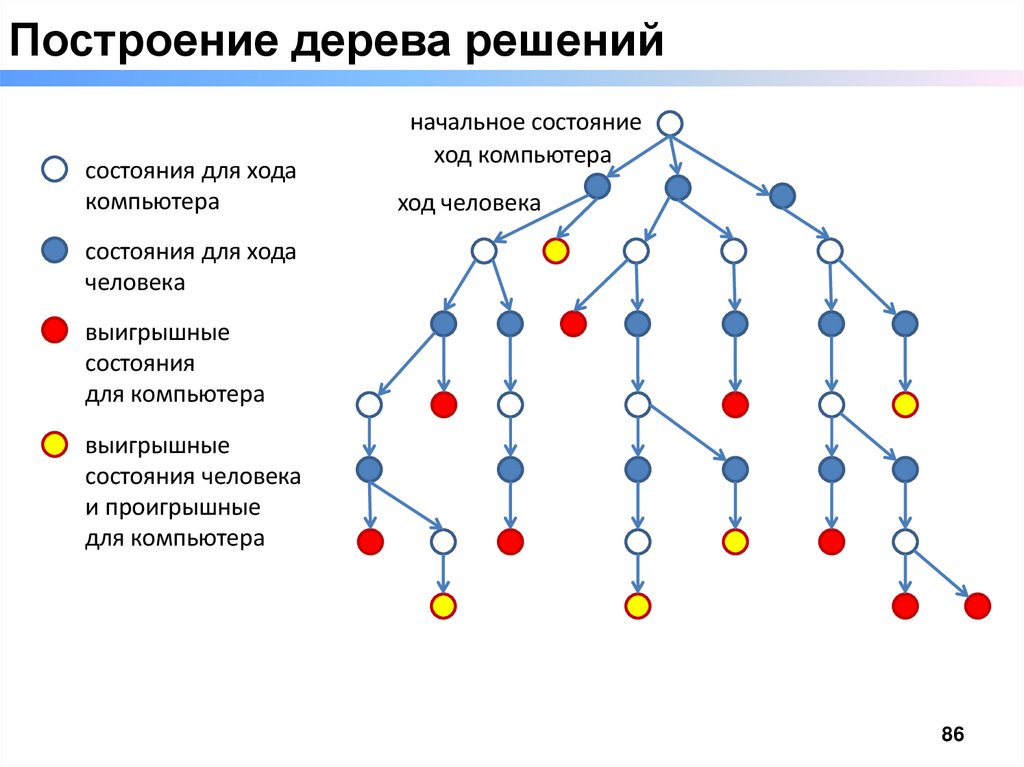
Построение дерева решенийсостояния для хода
компьютера
начальное состояние
ход компьютера
ход человека
состояния для хода
человека
выигрышные
состояния
для компьютера
выигрышные
состояния человека
и проигрышные
для компьютера
86
87.
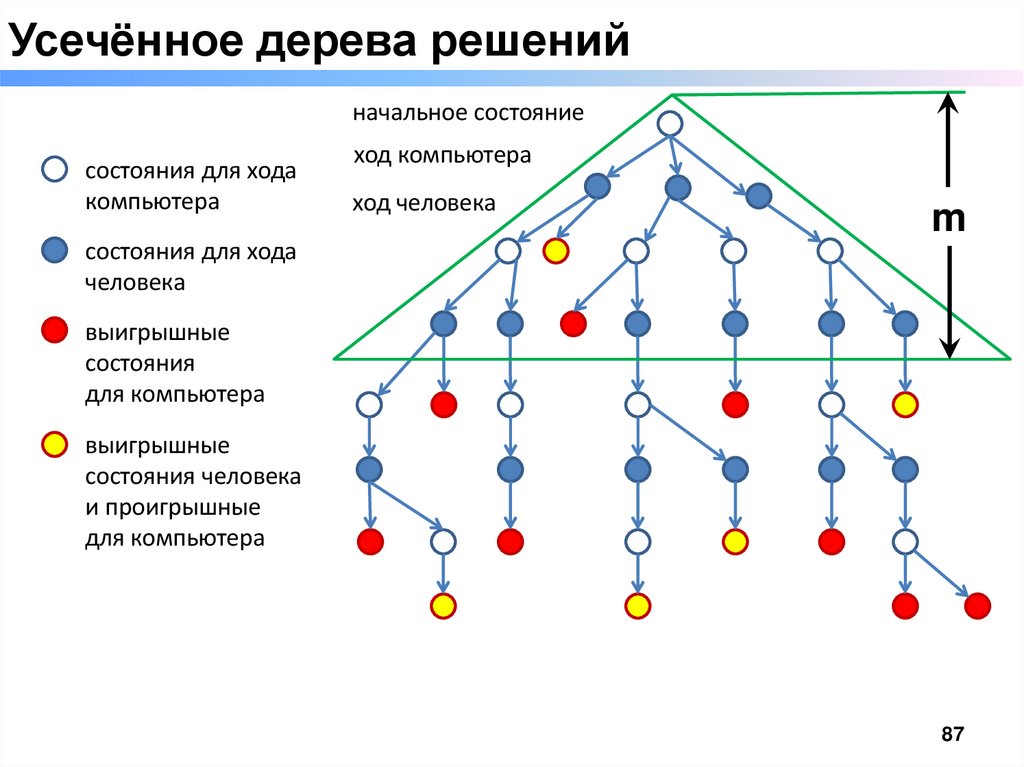
Усечённое дерева решенийначальное состояние
состояния для хода
компьютера
ход компьютера
ход человека
m
состояния для хода
человека
выигрышные
состояния
для компьютера
выигрышные
состояния человека
и проигрышные
для компьютера
87
88.
Цена игры□ Для классификации различных возможных ходов,
необходимо каждой конечной вершине поставить в
соответствие некоторое положительное или
отрицательное число
□ Это значение конечным вершинам дерева игры должно
присваиваться с помощью некоторой оценочной функции
(оценка(si))
□ Оценочная функция для шашек
F = (mb - mw) + 3*(kb-kw)
mb и mw – число простых шашек
kb и kw – число дамок.
88
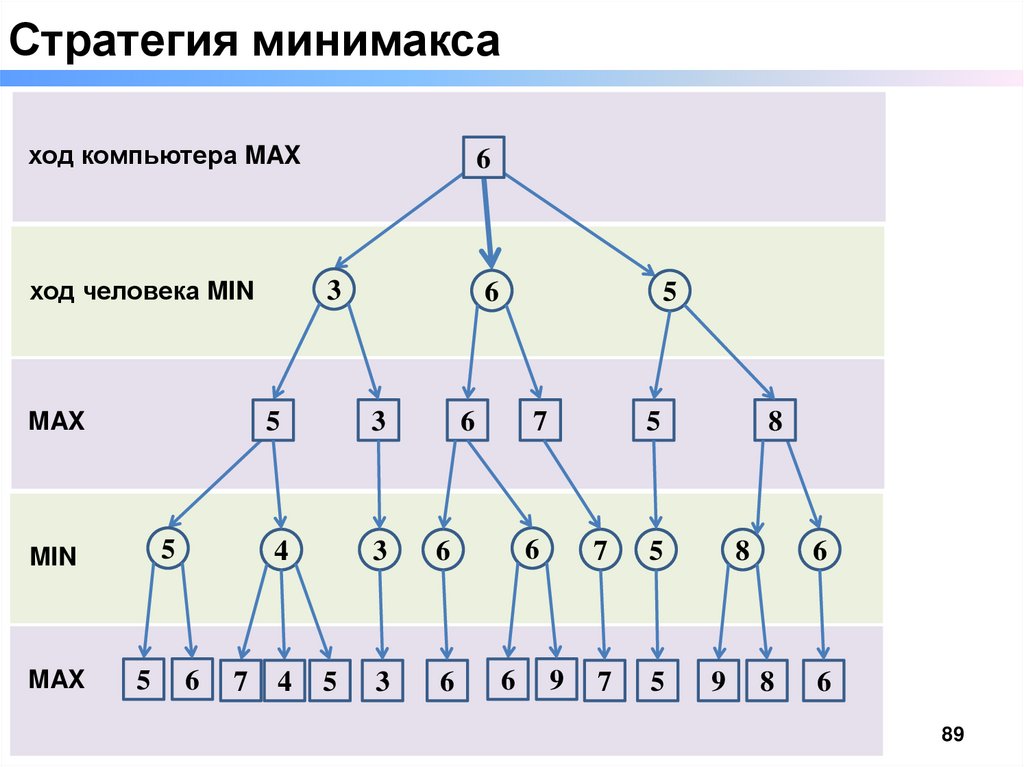
89.
Стратегия минимаксаход компьютера MAX
ход человека MIN
MAX
5
MIN
MAX
5
6
7
6
3
6
5
3
4
3
6
3
6
4
5
5
6
7
5
6
6
9
7
5
7
5
8
8
9
6
8
6
89
90.
Алгоритм минимаксаint MiniMax(pos,level)
{
if (level = leaf || IsWin() || IsLoss()) return eval(pos);
if (FindPrevPos(pos)) return eval(pos);
else Insert_Pos(pos);
if (level == max)
// level принадлежит уровню max
{
g := -∞;
pos_cur = FirstChild(pos);
while (pos_cur_с ≠ λ )
{
g = max(g, MiniMax(pos_cur , level + 1));
pos_сur = NextBrother(pos_cur);
}
}
else
// level принадлежит уровню min
{
g := +∞;
pos_cur = FirstChild(pos);
while (pos_cur ≠ λ )
{
g = min(g, MiniMax(pos_cur , level + 1));
pos_cur = NextBrother(pos_cur);
}
}
Delete_Pos(pos);
return g;
}
90
91.
Стратегия минимакса□ Число позиций, которое просмотривается этим
алгоритмом - WD
-- W - ширина дерева (среднее количество ходов, возможных в
каждой позиции)
-- D - глубина дерева
91
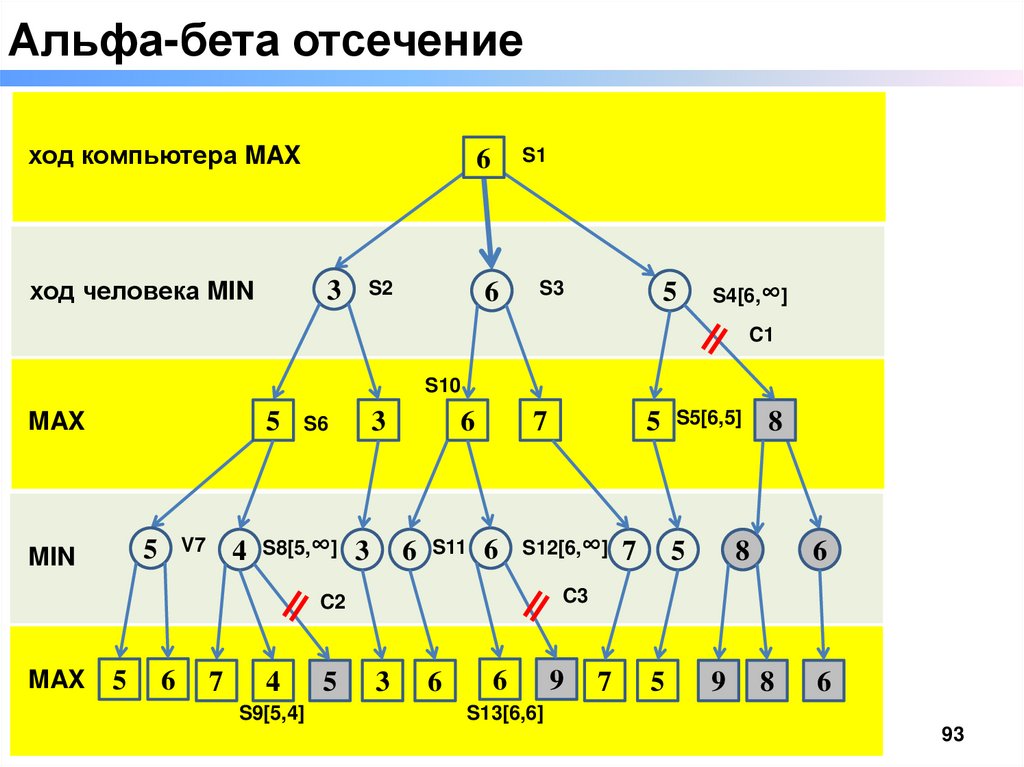
92.
Альфа-бета отсечение□ Альфа-бета отсечение основано на той идее, что анализ
некоторых ходов можно прекратить досрочно, игнорируя результат
их показаний
□ Эта стратегия оптимизации использует две дополнительные
переменные alpha и beta, где
- alpha — текущее максимальное значение, меньше которого игрок
максимизации (компьютер) никогда не выберет (изначально -∞)
alpha = max(alpha, f(Si));
- beta — текущее минимальное значение, больше которого игрок минимизации
(человек) никогда не выберет (изначально + ∞)
beta
= min(beta, f(Si));
92
93.
Альфа-бета отсечениеход компьютера MAX
S1
6
ход человека MIN
3
S2
6
S3
5
S4[6,∞]
C1
S10
5
MAX
3
4 S8[5,∞] 3
V7
5
MIN
S6
6
6 S11 6
S12[6,∞] 7
5
6
7
4
S9[5,4]
5
5
8
6
C3
C2
MAX
5 S5[6,5] 8
7
3
6
6
9
7
5
9
8
6
S13[6,6]
93
94.
Алгоритм «Альфа-бета отсечения»int AlphaBeta(pos,level,alpha,beta)
{
if (level = leaf || IsWin() || IsLoss()) return eval(pos);
if (FindPrevPos(pos)) return eval(pos);
else Insert_Pos(pos);
if (level == max)
// n принадлежит уровню max
{
g := -∞;
pos_cur = FirstChild(pos);
while ((с ≠ λ) && (g < beta))
{
g = max(g, AlphaBeta(cur_pos, level + 1, alpha, beta));
alpha = max(g,alpha);
с = NextBrother(c);
}
}
else
// n принадлежит уровню min
{
g := +∞;
pos_cur = FirstChild(pos);
while (с ≠ λ ) && (g > alpha)
{
g = min(g, AlphaBeta(cur_pos, level + 1, alpha, beta));
beta = min(g,beta);
с = NextBrother(c);
}
}
Delete_Pos(pos);
return g;
}
94
95.
Интересные случаи рекурсииint AlphaBeta(pos,level,alpha,beta)
{
if (level = leaf || IsWin() || IsLoss()) return eval(pos);
if (FindPrevPos(pos)) return eval(pos);
else Insert_Pos(pos);
95
96.
Заключительные штрихиint AlphaBeta(pos,level,alpha,beta)
{
if (level = leaf || IsWin() || IsLoss()) return eval(pos);
if (FindPrevPos(pos)) return eval(pos);
else Insert_Pos(pos);
96
97.
9798.
9899.
Robert Fathauer "Фрактальныерыбы – сгруппированные группы"
99
100.
Геометрическиефракталы
100






























































 programming
programming








