lec_4_Офгр

1.

Основы физики плазмы
4. Кулоновские столкновения. Кулоновский
логарифм.

2.

Траектории частиц

3.

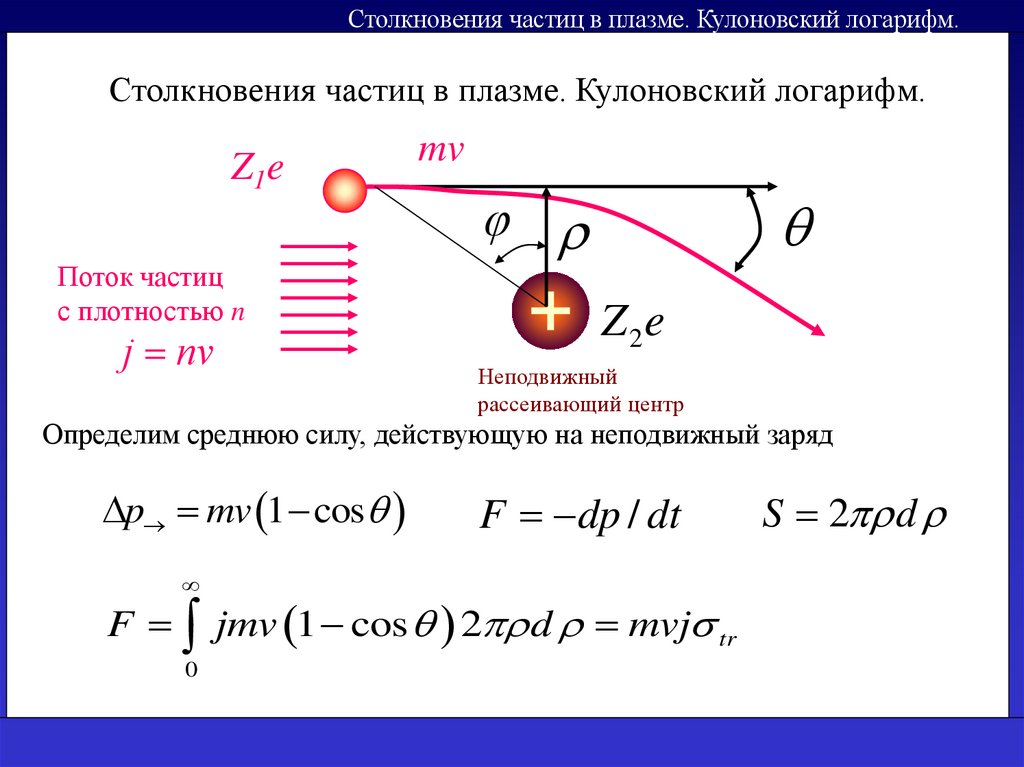
Столкновения частиц в плазме. Кулоновский логарифм.
Столкновения частиц в плазме. Кулоновский логарифм.
Z1e
Поток частиц
с плотностью n
j nv
mv
Z 2e
Неподвижный
рассеивающий центр
Определим среднюю силу, действующую на неподвижный заряд
p mv 1 cos
F dp / dt
F jmv 1 cos 2 d mvj tr
0
S 2 d

4.

Столкновения частиц в плазме. Кулоновский логарифм.
tr 2 1 cos d
0
Транспортное сечение имеет смысл площади
поперечного сечения, которое имел бы рассеивающий центр,
если бы он полностью поглощал импульс падающих на него
частиц.
Для вычисления транспортного сечения необходимо
знать зависимость
Воспользуемся формулой Резерфорда
2
Z1Z 2e
tg
2
2 m v

5.

Столкновения частиц в плазме. Кулоновский логарифм.
Формула получена в предположении, что масса
налетающей частицы гораздо меньше массы рассеивающего
центра (В лабораторной системе координат).
Основной вклад в транспортное сечение вносят
процессы рассеяния, происходящие на больших расстояниях.
В этом случае <<1
Это позволяет разложить тангенс в ряд по числам Бернулли
и оставить только первый член разложения:
2Z1Z 2e
2
m v
2

6.

Столкновения частиц в плазме. Кулоновский логарифм.
Используем разложение:
1 2
1 cos
2
Окончательно:
4Z Z e d
тр
mv
2
2 4
1
2
2 4
Интеграл логарифмически расходится на нижнем и
верхнем пределах.

7.

Столкновения частиц в плазме. Кулоновский логарифм.
Расходимость при малых прицельных параметрах связана
с использованием приближения далёких пролётов.
Интеграл зависит от нижнего предела только
логарифмически.
Поэтому точное значение min не очень существенно.
В качестве min можно выбрать прицельный параметр при
котором происходит рассеяние на угол порядка / 2:
min
2
Z1Z 2e
.
2
mv

8.

Столкновения частиц в плазме. Кулоновский логарифм.
Расходимость при больших значениях m ax связана с тем,
что кулоновский потенциал слишком медленно убывает с
расстоянием.
Однако, в плазме потенциал заряда экранируется.
Поэтому, на расстояниях, больших дебаевского радиуса rD,
поле спадает экспоненциально.
Поэтому, прицельные расстояния, большие rD, не
вносят вклада в интеграл.
В качестве верхнего предела можно взять величину rD:
max
T
2
4 ne

9.

Столкновения частиц в плазме. Кулоновский логарифм.
Точное значение max / min не очень существенно,
поскольку оно входит под знаком логарифма.
Величину
max
ln
min
называют кулоновским логарифмом.
Пусть для оценки v2 = 3T/m, Z1 = Z2 = 1, тогда
max
3T
1/2 3 1/2
min 2 e n
3/2
ND
1.

10.

Столкновения частиц в плазме. Кулоновский логарифм.
Обычно в качестве Λ берут число 10…15.
Для транспортного сечения получаем выражение:
4 Z Z e
тр
.
mv
2
2 4
1
2
2 4
Величина транспортного сечения уменьшается обратно
пропорционально квадрату кинетической энергии налетающих
частиц.

11.

Столкновения частиц в плазме. Кулоновский логарифм.
min
max
Z1Z 2e2
mv 2
при
T
rD
2
4 ne
max
ln
min
Е 100эВ,
/2
1/ 2
кулоновский _ логарифм
n 1014 см 3
14,3

12.

Столкновения частиц в плазме. Кулоновский логарифм.