Элементарные процессы в низкотемпературной плазме

1.

Элементарные
процессы в
низкотемпературной
плазме

2.

Лекция 8
Квантово-механические методы вычисления
эффективных сечений взаимодействий
План лекции 8
1. Теория возмущений.
2. Упругое рассеяние электронов.
3. Первое приближение теории
возмущений. Метод Борна.

3.

Теория возмущений
В волновой механике задача вычисления эффективных
сечений взаимодействия частиц друг с другом решается при
исследовании волнового уравнения системы сталкивающихся
частиц. При этом определяется амплитуда волн, связанных с
рассматриваемыми частицами, вдали от места взаимодействия
на расстояниях намного больших, чем атомные размеры
2
re a o
2
me

4.

Рассмотрим взаимодействие электрона с атомом, в этом
случае имеем:
me
mB me , mA m,
1, vA 0.
m
Пусть до взаимодействия атом находится в начальном n
состоянии, а электрон имеет энергию
e
с соответствующим волновым числом (волновым вектором)
ke
me ve
(2m eε e )
.

5.

После взаимодействия атом переходит в другое n
состояние и изменяется энергия электрона. Новое
значение энергии электрона равняется
ε nn ,
а новое значение волнового числа будет равно
k nn =
m e υnn
=
(2m e ε nn )
.

6.

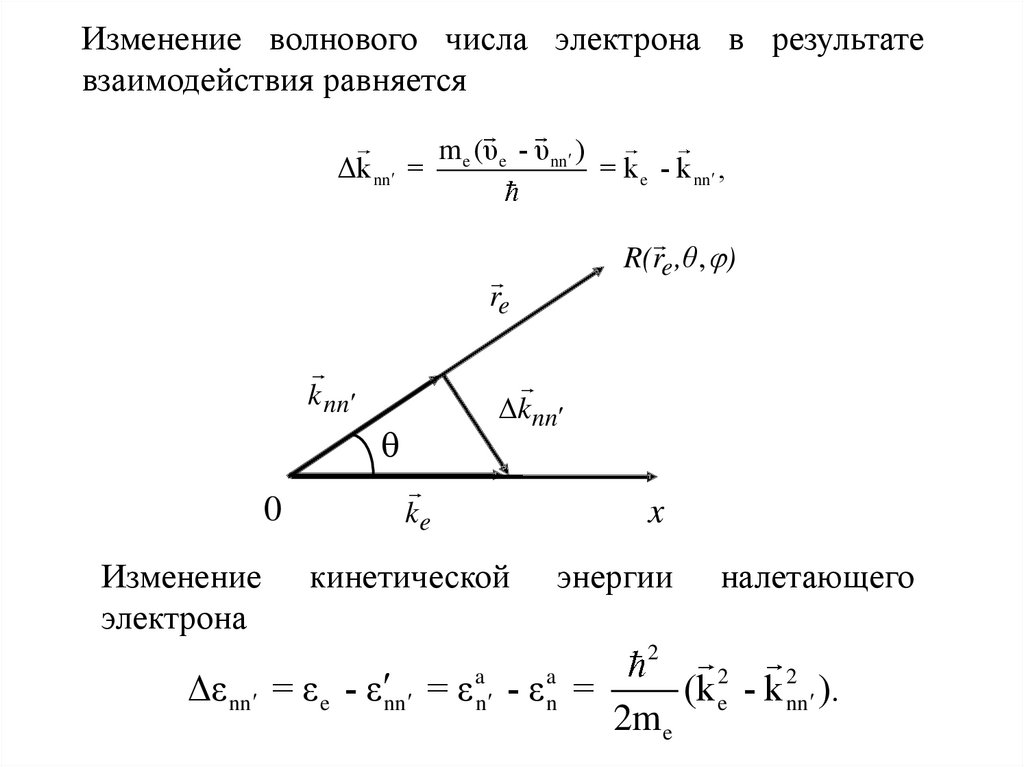
Изменение волнового числа электрона в результате
взаимодействия равняется
Δk nn =
m e (υe - υnn )
R(re ,θ , )
re
k nn
k nn
0
Изменение
электрона
= k e - k nn ,
ke
кинетической
x
энергии
Δε nn = ε e - ε nn = ε an - ε an =
налетающего
2
2m e
2
(k e2 - k nn
).

7.

Обозначим волновую функцию упруго рассеянных
электронов через
enn ,
Обозначим волновую функцию неупруго рассеянных
электронов через
enn ' .
e
Волновая функция nn упруго рассеянных электронов на
больших расстояниях от рассеивающего центра вблизи
точки
R( re , , )
должна представлять сумму двух потоков:

8.

• первичного потока налетающих частиц параллельно OX
и характеризуемого плоской волной
exp(ik e xe )
• и потока упруго рассеянных частиц, выражаемого
расходящейся сферической волной вида
1
fnn ( , ) exp(ik e re ),
re
где
1
fnn ( , )
re
- амплитуда волны упруго рассеянных электронов на
расстоянии re от атома в направлении, определяемом
углами и .

9.

en,n' ( n n')
Волновая функция
неупруго рассеянных электронов определяет вероятность
нахождения электронов с измененными энергиями (волновыми
числами) вблизи точки
R( re , , )
Таких электронов в первичном пучке нет.
Поэтому
enn '
r
1
fnn ' ( , ) exp(ik nn' re ).
re
Величина
e e * 1 f ( , ) 2
nn '
nn '
re2 nn '
выражает концентрацию
N nn ' ( re , , )
частиц, вызвавших переход частицы-мишени из начального n
состояния в конечное
n состояние и находящихся вблизи точки
R с координатами ( re , , ).

10.

k
Так как ve e ,
me
то плотность потока налетающих электронов равна
k e
Г e N e ve N e
me
Поэтому в первичной волне при условии Ne=1 плотность потока
налетающих электронов будет равна
k e
Гe
me
Поток рассеянных электронов, проходящих
через площадку dS,
центр которой расположен в точке R( re , , ) , будет равен
k nn' 1
2
dГ nn' ( re , , )
f
(
,
)
,
2 nn '
me re
здесь принято dS=1.

11.

По определению дифференциальное эффективное сечение
рассеяния на единичный телесный угол численно равняется
отношению потока рассеянных в заданном направлении частиц к
плотности потока налетающих частиц, т.е. в нашем случае будем
иметь
dГ nn ' dГ nn ' 2
nn ' ( ve , , )
re ,
Г ed
Гe
так как d
ds
,
2
re
а dS=1, то окончательно получим:
k nn '
2
nn ' ( ve , , )
fnn ' ( , ) .
ke
Отсюда
следует,
что
расчет
эффективных
сечений
взаимодействия квантово-механическими методами сводится к
вычислению амплитуды рассеянной волны
fnn' ( , ).

12.

Выведенная формула определяет понятие дифференциального
эффективного сечения рассеяния частиц в единичный телесный
угол с точки зрения квантовой механики. При этом частицамишень переходит из начального квантового состояния n в
другое состояние n , а налетающие частицы-снаряды (в нашем
случае электроны) меняют свои волновые числа от
до knn ' ,
а энергии – от
e
2
2me
ke2 до nn '
2
2me
knn2 '
ke
значения

13.

Для вычисления амплитуды рассеяния составляется волновое
уравнение системы атом - налетающий электрон в виде
( H a H e П ) W
Здесь:
H a H a ( r1,r2, ,rz ) - оператор энергии атома.
Собственные значения оператора
H a обозначим через H an , где n=1,2, ,
2
2 - оператор кинетической энергии налетающего
e
H
e
2 me
k 2 2
электрона с энергией
e
e
2 me
,
П П(re,r1,r2, ,rz ) - оператор энергии взаимодействия налетающего
электрона с атомом;
re,r1,r2 , ,rz
-
радиусы-вектора налетающего и атомных
электронов,
W const - полная энергия системы электрон-атом.

14.

Волновую функцию системы ищут в виде суммы произведений
e
волновых функций электрона nn ' и атома an ' , соответствующих
различным состояниям атома после столкновения с электроном:
an ' enn ' .
n'
Физически каждый член этой суммы соответствует совокупности атома,
перешедшего из n в n состояние, и электрона, вызвавшего этот переход,
изменив свою энергию на
nn' e nn' Wna' Wna ,
поэтому обладающего
новым значением волнового числа k nn' вместо
начального k e .
Ищут только асимптотические выражения решения волнового
уравнения, так как на опытах можно проверять только результаты
решений, характеризующие движение электрона на расстояниях во
много раз превышающих размеры атомов. Найти строгое решение
уравнения в виде, удовлетворяющем данным условиям, невозможно. Эта
задача решается различными приближенными методами

15.

Одним из них является первое приближение теории возмущений
(first order perturbation theory), обычно называемое методом Борна,
или
борновским
приближением,
в
котором
считается,
что
искажение падающей волны электрона полем атома мало и оно
может
рассматриваться
предположение
как
справедливо
малое
только
падающих электронов
mee4
e 2
или
e2
1
hve
для
возмущение.
больших
Это
энергий

16.

Решение уравнения Шредингера после подстановки в него
нулевого выражения в виде плоской волны
a
n exp(ik e x)
соответствующее отсутствию взаимодействия, дает решение
задачи в первом борновском приближении. В таком приближении,
когда
силы,
действующие
между
атомом
и
электроном,
центральные и П(r) - функция только расстояния, амплитуда
рассеяния выразится формулой
2 me
sin( kr ) 2
r dr.
fnn' ( , ) 2 П nn' ( r )
kr
0

17.

Дальнейший анализ требует раскрытия вида функции П(r). Чтобы
вычислить этот матричный элемент, необходимо задаться
определенным законом взаимодействия. Для точечных центров
притяжение (-) или отталкивания (+) пользуются стандартными
формулами. Так как рассматривается взаимодействие атома с
заряженной частицей (электроном), то можно положить
П ( re ) e ( re ),
Потенциал электрического поля вокруг атома с Z электронами
может быть выражен формулой
Z
Ze
1
( re )
e .
re
k 1 re rk
Здесь первый член выражает потенциал поля ядра, второй потенциал поля электронной оболочки атома. Подставив эти
выражения
в
предыдущие
формулы,
после
некоторых
преобразований получим

18.

2 me e2
fnn' ( , ) 2
Z nn ' Fnn' ,
2
k nn '
где Z - заряд ядра,
sin( kr ) 2
r dr - атомный фактор,
Fnn' 4 G nn ' ( r )
kr
0
nn'
( an )* an'dVa
(a)
Z
G nn' ( r )
1 для n n',
0 для n n'
( an' )* andVa
k 1( a )
Символ
dVa
(a)
дельта-функция Кронекера, и
представляет собой матричный элемент
плотности вероятности k электрона атома для
перехода n n .
обозначает интегрирование по координатам всех
электронов.

19.

Далее, после стандартных преобразований, получим выражение
для вычисления дифференциального эффективного сечения
рассеяния электронов на атомах в единичный телесный угол в
первом борновском приближении:
nn ' ( ve , , )
k nn '
ke
2
v nn '
2e 2
2
2
fnn ' ( , )
Z
F
nn' nn' .
2
me ( ve v nn ' ) ve
Эта формула описывает вероятность такого взаимодействия
электрона с атомом, в результате которого атом совершает переход
из n состояния в n , а налетающий электрон меняет свою скорость
на величину
ve v nn'
и рассеивается в направлении, определяемом углами и , внутри
единичного телесного угла.

20.

Упругое рассеяние электронов
При упругом взаимодействии частиц их квантовые состояния не
меняются, n=n , тогда nn=1. Также при упругих электрон-атомных
соударениях скорость электронов по абсолютной величине почти не
меняется. Поэтому с точностью до величин порядка me/mA будем
иметь
v nn
ve v nn
v nn
/2
/2
ve
k e k nn

21.

v nn
/2
/2
v nn
ve
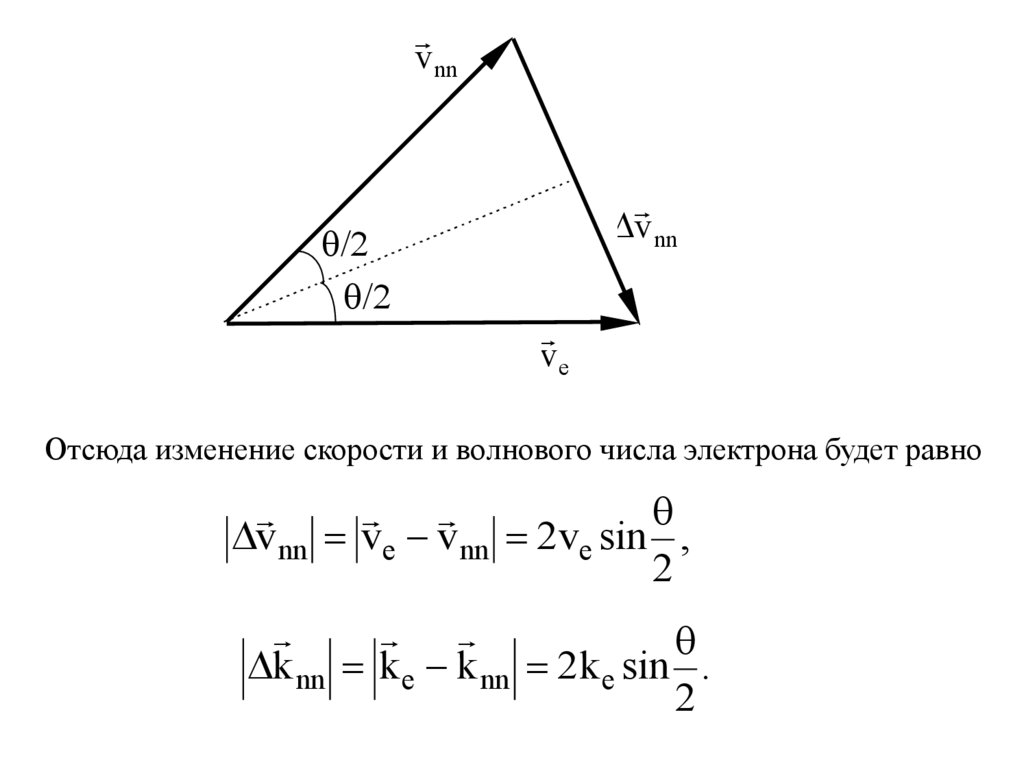
Отсюда изменение скорости и волнового числа электрона будет равно
vnn ve v nn 2ve sin ,
2
k nn k e k nn 2 k e sin .
2

22.

Для решения задачи упругого рассеяния электронов в ранее
приведенных общих выражениях для амплитуды рассеяния
fnn' ( , )
атомного фактора
Fnn'
и дифференциального эффективного сечения
nn ' ( ve , , )
Величины
k nn'
надо заменить на
k nn
2
e
1
2
nn ( ve , , )
Z Fnn
.
2
4
2 me ve
sin
2
2

23.

В простейших случаях, соответствующих распределению заряда в
атомах водорода и гелия в основных состояниях и без учета
поляризации атома плотность заряда убывает с расстоянием по
экспоненциальному закону. Для случая упругого рассеяния (n=n )
будем иметь
r
G nn ( r ) ( r ) o exp .
a
o
Zэф
8 a
3
,
ao
a
,
2 Zэф
Для водорода
H
Zэф
1,
2
8
ao
0
.
528
10
см
2
me
для гелия
He
Zэф
169
. .

24.

2 1 2a 2 k 2 sin 2
2
2
4e m Z a
e
e
эф
nn ( v e , , )
2
1 4a 2 k 2 sin 2
e
2
2
2
4
.
Исследуем это выражение для различных конкретных
условий соударений.
1)
k e a 1
me v e a .
Это означает, что скорость налетающего электрона во
много раз больше скорости орбитального движения
ve
1 .
v1

25.

Если и углы рассеяния не очень малы (на языке классической
физики - не очень большие прицельные расстояния) так, что
ak e sin 1,
2
2
e2 Z
1
эф
nn ( v e , , )
,
2m v2
e e sin 4
2
Эта формула совпадает с формулой Резерфорда, выведенной в
рамках классической физики для описания рассеяния легких
частиц на тяжелых ядрах, в предположении, что они
взаимодействуют друг с другом по закону Кулона

26.

Для случая рассеяния на малые углы, т.е. при больших
прицельных расстояниях формула Резерфорда дает
2)
nn ( ) 0 ,
в то время как волновая механика предсказывает при 0
конечное значение
nn ( ):
которое не зависит от энергии электронов
2
4e 2 m Z a 2
e эф
nn ( ) 0 nn (0)
,
2

27.

3) Рассеяние на большие углы, т.е.
, 0.
Для этих условий
sin 1
2
2
2
2
2
4e 2 m Z a 2 1 2a k e
e эф
nn ( )
.
2
4
1 4a 2 k 2e
ak e 1,
Так как мы решаем задачу в борновском приближении, т.е. когда
4e 2 m Z a 2
e эф
nn ( )
2
2
1
2 2 2
8a k e
nn (0)
2 2 2
8a k e
.

28.

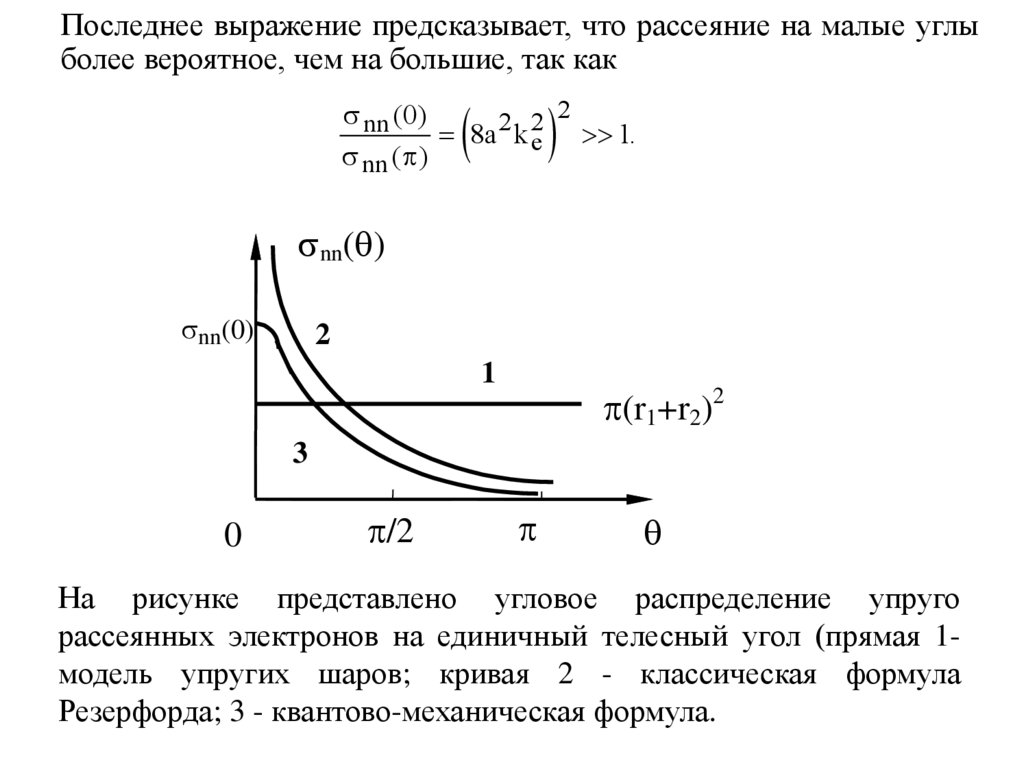
Последнее выражение предсказывает, что рассеяние на малые углы
более вероятное, чем на большие, так как
nn (0)
2 2 2
8a k e 1.
nn ( )
nn( )
nn(0)
2
1
(r1+r2)2
3
0
/2
На рисунке представлено угловое распределение упруго
рассеянных электронов на единичный телесный угол (прямая 1модель упругих шаров; кривая 2 - классическая формула
Резерфорда; 3 - квантово-механическая формула.

29.

4)
k ea 1.
Это условие означает малые скорости налетающих электронов. Этот
случай выходит за пределы применимости борновского
приближения. Все же рассмотрим и этот случай. Для этих условий
2
4e 2 m Z a 2
e эф
nn ( ) k a 1
nn (0),
2
e
то есть
nn ( )
1
nn (0)
Сечение не зависит от энергии электронов. Отсюда следует
предсказание, что электроны очень малых энергий должны
упруго рассеиваться изотропно, как упругие шары.

30.

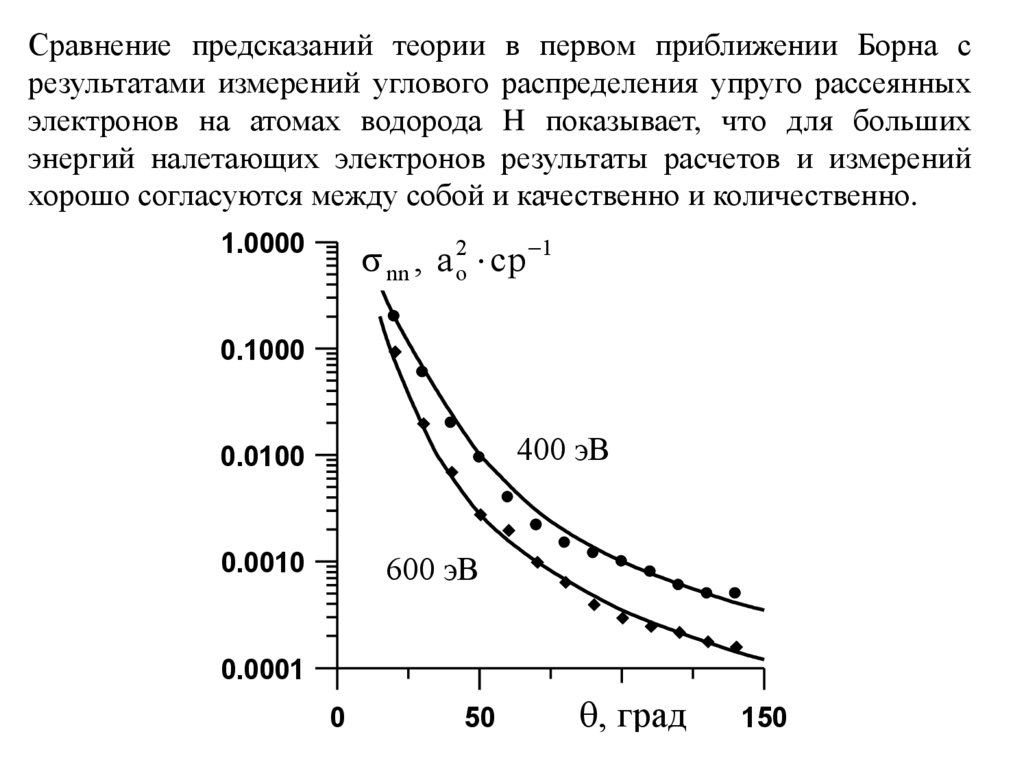
Сравнение предсказаний теории в первом приближении Борна с
результатами измерений углового распределения упруго рассеянных
электронов на атомах водорода H показывает, что для больших
энергий налетающих электронов результаты расчетов и измерений
хорошо согласуются между собой и качественно и количественно.
nn , a 2o с р 1
1.0000
0.1000
400 эВ
0.0100
600 эВ
0.0010
0.0001
0
50
,100
град
150

31.

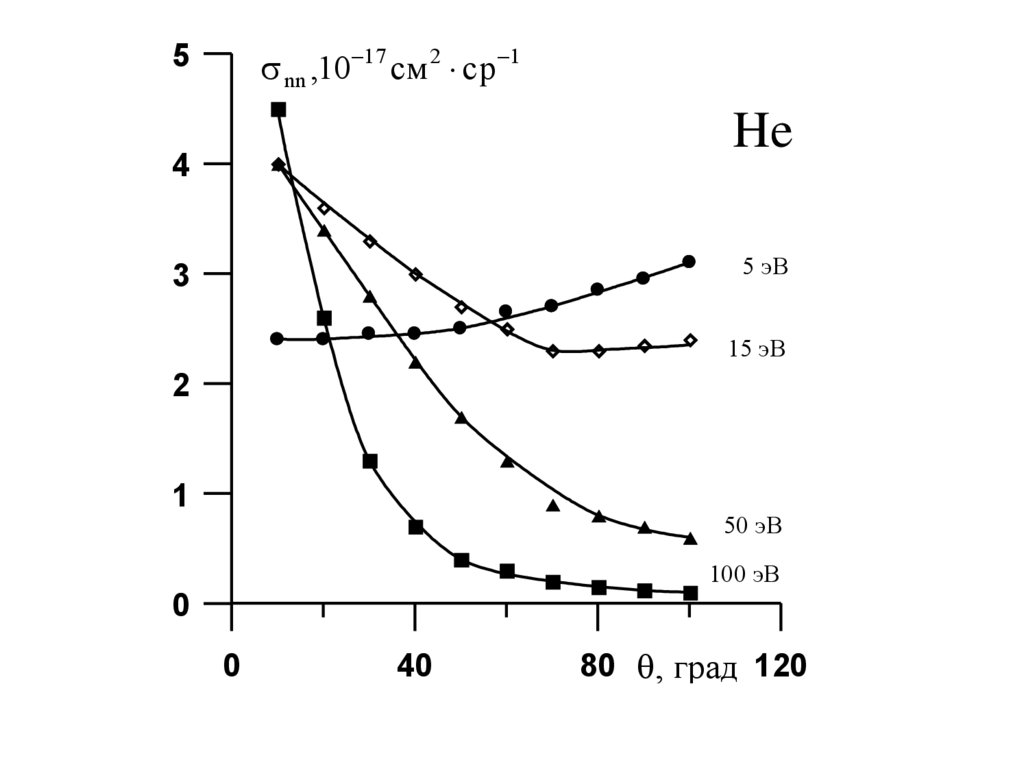
nn ,10 17 см 2 с р 1
5
He
4
5 эВ
3
15 эВ
2
1
50 эВ
100 эВ
0
0
40
80 , град 120

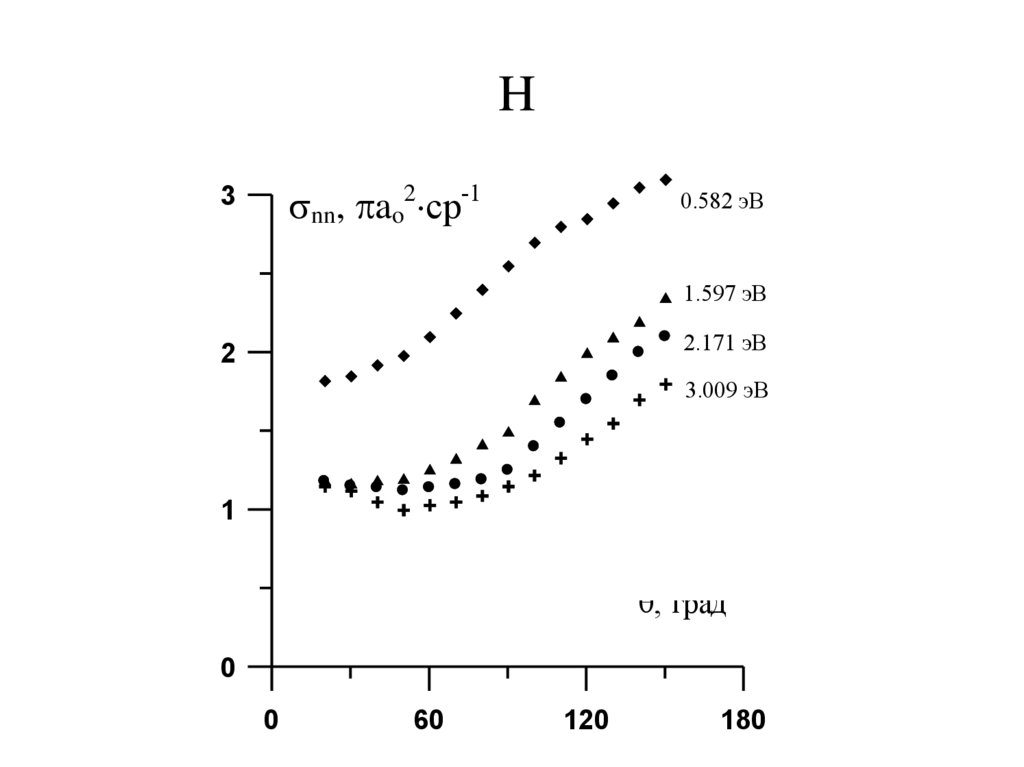
32.

H
nn, ao2 ср-1
3
0.582 эВ
1.597 эВ
2.171 эВ
2
3.009 эВ
1
, град
0
0
60
120
180

33.

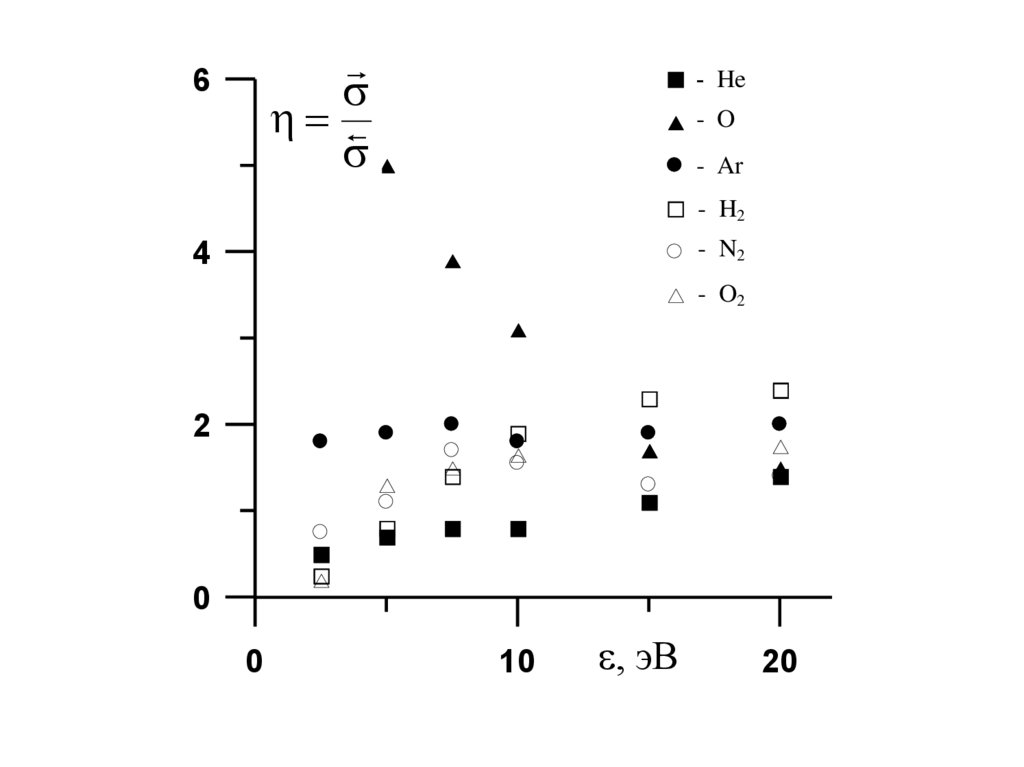
6
- He
- O
- Ar
- H2
- N2
4
- O2
2
0
0
10
, эВ
20

34.

Значение полного эффективного сечения упругого
рассеяния электронов атомами и молекулами получается
после
интегрирования
дифференциального
эффективного сечения упругого рассеяния для каждой
энергии налетающих электронов.
qnn (ke )
0
2
16 e 2 me Z э™ a 2 3 18a 2 ke2 4a 4 ke4
.
3
0 nn (ke , , ) sin d d
2
2
2
3
1 4a ke
2
Из этого выражения видно, что qnn(ve) - монотонно
убывающая зависимость от скорости электронов. Она
убывает при увеличении скорости ve (волнового числа
ke) электронов как ve-2 (ke-2 или как e-1.

35.

Возбуждение энергетических уровней и ионизация
атомов и молекул электронным ударом
n n , nn =0
2
v
2
2
e
nn' F2 ( , ).
nn' ( v e , , )
nn'
2 v
e
m
v
v
e e
nn'
Атомный фактор в выражении (2.90) пропорционален при малых
углах отклонения дипольному моменту для перехода n n , т.е.
Fnn' ( , )
k nn'
M nn' ,
e
2
nn' M n'n
me v e v nn' k ,
nn' ( v e , , )
4e 2
2 v 2e v 2nn'
v nn'
2
M nn'
ve

36.

То есть вероятность возбуждения перехода n n с рассеянием
электронов на малые углы пропорциональна квадрату
дипольного момента
M n' n
2
для перехода n n. Поэтому переходы, для которых
M n' n 0
(оптически запрещенные переходы: l=0, 2, ; S 0) имеют
малые вероятности возбуждения электронным ударом
Это
предсказание
теории
хорошо
согласуется
с
экспериментальными данными по изучению рассеяния
электронов с возбуждением энергетических уровней простых
атомов.

37.

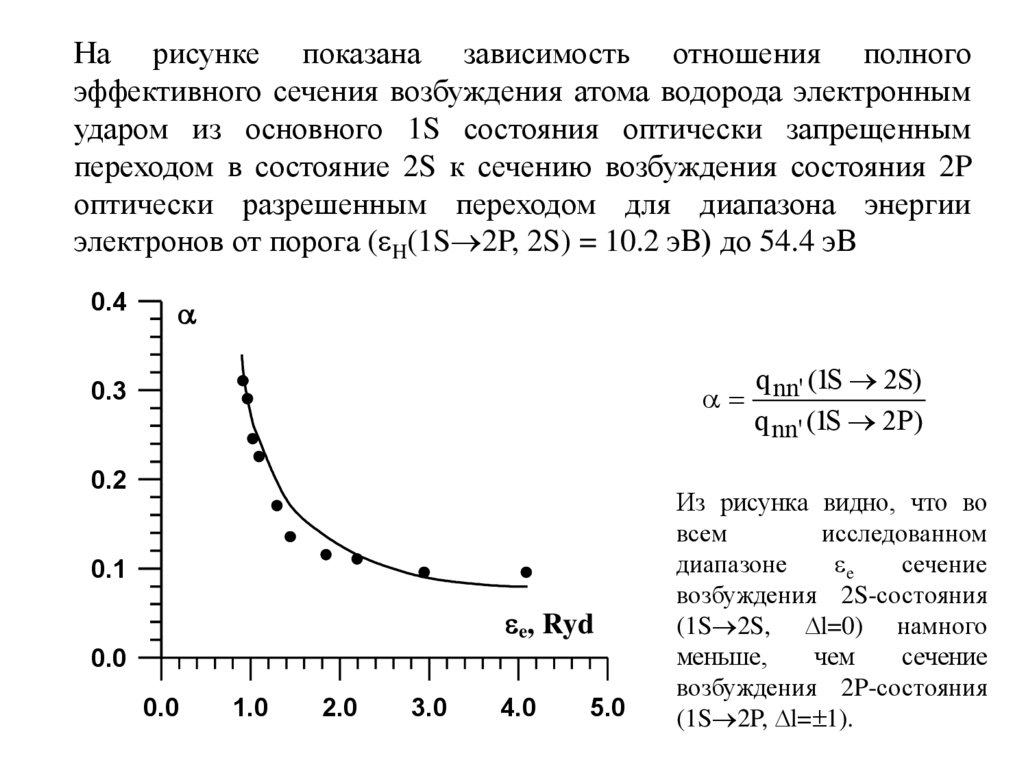
На рисунке показана зависимость отношения полного
эффективного сечения возбуждения атома водорода электронным
ударом из основного 1S состояния оптически запрещенным
переходом в состояние 2S к сечению возбуждения состояния 2P
оптически разрешенным переходом для диапазона энергии
электронов от порога ( H(1S 2P, 2S) = 10.2 эВ) до 54.4 эВ
0.4
q (1S 2S)
nn'
q nn' (1S 2 P)
0.3
0.2
0.1
e, Ryd
0.0
0.0
1.0
2.0
3.0
4.0
5.0
Из рисунка видно, что во
всем
исследованном
диапазоне
e
сечение
возбуждения 2S-состояния
(1S 2S, l=0) намного
меньше,
чем
сечение
возбуждения 2P-состояния
(1S 2P, l= 1).

38.

v nn'
v e v nn '
ve
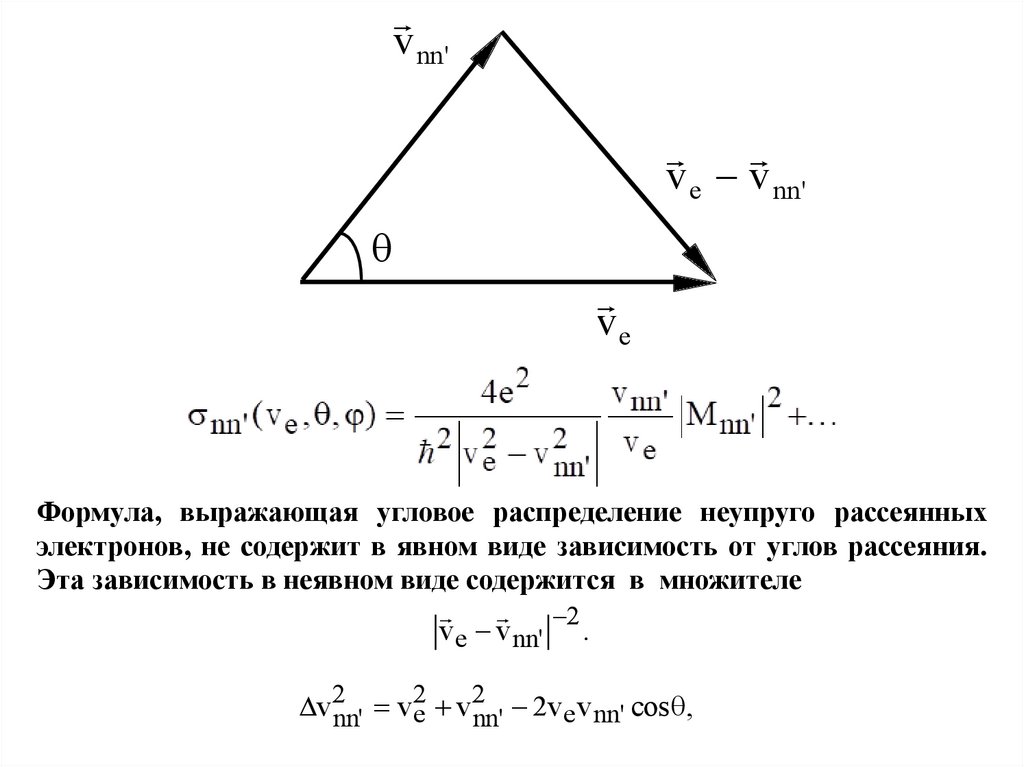
Формула, выражающая угловое распределение неупруго рассеянных
электронов, не содержит в явном виде зависимость от углов рассеяния.
Эта зависимость в неявном виде содержится в множителе
2
v e v nn' .
v2nn' v2e v2nn' 2ve v nn' cos ,

39.

Проинтегрировав дифференциальное эффективное сечение рассеяния в
единичный телесный угол по k, найдем полное сечение возбуждения
атома из n в n состояние, при котором волновое число электрона
изменяется (уменьшается) на величину
k nn' k e k nn' :
2
k nn' max
2 me e
k nn' max
q nn' ( k nn' )
,
nn' ( k nn' )d k nn' 2 2 M nn' ln k
ke
nn' min
k nn' min
Подставив значения
k nn' max
и
k nn' min
получаем выражение для полного эффективного сечения возбуждения
n n электронным ударом в первом борновском приближении:
q nn' ( e )
4 me e 2
2
M nn'
qnn ( e ) ~
1
e
2 1
e
ln e
ln
4 e
.
nn'