2

1. Примеры непосредственного интегрирования

Примеры
интегрирования
методом подстановки
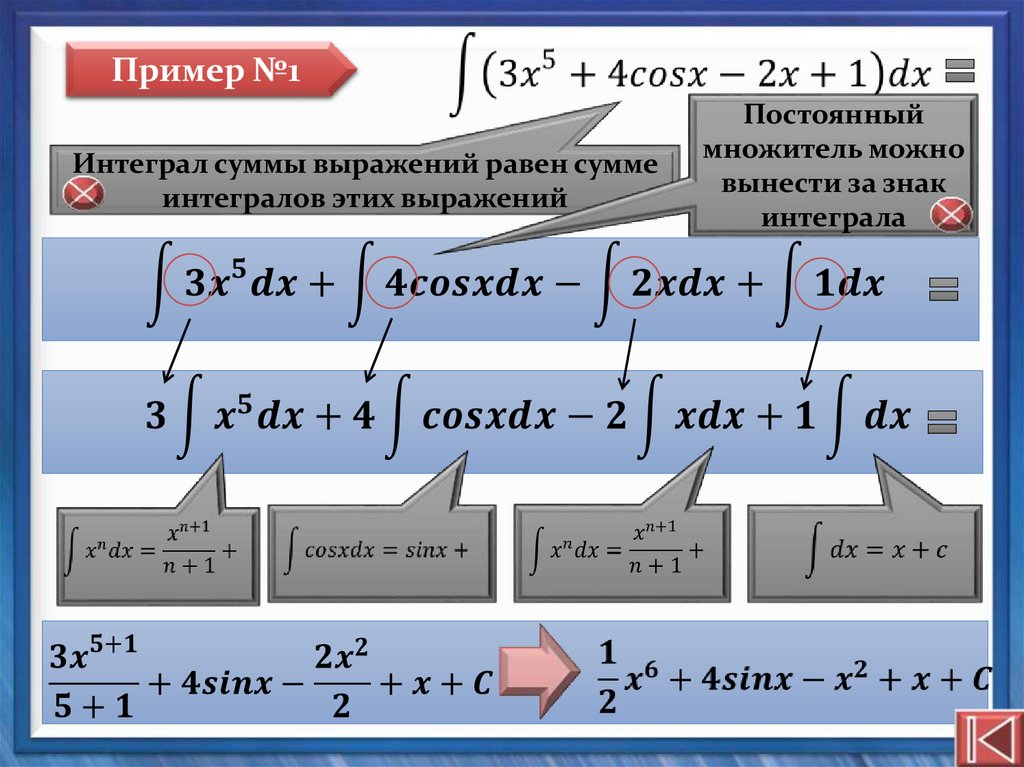
Пример №1
Пример №4
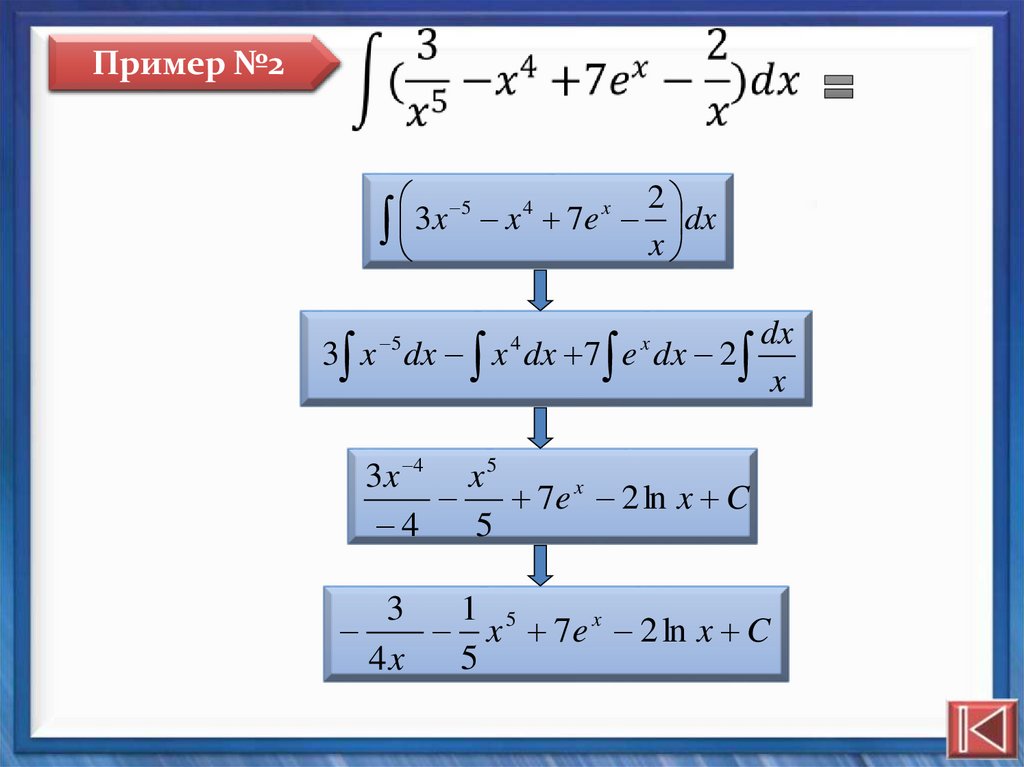
Пример №2
Пример №5
Пример №6
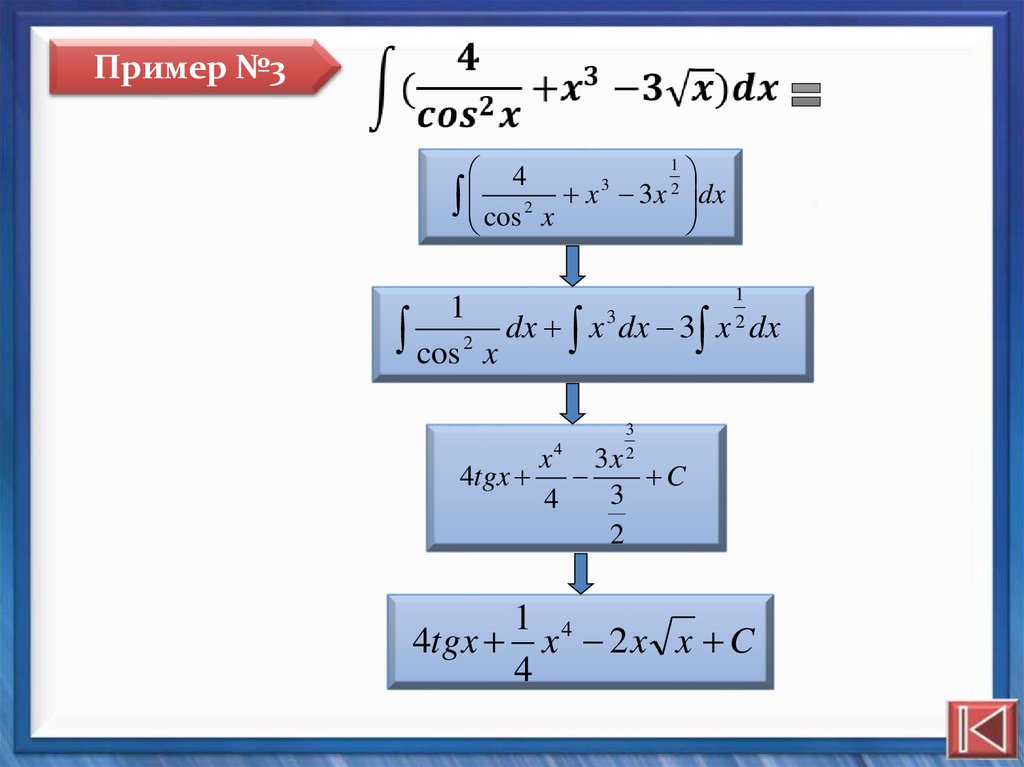
Пример №3
Пример №7

2.

Пример №2
2
5
4
x
3x x 7e x dx
dx
3 x dx x dx 7 e dx 2
x
5
4
x
3x 4 x 5
7e x 2 ln x C
4
5
3
1 5
x 7e x 2 ln x C
5
4x

3.

Пример №1
Интеграл суммы выражений равен сумме
интегралов этих выражений
Постоянный
множитель можно
вынести за знак
интеграла

4.

Пример №3
1
4
3
2
x
3
x
cos 2 x
dx
1
1
3
2
dx
x
dx
3
x
cos 2 x
dx
4tgx
4
3
2
x 3x
C
3
4
2
1 4
4tgx x 2 x x C
4

5.

Пример №4
Определяем, к какому табличному интегралу
приводится данный интеграл
Определяем, какую часть
подынтегральной функции нужно
заменить и записываем замену
Находим дифференциалы обеих частей,
выражаем старый дифференциал через новый
Производим замену в интеграле и
вычисляем его, используя таблицу
Производим обратную замену, то есть
возвращаемся к старой переменной

6.

Пример №5
u 6x 2
du 6dx
1
dx du
6
1
sin u 6 du
1
sin udu
6
1
cos 6 x 2 C
6
1
cos u C
6

7.

Пример №6
u 1 ln x
du
u du
2 3
u C
3
1
dx
dx
2
x
1
2
u du
2
u u C
3
3
2
2
u C
3
2
1 ln x 1 ln x C
3

8.

Пример №7
u 3 6x
du 6dx
1
dx du
6
1
u du
6
3
1
3 6 x 2 C
9
1
2
1
u du
6
3
1 2 2
u C
6 3
1
3 6 x 3 6 x C
9

9.

Алгоритм вычисления интегралов методом
непосредственного интегрирования
1. Преобразуем подынтегральную
функцию и представляем интеграл в
виде суммы или разности интегралов.
2. Выносим постоянные множители за
знаки интегралов.
3. Сводим полученные интегралы к
табличным интегралам.
4. Вычисляем и записываем ответ.

10.

Алгоритм вычисления интегралов методом
замены переменной
1. Определяем, к какому табличному интегралу
приводится данный интеграл.
2. Определяем, какую часть подынтегральной
функции нужно заменить и записываем замену.
3. Вычисляем дифференциал новой переменной,
выражаем старый дифференциал через новый.
4. Производим замену и вычисляем полученный
интеграл с помощью таблицы интегралов.
5. Возвращаемся к старой переменной и
записываем ответ.

11.

Проверить
решение
Найти неопределенный
интеграл
Проверить
решение

12.

Следует отметить, что для функции вида f(kx+b)
можно применять упрощенную формулу

13.

Применение интегралов к решению
профессионально-направленных задач
Задача: В результате значительной потери крови содержание железа в крови
уменьшилось на 210 мг. Скорость восстановления недостатка железа определяется
соотношением , где - время в сутках. Определите закон восстановления
недостатка железа.
Решение:
t
7
Постоянную С определяем,
используя начальные условия:
t
7
u 30e dt 30 e dt
Интеграл вычисляем методом замены переменной:
x
t
7
30 7 e dx 210e C 210e
x
0
7
C 210 C 0
t
7
1
u t 30 e dt dx dt
7
dt 7dx
x
210e
Закон восстановления недостатка
железа имеет вид:
t
7
C
u t 210e
t
7