Лекция 9-10 Пределы-

1. Введение в математический анализ

2.

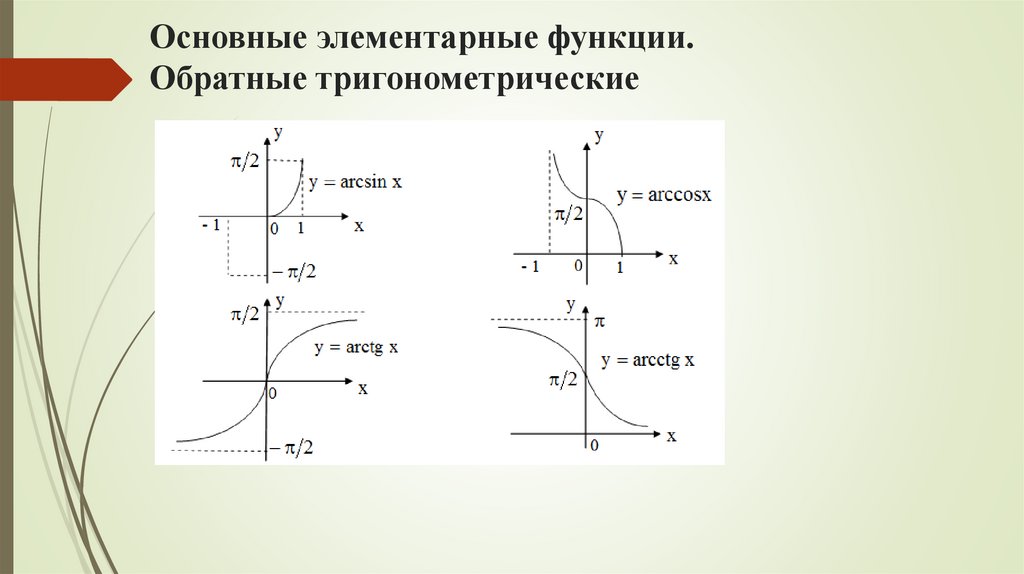
Функция. Способы задания функции. Свойства функций.
Основные элементарные функции и их графики
Предел функции.
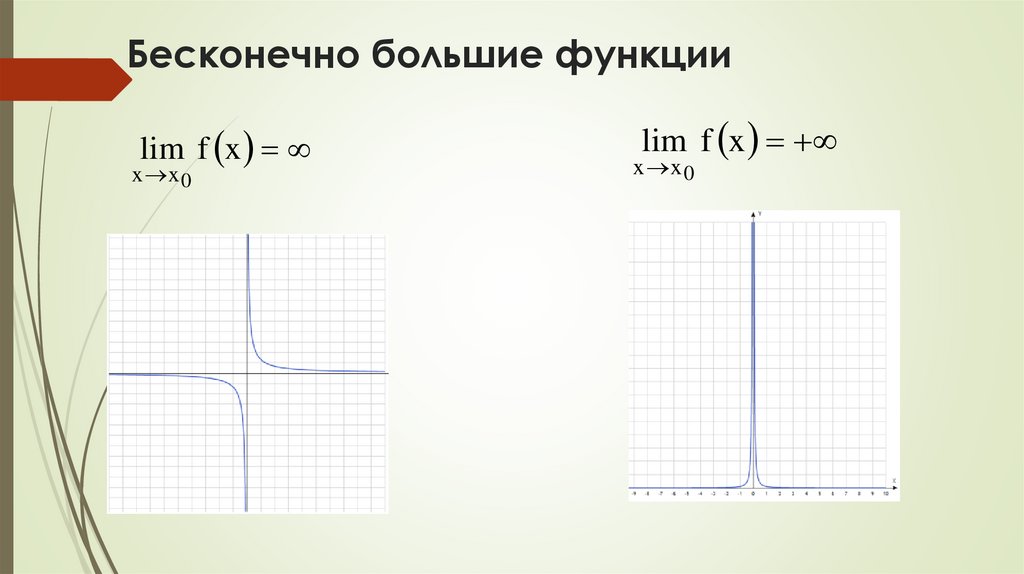
Бесконечно малые и бесконечно большие функции, их
свойства.
Дробно-рациональная функция и ее предел.
Первый и второй замечательные пределы.
Эквивалентные бесконечно-малые функции

3. Определения

.
Определения
Множество - совокупность некоторых объектов, объединенных в одно
целое по какому-либо признаку.
Пустое множество - множество, не содержащее ни одного элемента.
Обозначается символом ∅
Множество A называется подмножеством множества B, если каждый
элемент множества A является элементом множества B. A⊂ B
Равные множества - множества состоящие из одних и тех же элементов.
A= B
Объединением или суммой множеств и называется множество,
состоящее из элементов, каждый из которых принадлежит хотя бы одному
их этих множеств. A∪B
Пересечением или произведением множеств A и B называется
множество, состоящее из элементов, каждый из которых принадлежит
множеству A и множеству B. A ∩ B

4. ФУНКЦИЯ

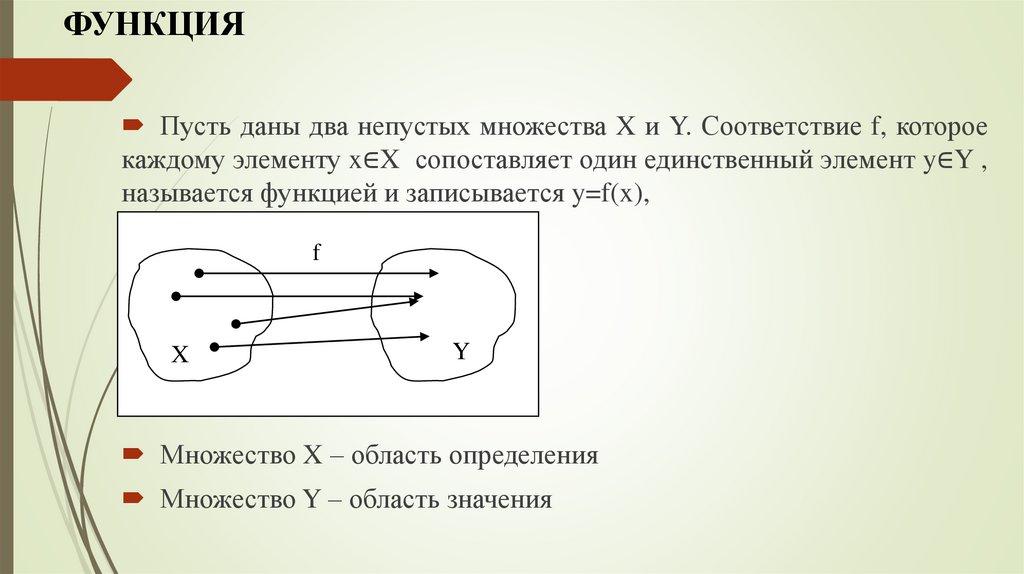
Пусть даны два непустых множества X и Y. Соответствие f, которое
каждому элементу x∈X сопоставляет один единственный элемент y∈Y ,
называется функцией и записывается y=f(x),
f
X
Y
Множество X – область определения
Множество Y – область значения

5. Способы задания функции

Табличный способ задания функции заключается в перечислении
значений аргумента и соответствующих значений функции.
Графический способ задается график функции.

6. Свойства

Функция