четные и нечетные функции

1.

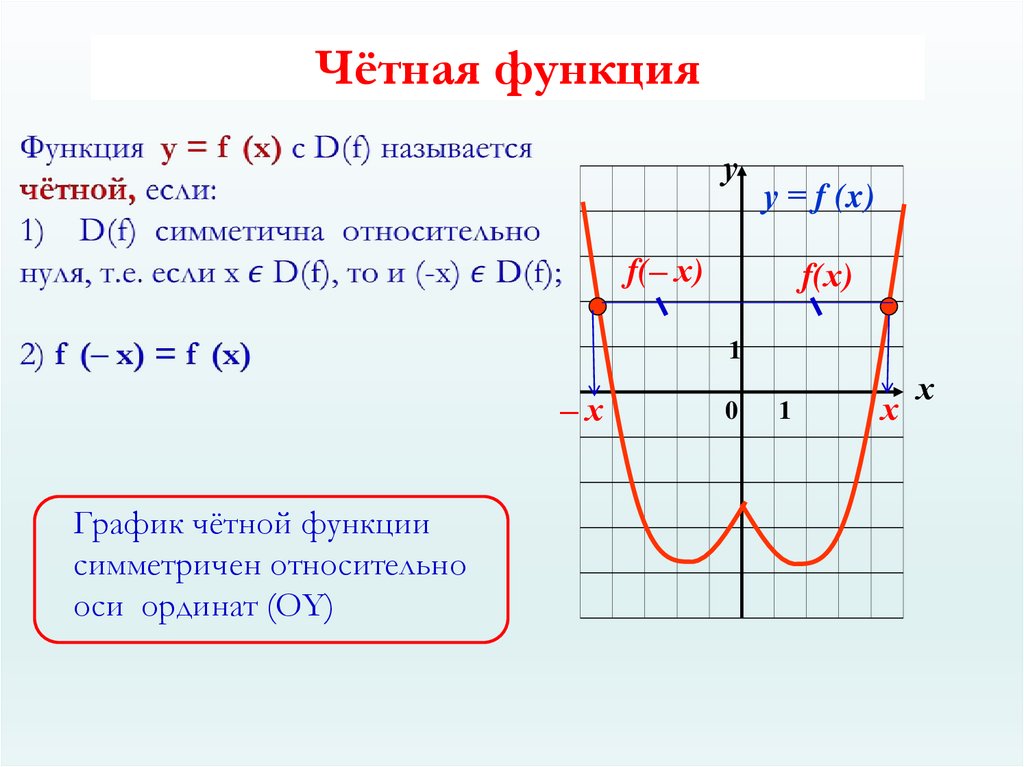
Чётные и нечётные функции.

2. Чётная функция

у
у = f (x)
f(‒ х)
f(х)
1
‒х
График чётной функции
симметричен относительно
оси ординат (ОY)
0
1
х
х

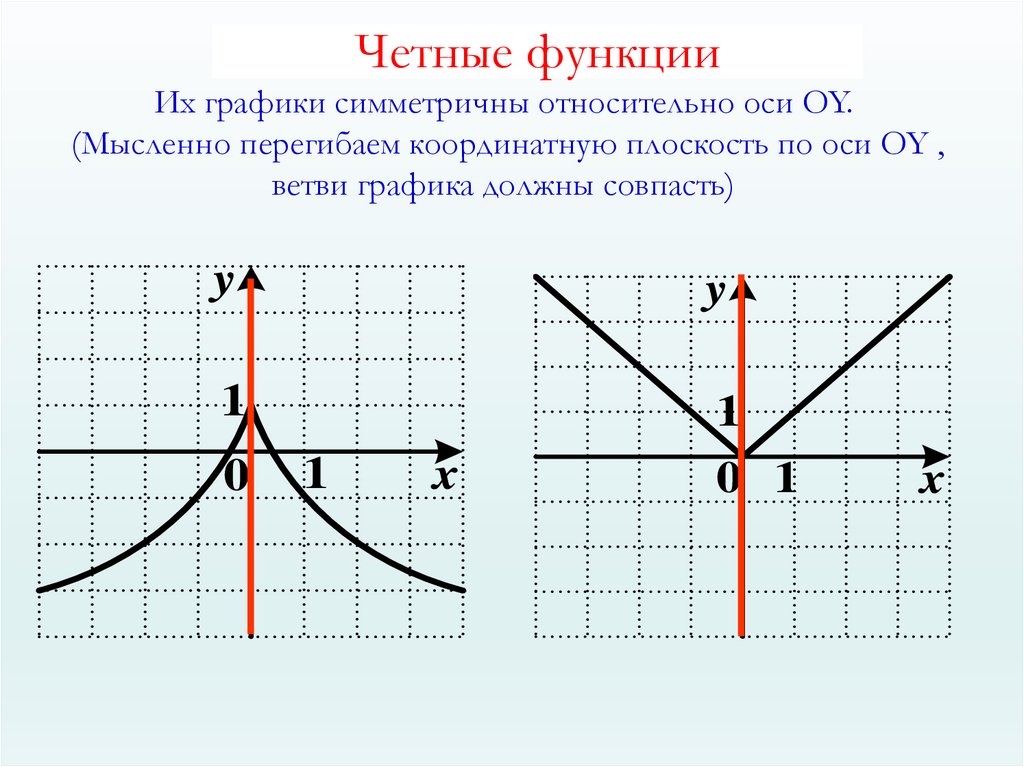
3. Четные функции

Их графики симметричны относительно оси OY.
(Мысленно перегибаем координатную плоскость по оси OY ,
ветви графика должны совпасть)
y
y
1
1
0 1
0
1
x
x

4.

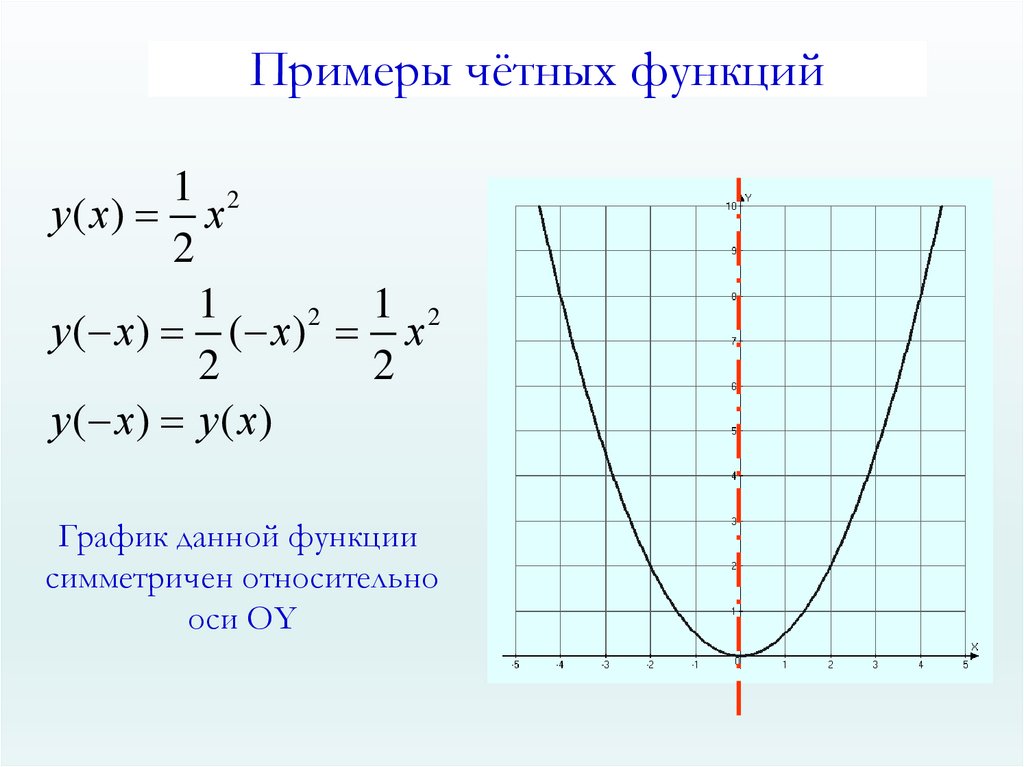
Примеры чётных функций
1 2
у ( х) х
2
1
1 2
2
у ( х) ( х) х
2
2
у ( х) у ( х)
График данной функции
симметричен относительно
оси ОY

5.

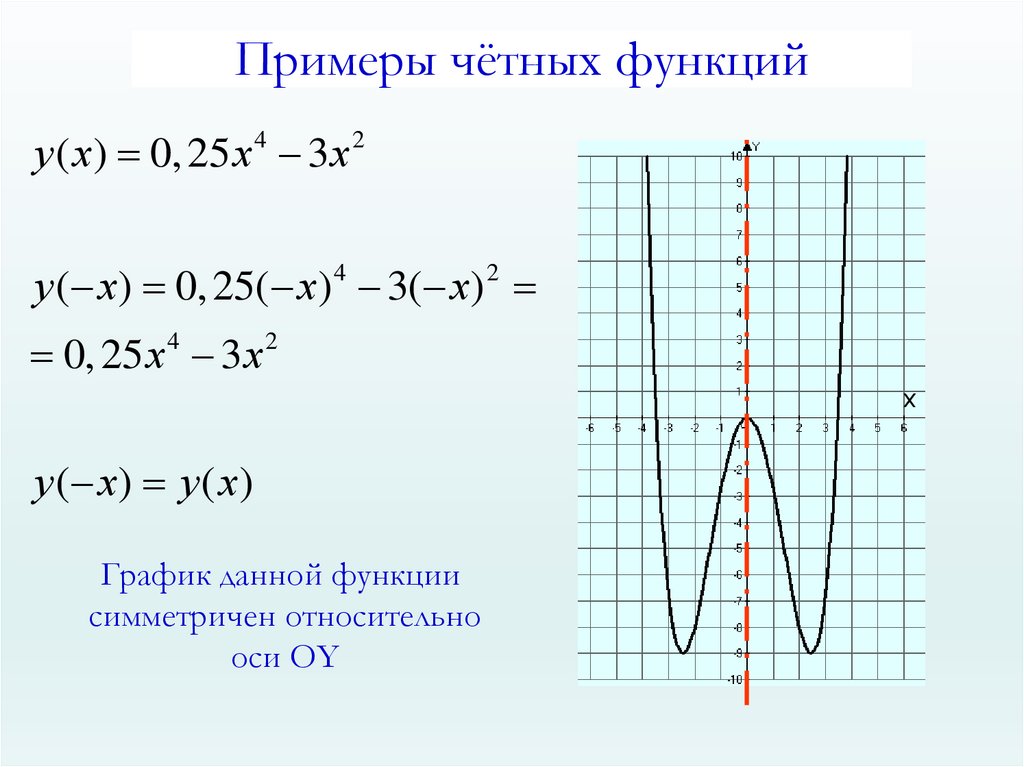
Примеры чётных функций
у ( х) 0, 25 х 4 3 х 2
у ( х) 0, 25( х) 4 3( х) 2
0, 25 х 4 3 х 2
х
у ( х) у ( х)
График данной функции
симметричен относительно
оси ОY

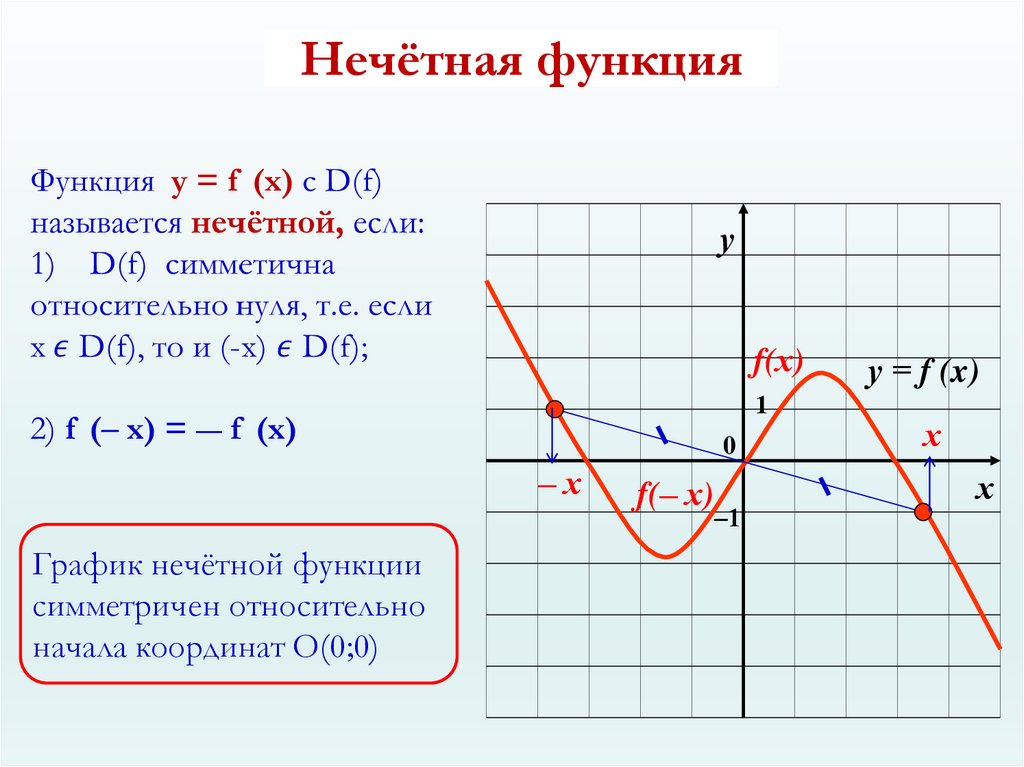
6. Нечётная функция

у
f(х)
1
0
‒х
График нечётной функции
симметричен относительно
начала координат О(0;0)
f(‒ х)
‒1
у = f (x)
х
х

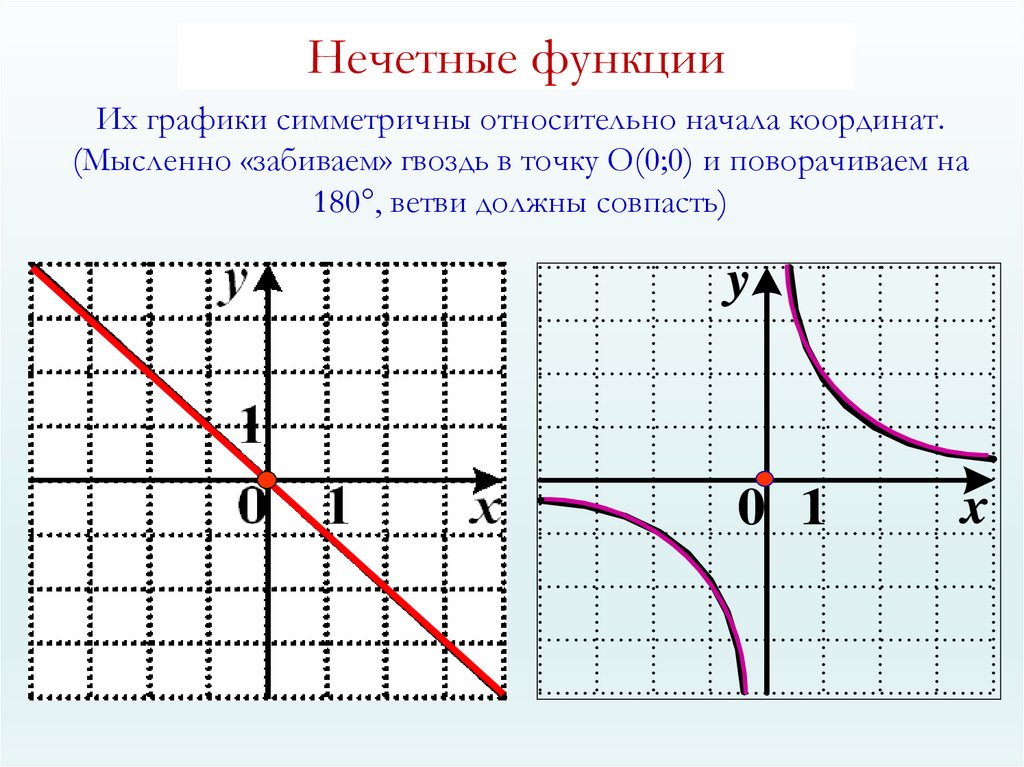
7. Нечетные функции

Их графики симметричны относительно начала координат.
(Мысленно «забиваем» гвоздь в точку O(0;0) и поворачиваем на
180°, ветви должны совпасть)
y
0 1
x

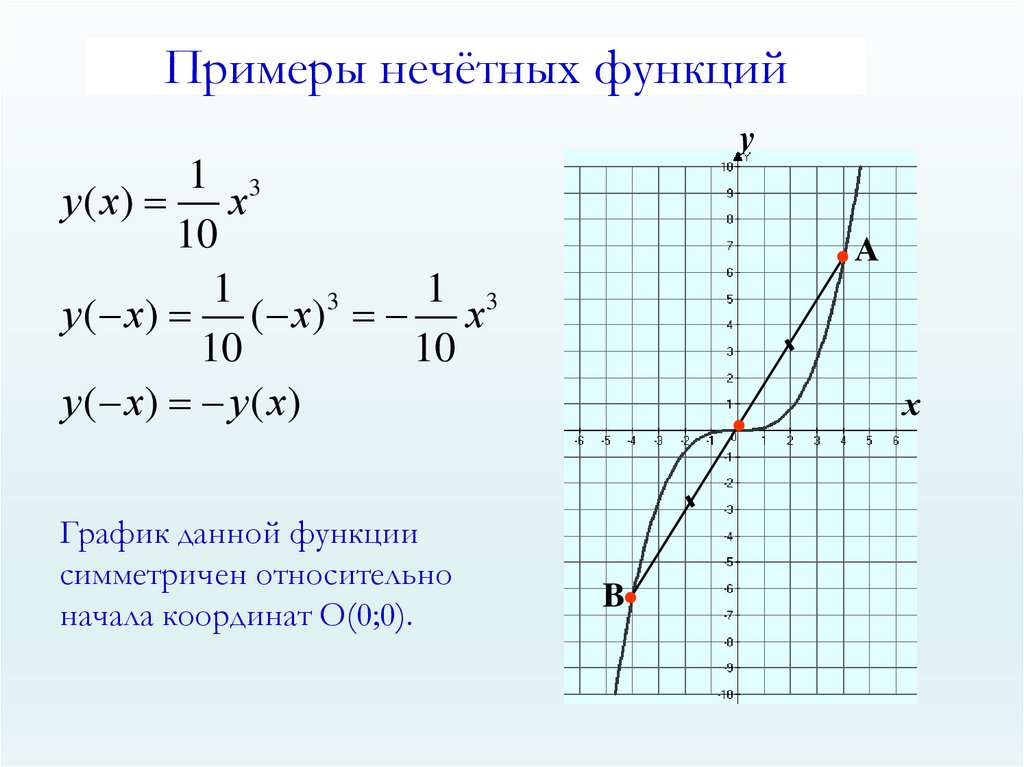
8.

Примеры нечётных функций
у
1 3
у ( х) х
10
1
1 3
3
у ( х) ( х) х
10
10
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат О(0;0).
А
х
B

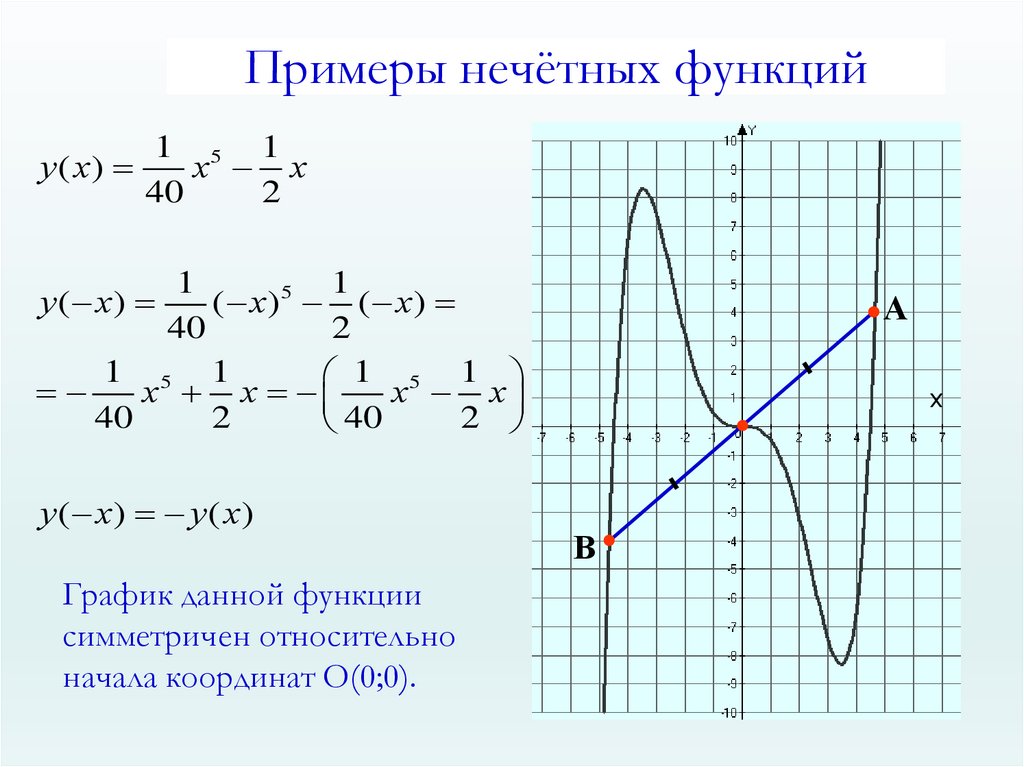
9.

Примеры нечётных функций
1 5 1
у ( х)
х х
40
2
1
1
5
у ( х)
( х) ( х)
40
2
1 5 1
1 5 1
х х
х х
40
2
2
40
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат О(0;0).
А
х
В

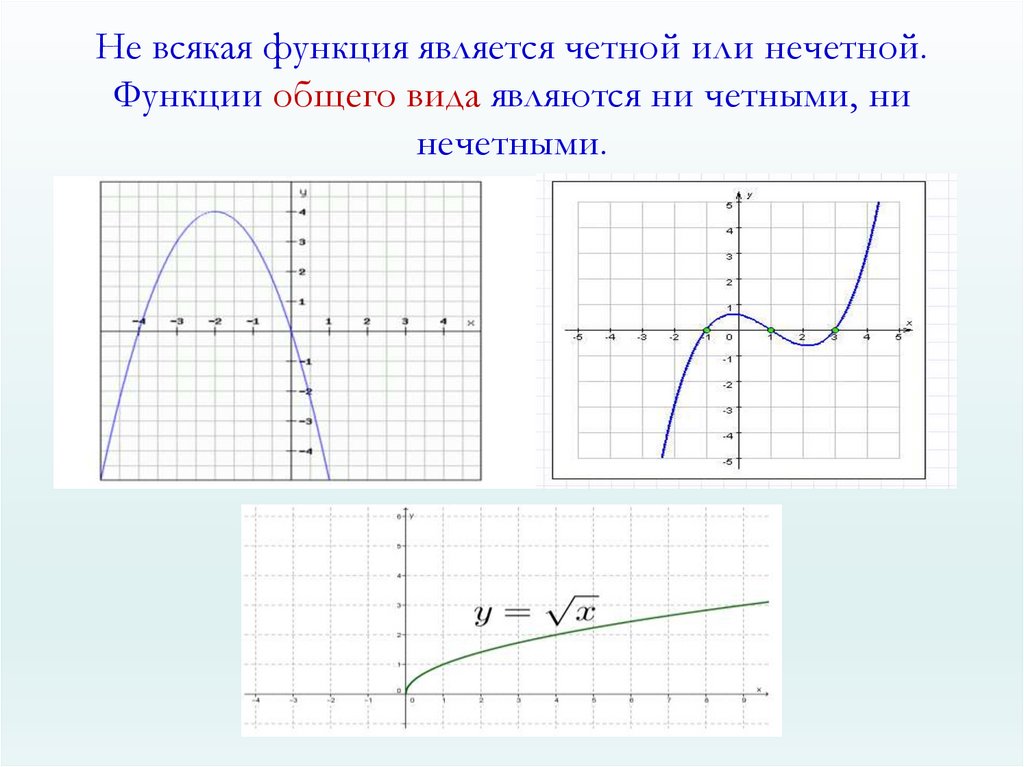
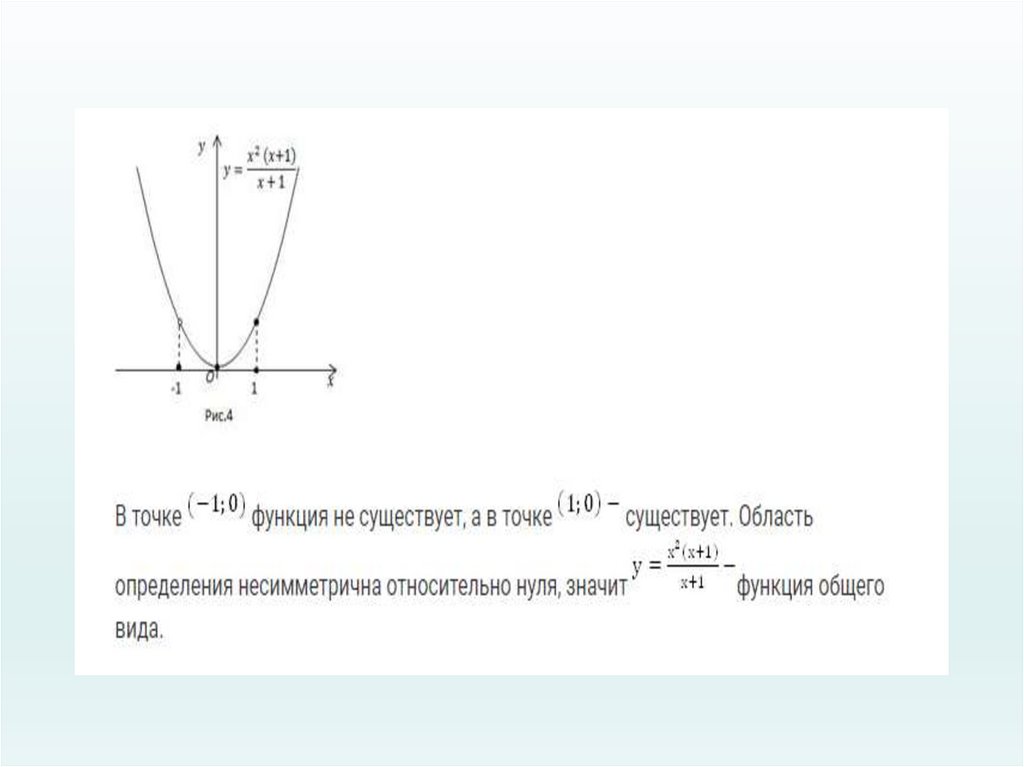
10. Не всякая функция является четной или нечетной. Функции общего вида являются ни четными, ни нечетными.

11.

12.

13.

14.

15.

16.

17. Ответь на вопросы:

• Может ли быть чётной или нечётной функция,
областью определения которой является:
а) промежуток [ - 2; 5 ] ;
б) промежуток ( - 7; 7 );
в) объединение промежутков [ - 10; - 2 ] U [ 2; 10 ] .
• а) Функция f – чётная, f (3) = 25. Найти f (- 3).
б) Функция f – нечётная, f (- 8) = 71. Найти f (8).