1 Линейные-1

1. ЛИНЕЙНЫЕ УРАВНЕНИЯ

ax + b = 0

2. Историческая справка: Древний Египет

В папирусе Ахмеса (Ринда) уже встречаются
задачи, сводящиеся к линейным уравнениям
вида ax=b . Египтяне использовали метод
«ложного положения» (регула фальси) — подбор
значения неизвестного с последующей
пропорциональной корректировкой.

3. Историческая справка: Древний Вавилон

Вавилоняне решали простейшие линейные
уравнения в рамках хозяйственных и
геометрических задач, хотя их записи были
табличными и алгоритмическими, без
символики.

4. Историческая справка: Древняя Греция

Диофант Александрийский в труде
«Арифметика» использовал буквенную
символику (в зачаточной форме) и решал
линейные уравнения как часть диофантовых
задач.

5. ОПРЕДЕЛЕНИЕ

ax + b = 0 где a ,
b – некоторые числа, x –
Уравнение вида
переменная, называется линейным
уравнением.

6. Линейное уравнение

Если а ≠ 0, то линейное
уравнение имеет
единственный корень х = -b/a
Если а = 0; b ≠ 0 , то линейное
уравнение не имеет решений.
Если а = 0; b = 0, то х – любое
число.

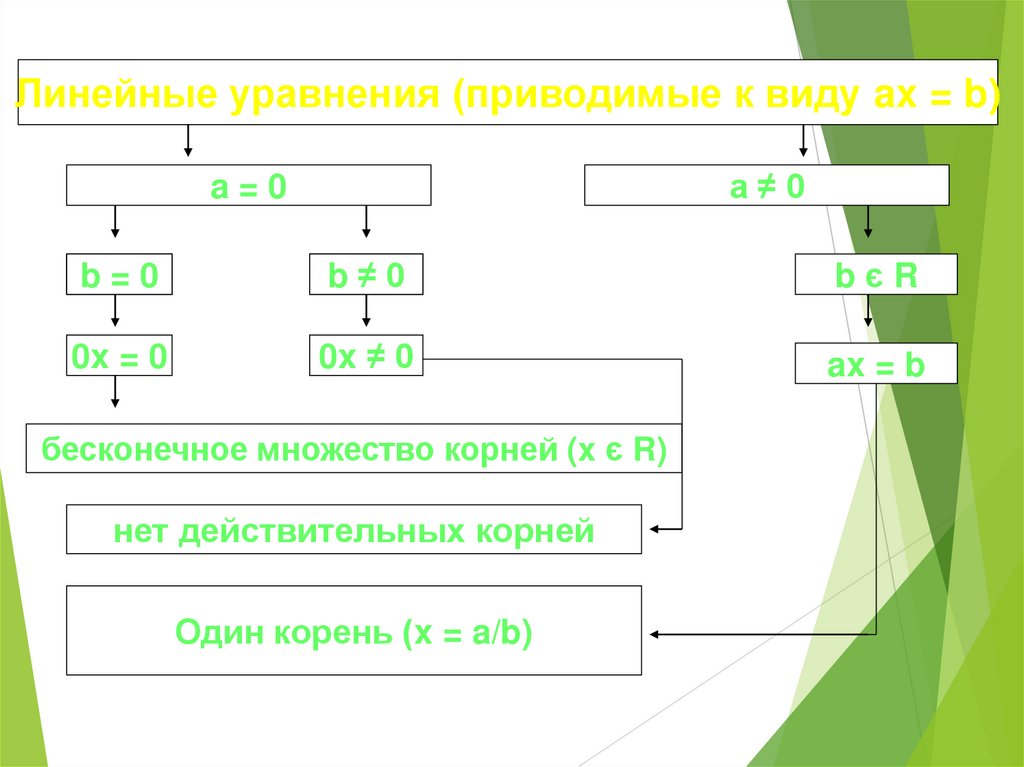
7.

Линейные уравнения (приводимые к виду ax = b)
a≠0
a=0
b=0
b≠0
bєR
0x = 0
0x ≠ 0
ax = b
бесконечное множество корней (x є R)
нет действительных корней
Один корень (x = a/b)

8. Методы решения

9. АЛГОРИТМ РЕШЕНИЯ ЛИНЕЙНОГО УРАВНЕНИЯ

Пример 1.
Решим уравнение 2x – 3 + 4(x – 1) = 5
Решение. 2x – 3 + 4x – 4 = 5
6x = 5 + 4 + 3
6x = 12
x = 12 : 6
x=2
Ответ: 2

10. АЛГОРИТМ РЕШЕНИЯ ЛИНЕЙНОГО УРАВНЕНИЯ

Пример 2.
Решим уравнение 2x – 8 – 2(x – 2) = 0
Решение. 2x – 8 – 2x + 4 = 0
-4=0
Ответ: решений нет!!!!!

11. АЛГОРИТМ РЕШЕНИЯ ЛИНЕЙНОГО УРАВНЕНИЯ

Пример 3.
Решим уравнение 3x + 6 – 3(x + 2) = 0
Решение. 3x + 6 – 3x – 6 = 0
0=0
Ответ: x – любое число.

12. Что такое система линейных уравнений?

13. Методы решения систем линейных уравнений: графический метод

14. Методы решения систем линейных уравнений: метод подстановки

15. Методы решения систем линейных уравнений: Метод сложения (алгебраического суммирования)