Лекция 6. Векторная алгебра ч.1

1. ВЕКТОРНАЯ АЛГЕБРА (основные понятия)

ЛЕКЦИЯ 6

2.

ЧТО ИЗУЧАЕТ ВЕКТОРНАЯ АЛГЕБРА?
Предметом изучения в векторной алгебре являются векторные
величины(векторы) и действия с ними. Понятие вектора возникает
там, где приходится иметь дело с объектами, которые
характеризуются величиной и направлением. Примерами таких
величин могут служить вектор перемещения (самолёта из точки А в
точку Б), вектор градиента (крутизны склона в определенном
направлении) и т.д.
Понятие вектора позволяет существенно упростить операции с
большими структурированными наборами чисел, ведь цифровые
данные, используемые в различных областях, также можно представить
в виде систем векторов.

3.

РАССМОТРИМ НА ПОНЯТНОМ ПРИМЕРЕ
ЭМОЦИОНАЛЬНЫЙ
ИНТЕЛЛЕКТ
Векторы состояния человека:
Ось X: уровень тревожности (от -10 "спокойствие" до +10 "паническая атака").
Ось Y: уровень энергии (от -10 "апатия" до +10 "мания").
Ось Z: уровень настроения (от -10 "депрессия" до +10 "эйфория").
Вектор студента А на момент перед модульной контрольной работой по математике: V1_A = (8, -5, -7).
Что это значит? Высокая тревожность, низкая энергия, подавленное настроение — классическая картина
депрессивного эпизода.
Вектор его же после получения положительной оценки: V2_А = (2, 2, 5).
Анализ: можно построить вектор изменения состояния: ΔV = V2_А – V1_A = (-6, 7, 12). Длина этого
вектора |ΔV| покажет величину улучшения, а его направление укажет, в какую именно сторону
сместилось состояние (снизилась тревожность и выросла энергия с настроением).

4.

ПРИМЕЧАТЕЛЬНО, что в 1901 году вышел
полноценный и обширный учебник по
векторному анализу американского физика
и математика Джозайи Уилларда Гиббса

5.

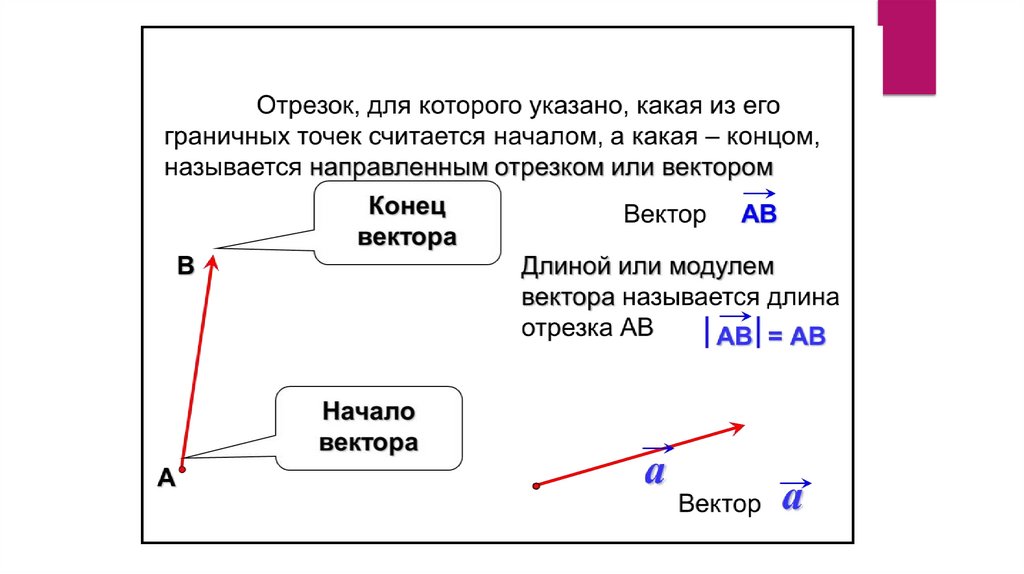
Определение:
Вектор — это направленный
прямолинейный отрезок, т. е.
отрезок, имеющий
определенную длину и
определенное направление.

6.

7. Свободные векторы

Свободный вектор – множество
одинаково направленных отрезков.
Таким образом, свободный вектор
можно отложить от любой точки
пространства, «клонируя» бесконечное
количество раз. Равные векторы- это
один и тот же СВОБОДНЫЙ
ВЕКТОР.

8.

9.

коллинеарность векторов записывают
привычным значком параллельности:
, при этом возможна детализация:
(векторы сонаправлены) или
(векторы направлены
противоположно).

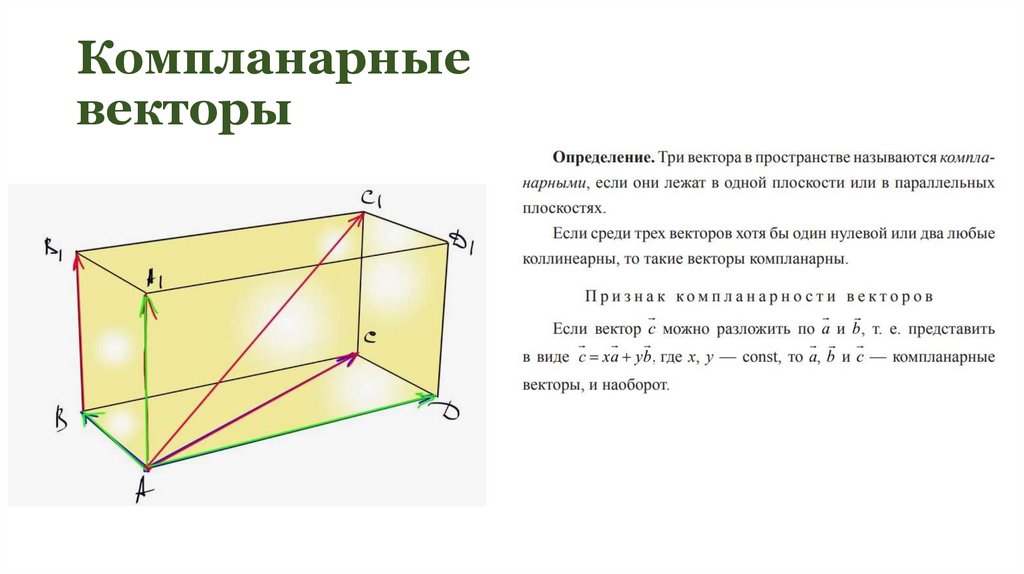
10. Компланарные векторы

11. Действия с векторами (линейные операции)

12.

13.

14. Свойства линейных операций над векторами

15.

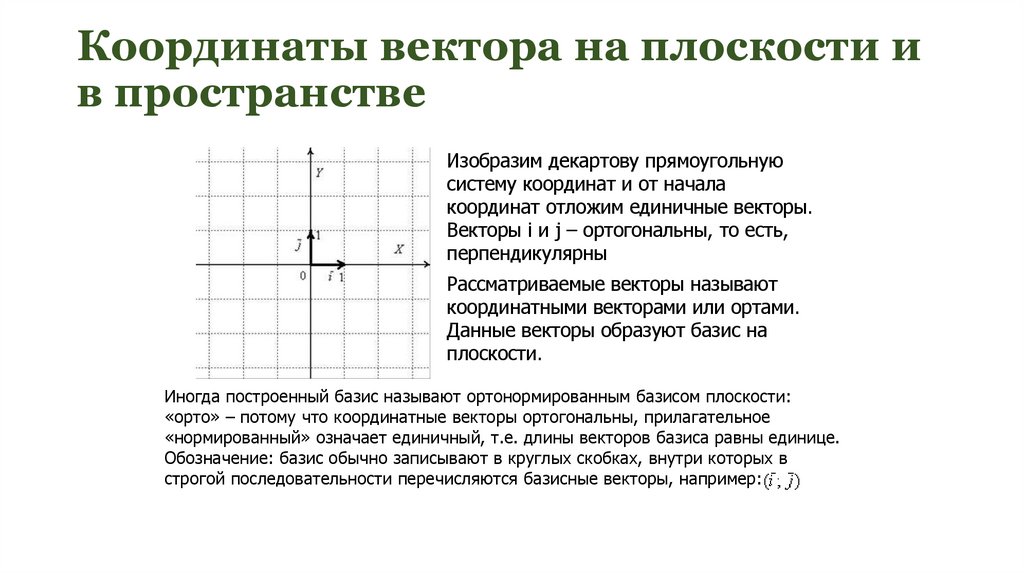
16. Координаты вектора на плоскости и в пространстве

Изобразим декартову прямоугольную
систему координат и от начала
координат отложим единичные векторы.
Векторы i и j – ортогональны, то есть,
перпендикулярны
Рассматриваемые векторы называют
координатными векторами или ортами.
Данные векторы образуют базис на
плоскости.
Иногда построенный базис называют ортонормированным базисом плоскости:
«орто» – потому что координатные векторы ортогональны, прилагательное
«нормированный» означает единичный, т.е. длины векторов базиса равны единице.
Обозначение: базис обычно записывают в круглых скобках, внутри которых в
строгой последовательности перечисляются базисные векторы, например:

17. Координаты вектора на плоскости и в пространстве

18. Ортонормированный вектор в трехмерном пространстве

19. Как найти вектор по двум точкам?

20. Как найти вектор по двум (трем) точкам?

21. Как найти длину отрезка?

22. Действия с векторами в координатах

23. Скалярное произведение векторов