Геометрические вектора

1.

Геометрические
вектора

2.

Основные представления
элементарной геометрии

3.

Геометрия — (греч. γεωμετρία, от γῆ — Земля и μετρέω
— измеряю) раздел математики, изучающий пространственные
отношения и формы, а также другие отношений и формы,
сходные с пространственными по своей структуре.
Пространство называется метрическим, если в нем
можно ввести расстояние между элементами. Для
геометрического пространства понятие расстояния (меры,
длины) является одним из основополагающих. Именно данное
понятие позволяет дать определение основным объектам
элементарной геометрии, такие как точка, пространство,
отрезок, прямая, плоскость, угол между прямыми.

4.

5.

6.

7.

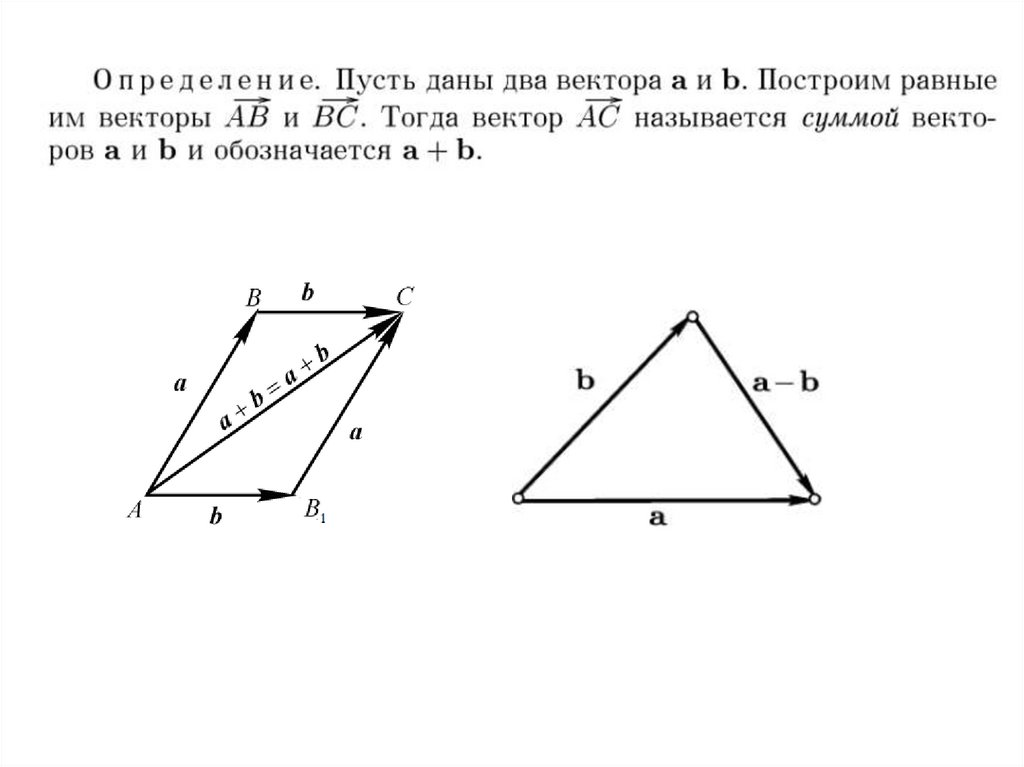
Геометрический вектор
Свободный вектор (вектор) - множество всех
сонаправленных отрезков одинаковой длины. Свободный вектор
может быть перенесен в любую точку пространства.
Скользящий вектор – множество направленных отрезков
равной длины, параллельных одной и той же прямой (вектор может
переноситься только вдоль этой прямой)
Приложенный вектор – направленный отрезок с
фиксированным положением начала или конца, переносить его
нельзя.

8.

9.

10.

11.

Поскольку геометрические вектора обладают всеми
свойствами элементов линейного пространства, пространство
геометрических векторов – линейное алгебраическое
пространство. В нем может быть введен базис (набор базисных
векторов), по которому мы сможем разложить любой
произвольный вектор, указав его координаты.
Построим базисные вектора так, чтобы их началом
являлась одна общая точка, которую мы назовем началом
координат. Направленные прямые, на которых лежат
построенные базисные вектора, называют осями координат.
Направления координатных осей совпадают с
направлением векторов базиса.
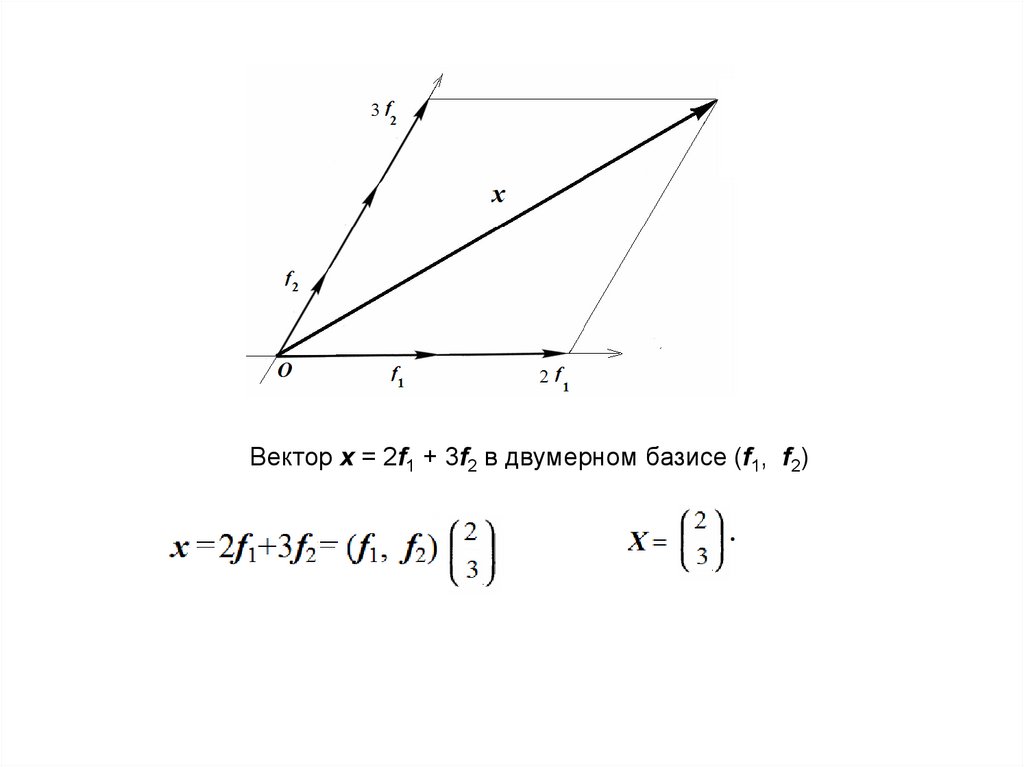
Таким образом, любой вектор (свободный!) можно
описать с помощью разложения по векторам базиса

12.

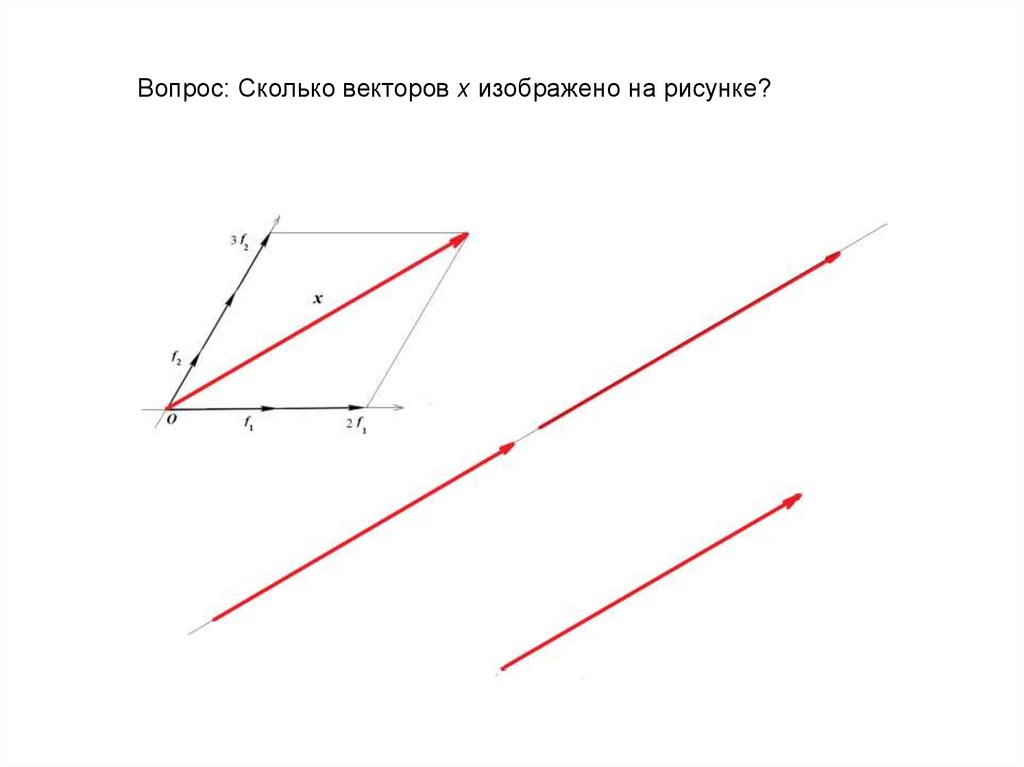
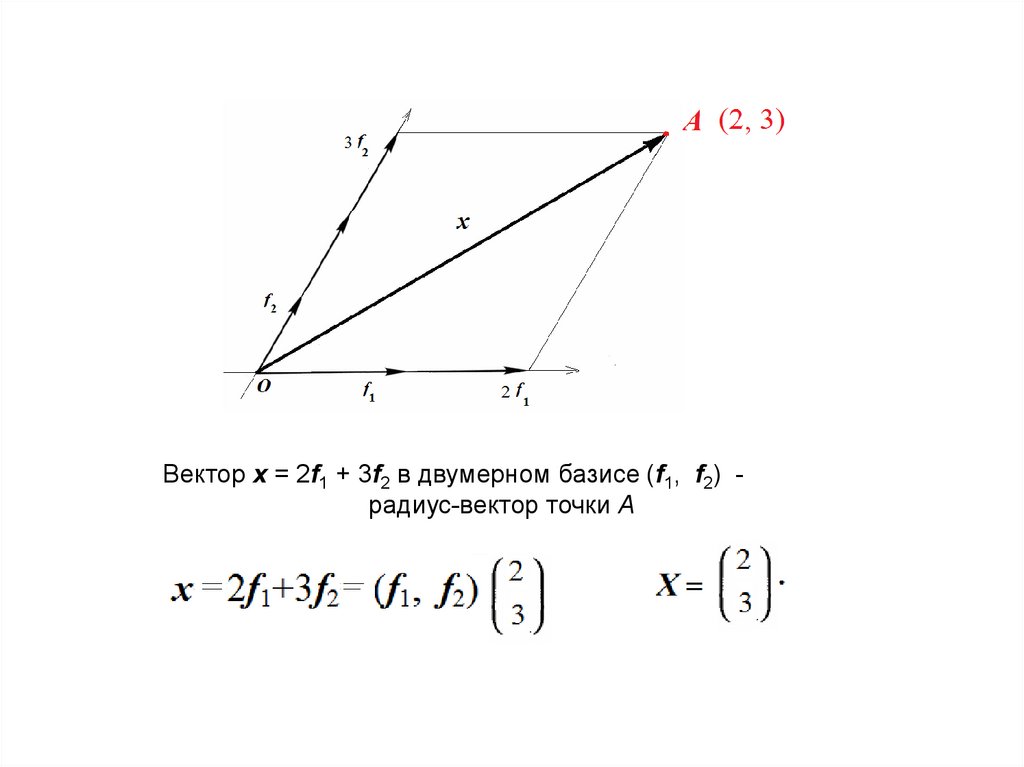
Вектор x = 2f1 + 3f2 в двумерном базисе (f1, f2)

13.

Вопрос: Сколько векторов x изображено на рисунке?

14.

Любую точку геометрического пространства можно
описать вектором (радиус-вектором), начало которого
совпадает с началом координат, а конец – с заданной точкой
пространства.
Координатный способ описания точек в пространстве
является основой аналитической геометрии. При этом для
определения положения точек мы используем приложенные
вектора (радиус-вектора), в качестве точки приложения
которых выступает начало координат (точка О на рис.).
При необходимости задать в пространстве положение
приложенного вектора, мы можем задать координаты двух точек
– точки, которая является началом вектора, и точки, которая
является его концом. Напомним, что начало свободного
вектора может быть перенесено в любую точку пространства.

15.

Вектор x = 2f1 + 3f2 в двумерном базисе (f1, f2) радиус-вектор точки А

16.

Скалярное произведение

17.

Скалярное произведение геометрических векторов обладает
всеми свойствами скалярного произведения в евклидовом пространстве, а
это означает, что в геометрическом пространстве, как и в любом другом
евклидовом векторном пространстве, может быть построен
ортонормированный базис. Напомним, что базис называется
ортонормированным в случае, когда все базисные вектора взаимно
ортогональны (взаимно перпендикулярны) и имеют длину, равную единице.
Декартова система координат строится на основе ортонормированного
базиса.

18.

Свойства ортонормированного базиса

19.

Декартова система координат строится на основе
ортонормированного базиса

20.

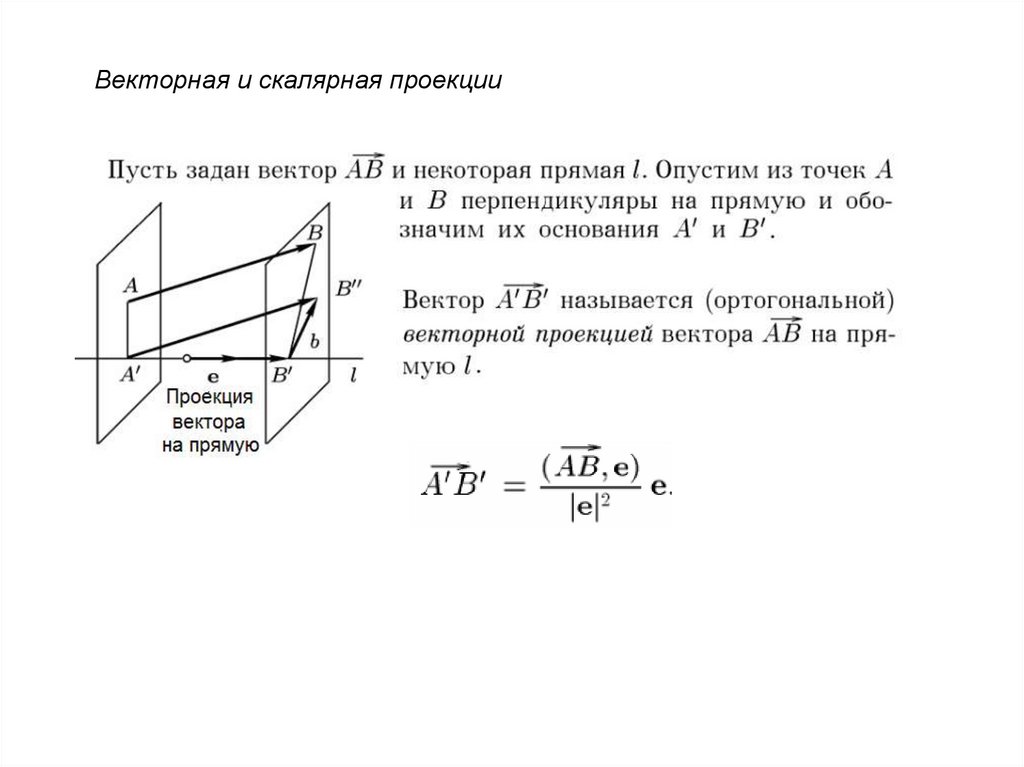
Векторная и скалярная проекции

21.

Координаты вектора в ортонормированном базисе (скалярные
произведения вектора с ортами) равны его скалярным проекциям
на оси координат:
Входящие в данное выражение косинусы углов i между заданным
вектором a и базисными векторами, называются направляющими
косинусами этого вектора.

22.

23.

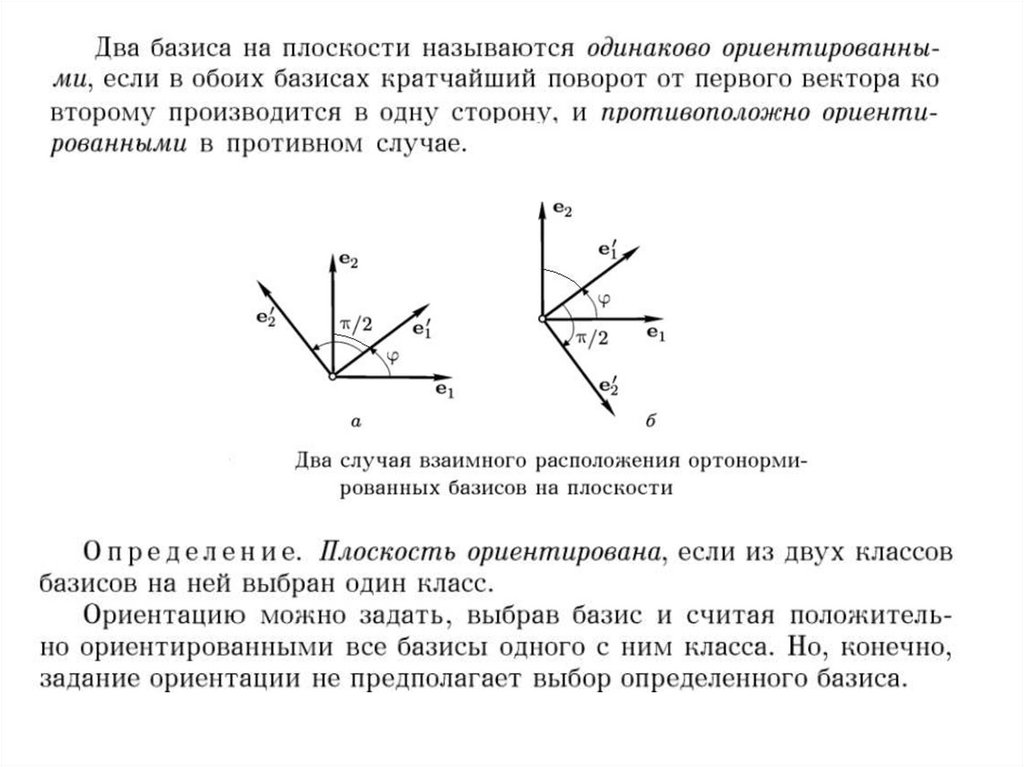
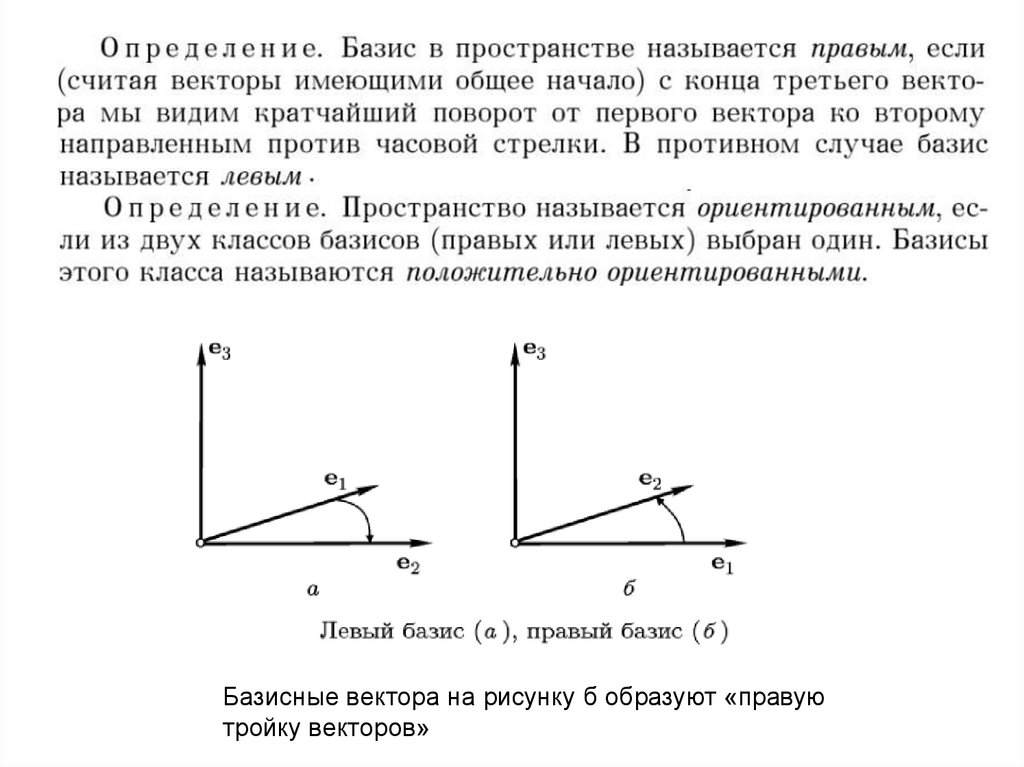
Ориентация базиса

24.

25.

Базисные вектора на рисунку б образуют «правую
тройку векторов»

26.

Векторное произведение

27.

Пусть имеются два вектора b и c. Построим для них вектор d,
обладающий следующими свойствами:
Для
обозначения
векторного
произведения
используются
прямоугольные скобки. Таким образом, для вектора d можно
написать:

28.

В ортогональном базисе для векторного произведения можно
использовать следующую формулу

29.

Поскольку векторное произведение – это вектор,
ортогональный заданным векторам, мы всегда можем
построить перпендикуляр к любой паре неколлинеарных
векторов, раскрыв определитель матрицы, содержащий в
качестве первой строки вектора ортонормированного базиса, а
в качестве второй и третьей строк – координаты исходных
векторов.
Кроме того, согласно определению, длина полученного
таким образом вектора будет равна площади
параллелограмма, построенного на исходных векторах
(напомним, что площадь параллелограмма можно вычислить,
умножив длину одной из его сторон на высоту, равную
произведению длины второй стороны на синус острого угла
параллелограмма).

30.

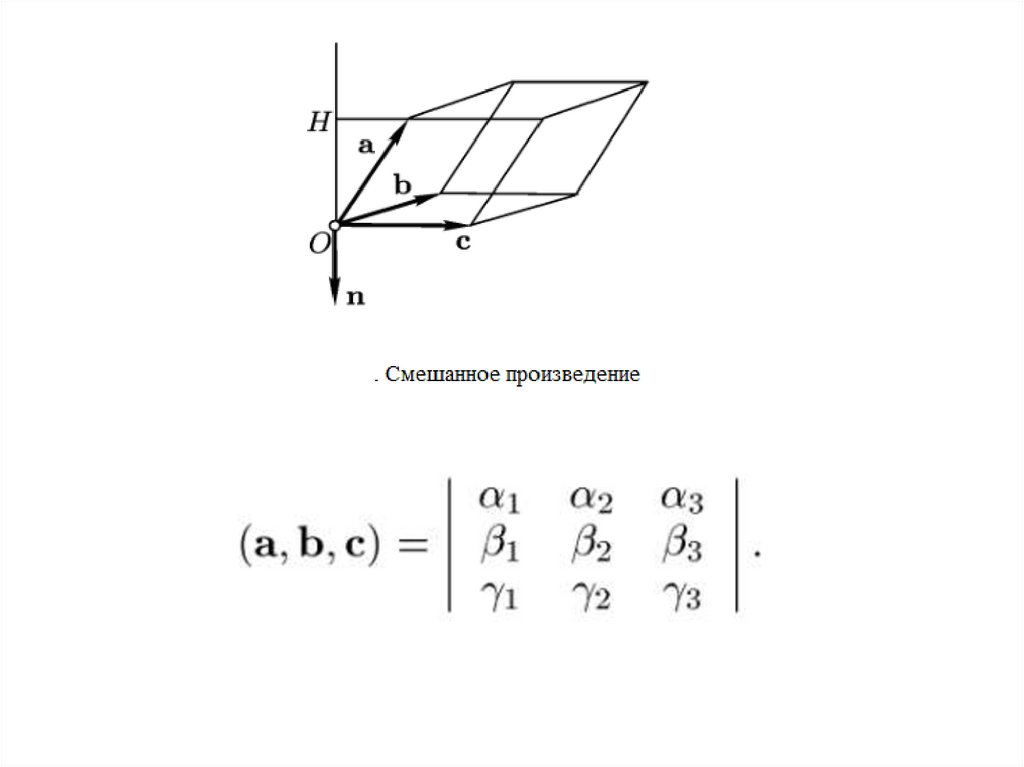
Смешанное произведение векторов

31.

Будем называть копланарными любые вектора, которые лежат в одной
и той же плоскости.
Для смешанного произведения выполняется:
Смешанное произведение векторов – это скалярное произведение
первого вектора с векторным произведением второго и третьего

32.

33.

Плоскости и прямые

34.

Плоскости в трехмерном
пространстве

35.

Простейшим примером алгебраической поверхности является плоскость

36.

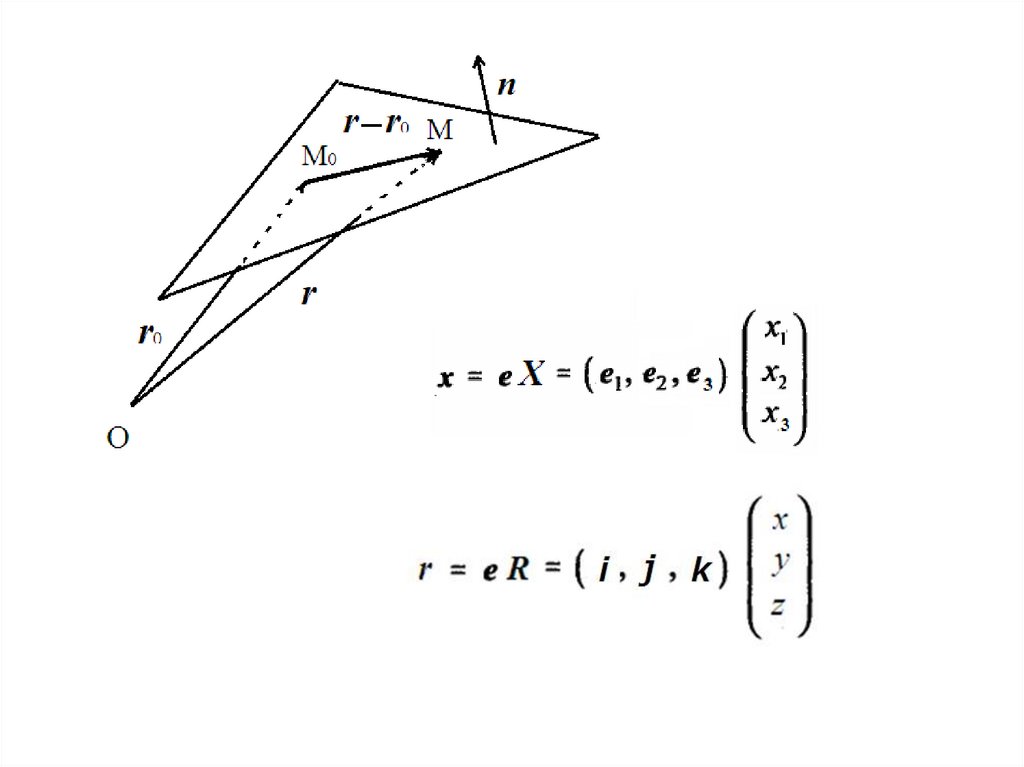
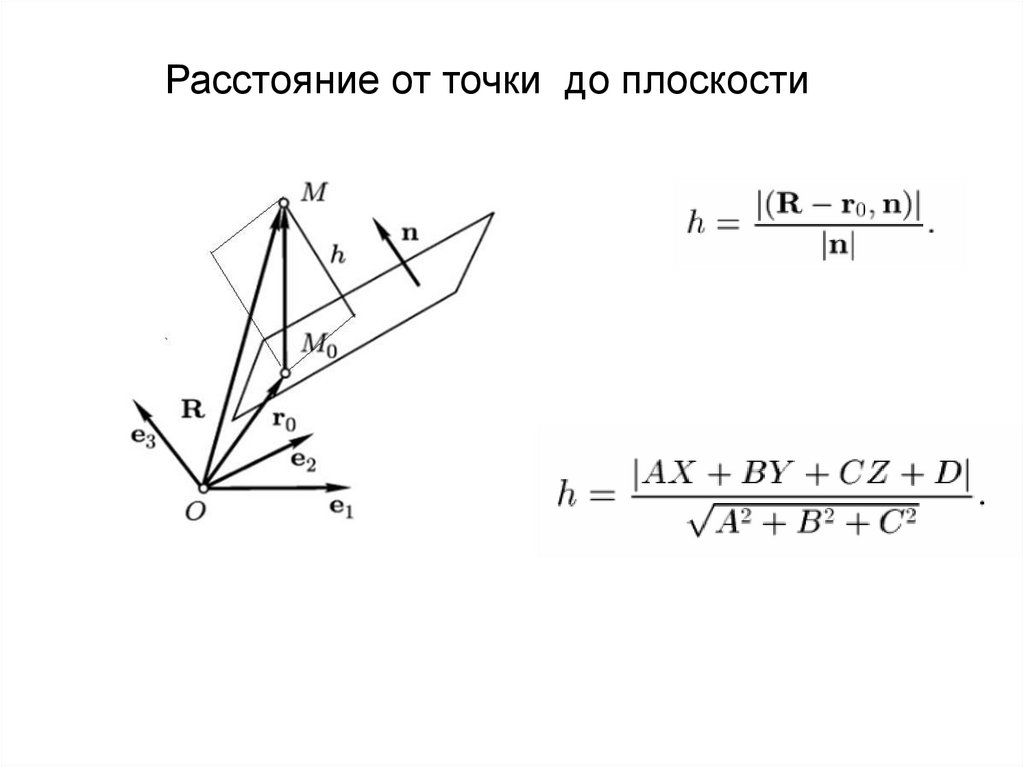
Векторное уравнение плоскости
Вектором нормали n к плоскости мы будем называть
вектор, перпендикулярный плоскости (лежащий на прямой,
перпендикулярной плоскости). Такой вектор образует
прямой угол с любым вектором, лежащим в плоскости.
Если положение произвольной точки плоскости M задать
с помощью радиус-вектора r , имеющего координаты x, y и z, то
для вектора r–r0, лежащего в плоскости на отрезке M0M, можно
записать:

37.

38.

Общее уравнение плоскости
Пусть у нас имеется вектор нормали к плоскости n, с
координатами A, B, C.
Общее уравнение плоскости:

39.

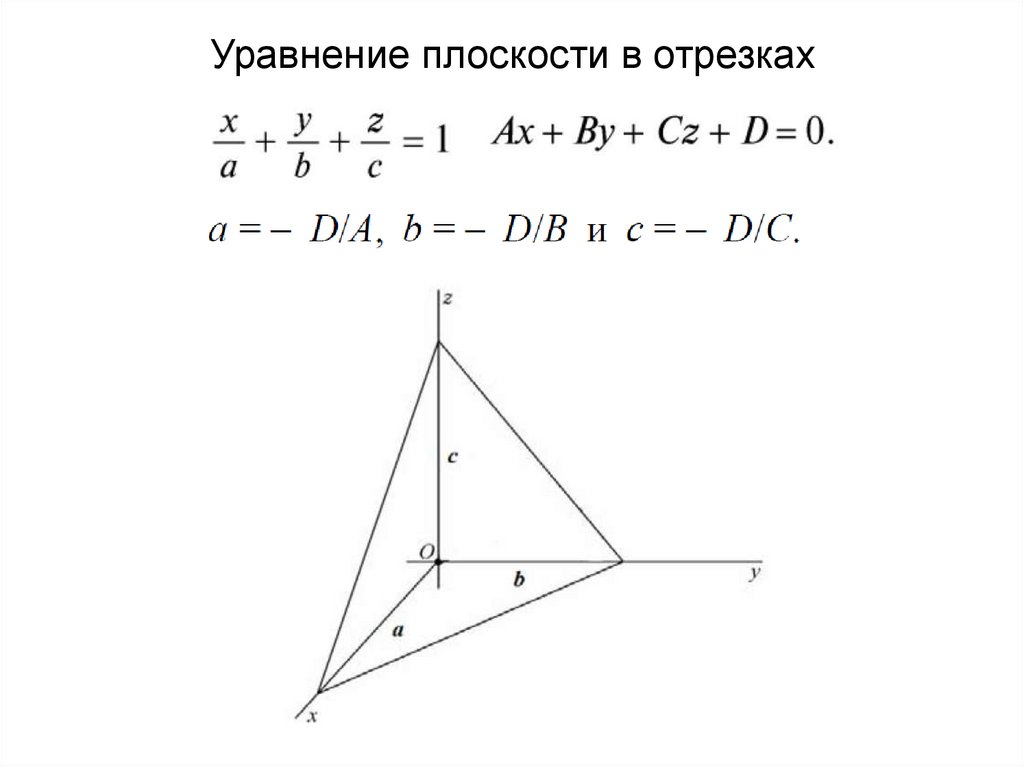
Уравнение плоскости в отрезках

40.

41.

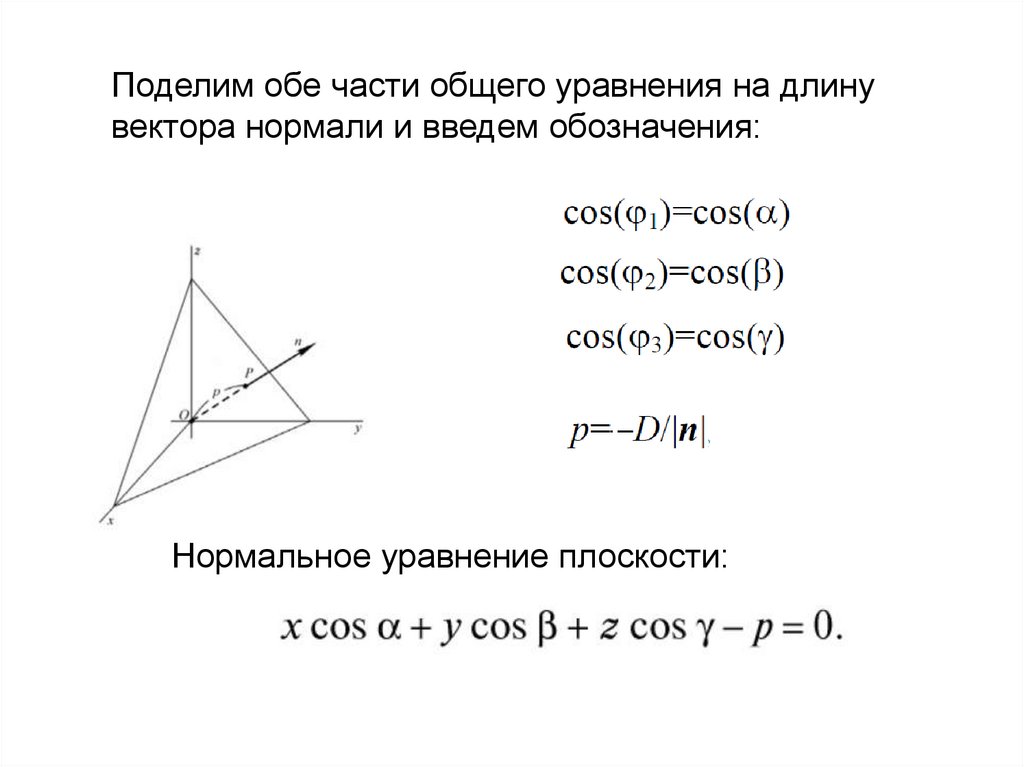
Нормальное уравнение плоскости
Пусть плоскость задана общим уравнением
Вектор нормали к плоскости n (с координатами A,
B, C) имеет длину:
и направляющие косинусы
.

42.

Поделим обе части общего уравнения на длину
вектора нормали и введем обозначения:
Нормальное уравнение плоскости:

43.

Расстояние от точки до плоскости

44.

Прямые в пространстве

45.

46.

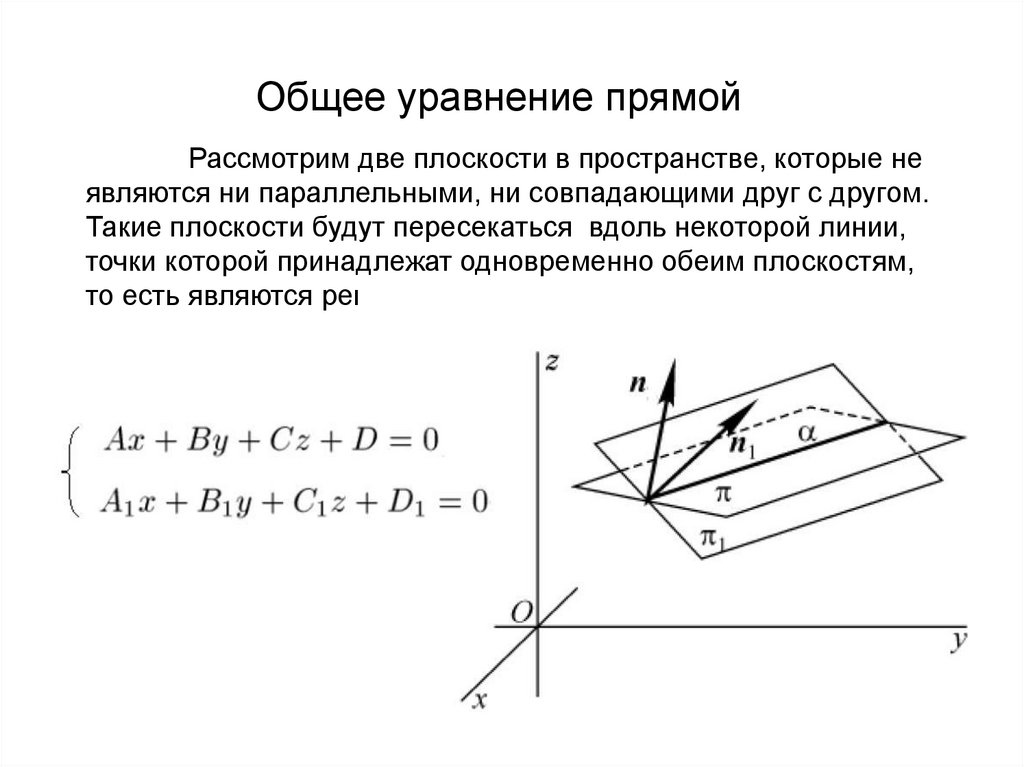
Общее уравнение прямой
Рассмотрим две плоскости в пространстве, которые не
являются ни параллельными, ни совпадающими друг с другом.
Такие плоскости будут пересекаться вдоль некоторой линии,
точки которой принадлежат одновременно обеим плоскостям,
то есть являются решением системы уравнений:

47.

Если плоскости совпадают - уравнения в системе
линейно-зависимы. Если плоскости параллельны – система
решений не имеет.
Система уравнений задает прямую, только если имеет
решение и ее уравнения линейно-независимы (Ранг основной
матрицы равен рангу расширенной и равен 2).

48.

Параметрическое уравнение прямой

49.

В двумерном случае (для прямой на
плоскости) можем написать:

50.

*** В случае, если рассматривается линейное пространство с
размерностью n, уравнение вида A1x1+A2X2+A3X3+….AnXn+B=0
называется уравнением гиперплоскости.
В трехмерном пространстве:
Точка:
Прямая:
Плоскость:
Совместная СЛАУ, состоящая из n линейно-независимых уравнений определяет
точку
Совместная СЛАУ, состоящая из n-1 линейно-независимых уравнений определяет
аналог прямой. Подпространство решений СЛАУ имеет одну степень свободы
(решение содержит одну свободную переменную)
Совместная СЛАУ, состоящая из единственного линейно-независимого уравнения
определяет гиперплоскость. Подпространство решений имеет n-1 степень свободы
(решение содержит n-1 свободную переменную)

51.

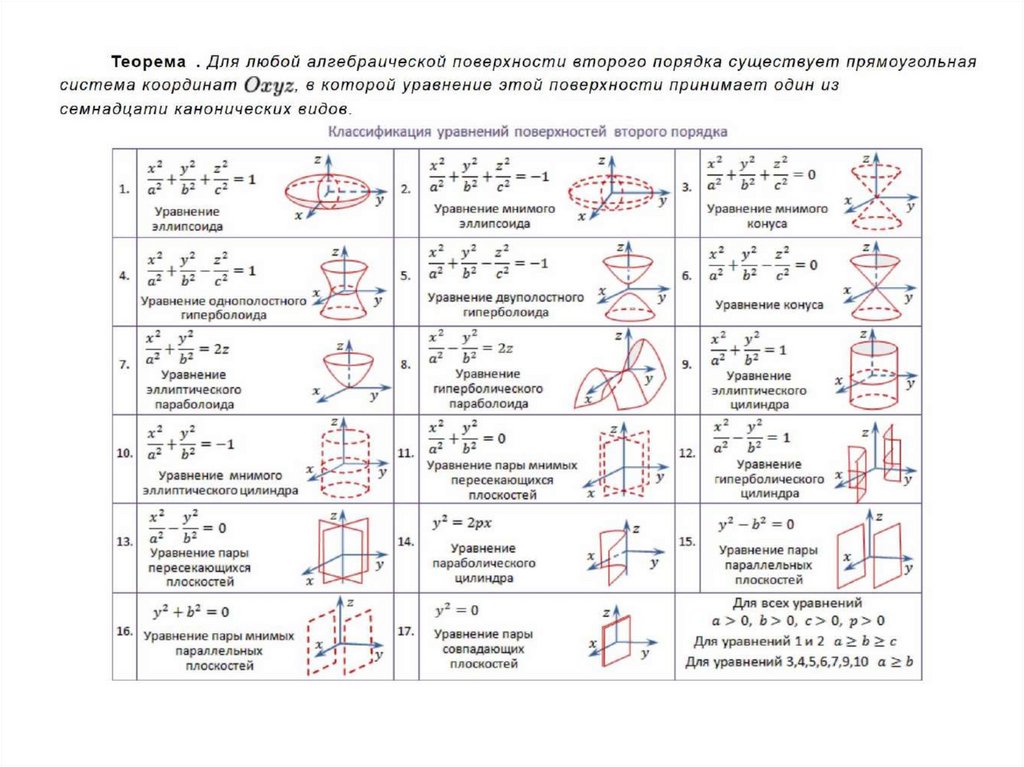
Линейные и
квадратичные
формы,
поверхности
второго порядка

52.

Векторная форма записи может быть использована и в случае,
когда уравнение линии (или поверхности) имеет более сложный вид, чем
уравнение плоскости или прямой.
Рассмотрим двумерное геометрическое пространство и определим, какая
фигура задается уравнением:
В данном уравнении r радиус вектор с координатами (x, y),
описывающий произвольную точку, принадлежащую заданной линии, a –
константа.
Очевидно, что уравнение можно переписать в виде |r|=a, то есть
оно задает множество точек на плоскости, принадлежащих окружности с
радиусом a и центром в точке О(0, 0).

53.

Перепишем уравнение в виде: x2+y2=a2, а затем в виде
x2+y2-a2=0 и определим порядок полученной алгебраической линии.
Уравнение окружности – уравнение алгебраической линии второго порядка

54.

В случае, если центр окружности находится в произвольной точке,
с радиус-вектором r0 , с координатами (x0 y0), можно упростить уравнение,
перейдя к новой системе координат с началом которой в точке О’,
расположенной в r0 (осуществив параллельный перенос начала координат
в данную точку).
Пример:
Выражение (x-3)2+(y-4)2=4 можно легко получить из выражения
x2-6x+y2-8y+21=0, используя формулу для квадрата разности и выделив
полные квадраты. В то же время данная данное выражение можно
записать в виде:
,
при a=2, X0=(3, 4)T.
Считая, что координаты точки в новой системе связаны с
координатами в старой системе выражением r’=r-r0, получим для системы
координат с началом в О‘ уравнение вида:

55.

Рассмотрим, что произойдет с уравнением окружности в
случае, если преобразование системы координат связано не с
параллельным переносом начала координат, а с ее поворотом. В
этом случае мы переходим к новому ортонормированному базису,
который может быть связан со старым с помощью соответствующей
матрицы перехода. В столбцах такой матрицы размещаются
координаты векторов нового базиса.
*Напомним, что в случае, если переход происходит между
ортогональными базисами, транспонированная матрица перехода
должна быть равна матрице, обратной для матрицы перехода.

56.

Пусть уравнение окружности имеет максимально простой вид
записи в «штрихованной» системе координат с базисом e’
Пусть также задана система координат с началом в той же точке О’=О,
и базисом e, связанным с исходным соотношением e =e’ A .
При таком выборе матрицы перехода координаты векторов в базисе e’
связаны с координатами в базисе e выражением
X’=AX
*Для проверки можно использовать равенство x=eX=e’X’.

57.

Запишем исходное уравнение через координаты и перейдем к новому
базису:
Выражение f(x, y) - квадратичная форма.
Это выражение можно записать
в матричном виде
f(x, y) = XTFX,
Симметризация исходной формы:

58.

В аналитической геометрии достаточно часто возникает задача приведения
имеющейся квадратичной формы к диагональному виду.
В нашем примере такой переход подразумевает поиск базиса, позволяющего
вместо
получить выражение
,
то есть перейти к квадратичной форме с матрицей:

59.

В общем случае для решения поставленной задачи необходимо
найти собственные значения и собственные вектора матрицы F. Для
симметричной матрицы квадратичной формы собственные значения всегда
вещественны, а собственные вектора – ортогональны, следовательно, их
можно использовать для построения искомого базиса
Рассмотренный пример описания линии в двумерном пространстве
можно обобщить и на случай пространства с более высокой размерностью,
в частности, рассмотреть вопрос о виде уравнения, возникающего при
описании поверхности второго порядка в трехмерном пространстве.