Л-1_Введение в мат.анализ (1)

1.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА ИМЕНИ АДМИРАЛА С.О. МАКАРОВА»
Введение в
математический
анализ
Доцент кафедры
высшей математики
Елена Ивановна Распутина

2.

«Математический анализ не менее всеобъемлющ, чем сама природа:
он определяет все ощутимые взаимосвязи, измеряет времена,
пространства, силы, температуры».
Ж. Фурье
фото Рена Марганна
(Ren McGann)

3.

Математический анализ ― раздел математики, в котором методом
анализа бесконечно малых и посредством предельных переходов
изучаются переменные величины и их функциональные зависимости.
Основные понятия:
переменная, функция, предел, бесконечно малая величина;
производная, дифференциал;
интеграл;
ряд.
Основа аппарата
правила предельных переходов,
дифференциальное и интегральное исчисления.

4.

:
Некоторые логические символы
:
квантор всеобщности (для всех, для каждого, для любого)
квантор существования (существует, найдется)
имеет место;
такое, что
знак логического следования (влечет)
из предложения следует предложение ;
достаточное условие для ; необходимое условие для
знак равносильности
(равносильно, необходимо и достаточно, тогда и только тогда)
Необходимость
Достаточность

5.

Величины
Постоянная величина
(константа)
Переменная величина
(переменная)
Переменные величины принимают значения из некоторого числового
множества, числового промежутка.
Числовые промежутки
отрезки
n N, N 1,2,3,
интервалы
полуинтервалы
— множество натуральных чисел;
x ; ; x R — множество действительных чисел
y 2;6 ;
С = Const
лучи

6.

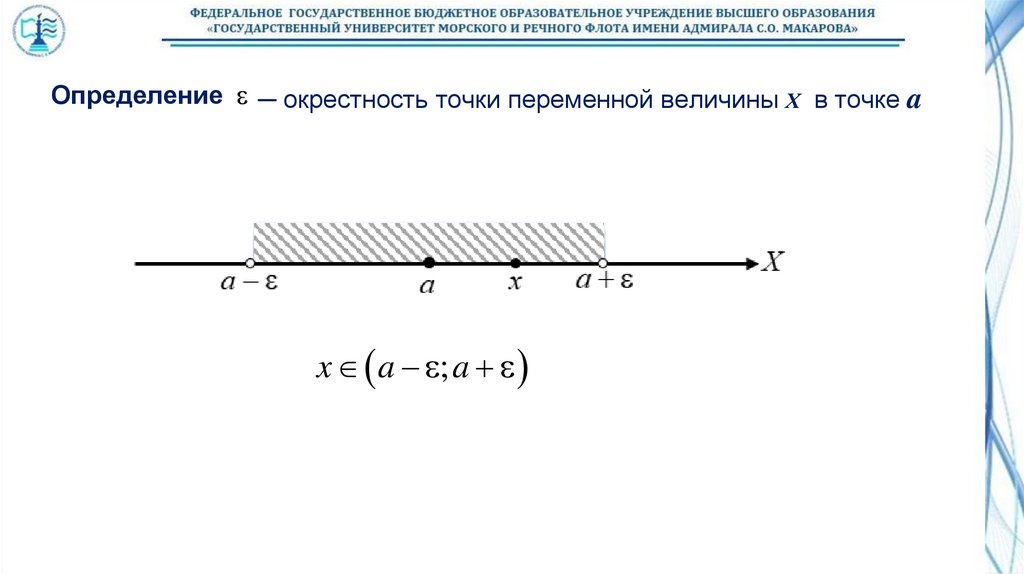
Определение ─ окрестность точки переменной величины Х в точке a
x a ; a

7.

Определение функции непрерывного аргумента
y y x f x ,
Определение функции натурального аргумента
xn f n ― формула общего члена последовательности.

8.

x
rn
yx
L
0N
2xf2
a
r r
xn ;2
n f 1x 3
n f y
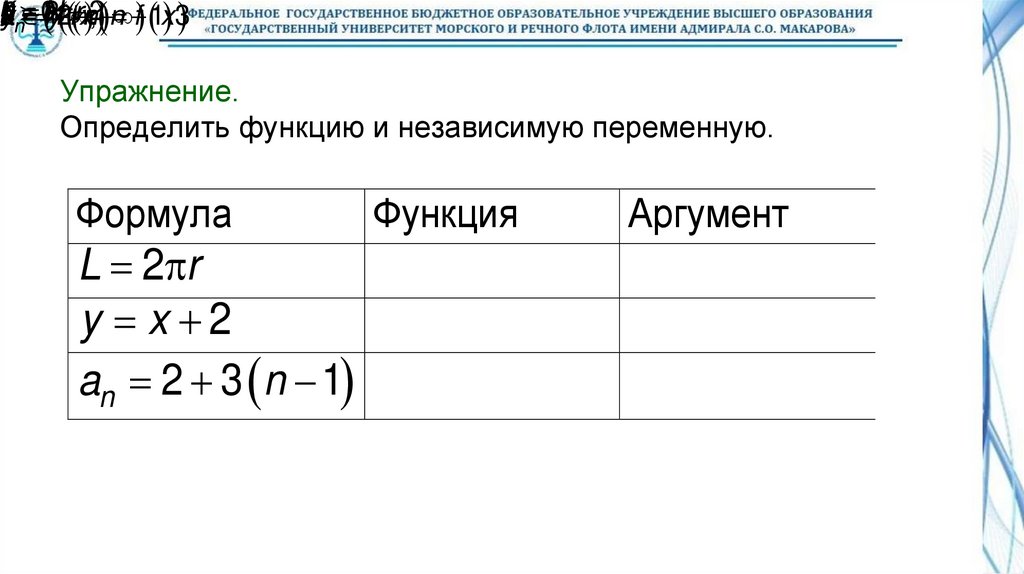
Упражнение.
Определить функцию и независимую переменную.
Формула
L 2 r
y x 2
an 2 3 n 1
Функция
Аргумент

9.

Упражнение.
Найти значение функции y = f (x) в точке xo.

10.

x
rn
yx
L
0N
2xf2
a
r r
xn ;2
n f 1x 3
n f y
Основные способы задания функции
1. Аналитический способ
1.1 явное задание функции
1.2 неявное задание функции
1.3 параметрическое задание функции
2. Табличный
3. Графический