123

1.

2.

Понятие о показательном уравнении и
основные методы его решения
Пусть а – данное положительное, не равное 1 число,
b – данное действительное число. Тогда уравнение
х
а =b
называют простейшим показательным уравнением.
Уравнение, в котором переменная содержится в
показателе степени, называется показательным.
Например: 2х = 8;
9
x 1
43 2
2x 3
6
(1/3)x = 9;
3 x
0
25х = -25

3. Способы решения показательных уравнений

Графический
1. Построить графики
двух функций
(левая и правая
части уравнения)
2. Найти абсциссы
точек пересечения
графиков
3. Записать ответ
Аналитические
1. Приравнивание
показателей
2. Вынесение общего
множителя за
скобки
3. Введение новой
переменной
4. Использование
однородности

4. Графический метод

Метод основан на использовании графических иллюстраций, или
каких-либо свойств функций.
• Решите уравнение
4
5 х
х
Построим в одной системе координат графики функций
у 4
и у = 5 - х.
х
х
-2
-1
0
1
2
у
1/16
1/4
1
4
16
х
0
1
у
5
4
Графики пересекаются в одной
точке (1; 4).
х=1 – решение уравнения.
Ответ: 1.

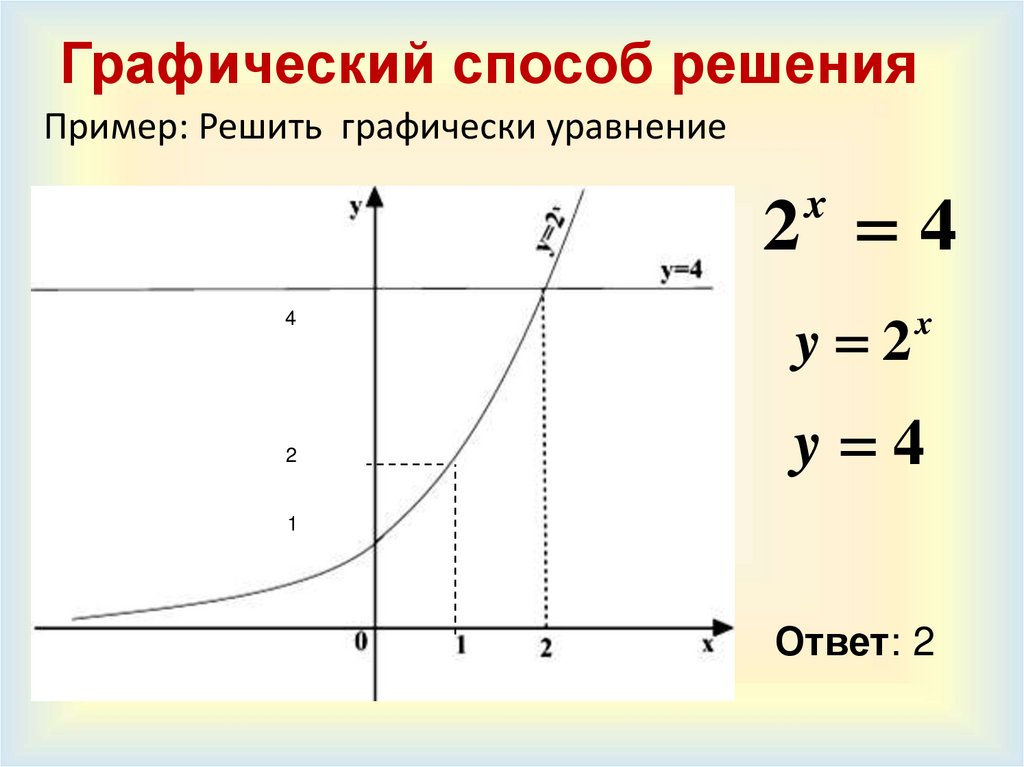
5. Графический способ решения

Пример: Решить графически уравнение
2 4
x
4
2
y 2
x
y 4
1
Ответ: 2

6. Аналитические способы

1. Приравнивание показателей
2. Вынесение общего множителя
за скобки
3. Введение новой переменной
4. Использование однородности
(деления на показательную
функцию)

7.

1. Метод приравнивания показателей
Показательное
уравнение
где
Равносильно
уравнению
a 0, a 1

8. 1. Приравнивание показателей

Суть метода:
1. Уединить слагаемое, содержащее
переменную
2. Привести степени к одному
основания
3. Приравнять показатели
4. Решить полученное уравнение
5. Записать ответ

9. Примеры:

3 27 0
x
3 27
x
3 3
x
3
1 2 x 1 1
( )
,
2
8
1 2 x 1
1 3
( )
( ) ,
2
2
2 x 1 3,
x 3
2 x 3 1,
Ответ: 3
x 1.
2 x 2,
Ответ: 1

10. 2. Метод разложения на множители.

Решите уравнение
2 3
x 1
6 3
x 1
x 1
3 9,
x
3 (2 3 6 3 ) 9,
3
x 1
3
2
1
9 9,
x 1
3
x 1
3 ,
0
x 1 0,
x 1.
1,
Ответ: 1

11. Используя формулу

а n
b n
( ) ( )
b
a
Решим уравнение
16 х
3 6
( ) ( ) ,
9
4
3 2 х
3 6
( )
( ) ,
4
4
Ответ: -3.
2 х 6,
х 6 : ( 2),
х 3.

12. 2. Вынесение общего множителя за скобки.

Примечание: выносим за скобки множитель с меньшим
показателем.
x
x 3
Пример:
3 3
78
3 1 3 78
x
3 26 78
x
3
3 3
x 1
Ответ: 1
x

13. 3. Введение новой переменной

2x
x
Пример 1: 4 5 4 4 0
Пусть
4 t
x
t 0
2
t
5t 4 0
Тогда уравнение примет вид:
D 25 16 9
5 3
t1
4
2
4x 4
x 1
Ответ: 0; 1
5 3
t2
1
2
x
0
4
4
4 1;
x
x 0

14.

2 2 2 0;
2х
Пример 2:
х
Пусть 2 х t , где t 0 , тогда t 2 t 2 0
По теореме, обратной теореме Виета,
получаем:
t1 t 2 1
t1 t 2 2
t1 2
t1 2
t2 1
не удовлетворяет условию t 0
Если t 1 ,то 2 x 1, 2 x 20 , x 0.
Ответ: 0

15. 4. Однородные уравнения (деление на показательную функцию)

Показательные уравнения вида a f ( x ) b f ( x )
называются однородными.
Суть метода: Так как показательная
функция не может принимать значение,
равное нулю, и обе части уравнения
можно делить на одно и то же неравное
нулю число, разделим обе части
f ( x)
уравнения, например, на b

16. Пример:

2 3
x
Пример:
x
x
x
2
3
x
x
3
3
x
2
1
3
Ответ: 0
x
2
2
3
3
x 0
0

17. Определите способ решения уравнений

18. Определите способ решения уравнений

(однородное уравнение)
(приравнивание показателей)
(замена переменной)
(приравнивание показателей)
(вынесение за скобки)

19.

Показательные неравенства
Неравенство, содержащее
неизвестную в показателе степени,
называется показательным
неравенством.
Неравенство в и д а
a
f ( x)
a
g ( x)
, a 0, a 1
называется простейшим показательным
неравенством.

20.

Методы решения показательных
неравенств.
1. Простейшие показательные неравенства
2. Сведение неравенства к простейшему
3. Метод введения новой переменной
4. Разложение на множители
5. Сведение к равносильной совокупности
6. Метод рационализации (замены множителей)

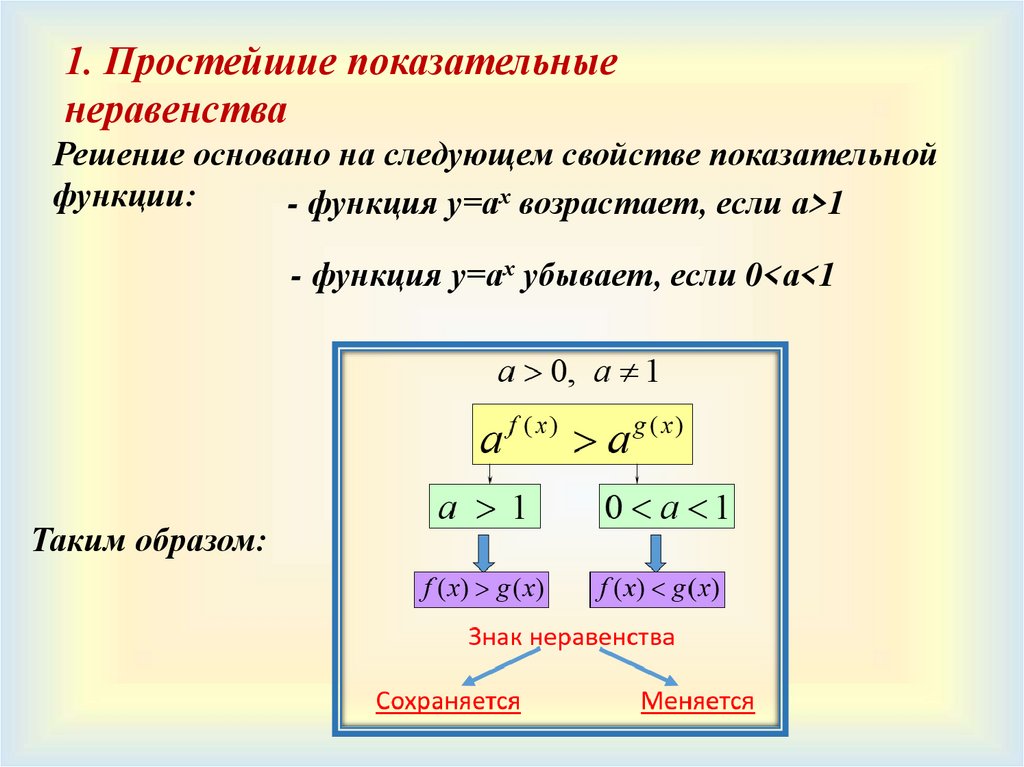
21.

1. Простейшие показательные
неравенства
Решение основано на следующем свойстве показательной
функции:
- функция у=ах возрастает, если а>1
- функция у=ах убывает, если 0<а<1
Таким образом:

22.

Простейшие показательные неравенства
Пример 1. 23 4 x 5 23 3 x 8
Пример 2. 0 ,234 x 5 0 ,233 x 8
23 1
4 x 5 3x 8
Ответ : x 13
0 0 ,23 1
4 x 5 3x 8
Ответ : x 13
Пример 3.
3 ,14 1
4 x 2 5 3 x 2
4 x2 3x 7 0
7
4
4 x 2 5
3 x 2
1
7
Ответ : ; 1;
4
Пример 4. 3
4 x 5
3 5
3 6 27
6
3
5
25
3
3
5
3
1
3
5
4 x 5 3x 8
Ответ : x 13
3 x 8

23.

2. Сведение неравенства к простейшему
Пример 5.
3
3
x 2 4 ,5
1
3
27
x 2 4 ,5
30 ,5 3 3
3
x 2 4
3 3
x 2 4 3
x2 1 0
1
Ответ :
1
; 1 1;

24.

Сведение неравенства к простейшему
Пример 6.
10
3
3 x2 3
10
2
3
3 x2 3
10
9
10
9
2 x
0 ,81
1
3 x2 3
2
1
3 x2 3
2
81
100
9
10
10
9
2 x
1
( 3 x2 3 ) 4 x
2
3 x2 3 8 x
3x2 8 x 3 0
4 x
4x
1
3
1
Ответ : ;3
3
3

25.

Сведение неравенства к простейшему
Пример 7. 5 x 1 2 x 2 8 10 x 3 x 2
2
5
x 1
2
x 2
2 (5 2 )
3
5 x 1 2 x 2
2 2
3
5
5
x2 3 x 2
5
x 1 ( x 2 3 x 2 )
x 2 4 x 3
10
2
x 2 4 x 3
x2 3 x 2
2
x 2 3 x 2
10 0
x2 4 x 3 0
x2 4 x 3 0
x 2 3 x 2
)
1
x 2 3 ( x 2 3 x 2 )
x 2 4 x 3
( 2 (5 2 )
3
1
1
1
3
Ответ : ( 1;3 )
26

26.

Сведение неравенства к простейшему
Пример 8.
1
16
4 x 1
4 x 2
1
2
1 1
2 2
1
2
4x
x 0 , 25
1
4
1
2
2
1 1
2 2
4x
4 x 3
5 1
8 2
4x
5
4
3
5
8
1
2
3
4x
4 x 3
5
4
1 1
2 2
1 1 1 1
2 2 2 2
2
2 x 1
5
4
4x
5
4
5
4
1
2
1
2
4x
4x
2
1
2
1
4 x 1
1
Ответ : x 4
27

27.

Сведение неравенства к простейшему
Пример 8.
2 2 x 1 3 2 x 1 3 2 x 7 2 2 x
2 2 2 x 3 32 x 32 x 7 2 2 x
2 7 2 2 x 1 3 32 x
9 2 2 x 4 3 2 x 32 x 9
22 x 4
2x
3
9
2
3
2x
2
3
2x 2
2
Ответ : x 1

28.

Метод введения новой переменной
Пример 9.
25 x 4 5 x 5 0
5
2x
4 5 5 0
x
Замена : 5 x t 5 2 x t 2
t2 4t 5 0
( t 5 )( t 1 ) 0
5
t 5
t 1
1
5 х 5
x
5 1
нет решений
x
0
5
5
Ответ : x 0

29.

3. Метод введения новой переменной
Пример 10.
25 x 4 5 x 5 0
5
2x
Замена : 5 x t 5 2 x t 2
4 5 5 0
x
t2 4t 5 0
( t 5 )( t 1 ) 0
5
t 5
t 1
1
5 x 5
x
5 1
x R
x
0
5
5
Ответ : x 0

30.

Метод введения новой переменной
Пример 11.
5
5
12 x 143 12 x 2
5
5
12 x 143 12 x 144
5
5
t 143 144 t
Замена : 12 x t
144 t ( t 144 ) 0
5 144 t 5 ( t 143 ) 0 5
144 t ( t 143 ) 0
t 1
143t 143 0
5x 1
5 x 50
Ответ : x 0

31.

Метод введения новой переменной
Пример 12. ( 19 6 10 ) x 6 ( 10 3 ) x 1 0
Заметим, что выражение
( 10 3 )2 x 6 ( 10 3 ) x 1 0 в первой скобке равно
квадрату выражения,
t2 6 t 1 0
находящегося во второй
скобке
( t ( 3 10 )( t ( 3 10 )) 0
Замена : ( 10 3 ) x t
3 10
3 10
t 3 10 ( 10 3 ) x 3 10 x R
x
t 3 10 ( 10 3 ) 3 10 ( 10 3 ) x ( 10 3 )0
0 10 3 1
Ответ : x 0

32.

Метод введения новой переменной
( 3 2 2 )x ( 3 2 2 )x 6 0
Числа (a-b) и (a+b)
1
t 6 0 t 0
являются взаимно
t
2-b2=1
обратными,
если
a
t2 6t 1 0
(наш случай)
( t ( 3 2 2 )( t ( 3 2 2 )) 0
Замена : ( 3 2 2 ) x t
Пример 13.
1
(3 2 2 )
t
x
3 2 2
t 3 2 2
t 3 2 2
3 2 2
( 3 2 2 ) x ( 3 2 2 )1
x 1
0 3 2 2 1
x
1
x 1
( 3 2 2 ) ( 3 2 2 )
Ответ : ( ; 1 ) ( 1; )

33.

4. Разложение на множители
Пример 14.
8 x 3 4 x 2 x 2 12 0
2 3 x 3 2 2 x 4 2 x 12 0
Замена : 2 x t
t 3 3 t 2 4 t 12 0
t 2 ( t 3 ) 4( t 3 ) 0
( t 2 4 )( t 3 ) 0
( t 2 )( t 2 )( t 3 ) 0
( 2 x 2 )( 2 x 2 )( 2 x 3 ) 0 ( 2 x 2 )( 2 x 3 ) 0
2x 2 0
2 x 21
Ответ : x 1

34.

Разложение на множители
Пример 15. 4 8 x 6 12 x 2 18 x 3 27 x 0
4 2 3 x 6 2 2 x 3 x 2 2 x 32 x 3 33 x 0
Замена : 2 x a
3x b
4 a 6 a b 2 a b 3 b 0
3
2
2
3
2 a 2 ( 2 a 3b ) b 2 ( 2 a 3b ) 0
( 2a 2 b 2 )( 2a 3b ) 0
( 2 2 2 x 3 2 x )( 2 2 x 3 3 x ) 0 ( 2 2 x 3 2 x ) 0
2 2 x 1 3 2 x 1 0
2
2 x 1
2
3
3
2 x 1
2 x 1
1
3
2 x 1
0
2
3
2 x 1
2
3
2x 1 0
0
Ответ : x 0 ,5

35.

Разложение на множители
3 3 x 3 2 x 1 3 x 1 1 0
Пример 16.
33 x 3 32 x 3 3 x 1 0
Замена : 3 x a
a 3 3a 2 3a 1 0
( a 3 1 ) ( 3a 2 3a ) 0
( a 1 )( a 2 a 1 ) 3a( a 1 ) 0
( a 1 )( a 2 a 1 3a ) 0
a 1 0
( a 1 )( a 2 2a 1 ) 0
a 1
( a 1 )( a 1 ) 0
3x 1
( a 1) 0
3 x 30 Ответ :
2
3
x 0

36.

5. Сведение к равносильной совокупности
Пример 17.
( x 4x )
2
x 2 5 x
( x 4x )
2
x 2 5 x
1
( x 2 4 x )0
Если х2-4х≠1, то необходимо
рассматривать два случая:
x 4 x 1
2
x 5 x 0
2
0
x
4x 1
x 2 5 x 0
2
Во первых, заметим, что
если х2-4х=1, то неравенство
выполнено; при х=0 - не имеет
смысла
x 2 5 решения
1) x 4 x 1 0
2
x 5 x 0
2
( x ( 2 5 ))( x ( 2 5 )) 0
x( x 5 ) 0
5
2 5
0
2 5

37.

Сведение к равносильной совокупности
Пример 17.
( x 4x )
2
x 2 4 x 1
2
1)
x
5
x
0
2
0
x
4x 1
x 2 5 x 0
x 2 5 x
1
5
x 2 5 решения
2 5
2 5
0
2
0
x
4x 1
2)
2
x 5 x 0
( x ( 2 5 ))( x ( 2 5 )) 0
x( x 4 ) 0
2 5
5
x( x 5 ) 0
0
4
Решение – объединение решений двух случаев
Ответ : ( ; 5 ] [ 2 5 ;0 ) [ 2 5 ; )
2 5

38.

6. Метод замены множителей
Знак выражения hf-hg совпадает со знаком выражения
(h-1)(f-g)
Пример 17 (второй способ). ( x 4 x )
2
( x 4x )
2
x 2 5 x
x 2 5 x
( x 2 4 x )0 0
1 при х=0 - не имеет
смысла
( x 2 4 x 1 )( x 2 5 x ) 0
x( x ( 2 5 ))( x ( 2 5 ))( x 5 ) 0
5
2 5
0
2 5
Ответ : ( ; 5 ] [ 2 5 ;0 ) [ 2 5 ; )

39.

Решите
самостоятельно:

40.

Решите уравнения:
х
х
9 - 8·3 = 9
2
2-х
–2
х–1
=1

41.

Решите уравнения (замена переменной):
9х - 8·3х = 9
32 x 8 3 x 9 0
3 x t , (t 0)
t2 8 t 9 0
D 64 36 100
8 10
t
9
1
2
8 10
t
1,
2
2
3х 9
3 х 32
x 2
Ответ : x 2
2
2-х
–2
х–1
=1
2 2 2 x 2 x 2 1 1
4
2x
1 0
x
2
2
2 x t , (t 0)
4
t
1 0 / 2t
t
2
t 2 2t 8 0
D 4 32 36
2 6
t1
2
2
2 6
t2
4
2
2x 2
x 1
Ответ : х 1

42.

Решите уравнения

43.

Решите уравнения
(Вынесение общего множителя за скобки)
2 x 1 1 2 2 12
2 x 1 3 12
5 x 2 3 5 200
5 x 2 8 200
2 x 1 4
5 x 2 25
2 x 1 2 2
x 1 2
5 x 2 52
x 2 2
x 1
x 4
Ответ : x 1
Ответ : x 4

44.

Решите уравнение:
3 25 8 15 5 9 0
х
х
х

45.

Решите уравнения
(деление на показательную
функцию )
3 25 х 8 15 х 5 9 х 0
х
x
25
15
3 х 8 x 5 0
9
9
2x
x
5
5
3 8 5 0
3
3
5
t
3
х
(t 0)
3t 8t 5 0
: 9х
D 64 4 3 5 4 2 2
8 2 10 5
t1
;
6
6 3
8 2
t2
1.
6
х
х
5
5
3
3
х 1
5
1
3
х
5 5
3 3
х 0
2
Ответ: 0; 1
0

46.

Решите графически уравнение
3
х
4 х