Транспортная задача

1. Транспортная задача

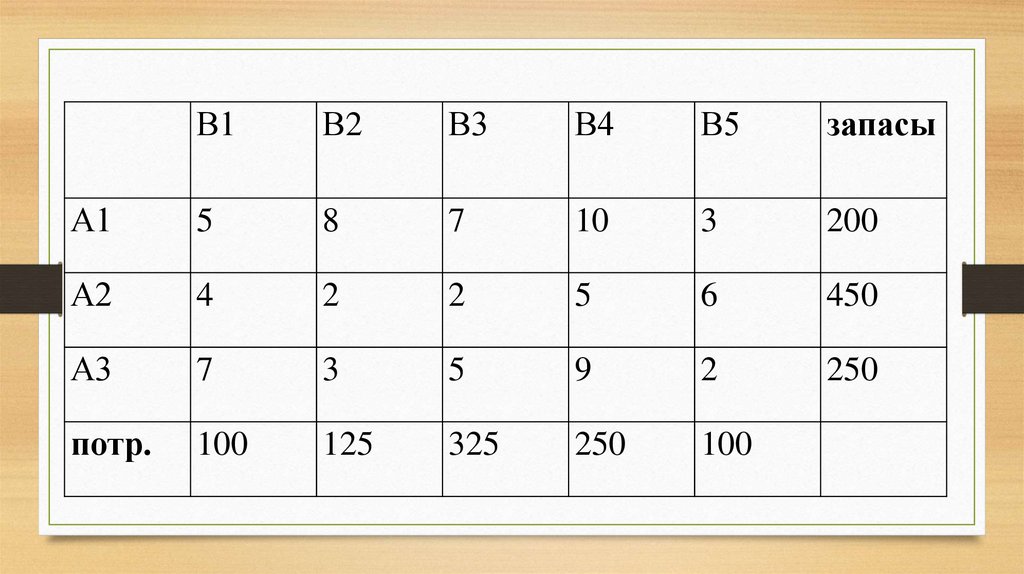
2. Составить математическую модель следующей задачи. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1,

В2, В3, В4, В5 потребления
этого груза. На пунктах А1, А2 и А3 находится груз
соответственно в количестве 200, 450, 250 тонн. В
пункты В1, В2, В3, В4, В5 требуется доставить
соответственно 100, 125, 325, 250, 100 тонн груза.
Расстояние между пунктами поставки и пунктами
потребления приведено в таблице:

3.

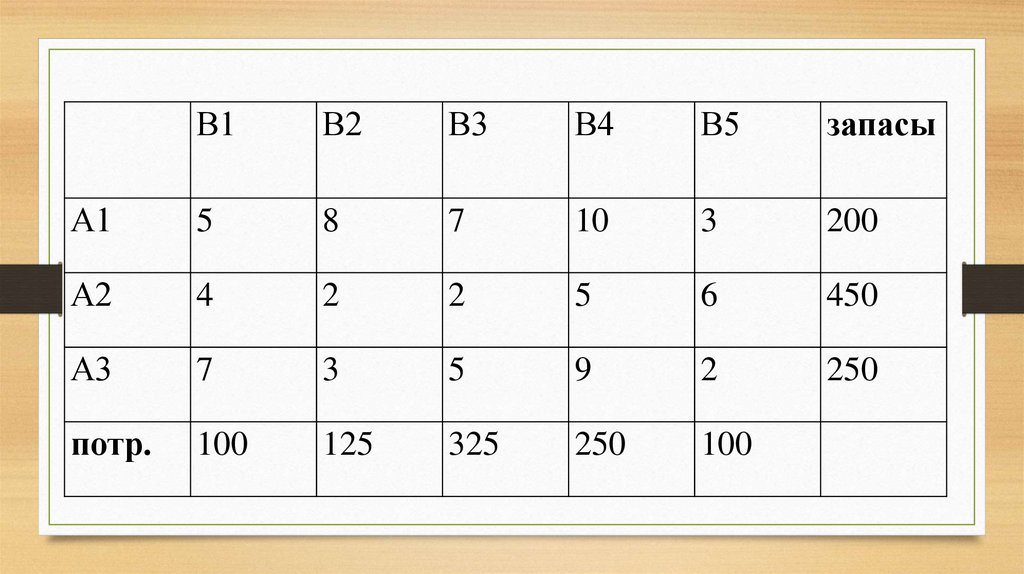
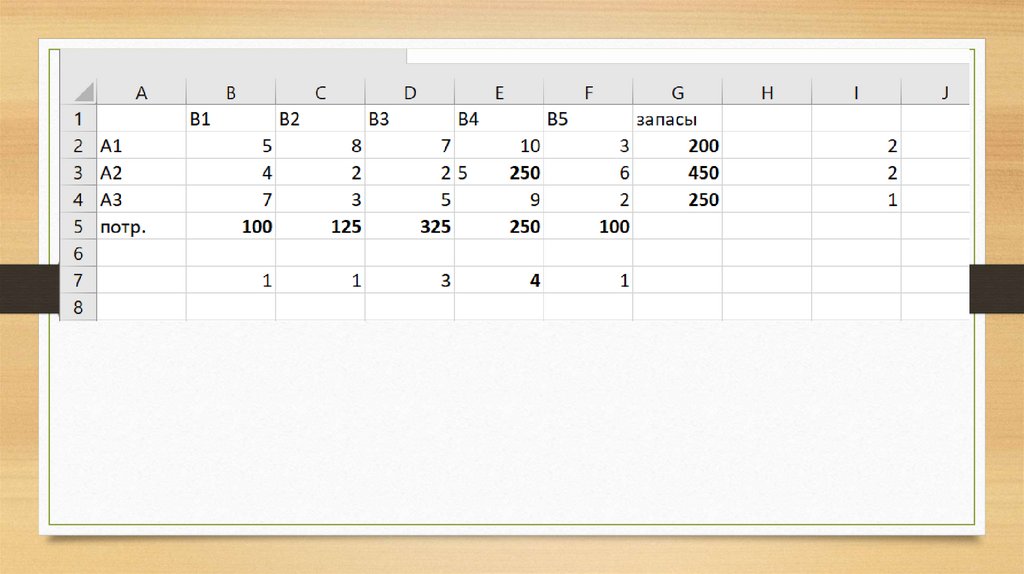
В1
В2
В3
В4
В5
запасы
А1
5
8
7
10
3
200
А2
4
2
2
5
6
450
А3
7
3
5
9
2
250
потр.
100
125
325
250
100

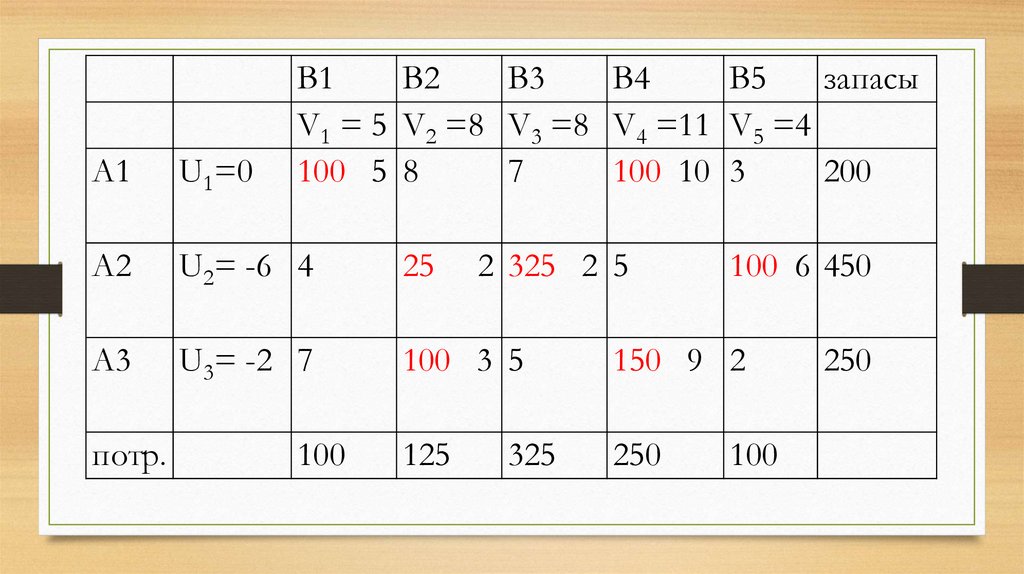
4. Описание транспортной задачи

5. Решить транспортную задачу – это найти оптимальный план перевозок (х11, х12,…, х34), который минимизирует его стоимость

перевозок.

6. Общая стоимость перевозок F, выраженная в тонно-километрах

хіjсіj - количество тонно-километровая
характеристика перевозки.
3
4
F x ijcij
i 1 j 1

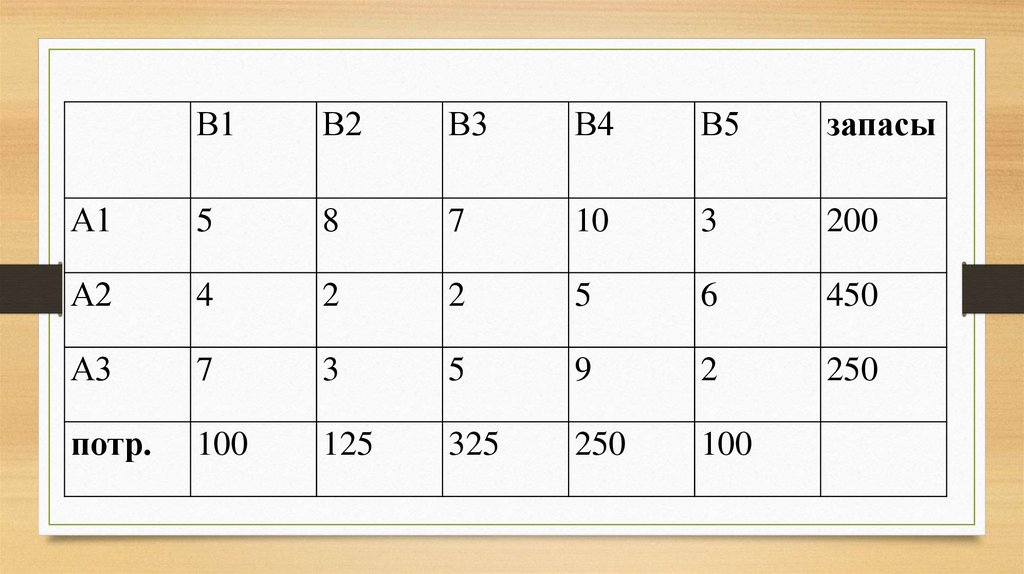
7.

В1
В2
В3
В4
В5
запасы
А1
5
8
7
10
3
200
А2
4
2
2
5
6
450
А3
7
3
5
9
2
250
потр.
100
125
325
250
100

8. Нахождение оптимального плана перевозок (х11, х12,….). Сводится к решению системы линейных уравнений, относительно определяемых

переменных хіj

9. Примечание

Если сij означает расстояния между базами и
заказчиками, то F (общая стоимость) выражается в в
тонно-километрах.
Если сij означает стоимость перевозки одной тонны
груза между базами и заказчиками, то F (общая
стоимость) выражается в рублях.

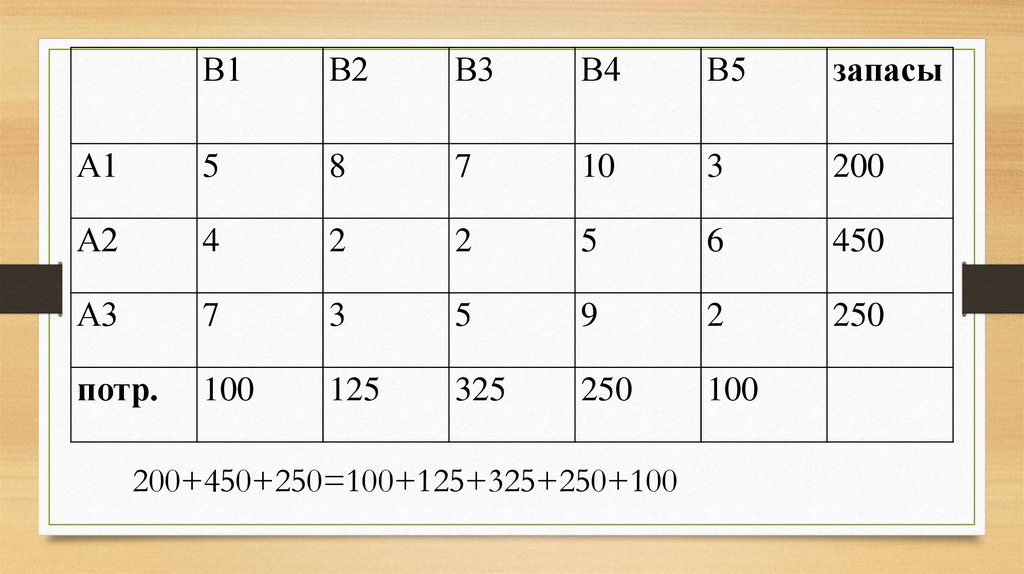
10. Если суммарный объем груза, содержащийся на базах, равен суммарной потребности заказчиков, то транспортная задача называется

закрытой или сбалансированной.
(то есть, при вывозе всего груза,
имеющегося на базах, потребности всех
заказчиков будут полностью удовлетворены)
.

11.

В1
В2
В3
В4
В5
запасы
А1
5
8
7
10
3
200
А2
4
2
2
5
6
450
А3
7
3
5
9
2
250
потр.
100
125
325
250
100
200+450+250=100+125+325+250+100

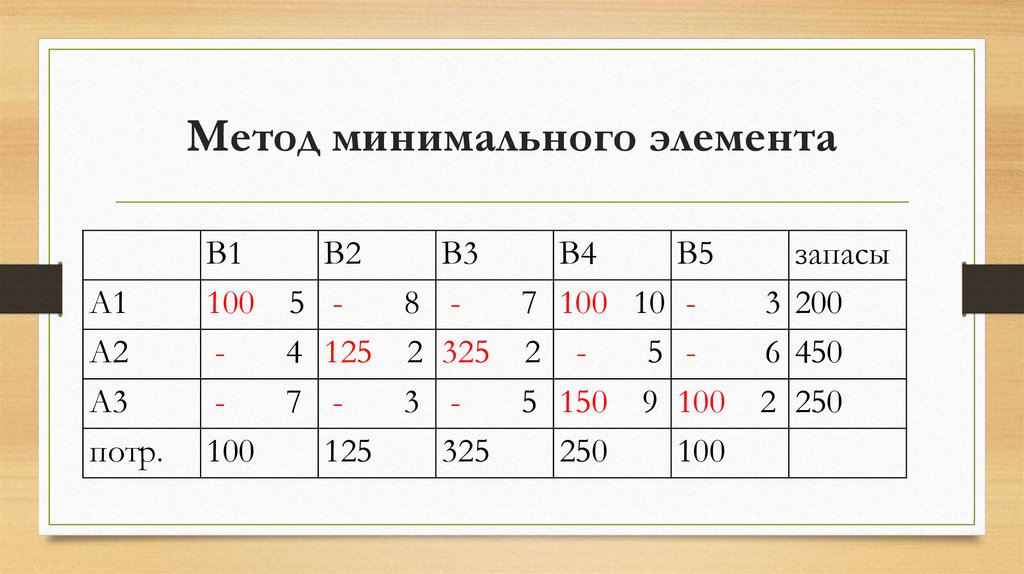
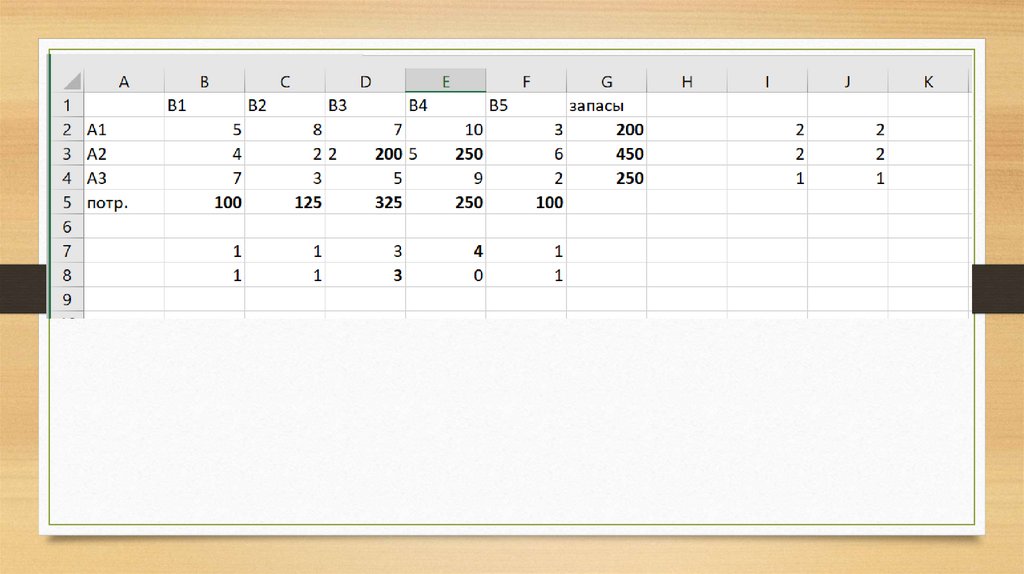
12. Метод минимального элемента

А1
А2
А3
потр.
В1
В2
В3
В4
В5
запасы
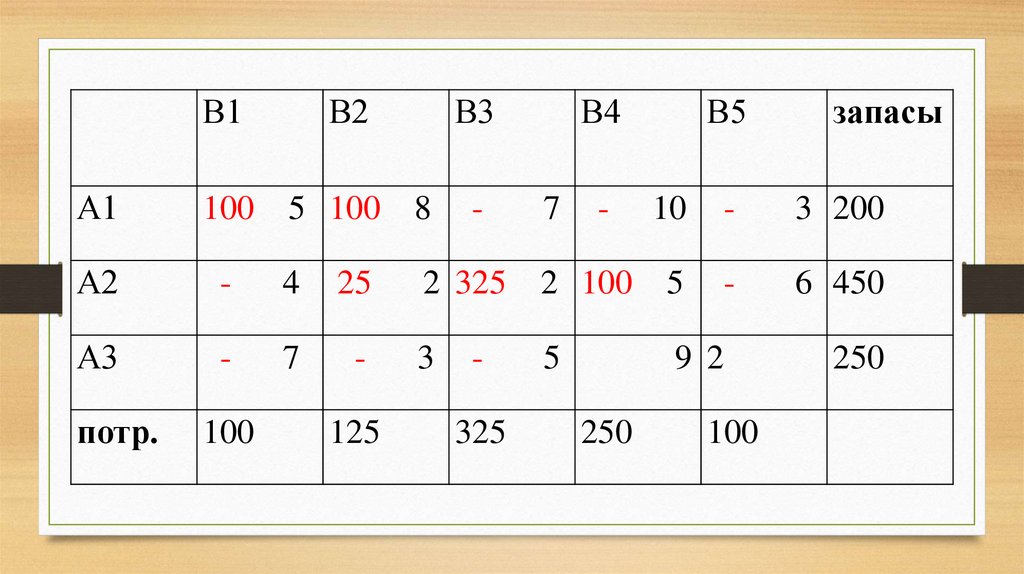
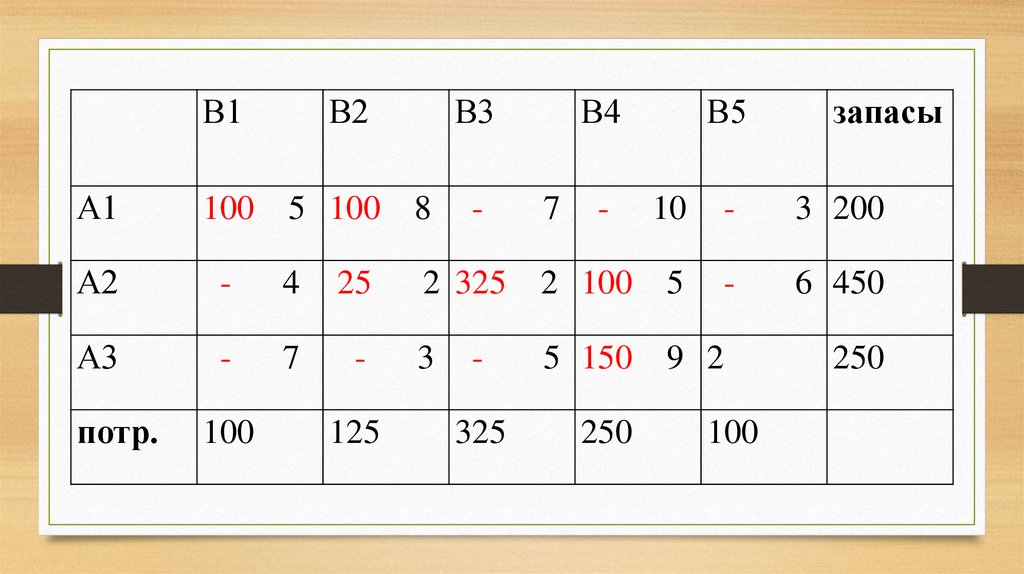
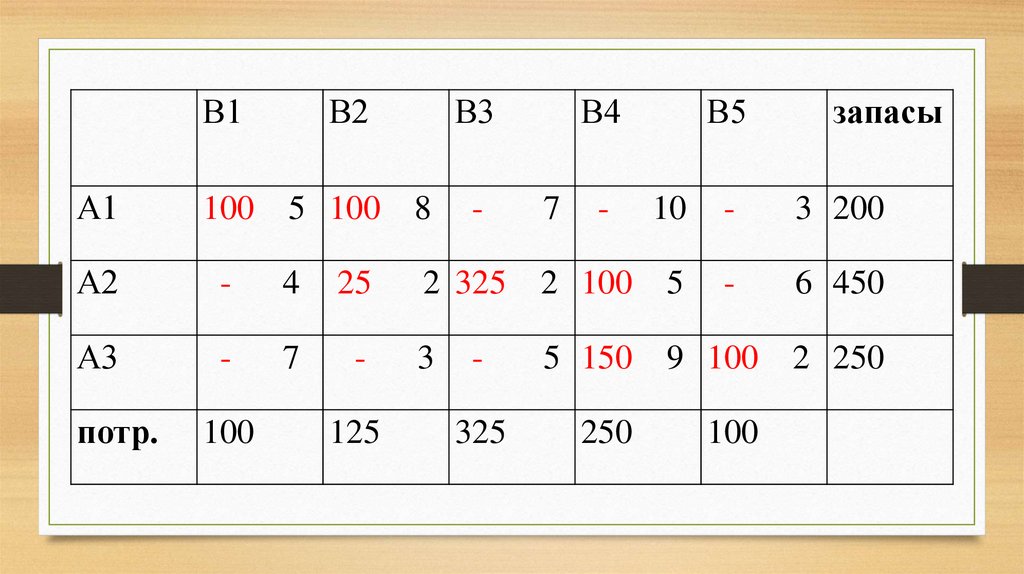
100 5 8 7 100 10 3 200
4 125 2 325 2 5 6 450
7 3 5 150 9 100 2 250
100
125
325
250
100

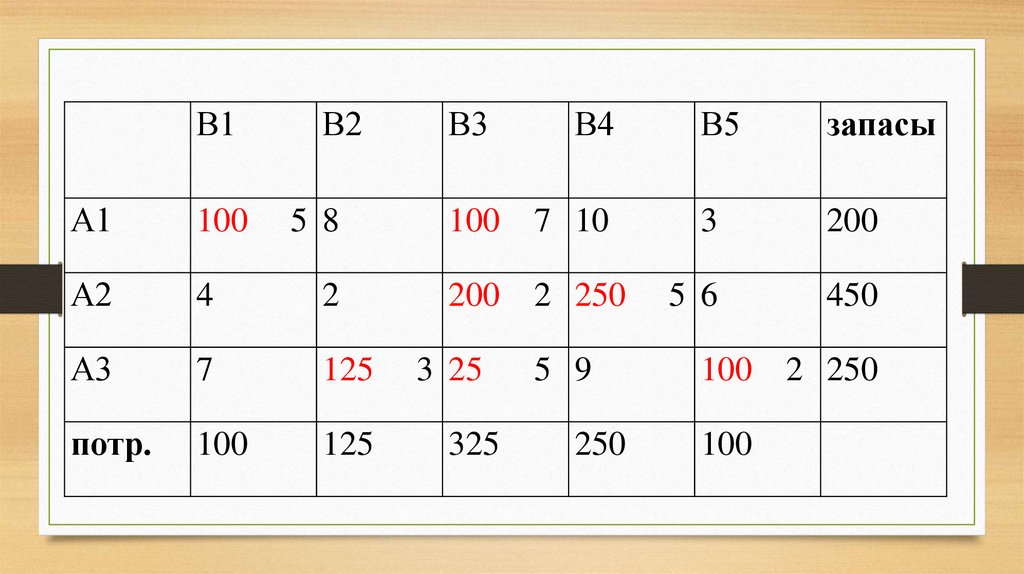
13. Согласно данному плану перевозок, общая стоимость перевозок всего груза составляет: Z1 = 5*100 + 2*125 + 2*325 + 10*100 + +

9*150 + 2*100 = 3950

14. 1. Формирование опорного решения

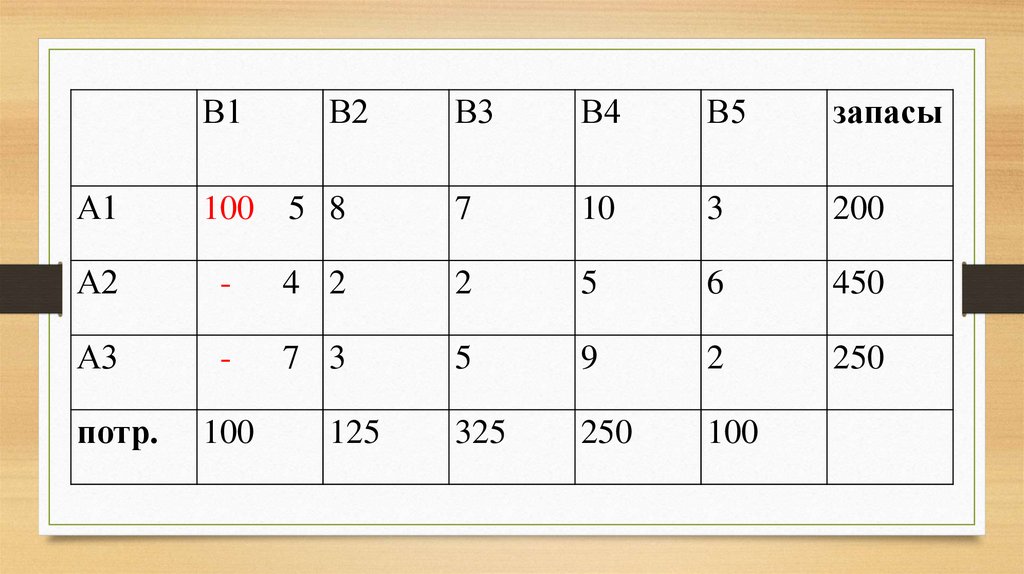
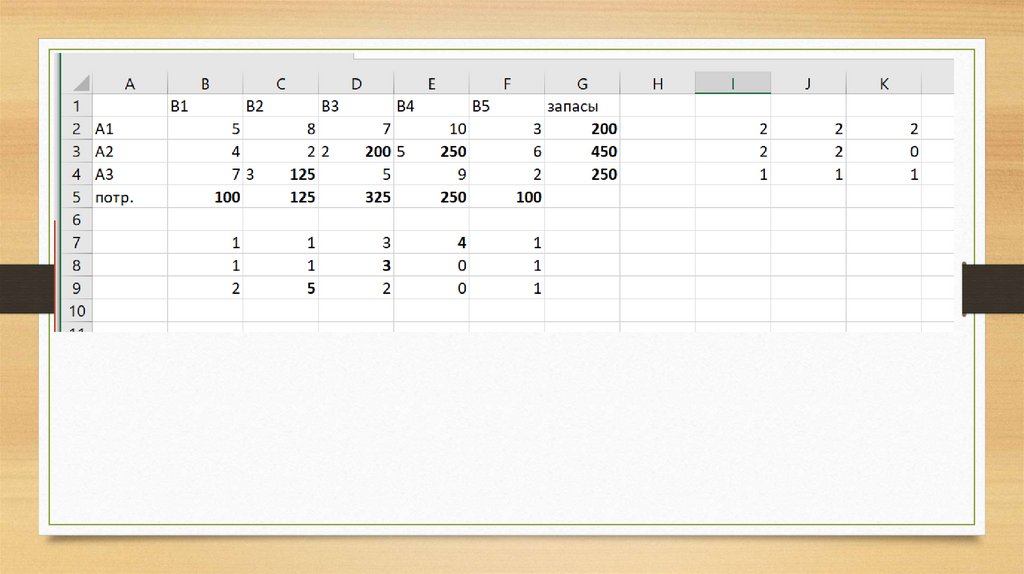
15. Формирование опорного решения методом северо-западного угла Вначале заполняется левая верхняя клетка (северо-западный угол)

исходной таблицы
или её оставшейся части.
После заполнения северо-западного угла с
учетом предельных возможностей базы, из
таблицы исключается или очередной
столбец слева, или очередная строка сверху.

16.

17.

В1
В2
В3
В4
В5
запасы
А1
100 5 8
7
10
3
200
А2
-
4 2
2
5
6
450
А3
-
7 3
5
9
2
250
потр.
100
325
250
100
125

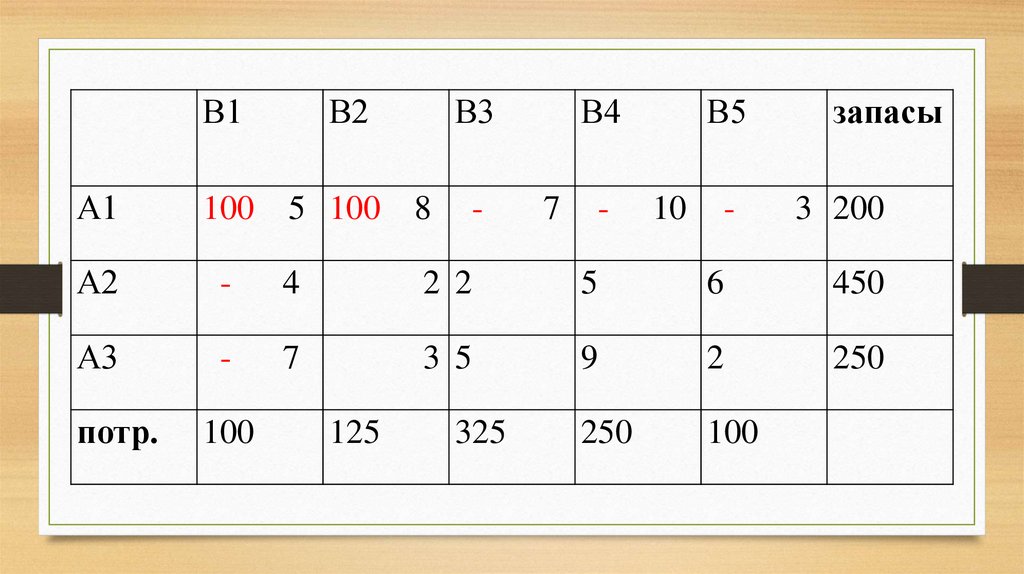
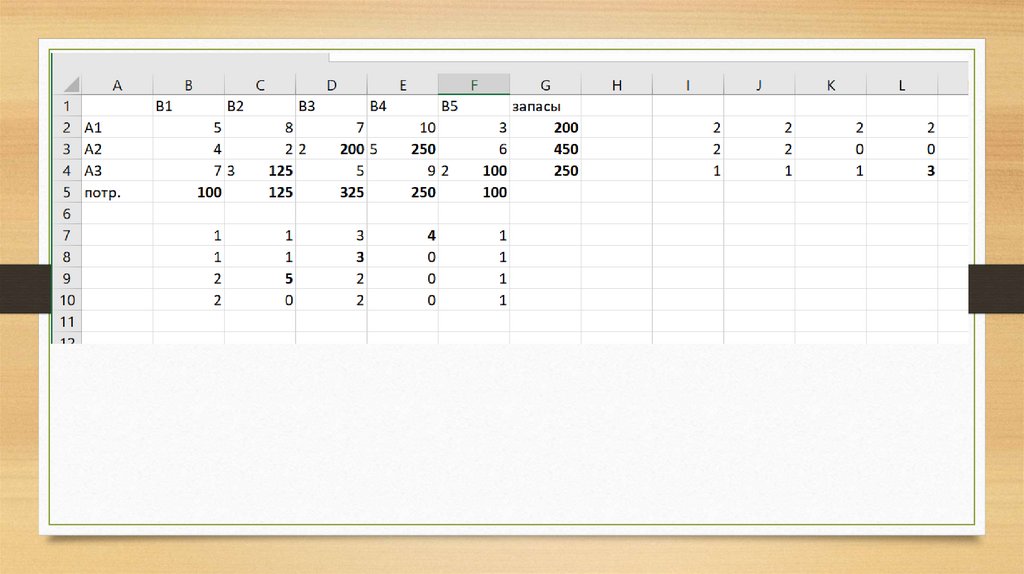
18.

В1
В2
В3
А1
100 5 100 8
А2
-
4
2 2
А3
-
7
3 5
потр.
100
125
-
325
В4
7
-
В5
10
запасы
-
3 200
5
6
450
9
2
250
250
100

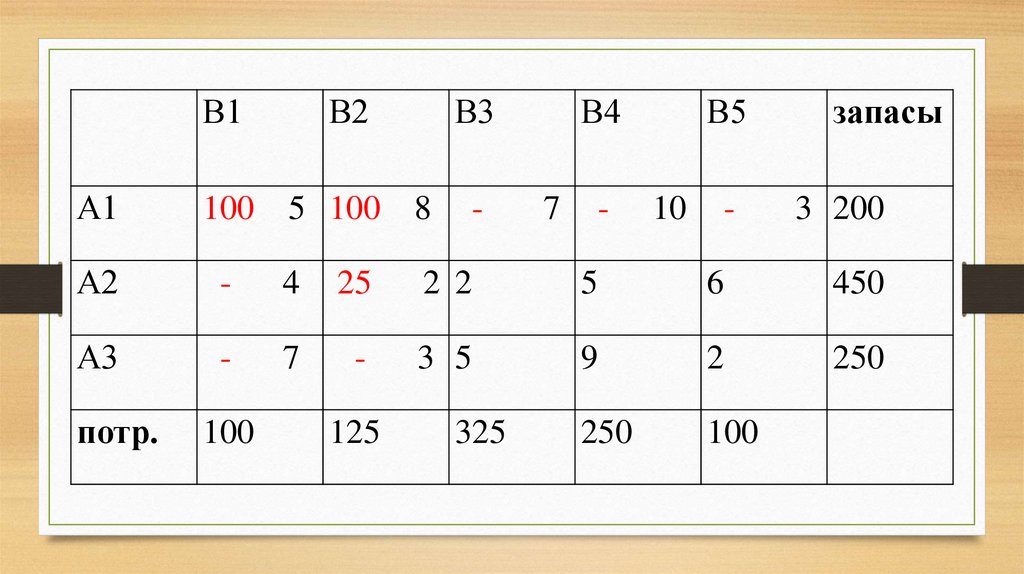
19.

В1
В2
В3
А1
100 5 100 8
А2
-
4
25
2 2
А3
-
7
-
3 5
потр.
100
125
-
325
В4
7
-
В5
10
запасы
-
3 200
5
6
450
9
2
250
250
100

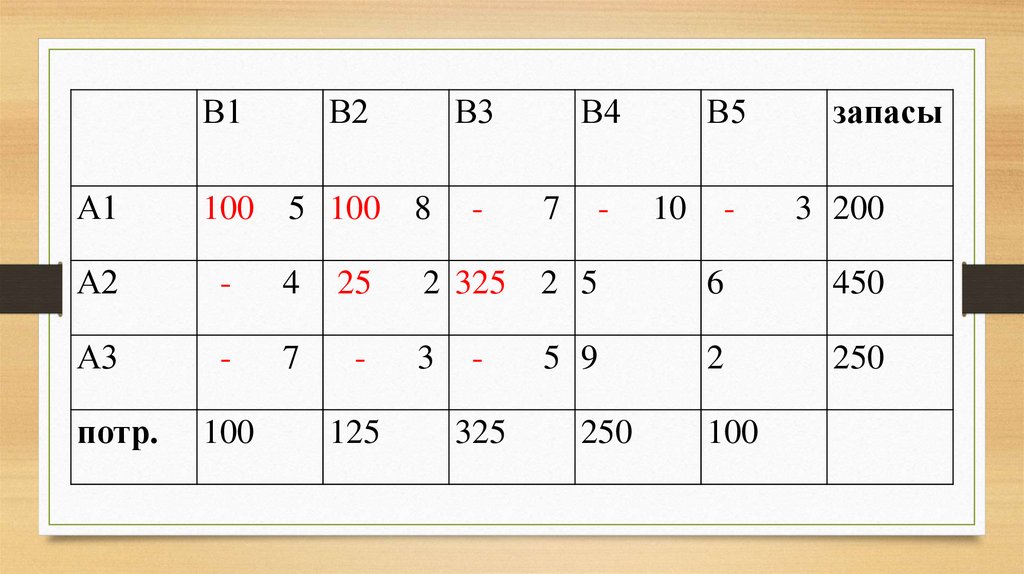
20.

В1
В2
В3
А1
100 5 100 8
А2
-
4
25
А3
-
7
-
потр.
100
125
-
В4
3 200
2 325 2 5
6
450
3
2
250
325
-
5 9
250
10
запасы
-
-
7
В5
100

21.

В1
В2
В3
А1
100 5 100 8
А2
-
4
А3
-
7
потр.
100
3 200
25
2 325 2 100 5
-
6 450
-
3
9 2
250
325
-
запасы
-
-
7
В5
10
125
-
В4
5
250
100

22.

В1
В2
В3
А1
100 5 100 8
А2
-
4
А3
-
7
потр.
100
3 200
25
2 325 2 100 5
-
6 450
-
3
5 150 9 2
250
325
-
запасы
-
-
7
В5
10
125
-
В4
250
100

23.

В1
В2
В3
А1
100 5 100 8
А2
-
4
А3
-
7
потр.
100
3 200
25
2 325 2 100 5
-
6 450
-
3
325
-
запасы
-
-
7
В5
10
125
-
В4
5 150 9 100 2 250
250
100

24. Стоимость перевозок по опорному (первоначальному) плану составит: Z1 = 5*100 + 8*100 + 2*25 + 2*325 + 5*100 + 9*150 + 2*100 =

4050

25. Метод аппроксимации Фогеля

26. При составлении первоначального опорного плана данным методом по всем строкам и столбцам определяют разность между двумя

наименьшими тарифами. Эти
разности записывают в отдельные строку и
столбец распределительной таблицы.

27. Среди указанных разностей выбирают максимальную. В строке (столбце) с максимальной разностью определяют минимальный тариф и

заполняют
соответствующую этому тарифу клетку.

28. Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая

расположена в столбце (строке),
соответствующем наибольшей разности
между двумя минимальными тарифами,
находящимися в данном столбце (строке).

29.

В1
В2
В3
В4
В5
запасы
А1
5
8
7
10
3
200
А2
4
2
2
5
6
450
А3
7
3
5
9
2
250
потр.
100
125
325
250
100

30.

31.

32.

33.

34.

35.

В1
В2
А1
100
А2
В3
В4
В5
запасы
5 8
100 7 10
3
200
4
2
200 2 250
5 6
450
А3
7
125
3 25
потр.
100
125
325
5 9
250
100 2 250
100

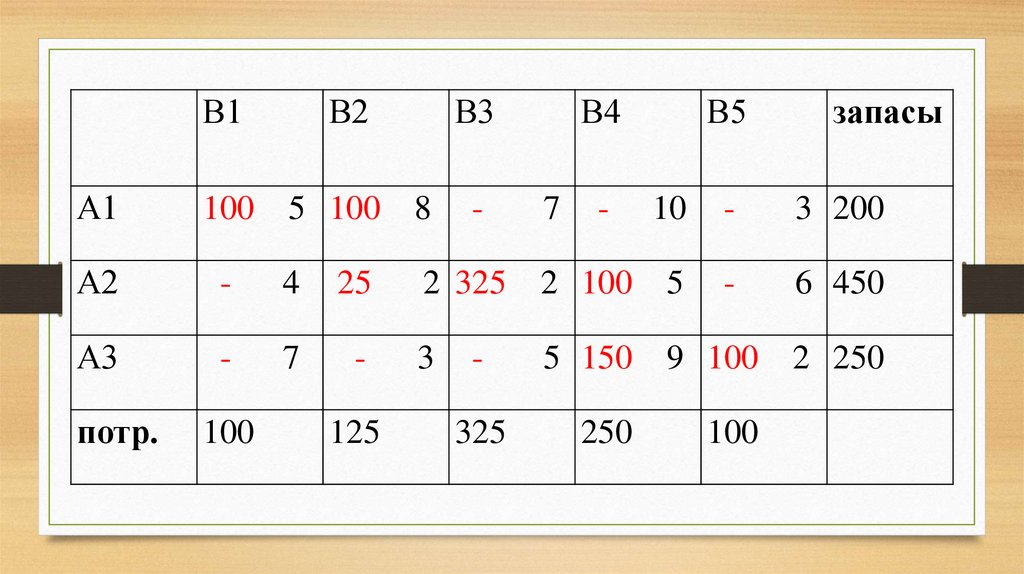
36. Суммарная стоимость перевозки по этому плану: Z1 = 5*100 + 7*100 + 2*200 + 5*250 + 3*125 + 5*25 + 2*100 = 3550

37. Решение транспортной задачи методом потенциалов

38. Пересчитывать опорный план можно с помощью потенциалов.

Тариф сij базисных переменных
представляется в виде суммы
сij = Ui + Vj
Ui - потенциалы баз,
Vj – потенциалы заказчиков.

39.

В1
В2
В3
А1
100 5 100 8
А2
-
4
А3
-
7
потр.
100
3 200
25
2 325 2 100 5
-
6 450
-
3
325
-
запасы
-
-
7
В5
10
125
-
В4
5 150 9 100 2 250
250
100

40. образуется система уравнений

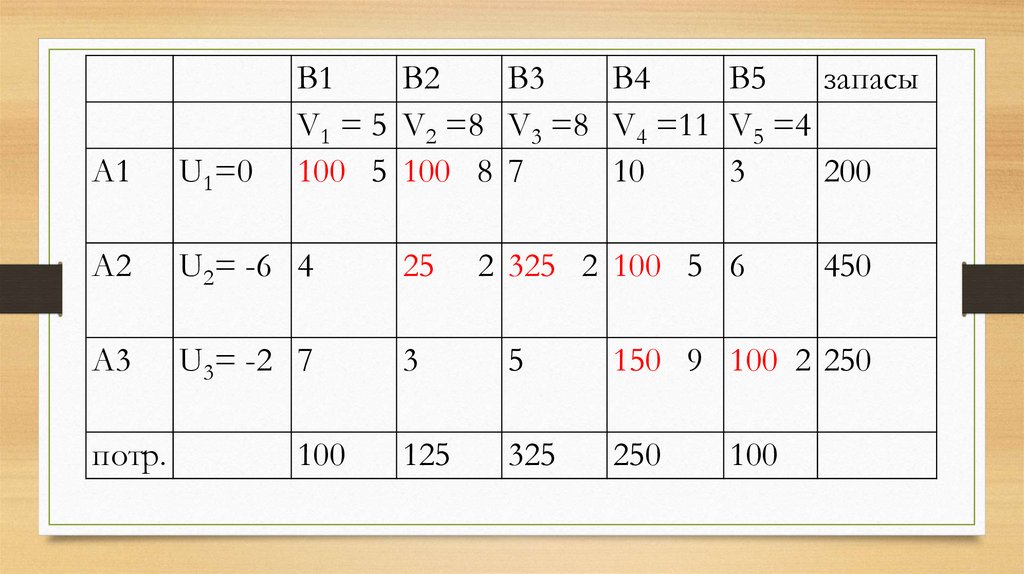
41. Значение одного из данных неизвестных можно выбирать произвольно. Например, можно принять, что U1 = 0. Тогда решение системы

примет вид:

42. Значение одного из данных неизвестных можно выбирать произвольно. Например, можно принять, что U1 = 0. Тогда решение системы

примет вид:

43.

В1
В2
В3
В4
В5
запасы
V1 = 5 V2 =8 V3 =8 V4 =11 V5 =4
100 5 100 8 7
10
3
200
А1
U1=0
А2
U2= -6 4
25
А3
U3= -2 7
3
5
150 9 100 2 250
125
325
250
потр.
100
2 325 2 100 5 6
100
450

44. Посчитаем алгебраические суммы свободных клеток

Проверим
критерий
оптимальности :
Ui + Vj ≤ dij для
свободных
клеток.

45. Из тех условий, где критерий не выполняется, выбираем то условие, где разница максимальна. Это – ячейка (3 , 2)

46. Перебросим в ячейку (3 , 2) 100 единиц груза из ячейки (1 , 2). Чтобы компенсировать недостаток в первой строке, перебросим те

же 100 единиц
груза из ячейки (2 , 4) в ячейку (1 , 4).
Теперь чтобы компенсировать недостаток в
строке 2, перебросим из ячейки (3 , 5) 100 единиц
в ячейку (2 , 5).

47.

В1
В2
В3
В4
В5
запасы
V1 = 5 V2 =8 V3 =8 V4 =11 V5 =4
100 5 8
7
100 10 3
200
А1
U1=0
А2
U2= -6 4
25
А3
U3= -2 7
100 3 5
150 9 2
125
250
потр.
100
2 325 2 5
325
100 6 450
100
250

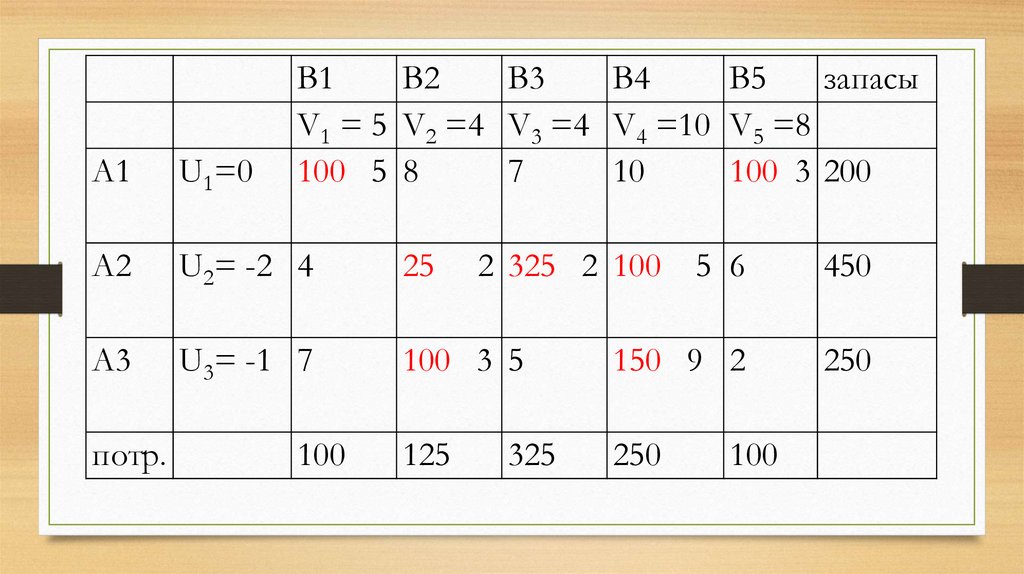
48. Получаем новую таблицу, для которой повторяем расчет потенциалов: Полагаем U1=0, а далее Ui + Vj = dij для занятых клеток

таблицы.

49.

50.

В1
В2
В3
В4
В5
запасы
V1 = 5 V2 =4 V3 =4 V4 =10 V5 =8
100 5 8
7
10
100 3 200
А1
U1=0
А2
U2= -2 4
25
А3
U3= -1 7
100 3 5
150 9 2
125
250
потр.
100
2 325 2 100 5 6
325
100
450
250

51. Проверим критерий оптимальности : Ui + Vj ≤ dij для свободных клеток.

Критерий не
выполнен

52. К новой таблице применяют еще раз метод потенциалов для минимизации стоимости перевозок до тех пор, пока алгебраические суммы

тарифов для всех свободных клеток
таблицы не окажутся положительными.