Тема 3. Системы НУ

1.

Андреева Анна Дмитриевна

2. Итерационные методы решения систем нелинейных уравнений

1
F(X ) 0
f1 x1 , x2 , , xm 0
f ( x , x , , x ) 0
2 1 2
m
f m ( x1 , x2 , , xm ) 0
- вектор решения, полученный на
X 0 x10 , x20 , , xm0
X n x1n , x2n , , xmn
- начальное приближение
(заданный вектор)
n-ой итерации
0 1
- точность решения (задана)

3. Каноническая форма одношаговых итерационных методов

Каноническая форма
одношаговых итерационных
F(X ) 0
методов
Bn 1
X n 1 X n
n 1
Метод сходится, если
F(X ) 0
n
2
X n 1 X n 0, n
3
max xin 1 xin
Явный метод, если Bn+1=E
1 i m
Неявный метод, если Bn+1≠ E
Cтационарный метод, если B = const, τ = const
Нестационарный метод, если B ≠ const или τ ≠ const

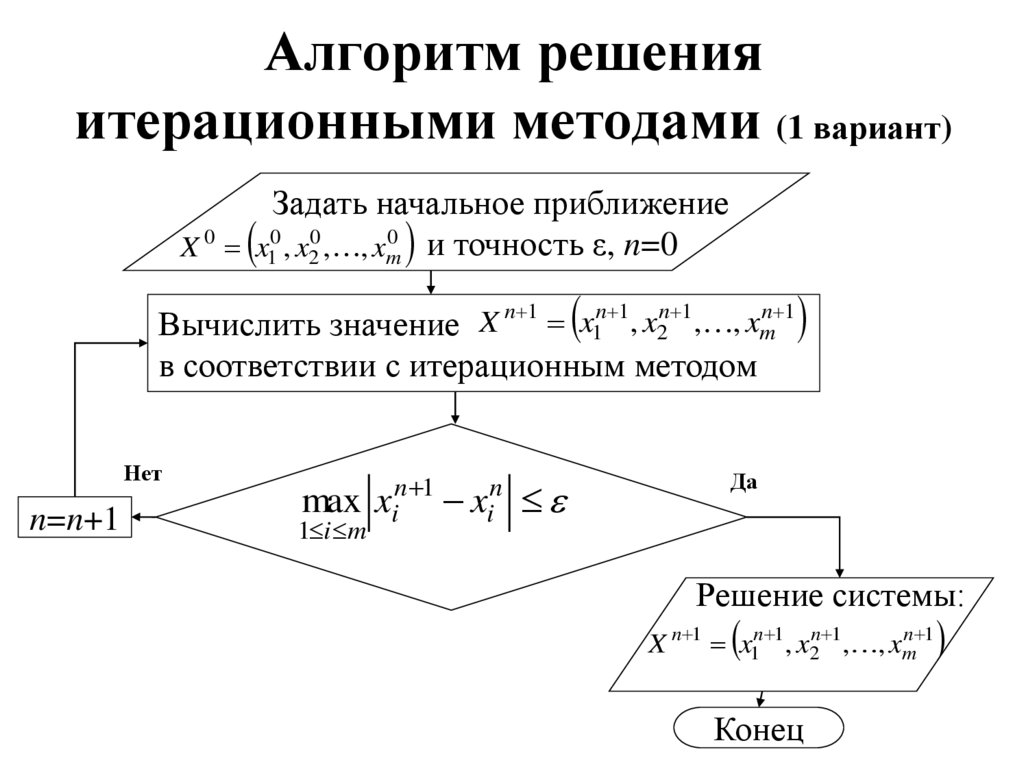
4. Алгоритм решения итерационными методами (1 вариант)

Задать начальное приближение
X 0 x10 , x20 , , xm0 и точность ε, n=0
Вычислить значение X n 1 x1n 1, x2n 1, , xmn 1
в соответствии с итерационным методом
Нет
n=n+1
max xin 1 xin
1 i m
Да
Решение системы:
X n 1 x1n 1, x2n 1, , xmn 1
Конец

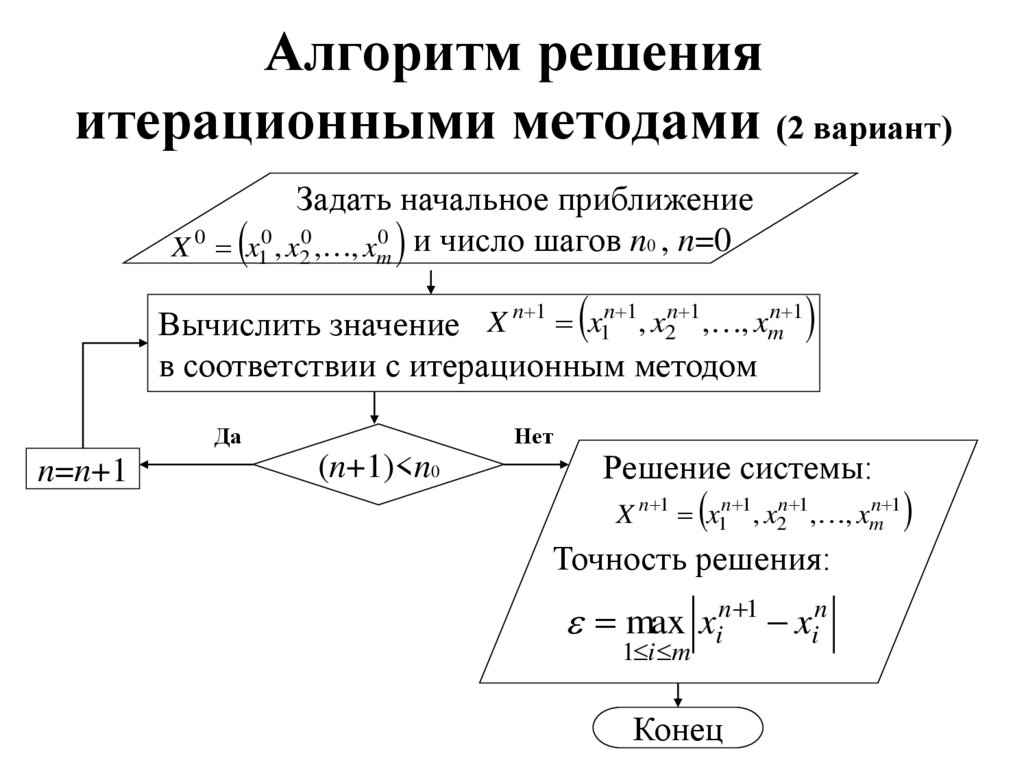
5. Алгоритм решения итерационными методами (2 вариант)

Задать начальное приближение
X 0 x10 , x20 , , xm0 и число шагов n0 , n=0
Вычислить значение X n 1 x1n 1, x2n 1, , xmn 1
в соответствии с итерационным методом
Да
n=n+1
Нет
(n+1)<n0
Решение системы:
X n 1 x1n 1, x2n 1, , xmn 1
Точность решения:
max xin 1 xin
1 i m
Конец

6. Методы решения систем нелинейных уравнений

1. Метод простой итерации
X n 1 X n F ( X n ) 0
4
X n 1 X n F ( X n )
n 1
n
n n
n
xi xi f i ( x1 , x2 , , xm ),
i 1, m
4.1

7.

2. Метод Ньютона
X n x1n , x2n , , xmn
j m
n
n
f
(
x
,
x
n
n
n
n 2
i 1
m)
f i ( x1 , , xm ) f i ( x1 , , xm ) ( x j x j )
( X X ),
x j
j 1
i 1, m
j m
n f i ( X
(x j x j )
x j
j 1
j m
n
)
n 1
n f i ( X
(x j x j )
x j
j 1
f i ( X n ) 0, i 1, m
n
)
f i ( X n ) 0, i 1, m
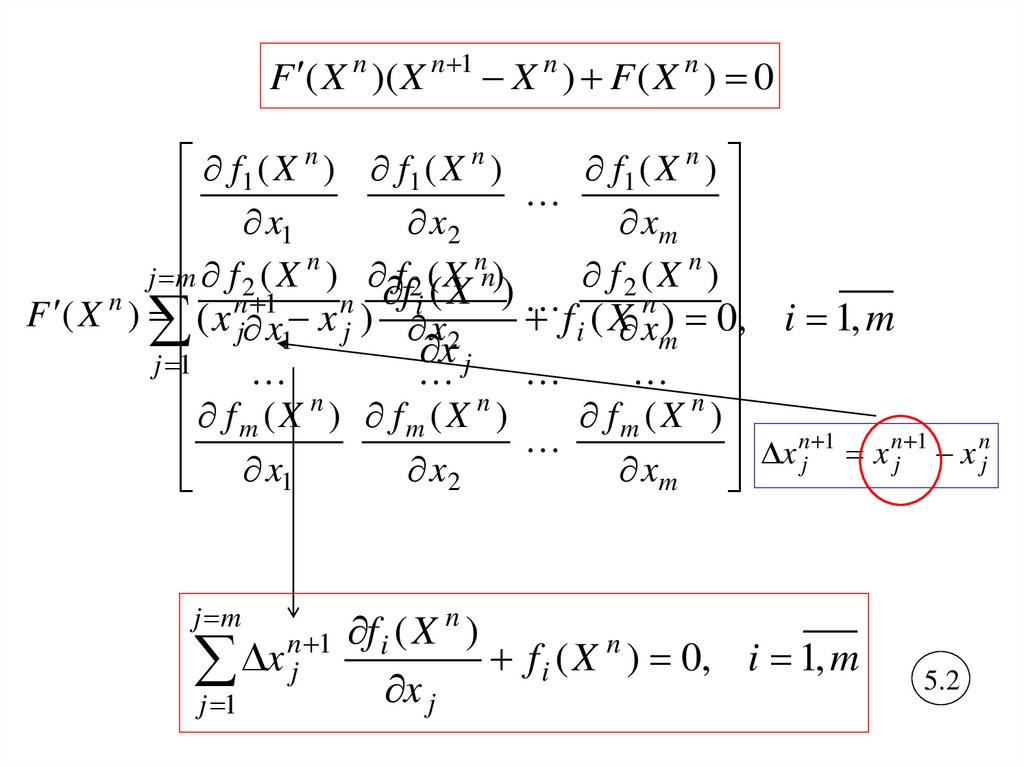
F ( X n )( X n 1 X n ) F ( X n ) 0
5
5.1

8.

F ( X n )( X n 1 X n ) F ( X n ) 0
f1 ( X n ) f 1 ( X n )
f1 ( X n )
x2
xm
x1
n
f 2 ( X n ) f 2 ( X nn)
f
(
X
)
j m
2
f
(
X
)
n
, i 1, m
F ( X n ) ( x nj 1x x nj ) i x
f
(
X
)
0
i xm
1
2
x j
j 1
fm (X n ) fm ( X n )
fm (X n )
x nj 1 x nj 1 x nj
x2
xm
x1
j m
n 1 f i ( X
x j
x j
j 1
n
)
f i ( X n ) 0, i 1, m
5.2

9. Нелинейные итерационные методы

f1 x1 , x2 , , xm 0
f ( x , x , , x ) 0
2 1 2
m
f m ( x1 , x2 , , xm ) 0
x1 g1 x1 , x 2 , , x m
x g ( x , x , , x )
2
2 1 2
m
x m g m ( x1 , x2 , , xm )
6
3. Метод Якоби
n 1
n
n
n n
n
xi gi ( x1 , , xi 1, xi , xi 1, , xm ),
i 1, m
7
4. Метод Зейделя
n 1
n 1
n 1 n n
n
xi gi ( x1 , , xi 1 , xi , xi 1, , xm ),
i 1, m 8

10. Численные методы решения нелинейных уравнений

f ( x) 0
1
Трансцендентные
Алгебраические
a0 x n a1 x n 1 an 1 x an 0
2
Примеры
2x3 x 2 5 0
ln x x 0
2

11. Основные положения методов решения нелинейных уравнений

f ( x) 0
Решение производится в два этапа:
Этап отделения корня получение начального
приближения корня
x0
Условия
окончания
итераций:
Этап уточнения корня последовательное уточнение
приближения корня:
3
x n 1 x n
n0
x1 , x 2 , , x n
ε – заданная точность
- заданное число итераций

12. Отделение корней алгебраических уравнений

a0 x n a1 x n 1 an 1 x an 0
2
1. Имеет n корней
2. Число «+» корней равно числу перемен знаков в последовательности коэффициентов a0 , a1 , , an
3. Число «-» корней равно числу перемен знаков в последовательности коэффициентов a0 , a1 , , an , где x заменено на -x
4. Интервалы существования «+» и «-» корней:
an
M
x 1
m an
a0
где
m max a0 , a1 , , an 1 ,
an
M
1
x
a0
m an
M max a1 , a2 , , an

13. Шаговый метод отделения корня

f ( x) 0
1
[xн , xв], хн < хв
1) на отрезке [xн,xв] есть корень?
2) сузить отрезок до величины h, h <1
f (x)
f (x)
f(xн)f(xв)>0 – нет корня
f(xн)f(xв)<0 – есть корень
f (xв)
xн
xн+h xxнн+hxн+h xв
x
f (xн)
f(xн)f(xн+h)>0 – нет корня
f(xн)f(xн+h)<0 – есть корень

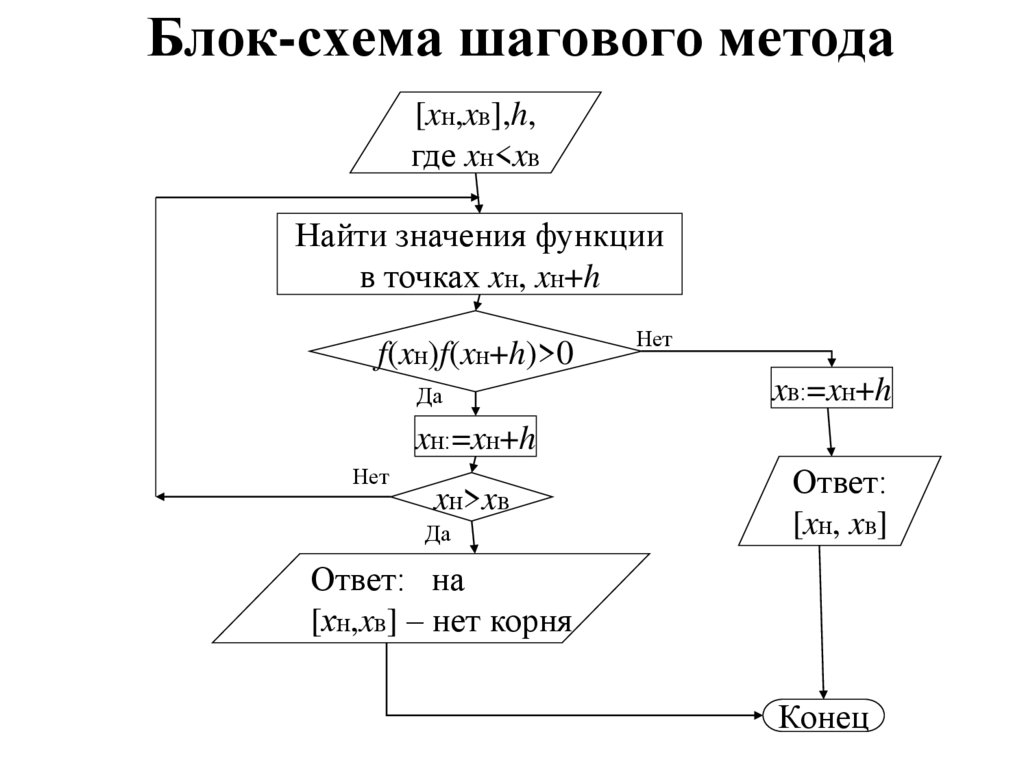
14. Блок-схема шагового метода

[xн,xв],h,
где xн<xв
Найти значения функции
в точках xн, xн+h
f(xн)f(xн+h)>0
Да
Нет
xв:=xн+h
xн:=xн+h
Нет
xн>xв
Да
Ответ:
[xн, xв]
Ответ: на
[хн,xв] – нет корня
Конец

15. Метод половинного деления

f ( x) 0
f (x)
1
f(xн)f(xв)<0 – есть корень
f (x)
f (xв)
xн
x1
x2 x
в
x
f (xн)
x
n 1
x
n

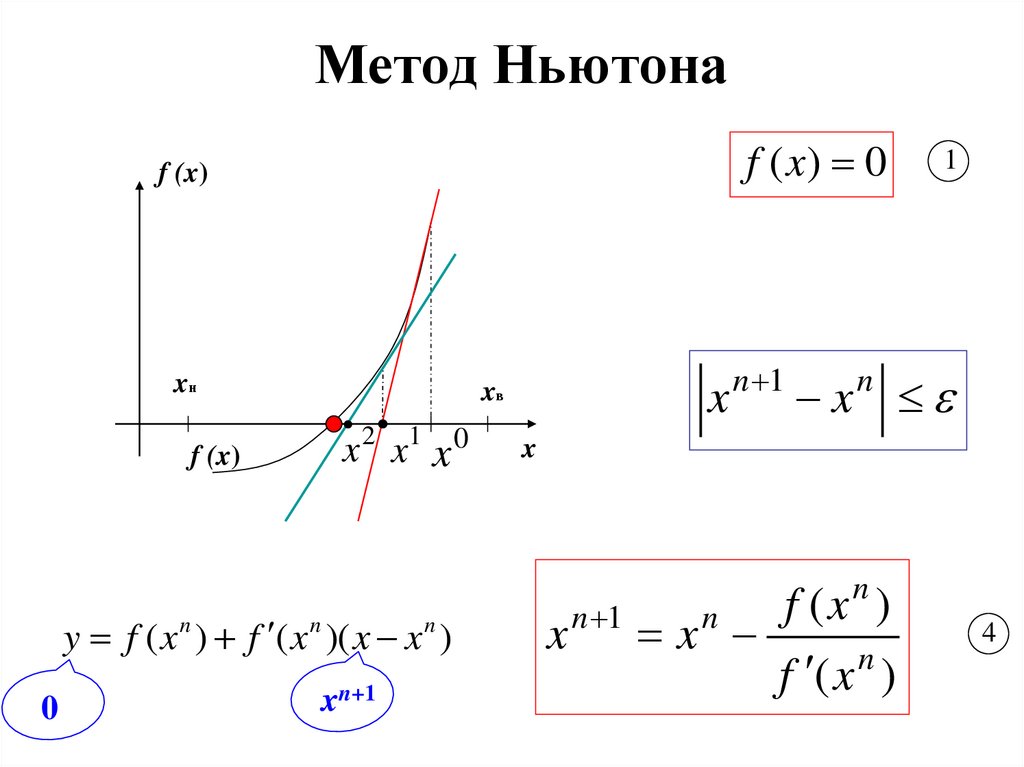
16. Метод Ньютона

f ( x) 0
f (x)
xн
f (x)
x 2 x1 x 0
y f ( x n ) f ( x n )( x x n )
0
x
xв
xn+1
n 1
1
x
n
x
n
f
(
x
)
n 1
n
x x
n
f (x )
4

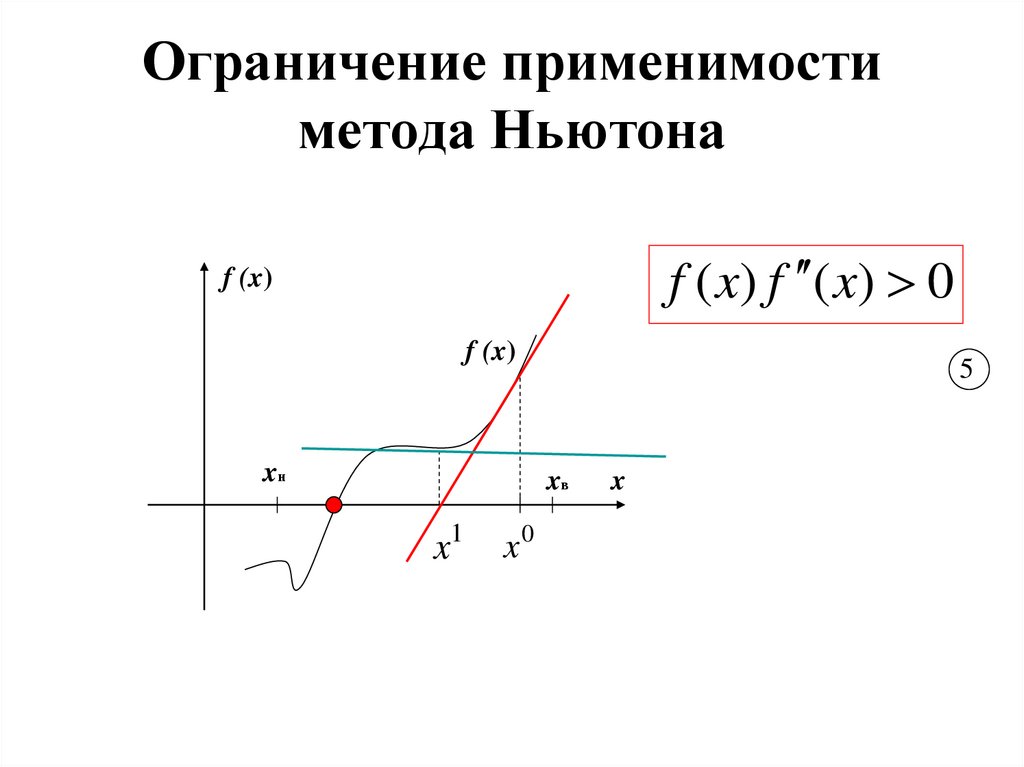
17. Ограничение применимости метода Ньютона

f ( x) f ( x) 0
f (x)
f (x)
xн
5
xв
x1
x0
x

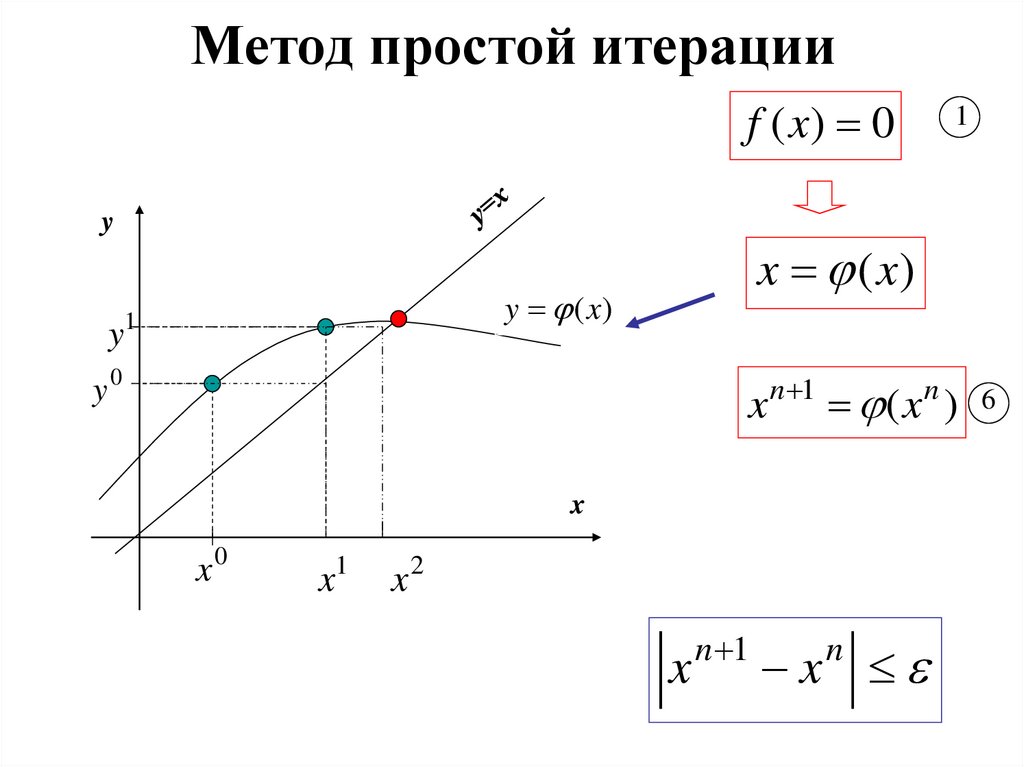
18. Метод простой итерации

f ( x) 0
y
x (x)
y (x)
1
y
1
y0
x n 1 ( x n ) 6
x
x0
x1
x2
x
n 1
x
n

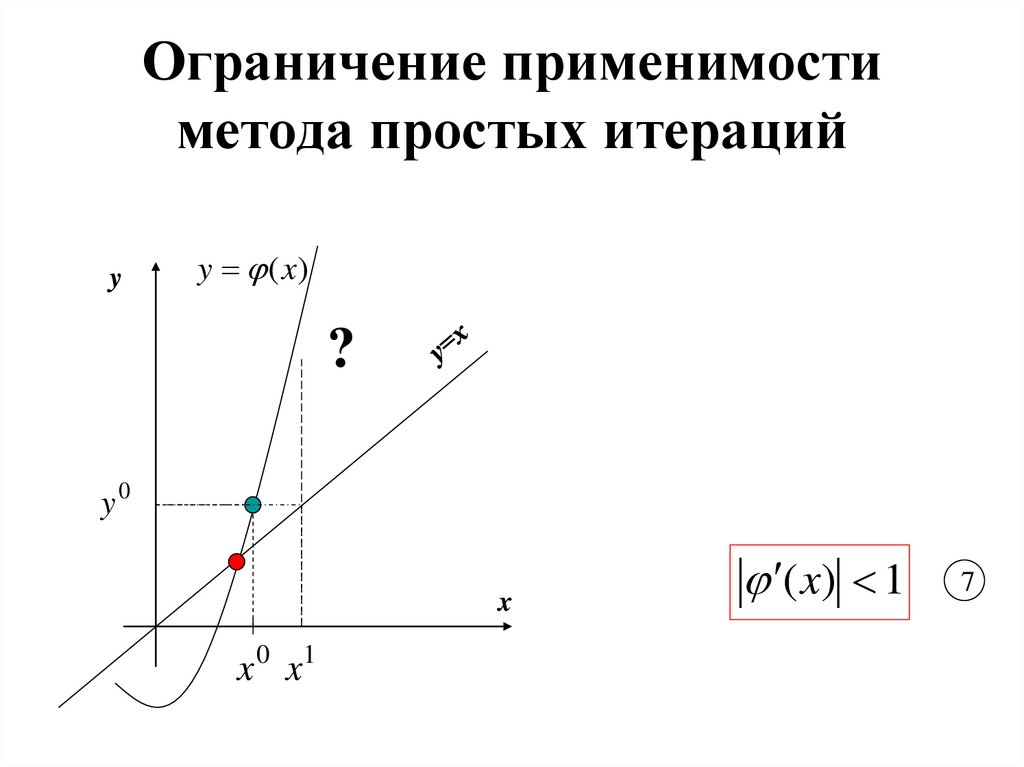
19. Ограничение применимости метода простых итераций

y
y (x)
?
y0
x
x 0 x1
( x) 1
7

20. Ограничение на значение точности ε

T x
n 1
x
n
Т
min 10 7
εmin
min
n
x x
n 1
x [ x n 1 , x n 1 ]