Презентация_по_алгебре_Задание_11_ЕГЭ_профильного_уровня_по_математике

1. «Задание 11 ЕГЭ-профильного уровня по математике (графики функций)

«Задание 11 ЕГЭпрофильного уровня по
математике
(графики функций)

2. Задание 11 Функции и их графики.

Проверяется умение определять значение функции
по значению аргумента при различных способах
задания функции; описывать по графику
поведение и свойства функции, находить по
графику функции наибольшее и наименьшее
значения; строить графики изученных функций.

3.

Как формулируется задание 11 ЕГЭ по математике?
По графику функции, который дается в условии, нужно
определить неизвестные параметры в ее формуле.
Возможно — найти значение функции в некоторой точке
или координаты точки пересечения графиков функций.
Чтобы выполнить это задание, надо знать, как выглядят
и какими свойствами обладают графики элементарных
функций. Надо уметь читать графики, то есть получать
из них необходимую информацию. Например,
определять формулу функции по ее графику.

4. Функции

Линейная функция, её график
Функция, описывающая обратную пропорциональную зависимость,
её график
Квадратичная функция, её график
Степенная функция с натуральным показателем, её график
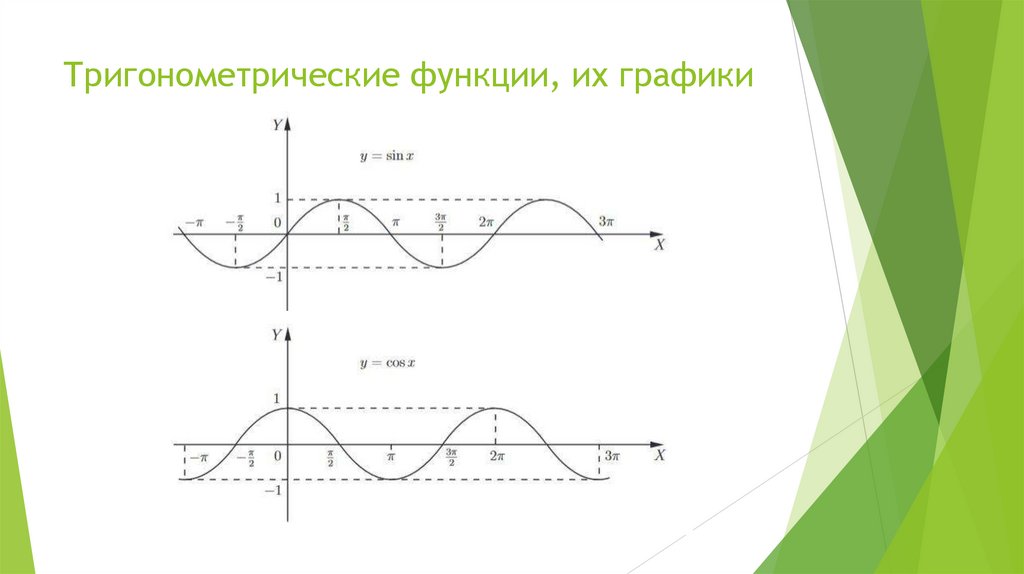
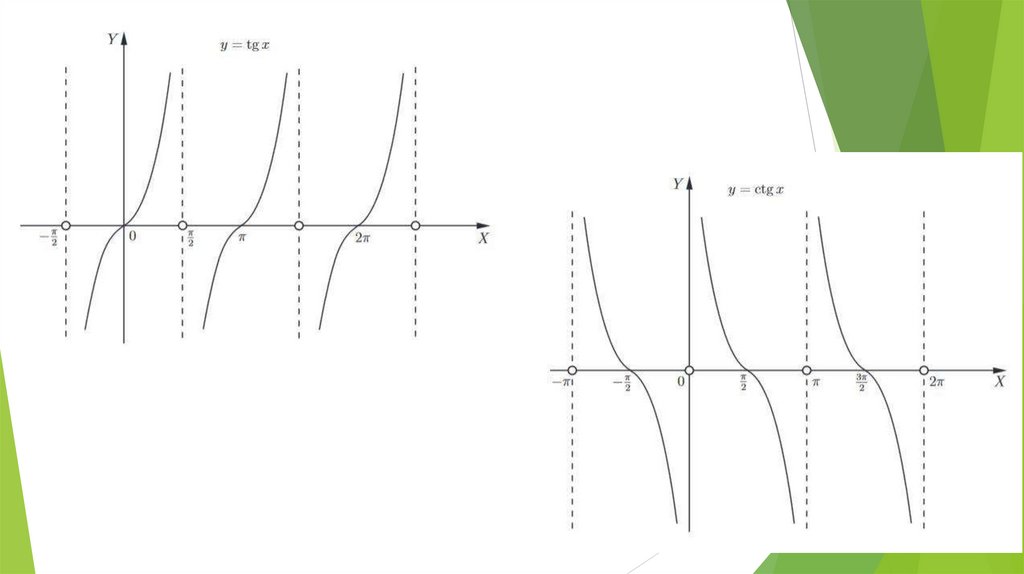
Тригонометрические функции, их графики
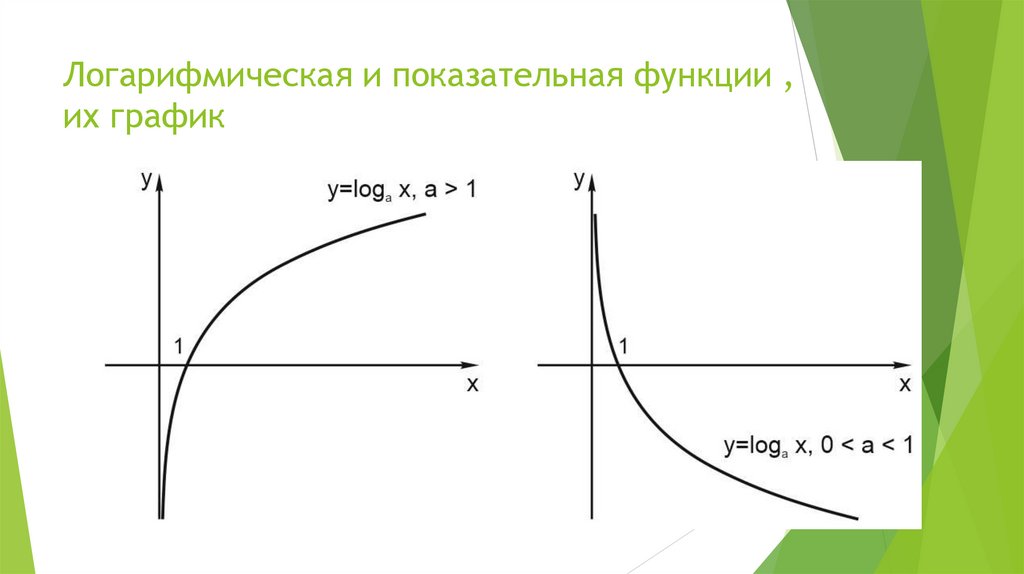
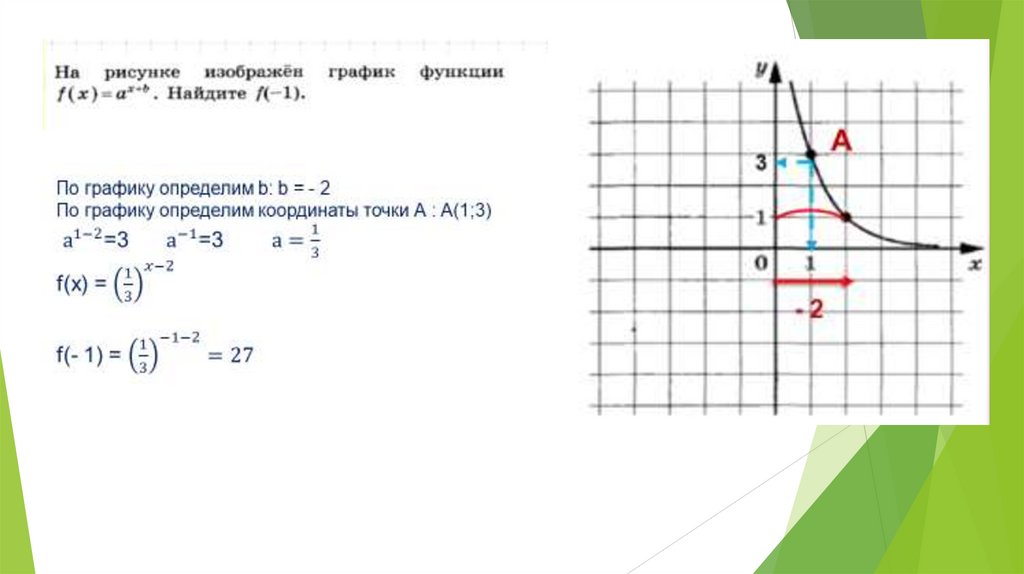
Показательная функция, её график
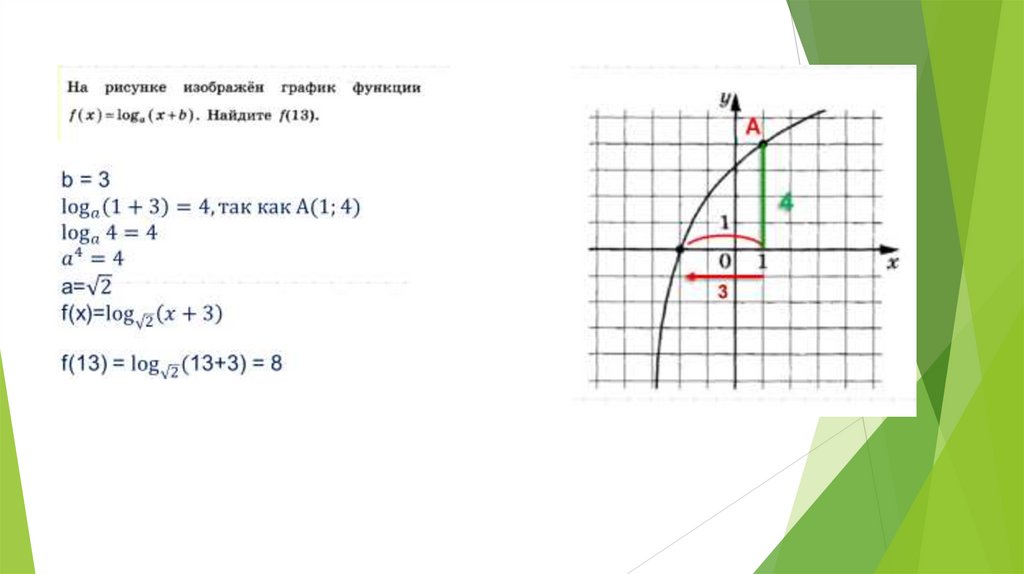
Логарифмическая функция, её график

5. Способы решения:

1. Нахождение коэффициентов функции через решение
систем уравнений, используя целочисленные координаты
точек графика ( в том числе и точек пересечения с
осями).
2. Нахождение коэффициентов, используя
вспомогательные формулы. Например, формулу тангенса
угла наклона прямой, абсциссы вершины параболы,
периодичности функции и др.)
3. Преобразование формулы, задающую функцию.
4. Нахождение коэффициентов через преобразования
графиков функций.

6. Линейная функция, её график

Линейная функция — функция вида y = kx+b.
График линейной функции — прямая.
Для построения графика линейной функции достаточно
двух точек — потому что через две несовпадающие
точки всегда можно провести прямую, причем
единственную.

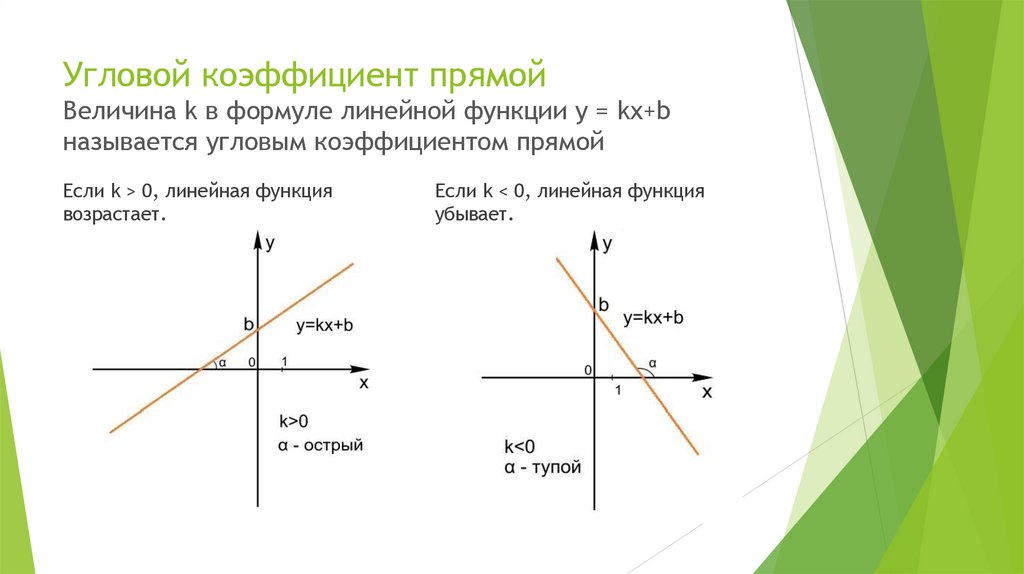
7. Угловой коэффициент прямой Величина k в формуле линейной функции y = kx+b называется угловым коэффициентом прямой

Если k > 0, линейная функция
возрастает.
Если k < 0, линейная функция
убывает.

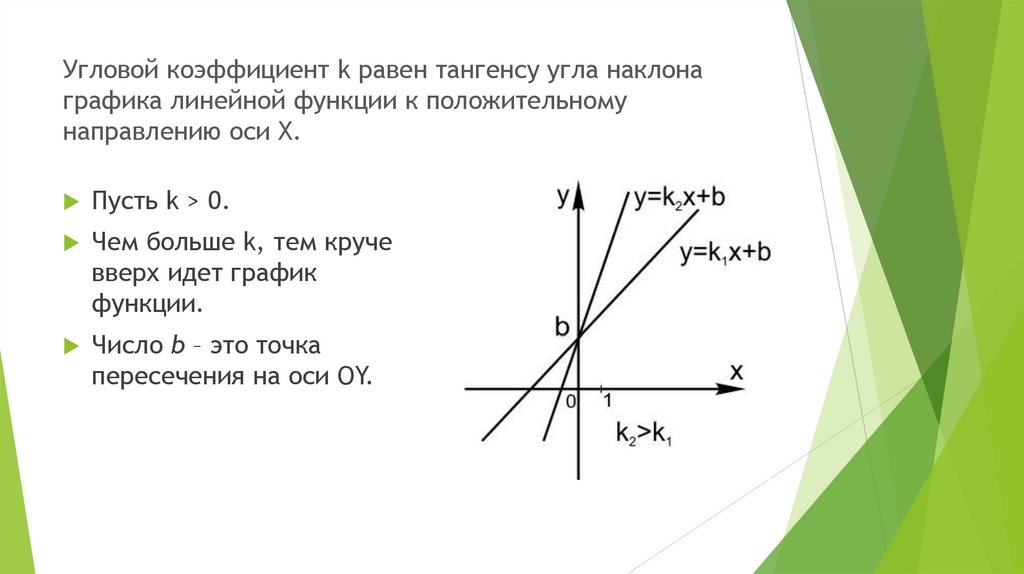
8. Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.

Пусть k > 0.
Чем больше k, тем круче
вверх идет график
функции.
Число b – это точка
пересечения на оси OY.

9.

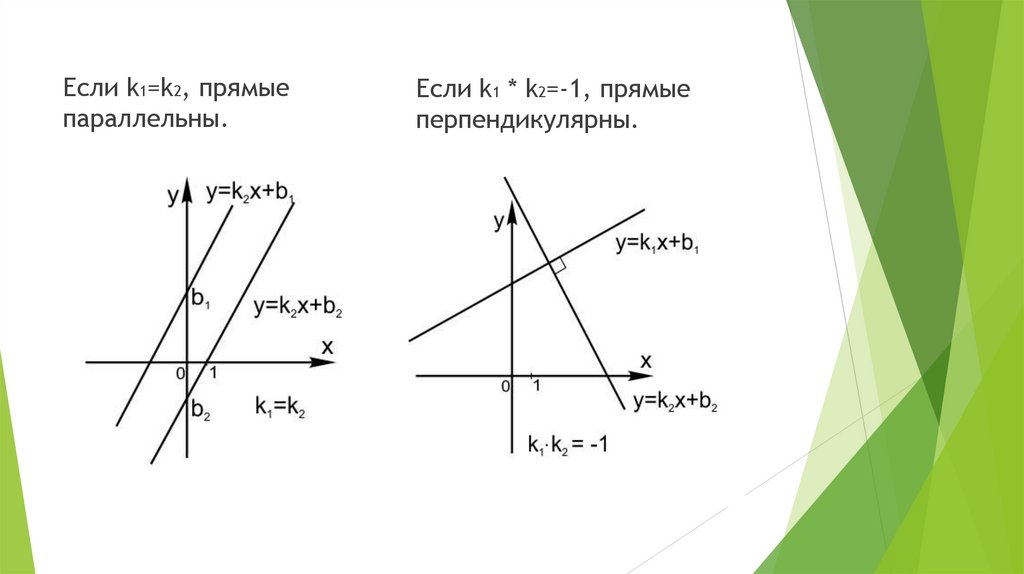
Если k1=k2, прямые
параллельны.
Если k1 * k2=-1, прямые
перпендикулярны.

10. Пример 1

11.

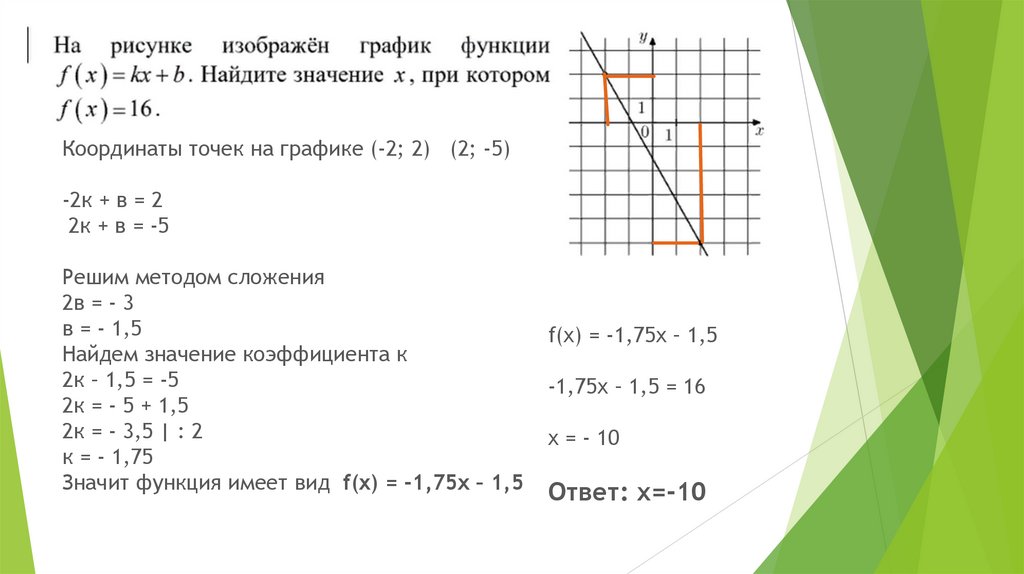
Координаты точек на графике (-2; 2) (2; -5)
-2к + в = 2
2к + в = -5
Решим методом сложения
2в = - 3
в = - 1,5
Найдем значение коэффициента к
2к – 1,5 = -5
2к = - 5 + 1,5
2к = - 3,5 | : 2
к = - 1,75
Значит функция имеет вид f(x) = -1,75х – 1,5
f(x) = -1,75х – 1,5
-1,75х – 1,5 = 16
x = - 10
Ответ: х=-10

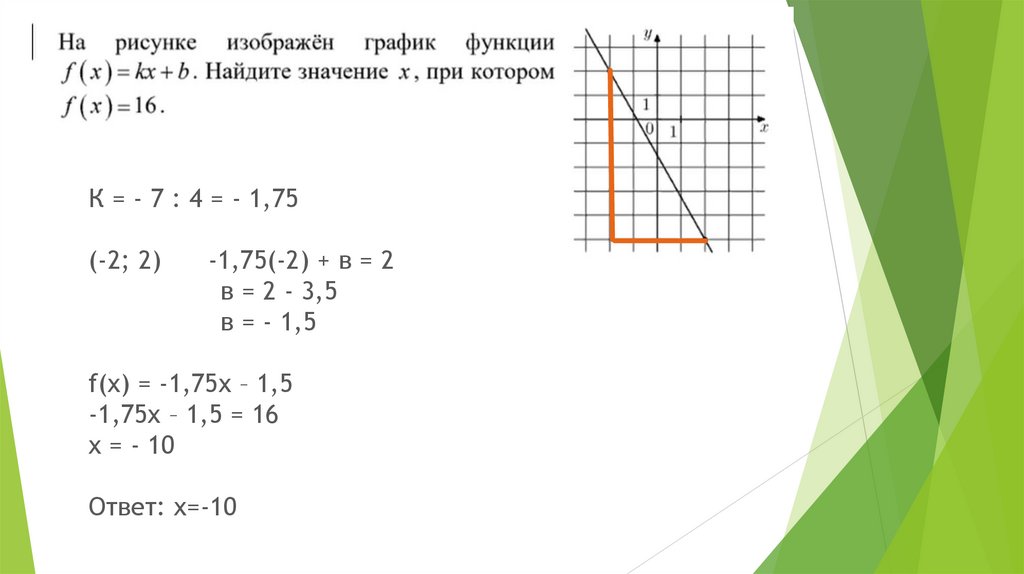
12.

К = - 7 : 4 = - 1,75
(-2; 2)
-1,75(-2) + в = 2
в = 2 - 3,5
в = - 1,5
f(x) = -1,75х – 1,5
-1,75х – 1,5 = 16
x = - 10
Ответ: х=-10

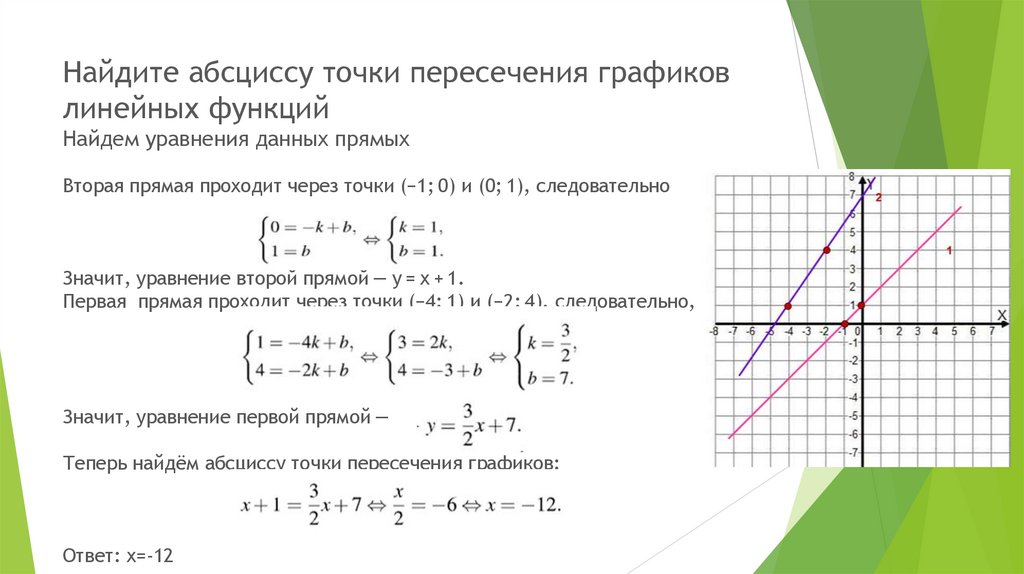
13. Найдите абсциссу точки пересечения графиков линейных функций Найдем уравнения данных прямых

Вторая прямая проходит через точки (−1; 0) и (0; 1), следовательно
Значит, уравнение второй прямой — y = x + 1.
Первая прямая проходит через точки (−4; 1) и (−2; 4), следовательно,
Значит, уравнение первой прямой —
Теперь найдём абсциссу точки пересечения графиков:
Ответ: х=-12

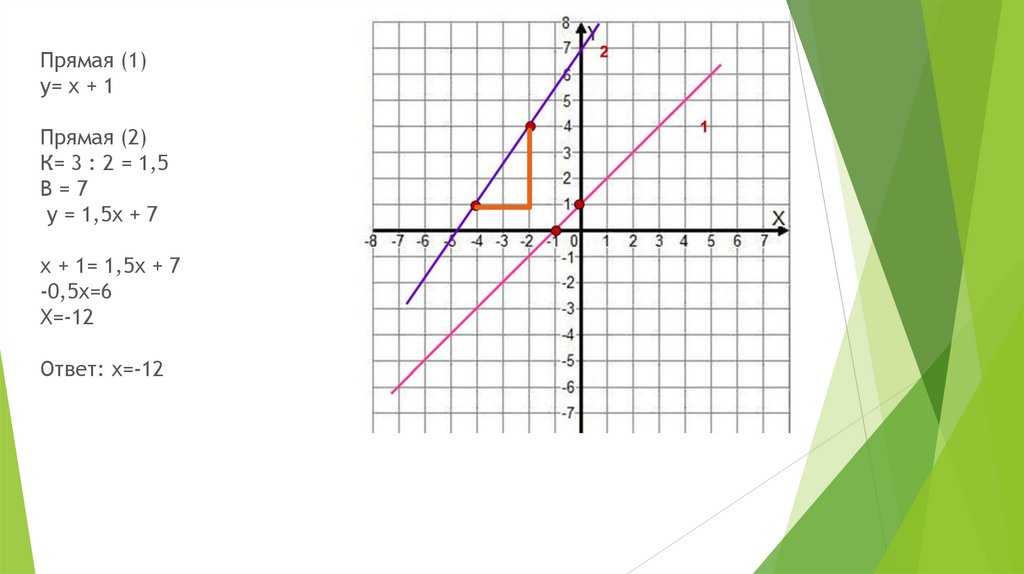
14.

Прямая (1)
у= х + 1
Прямая (2)
К= 3 : 2 = 1,5
В=7
у = 1,5х + 7
х + 1= 1,5х + 7
-0,5х=6
Х=-12
Ответ: х=-12

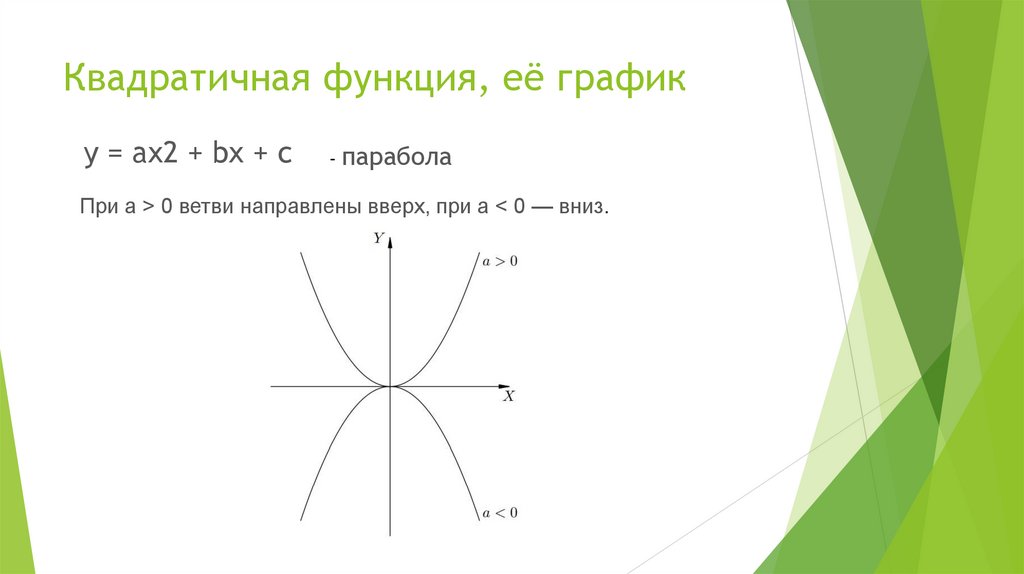
15. Квадратичная функция, её график

y = ax2 + bx + c
- парабола
При a > 0 ветви направлены вверх, при a < 0 — вниз.

16.

Абсцисса вершины параболы y = ax2 + bx + c находится по формуле:
Для нахождения ординаты вершины y0 удобнее всего подставить
x0 в уравнение параболы
или по формуле
Точки пересечения параболы y = ax2 + bx + c с осью X находятся с
помощью решения квадратного уравнения ax2 + bx + c = 0. Если
дискриминант равен нулю, то парабола касается оси X. Если
дискриминант меньше нуля, то парабола не пересекает ось X.
Точка пересечения с осью Y находится легко: мы просто
подставляем x = 0 в уравнение параболы. Получается точка (0, c).

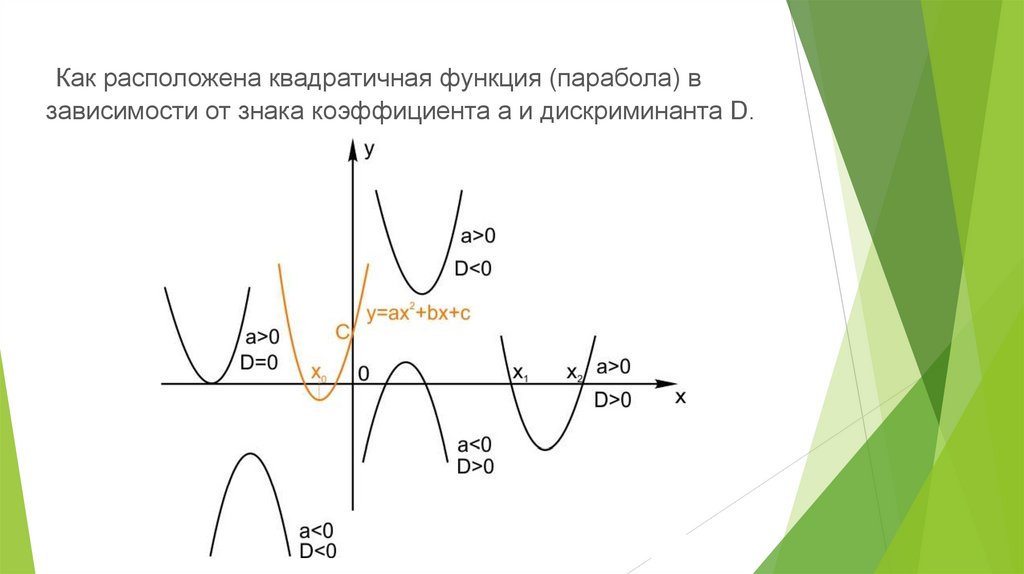
17.  Как расположена квадратичная функция (парабола) в зависимости от знака коэффициента а и дискриминанта D.

Как расположена квадратичная функция (парабола) в
зависимости от знака коэффициента а и дискриминанта D.

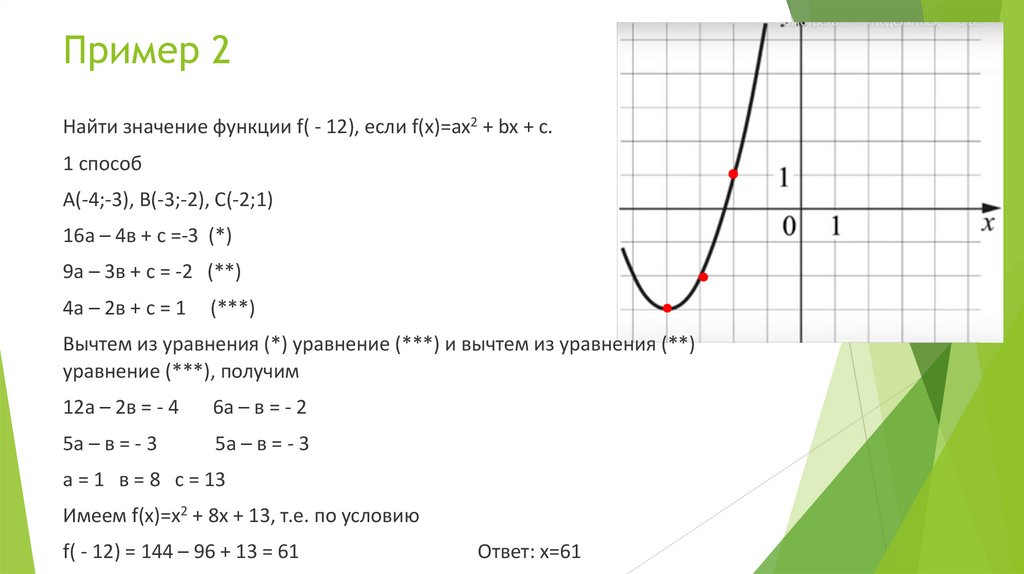
18. Пример 2

Найти значение функции f( - 12), если f(x)=ax2 + bx + c.
1 способ
А(-4;-3), В(-3;-2), С(-2;1)
16а – 4в + с =-3 (*)
9а – 3в + с = -2 (**)
4а – 2в + с = 1
(***)
Вычтем из уравнения (*) уравнение (***) и вычтем из уравнения (**)
уравнение (***), получим
12а – 2в = - 4
6а – в = - 2
5а – в = - 3
5а – в = - 3
а = 1 в = 8 с = 13
Имеем f(x)=x2 + 8x + 13, т.е. по условию
f( - 12) = 144 – 96 + 13 = 61
Ответ: х=61

19.

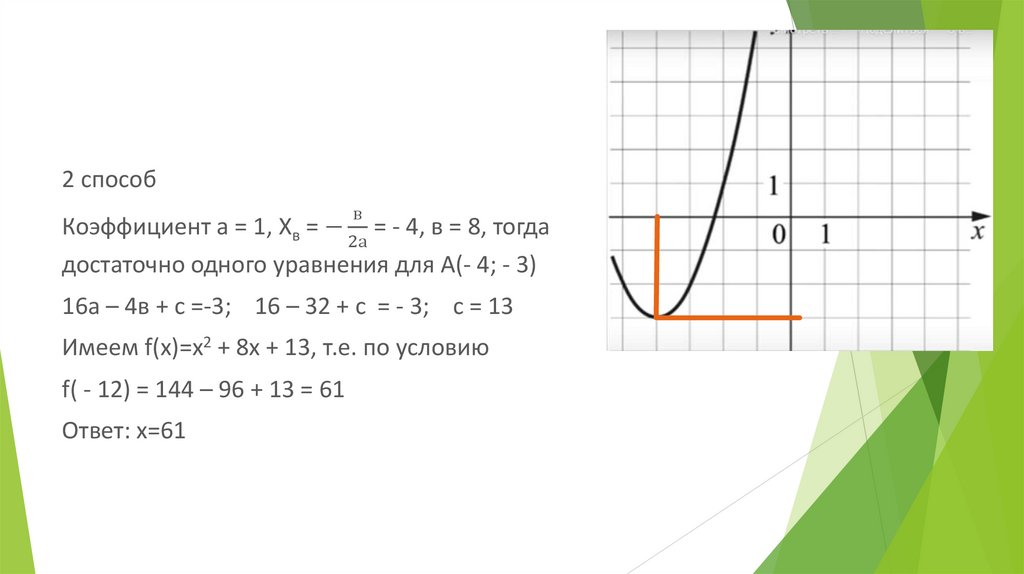
2 способ
в
Коэффициент а = 1, Хв = − = - 4, в = 8, тогда
2а
достаточно одного уравнения для А(- 4; - 3)
16а – 4в + с =-3; 16 – 32 + с = - 3; с = 13
Имеем f(x)=x2 + 8x + 13, т.е. по условию
f( - 12) = 144 – 96 + 13 = 61
Ответ: х=61

20.

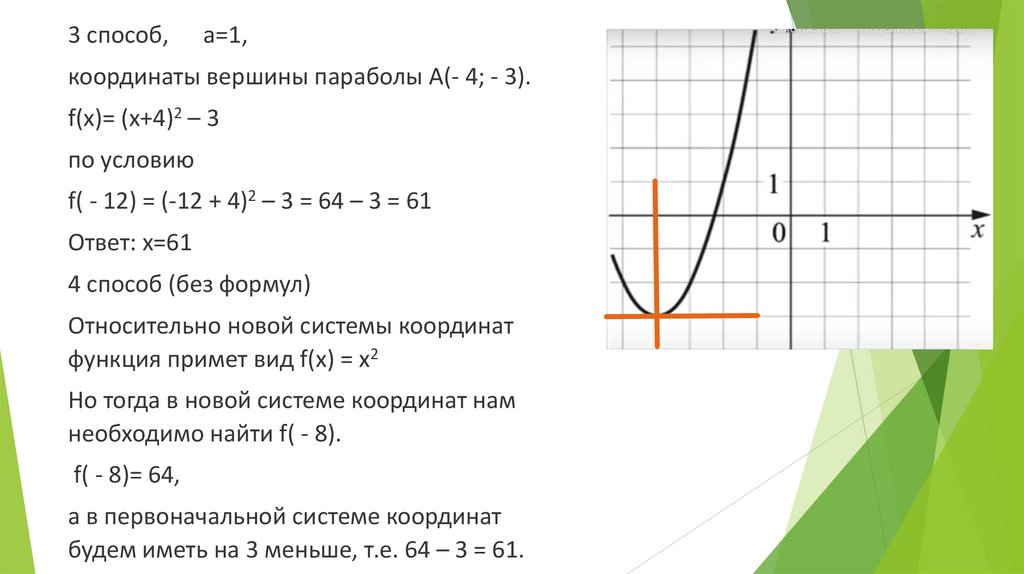
3 способ,
а=1,
координаты вершины параболы А(- 4; - 3).
f(x)= (x+4)2 – 3
по условию
f( - 12) = (-12 + 4)2 – 3 = 64 – 3 = 61
Ответ: х=61
4 способ (без формул)
Относительно новой системы координат
функция примет вид f(x) = x2
Но тогда в новой системе координат нам
необходимо найти f( - 8).
f( - 8)= 64,
а в первоначальной системе координат
будем иметь на 3 меньше, т.е. 64 – 3 = 61.

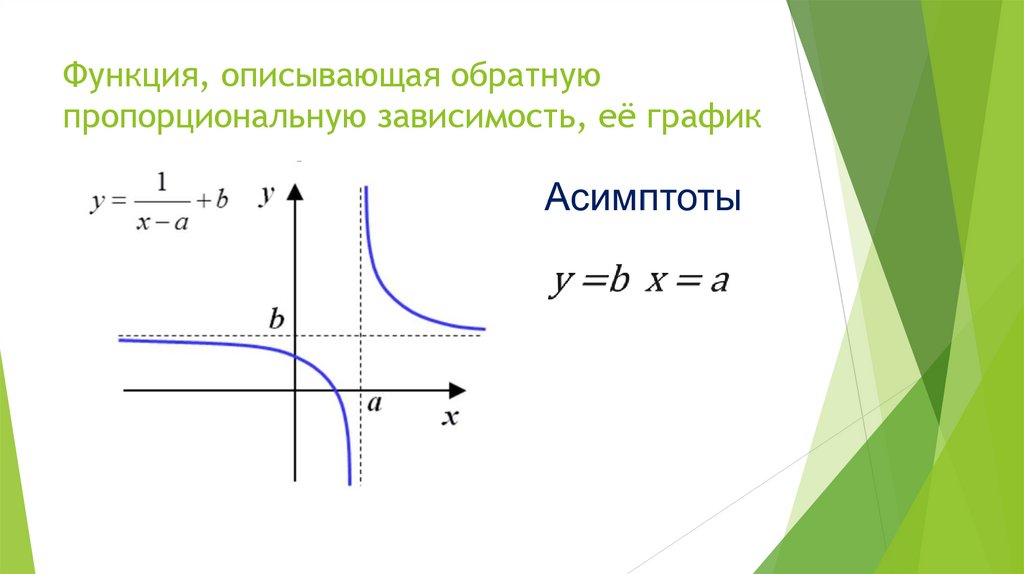
21. Функция, описывающая обратную пропорциональную зависимость, её график

22.

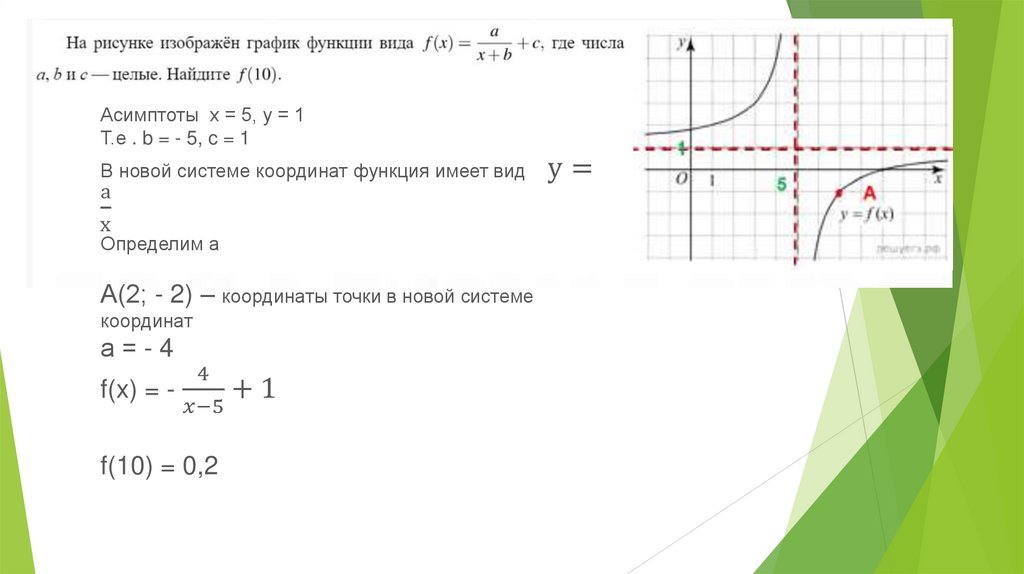
Асимптоты х = 5, у = 1
Т.е . b = - 5, c = 1
В новой системе координат функция имеет вид
а
х
Определим а
А(2; - 2) – координаты точки в новой системе
координат
а=-4
4
f(x) = +1