https___myschool.72to.ru_ej_attachments_files_002_248_797_original_9BBEBCB0BD8BB5D020BCBDBEB3BE83B3BEBB8CBDB8BAB8

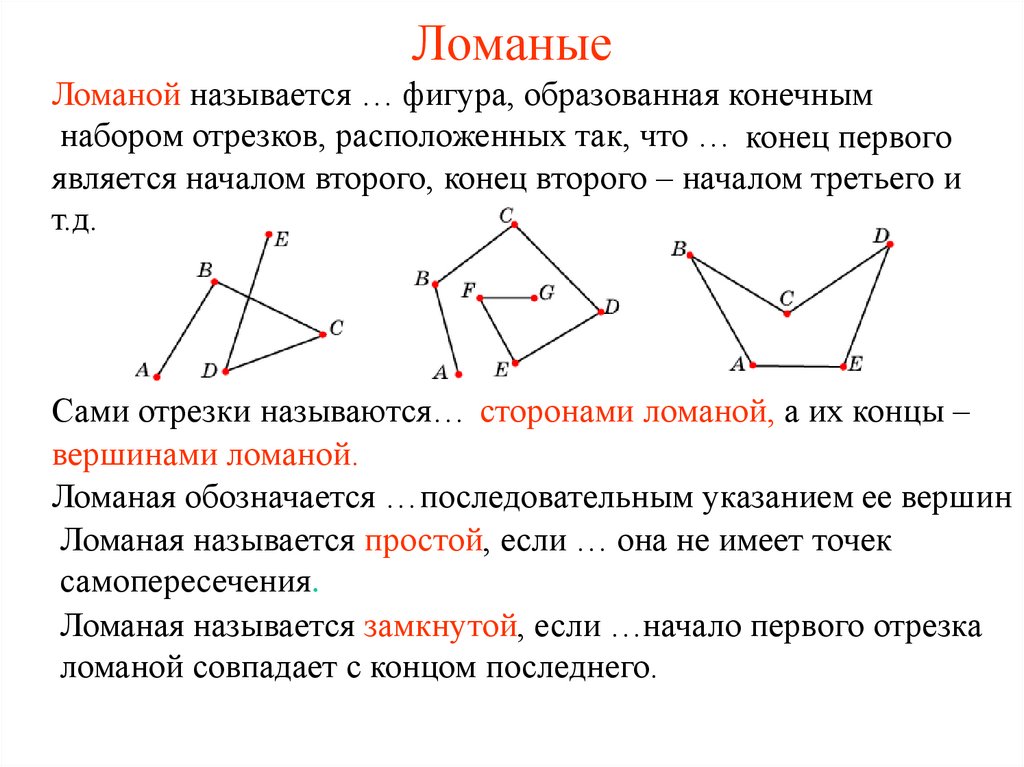
1. Ломаные

Ломаной называется … фигура, образованная конечным
набором отрезков, расположенных так, что … конец первого
является началом второго, конец второго – началом третьего и
т.д.
Сами отрезки называются… сторонами ломаной, а их концы –
вершинами ломаной.
Ломаная обозначается …последовательным указанием ее вершин
Ломаная называется простой, если … она не имеет точек
самопересечения.
Ломаная называется замкнутой, если …начало первого отрезка
ломаной совпадает с концом последнего.

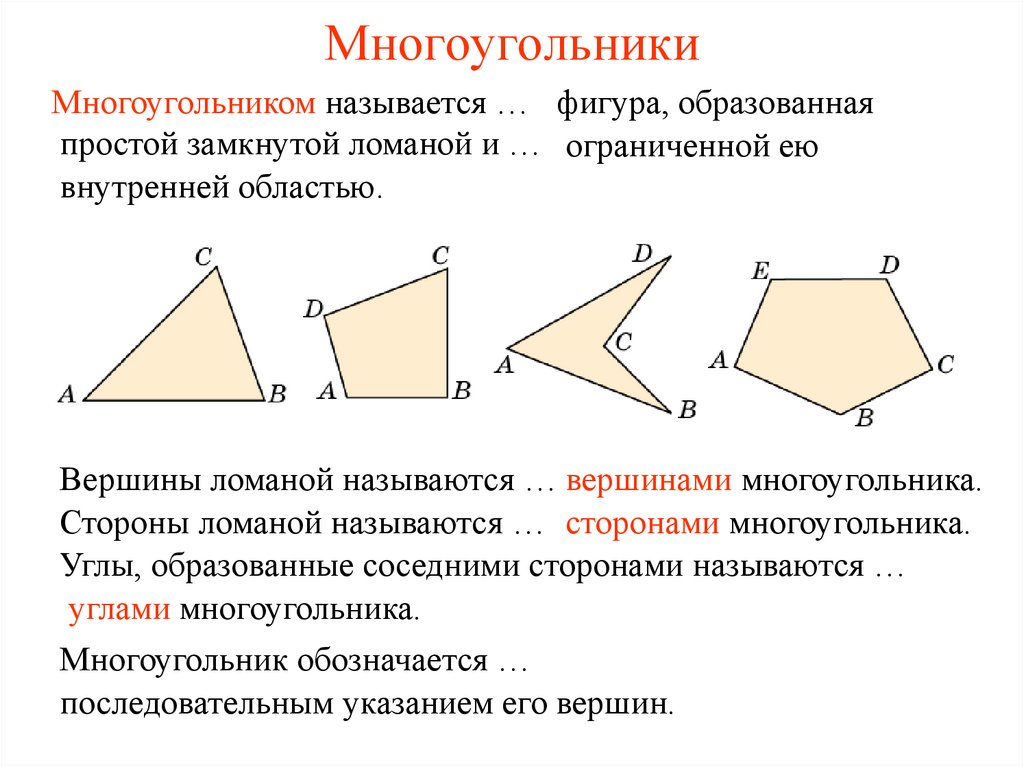
2. Многоугольники

Многоугольником называется … фигура, образованная
простой замкнутой ломаной и … ограниченной ею
внутренней областью.
Вершины ломаной называются … вершинами многоугольника.
Стороны ломаной называются … сторонами многоугольника.
Углы, образованные соседними сторонами называются …
углами многоугольника.
Многоугольник обозначается …
последовательным указанием его вершин.

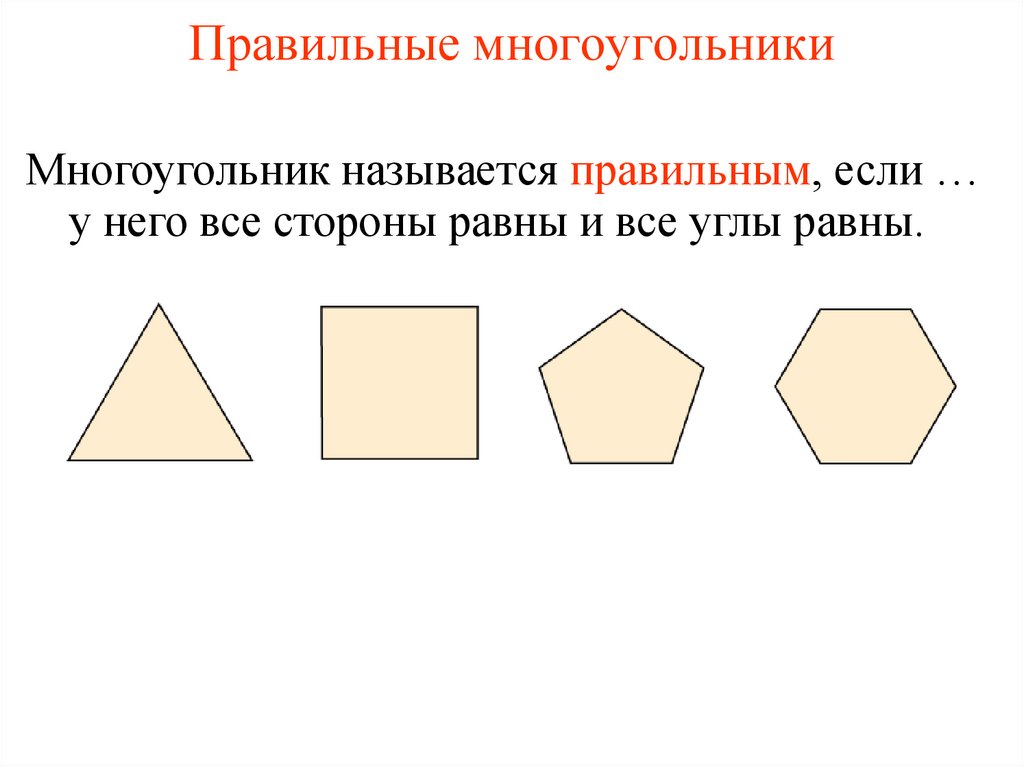
3. Правильные многоугольники

Многоугольник называется правильным, если …
у него все стороны равны и все углы равны.

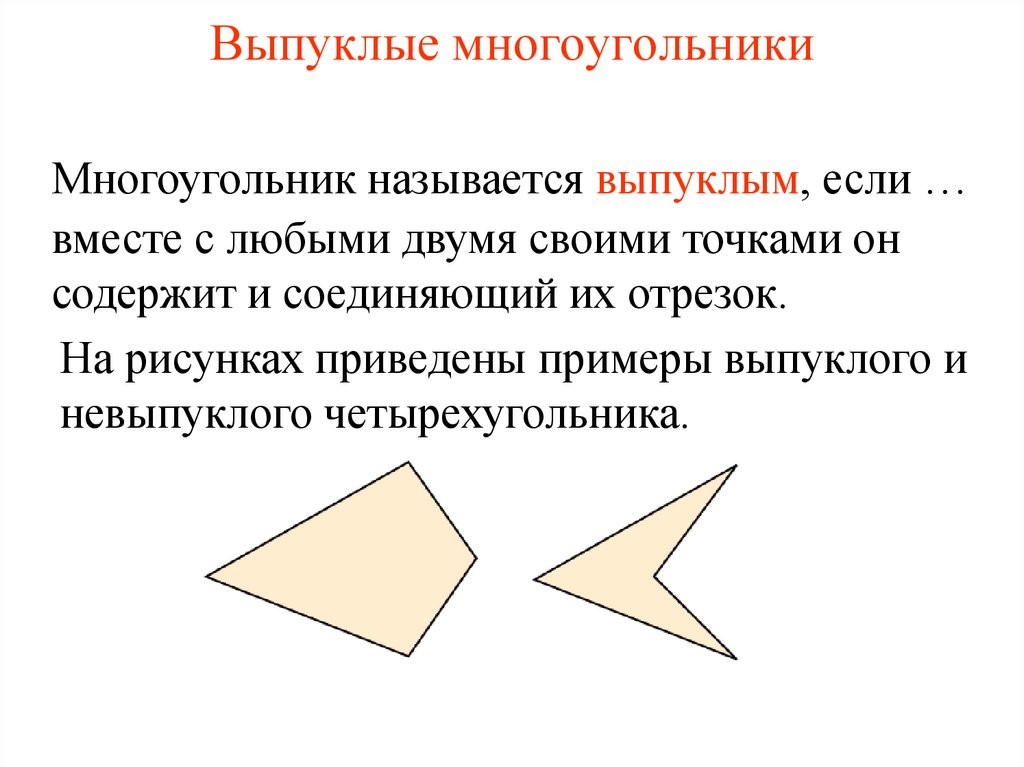
4. Выпуклые многоугольники

Многоугольник называется выпуклым, если …
вместе с любыми двумя своими точками он
содержит и соединяющий их отрезок.
На рисунках приведены примеры выпуклого и
невыпуклого четырехугольника.

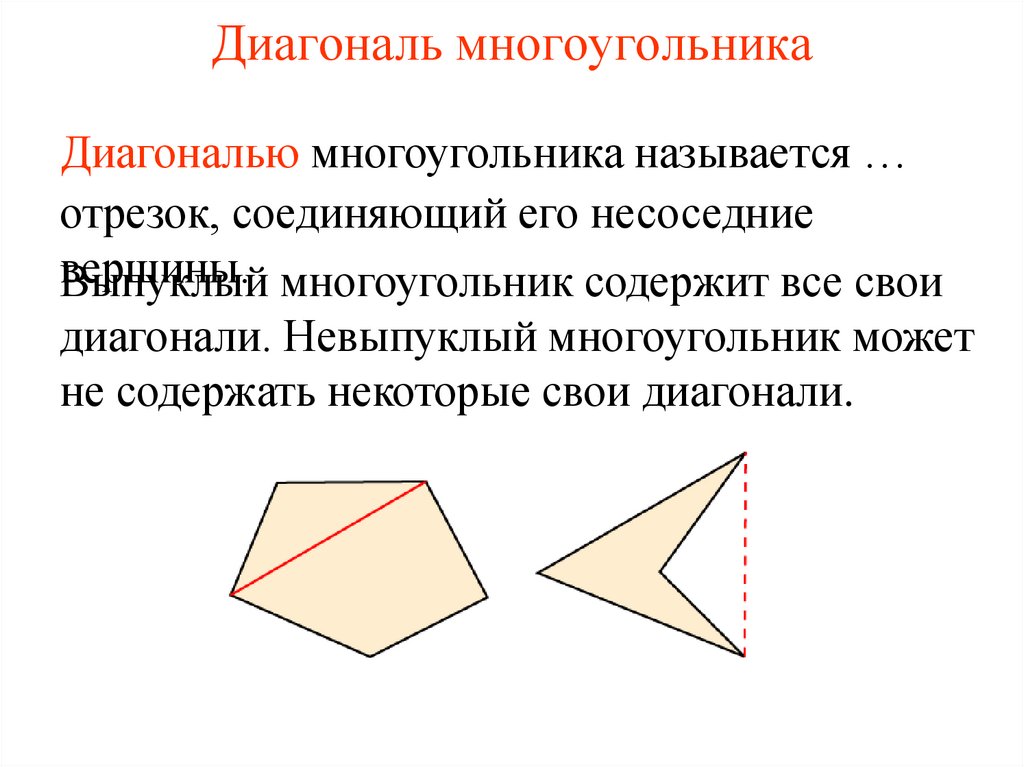
5. Диагональ многоугольника

Диагональю многоугольника называется …
отрезок, соединяющий его несоседние
вершины.
Выпуклый многоугольник содержит все свои
диагонали. Невыпуклый многоугольник может
не содержать некоторые свои диагонали.

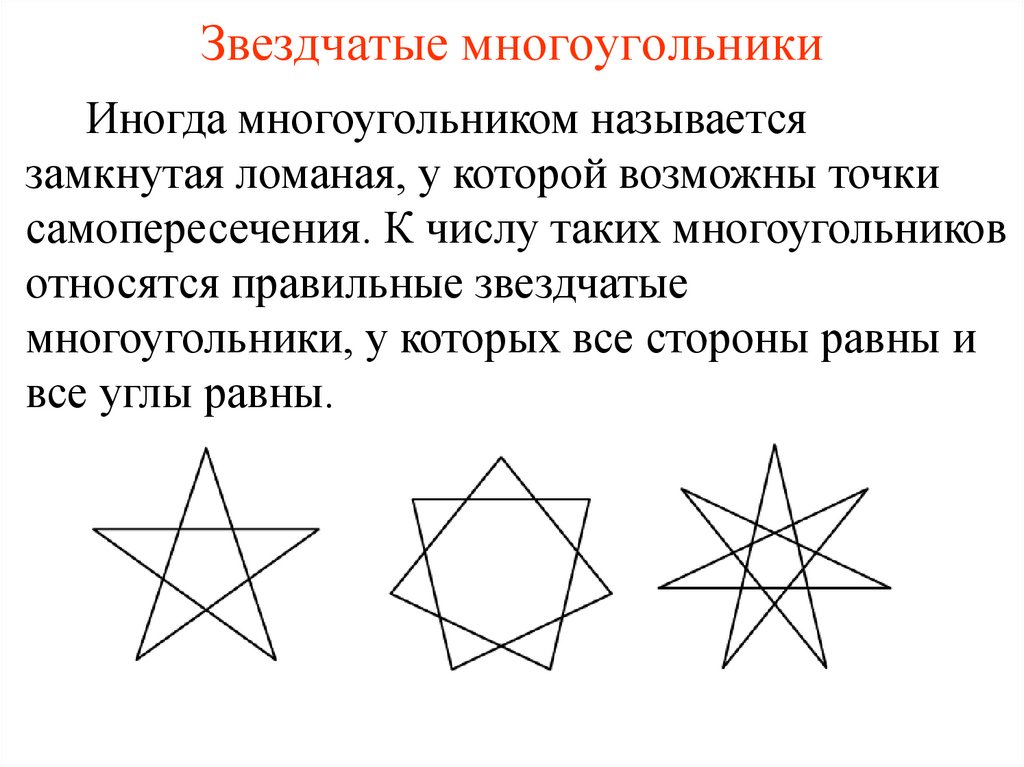
6. Звездчатые многоугольники

Иногда многоугольником называется
замкнутая ломаная, у которой возможны точки
самопересечения. К числу таких многоугольников
относятся правильные звездчатые
многоугольники, у которых все стороны равны и
все углы равны.

7. Вопрос 1

Что называется ломаной, сторонами и
вершинами ломаной?
Ответ: Ломаной называется фигура,
образованная конечным набором отрезков,
расположенных так, что конец первого
является началом второго, конец второго –
началом третьего и т.д. Сами отрезки
называются сторонами ломаной, а их концы –
вершинами ломаной.

8. Вопрос 2

Как обозначается ломаная?
Ответ: Ломаная обозначается
последовательным указанием ее вершин.

9. Вопрос 3

Что называется длиной ломаной?
Ответ: Длиной ломаной называется сумма
длин ее сторон.

10. Вопрос 4

Какая ломаная называется простой?
Ответ: Ломаная называется простой, если
она не имеет точек самопересечения

11. Вопрос 5

Какая ломаная называется замкнутой?
Ответ: Ломаная называется замкнутой,
если начало первого отрезка ломаной
совпадает с концом последнего.

12. Вопрос 6

Какой многоугольник называется
правильным?
Ответ: Многоугольник называется правильным,
если у него все стороны равны и все углы равны.

13. Вопрос 7

Какой многоугольник называется
выпуклым?
Ответ: Многоугольник называется выпуклым,
если вместе с любыми двумя своими точками он
содержит и соединяющий их отрезок.

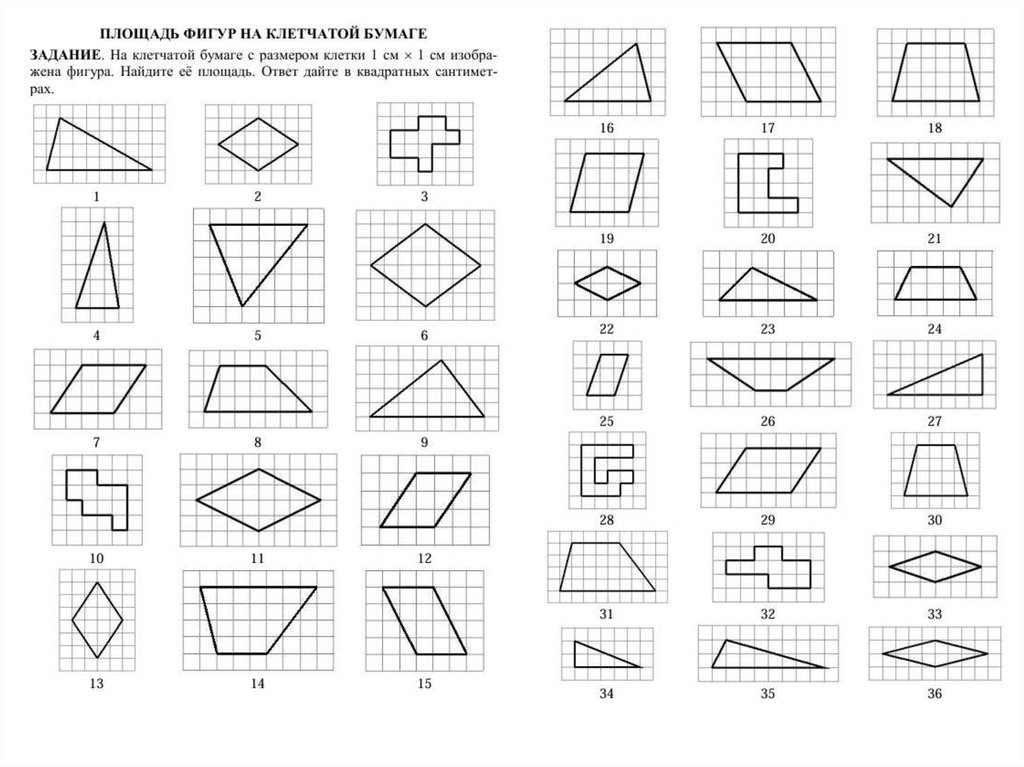
14. Вычисление периметров и площадей многоугольников на клетчатой бумаге

15.

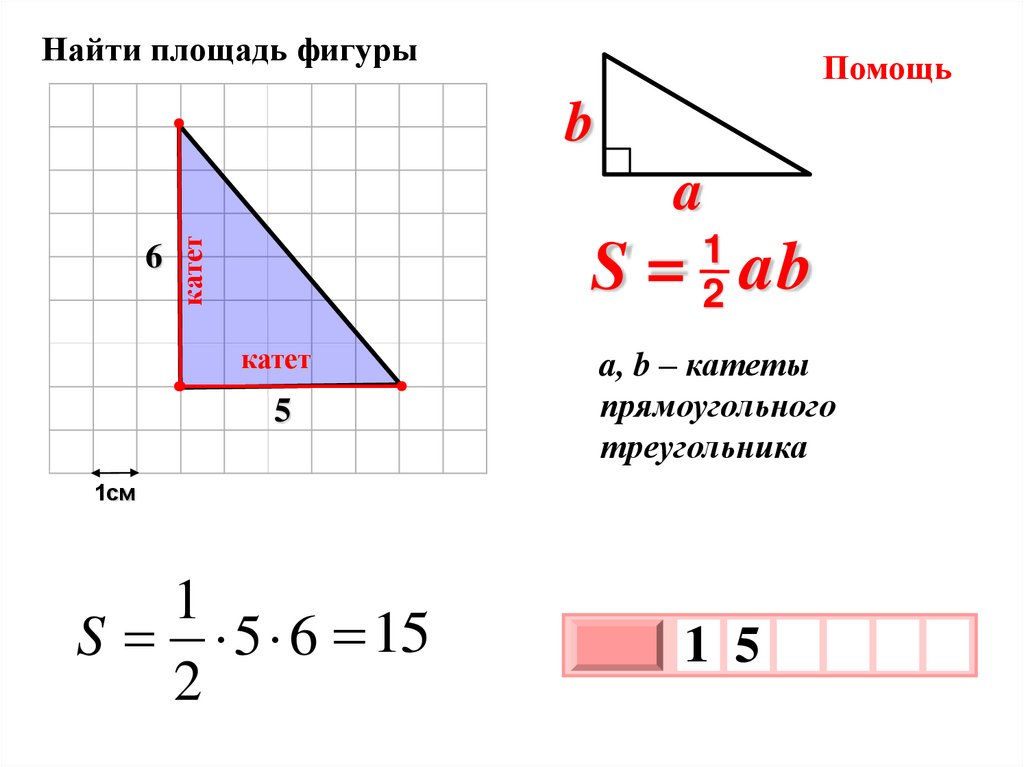
Найти площадь фигуры
Помощь
b
a
1
2
катет
6
S = ab
катет
5
a, b – катеты
прямоугольного
треугольника
1см
1
S 5 6 15
2
1 5
3
10 х
х

16.

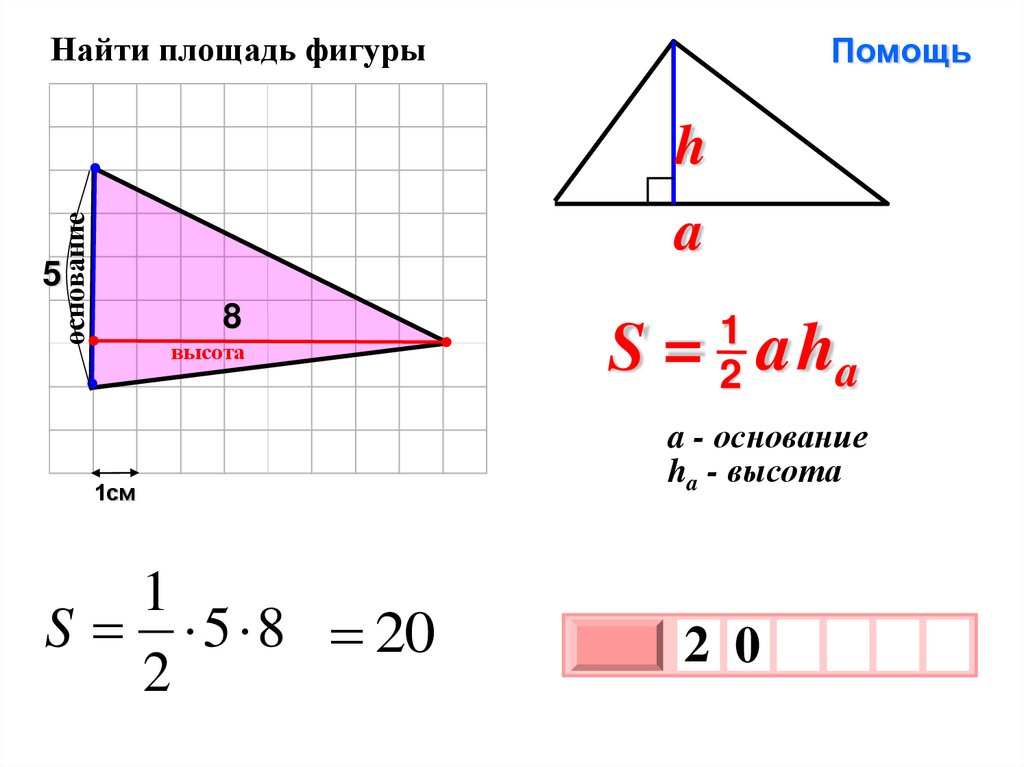
Найти площадь фигуры
Помощь
h
основание
a
5
8
высота
1см
1
S 5 8 20
2
1
2
S = aha
a - основание
ha - высота
2 0
3
10 х
х

17.

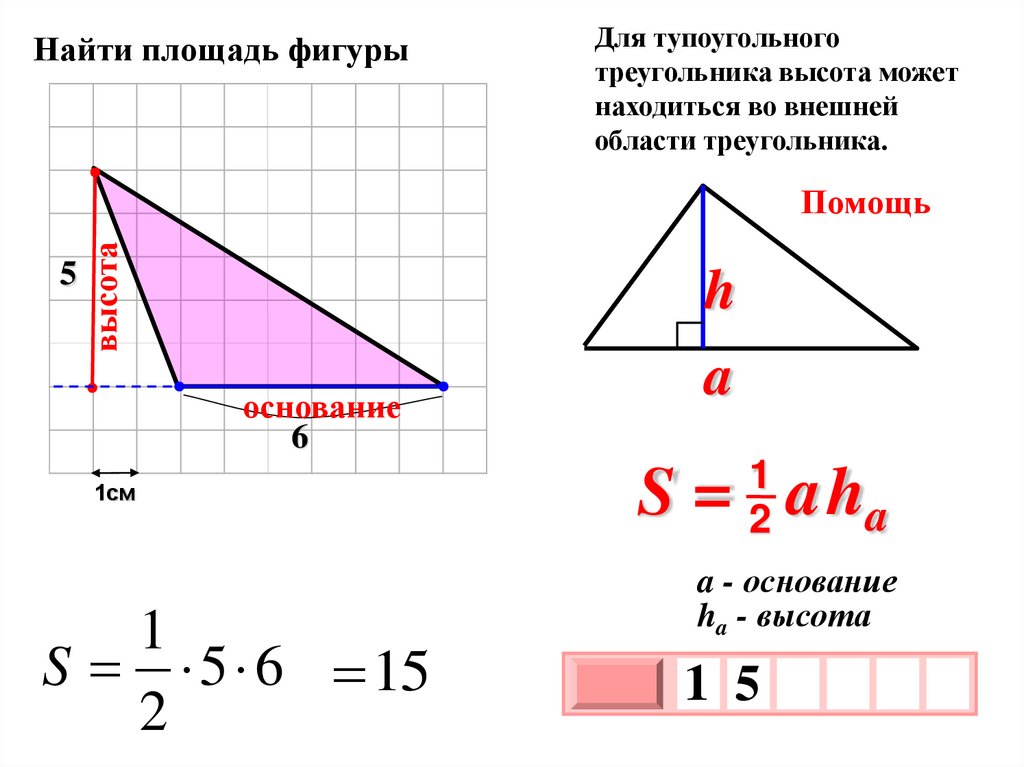
Найти площадь фигуры
Для тупоугольного
треугольника высота может
находиться во внешней
области треугольника.
5
высота
Помощь
h
основание
6
1см
1
S 5 6 15
2
a
1
2
S = aha
a - основание
ha - высота
1 5
3
10 х
х

18.

Формула Пика
Если вершины многоугольника
находятся в точках с целочисленными
координатами (в декартовой системе
координат), то его площадь можно
вычислить по формуле Пика:
S = В + Г/2 − 1
Это соотношение открыл и доказал
австрийский математик Георг Александр
Пик (Georg Alexander Pick) в 1899 г.

19.

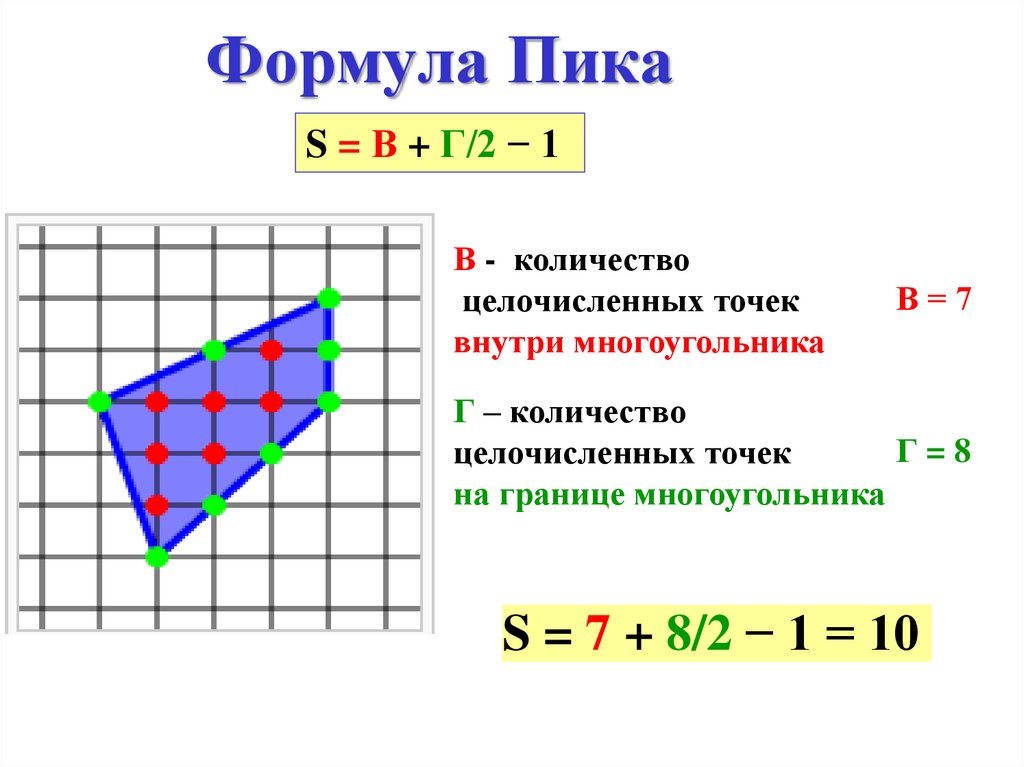
Формула Пика
S = В + Г/2 − 1
В - количество
целочисленных точек
внутри многоугольника
В=7
Г – количество
Г=8
целочисленных точек
на границе многоугольника
S = 7 + 8/2 − 1 = 10

20.

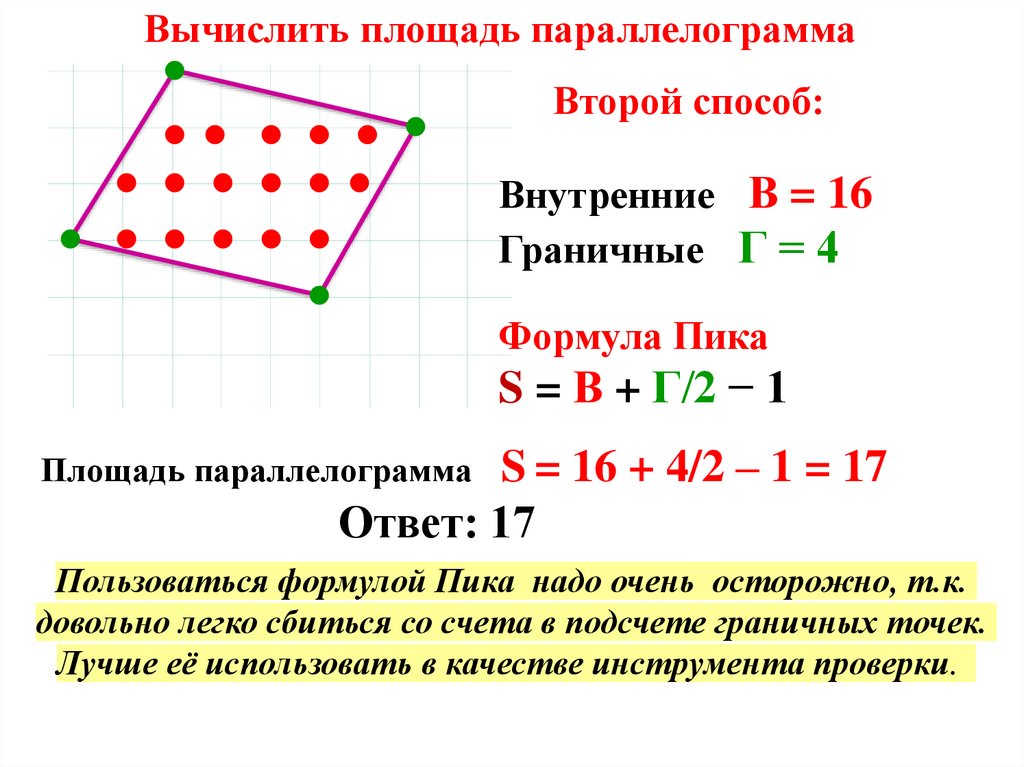
Вычислить площадь параллелограмма
Второй способ:
Внутренние В = 16
Граничные Г = 4
Формула Пика
S = В + Г/2 − 1
S = 16 + 4/2 – 1 = 17
Ответ: 17
Площадь параллелограмма
Пользоваться формулой Пика надо очень осторожно, т.к.
довольно легко сбиться со счета в подсчете граничных точек.
Лучше её использовать в качестве инструмента проверки.

21.

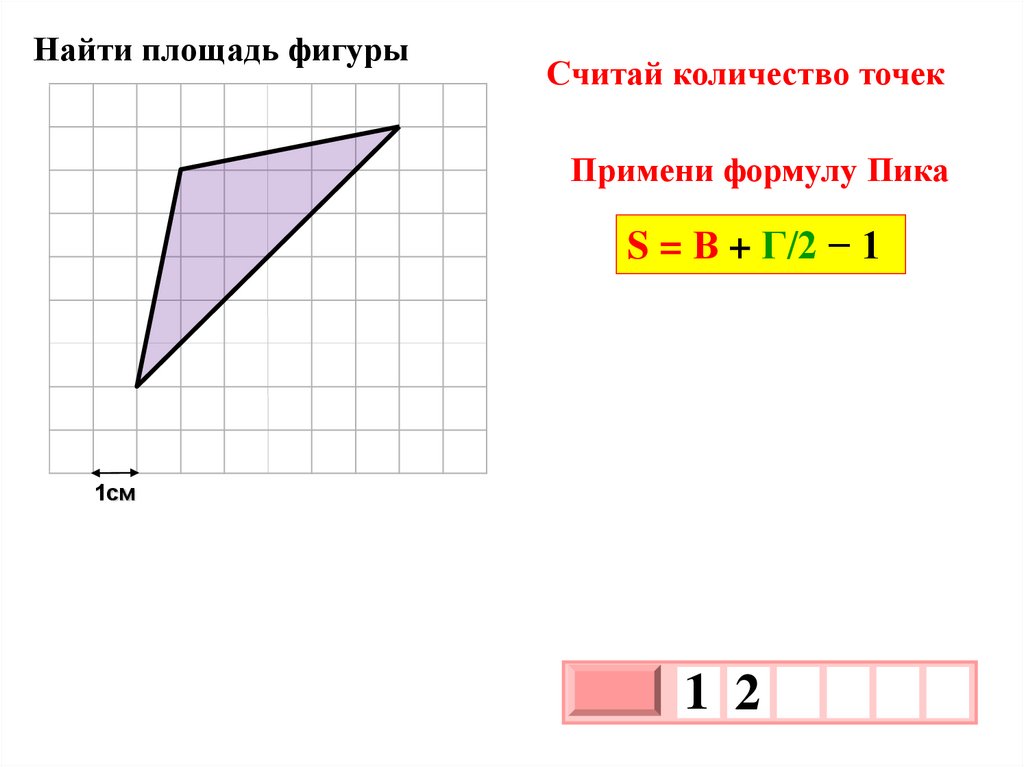
Найти площадь фигуры
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
1см
1 2
3
10 х
х