https___school.mos.ru_ej_attachments_files_217_186_925_original_%D0%9E%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F%20%D0%BE%D0%BA%D1%80%D1%83%D0%B6%D0%BD%D0%BE%D1%81%D1%82%D1%8C

1.

Лицей №1523 г.Москвы
Геометрия
9 класс
Теоретический материал
2025-2026
ЗОВ

2.

Описанная около
многоугольника окружность

3.

I. Определение описанной окружности.
.
Окружность
называется
описанной
около
многоугольника, если она проходит через все его
вершины. При этом многоугольник называется
вписанным в окружность (рисунок 15).
Замечание: Далеко не около всякого многоугольника можно описать
окружность. Около многоугольника можно описать окружность тогда и
только тогда, когда серединные перпендикуляры ко всем его сторонам
пересекаются в одной точке. При этом центром описанной окружности как
раз и является точка пересечения серединных перпендикуляров к сторонам
многоугольника, а радиус описанной окружности равен расстоянию от ее
центра до любой из вершин многоугольника.

4.

II. Описанная около треугольника окружность.
Теорема о существовании и единственности описанной около
треугольника окружности: Около всякого треугольника можно описать
единственную окружность, центр которой лежит на пересечении
серединных перпендикуляров к его сторонам.

5.

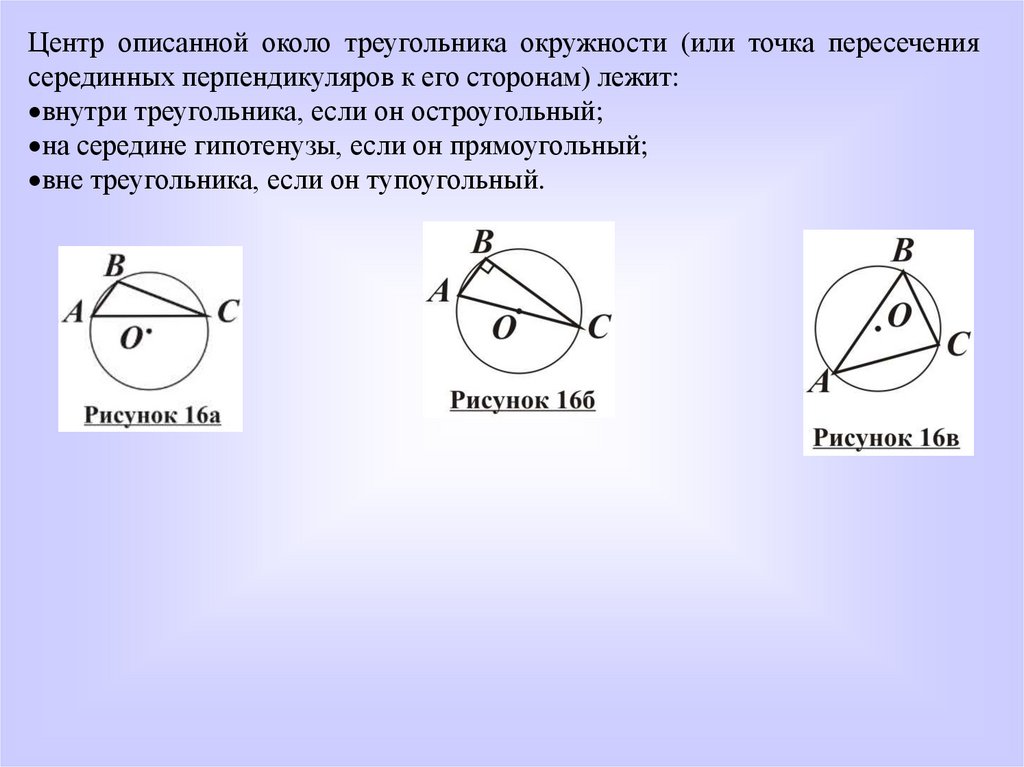
Центр описанной около треугольника окружности (или точка пересечения
серединных перпендикуляров к его сторонам) лежит:
внутри треугольника, если он остроугольный;
на середине гипотенузы, если он прямоугольный;
вне треугольника, если он тупоугольный.

6.

Формула для вычисления радиуса описанной около треугольника
.
.
окружности: Радиус описанной около треугольника окружности равен
отношению его стороны к двум синусам противолежащего угла:
.
AB
Дано:
R
2sin C
(O; R)
1. Проведем диаметр AD (рисунок 17).
Описана
Тогда по следствию из теоремы о
около ΔABC.
вписанном угле ABD = 90°.
Доказать:
Из п/у Δ-ка ABD
R
AB
2sin C
sin ADB
AB AB
AD 2 R
R
AB
2sin ADB
2. По теореме о вписанном угле
ADB
R
AB
C
2
AB
AB
2sin ADB 2sin C

7.

Следствие 1: Умножив числитель и знаменатель дроби в правой части формулы
R
AB
2sin C
на произведение BC·AC, получим еще одну формулу для вычисления радиуса
описанной около треугольника окружности:
R
AB BC AC
AB BC AC
AB BC AC
2 BC AC sin C 4 1 BC AC sin C
4S ABC
2
S ABC
Полученной формулой
R
AB BC AC
4S ABC
удобно пользоваться в случае, когда треугольник задан тремя сторонами (в
этом случае площадь SΔABC рассчитывается по формуле Герона).

8.

Следствие 2: Из выведенной только что формулы следует, что
.
R
AB
BC
AC
2sin C 2sin A 2sin B
AB
BC
AC
2R
sin C sin A sin B
т.е. стороны треугольника пропорциональны синусам противолежащих углов.
Это утверждение называется теоремой синусов, которая активно используется
для решения треугольников:
Теорема синусов: Стороны произвольного треугольника пропорциональны
синусам противолежащих углов, т.е. для всякого Δ-ка ABC выполняется
равенство:
AB
BC
AC
sin C
sin A
sin B

9.

.
III. Свойство и признак вписанного четырехугольника.
Сумма противоположных углов вписанного четырехугольника равна 180° .
,
Доказательство:
Дано:
ABCD вписан в (O; R).
1. По теореме о вписанном
Доказать:
угле
A + C = B + D = 180°.
BAD
A
A C
BCD
2
C
2
BCD BAD BCD BAD 360
180
2
2
2
2
2. Т.к. сумма внутренних углов четырехугольника равна 360°,
B D 360 A C 360 180 180
180

10.

Признак
вписанного
четырехугольника:
Если
сумма
двух
противоположных углов четырехугольника равна 180°, то около этого
четырехугольника можно описать окружность (без доказательства).
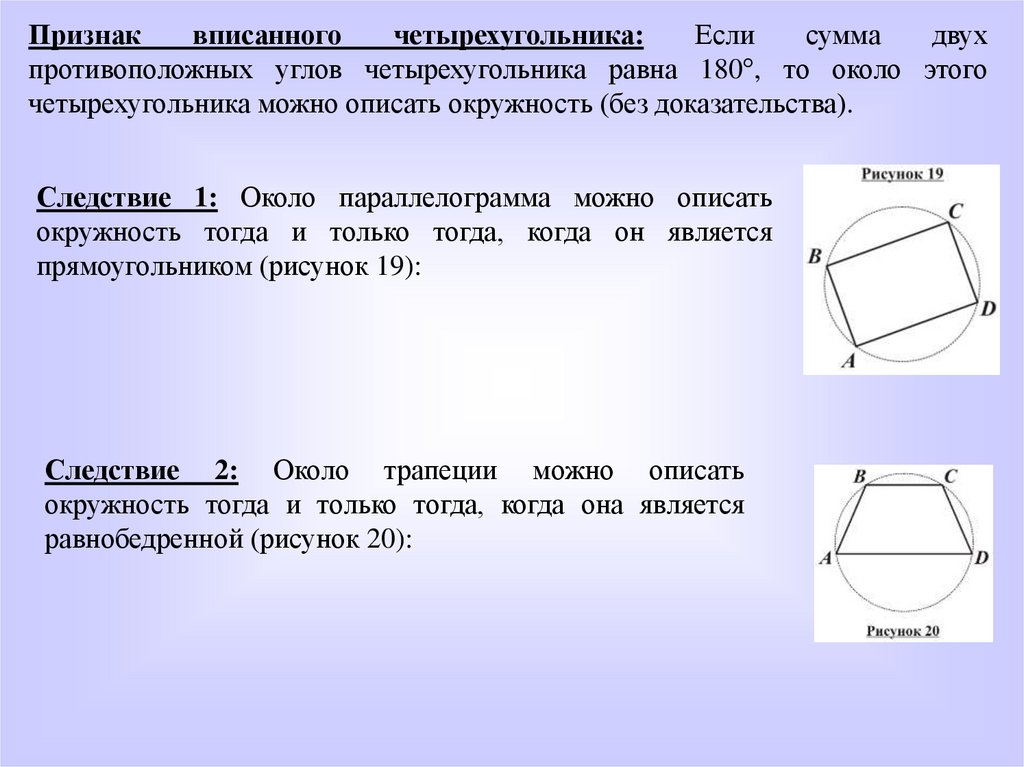
Следствие 1: Около параллелограмма можно описать
окружность тогда и только тогда, когда он является
прямоугольником (рисунок 19):
Следствие 2: Около трапеции можно описать
окружность тогда и только тогда, когда она является
равнобедренной (рисунок 20):