https___school.mos.ru_ej_attachments_files_217_169_450_original_%D0%9C%D0%B5%D1%82%D0%BE%D0%B4%20%D0%B8%D0%BD%D1%82%D0%B5%D1%80%D0%B2%D0%B0%D0%BB%D0%BE%D0%B2.(%D0%B4%D0%BB%D1%8F%20%D1%80%D0%B5%D0%B1%D1%8F%D1%82)

1.

Применение метода
интервалов для
решения неравенств

2.

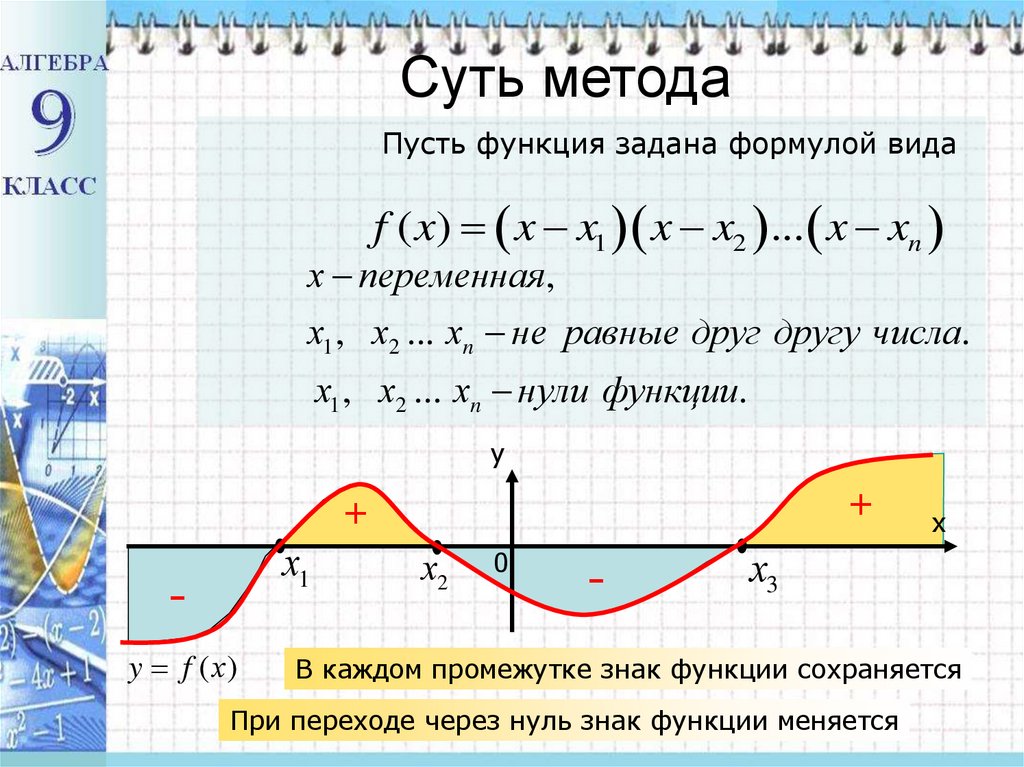
Суть метода
Пусть функция задана формулой вида
f ( x) x x1 x x2 ... x xn
х переменная,
х1 , х2 ... хn не равные друг другу числа.
х1 , х2 ... хn нули функции.
у
+
+
х1
y f ( х)
х2
0
-
х
х3
В каждом промежутке знак функции сохраняется
При переходе через нуль знак функции меняется

3.

f (x )
Функция
Свойство непрерывной функции.
Функция f ( x) непрерывна на области
определения и имеет различные
нули. Нули функции разбивают
область определения на промежутки
знакопостоянства, при переходе
через нуль знак функции меняется.

4.

План применения метода интервалов
!
• Разложить многочлен на простые
множители;
• найти корни многочлена;
• изобразить их на числовой прямой;
• разбить числовую прямую на интервалы;
• определить знаки множителей на
интервалах знакопостоянства;
• выбрать промежутки нужного знака;
• записать ответ (с помощью скобок или
знаков неравенства).

5.

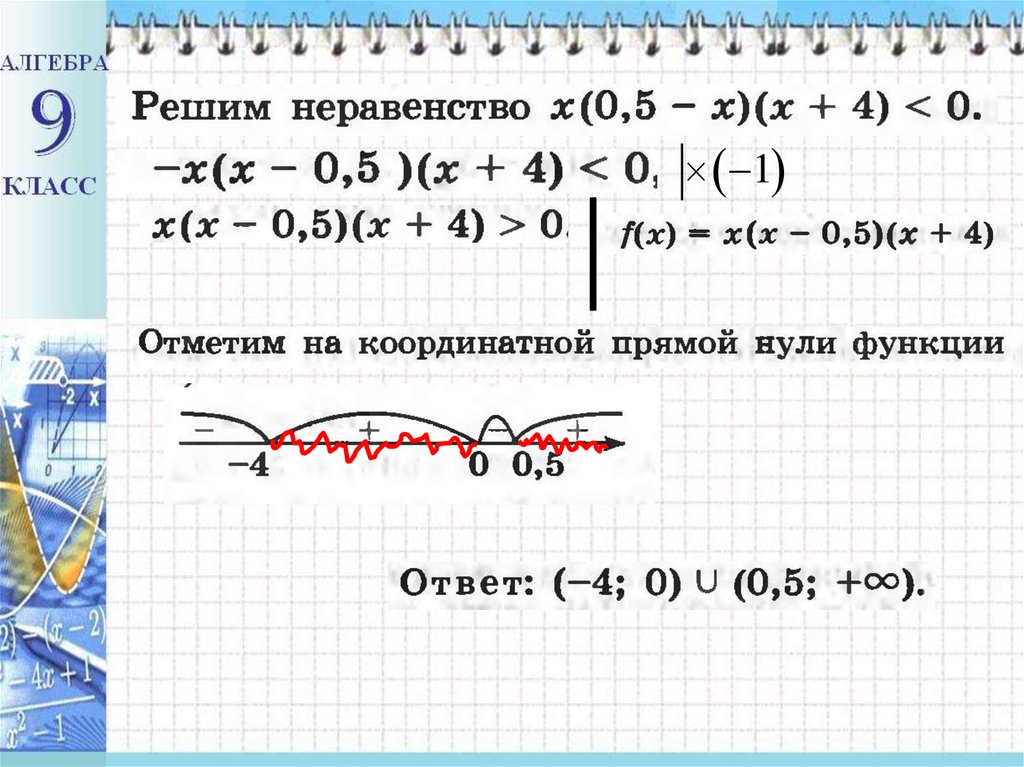
Решить неравенство
х 2 х 5 х 4 0
х1 2, х2 5, х3 4
нули функции
f ( x) х 2 х 5 х 4 .
-
+
?
-6
0
-5
+
-
2
3
4
5
(3)
05
ffх
f((0)
(5)
6)
622
23
305
44
30
48 80
6 40
0355;
556
4;

6.

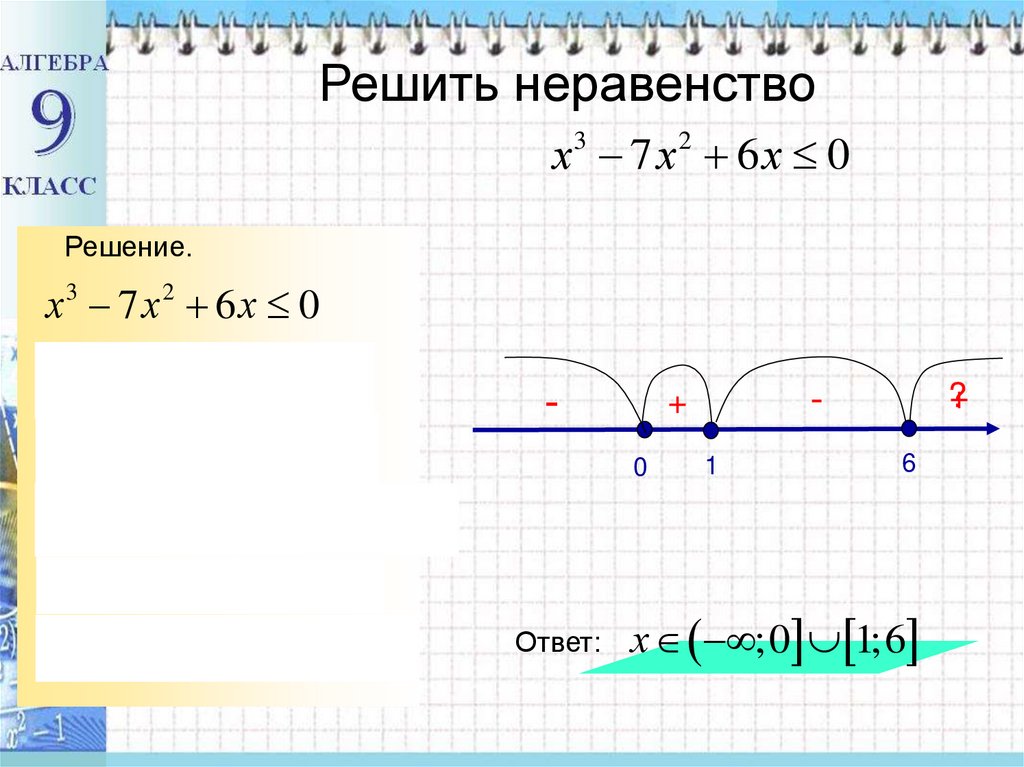
Решить неравенство
х3 7 х 2 6 х 0
Решение.
х 7х 6х 0
3
2
х х2 7 х 6 0
х х 1 х 6 0
0
?
+
-
+
1
6
х1 0, х2 1, х3 6
нули функции
f ( x) х 7 х 6 х.
3
2
Ответ:
х ;0 1;6

7.

1

8.

5

9.

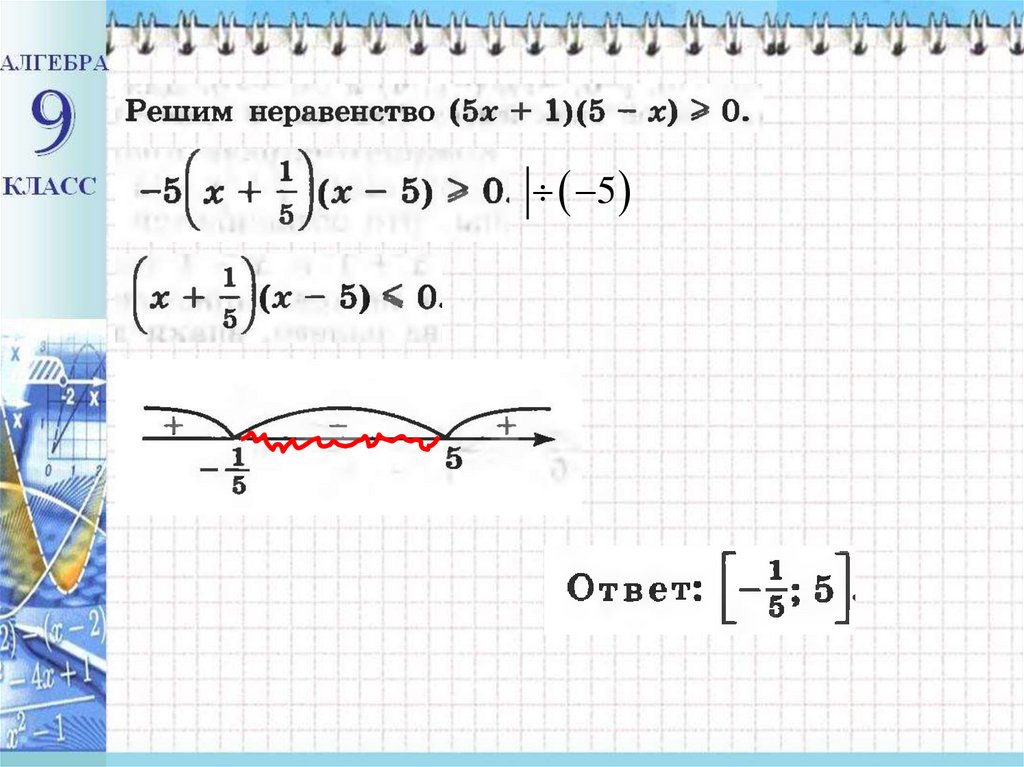
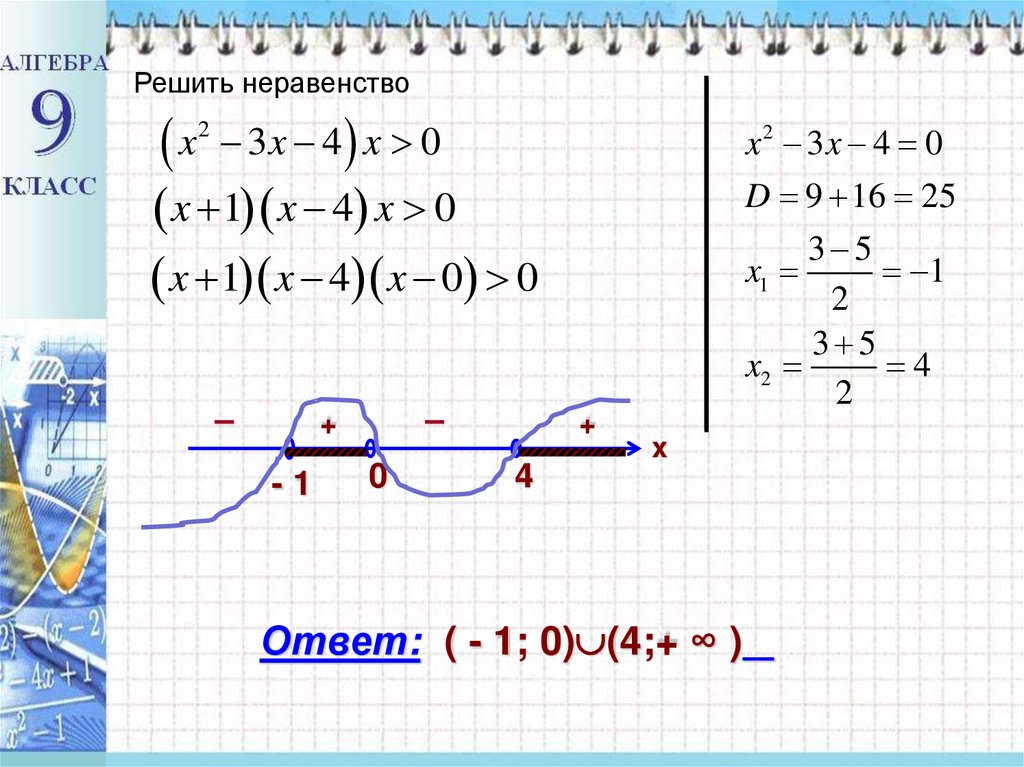
Решить неравенство
2
x
3x 4 x 0
x 2 3x 4 0
x 1 x 4 x 0
x 1 x 4 x 0 0
–
–
+
-1
0
D 9 16 25
3 5
x1
1
2
3 5
x2
4
2
+
4
x
Ответ: ( - 1; 0) (4;+ ∞ )

10.

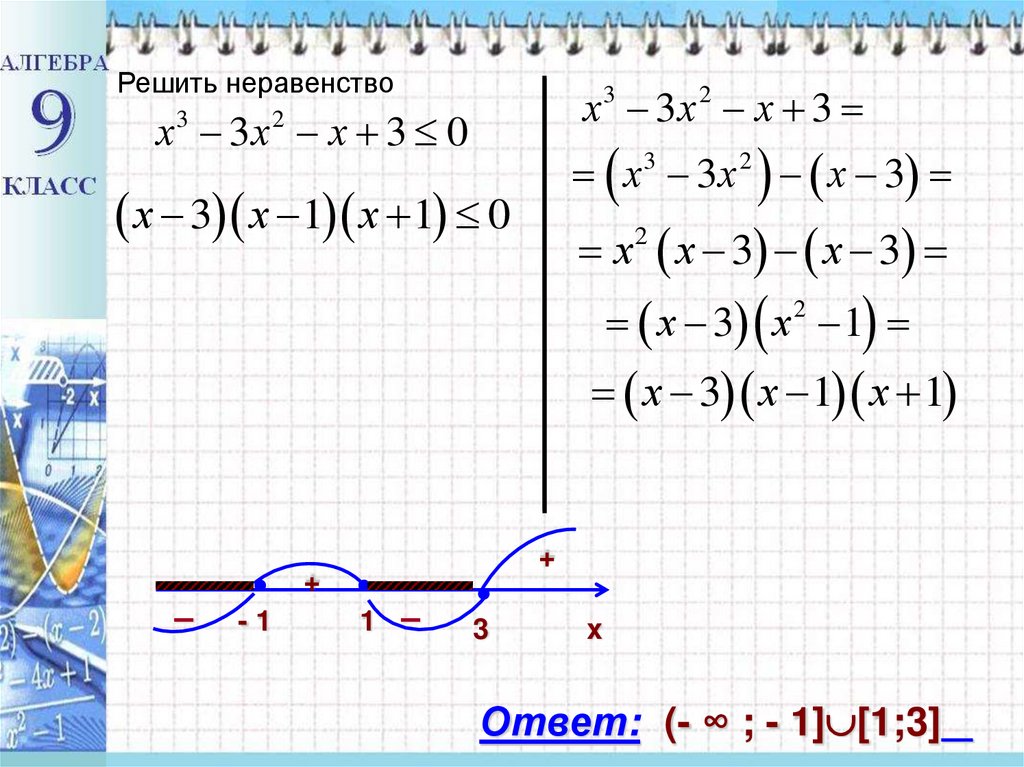
Решить неравенство
х3 3х 2 х 3
х3 3х 2 х 3 0
х 3 х х 3
3
х 3 х 1 х 1 0
2
х2 х 3 х 3
х 3 х 1
2
х 3 х 1 х 1
+
+
–
-1
1 –
3
x
Ответ: (- ∞ ; - 1] [1;3]

11.

Метод интервалов
используется тогда и только
тогда, когда многочлен или
дробное выражение
сравниваются с нулем
Во вторую очередь,
раскладывают на
множители: многочлен или
числитель и знаменатель
дробного выражения

12.

Знак неравенства
«нестрогий»: на числовой
прямой корни многочлена
или числителя закрашенные кружки.
Корни знаменателя для
«строгих» и «нестрогих»
неравенств - «пустые»
кружки.
Надо штриховать
промежутки.
Штриховка
соответствует знаку
неравенства

13.

Проверь своё решение
Вариант 1.
Вариант 2.
№2. Найдите область определения функции:
y 6 x x2 3 3 2 x 5
y 2 7 x x 2 5 5 3x 4
Решение.
Решение.
6 x x 0 1
7 x x 0 1
x2 6 x 0
x( x 6) 0
x 7x 0
x( x 7) 0
2
2
–
+
0
Ответ:
+
6
0; 6
2
–
+
x
0
Ответ:
0; 7
+
7
x

14.

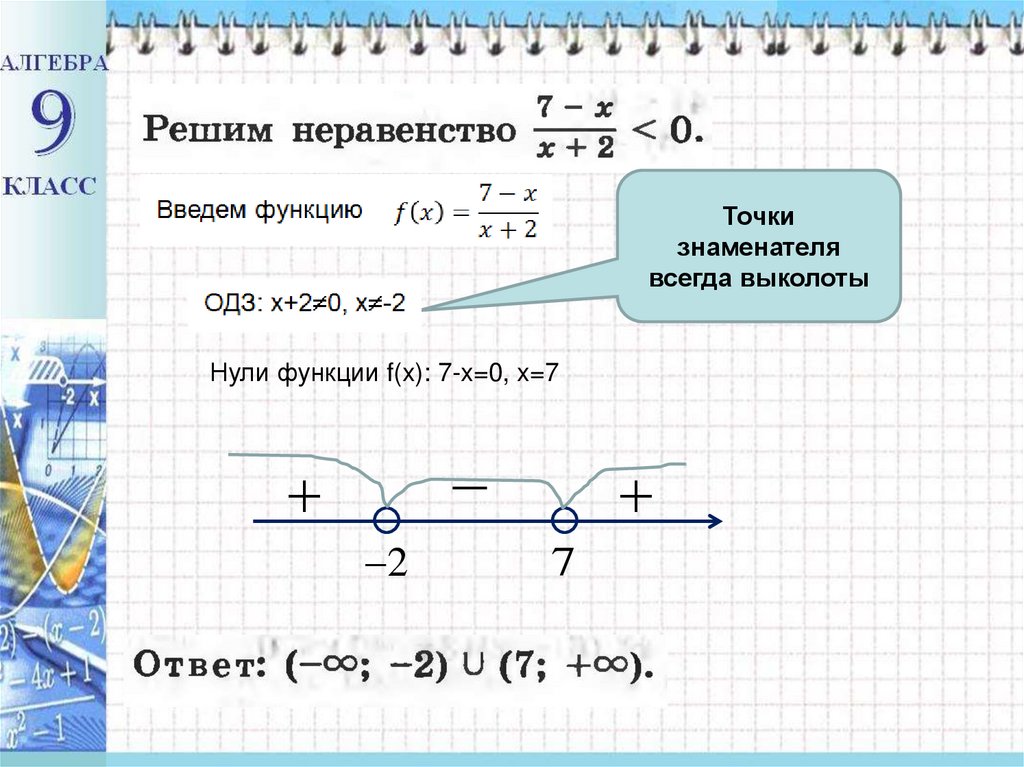
Точки
знаменателя
всегда выколоты
Нули функции f(x): 7-x=0, x=7
2
7

15.

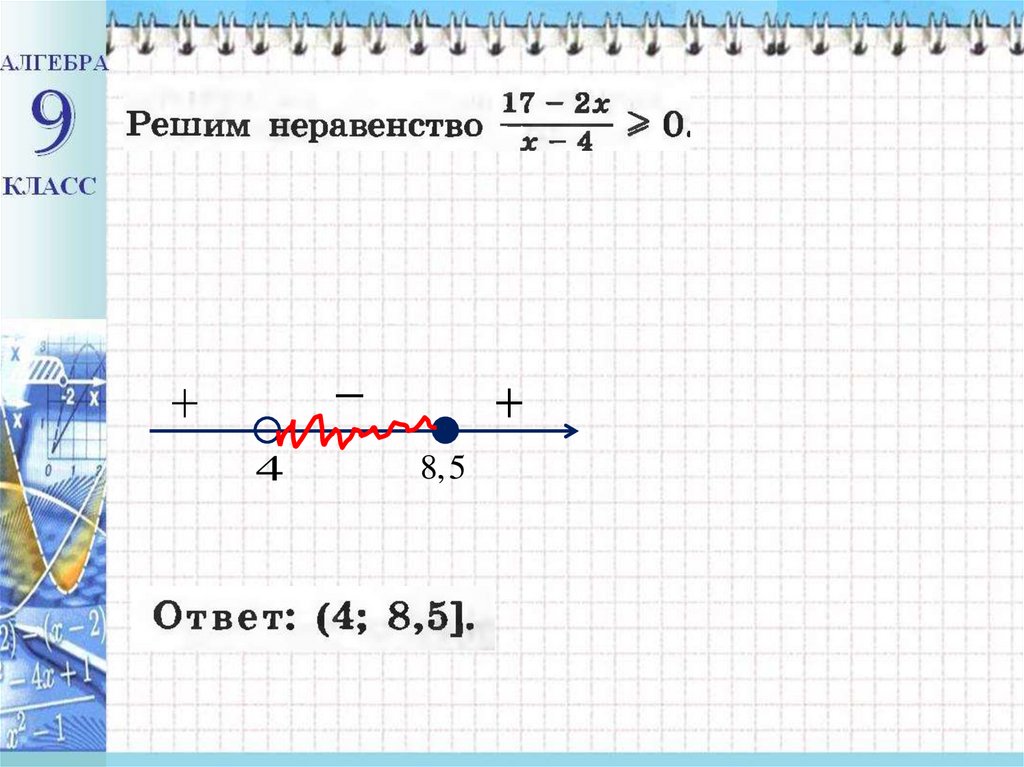
4
8,5

16.

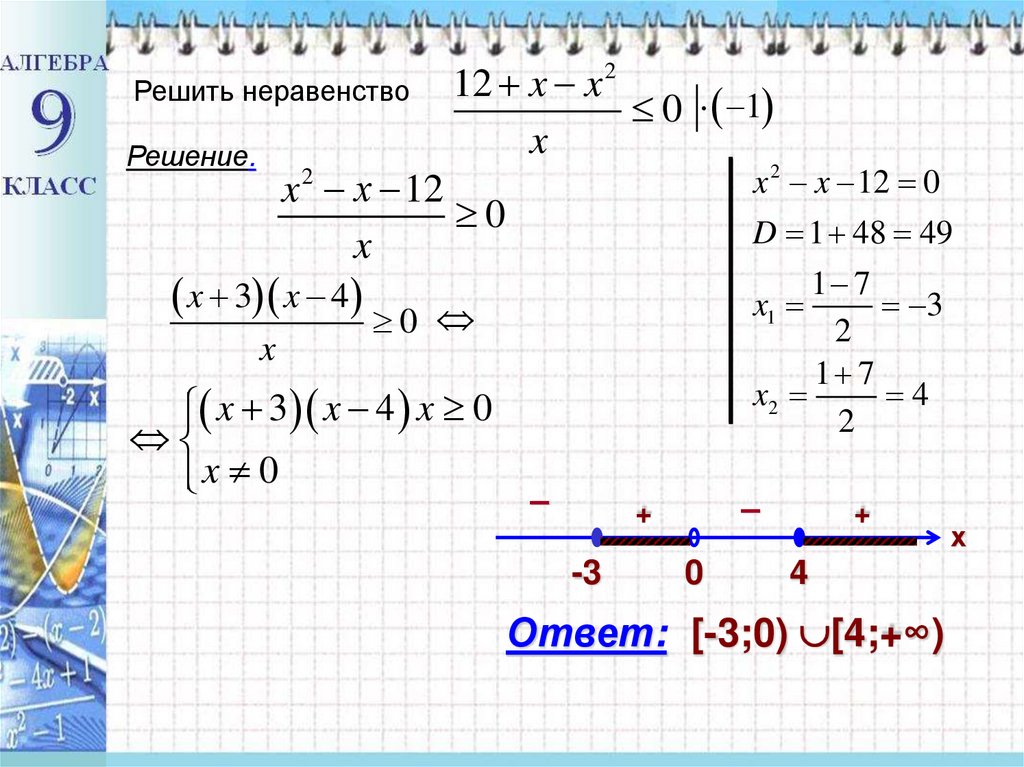
Решить неравенство
Решение.
12 x x 2
0 1
x
x 2 x 12 0
D 1 48 49
1 7
x1
3
2
1 7
x2
4
2
x х 12
0
x
2
x 3 x 4 0
x
x 3 x 4 x 0
x 0
–
–
+
-3
0
+
4
Ответ: [-3;0) [4;+∞)
х