Similar presentations:
Решение неравенств методом интервалов далее
1.
Решениенеравенств
методом
интервалов
далее »
2.
Цели урока:1. Познакомить учащихся с решением неравенств методом
интервалов.
2. Отработка навыка решения неравенств методом
интервалов.
3. Повторить решение неравенств второй степени с одной
переменной с помощью графика.
4. Для подготовки к ГИА повторить нахождение «нулей
функции», решение квадратных уравнений по формуле,
решение неполных квадратных уравнений.
5. Воспитание внимания, ответственного отношения к
учебе; тренировать память.
3.
Проверяем домашнее задание.Правило
№305
А)
2 х 3х 5 0
2
-2,5
2 х 3х 5 0
2
D =49
Х1 =1; Х2 = -2,5
Б)
Ответ: ( ; 2,5] [1; )
6 х 6 х 36 0
2
6 х 2 6 х 36 0
D=900
-2
Х1 = -2; Х2 = 3
Ответ: [ 2;3]
3
1
4.
В)х 5 0
2
х 5 0
2
Х1 =
5; Х = - 5
2
- 5
5
Ответ: ; 5 5;
5.
Проверяем домашнее задание.№304(д-з)
Д)
4 х 12 х 9 0
2
1,5
Ответ: ( ;1,5) (1,5; )
Е) 25 х 2 30 х 9 0
-0,6
Ответ: Решений нет
Ж)
10 х 9 х 0
2
Ответ:
З)
2 х 7 х 0
(0;0,9)
0
0,9
2
Ответ: ( ;0) (3,5; )
0
3,5
6.
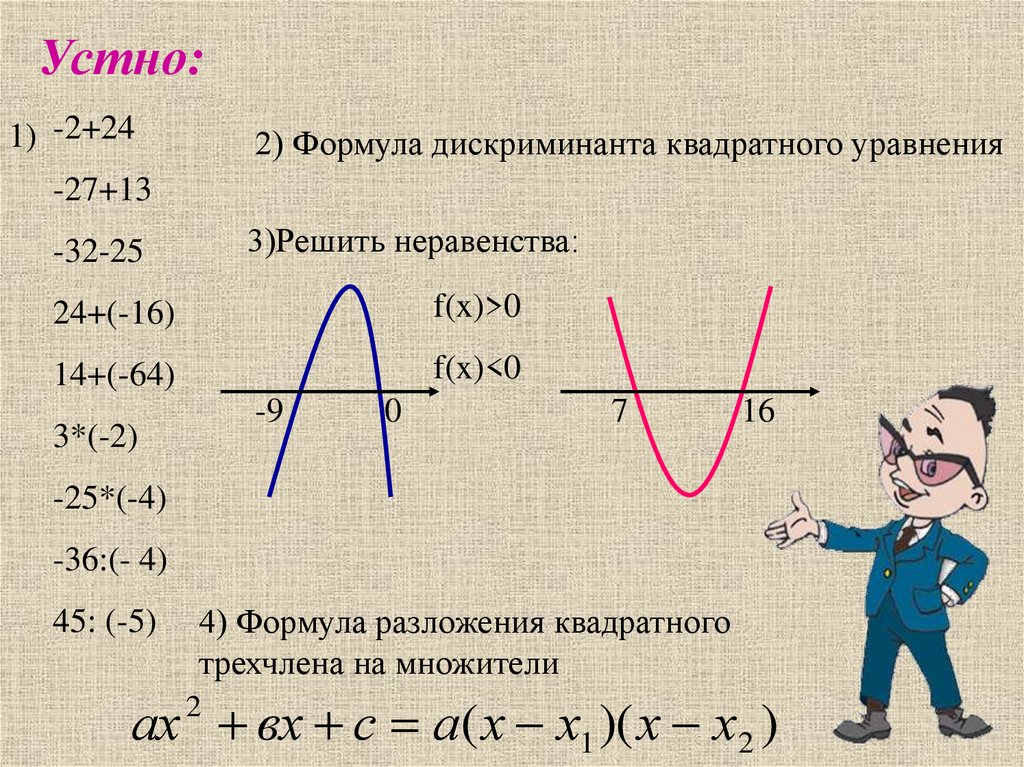
Устно:1) -2+24
2) Формула дискриминанта квадратного уравнения
-27+13
3)Решить неравенства:
-32-25
24+(-16)
f(x)>0
14+(-64)
f(x)<0
-9
3*(-2)
0
7
16
-25*(-4)
-36:(- 4)
45: (-5)
4) Формула разложения квадратного
трехчлена на множители
ах вх с а( х х1 )( х х2 )
2
7.
Гимнастика для глаз8.
Рассмотримрешение неравенств
второй степени с
одной переменной.
1
2
решение с помощью графика квадратичной
функции;
методом интервалов.
Назад на титульный лист
9.
Метод рассмотрения квадратичной функции1) Рассмотрим квадратичную функцию f(x) = x2 – 5 x - 50 и
найдем такие значения x, для которых f(x) < 0.
2) Графиком рассматриваемой функции является парабола,
ветви которой направлены вверх, так как a = 1, 1 > 0.
3) Найдем нули функции (то есть абсциссы точек пересечения
параболы с осью Ox), для этого решим квадратное уравнение
x2 – 5 x – 50 = 0.
x2 – 5 x – 50 = 0, a = 1, b = -5, c = -50.
D = b2 – 4ac;
D = (-5)2 –4*1*(-50) = 25 + 200 = 225 = 152, 225 > 0, значит
уравнение имеет два действительных корня.
x1 = (-(-5) – 15) : 2 = -5;
x2 = (-(-5) + 15) : 2 = 10.
« назад
далее »
Нули функции: x = -5 и x = 10.
10.
4) Изобразим схематично параболу f(x) = x2 – 5x –50 вкоординатной плоскости Oxy.
5) Из рисунка видим, что
f(x) < 0, при –5 < x < 10
(то есть берем в рассмотрение
ту часть параболы, которая
лежит ниже оси Ox).
Замечание: ответ записываем
в виде числового промежутка.
Ответ: (-5; 10).
« назад
11.
Метод интервалов1) Рассмотрим функцию f(x) = (х+2)(х-3)(х-5) .
Область определения D(f) = R (то есть множество всех
действительных чисел).
2) Найдем нули функции, т.е.решим уравнений f(x)=0.
(х+2)(х-3)(х-5)=0
х+2=0 или х-3=0 или х-5=0
или
х = -2 или х = 3
х=5
Числа -2, 3, 5 – нули функции, они разбивают область определения
функции на промежутки
( ; 2)
-2
3
( 2;3)
5
(3;5)
(5; )
« назад
далее »
12.
Выясним, каковы знаки этой функции в каждом изуказанных промежутков
-2
3
5
Выражение (х+2)(х-3)(х-5) представляет собой произведение
3 множителей. Знак каждого из этих множителей в
рассматриваемых промежутках указан в таблице
Мы видим, что в каждом из промежутков ( ; 2) ( 2;3) (3;5)
(5; )
функция сохраняет знак, а при переходе через точки -2, 3, 5
ее знак изменяется.
« назад
далее»
Правило: стр 89
13.
Это свойство используется для решения неравенств вида(х-х )(х-х )(х-х )…(х-х )>0 или
(х-х )(х-х )(х-х )…(х-х )<0,
1
2
1
3
2
n
3
n
где х1, х2, …хn – не равные нулю числа.
№1. Решить неравенство (х+6)(х+1)(х-4)<0
Находим нули функции
(х+6)(х+1)(х-4)=0
х+6=0 или х+1=0 или х-4=0
х = -6 или х = -1 или х = 4
Отмечаем эти числа -6, -1, 4 (нули функции) пустыми
кружками (т.к неравенство строго больше 0) на числовой
прямой. Числа разбивают числовую прямую на промежутки,
в каждом из которых функция сохраняет знак.
-6
-1
4
далее »
14.
-7+
-3
+
6
-6
-1 0 4
Определим знак функции f(x)= (х+6)(х+1)(х-4)
на каждом из промежутков
-
Если х = -7, то f(-7) = (-7+6)(-7+1)(-7-4) < 0
+
Если х = -3, то f(-3) = (-3+6)(-3+1)(-3-4) > 0
+
+
+
Если х = 0, то f(0) = (()+6)(0+1)(()-4) < 0
+
+
+
Если х = 6, то f(6) = (6+6)(6+1)(6-4)
+
Мы решаем неравенство (х+6)(х+1)(х-4)<0. Нас
интересует, на каких промежутках функция принимает
значения меньшие нуля.
Ответ: ( ; 6) ( 1;4)
15.
Данный метод решения неравенствназывается методом интервалов
Попробуйте решить неравенства данным методом:
№325
(х+8)(х-5) > 0
(х+8)(х-5)=0
х+8=0 или х-5=0
х = - 8 или х = 5
+
+
-10
-8
0
5
7
f(x) = (x+8)(x-5)
х = - 10, f(-10)=(-10+8)(-10-5) > 0
х = 0,
f(0)=(0+8)(0-5) < 0
х = 7,
f(7)=(7+8)(7-5)>0
Ответ: ( ; 8) (5; )
16.
Самостоятельная работа № 326Проверяем
Ответы
Б)
( 10;14)
В) ; 8,5 3,5;
1 1
Г) [ ; ]
3 8
№ 327.
Ответы № 327
А)
( 2;5) (12; )
Б)
; 7 1;4
В)
; 5 1;0
17.
Домашнее задание:Правило на стр 89
№ 326 - решить методом
интервалов,
№ 306 – решить с помощью
параболы (графически)
Итог урока:
Что узнали нового?
Как называется новый метод решения неравенств второй
степени с одной переменной?
Какой способ решения неравенств вам больше понравился?
Есть ли вопросы по д/з? Сможете ли вы его решить?
Оценки
18. С каким настроением вы пришли сегодня на урок?
19.
«Образовательный портал Мой университет – www.moi-universitet.ru,факультет «Реформа образования» – www.edu-reforma.ru»
20.
Спасибо заурок!



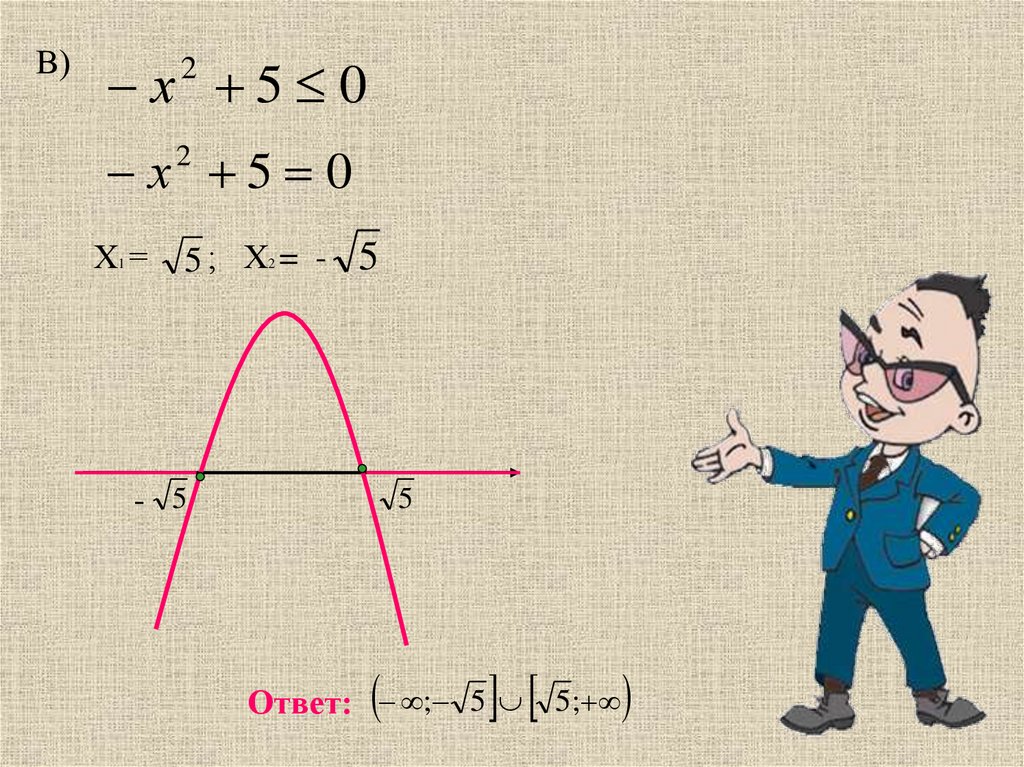















 mathematics
mathematics








