Similar presentations:
Предел функции. Замечательные пределы, раскрытие неопределенностей
1.
Лекция 2.Предел функции. Замечательные
пределы, раскрытие
неопределенностей. Односторонние
пределы, классификация точек
разрыва.
2. Предел функции в точке
Пусть функция y = f(x) определена в некоторой окрестности точки x0,кроме, быть может самой точки x0.
Число А называют пределом функции в точке x0 (или при x x0),
если для любого положительного ε найдется такое положительное
число δ, что для всех х из δ – окрестности точки x0 справедливо
неравенство:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x) A
x x0
3. Предел функции в точке
0; 0; x : x x0 f ( x ) Aε окрестность точки А
y
2
А
0
х0
х
δ окрестность точки x0
Геометрический смысл предела: для всех х из δ –
окрестности точки x0 точки графика функции лежат
внутри полосы, шириной 2ε, ограниченной прямыми: у
=А+ε,у=А-ε.
4. Односторонние пределы
В определении предела функцииlim f ( x ) A
x x0
предполагается, что x стремится к x0 любым способом: оставаясь
меньше, чем x0 (слева от x0), большим, чем x0 (справа от x0), или
колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента x к x0 существенно
влияет на значение предела, поэтому вводят понятия односторонних
пределов.
Число А1 называют пределом функции слева в точке x0, если для любого
ε > 0 найдется такое δ >0, что для всех x ( x0 ; x0 ) справедливо
неравенство:
f ( x ) A1
Предел слева записывают так:
lim f ( x) A1
x x0 0
5. Односторонние пределы
Число А2 называют пределом функции справа в точке x0, если0; 0; x x0 ; x0 f ( x ) A2
Предел справа записывают так:
Пределы функции слева и справа
называют односторонними
пределами.
y
А2
А1=А2=А
А1
0
lim f ( x ) A2
x x0 0
Очевидно, если существует
х0
х
lim f ( x ) A
x x0
то существуют и оба
односторонних предела, причем
А = А1 = А2
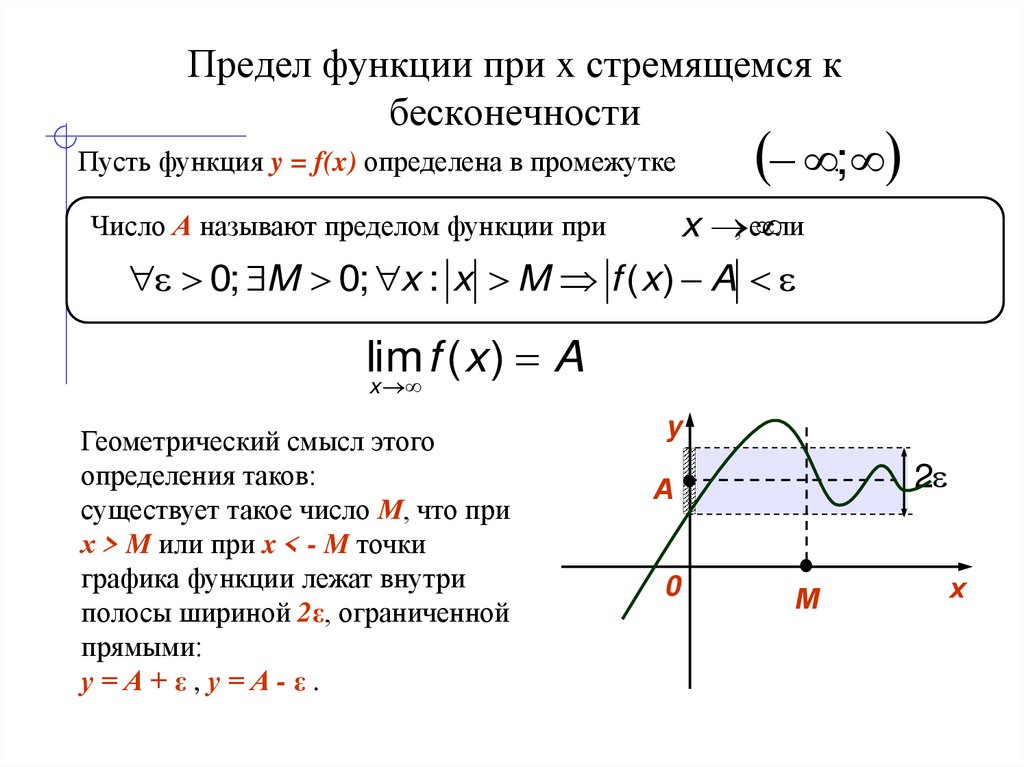
6. Предел функции при x стремящемся к бесконечности
.;Пусть функция y = f(x) определена в промежутке
x , если
Число А называют пределом функции при
0; M 0; x : x M f ( x ) A
lim f ( x ) A
x
Геометрический смысл этого
определения таков:
существует такое число М, что при
х > M или при x < - M точки
графика функции лежат внутри
полосы шириной 2ε, ограниченной
прямыми:
у=А+ε,у=А-ε.
y
2
А
0
М
х
7. Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределовфункций.
Формулировка теорем, когда x x0 или x аналогичны,
поэтому будем пользоваться обозначением: lim f ( x ).
Предел суммы (разности) двух функций равен сумме (разности)
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) limf2 ( x )
Предел произведения двух функций равен произведению
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Постоянный множитель можно выносить за знак предела:
lim C f ( x ) C lim f ( x )
8. Основные теоремы о пределах
Предел дроби равен пределу числителя, деленному на пределзнаменателя, если предел знаменателя не равен нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Предел степени с натуральным показателем равен той же
степени предела:
lim f ( x ) lim f ( x )
n
n
Предел показательно – степенной функции:
lim f ( x )
g(x)
lim f ( x )
lim g ( x )
9. Основные теоремы о пределах
Если между соответствующими значениями трех функцийu u( x );
z z( x ); v v ( x )
выполняются неравенства: u z v, при этом:
lim u( x ) lim v ( x ) A тогда: lim z( x ) A
Если функция f(x) монотонна и ограничена при x < x0 или при
x > x0, то существует соответственно ее левый предел:
lim
f
(
x
)
A
1
x x 0
0
или ее правый предел:
lim f ( x ) A2
x x0 0
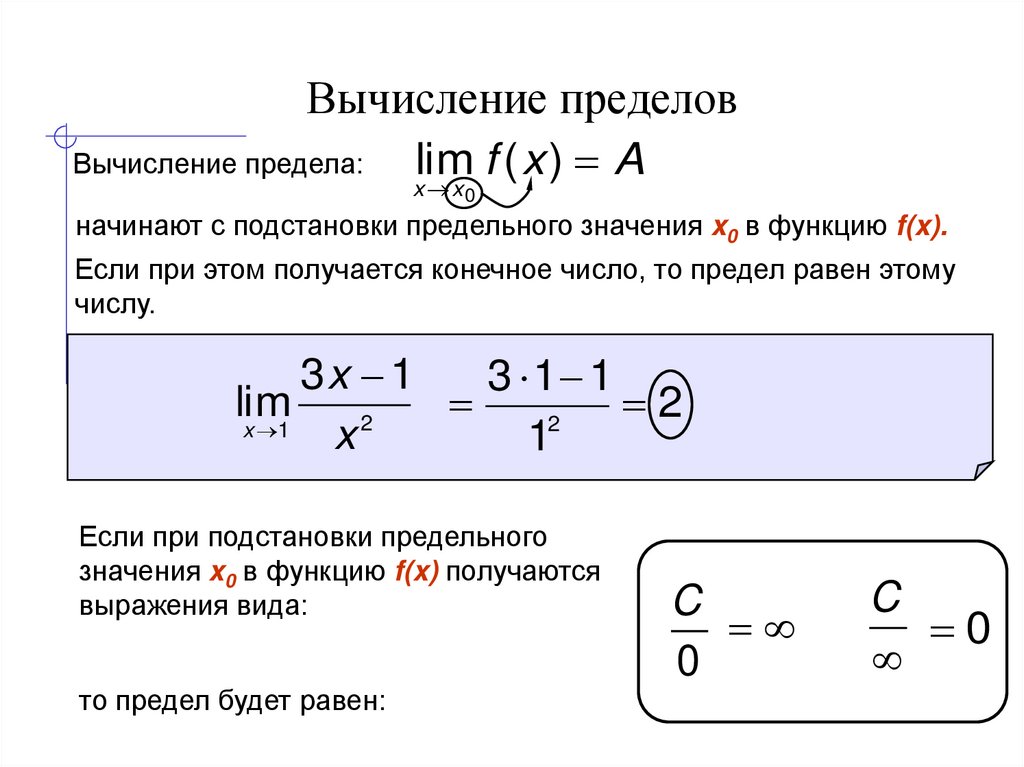
10. Вычисление пределов
Вычисление предела:lim f ( x ) A
x x
0
начинают с подстановки предельного значения x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому
числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Если при подстановки предельного
значения x0 в функцию f(x) получаются
выражения вида:
то предел будет равен:
C
0
C
0
11. Вычисление пределов
Часто при подстановке предельного значения x0 в функцию f(x)получаются выражения следующих видов:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Эти выражения называются неопределенности, а вычисление
пределов в этом случае называется раскрытие
неопределенности.
12. Раскрытие неопределенностей
Раскрытие неопределенности0
0
x 2 14 x 32
0
x 2 x 16
lim
lim
2
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
необходимо разложить
наlim
lim
Если f(x) – иррациональная
x
0
x 0
0
x
множители
числитель
и
x 1 умножить
1
дробь, x
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2
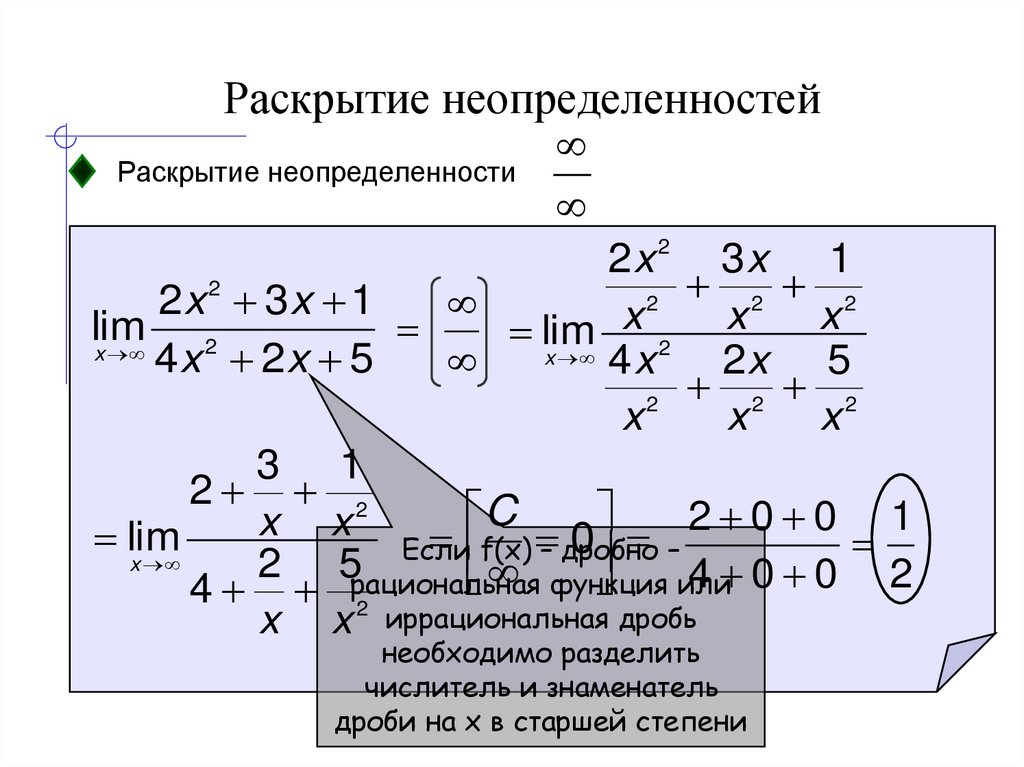
13. Раскрытие неопределенностей
Раскрытие неопределенности2
2x
3x 1
2 2
2
2x 2 3 x 1
x
x
x
lim
lim
x
x 4 x 2
4 x 2 2x 5
2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
f(x) – дробно
0 –
Если
x
2 5рациональная
4 0 0 2
функция
или
4 2
x x иррациональная дробь
необходимо разделить
числитель и знаменатель
дроби на x в старшей степени
14. Раскрытие неопределенностей
Раскрытие неопределенности2
2
lim
x
1
x
1
x
x 1 x 1 x 1 x 1
lim
x 1 x 1
2
x
lim
x
2
2
2
2
2
Умножим и разделим
2
( x 1) ( x функцию
1)
на
сопряженное
lim
2
x
2
2
выражение.
2
2
x 1 x 1
2
0
x 1 x 1
2
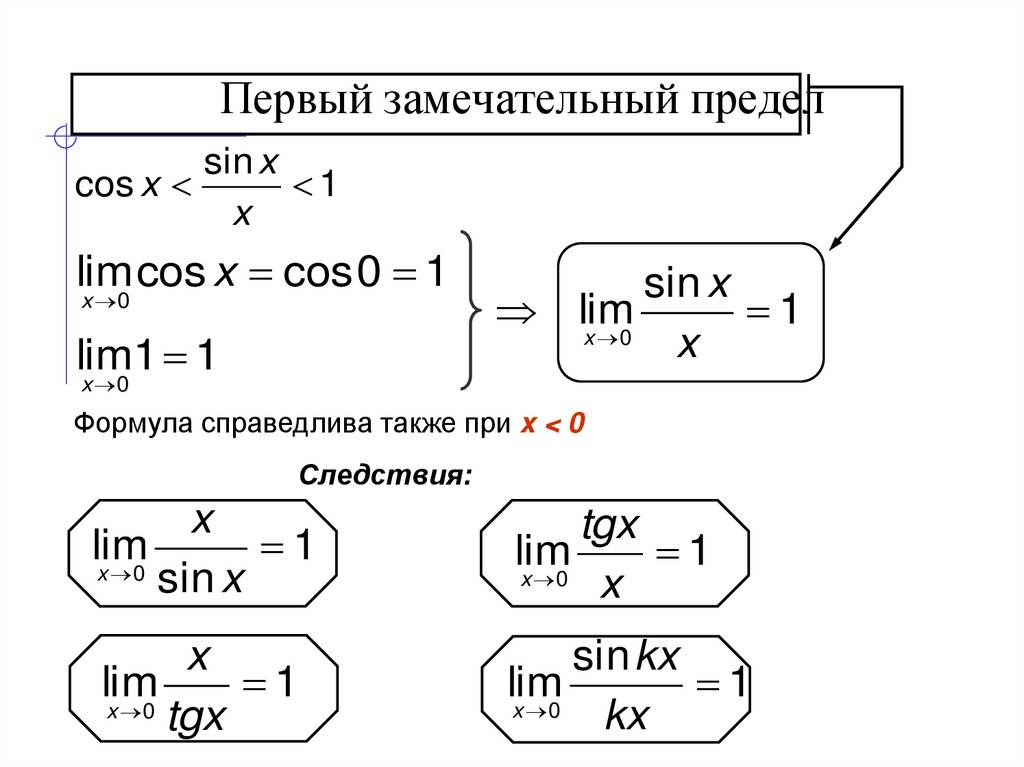
15. Первый замечательный предел
Функцияsin x
x
не определена при x = 0.
Найдем предел этой функции при
М С
x
О В А
OA 1
x 0
0 x
2
Обозначим:
S1 - площадь треугольника OMA,
S2 - площадь сектора OMА,
S3 - площадь треугольника OСА,
Из рисунка видно, что S1< S2 < S3
1
1
1
S1 OA MB OA 0M sin x sin x
2
2
2
16. Первый замечательный предел
М Сx
О В А
1
1
S 2 OA ОM x
2
2
1
1
S3 OA AC 1 tgx
2
2
1
1
1
sin x x tgx
2
2
2
sin x x tgx
sin x
cos x x
x tgx
sin x
x sin x
1
x
sin x
cos x
1
x
17. Первый замечательный предел
sin xcos x
1
x
lim cos x cos 0 1
x 0
lim1 1
sin x
lim
1
x 0
x
x 0
Формула справедлива также при x < 0
Следствия:
x
lim
1
x 0
sin x
tgx
lim
1
x 0
x
x
lim
1
x 0
tgx
sin kx
lim
1
x 0
kx
18. Первый замечательный предел
01 cos 4 x
2 sin 2x
sin 2 x
lim
lim
2 lim
2
2
x 0
x
0
x
0
0
x
x
x
2
2
sin 2 x 2 lim 2 sin 2 x
x 0
2 lim
2x
x 0 x
2
2
sin 2 x
2
2 2 lim
2 2 1 8
x 0
2x
2
19.
СЛЕДСТВИЯ ПЕРВОГО ЗАМЕЧАТЕЛЬНОГО ПРЕДЕЛАtg ax
sin ax
sin ax
1
lim
lim
lim
lim
1
x 0
x 0 ax cos ax
x 0
x 0 cos ax
ax
ax
tg ax
lim
1
x 0
ax
arctg ax
lim
1
x 0
ax
arcsin ax
lim
1
x 0
ax
19
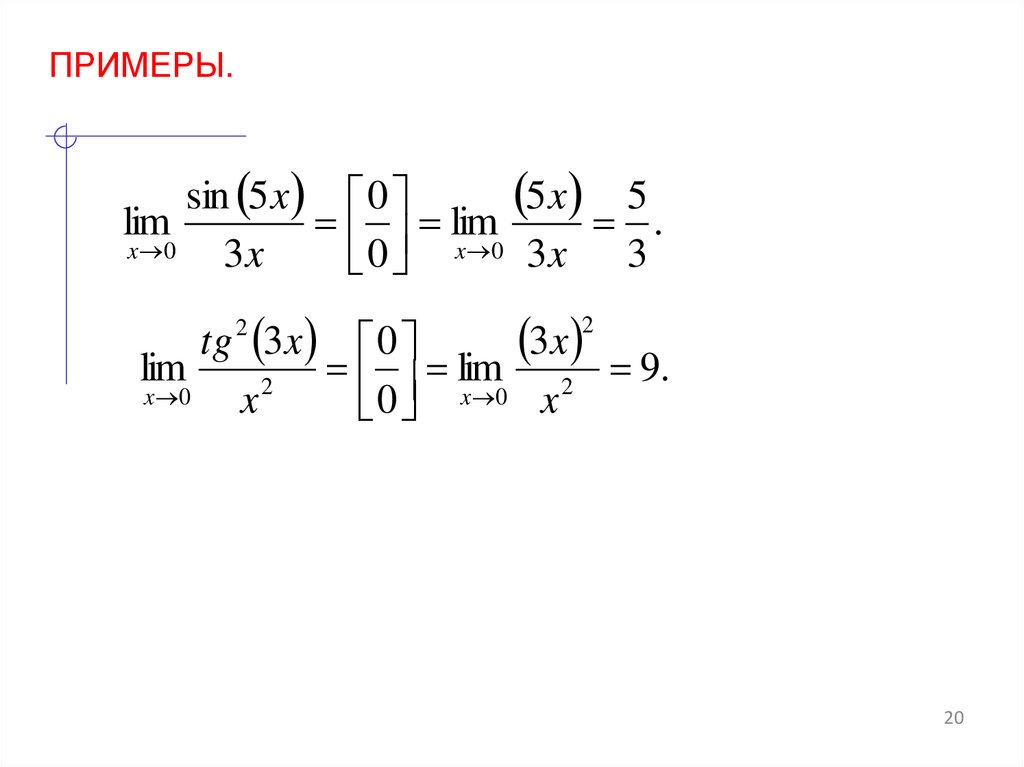
20.
ПРИМЕРЫ.sin 5 x 0
5x 5
lim
lim
.
x 0
3x
0 x 0 3 x 3
tg 3x 0
3x
lim
lim 2 9.
2
x 0
x
0 x 0 x
2
2
20
21.
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛx
1
lim 1 e
x
x
СЛЕДСТВИЯ ВТОРОГО ЗАМЕЧАТЕЛЬНОГО ПРЕДЕЛА
1
t
t
1
1/ x
lim 1 x
lim 1 e
x
x 0
t
t
x 0 t
lim 1 x
1/ x
x 0
e
21
22.
ln x 1ln x 1
1/ x
1
lim
lim ln 1 x ln e 1 lim
x 0
x 0
x 0
x
x
t ex 1
еx 1
t
еx 1
lim
x ln t 1
lim
1 lim
1
x 0
t 0 ln t 1
x 0
x
x
x 0 t 0
22
23.
ax1
lim 1 e
x
ax
lim 1 ax
1/ ax
x 0
e
ln ax 1
lim
1
x 0
ax
е ax 1
lim
1
x 0
ax
23
24.
ПРИМЕРЫ.е7 x 1
7x
lim
lim
7.
x 0
x 0 x
x
ln 2 x 1
2x 2
lim
lim
.
x 0
x 0 7 x
7x
7
lim 1 3x 1 0
x 0
1
5x
lim 1 3x
x 0
1
3x
3 x
1
5x
3
5
e .
24
25. Таблица эквивалентности
1) sin x x, x 03) arcsin x x, x 0
x2
5)1 cos x , x 0
2
x
7)а 1 x ln a, x 0
9) log a (1 x) x log a e, x 0
2)tgx x, x 0
4)arctgx x, x 0
6) е x 1 x , x 0
8) ln( 1 x) x, x 0
10)(1 x) k 1 kx, k 0, x 0
x
11) 1 x 1 , x 0
2
26. Определение непрерывности функции
Функция y = f (x) называется непрерывной вточке x0 , если выполняются условия:
1) Функция определена в точке x0 ;
2) Односторонние пределы функции в точке x0
равны между собой:
lim
f
(
x
)
lim
f
(
x
)
;
x x 0
x x0 0
0
3) Односторонние пределы равны значению
функции в точке x0:
f ( x) lim f ( x) lim f ( x) f ( x0 ) .
x lim
x x0 0
x x0
x0 0
27. Свойства непрерывных функций
1. Если даны две непрерывные функции вточке x0, то их сумма, разность и
произведение является непрерывной
функцией.
2. Основные элементарные функции
непрерывны в своей области определения;
3. Функция является непрерывной на
интервале, если она непрерывна в каждой
точке этого интервала.
28. Определение точки разрыва функции
Если в точке x0 нарушается хотя быодно
условие
определения
непрерывности в точке x0 , то такая
точка называется точкой разрыва
функции y = f (x).
29. Точки разрыва функции
Точка x=x0 называется точкой разрыва функции y=f(x),если в ней не выполняется по крайней мере одно из
условий непрерывности функции
30. Точки разрыва
Точка x=x0 называется точкой разрыва функции y=f(x) I рода,если существуют конечные пределы
f ( x 0) xlim
f ( x) ,
x 0
причем не все 3 числа 0
0
f ( x 0) lim f ( x)
0
x x0 0
равны между
собой
f ( x0 ), f ( x0 0), f ( x0 0)
Точка x=x0 называется точкой разрыва функции y=f(x) II рода,
если по крайней мере один из односторонних пределов в этой
точке
f ( x 0) xlim
f ( x) ,
x 0
0
не существует или равен
0
f ( x0 0) xlim
f ( x)
x 0
0
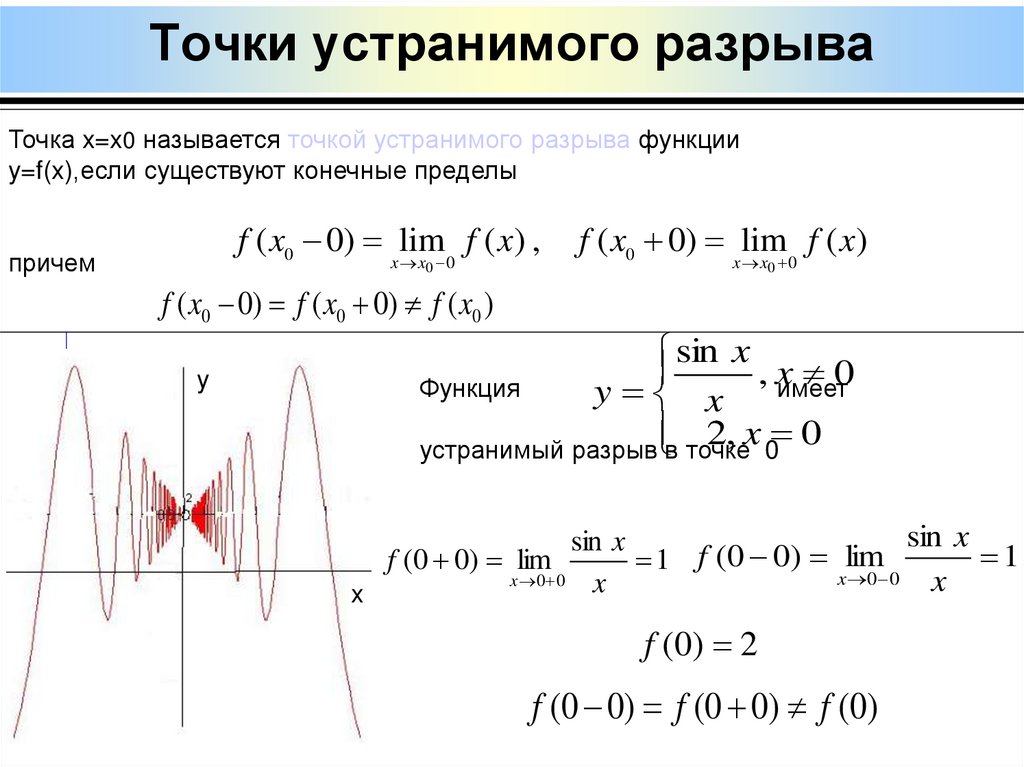
31. Точки устранимого разрыва
Точка x=x0 называется точкой устранимого разрыва функцииy=f(x),если существуют конечные пределы
f ( x0 0) xlim
f ( x) ,
x 0
причем
0
f ( x0 0) xlim
f ( x)
x 0
0
f ( x0 0) f ( x0 0) f ( x0 )
y
sin x
, xимеет
0
Функция
y x
2, x 0
устранимый разрыв в точке 0
sin x
sin x
1
f (0 0) lim
1 f (0 0) lim
x
0
0
x 0 0
x
x
x
f ( 0) 2
f (0 0) f (0 0) f (0)
32. Точки скачка
Точка x=x0 называется точкой скачка функции y=f(x),еслисуществуют конечные пределы
f ( x0 , где
0) xlim
f ( x) , - скачок
f ( x0 функции
0) xlim
f ( x)
причем
x0 0
x0 0
y=f(x) в точке
y f (xx0 0) f ( x 0)
f ( x 0) f ( x 0)
0
0
0
y
Функция
0
x 1, 1 x 2
имеет
y
2 x, 2 x 5
скачок в точке 2
x
-1
2
5
f (2 0) lim f ( x) 0
x 2 0
f (2 0) lim f ( x) 1
x 2 0
f ( 2) 0
f (2 0) f (2 0)
f (2 0) f (2 0) 1 - скачок
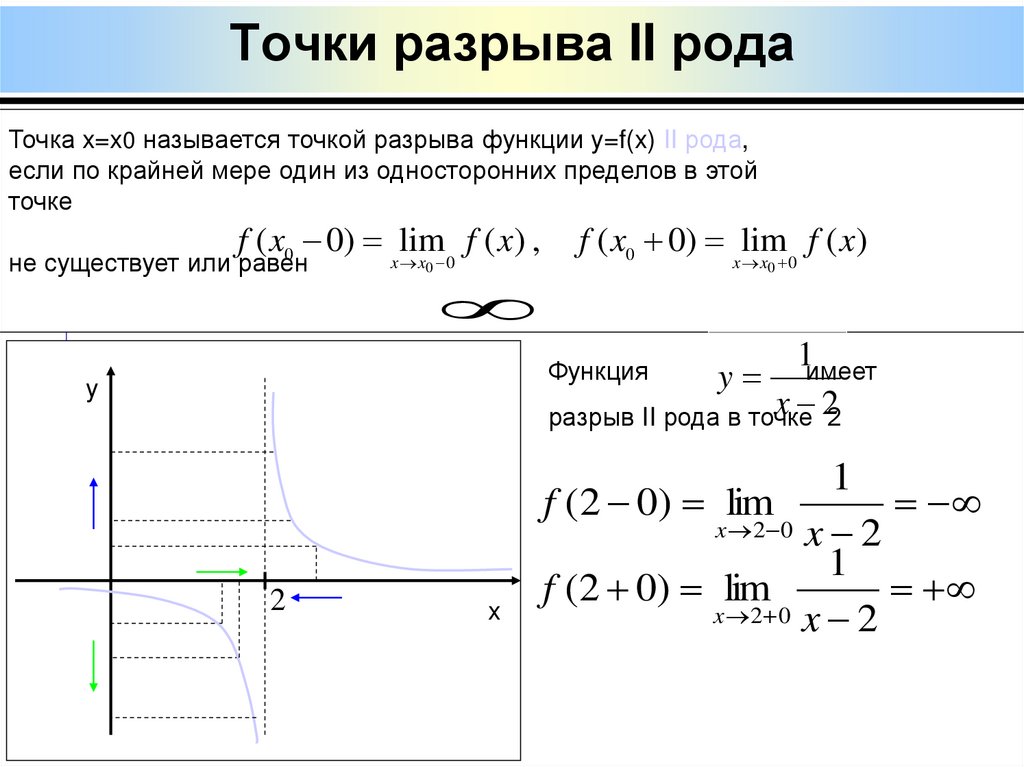
33. Точки разрыва II рода
Точка x=x0 называется точкой разрыва функции y=f(x) II рода,если по крайней мере один из односторонних пределов в этой
точке
f ( x 0) xlim
f ( x) ,
x 0
0
не существует или равен
0
f ( x0 0) xlim
f ( x)
x 0
0
1имеет
y
x 22
разрыв II рода в точке
Функция
y
2
x
1
f (2 0) lim
x 2 0 x 2
1
f (2 0) lim
x 2 0 x 2
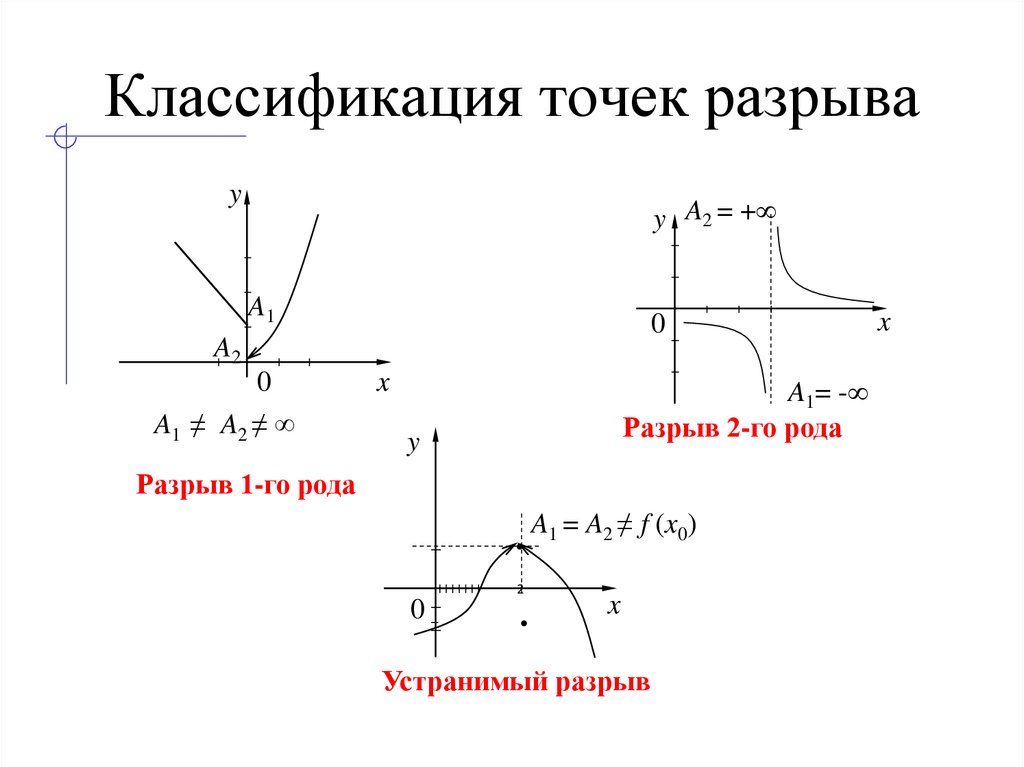
34. Классификация точек разрыва
yy A2 = +
A1
0
A2
0
A1 ≠ A2 ≠ ∞
x
A1= -
Разрыв 2-го рода
y
Разрыв 1-го рода
A1 = A2 ≠ f (x0)
2
0–
x
Устранимый разрыв
x
















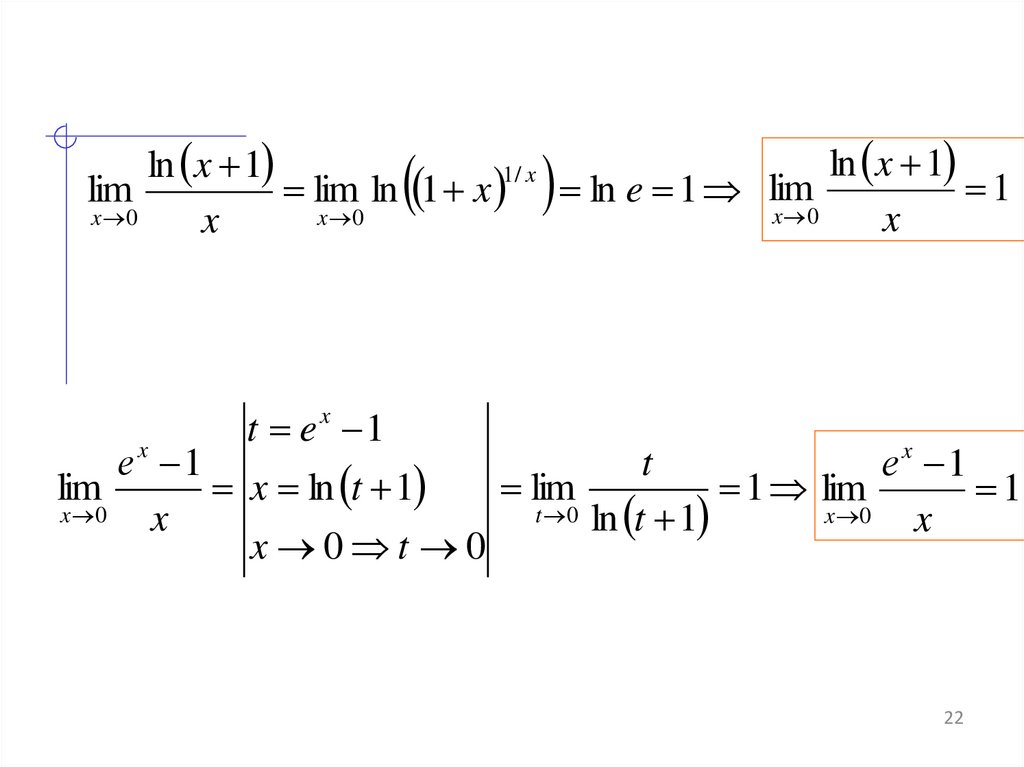









 mathematics
mathematics








