Ликбез. Лекция 2

1.

Лекция 2
Ликбез
3 курс

2.

• ОСНОВНЫЕ ТЕРМОДИНАМИЧЕСКИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.
• АДИАБАТИЧЕСКИЙ ПРОЦЕСС. СКОРОСТЬ ЗВУКА.
• КРИТИЧЕСКИЕ ПАРАМЕТРЫ ПОТОКА.
• ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ.
• ЗАПИСЬ ОСНОВНЫХ УРАВНЕНИЙ СОХРАНЕНИЯ С ИСПОЛЬЗОВАНИЕМ ГАЗОДИНАМИЧЕСКИХ
ФУНКЦИЙ.
• УРАВНЕНИЕ НЕРАЗРЫВНОСТИ.
• УРАВНЕНИЕ СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ.
• ПРЯМОЙ СКАЧОК УПЛОТНЕНИЯ.
• ПОДОБИЕ. ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В ЭЛЕМЕНТАХ ДВИГАТЕЛЯ.

3.

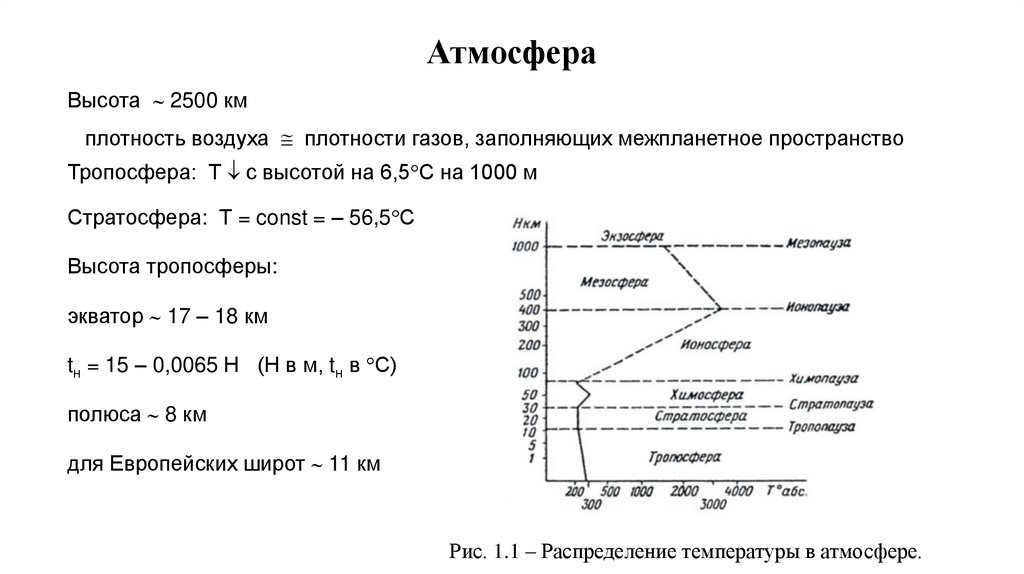
Атмосфера
Высота 2500 км
плотность воздуха плотности газов, заполняющих межпланетное пространство
Тропосфера: Т с высотой на 6,5 С на 1000 м
Стратосфера: Т = const = – 56,5 С
Высота тропосферы:
экватор 17 – 18 км
tн = 15 – 0,0065 Н (Н в м, tн в С)
полюса 8 км
для Европейских широт 11 км
Рис. 1.1 – Распределение температуры в атмосфере.

4.

Физические свойства воздуха
Давление
• Атмосферное давление измеряется в мм рт. ст.
Нормальное
давление: 760 мм рт. ст.
• Связь между единицами измерения давления:
1 кг/см2 = 10000
кг/м2 = 735,6 мм рт.ст.
• 1 ат = 10333 кг/м2 = 10333 мм вод. ст. = 1,0333 кг/см2 = 760 мм рт. ст.

5.

Физические свойства воздуха
Плотность
Измеряется массой тела, заключённой в единице его объема:
Переход от плотности в начальных к плотности в рассматриваемых условиях:
, т.к. для норм. условий р = В0 = 760 мм рт. ст.
и t = t0 = 15 С
= 0 = кг с2/м4
– относительная плотность воздуха

6.

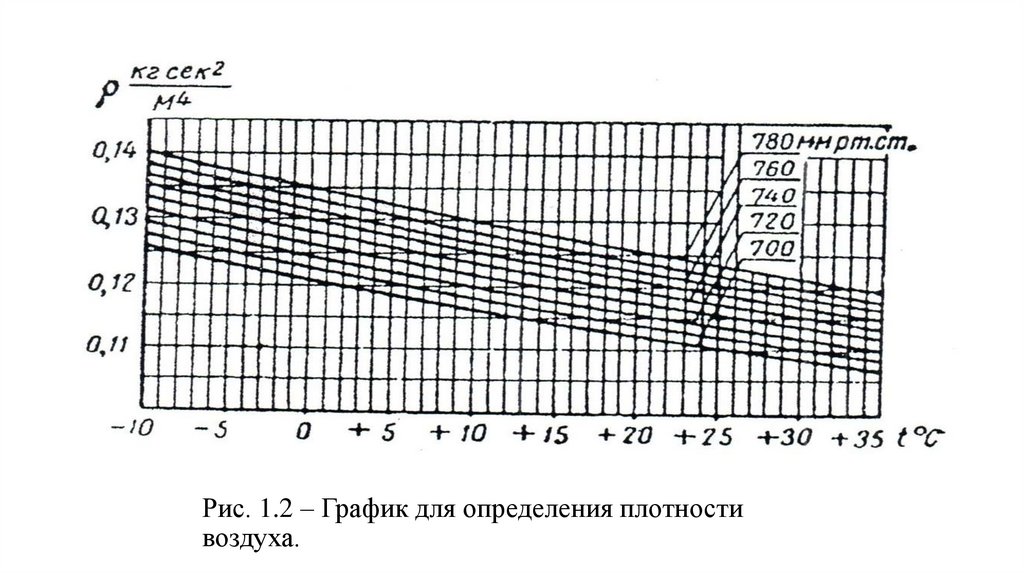
Рис. 1.2 – График для определения плотности
воздуха.

7.

Физические свойства воздуха
Вязкость
Силы
вязкости,
действующие
вдоль
рассматриваемой
элементарной
поверхности при движении выделенного объёма, характеризуют касательные
напряжения.
Сила вязкости:
абсолютный, либо динамический коэффициент вязкости –
Кинематический коэффициент вязкости:
= см2 с-1 = стокс
Рис. 1.3 – К определению силы вязкости.

8.

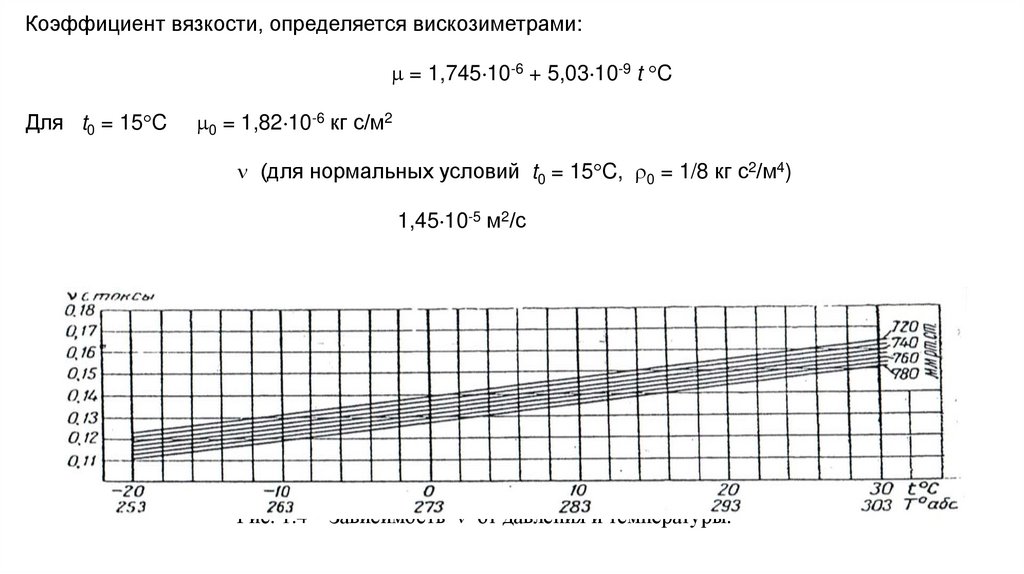
Коэффициент вязкости, определяется вискозиметрами:
= 1,745 10-6 + 5,03 10-9 t C
Для t0 = 15 C
0 = 1,82 10-6 кг с/м2
(для нормальных условий t0 = 15 C, 0 = 1/8 кг с2/м4)
1,45 10-5 м2/с
Рис. 1.4 – Зависимость от давления и температуры.

9.

Физические свойства воздуха
Упругость
Под упругостью понимают способность тел испытывать обратимые деформации.
Мера упругости – давление, оказываемое им на тела, ограничивающие расширение газа.
Сжимаемость – свойство газа изменять свой объем и плотность при изменении давления и температуры.
Для неизменности объема газа: упругость газа = внешнему действующему на него давлению.
Уравнение состояния:
,
здесь
– уравнение Майера;
ср и сv – теплоёмкость при постоянном р и v – соответственно;
с = dq / dT – отношение количества теплоты в б/м процессе к изменению температуры.
Адиабатический процесс:
Q = 0 – относительные скорости движения газов, настолько велики, что теплообмен между
струйками невозможен из-за малого времени соприкосновения. Тогда , (1,4 для воздуха), – константа Пуассона. 1 – атомные газы
= 1,6; 2 – атомные газы = 1,4; 3 – атомные газы = 1,29
Изоэнтропический процесс – отсутствие притока тепла, как извне, так и от внутреннего трения в газе.
Энтропия

10.

Стандартная Атмосфера (СА)
Введена для сравнения результатов испытаний, полученных в разных условиях.
Выведем формулы для СА.
Условия равновесия элементарного объёма воздуха с
единичной площадью сечения.
, т.к.
;
– удельный вес
Делаем предположение о распределении Т по высоте
1. Принимаем Т = const, и
в пределах от р0 до р и от 0 до Н
, Н* = RT – высота однородной атмосферы, если
= const (по высоте)
– формула Галлея,
(т.к. Т = const)
2. Предположим T – убывает при Н
преобразуем;
Рис.1

11.

затем в пределах от р0 до р и от 0 до Н
– градиент Т по высоте
обозначаем
,
тогда
для плотности
При разработке СА были приняты законы распределения Т по высоте
Для 1. Тропосферы:
tн = 15 – 0,0065 Н
2. Стратосферы: t = –56,5 С
Принимая: р0 = 760 мм рт. ст., Т0 = 288 К и 0 = кг м-4 с2
1.
,
2.
Для прикидочных расчётов: формула Ветчинкина для тропосферы:

12.

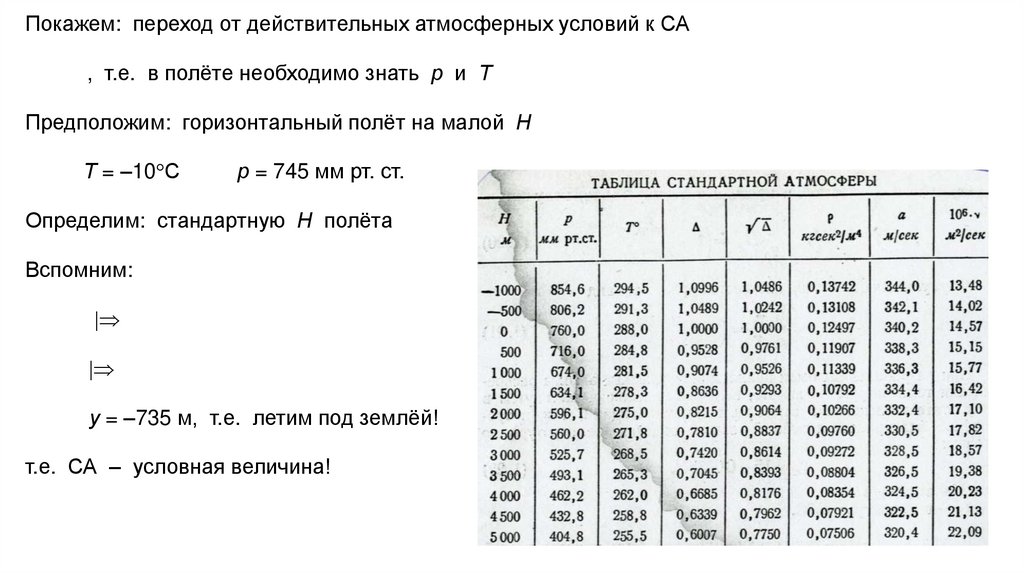
Покажем: переход от действительных атмосферных условий к СА
, т.е. в полёте необходимо знать р и Т
Предположим: горизонтальный полёт на малой Н
Т = –10 С
р = 745 мм рт. ст.
Определим: стандартную Н полёта
Вспомним:
у = –735 м, т.е. летим под землёй!
т.е. СА – условная величина!

13.

Основные законы движения жидкости
Закон обращения движения
Уравнение неразрывности (Закон постоянства массы)
Уравнение неразрывности – является выражением закона постоянства
массы.
m1, m2 – секундные массы
;
т.к. в выделенной струйке, все скорости параллельны оси струйки, а m
можно выразить, как: m = F V, то уравнение неразрывности:
1 F1 V1 = 2 F2 V2 = const
либо: Gс = 1 F1 V1 = 2 F2 V2 = const, где:
Gс – весовой расход кг/с; – удельный вес.
Если
справедливо
уравнение
неразрывности,
Рис. 1.5 – К выводу уравнения неразрывности.
то
это
исключает
возможность существования разрывов сплошности (т.е. несоответствие
плотности
и
объёма
в
различных
сечениях
текущей
жидкости).

14.

Уравнение теплосодержания
(уравнение энергии)
• Связывает Тгаза со скоростью движения с учётом
энергетических
воздействий
(подвод
тепла,
техническую работу и т.д.).
• В аэродинамике используют иную (механическую)
форму уравнения энергии, где скорость движения
связана с р и .

15.

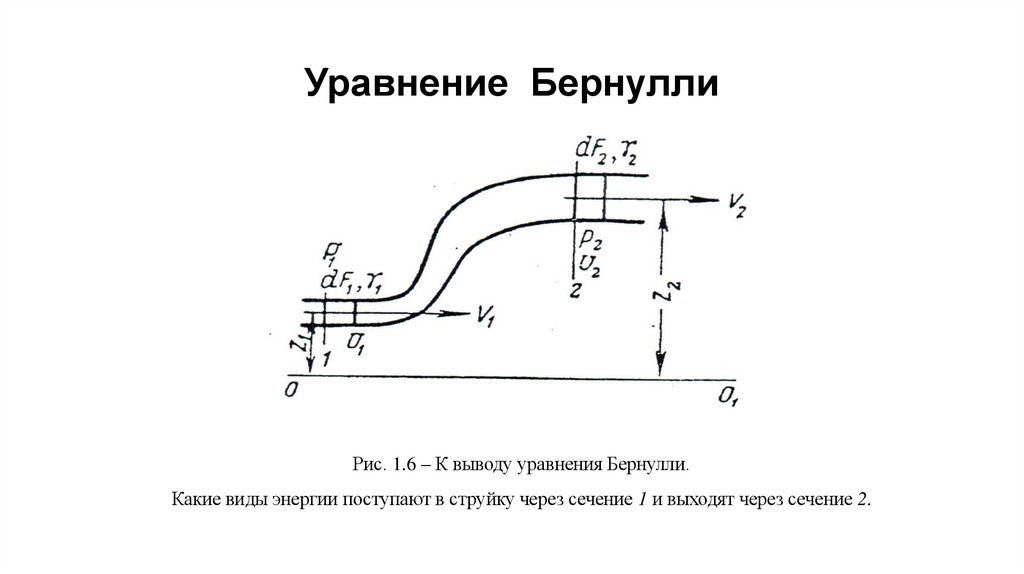
Уравнение Бернулли
Рис. 1.6 – К выводу уравнения Бернулли.
Какие виды энергии поступают в струйку через сечение 1 и выходят через сечение 2.

16.

Энергия веса
Секундный объём жидкости (dF1V1) на удельный вес ( 1) на нивелирную высоту dF1V1 1z1
Отнесем к единице веса протекающей жидкости
м – энергия 1 кг протекающей жидкости
Энергия давления
p1 dF1 V1, отнесем к единице веса протекающей жидкости
Кинетическая энергия
Отнеся к единице веса протекающей жидкости:
м.
м
Внутренняя тепловая энергия
Внутренняя энергия 1 кг жидкости, протекающего через сечение 1
где А – тепловой эквивалент работы.
м,

17.

Полная энергия в сечении 1, отнесённая к 1 кг жидкости
Для несжимаемой жидкости 1 = 2 и U1 = U2
При выводе предполагали: отсутствие потерь теплового и механического характера.
Если между струйками: потери тепла и трение, либо подвод энергии, то в зависимости от скорости струек возможны
варианты:
1. Высокая скорость (нет теплообмена) – течение адиабатическое.
2. Средняя скорость (теплообмен существует)
потери энергии (hп) между сечениями 1 и 2 для несжимаемой жидкости:
Часто применяемый вид записи: энергию относят не 1 кг, а 1 м3
– скоростной напор.

18.

Вернёмся к:
(*)
(**)
Свяжем внутреннюю энергию с энергией давления, используя 1 закон термодинамики
dQ = ApdV + dU, где dQ – подведённое тепло, ApdV – работа сил давления, dU – изменение
внутренней энергии
Если процесс изоэнтропический dQ = 0
Интегрируем:
интегрируем по частям, заменяем удельный объём удельной плотностью и подставляем в (**)

19.

,
где
– различна
Для использования уравнения Бернулли для сжимаемого газа надо знать процесс
1. Изохорический процесс: V = const, т.е. = const
– несжимаемая жидкость
z2 = z1
2. Изобарический процесс: технической работы – нет (), работы сил трения – нет
3. Адиабатический процесс :
т.е. если изменением потенциальной энергии можно пренебречь, нет технической работы
(L = 0), процесс идеально адиабатический, то
уравнение Бернулли:

20.

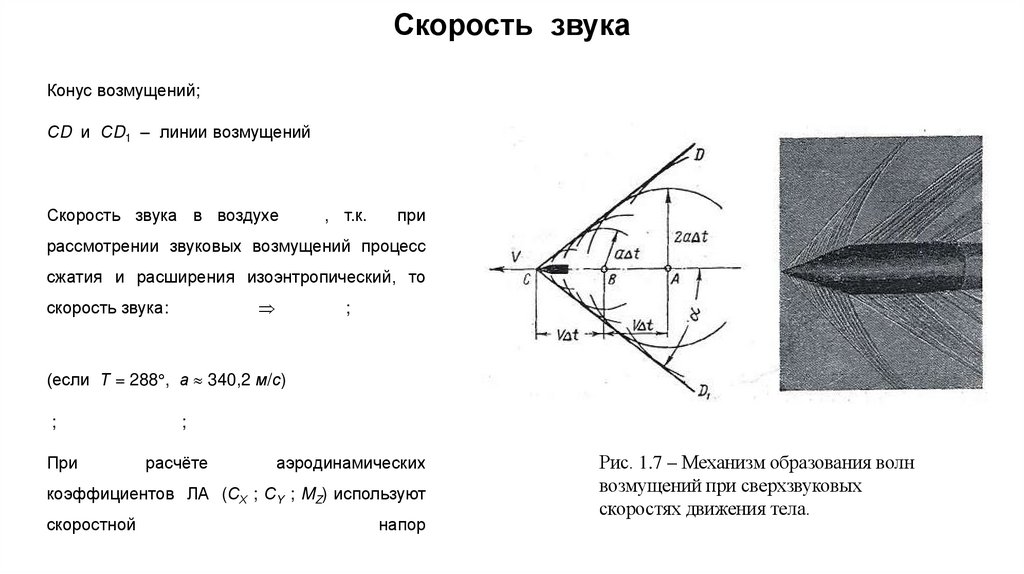
Скорость звука
Конус возмущений;
СD и СD1 – линии возмущений
Скорость звука в воздухе
, т.к.
при
рассмотрении звуковых возмущений процесс
сжатия и расширения изоэнтропический, то
скорость звука:
;
(если Т = 288 , а 340,2 м/с)
;
;
При
расчёте
аэродинамических
коэффициентов ЛА (СХ ; СY ; MZ) используют
скоростной
напор
Рис. 1.7 – Механизм образования волн
возмущений при сверхзвуковых
скоростях движения тела.

21.

,
р – связана с высотой, определяем по таблицам
Энтальпия
i = h + pv ,
После преобразований:
где h – внутренняя энергия, p – давление, v – удельный объём
i = cpT
В случае энергоизолированного течения газа используя уравнение 1-го закона термодинамики:
– уравнение Бернулли – Сен-Венана
Уменьшение кинетической энергии
энтальпии
– энтальпия адиабатного торможения – т.е. полная энтальпия
Энтропия
Функция состояния:
1-ый закон термодинамики:
,
Преобразуем:
dQ = cv dT + p dV
т.к. R = cp – cv
Если изменение параметров воздуха происходит по адиабате S2 = S1

22.

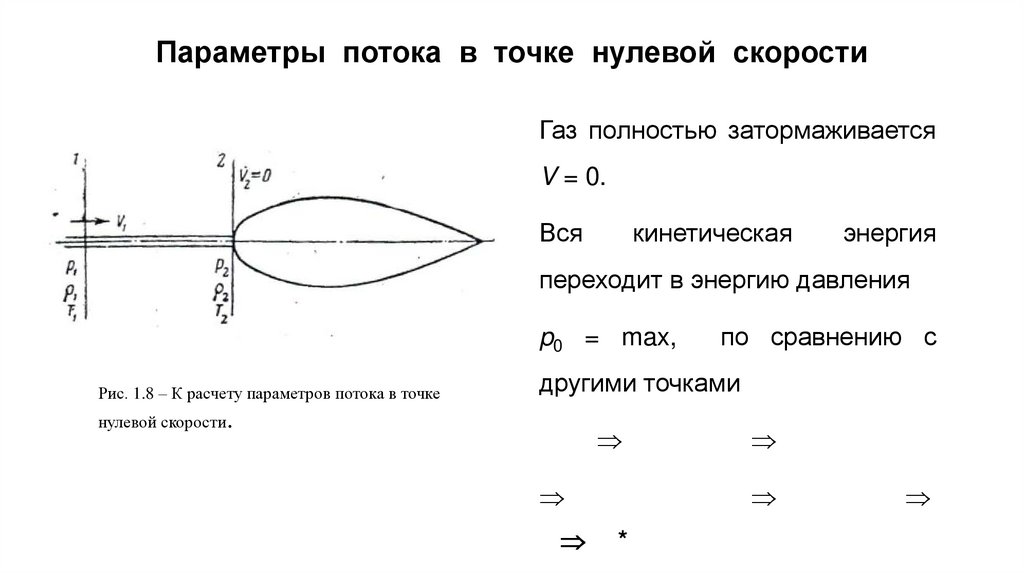
Параметры потока в точке нулевой скорости
Газ полностью затормаживается
V = 0.
Вся
кинетическая
энергия
переходит в энергию давления
p0 = max,
Рис. 1.8 – К расчету параметров потока в точке
по сравнению с
другими точками
нулевой скорости.
*

23.

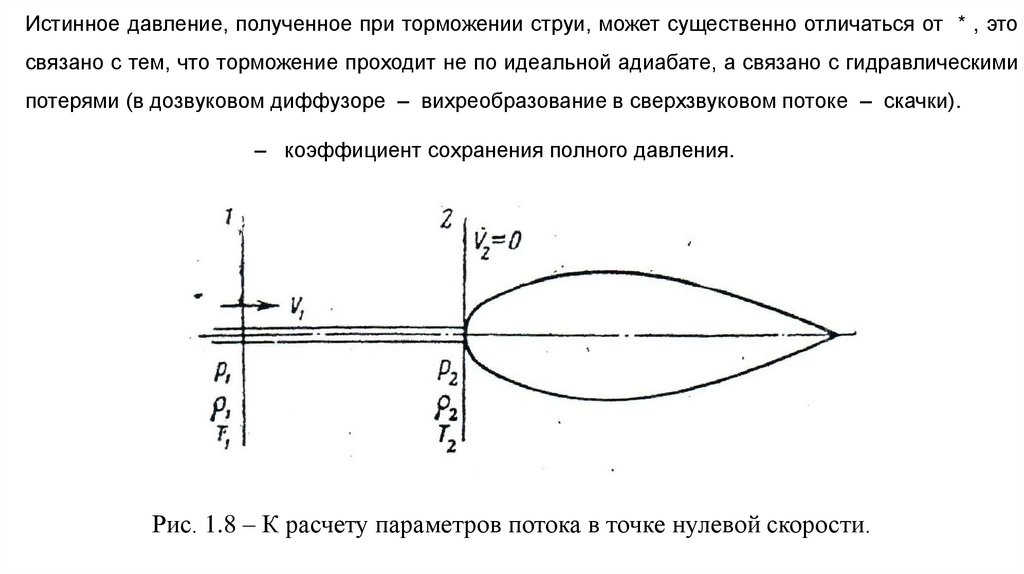
Истинное давление, полученное при торможении струи, может существенно отличаться от * , это
связано с тем, что торможение проходит не по идеальной адиабате, а связано с гидравлическими
потерями (в дозвуковом диффузоре – вихреобразование в сверхзвуковом потоке – скачки).
– коэффициент сохранения полного давления.
Рис. 1.8 – К расчету параметров потока в точке нулевой скорости.

24.

Запишем зависимости для отношений:
и
Получим приведенные зависимости для
Критические параметры: Ткр; ркр; кр; акр
,
т.к. М2 = 1; ;
Связь: а0 и а
,
т.к. ,
то
, т.к.

25.

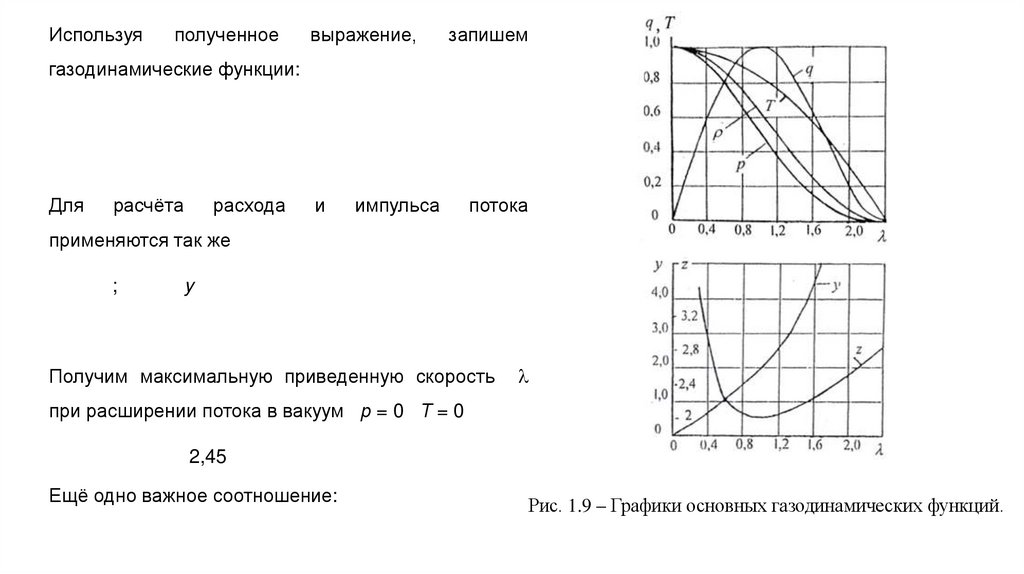
Используя
полученное
выражение,
запишем
газодинамические функции:
Для
расчёта
расхода
и
импульса
потока
применяются так же
;
y
Получим максимальную приведенную скорость
при расширении потока в вакуум р = 0 Т = 0
2,45
Ещё одно важное соотношение:
Рис. 1.9 – Графики основных газодинамических функций.

26.

Уравнение сохранения расхода (уравнение неразрывности)
, где
Уравнение расхода воздуха, протекающего по трубке между сечениями 1 – 1 и 2 – 2
= const;
,
т.к.
,
– характеризует теплоподвод,
если он отсутствует, то уравнение принимает форму:
,
– характеризует потери в потоке

27.

Уравнение сохранения количества движения

28.

Выразим М через :
После преобразований:
подставим m из уравнения расхода:
В случае энергоизолированного течения; при k = const:

29.

Прямой скачок уплотнения
Рассмотрим энергоизолированный цилиндрический канал между сечениями 1–1 и 2–2
Уравнение сохранения расхода:
Уравнение количества движения:
q( 1) F1 = q( 2) F2 V1–2
Пренебрегаем силами трения на цилиндрической стенке, т.е. R = 0; V1–2 = Vn
и
z( 2) = z( 1),
т.к. z( ) = + 1 / ,
то два решения:
2 = 1 – скачка нет, параметры неизменны и
2 = 1 / 1
Коэффициент восстановления полного давления в прямом скачке
1 2 = 1;
(т.к. = u / a0)
в скачке переход от сверхзвуковой скорости (u1 a0) к дозвуковой (u2 a0), причём, чем она выше на входе в
скачок, тем меньше после.

30.

ПОДОБИЕ. ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
В ЭЛЕМЕНТАХ ДВИГАТЕЛЯ
Для определения характеристик двигателя необходимо определить характеристики его
элементов.
Характеристики – это зависимости параметров эффективности от главных факторов,
определяющих режимы работы. Характеристики элементов двигателя исследуют на модельных
либо натурных объектах.
Возникают вопросы: о подобии физических явлений для модельного и натурного объекта.
Важное значение имеет:
– обработка экспериментальных данных;
– их предоставление в универсальной форме.
Эти вопросы и ряд других рассмотрены в теории подобия.
• Подобные физические явления реализуются только в геометрически подобных системах.

31.

• Геометрическое подобие – означает отношение любых их сходственных размеров постоянно, т.е.
, где – масштаб геометрического подобия.
Рис. 1 – Обтекание двух
геометрически подобных тел
Явления, протекающие в геометрически подобных системах и имеющие сходственную физическую
природу, могут быть подобны физически.
Физическое подобие – равенство отношений одноимённых физических величин в сходственных точках
в сходственные моменты времени.
, где – масштаб подобия данной физической величины.

32.

Если Ф – вектор скорости потока, (Ф = ) – кинематическое подобие
– равенство отношений векторов скоростей в любых сходственных точках в
сходственные моменты времени; – масштаб кинематического подобия.
Следствие кинематического подобия: подобие полей скоростей и линий тока.
Динамическое подобие – если Ф есть сила (Ф = ), т.е. равенство отношений векторов сил в
сходственных точках в сходственные моменты времени.
, где – масштаб динамического подобия.
Частный случай динамического подобия, равенство давления газа в сходственных точках:
.
Температурное подобие – равенство отношений температур потока в любых сходственных точках в
сходственные моменты времени.
, где – масштаб температурного подобия.
Подобие скоростей и сил в газовых потоках – газодинамическое подобие.
Тепловое подобие – газодинамическое подобие + подобие полей температур.

33.

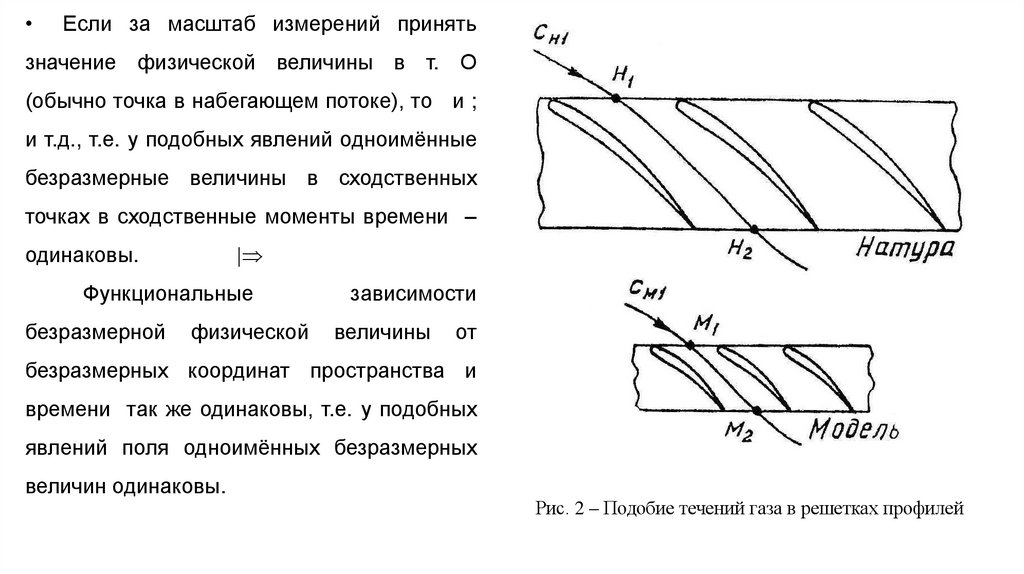
Если за масштаб измерений принять
значение физической величины в т. О
(обычно точка в набегающем потоке), то и ;
и т.д., т.е. у подобных явлений одноимённые
безразмерные величины в сходственных
точках в сходственные моменты времени –
одинаковы.
Функциональные
безразмерной
физической
зависимости
величины
от
безразмерных координат пространства и
времени так же одинаковы, т.е. у подобных
явлений поля одноимённых безразмерных
величин одинаковы.
Рис. 2 – Подобие течений газа в решетках профилей

34.

Первая теорема подобия:
У подобных физических явлений безразмерные уравнения движений – одинаковы, а безразмерные комплексы при
основных членах этих уравнений, называемые критериями подобия численно равны.
Критерии подобия, получаемые из уравнения движения газа, характеризуют определённые свойства газа.
Для газодинамического подобия необходимо равенство 5 критериев подобия:
– критерий Рейнольдса Re,
– критерий (число) М,
– критерий Фруда Fr,
– число Струхаля Sh,
– критерий Пуассона, показатель адиабаты k.
– характеризует степень влияния вязкости газа
– отношение сил вязкости к силам инерции,
где с – скорость, – плотность, – динамическая вязкость, l – линейный размер.

35.

При малых Re – силы вязкости преобладают; течение ламинарное, газ движется в виде
несмешивающихся слоёв.
При больших
Re
(Re 106) преобладает влияние сил инерции с2; турбулентное
течение газа (беспорядочное перемешивание частиц во всём занятом объёме газа).
Критическое число Re: завершение перехода от ламинарного к турбулентному
течению.
Обеспечение подобия по если неизменны физические свойства ( м = н и м = н), то
см lм = сн lн, т.е. скорость обратно пропорциональна линейному масштабу. Сохранить
условия см = сн можно в модельном течении: , либо за счёт снижения вязкости:
(например, вместо воздуха использовать фреон).

36.

Критерий
– характеризует сжимаемость движущегося газового потока.
Вспомним одномерное уравнение энергии, уравнение Бернулли:
процесс адиабатный, перейдём к а и М
, т.е. число М – характеризует степень влияния относительного изменения скорости (с) на относительное
изменение объёма (v), т.е. сжимаемость, чем выше М, тем сильнее это влияние, т.к. , то для подобия по М
при одинаковых физических свойствах (kм = kн и Rм = Rн) необходимо .
Критерий Фруда:
– оценивает влияние силы тяжести, т.к. является мерой отношения сил инерции к
силам тяжести: ,
– сила инерции (динамический напор),
– сила тяжести (статическое давление столба жидкости высотой l с плотностью ).
Критерий Струхаля: – характеризует нестационарность газовых потоков в элементах двигателя; t –
характерное для нестационарных процессов время (например, период колебаний).
Критерий Пуассона: k – характеризует физические свойства газа (отношение теплоёмкостей газа при
p = const и v = const), зависит от природы рабочего тела и его температуры.

37.

Для теплового подобия т.е. при учитывание теплообмена необходимо добавить критерии:
– число Прандтля,
– число Фурье,
где – коэффициент теплопроводности, – коэффициент динамической вязкости,
– плотность тока, cp – теплоемкость при постоянном давлении.
Критерий Pr – физический параметр составлен из параметров, характеризующих физические
свойства среды.
Для газов Pr = 0,6…1,0 мало изменяется с изменением давления и температуры.
У жидкостей Pr меняется в широких пределах.
Критерий Фурье – безразмерная временная характеристика нестационарного теплового
процесса.
Для газодинамического и теплового подобия необходимо: равенство определяющих критериев
М = idem; Re = idem; k = idem; Sh = idem; Fo = idem; Pr = idem.

38.

Вторая теорема подобия:
Решение дифференциальных уравнений, описывающих физические явления можно представить,
как зависимости искомых безразмерных величин от определяющих критериев подобия и безразмерных
координат пространства и времени:
безразмерная скорость
–
= f (М; Re; k; Sh; Fo; Pr; ; ; ; t);
безразмерное давление
–
= f (М; Re; k; Sh; Fo; Pr; ; ; ; t);
безразмерная температура
–
= f (М; Re; k; Sh; Fo; Pr; ; ; ; t).
Критериальные зависимости, полученные из данного конкретного опыта, справедливы для всех
подобных явлений.
Для определяемых безразмерных параметров (параметров эффективности, например ) так же
могут быть получены критериальные зависимости.
Т.е. характеристики элементов двигателя могут быть выражены через критерии подобия в виде
уравнений, либо графиков.

39.

Третья теорема подобия
–
устанавливает условия, чтобы рассматриваемые явления были
подобны.
Для получения подобных физических явлений необходимо и достаточно, чтобы условия
однозначности явлений были между собой подобны, а их одноимённые численные критерии были
численно одинаковы.
Т.е. 1. Соблюдение условий однозначности для граничных и начальных условий (подобие полей
величин скоростей, давлений, температур в набегающем потоке и во всём потоке в начальный момент
времени).
2. Равенство одноимённых критериев подобия.
Т.е. 1 и 2 теорема подобия описывает свойства и признаки подобных явлений.
3 теорема – устанавливает условия, подобия явлений.
НО, Получить равенство нескольких критериев подобия сложно, т.к. это приводит к
противоречивым требованиям.
Например: если рабочие тела натуры и модели одинаковы, то для
при l надо с, а для
при

40.

Выход:
пренебрежение критериями подобия, слабо влияющими на режим течения – свойство
автомодельности:
– для установившегося течения газа: можно пренебречь критерием Струхаля Sh и числом Фурье
Fo;
– если пренебречь силами тяжести, то не учитывается критерий Fr;
– критерий Pr – мало изменяется 1% для потока газа;
– показатель адиабаты k требуется в случаях, когда у натуры и модели различная температура в
потоке.
Два определяющих критерия: число М и критерий Рейнольдса Re.
Т.е. при испытаниях в воздушной среде необходимо: (Мн = Мм).
Для Reн = Reм необходимо изменить коэффициент кинематической вязкости: = / .
зависит от давления
испытания необходимо проводить в скоростных трубах, переменного
давления.
Подобие по М и Re – частичное подобие.