Similar presentations:
Основные задачи, решаемые теорией аэродинамического подобия
1.
ОСНОВЫ АЭРОДИНАМИКИЛЕКЦИЯ № 4
Тема 4
Аэродинамическое подобие
2.
Лекция № 4. Основные задачи, решаемыетеорией аэродинамического подобия
2
Рассматриваемые вопросы:
4.1 Аэродинамическое подобие и его составляющие.
4.2 Полное и неполное подобие.
4.3 Критерии подобия.
4.4 Системы координат.
4.5 Аэродинамические силы и моменты, их коэффициенты.
4.6 Коэффициент давления.
Литература:
1. Гарбузов В. М., Ермаков А. Л., Кубланов М. С., Ципенко В. Г.
Аэромеханика: Учебник для студентов вузов гражданской авиации –
М.: МГТУГА, 2000, 288 с.
2. Логвинов И. И. Аэромеханика: Учебное пособие М.
Иркутск: ИГТУ, 1998, 144 с.
3. Ништ М. И. Аэродинамика летательных аппаратов. Учебник для
ВУЗов. М.: ВВИА им. проф. Н. Е. Жуковского, 1994, 570 с.
3.
Введение в аэродинамическое подобие3
Аэродинамическое подобие (АП) наука об
возможности исследовании характеристик и свойств
аэродинамических тел посредством их моделей в поле
течения, искусственно созданного для указанной цели.
Факторы, побуждающие появления АП:
потери персонала при испытании натурных образцов;
дороговизна процесса испытания натурных образцов;
отсутствие предсказуемости ожидаемых результатов;
отсутствие экспериментальной базы модельного
эксперимента (от мастерских ВВИА до ЦАГИ);
отсутствие совместимости характеристик испытуемых
натурных образцов, экспериментальных моделей и
теоретического обоснования создаваемых аэродинамических
изделий.
4.
4.1 Аэродинамическое подобие и его составляющие4
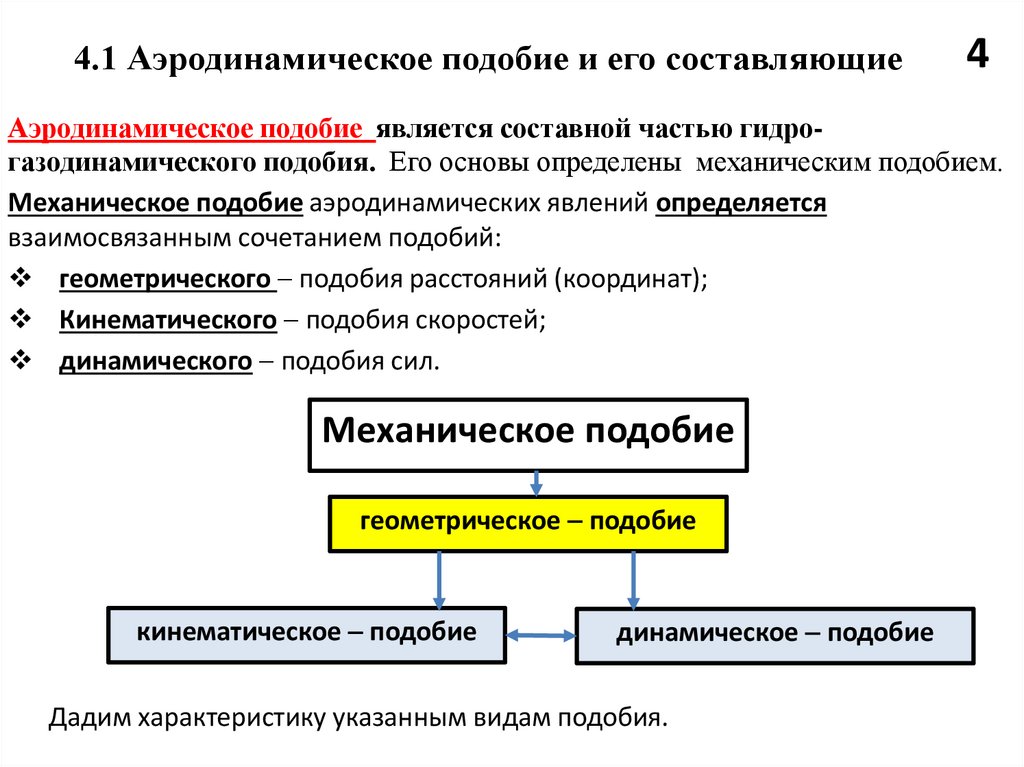
Аэродинамическое подобие является составной частью гидрогазодинамического подобия. Его основы определены механическим подобием.
Механическое подобие аэродинамических явлений определяется
взаимосвязанным сочетанием подобий:
геометрического подобия расстояний (координат);
Кинематического подобия скоростей;
динамического подобия сил.
Механическое подобие
геометрическое подобие
кинематическое подобие
динамическое подобие
Дадим характеристику указанным видам подобия.
5.
4.2 Основные задачи, решаемые теорией 5аэродинамического подобия
разработка теорем и критериев подобия,
востребованных не только в гидрогазодинамике, но и в других направлениях;
совершенствование критериев подобия
и методик их применения;
установление необходимого и достаточного
количества критериев, отвечающих
требованиям полного подобия;
применение теории подобия в области
решения практических задач и др.
6.
4.3 Аэродинамическое подобие и егосоставляющие
6
Определение подобных течений
Течения газа считаются подобными, если при обтекании
геометрически подобных аэродинамических тел (рис. 4.1) отношения
давления, скорости и температуры в любых сходственных точках
потока вокруг этих тел в сходственные моменты времени постоянны,
а векторы скоростей - одинаково ориентированы относительно этих
обтекаемых тел.
Натурный образец
Модель
Рисунок 4.1 К условию геометрически подобных тел
Определяющее условие подобия о:
Подобие течений реализуется только при
геометрически подобных системах.
7.
Геометрически подобные системы7
Геометрически подобные системы у которых соблюдено
равенство отношений любых размеров сходственных
элементов натурного образца и его модели.
Для аэродинамических профилей линейные размеры l:
b хорда; c толщина; f стрела прогиба средней линии и др.
Условие геометрического подобия можно
представить в виде линейного масштаба k1
k1= const1:
м модель;
сmax
н натурное тело.
l м bм cм f м
k1 const1
l н bн cн f н
b
fmax
8.
Физическое подобие теченияФизически подобными называется течения, у которых равенство
отношений одноименных физических величин
в сходственных точках геометрически подобных систем
в сходственные моменты времени – постоянны.
Сходственные точки, координаты которых удовлетворяют
условию геометрического подобия:
ха
yа
zа
lн
const1
ха
yа z а l м
Физические явления характеризуются множеством физических
параметров – скоростью, силой, температурой . Следовательно:
Физическое подобие может быть представлено совокупностью
составляющих его подобий:
– кинематическим;
– динамическим;
– температурным подобием.
8
9.
Кинематически подобные течения9
Кинематически подобными называется течения, у
которых равенство отношений скорости потока «V» в
сходственных точках геометрически подобных
натурного объекта и модели в сходственные моменты
времени – постоянны.
Кинематическим условием подобия называется
постоянство в сходственные моменты времени
отношений скорости потока в сходственных точках
геометрически подобных натурного объекта и его
модели.
Vа Vе
kV const 2
Vа Vе
Здесь kV – масштаб кинематического подобия.
10.
Динамически подобные течения10
Динамически подобные течения у которых
равенство отношений силы Р (давления "р") в
сходственных точках геометрически подобных
натурного объекта и модели в сходственные
моменты времени – постоянны.
Определение динамического условия подобия
течений и его математическая формулировка:
Динамическе условие подобия постоянство в
сходственные моменты времени отношений
давления потока в сходственных точках
геометрически подобных натурного объекта и
ра ре
его модели.
k const
ра
ре
р
3
11.
Температурное подобие11
Температурно-подобными течения у
которых равенство отношений
температуры Т в сходственных точках
геометрически подобных натурного
объекта и модели в сходственные
моменты времени – постоянны.
Температурное условие подобия течений в
сходственные моменты и в сходственных точках
геометрически подобных натурного объекта и его
модели можно представить в виде:
Та Те
kТ const 4
Т а Т е
12.
4.4 Полное и неполное подобие12
Соответствия модели и натуры геометрическое подобие, не
раскрывает подобия всех физических явлений. Следовательно, оно
обязательно, но не полное.
Физическое подобие требует соблюдения :
геометрического подобия;
кинематического подобия подобия скоростей и ускорений в
сходственных точках модели и натуры;
динамического подобия подобия сил в соответствующих
точках модели и натуры.
Физическое подобие может быть полным, неполным, приближенным.
Полное подобие – протекание во времени и пространстве
физических процессов, достаточно полно характеризующих явление.
Основная задача исследования – полное подобие.
Не всегда удаётся обеспечить полное моделирование.
Следствие прибегают к неполному или приближенному,
обеспечивая подобие процесса только во времени или в пространстве.
13.
134.5 Критерии подобия
Критериями подобия называются параметры, удовлетворение
которым в полном объёме обеспечивает подобие течения у
геометрически подобных натурного объекта и модели в
сходственных точках и в сходственные моменты времени.
Газодинамическое подобие (при отсутствии теплообмена)
обеспечивают, пять критериев подобия:
u
1. Критерий (число) Маха Мс
Mc =
a
.
Характеризует сжимаемость газового потока, то есть влияние
относительного изменения скорости на относительное изменение
удельного объёма РТ.
ρ u l u l
Re
,
2. Критерий Рейнольдса Re
μ
характеризующий влияние вязкости газа.
Здесь l – характерный линейный размер,
- коэффициент динамической вязкости,
ρ – плотность газа.
14.
(продолжение сл. 13)При малых числах Рейнольдса в обтекании тела
преобладают силы вязкости . Течение ламинарное
(упорядоченное). Слои газа не смешиваются.
При больших числах Рейнольдса в обтекании тела
преобладает влияние сил инерции . Частички РТ,
обладающие запасом кинетической энергии, проникают в
смежные слои. Беспорядочное перемешивание частичек во
всем занятом ими объёме.
Слоистое течение потока исчезает и переходит в
турбулентное. Граница перехода по числам Re от
ламинарного течения к турбулентному соответствует
критическому числу Рейнольдса Reкр.
14
15.
Критерий Фрудаu
Fr ,
g
l
Здесь g – ускорение свободного падения.
3. Критерий Фруда Fr
Критерий Фруда оценивает влияние сил тяжести.
Он является мерой отношения сил инерции к силе ρgl
статического давления столба жидкости или газа с плотностью ρ и
высотой l.
4. Критерий Струхаля Sh характеризует влияние
нестационарности течения.
В формуле Sh:
- характерное время, например период колебаний.
где, cр и cv – удельные теплоёмкости газа при постоянном
давлении и удельном объеме газа соответственно. Величина
показателя адиабаты указывается в справочниках и зависит от
природы РТ и от температуры.
16.
Показатель адиабаты k(критерий Пуассона)
15
Тепловое подобие обеспечивают критерии
Нуссельта Nu, Прандтля Pr и Фурье Fo.
Критерий Нуссельта Nu: Самостоятельно
где: - коэффициент теплоотдачи; - коэффициент теплопроводности.
Критерий Нуссельта характеризует интенсивность теплообмена
между теплоносителем и элементами ОК при вынужденном движении.
7. Критерий Прандтля Pr:
• Критерий Прандтля Pr характеризует физические свойства среды. Для
газов его величина лежит в пределах Pr = 0,6 … 1,0 и мало
изменяется.
17.
4.6 Системы координатВ аэродинамике применяются системы
координат:
1. Земная система координат.
2. Скоростная система координат.
3. Связанная система координат.
Существуют также:
1. Полярная система координат
2. Нормальная система координат.
3. Траекторная система координат.
17
18.
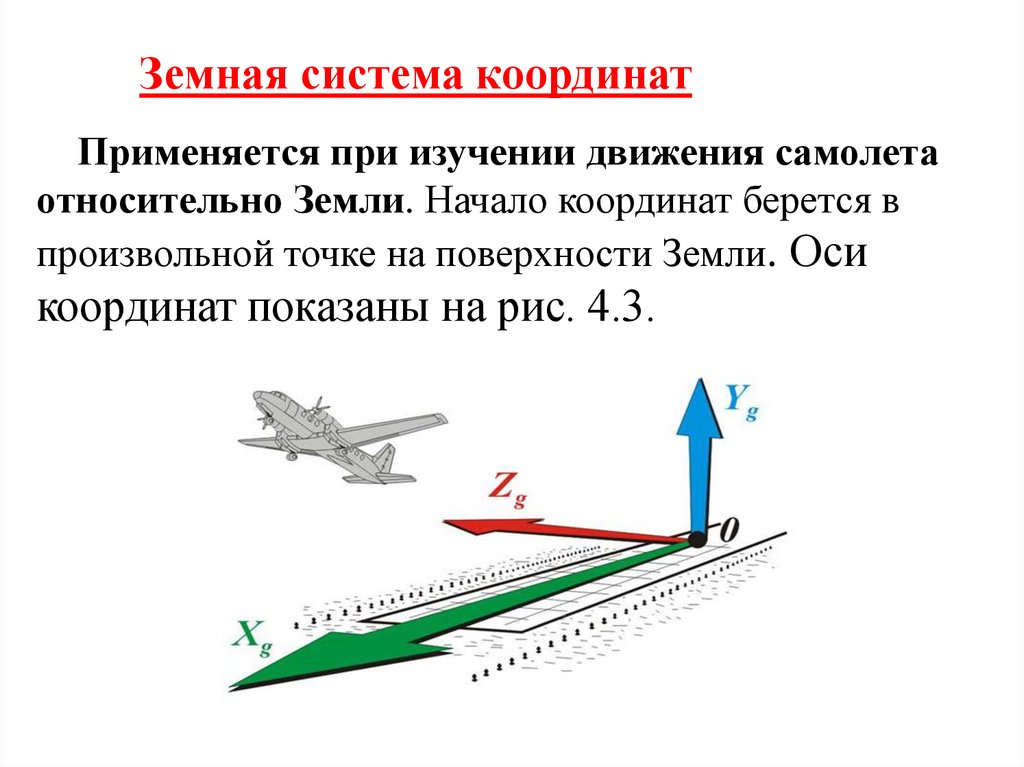
Земная система координатПрименяется при изучении движения самолета
относительно Земли. Начало координат берется в
произвольной точке на поверхности Земли. Оси
координат показаны на рис. 4.3.
19.
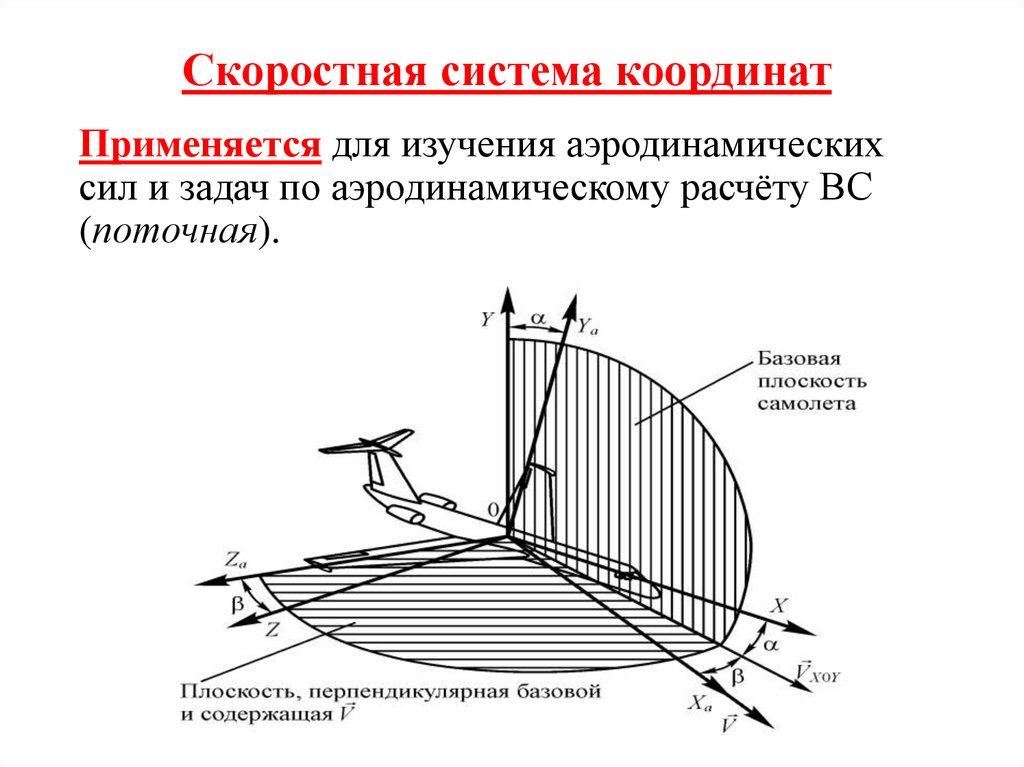
Скоростная система координатПрименяется для изучения аэродинамических
сил и задач по аэродинамическому расчёту ВС
(поточная).
20.
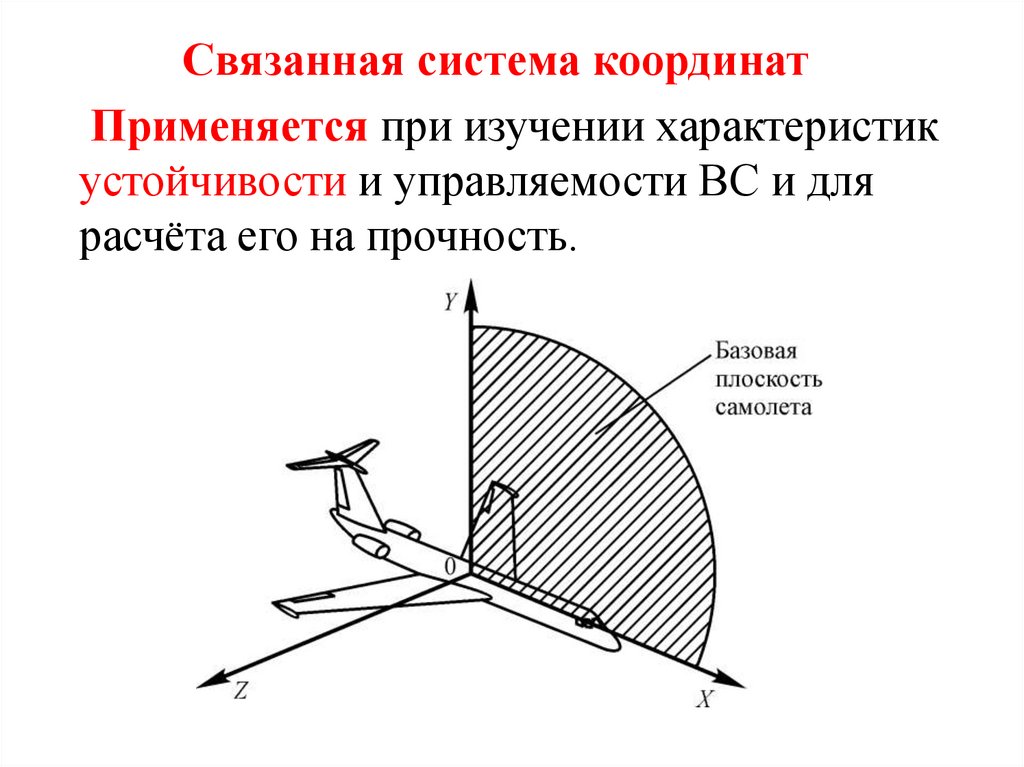
Связанная система координатПрименяется при изучении характеристик
устойчивости и управляемости ВС и для
расчёта его на прочность.
21.
4.7 Аэродинамические силы и моменты и ихкоэффициенты
Положение ВС в потоке воздуха задаётся
углами атаки, скольжения и крена.
Угол атаки угол между продольной
осью самолета и проекцией вектора V
скорости потока на плоскость симметрии
самолёта.
Угол скольжения угол между
направлением вектора скорости потока V
и его проекцией на плоскостью
симметрии самолёта.
22.
Положение ВС в пространствеПоложение самолёта в пространстве
характеризуется углами рысканья, тангажа, крена.
Угол рысканья угол между проекцией
траектории (осью OXg в земной системе координат)
и проекцией продольной оси самолёта ОХ на
горизонтальную плоскость.
Угол тангажа угол между продольной осью
самолёта и горизонтом.
Угол крена угол между вертикальной
плоскостью, проходящей через продольную ось
самолета, и нормальной плоскостью
самолета(XOY).
23.
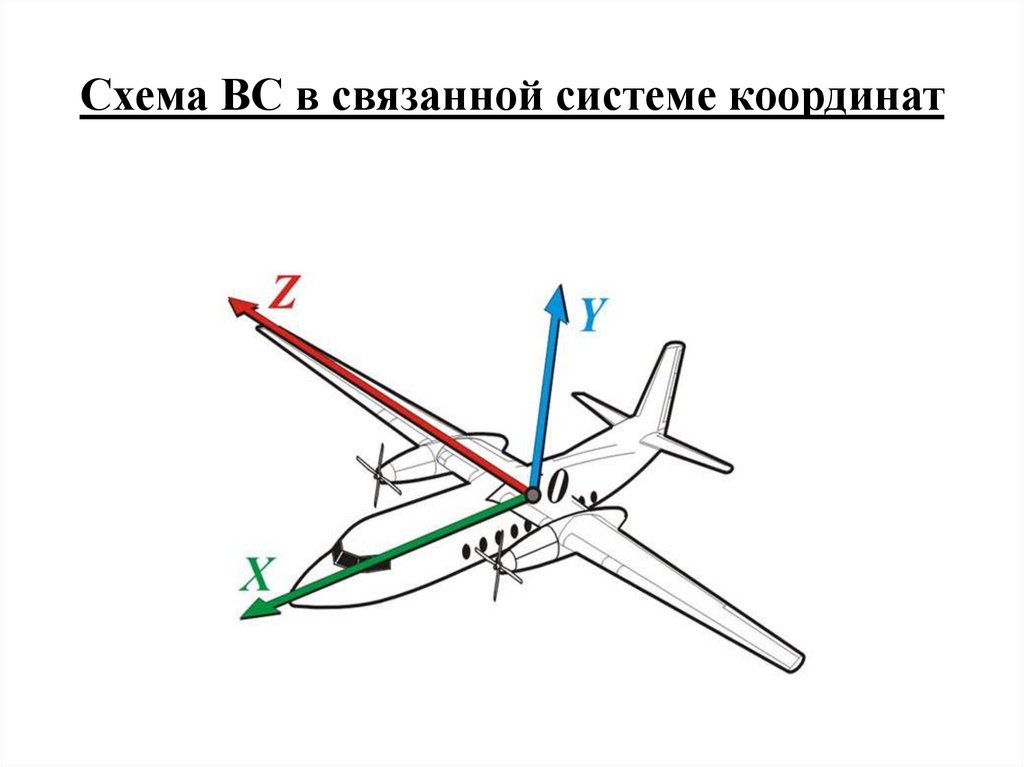
Схема ВС в связанной системе координат24.
Силы и моменты а в скоростнойсистеме координат
Xa — сила лобового сопротивления;
Ya — подъемная сила;
Za — боковая сила;
Мх a — момент крена;
My a — момент рысканья (путевой
момент);
Mz a — момент тангажа (продольный
момент) пикирующий и кабрирующий.
25.
Представление аэродинамических сил,18
моментов и их коэффициентов в связанной
системе координат
.
26.
4.8 Коэффициент давления20
4.8 Коэффициент давления
Определение:
Коэффициентом давления называется отношение
разности полного и статического давления к
величине скоростного напора потока, омывающего
исследуемое аэродинамическое тело.
Формула коэффициента давления Сp
Область применения:
pн* - pст
p* - pст
Cp =
2
2
ρV
ρV 2
2
построение эпюр;
расчёт аэродинамических сил и моментов.





















 physics
physics








