Similar presentations:
Методы расчета и анализа нелинейных цепей. Лекция 2
1. Лекция 2 Методы расчета и анализа нелинейных цепей
1 Графический метод расчета нелинейныхцепей.
2 Расчет нелинейных цепей методом двух
узлов и методом эквивалентного генератора
3 Аналитические методы расчета нелинейных
цепей.
Литература: Кононенко, В.В. Электротехника и
электроника: учеб. пособие для вузов / В. В.
Кононенко и др. ; под ред. В. В. Кононенко. - 5-е
изд. - Ростов н/Д : Феникс, 2008. – с. 98-109.
2. Методы расчета нелинейных электрических цепей
• Графические, в виде геометрических построений наоснове заданных характеристик;
• Аналитические, основанные на том, что
характеристика нелинейного элемента выражается
приближенной аналитической функцией;
• Графо-аналитические, линейная часть цепи
описывается аналитически, а характеристики НЭ
представлены в виде графиков;
• Итерационные (численные), основаны на
приближенных способах решения алгебраических и
дифференциальных уравнений.
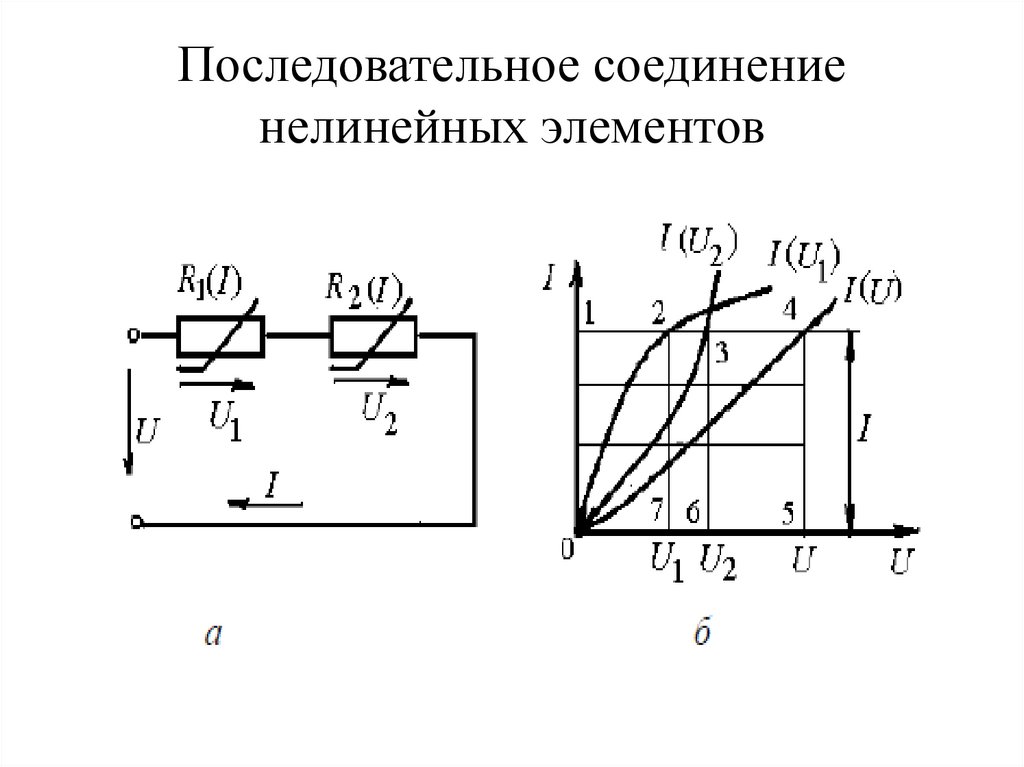
3. Последовательное соединение нелинейных элементов
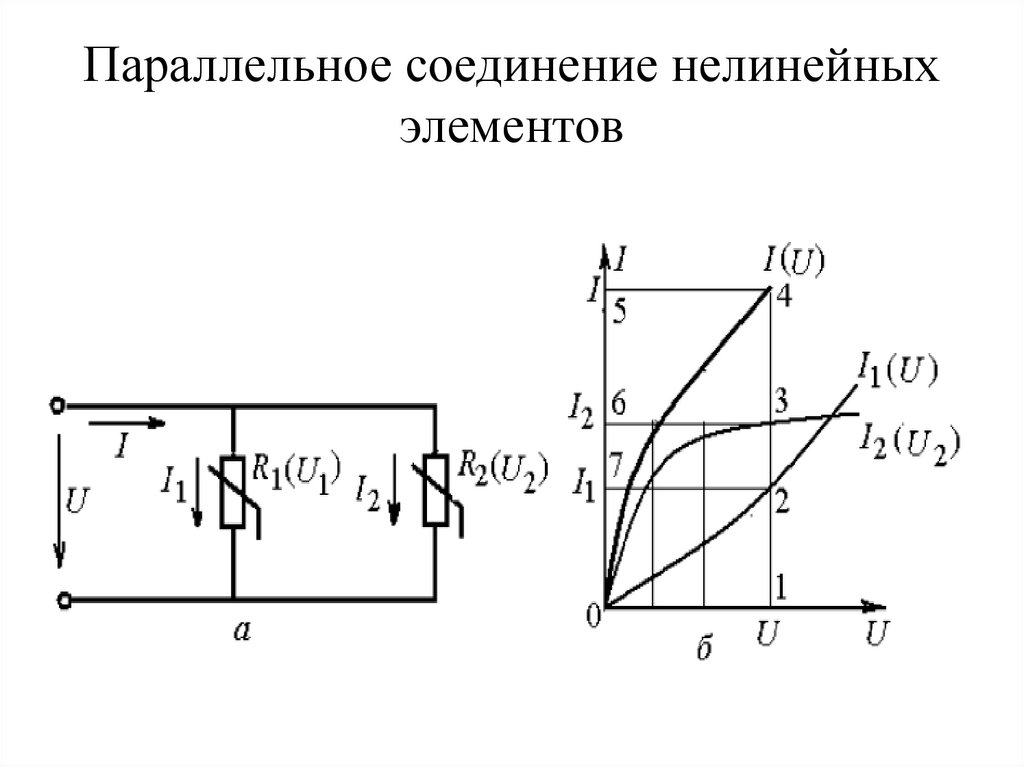
4. Параллельное соединение нелинейных элементов
5. Смешанное соединение нелинейных элементов
Расчет таких цепей производится в следующей последовательности:• исходная схема сводится к цепи с последовательным соединением
резисторов, для чего строится результирующая ВАХ параллельно
соединенных элементов;
• проводится расчет полученной схемы с последовательным соединением
резистивных элементов, на основании которого затем определяются токи в
исходных параллельных ветвях.
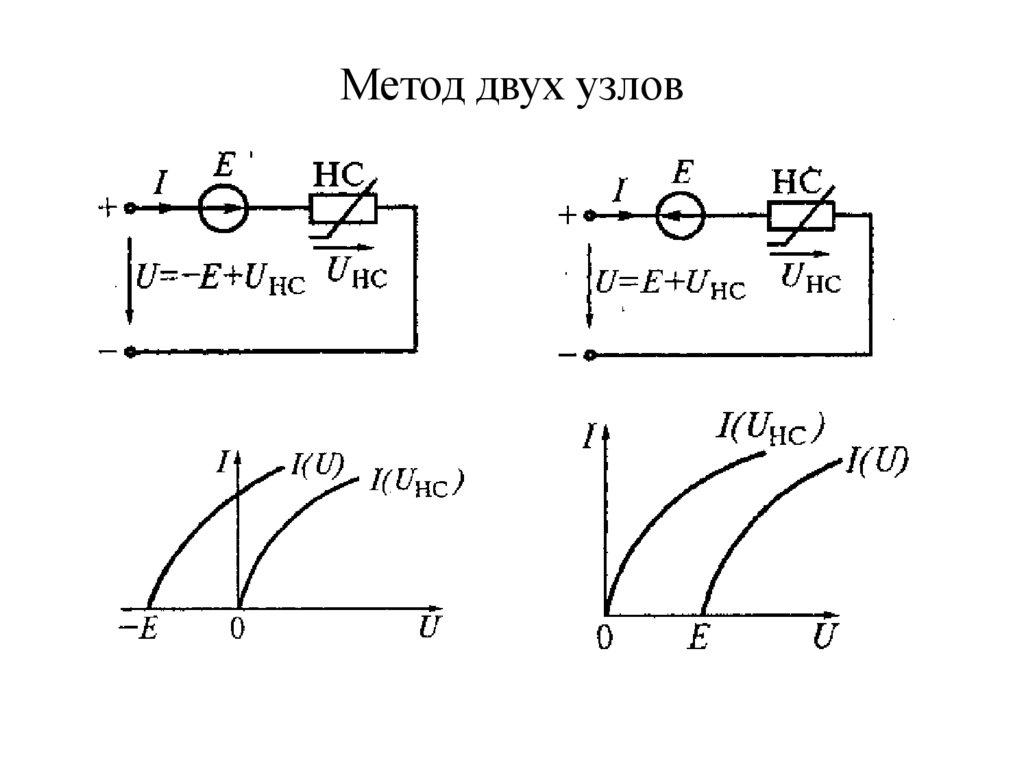
6. Метод двух узлов
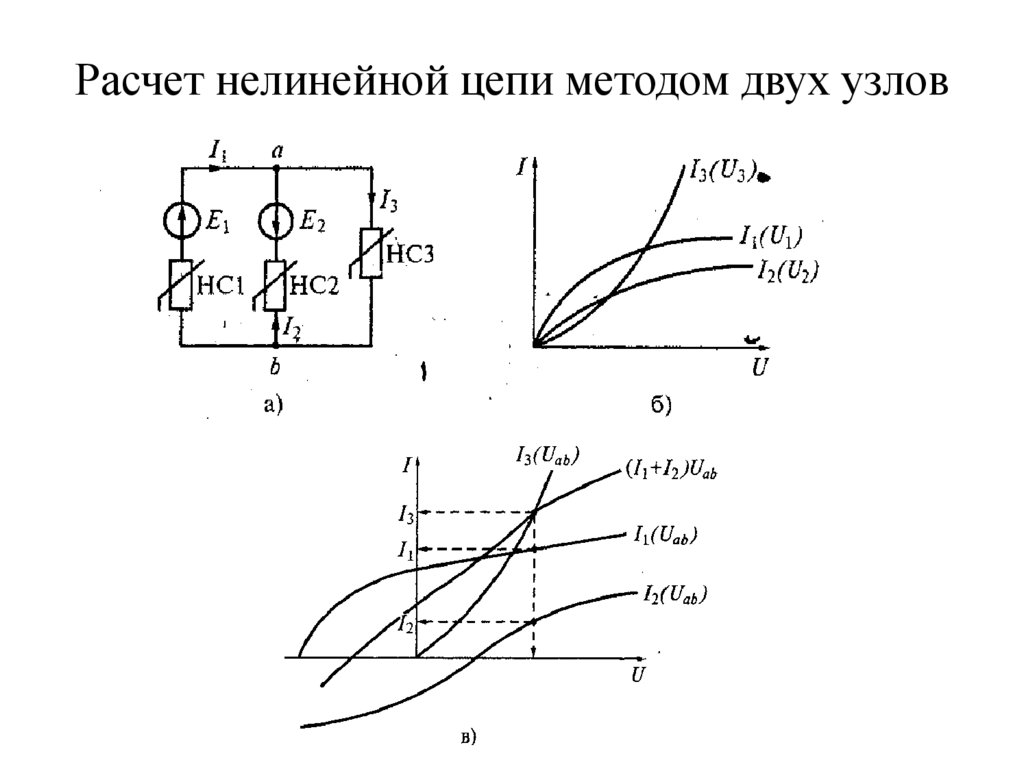
7. Расчет нелинейной цепи методом двух узлов
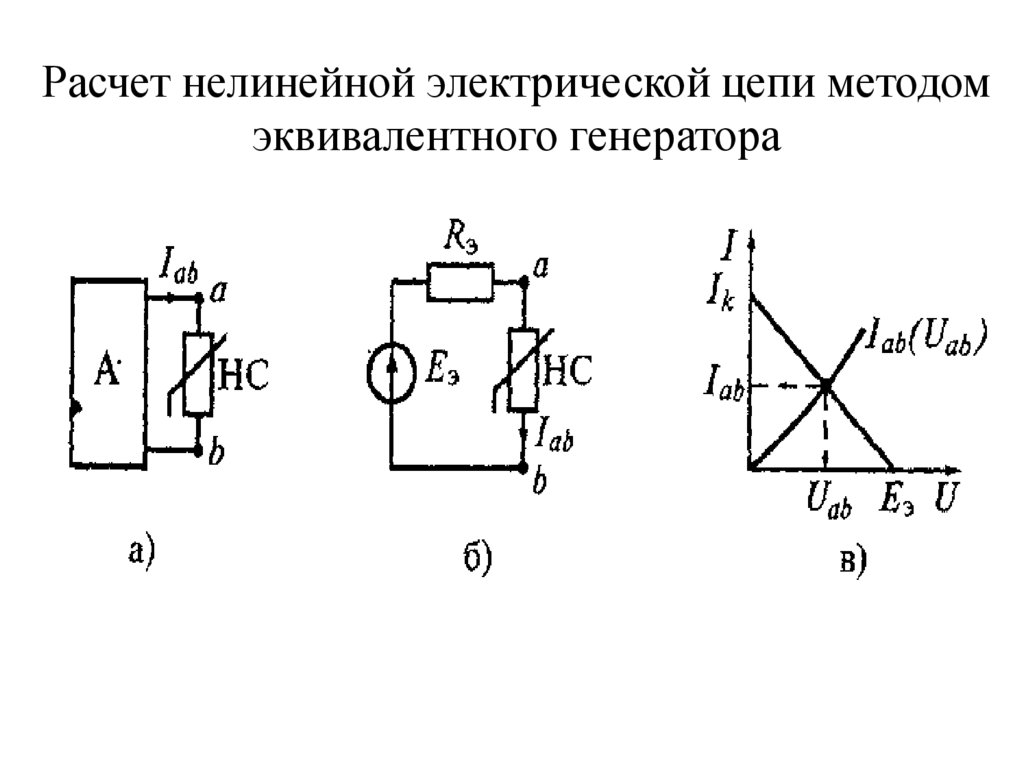
8. Расчет нелинейной электрической цепи методом эквивалентного генератора
9. Аналитические методы
К аналитическим методам относятся:• метод аппроксимации, когда ВАХ
нелинейного элемента заменяется
аналитическим выражением;
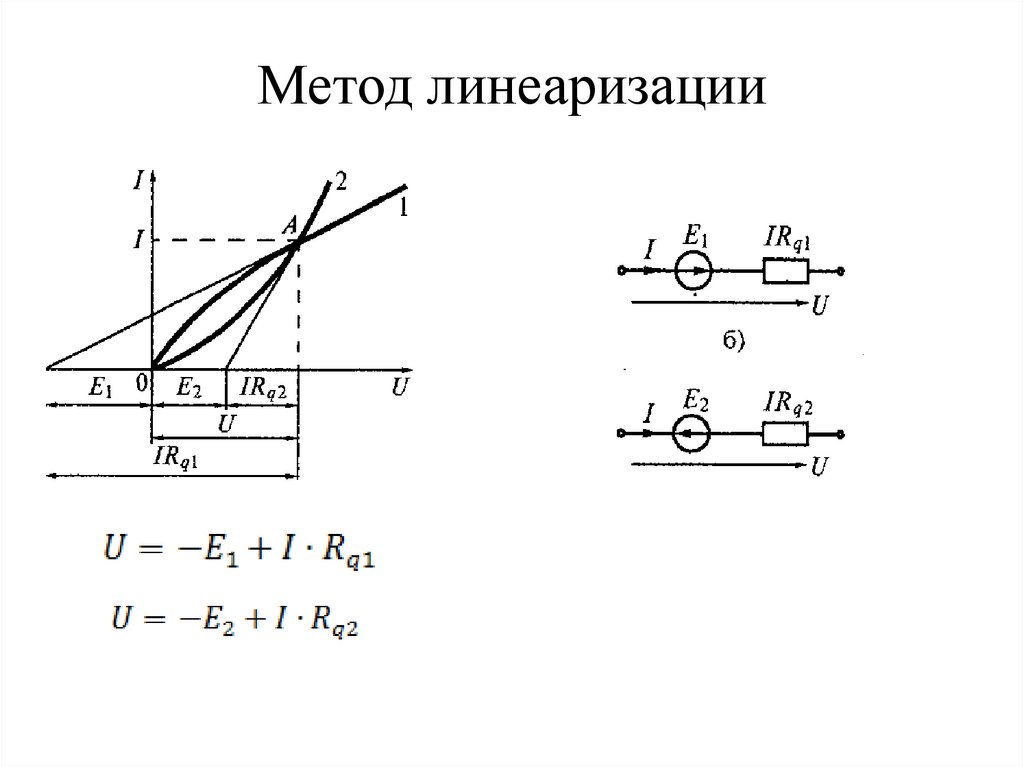
• метод линеаризации, когда НЗ заменяется
эквивалентной схемой, состоящего из
источника ЭДС и линейного элемента.
10.
Для целей аппроксимации чаще всего применяются следующие функции:1. Степенной полином в виде
n
y A0 A1 x A2 x ... An x An x n
2
n
n 0
2. Экспоненциальный полином
y A0 A1 e
1 x
A2 e
2 x
... An e
n x
n
А0 An е n x
n 0
3. Тригонометрический полином
y A0 A1 sin x 1 A2 sin 2 x 2 ... An sin nx n
n
А0 An sin nx n .
n 0
4. Дробно-степенная функция
y A x
где – дробное число.
11. Метод аппроксимации
Задача аппроксимации решается в два этапа:1) выбирают подходящую структуру аппроксимирующей
функции;
2) рассчитывают неизвестные коэффициенты, входящие в
аппроксимирующую функцию
- степенной полином






 physics
physics








