функция1

1. «Функции»

2.

Определение
Функциональной
зависимостью
(функцией) называют такую зависимость, для
которой указано правило, с помощью которого
для
каждого
значения
независимой
переменной (аргумента) можно найти
единственное значение зависимой переменной
(значение функции).
у=f(х)

3.

Множество X всех допустимых действительных
значений аргумента, при которых функция y = f (x)
определена, называется областью определения функции.
D(f)
Множество Y всех действительных значений , которые
принимает функция, называется областью значений
функции.
Е(f)

4.

Способы задания функций.
Табличный способ.
Графический способ
Аналитический способ
Словесный способ.

5.

Основные свойства функции.
1. Четность и нечетность
Функция называется четной, если – область определения
функции симметрична относительно нуля; – для любого х
из области определения f(-x) = f(x).
График четной функции симметричен относительно оси 0y.
Функция называется нечетной, если – область определения
функции симметрична относительно нуля; – для любого х
из области определения f(-x) = –f(x).
График нечетной функции симметричен относительно
начала координат

6.

2. Периодичность.
Функция f(x) называется периодической с
периодом Т, если для любого х из области
определения f(x) = f(x+Т) = f(x-Т). График
периодической функции состоит из
неограниченно повторяющихся
одинаковых фрагментов.

7.

3. Монотонность (возрастание, убывание).
Функция f(x) возрастает на множестве Р ,
если для любых x и x из этого множества,
таких, что x < x выполнено неравенство
f(x )< f(x ). Функция f(x) убывает на
множестве Р, если для любых x и x из этого
множества, таких, что x < x выполнено
неравенство f(x ) > f(x ).
1
1
1
2
2
2
1
1
1
2
2
2

8.

4. Нули функции
Нулем функции y = f(x) называется такое
значение аргумента х , при котором функция
обращается в нуль: f(x) = 0.
5. Ограниченность. Функция называется
ограниченной, если существует такое
положительное число M, что |f ( x )|< M для всех
значений x . Если такого числа не существует, то
функция - неограниченная

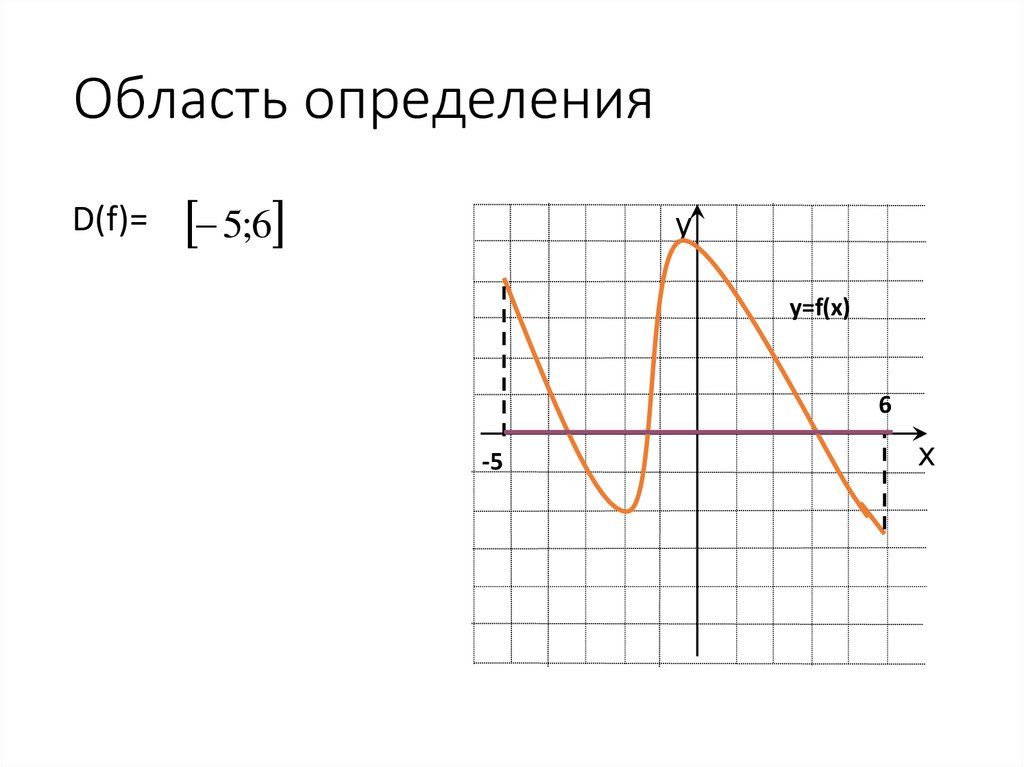
9. Область определения

D(f)=
5;6
у
y=f(x)
6
-5
х

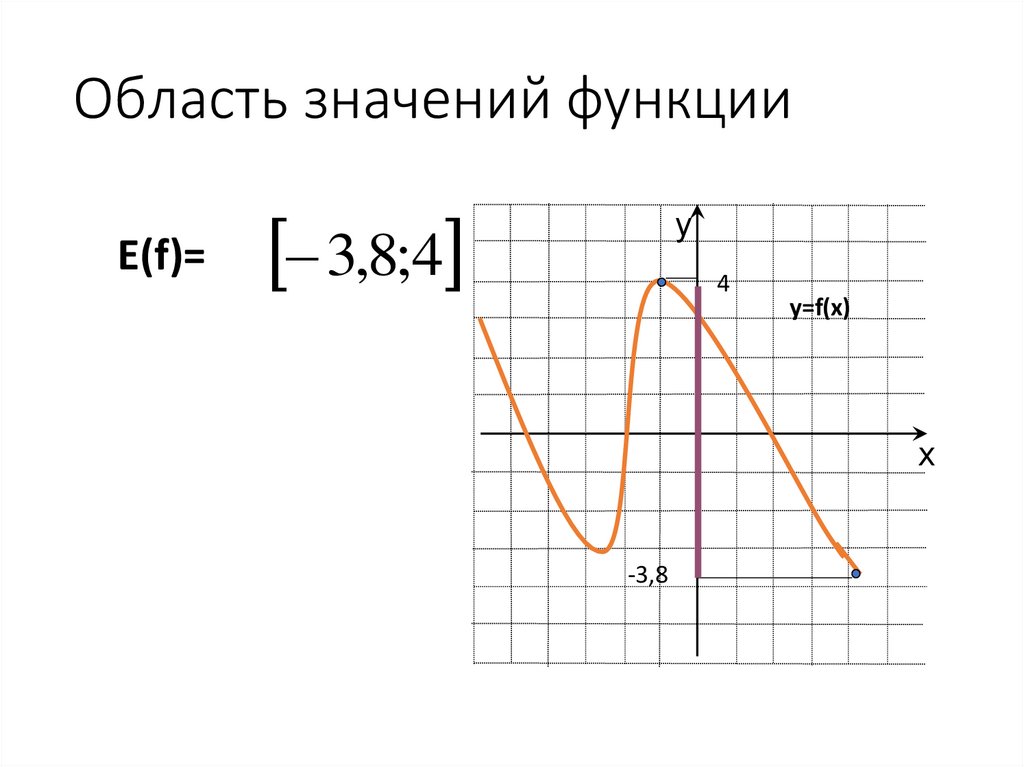
10. Область значений функции

Е(f)=
3,8;4
у
4
y=f(x)
х
-3,8

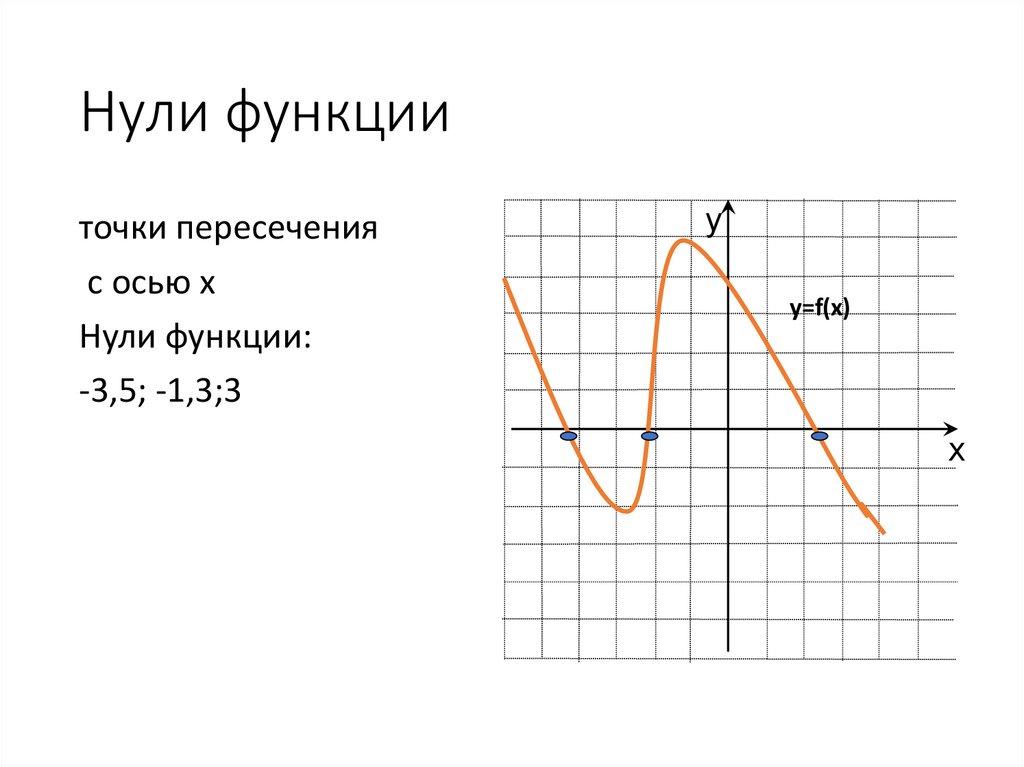
11. Нули функции

точки пересечения
с осью х
Нули функции:
-3,5; -1,3;3
у
y=f(x)
х

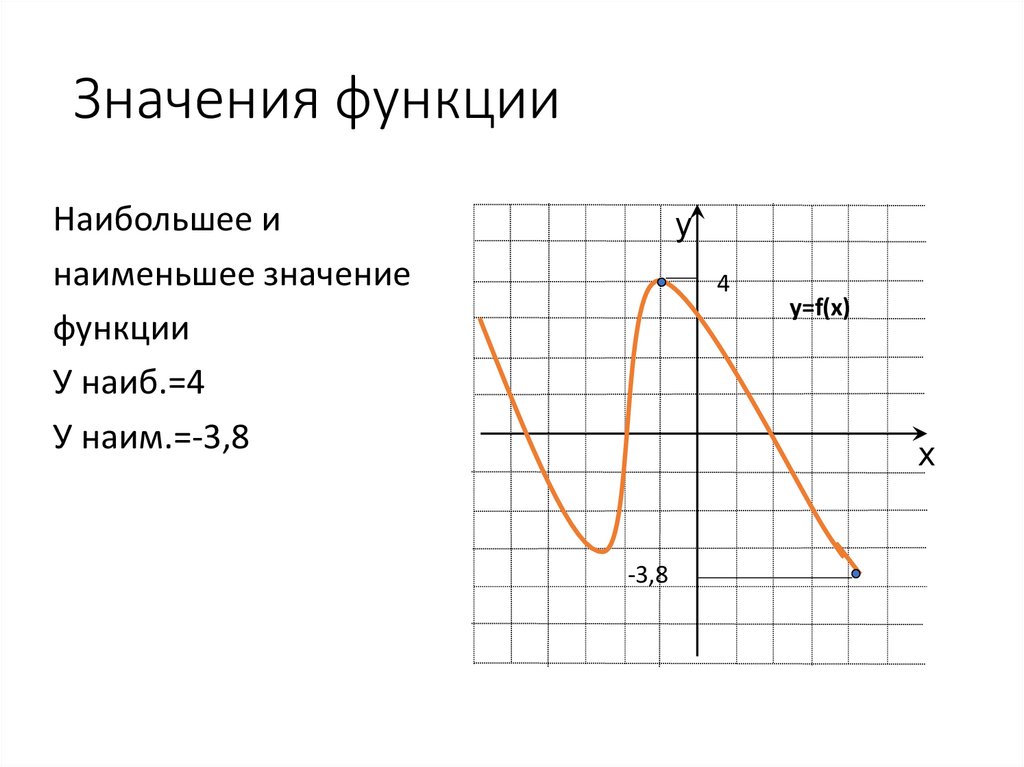
12. Значения функции

Наибольшее и
наименьшее значение
функции
У наиб.=4
У наим.=-3,8
у
4
y=f(x)
х
-3,8

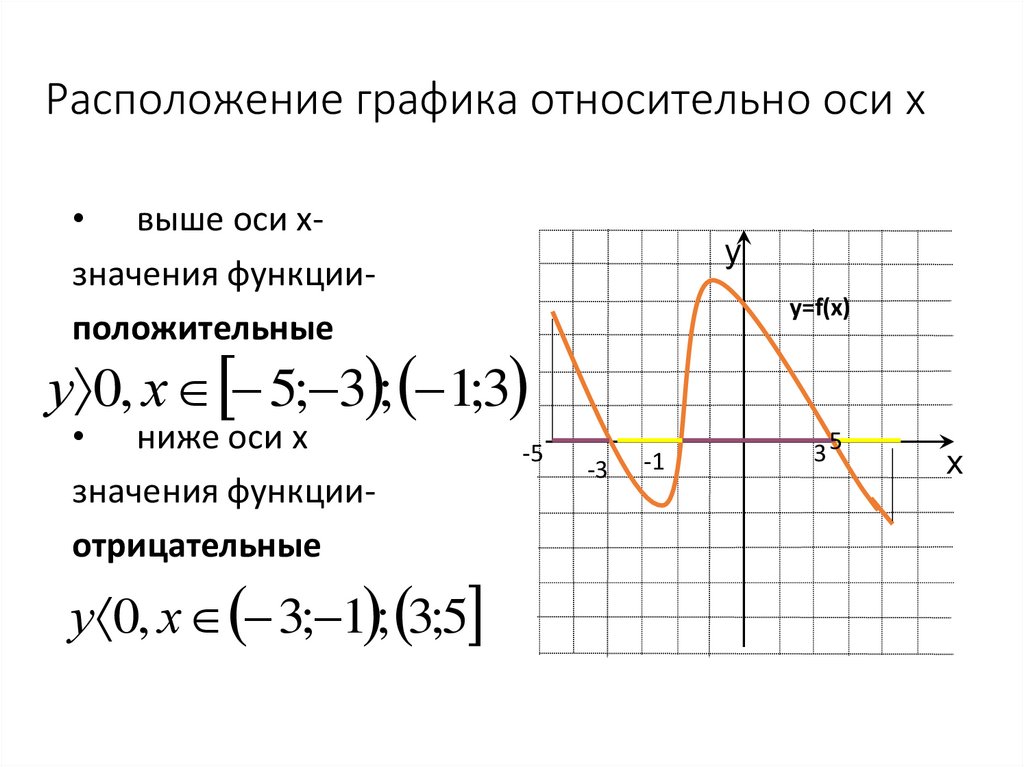
13. Расположение графика относительно оси х

• выше оси хзначения функцииположительные
у
y=f(x)
у 0, х 5; 3 ; 1;3
• ниже оси х
значения функцииотрицательные
у 0, х 3; 1 ; 3;5
-5
-3
-1
35
х

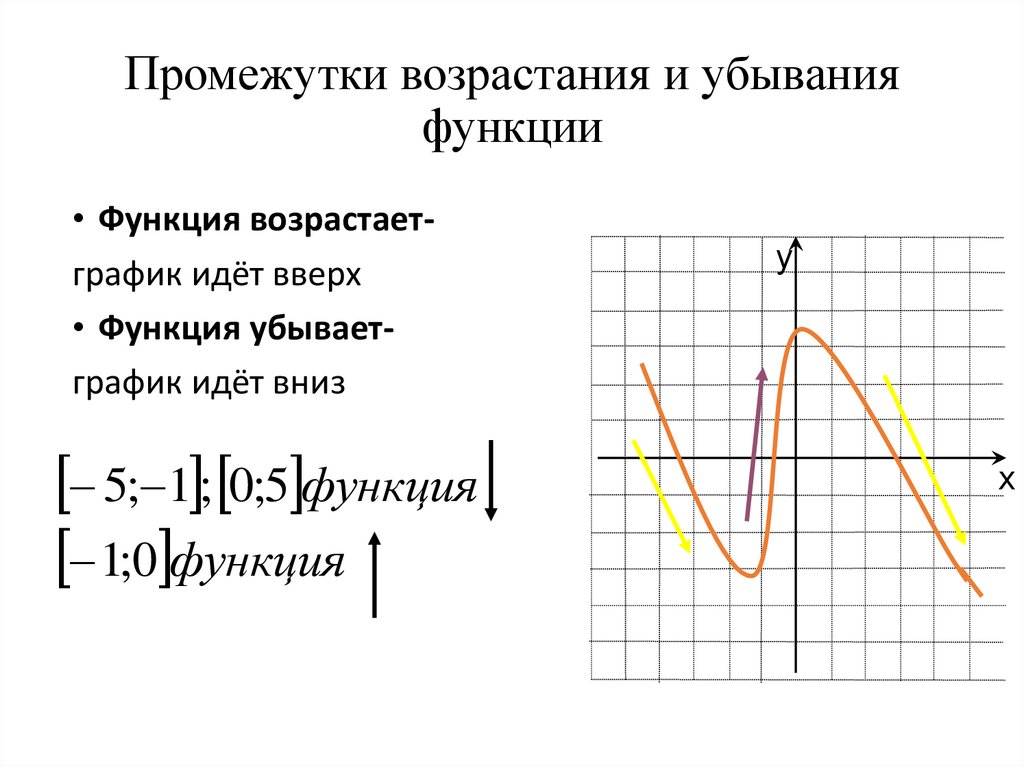
14. Промежутки возрастания и убывания функции

• Функция возрастаетграфик идёт вверх
• Функция убываетграфик идёт вниз
5; 1 ; 0;5 функция
1;0 функция
у
х

15.

Линейная функция
f (x) = kx + b.
D(f) = R,
E(f) = R.
График функции y = kx + b — прямая линия.
Функция монотонно возрастает при k > 0 и убывает при k < 0.
При b = 0 прямая линия проходит через начало координат, при
этом функция y = kx — нечетная.
Промежутки постоянного знака для функции y = kx зависят от
знака параметра k: k > 0, то y > 0 при x > 0; y < 0 при x < 0;
k < 0, то y > 0 при x < 0; y < 0 при x > 0.

16.

Свойства линейной функции
:
•Область определения
:
•Область значений
:
(если
),
(если
)
•Четность/нечетность:
1.если
, функция общего вида
2.если
, функция нечетная (функция вида
называется прямой
пропорциональностью)
3.если
, функция четная
4.если
, функция равна нулю, то есть одновременно и четная, и
нечетная
•Монотонность функции:
1.если
, то функция возрастает
2.если
, то функция убывает
3.если
, то функция постоянна (параллельна оси абсцисс)
Взаимное размещение графиков линейных функций:
1.если
, графики функций
и
пересекаются в
одной точке
2.если
,
, графики
функций
и
являются параллельными прямыми
3.если
,
, графики
функций
и
прямые совпадают

17.

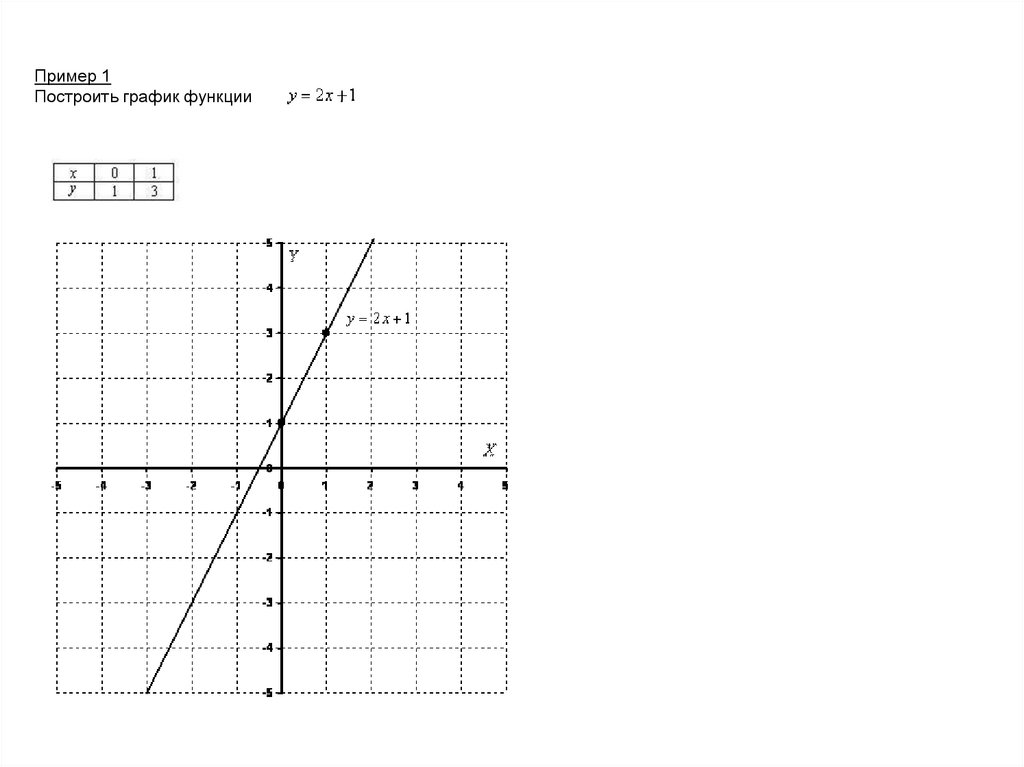
Пример 1
Построить график функции
.