Решение уравнений с модулем. Метод интервалов

1.

24.09.2025
Тема урока:

2.

Алгоритм решения уравнения с модулем
Дано неравенство:
│х + а│+│х + b│+│х + c│+ х + m >(<) d,
где a, b, c, d, m − заданные числа и пусть a < b < c.
1. Решаем каждое из уравнений:
х + а = 0,
х = − a;
х + b = 0,
x = − b;
х + с = 0,
x = − с.
получаем
2. Разбиваем числовую прямую на промежутки
)[
−с
)[
−b
)[
−a
3. Раскрываем модули и решаем уравнение на
каждом промежутке.
4. Записываем ответ.
х

3.

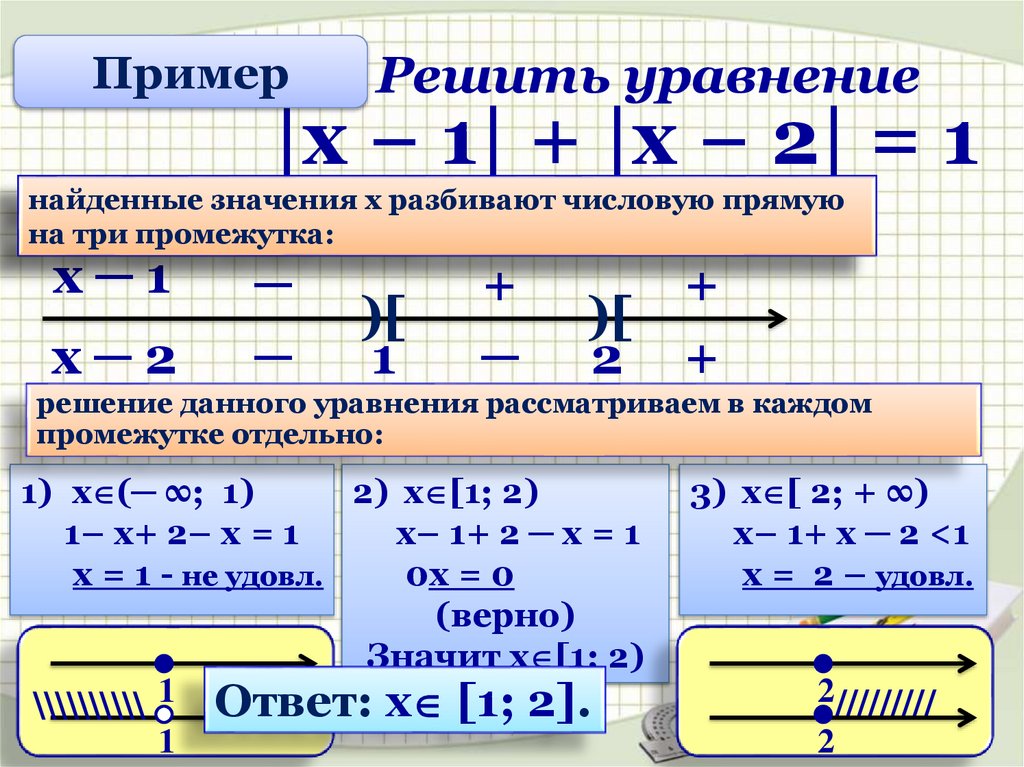
Пример
Решить уравнение
|х − 1| + |х − 2| = 1
найденные
Найдём
корни(нули)
значения каждого
х разбивают
выражения,
числовую прямую
содержащего
на
три промежутка:
знак модуля:
х─1
х─2
─
─
)[
1
+
─
+
)[
2 +
решение данного уравнения рассматриваем в каждом
промежутке отдельно:
1) х (─ ∞; 1)
2) х [1; 2)
1– х+ 2– х = 1
х– 1+ 2 ─ х = 1
х = 1 - не удовл.
0х = 0
(верно)
Значит х [1; 2)
\\\\\\\\\\ 1 Ответ: х [1; 2].
1
3) х [ 2; + ∞)
х– 1+ х ─ 2 <1
х = 2 – удовл.
2/////////
2

4.

Решить уравнения
|5– 2х|+|х+ 3|= 2–3х.
|х|– 2∙|х+1|+3∙|х+2|= 0