2-тема. Логика составных высказываний (The Logic of Compound Statements)

1.

2-тема. Логика составных высказываний
(The Logic of Compound Statements).
План:Логические связки.Сложные
высказывания.Логические
выражения.Логические операции над
выражениями.Операции : отрицание (NOT),
конъюкция (AND), дизъюнкция(OR),
исключающее ИЛИ (XOR), импликация (If p
then q condition),эквиваленция (XNOR), штрих
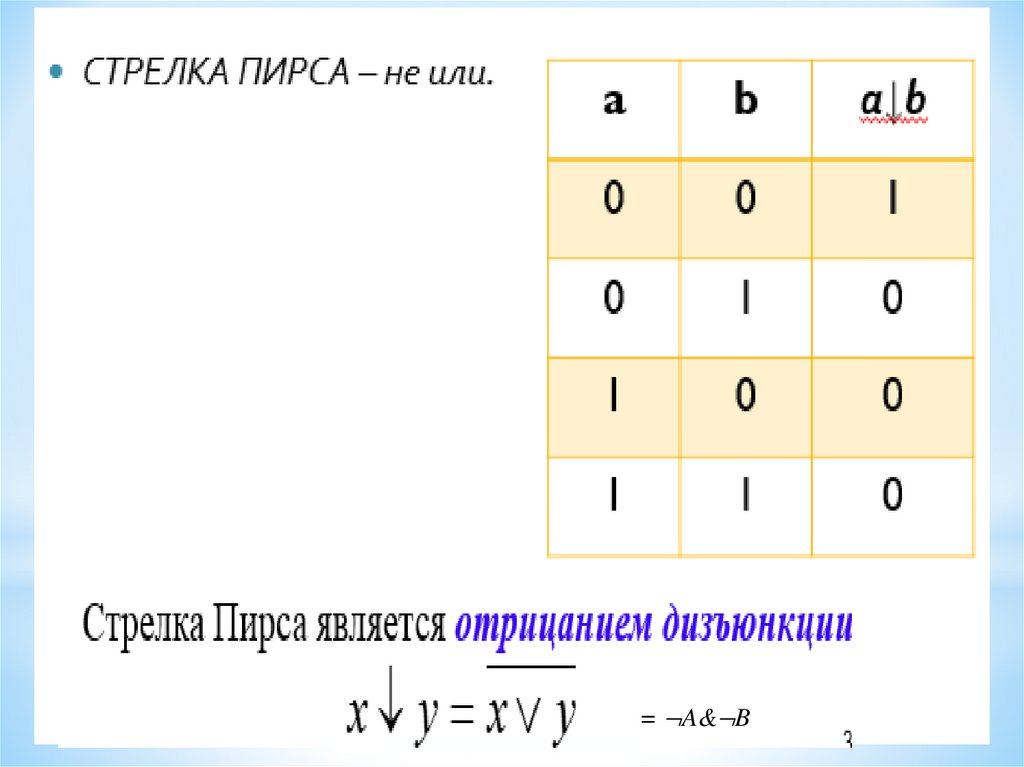
Шеффера (NAND), стрелка Пирса(NOR) и их
таблиы истинности (true/false).
Создание таблицы истинности для логических
выражений (trouth table).

2.

*Высказывание-это утверждение или
повествовательное предложение какого-либо
языка, о содержание которого можно сказать,
истинно оно или ложно.(т.е.говорят,что оно имеет
значение истинности: может быть истинным, то
обозначается буквой И или ложным ,то - Л )
*( в дальнейшем мы дадим более строгое
определение!)

3.

Высказывание называется простым,
если никакая его часть сама не
является высказыванием.
Высказывание, состоящие из
простых высказываний, называется
сложным или составным.

4.

Основные логические связки это связки: и, или, не, если … то…,
которые в логике высказываний имеют специальные названия и
обозначения. Иногда к ним добавляют еще две связки либо …, либо
…(или …, или …); если, и только если (тогда и только тогда).
*Используя их, можно построить новые высказывания, называемые
«сложные или составные высказывания».

5.

Если мы рассматриваем высказывания и операции над ними, то
можно говорит об «алгебре логики».
В формулах алгебры логики переменные – это высказывания.
Они принимают только 2 значения – ложь и истина, которые
обозначаются либо Л и И, либо false и true,
либо 0 и 1.
Каждая формула задает логическую функцию, которая сама
может принимать только два логических значения.
*
Если высказывание А истинно, то можно писать А=1;
если высказывание А ложно, то А=0

6.

Из простых высказываний можно получать более сложные
(составные высказывания) с помощью так называемых
логических связок или логических операций .
Основные логические операции
1. Из высказывания А можно получить высказывание
"неверно, что А” ( можно просто «не А» ).
Например, пусть A="2·2=5", тогда получаем высказывание
"неверно, что А".
ОПРЕДЕЛЕНИЕ 1.Высказывание "неверно, что А" называется
отрицанием А и обозначается
(или ~ A, или
).
Задается действие отрицания с помощью таблицы
истинности:

7.

2. Из высказываний А, В можно образовать высказывание
"А и В".
Например,
"2·2=4 и 5+3=9"
Поскольку результат конъюнкции похож на результат
обычного умножения чисел 0 и 1, эту операцию часто
называют логическим умножением.

8.

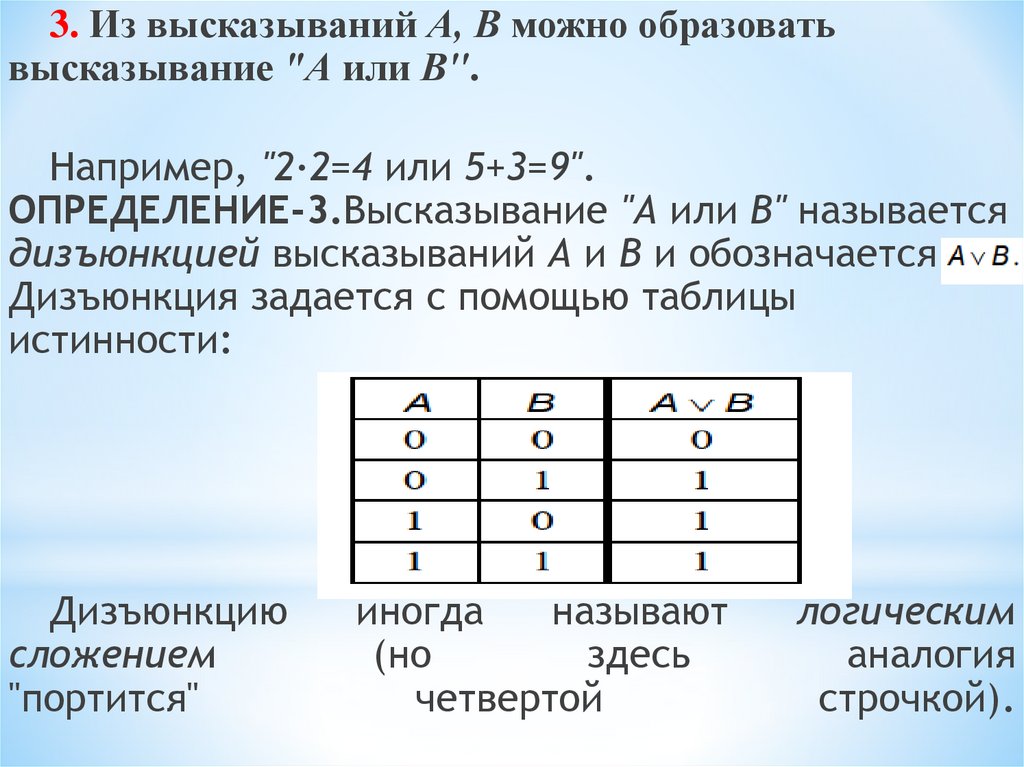
3. Из высказываний А, В можно образовать
высказывание "А или В".
Например, "2·2=4 или 5+3=9".
ОПРЕДЕЛЕНИЕ-3.Высказывание "А или В" называется
дизъюнкцией высказываний А и В и обозначается
Дизъюнкция задается с помощью таблицы
истинности:
Дизъюнкцию
сложением
"портится"
иногда
называют
(но
здесь
четвертой
логическим
аналогия
строчкой).

9.

4. Из высказываний А, В можно образовать
следующее высказывание: "А тогда и только тогда,
когда В".
Например, треугольник является
равносторонним тогда и только тогда, когда все его
углы равны между собой.
Синонимами служат фразы:
-"А в том и только в том случае, когда В”;
-"А необходимо и достаточно для того, чтобы
выполнялось В”;
-"А равносильно В”;
-"А эквивалентно B".
ОПРЕДЕЛЕНИЕ-4. Высказывание "А равносильно В"
называется эквивалентностью высказываний А и В
и обозначается

10.

Эквивалентность(ЭКВИВАЛЕНЦИЯ) задается таблицей истинности:
5. Из высказываний А и В можно образовать так называемое
условное высказывание "если А, то В".
Например, если две прямые параллельны третьей, то они
параллельны между собой.
Синонимами служат следующие фразы:
-"из А следует В“;
- "В является следствием А“;
- "А влечет В“;
- "А достаточное условие для В";
- "В необходимое условие для А" и т.п.

11.

* При определении истинностного значения условного
высказывания ,необходимо различать фактическую истину и
логическую.
* Пример. Пусть Р — (ложное) высказывание 1 = 5, Q —
(тоже ложное) высказывание 3 = 7 и R — (истинное) утверждение
4 = 4. Показать, что условные высказывания: 1)«если Р, то Q» и
2) «если Р, то R », — оба истинны.
Решение. 1)Если 1 = 5, то, прибавляя 2 к обеим частям равенства,
мы получим, что 3 = 7. Следовательно, высказывание «если Р, то
Q» справедливо.
2) Вычтем теперь из обеих частей равенства 1 = 5 число

12.

ОПРЕДЕЛЕНИЕ -5.Высказывание "если А, то В" называется
импликацией высказываний А и В и обозначается
.
В этой ситуации высказывание А называется
(пред)посылкой, а В – заключением.
Задается импликация cл. таблицей истинности:
Замечания для запоминания:

13.

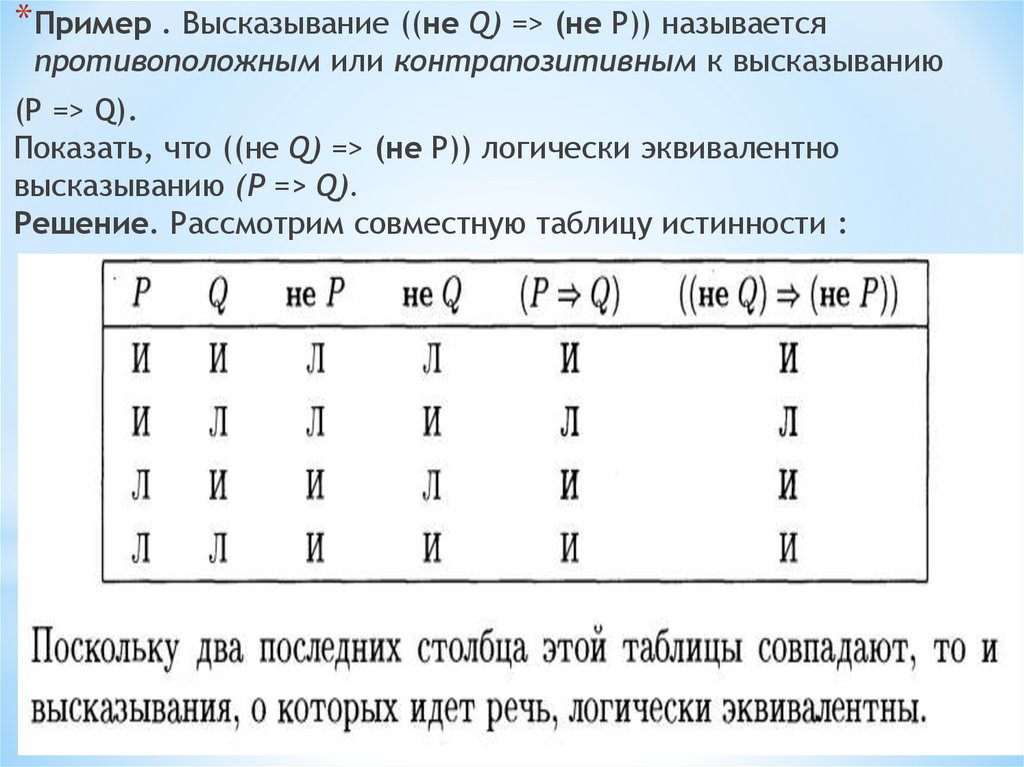
* Пример . Высказывание ((не Q) => (не Р)) называется
противоположным или контрапозитивным к высказыванию
(Р => Q).
Показать, что ((не Q) => (не Р)) логически эквивалентно
высказыванию (Р => Q).
Решение. Рассмотрим совместную таблицу истинности :

14.

6.
= A B

15.

* Свойства для операции штрих Шеффера:

16.

7.
= A& B

17.

* Свойства для операции стрелка Пирса: