5) Эквивалентность (логическая равнозначность)

Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z)

Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Закон коммутативности (переместительный)

Закон дистрибутивности (распределительный)

Множество. Мощность множества. Операции над множествами

2.90M

Category:

informatics

Логика как наука. Высказывания

1. Логика как наука. Высказывания

2. Логика как наука

Слово «логика» происходит от греческого logos, что
означает «мысль», «слово», «разум»,
«закономерность».
Логика как наука изучает логические формы,
операции с ними и законы мышления.

3. Алгебра логики

Алгебра логики — это математический аппарат, с
помощью которого записывают, вычисляют,
упрощают и преобразовывают логические
высказывания.
Логическое высказывание (суждение) — это
любое
повествовательное
предложение,
в
отношении которого можно однозначно сказать,
истинно оно или ложно (обозначаемые,
соответственно, "1" и "0" ).

4.

Высказывательной формой называется
логическое высказывание, в котором один из
объектов заменён переменной. При
подстановке вместо переменной какого-либо
значения высказывательная форма
превращается в высказывание.
Пример: «В городе Х идёт дождь.» —
высказывательная форма.
«В городе Архангельске идёт дождь.» —
высказывание.

5.

Умозаключение – это форма мышления,
посредством которой из одного или
нескольких
суждений,
называемых
посылками, по определенным правилам
логического вывода получается новое
истинное
суждение,
называемое
заключением.

6.

Посылка: при выполнении всех заданий
верно учащийся получает оценку «5».
Посылка: нужно выполнить 10 заданий.
Заключение: чтобы получить «5», надо верно
выполнить 10 заданий.

7.

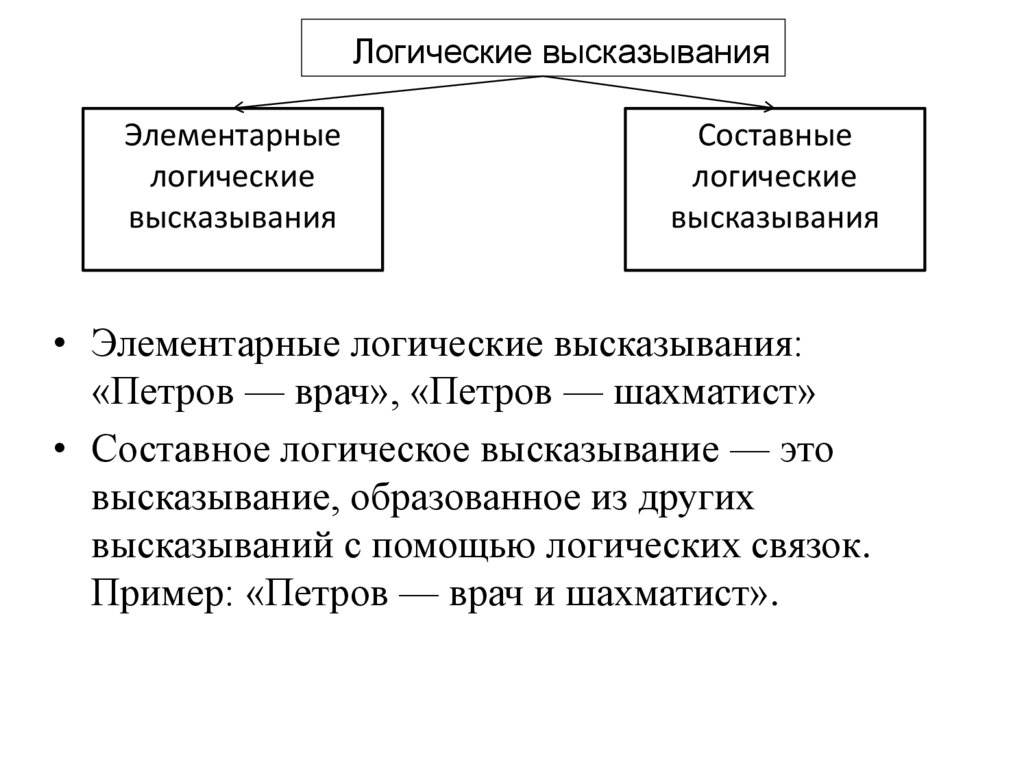
Логические высказывания
Элементарные
логические
высказывания
Составные
логические
высказывания
• Элементарные логические высказывания:
«Петров — врач», «Петров — шахматист»
• Составное логическое высказывание — это
высказывание, образованное из других
высказываний с помощью логических связок.
Пример: «Петров — врач и шахматист».

8.

Логическая связка — это любая логическая
операция над высказыванием.
Например, употребляемые в обычной речи
слова и словосочетания «не», «и», «или»,
«если… , то», «тогда и только
тогда» являются логическими связками

9. Этапы развития логики

1 этап – Аристотель (384-322г. до н. э.)
Он пытался найти ответ на вопрос: "Как мы
рассуждаем".
Возникла формальная логика – наука о законах и
формах мышления.
2 этап – появление математической или
символической логики (Г. В. Лейбниц (1646-1716)).
Он сделал попытку заменить простые рассуждения
действиями со знаками.

10. Этапы развития логики

3 этап - (Джордж Буль (1815-1864))
В его работах логика приобрела свой алфавит,
орфографию и грамматику.
Начальный раздел математической логики
назвали алгеброй логики или Булевой
алгеброй.
Джон фон Нейман (1903 — 1957) в основу
работы компьютера заложил математический
аппарат, использующий законы
математической логики.

11. Простые логические операции

12. Обозначение высказываний

Пусть А - высказывание "Тимур поедет
летом на море",
В — высказывание "Тимур летом
отправится в горы".
Тогда составное высказывание "Тимур летом
побывает и на море, и в горах" можно
кратко записать как А и В.
Здесь "и" — логическая связка, А, В —
логические переменные, которые могут
принимать только два значения "истина" или "ложь", обозначаемые,
соответственно, "1" и "0".

13. Таблицы истинности (ТИ)

Таблица истинности логической
формулы выражает соответствие
между всевозможными наборами
значений переменных и значениями
формулы.

14. 1) Отрицание - инверсия

Отрицанием Ā некоторого высказывания А называется
такое высказывание, которое истинно, когда А ложно, и
ложно, когда А истинно.
(Отрицание лжи есть истина, отрицание истины есть ложь)

15. 1) Отрицание - инверсия

16. 2) Конъюнкция - логическое умножение

Конъюнкцией двух высказываний А и В
называется такое новое высказывание, которое
истинно тогда и только тогда, когда истинны оба
высказывания А и В.
Обозначения
A B A B A& B

17. 2) Конъюнкция - логическое умножение

18.

Определение конъюнкции 2-х высказываний
распространяется на любое конечное число
составляющих:
конъюнкция А1 & A2 & A3 &...& An истинна
тогда и только тогда, когда истинны все
высказывания А1, A2, A3, ...An;
конъюнкция ложна, когда хотя бы одно из
этих высказываний ложно.

19. 3) Дизъюнкция - логическое сложение

Дизъюнкцией двух высказываний
называется такое новое
высказывание, которое истинно
тогда и только тогда, когда истинно
хотя бы одно из этих
высказываний.
Обозначения:
A B
A B

20. 3) Дизъюнкция - логическое сложение

21.

Определение дизъюнкции 2-х высказываний
распространяется на любое конечное число
составляющих:
дизъюнкция А1 v А2 v А3 v ... v Аn истинна тогда
и только тогда, когда истинно хотя бы одно из
высказываний А1, А2, А3, ..., Аn;
дизъюнкция ложна, если ложны все
высказывания.

22. 4) Импликация

Импликацией А => В называется
высказывание, которое ложно тогда и только
тогда, когда А истинно и В ложно.
Обозначения: →

23. 4) Импликация

Импликацией А => В называется
высказывание, которое ложно тогда и только
тогда, когда А истинно и В ложно.
Обозначения: →
A
B
А→В
1
1
1
1
0
0
0
1
1
0
0
1

24.

Утверждение:
«Если каждое слагаемое делится на 3, то и
сумма делится на 3» истинно.
Из высказывания «каждое слагаемое делится на
3» => высказывание «сумма делится на 3».

25.

Утверждение:
«Если каждое слагаемое делится на 3, то и сумма
делится на 3» истинно.
Из высказывания «каждое слагаемое делится на 3»
=> высказывание «сумма делится на 3».
Слагаемые числа:
6 и 9 => истинны посылка и заключение => истинно
все утверждение;
4 и 5 => посылка ложная, а заключение истинно;
4 и 7 => и посылка и заключение ложны.

26. 5) Эквивалентность (логическая равнозначность)

Это сложное логическое выражение, которое
является истинным тогда и только тогда, когда
оба простых логических выражения имеют
одинаковую истинность.
Обозначение: ≡; ↔.

27. 5) Эквивалентность (логическая равнозначность)

Это сложное логическое выражение, которое
является истинным тогда и только тогда, когда
оба простых логических выражения имеют
одинаковую истинность.
Обозначение: ≡; ↔.
A
B
A≡B
0
0
1
0
1
0
1
0
0
1
1
1

28.

Высказывания эквивалентны (равносильны),
когда их значения истинности одинаковы,
например:
«Железо тяжелое» и «Пух легкий»

29.

Высказывания эквивалентны (равносильны),
когда их значения истинности одинаковы,
например:
«Железо тяжелое» и «Пух легкий»
«Железо легкое» и «Пух тяжелый»

30. Порядок выполнения логических операций

1) отрицание (не);
2) конъюнкция (и);
3) дизъюнкция (или)
4) Импликация
5) Эквивалентность

31. Порядок выполнения логических операций

1) отрицание (не);
2) конъюнкция (и);
3) дизъюнкция (или)
4) Импликация
5) Эквивалентность
6) сумма по модулю два,
7) стрелка Пирса
8) штрих Шефера

32.

Количество строк в ТИ находится по формуле
Q=2n, где n – количество переменных.

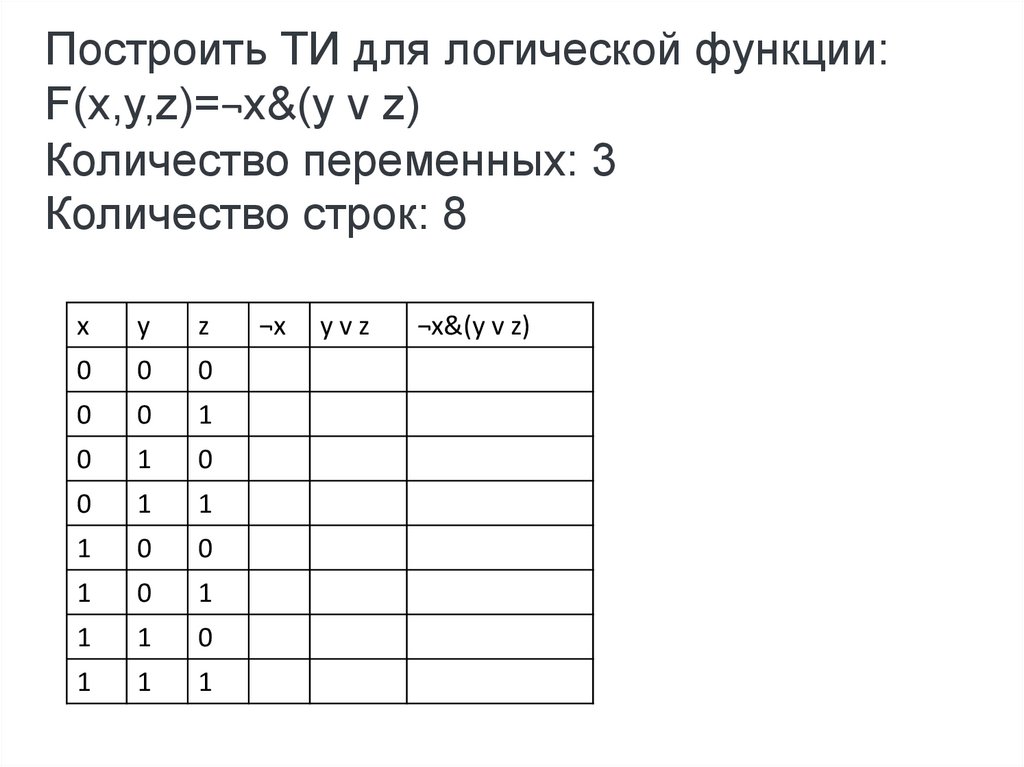
33. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z)

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)

34. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8

35. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8
x
y
z

36. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8
x
y
z
¬x

37. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8
x
y
z
¬x
yvz
¬x&(y v z)

38. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8
x
y
z
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
¬x
yvz
¬x&(y v z)

39. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8
x
y
z
¬x
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
0
yvz
¬x&(y v z)

40. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8
x
y
z
¬x
yvz
0
0
0
1
0
0
0
1
1
1
0
1
0
1
1
0
1
1
1
1
1
0
0
0
0
1
0
1
0
1
1
1
0
0
1
1
1
1
0
1
¬x&(y v z)

41. Построить ТИ для логической функции: F(x,y,z)=¬x&(y v z) Количество переменных: 3 Количество строк: 8

Построить ТИ для логической функции:
F(x,y,z)=¬x&(y v z)
Количество переменных: 3
Количество строк: 8
x
y
z
¬x
yvz
¬x&(y v z)
0
0
0
1
0
0
0
0
1
1
1
1
0
1
0
1
1
1
0
1
1
1
1
1
1
0
0
0
0
0
1
0
1
0
1
0
1
1
0
0
1
0
1
1
1
0
1
0

42. Основные законы алгебры логики

43. Закон идемпотентности (одинаковости)

A& A A
A A A

44.

Действия с константами
A &1 A
A 1 1
A&0 0
A 0 A

45. Закон двойного отрицания

A A
Закон исключенного третьего
A A 1
Закон противоречия
A& A 0

46. Закон коммутативности (переместительный)

x&y y&x
x y y x

47. Закон дистрибутивности (распределительный)

x & (y z) (x & y) (x & z)
x (y & z) (x y) & (x z)

48. Закон ассоциативности (сочетательный)

(x & y) & z x & (y & z)
(x y) z x (y z)

49. Закон де Моргана

x& y x y
x y x& y

50. Формулы склеивания

(A & B) (A & B) A
(A B) & (A B) A

51. Формулы поглощения

A ( A & B) A
A & ( A B) A
A ( A & B) A B
A & ( A B) A & B

52. Упростите выражение

( A A) B
A B A B
A B A

53. Множество. Мощность множества. Операции над множествами

54.

Множество обычно представляют как объект,
образованный за счет мысленного собирания
в единое целое каких-либо предметов, в том
числе, возможно, и самих множеств.

55.

• Объекты, входящие в множество,
называются элементами этого множества.

56.

57.

58.

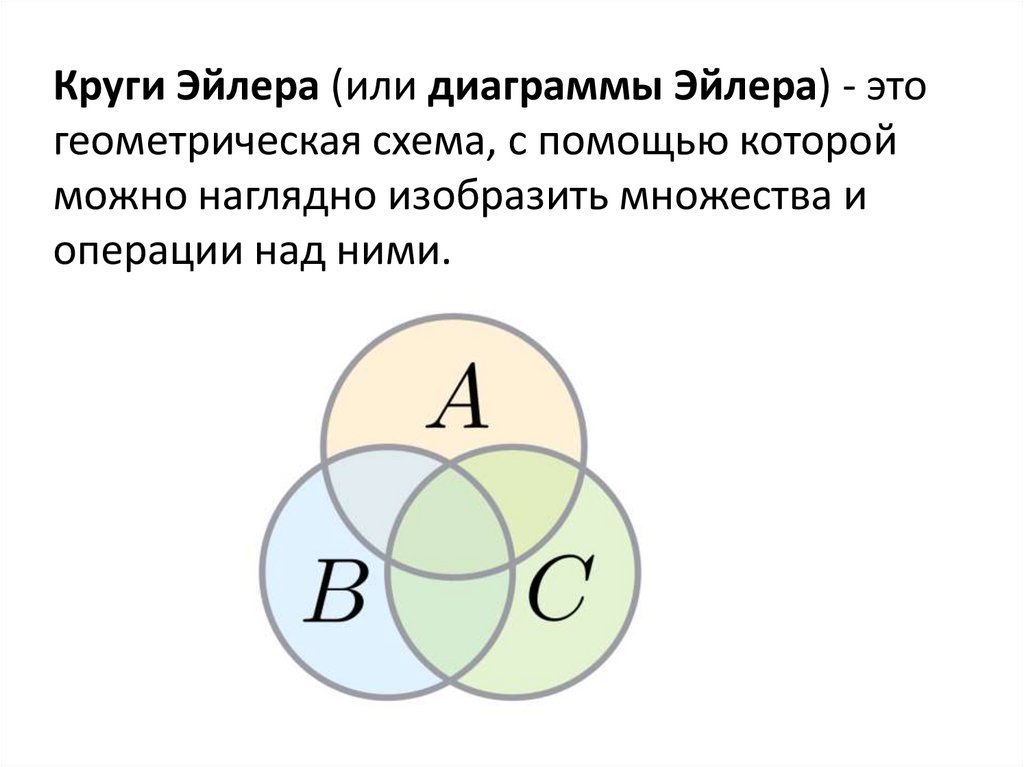
Круги Эйлера (или диаграммы Эйлера) - это
геометрическая схема, с помощью которой
можно наглядно изобразить множества и
операции над ними.