Ранг матрицы

1.

ЛИНЕЙНАЯ АЛГЕБРА
РАНГ МАТРИЦЫ
Теорема о ранге матрицы

2. Основное понятие

Ранг матрицы - это наивысший из порядков миноров
этой матрицы, определитель которых отличен от нуля
Обозначают: r, rang(A), r(A).
Рассмотрим пример
1
М3 =
1 7 -1
0 2 3
8 4 6
Пусть А =
1 7 -1 9
0 2 3 -2
8 4 6 5
3 х4
= 1(12-12) + 8(21+2) = 184 = 0
1
так как ее минор старшего порядка М3
отличен от нуля, тогда rang(A)= 3

3. Рассмотрим пример 1

Пусть D =
0 0 0
0 0 -1
0 0 0
тогда rang(A)= 1
3 х3
потому что все миноры 3-го порядка равны нулю,
все миноры 2-го порядка тоже равны нулю и только
один минор −1 = −1 ≠ 0 , а он первого порядка.
φ
М3 = 0
φ
М2 = 0
1
М1 = −1 = −1 ≠ 0
ПРИМЕЧАНИЕ
Если матрица A нулевая, т. е. все ее элементы равны
нулю, то и все миноры матрицы равны нулю. Ранг такой
матрицы считается равным нулю.

4. Рассмотрим пример 2

Задание.
Посчитать миноры матрицы
1
0
С= 0
0
0
0
3
0
0
0
0
0
Решение.
4 х3
Самый старший минор для этой матрицы –это минор
3-го порядка. Таких миноров три. И каждый равен нулю.
Среди миноров 2-го порядка есть один - отличный от нуля
М2
1
1 0
= 0 3
вывод: чем больше в матрице
нулей, тем легче считать ее
определитель
=3–0≠ 0
Ответ: rang(С) = 2.
≠

5. Методы нахождения ранга матрицы

1. Метод окаймляющих миноров
Пусть в матрице А найден ненулевой минор k -го порядка .
Рассмотрим все миноры k+1 -го порядка, включающие в себя
(окаймляющие) минор Мkφ ; если все они равны нулю, то ранг
матрицы равен k . В противном случае среди окаймляющих
миноров найдется ненулевой, и вся процедура повторяется.
2. Метод элементарных преобразований
Ранг матрицы равен числу ненулевых строк в матрице
после приведения её к ступенчатой форме при помощи
элементарных преобразований над строками матрицы.

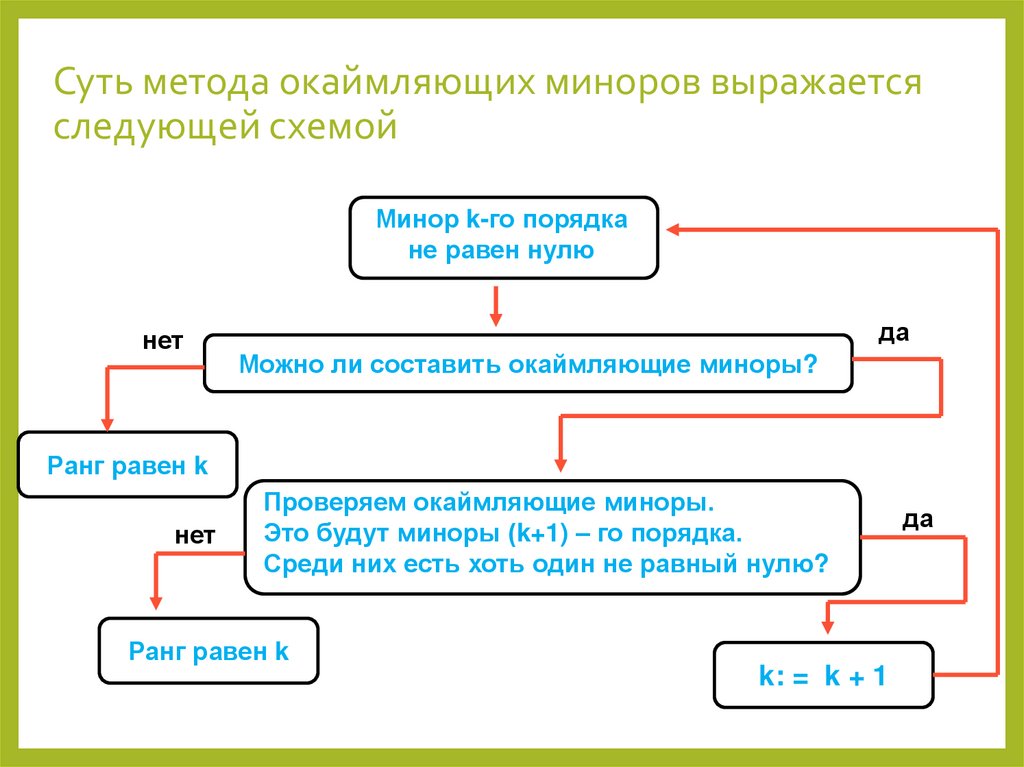
6. Суть метода окаймляющих миноров выражается следующей схемой

Минор k-го порядка
не равен нулю
нет
да
Можно ли составить окаймляющие миноры?
Ранг равен k
нет
Проверяем окаймляющие миноры.
Это будут миноры (k+1) – го порядка.
Среди них есть хоть один не равный нулю?
Ранг равен k
k: = k + 1
да

7. Метод окаймления миноров

Задание.
Найти ранг матрицы А
методом окаймления миноров
1 2 -1 -2
А= 2 4 3 0
-1 -2 6 6
Решение.
1. Рассмотрим миноры 1-го порядка матрицы А
1
М1 = 1 = 1 ≠ 0
( условие выполнено )
3 х4

8.

2. Рассмотрим миноры 2-го порядка матрицы А
1 2 -1 -2
А= 2 4 3 0
-1 -2 6 6
1
М2 =
2
М2 =
1 2
2 4
1 -1
2 3
=1 4-2 2= 4–4=0
( не подходит )
= 1 3 – 2 (-1) = 3 + 2 = 5 ≠ 0
( условие выполнено)
3 х4

9.

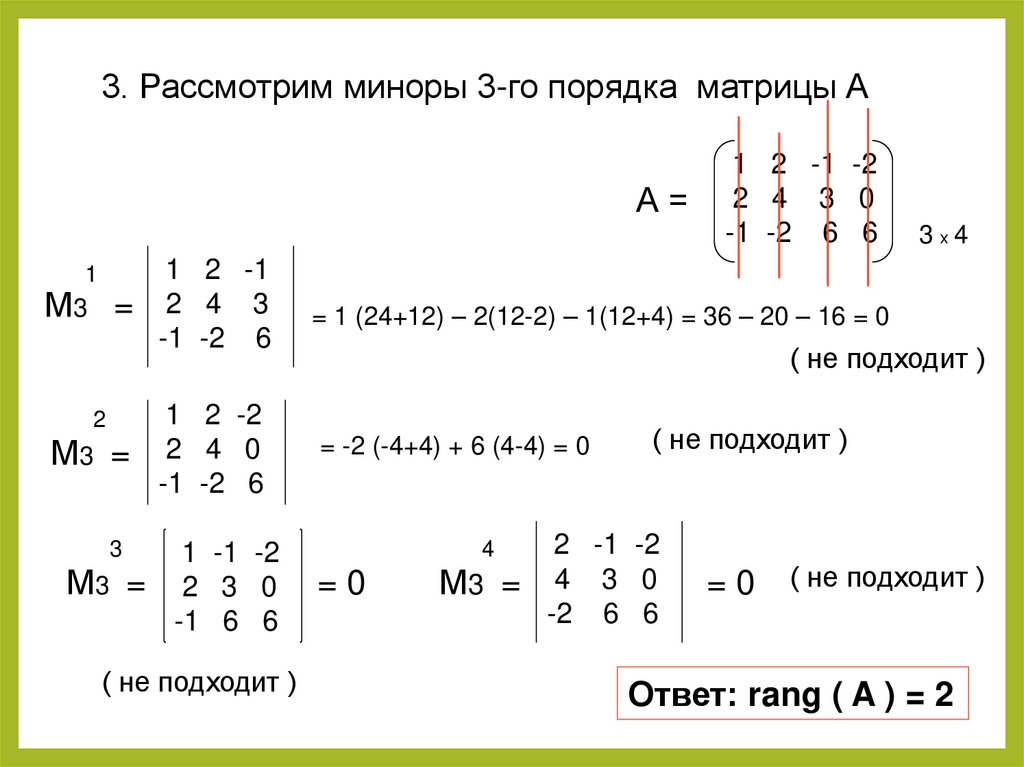
3. Рассмотрим миноры 3-го порядка матрицы А
А=
1 2 -1 -2
2 4 3 0
-1 -2 6 6
1 2 -1
М3 = 2 4 3
-1 -2 6
= 1 (24+12) – 2(12-2) – 1(12+4) = 36 – 20 – 16 = 0
1 2 -2
М3 = 2 4 0
-1 -2 6
= -2 (-4+4) + 6 (4-4) = 0
3 х4
1
( не подходит )
2
3
1 -1 -2
М3 = 2 3 0
-1 6 6
( не подходит )
( не подходит )
2 -1 -2
М3 = 4 3 0
-2 6 6
4
=0
=0
( не подходит )
Ответ: rang ( A ) = 2

10. Эквивалентные преобразования

1
умножение строки на ненулевое число
2
перестановка двух строк
3
прибавление к одной строке матрицы другой ее
строки, умноженной на некоторое ненулевое число
4
при транспонировании матрицы
Эти преобразования называются эквивалентными
при этом ранг матрицы не изменяется
употребляется знаки: ~; ⇔ ; ↔

11. Рассмотрим пример эквивалентных преобразований

А=
Пусть задана матраца
1 3 3
3 2 2
2 х3
1) Умножим первую строку матрицы на два, то есть
каждый элемент первой строки умножаем на двойку
А=
1 3 3
3 2 2
⇔ В=
Получили матрицу В =
1 2 3 2 3 2
3
2
2
2 6 6
3 2 2
=
2 6 6
3 2 2
такую, что А ⇔ В
ПРЕОБРАЗОВАНИЕ 1
2 х3

12. Эквивалентные преобразования

Пусть задана матраца
В=
2 6 6
3 2 2
2 х3
2) Поменяем первую и вторую строки матрицы местами
В=
2 6 6
3 2 2
Получили матрицу С =
⇔ С=
3
2
2
6
2
6
3
2
2
6
2
6
такую, что В ⇔ С
ПРЕОБРАЗОВАНИЕ 2

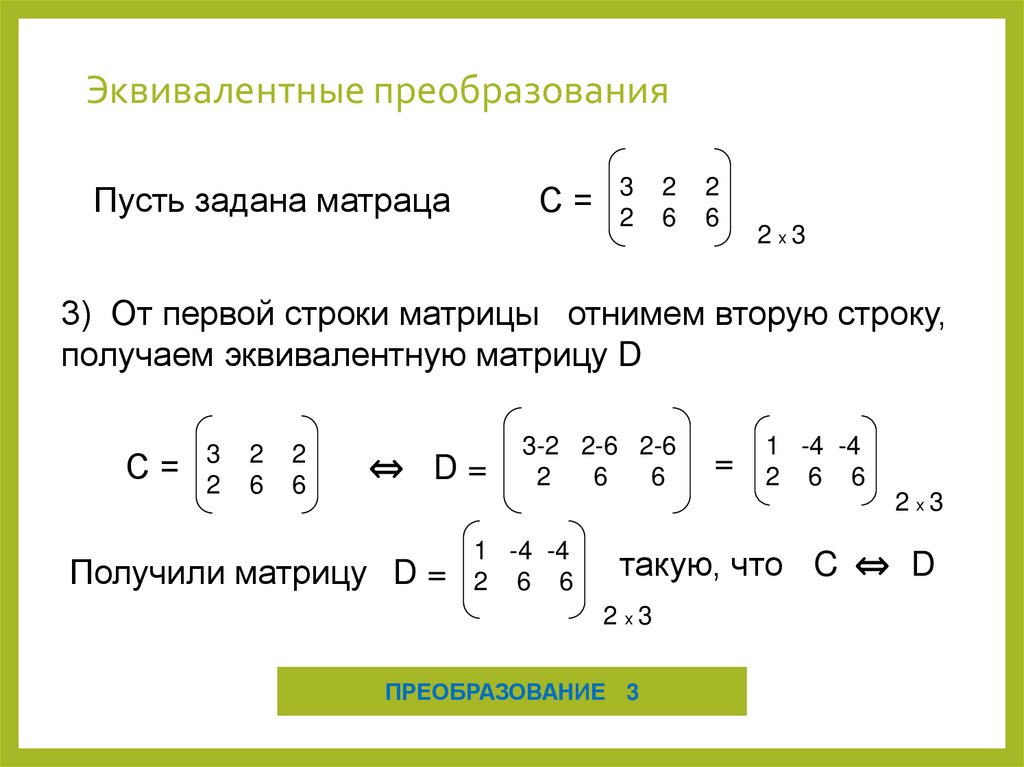
13. Эквивалентные преобразования

Пусть задана матраца
С=
3
2
2
6
2
6
2 х3
3) От первой строки матрицы отнимем вторую строку,
получаем эквивалентную матрицу D
С=
3
2
2
6
2
6
⇔ D=
3-2 2-6 2-6
2
6
6
=
1 -4 -4
2 6 6
2 х3
Получили матрицу D =
1 -4 -4
2 6 6
такую, что C ⇔ D
2 х3
ПРЕОБРАЗОВАНИЕ 3

14. Эквивалентные преобразования

Пусть задана матраца
D=
1 -4 -4
2 6 6
2 х3
4) Проведём транспонирование матрицы D, получаем
эквивалентную матрицу F
D=
1 -4 -4
2 6 6
⇔
2 х3
F=
1
-4
-4
2
6
6
3 х2
Вывод: Матрицы А ⇔ F ,
так как от одной из них перешли к другой при помощи
эквивалентных преобразований над строками.
ПРЕОБРАЗОВАНИЕ 4

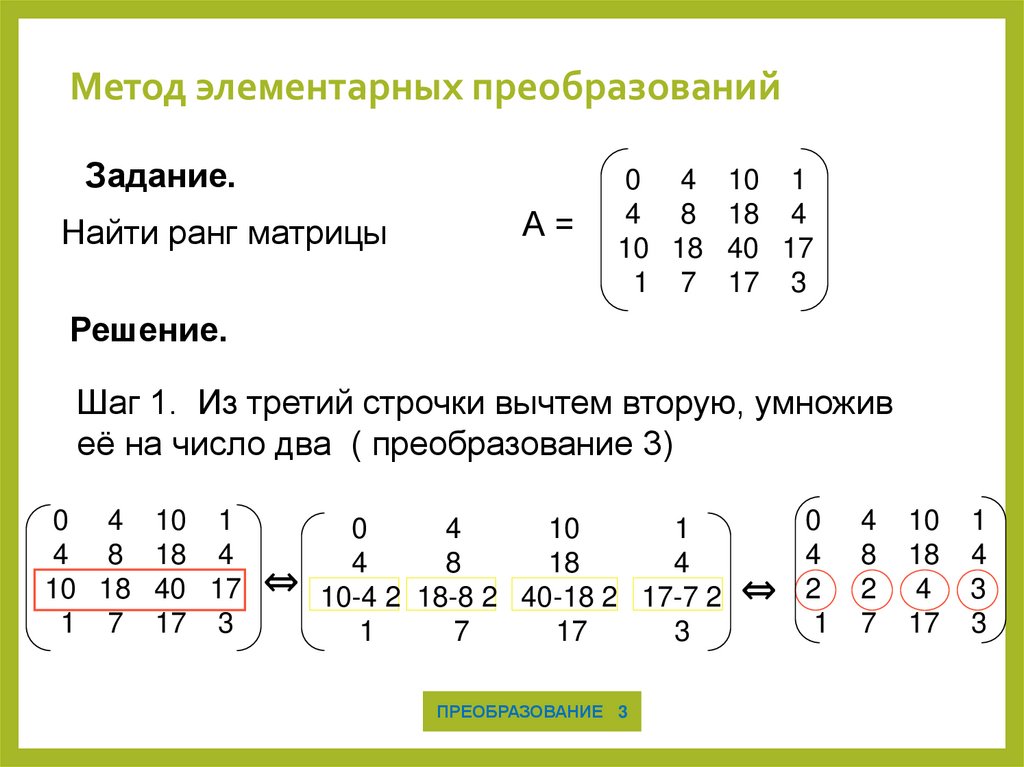
15. Метод элементарных преобразований

Задание.
Найти ранг матрицы
А=
0 4 10 1
4 8 18 4
10 18 40 17
1 7 17 3
Решение.
Шаг 1. Из третий строчки вычтем вторую, умножив
её на число два ( преобразование 3)
0 4 10 1
0
4
10
1
4 8 18 4
4
8
18
4
10 18 40 17 ⇔ 10-4 2 18-8 2 40-18 2 17-7 2 ⇔
1 7 17 3
1
7
17
3
ПРЕОБРАЗОВАНИЕ 3
0
4
2
1
4
8
2
7
10
18
4
17
1
4
3
3

16.

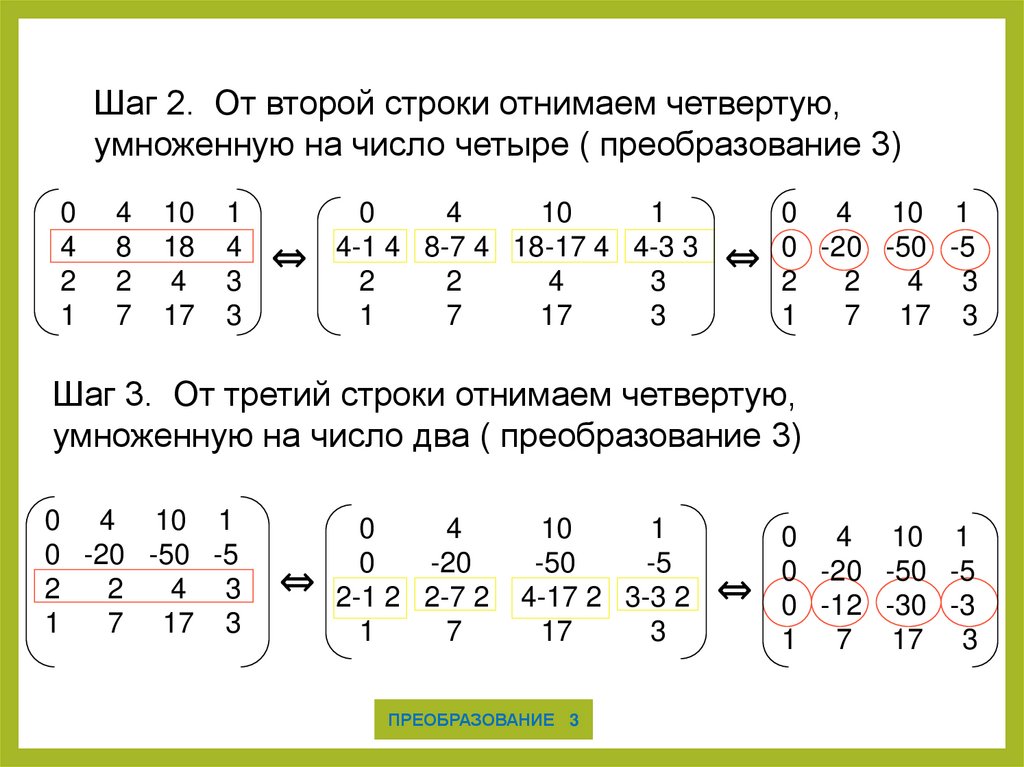
Шаг 2. От второй строки отнимаем четвертую,
умноженную на число четыре ( преобразование 3)
0
4
2
1
4
8
2
7
10
18
4
17
1
4
3
3
⇔
0
4
10
1
0 4 10 1
4-1 4 8-7 4 18-17 4 4-3 3 ⇔ 0 -20 -50 -5
2
2
4
3
2
2
4 3
1
7
17
3
1
7 17 3
Шаг 3. От третий строки отнимаем четвертую,
умноженную на число два ( преобразование 3)
0 4 10 1
0 -20 -50 -5
2
2
4 3
1
7 17 3
0
4
0
-20
⇔ 2-1 2 2-7 2
1
7
10
1
-50
-5
4-17 2 3-3 2 ⇔
17
3
ПРЕОБРАЗОВАНИЕ 3
0 4 10 1
0 -20 -50 -5
0 -12 -30 -3
1 7 17 3

17.

Шаг 4. К второй строки прибавим первую, умноженную
на число тять ( преобразование 3)
0 4 10 1
0
4
10
1
0 4 10 1
0 -20 -50 -5 ⇔ 0-0 5 -20+4 5 -50+10 5 -5+1 5
0 0 0 0
⇔
0 -12 -30 -3
0
-12
-30
-3
0 -12 -30 -3
1 7 17 3
1
7
17
3
1 7 17 3
Шаг 5. К третий строки прибавим первую, умноженную на
число три ( преобразование 3)
0 4 10 1
0 0 0 0
0 -12 -30 -3
1 7 17 3
0
4
10
1
0
0
0
0
0
0
⇔ 0+0 3 -12+ 4 3 -30+10 3 -3+1 3 ⇔ 0
1
7
17
3
1
ПРЕОБРАЗОВАНИЕ 3
4 10
0 0
0 0
7 17
1
0
0
3

18.

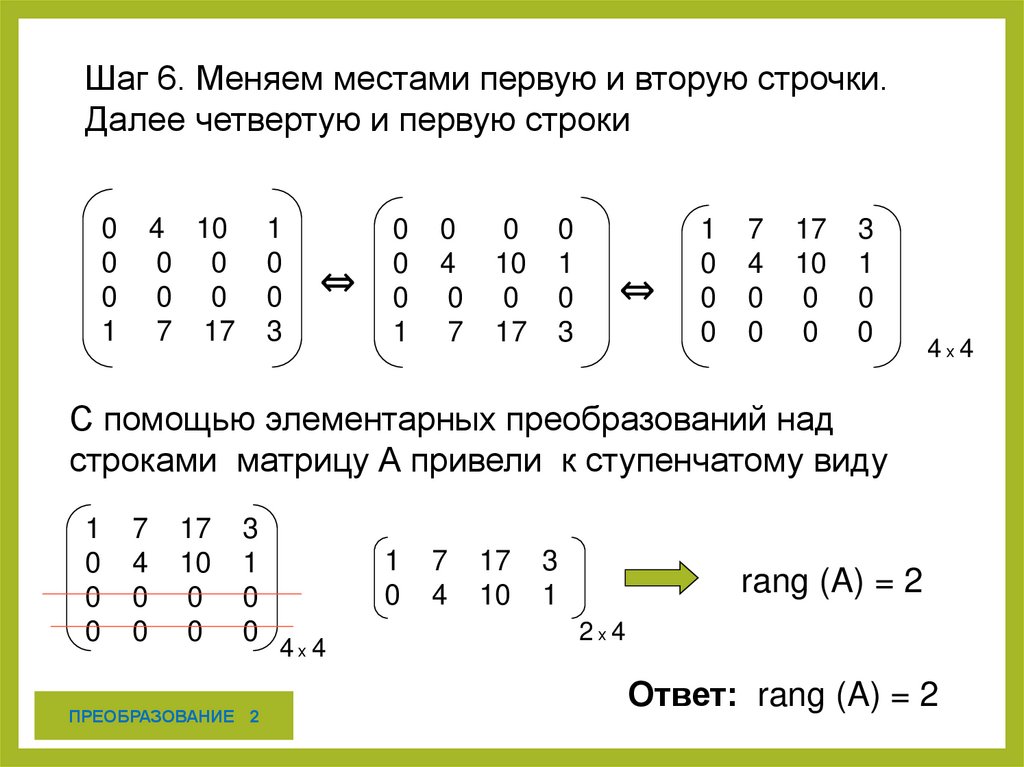
Шаг 6. Меняем местами первую и вторую строчки.
Далее четвертую и первую строки
0
0
0
1
4 10
0 0
0 0
7 17
1
0
0
3
⇔
0
0
0
1
0
4
0
7
0
10
0
17
0
1
0
3
⇔
1
0
0
0
7
4
0
0
17
10
0
0
3
1
0
0
4х4
С помощью элементарных преобразований над
строками матрицу А привели к ступенчатому виду
1
0
0
0
7
4
0
0
17
10
0
0
3
1
0
0
ПРЕОБРАЗОВАНИЕ 2
1
0
4х4
7
4
17
10
3
1
rang (A) = 2
2х4
Ответ: rang (A) = 2