Понятия и методика их формирования. Лекция 2

1. Лекция 2. Понятия и методика их формирования

План:
I. Понятие как форма мышления.
II. Этапы методики формирования
понятий.
III. Примеры студенческих проектов.

2. Вопросы лекции, вынесенные на отчет:

Какую форму мышления называют понятием?
Какая совокупность называется содержанием понятия?
Какая совокупность называется объёмом понятия?
Какая связь существует между содержанием и объёмом понятия?
Каковы 3 этапа формирования понятий?
Каковы 3 правила работы на первом этапе методики формирования понятий?
На какие вопросы отвечает мотивация понятия?
В чем сущность конкретно-индуктивного метода введения определения, и какова
последовательность действий этим методом?
9.
В чём сущность абстрактно-дедуктивного метода введения определения, и какова
последовательность действий этим методом?
10. Какие 2 цели этапа усвоения определения понятия выделяют?
11. Как называются упражнения для этапа усвоения определения, как они
формулируются, и почему свои ответы учащиеся должны аргументировать? Как
конструируются примеры для этапа усвоения определения?
1.
2.
3.
4.
5.
6.
7.
8.

3. I. Понятие как форма мышления (4 раздела)

1. Сущность понятия.
Понятие - это форма мышления, в
которой отражены существенные свойства
совокупности объектов (предметов, явлений).
Приём промежуточных вопросов?
Каждое понятие связано со словом-термином,
которое соответствует данному понятию.
Важно знать происхождение термина, поскольку
оно отражает существенные свойства понятия.
Например:
«синус», «косинус» (М),
«бит», «пиксель» (И),
«инерция» (Ф).

4.

2. Характеристики понятия и связь между ними.
Всякое
понятие
имеет
две
логические
характеристики: содержание и объем.
Содержанием понятия называется совокупность
всех существенных свойств объектов, относящихся к
понятию.
Объемом понятия называется совокупность всех
объектов, относящихся к понятию.
Замечание. Свойство называется существенным, если
оно присуще всем объектам, входящим в объем понятия.
Между содержанием понятия и объемом существует
следующая связь: чем больше объем понятия, тем меньше
его содержание, и наоборот.

5.

Примеры
(М). Термин (название) – параллелограмм.
Содержание понятия: ___________________________
(И). Термин – алгоритм.
Содержание понятия: ___________________________
(Ф). Термин – сила.
Содержание понятия: ___________________________
Объем понятия.
Пример (М): _______________________________
Пример (И): _______________________________
Пример (Ф): _______________________________

6.

Замечание.
Свойство
называется
несущественным, если оно ____________________
_____________________________________________
Несущественные свойства позволяют отличать
один объект от другого.
Приведите пример, относящийся к несущественным
свойствам понятия «параллелограмм».
Приведите пример, относящийся к несущественным
свойствам понятия «алгоритм».
Приведите пример, относящийся к несущественным
свойствам понятия «сила».

7.

Какая связь существует между объемом и содержанием понятия?
Пример (М). Параллелограмм – ромб.
Сравните объемы.
Сравните содержание.
Пример
(И).
Информационная
компьютерная модель.
Сравните объемы.
модель
Сравните содержание.
Пример (Ф). Сила – сила тяжести.
Сравните объемы.
Сравните содержание.
–

8.

Если объем одного понятия входит как часть в объем
другого понятия, то первое понятие называют видовым, а второе
родовым.
Пример (М). Родовым понятием для параллелограмма
является понятие «четырёхугольник».
Почему?
Другим видом четырёхугольников является ___________
В свою очередь параллелограмм является родовым
понятием для видов параллелограммов.
Пример (И). Родовым понятием для информационной
модели является понятие «модель». Почему?
Другим видом моделей является ____________________
В свою очередь информационная модель является
родовым понятием для видов информационных моделей.
Пример (Ф). Родовым понятием для идеальной модели
является понятие «модель».

9.

3. Сущность определения понятия.
В содержание понятия о каком-либо математическом
объекте входит много различных существенных свойств этого
объекта. Однако чтобы распознать объект, установить,
принадлежит ли он к данному понятию или нет, достаточно
проверить наличие у него некоторых существенных свойств.
Определение понятия – это предложение, в котором
перечисляется минимальное число
необходимых и
достаточных признаков понятия.
Приём промежуточных вопросов?

10.

4. Классификация понятий.
Классификация – это распределение объектов
какого-либо понятия на взаимосвязанные классы (виды,
типы) по наиболее существенным признакам (свойствам).
Признак
(свойство),
по
которому
происходит классификация (деление) понятия
на
виды
(классы),
называется
_____________________________

11.

Пример 1 (М). Классификация треугольников.
Основание классификации: число равных сторон.
Члены классификации:
______________________________________________
Такая
классификация
называется
классификацией по видоизмененному признаку.
Пример 2 (М). Классификация треугольников.
Основание классификации: наличие равных сторон.
Члены классификации: __________________________
Такая
классификация
называется
дихотомической классификацией (dicha и tome(греч)«сечение на две части»).

12.

Пример 1 (И). Классификация информационных
моделей.
Основание
классификации:
форма
представления. Члены классификации:
________________________________________________
Такая классификация называется классификацией по
____________________________.
Пример 2 (И). Классификация сообщений. Основание
классификации: информативность сообщения. Члены
классификации:
________________________________________
Такая классификация называется
_________________________________________
(dicha и tome (греч) - «сечение на две части»).

13.

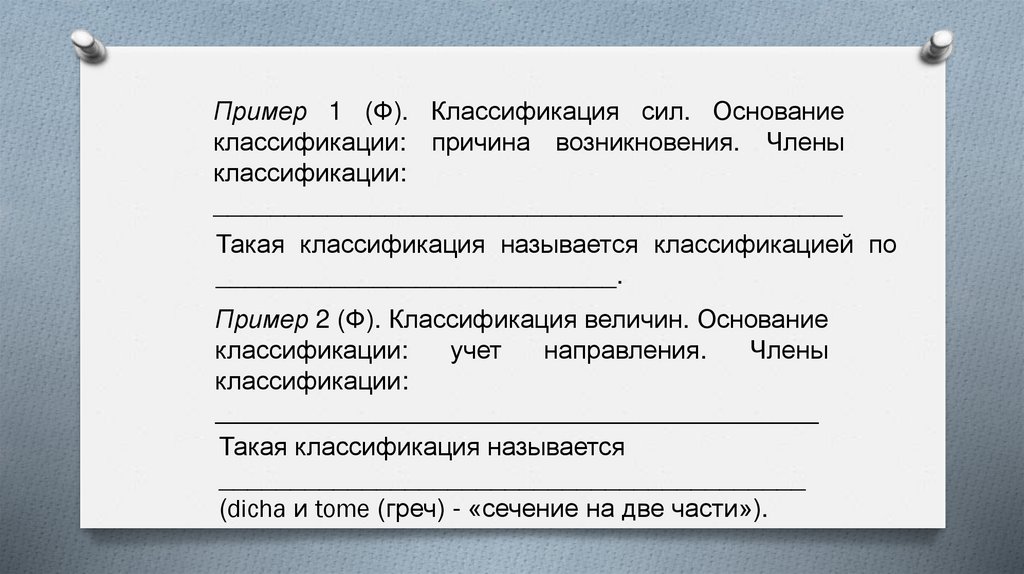
Пример 1 (Ф). Классификация сил. Основание
классификации: причина возникновения. Члены
классификации:
____________________________________________
Такая классификация называется классификацией по
____________________________.
Пример 2 (Ф). Классификация величин. Основание
классификации:
учет
направления.
Члены
классификации:
_____________________________________
Такая классификация называется
_________________________________________
(dicha и tome (греч) - «сечение на две части»).

14.

При проведении классификации
соблюдать следующие 3 правила:
необходимо
1. В качестве основания классификации можно брать лишь
один общий признак всех объектов данного понятия, он
должен оставаться неизменным в процессе классификации.
Пример ошибки (М): «параллелограммы делятся на ромбы,
прямоугольники и квадраты».
Пример ошибки (И): «алгоритмы бывают линейными и на
языке Паскаль».
Пример ошибки (Ф): «движения бывают равномерными и
прямолинейными»

15.

2. Каждый объект понятия должен попасть в результате
классификации только в один класс.
Пример ошибки (М): «параллелограммы делятся на
ромбы, прямоугольники и квадраты».
Пример ошибки (И): «модели бывают натуральные,
информационные, компьютерные».
Пример ошибки (Ф):

16.

3. Классификация должна быть соразмерной, то
есть объединение классов объектов составляют
объем понятия (нет объекта, который не попал
бы ни в один класс).
Пример ошибки (М): «параллелограммы делятся
на ромбы, прямоугольники и квадраты».
Пример ошибки (И): «системы счисления бывают
двоичными и десятичными».
Пример
ошибки
(Ф):
«Поля
эклектическими и магнитными».
бывают

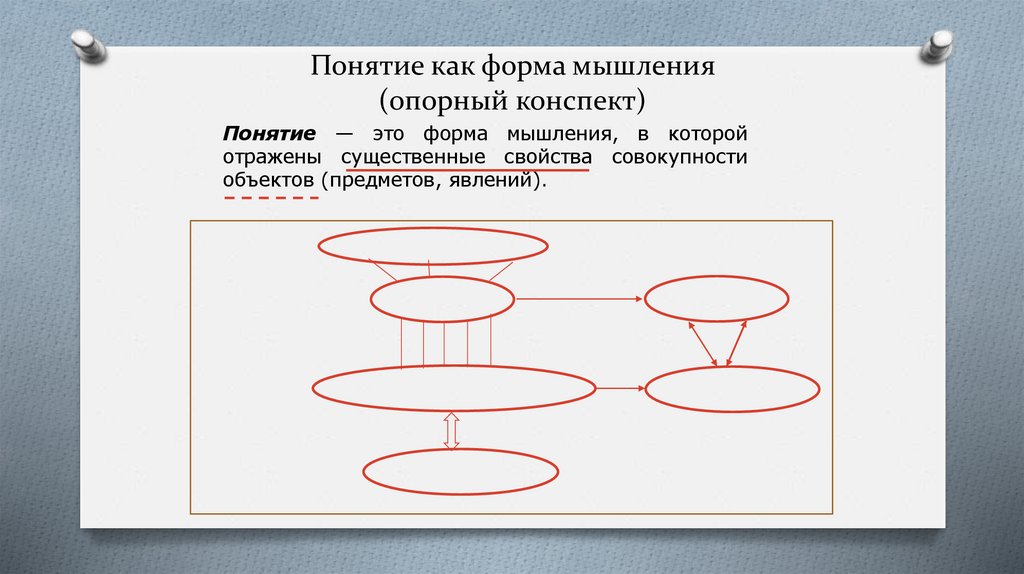
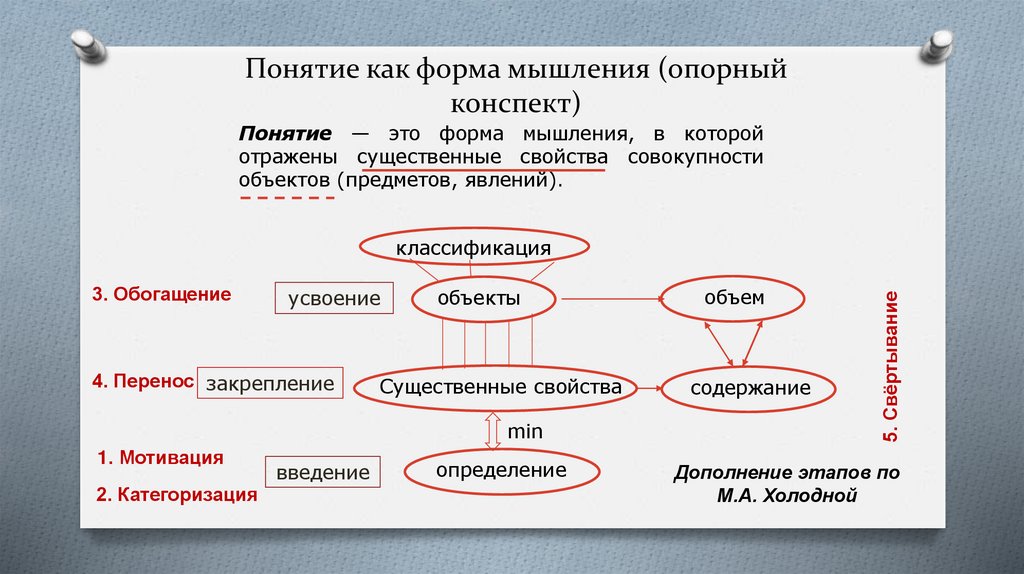
17. Понятие как форма мышления (опорный конспект)

Понятие — это форма мышления, в которой
отражены существенные свойства совокупности
объектов (предметов, явлений).

18.

II. Этапы методики формирования понятий
При
формировании
соблюдать три этапа:
1. Введение определения.
2. Усвоение определения.
3. Закрепление понятия.
понятий
следует

19.

Этап 1.
Введение определения
Методические правила работы на этапе введения
определения
Правило 1. Желательно мотивировать новое понятие.
Мотивация отвечает на вопросы:
«Что послужило поводом к появлению данного
понятия?», «Почему будем рассматривать новое
понятие?».

20.

Правило 2. Желательно раскрыть происхождение термина.
Правило 3. Необходимо следовать методам введения определения.
1. Конкретно-индуктивный метод (на основе
рассмотрения конкретных примеров или задач приходят к
новому понятию и его определению).
Последовательность действий на этапе введения
конкретно-индуктивным методом: конкретный пример
существенные признаки определение.
2. Абстрактно-дедуктивный метод (определение
понятия формулируется сразу после объявления нового термина).
Последовательность действий на этапе введения
абстрактно-дедуктивным
методом:
определение
существенные признаки конкретный пример.

21.

Пример (М). Определение понятия параллелограмма можно ввести
конкретно-индуктивным методом через практическую работу, через
классификацию рисунков (примеров), а можно – абстрактнодедуктивным (для параллелограмма ещё и через расшифровку
термина).
Пример (И). Определение понятия логического выражения можно
ввести конкретно-индуктивным методом через аналогию с
алгебраическим выражением, а понятие полного имени файла –
абстрактно-дедуктивным методом.
Пример (Ф). Определение понятия массы можно ввести
конкретно-индуктивным методом, наблюдая за связью скорости
движения с величиной груза, а определение плотности вещества –
абстрактно-дедуктивным методом.

22.

Этап 2.
Усвоение определения.
На этапе усвоения преследуются две цели:
1) научиться проверять, подходит объект под рассматриваемое понятие или нет;
2) запомнить определение.
Это достигается с помощью специально составленных упражнений –
упражнений на “да” и “нет”, которые формулируются, начиная со слов “Является
ли...”.
Аргументируя свой ответ, учащиеся а) осваивают признаки понятия и б)
выучивают определение.
При составлении примеров на “да”, учитель варьирует несущественные
признаки (включает частные случаи, изменяет размеры, расположение данных…).
При составлении примеров на “нет” учитель отвергает один или несколько
существенных признаков.
Этап усвоения требует подведения итогов, где повторяется определение, его
существенные признаки, а также некоторые несущественные признаки (расположение,
размеры, частные случаи).

23.

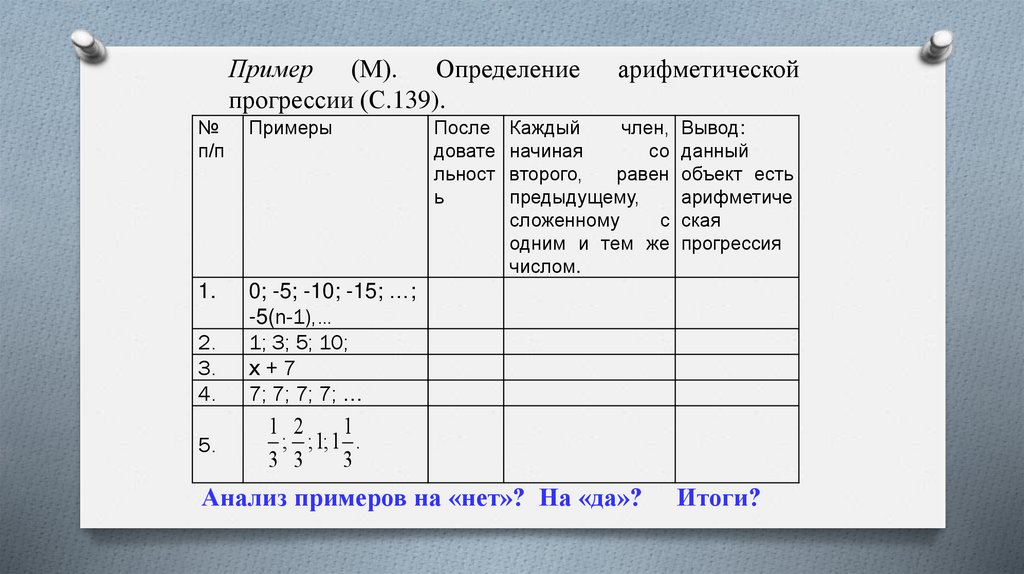
Пример (М). Определение
прогрессии (С.139).
№
п/п
Примеры
1.
0; -5; -10; -15; …;
-5(n-1),…
1; 3; 5; 10;
х+7
7; 7; 7; 7; …
2.
3.
4.
5.
После
довате
льност
ь
арифметической
Каждый
член, Вывод:
начиная
со данный
второго,
равен объект есть
предыдущему,
арифметиче
сложенному
с ская
одним и тем же прогрессия
числом.
1 2
1
; ; 1; 1 .
3 3
3
Анализ примеров на «нет»? На «да»?
Итоги?

24.

Пример (И). Понятие «маска файла».
В текущем каталоге имеются файлы:
1) zzz.cpp
2) zzz.cpppc 3)z.c 4) 1.cpp 5) 123.pc
Какие файлы будут выбраны из текущего каталога по маске
(___); (отрабатываем ___);
а)*.срр
б) ?.срр ( ); (отрабатываем ___);
в) *z*.c?p ( ); (_________________);
г) *.*с (2, 3, 5)
(...………………………………………………….……….)

25.

Примеры (Ф). Понятия механического и электрического явлений

26.

Этап 3. Закрепление понятия.
На этом этапе преследуются цели:
1) выявление новых свойств данного понятия, кроме тех, которые
отражены в формулировке определения (это закрепление может
быть не только на первом уроке изучения нового, но и на
последующих, в другой теме);
2) решение более сложных задач, включающих рассматриваемые
понятия;
3) решение комплексных заданий (прямые и обратные задачи;
после решения одной задачи обсуждаем, что изменится, если
изменить …);
4) систематическое подведение итогов .

27.

Вопросы для итогов на этапе закрепления:
а) с каким понятием работали;
б) что о нем нового узнали;
в) что учились делать в связи с этим понятием;
г) какие виды задач учились решать;
д) в каких ситуациях можно применять данное понятие.

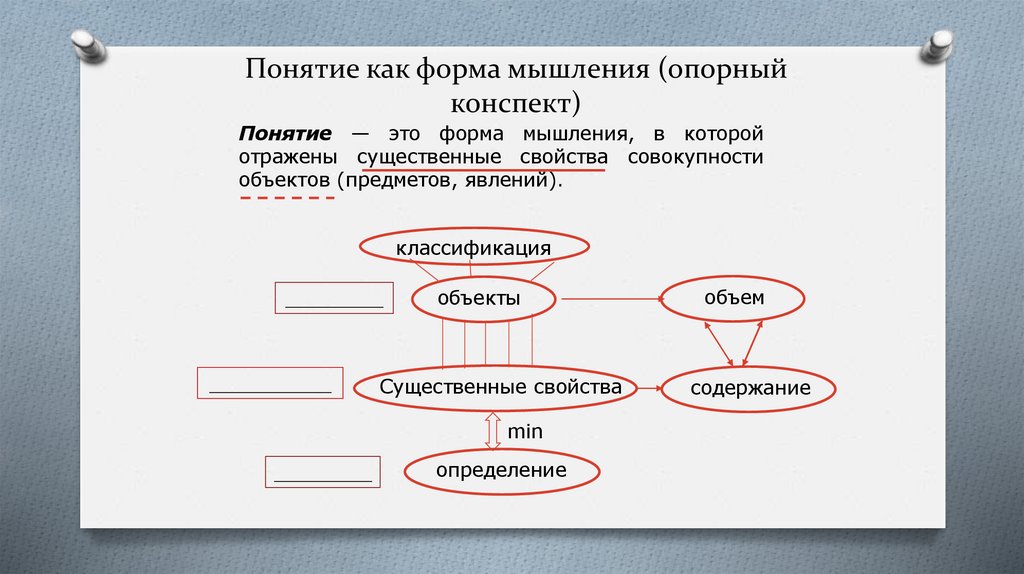
28. Понятие как форма мышления (опорный конспект)

Понятие — это форма мышления, в которой
отражены существенные свойства совокупности
объектов (предметов, явлений).
классификация
________
__________
объекты
Существенные свойства
min
________
определение
объем
содержание

29. Понятие как форма мышления (опорный конспект)

Понятие — это форма мышления, в которой
отражены существенные свойства совокупности
объектов (предметов, явлений).
3. Обогащение
усвоение
4. Перенос закрепление
объекты
Существенные свойства
min
1. Мотивация
2. Категоризация
введение
определение
объем
содержание
5. Свёртывание
классификация
Дополнение этапов по
М.А. Холодной

30.

С.137-154
(описание
методики с примерами реализации),
С. 233-246 (конспекты
уроков по НОД),
С. 292-295 (карты изучения
функций),
С. 299-306 (конспект урока
при изучении тригонометрических
понятий в геометрии),
С. 311-319 (конспект урока
по
изучению
арксинуса
и
арккосинуса),
С. 323-334 (модульная
технология изучения производной),
С.
399-402
(введение
определения
при
личностно
ориентированном
обучении
–
примеры)

31. III. Примеры студенческих проектов.

Проект 1. Организация этапов введения и усвоения
определения корня уравнения (проект Кирилловой
Анастасии).
Проект 2. Организация этапов введения и усвоения
определения шифрования (проект Веселовой Полины).
Проект 3. Организация этапов введения усвоения
определения инерции (проект Зарубиной Вероники).

32.

Организация этапов введения и
усвоения определения корня уравнения
Учебник Макарычев Ю.Н., Миндюк
Н.Г., Нешков К.И., Суворова С.Б.; под
редакией Теляковского С.А.
«Алгебра», 7класс, пункт 6
Подготовил:
Студент физико-математического
факультета
3 курса 4 группы
Кириллова Анастасия
Методист:
Профессор кафедры математического
анализа, алгебры и геометрии
Доктор педагогических наук
Малова Ирина Евгеньевна
2023, г. Брянск

33.

Введение определения корня уравнения
Решим данную задачу, используя уравнение:
Обозначим буквой x число книг на верхней полке. Так как на нижней книг в 4 раза больше, тогда на нижней полке
было ________
С нижней полки переставляют на верхнюю полку 15 книг. Отсюда: на нижней полке останется ________,
а на верхней будет ____________
После перестановки книг на полках окажется поровну.
Составим уравнение:
_____________________
Какое число нужно найти, чтобы считать, что решили уравнение?
Нужно найти число, при котором уравнение обращается в верное равенство.
Это число называется решением уравнения
или корнем уравнения.
Попробуйте сформулировать определение
корня уравнения.

34.

Усвоение определения корня уравнения
Что нужно сделать, чтобы проверить, является ли число
корнем уравнения?
Подставить вместо переменной заданное число, если
уравнение обратится в верное равенство, то число будет
корнем, если нет, то нет.
Упражнения на «да» и «нет»
Является ли 0 корнем уравнения?
1) 3