Similar presentations:
Двоичная система: от перевода до вычислений
1.
Двоичная система: от переводадо вычислений
2.
01. Зачем компьютеру двоичный кодCONTENTS
02. Перевод чисел
03. Сложение в двоичной системе
04. Вычитание и заём
05. Итоги и переход к новым системам
3.
Зачем компьютеру двоичный код01
4.
Двоичная система — язык компьютера01
Основание 2 и состояния
Арифметические операции в двоичной системе сведены к минимуму правил, что делает
логические схемы компьютера простыми и быстрыми в обработке данных.
Простота арифметики
Двоичная система использует основание 2, что позволяет компьютерам работать с
элементами, имеющими два состояния: включено и выключено. Это упрощает создание
надёжных и дешёвых электронных устройств.
03
Универсальность двоичного кода
Все данные в компьютере хранятся и обрабатываются в виде двоичных чисел. Это
обеспечивает единый язык для всех видов данных, от текста до изображений.
02
5.
Достоинства и недостатки для человека01
02
Достоинства для компьютера
Недостатки для человека
Двоичная система идеальна для компьютеров
Двоичная запись больших чисел становится
из-за простоты аппаратной реализации и
громоздкой и однородной, что затрудняет
надёжности. Однако для человека она имеет
чтение и увеличивает вероятность ошибок.
существенные недостатки.
Поэтому для человека используются другие
системы счисления.
6.
Перевод чисел02
7.
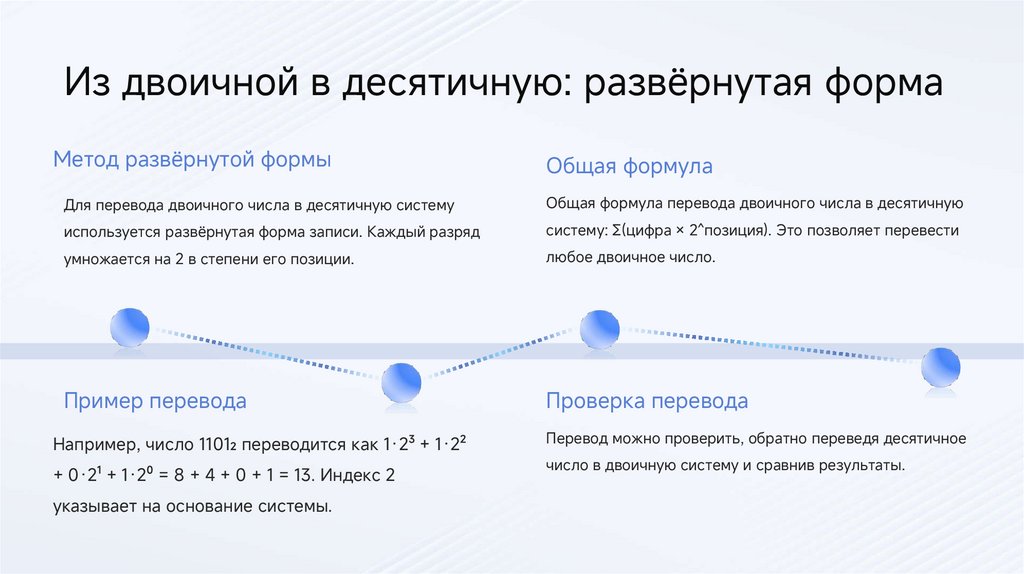
Из двоичной в десятичную: развёрнутая формаМетод развёрнутой формы
Общая формула
Для перевода двоичного числа в десятичную систему
Общая формула перевода двоичного числа в десятичную
используется развёрнутая форма записи. Каждый разряд
систему: ∑(цифра × 2^позиция). Это позволяет перевести
умножается на 2 в степени его позиции.
любое двоичное число.
Пример перевода
Проверка перевода
Например, число 1101₂ переводится как 1·2³ + 1·2²
+ 0·2¹ + 1·2⁰ = 8 + 4 + 0 + 1 = 13. Индекс 2
указывает на основание системы.
Перевод можно проверить, обратно переведя десятичное
число в двоичную систему и сравнив результаты.
8.
Из десятичной в двоичную: делениена 2
Метод деления на 2
Для перевода числа из десятичной системы в двоичную, нужно
делить число на 2, записывая остатки на каждом шаге, пока не
получится 0. Затем остатки записываются в обратном порядке.
9.
Признаки чётности и делимостиЧётность числа
Делимость на 4
Последняя цифра двоичного
Общие признаки
числа показывает его чётность:
Если двоичное число
0 — чётное, 1 — нечётное. Это
заканчивается на два нуля, оно
Общие признаки делимости на
позволяет быстро определить
делится на 4. Это свойство
2ⁿ: число делится на 2ⁿ, если его
свойства числа без перевода.
используется для быстрой
последние n цифр равны нулям.
проверки делимости.
Это упрощает анализ чисел.
10.
Сложение в двоичной системе03
11.
Правила сложения и переноса01
02
Основные правила сложения
Перенос в следующий разряд
Сложение в двоичной системе выполняется по
Перенос происходит, когда сумма в текущем
простым правилам: 0+0=0, 1+0=1, 1+1=10₂
разряде превышает 1. Это аналогично
(записываем 0, перенос 1), 1+1+1=11₂
десятичной системе, когда сумма превышает
(записываем 1, перенос 1).
9.
12.
Пример сложения и проверка1
Пример сложения
Сложим числа 1011101₂ и 110111₂
столбиком, учитывая переносы.
Результат будет 10010100₂.
2
Проверка в
десятичной системе
Переведём слагаемые в
десятичную систему: 93 + 55 =
148. Перевод результата
10010100₂ также даёт 148,
подтверждая правильность.
3
Важность проверки
Проверка перевода и
вычислений в обеих системах
счисления помогает избежать
ошибок и подтверждает
правильность алгоритма.
13.
Вычитание и заём04
14.
Правила вычитания и случаи займаОсновные правила вычитания
Аналогия с десятичной
системой
Вычитание в двоичной системе выполняется по
Механизм займа аналогичен десятичной системе,
правилам: 0-0=0, 1-0=1, 1-1=0, 10₂-1=1. Если в
но проще, поскольку возможны только два
разряде 0, а вычитаем 1, берём заём.
состояния разряда.
Механизм займа
Пример займа
При заёме старший разряд уменьшается на 1,
Например, при вычитании 1000₂ - 1₂, заём
промежуточные нули становятся единицами, а
превращает 1000₂ в 0110₂, и результат становится
текущий разряд получает 10₂=2.
111₂.
15.
Пример вычитания и контрольПример вычитания
Проверка в десятичной
системе
Вычтем 110111₂ из 1011101₂ столбиком,
Переведём числа в десятичную систему:
учитывая займы. Результат будет 100110₂.
93 - 55 = 38. Перевод результата 100110₂
также даёт 38, подтверждая
правильность.
16.
Вычитание из меньшего большегоВычитание с инверсией знака
Если уменьшаемое меньше вычитаемого, инвертируем знак
и вычитаем наоборот. Например, 10111₂ - 110101₂ становится (110101₂ - 10111₂), результат -11110₂.
17.
Итоги и переход к новым системам05
18.
Ключевые выводы о двоичной арифметикеУниверсальность двоичной
системы
Правила арифметики
Двоичная система обеспечивает универсальный
Сложение и вычитание в двоичной системе
способ хранения и обработки данных в
выполняются по простым правилам с переносом
компьютерах, используя только два символа: 0 и 1.
и займом, аналогичным десятичной системе.
Методы перевода
Признаки свойств чисел
Перевод из двоичной в десятичную систему
Последняя цифра двоичного числа показывает
осуществляется через развёрнутую форму, а из
его чётность, а два младших нуля — делимость на
десятичной в двоичную — через деление на 2.
4. Эти признаки упрощают анализ чисел.
19.
От двоичной к восьмеричной ишестнадцатеричной
Переход к восьмеричной и
Недостатки двоичной
шестнадцатеричной
системы для человека
системам
Длинные цепочки нулей и единиц в
Для упрощения работы с данными
двоичной системе неудобны для
используются восьмеричная и
человека из-за их громоздкости и
шестнадцатеричная системы, которые
однородности, что увеличивает
сокращают запись и сохраняют
вероятность ошибок.
простоту перевода.



















 informatics
informatics